A Watt-Level, High-Quality LG0,±1 Vortex Beam made from a Nd:YVO4 Laser Pumped by an Annular Beam
Abstract
1. Introduction
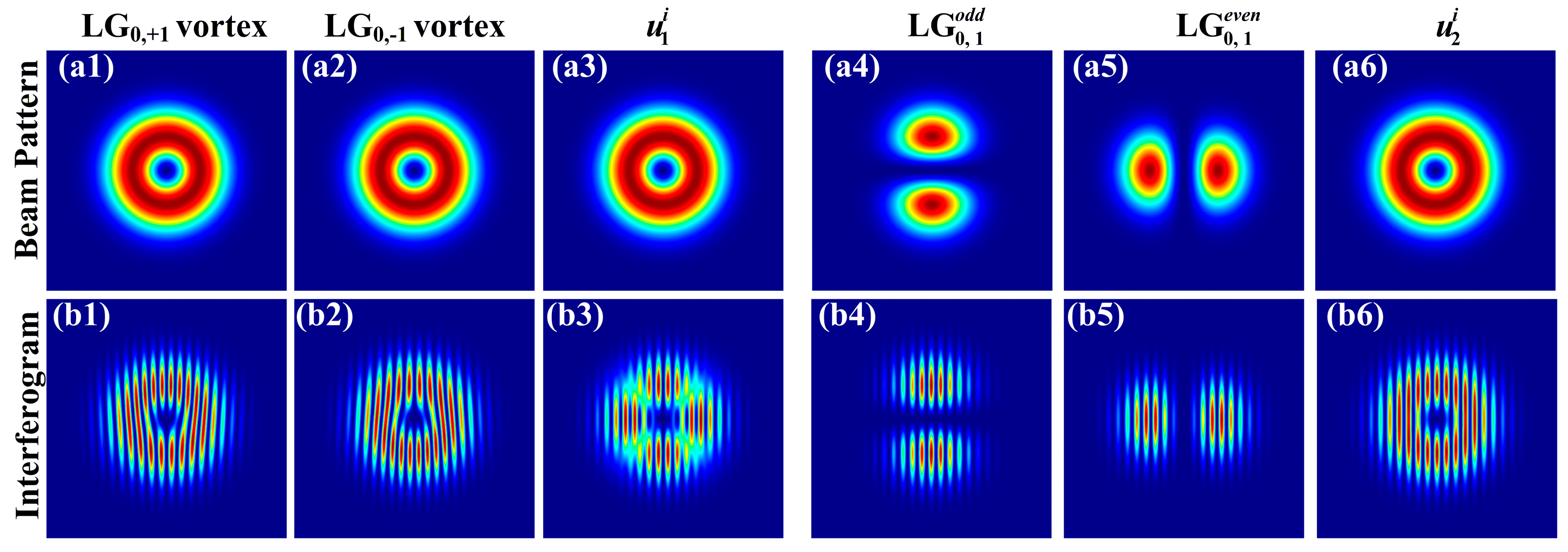
2. Theoretical Model
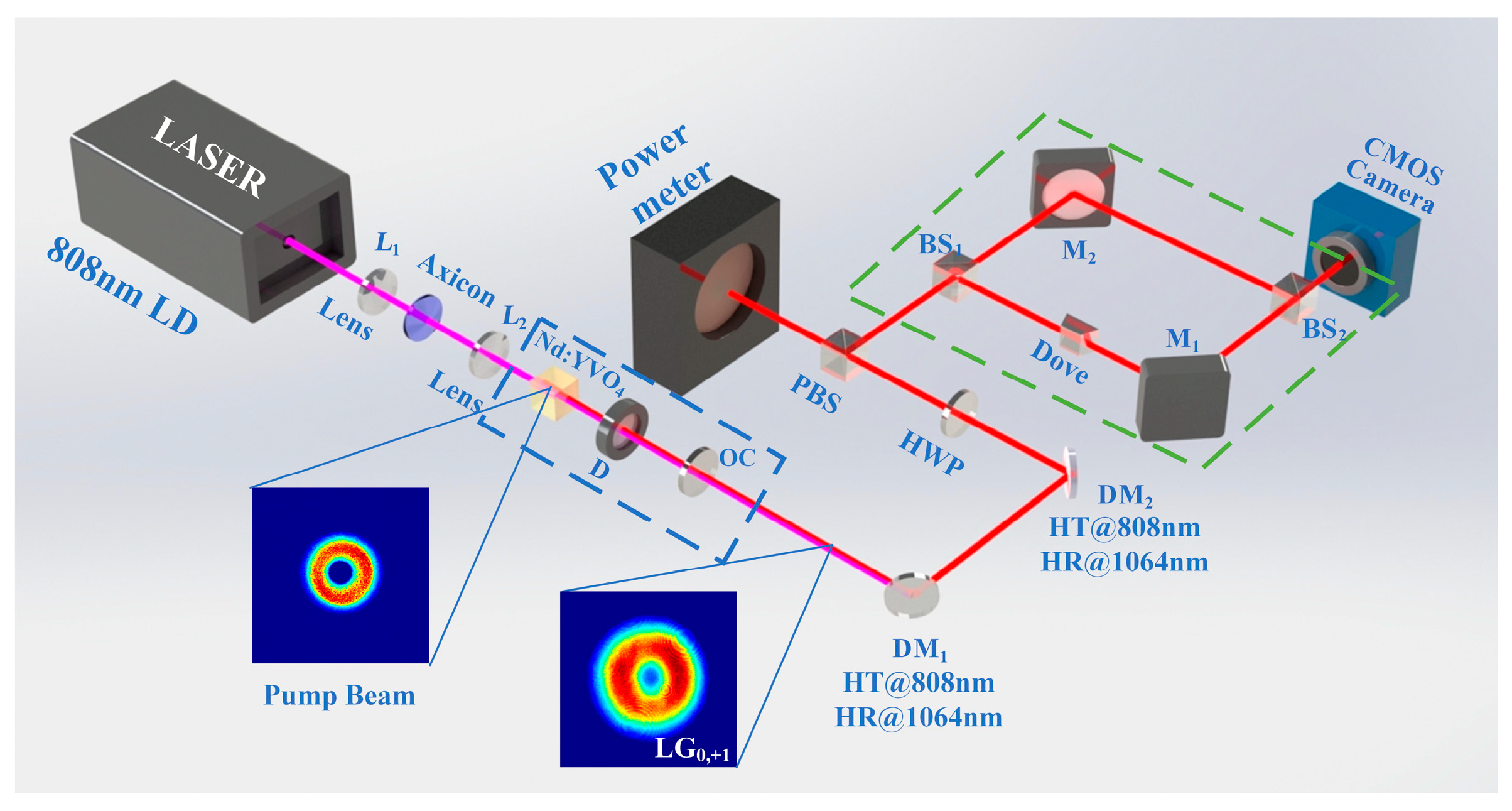
3. Experimental Setup
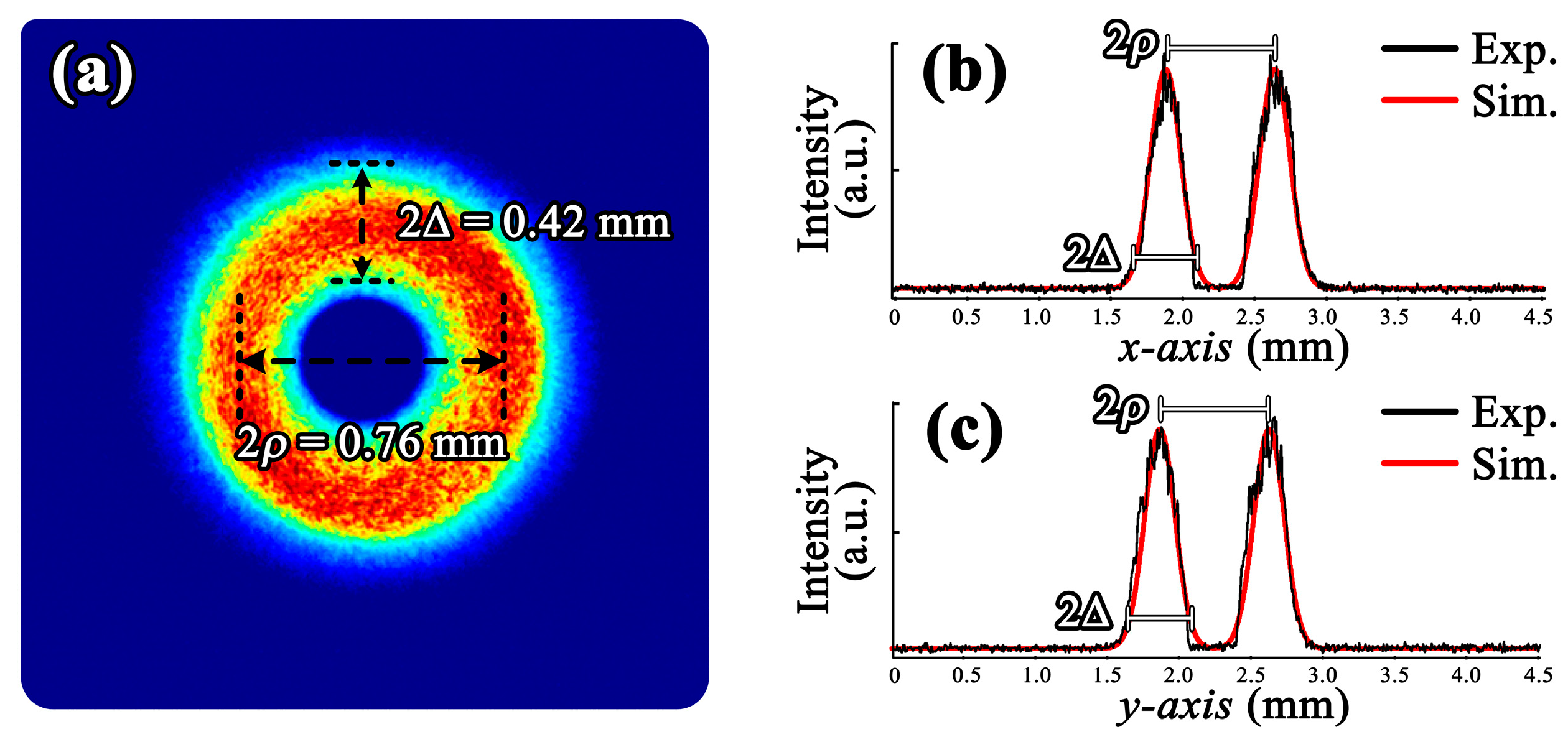
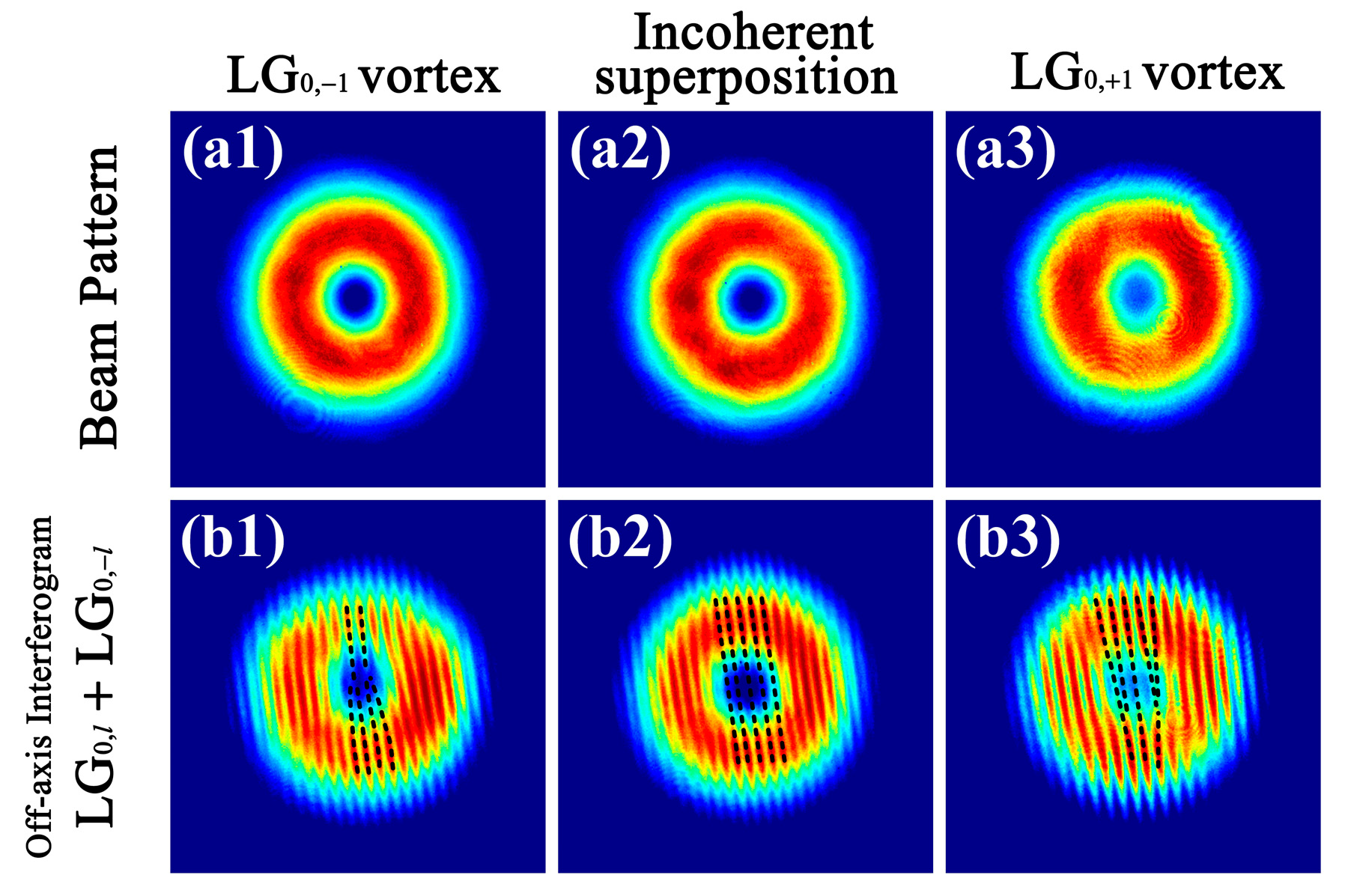
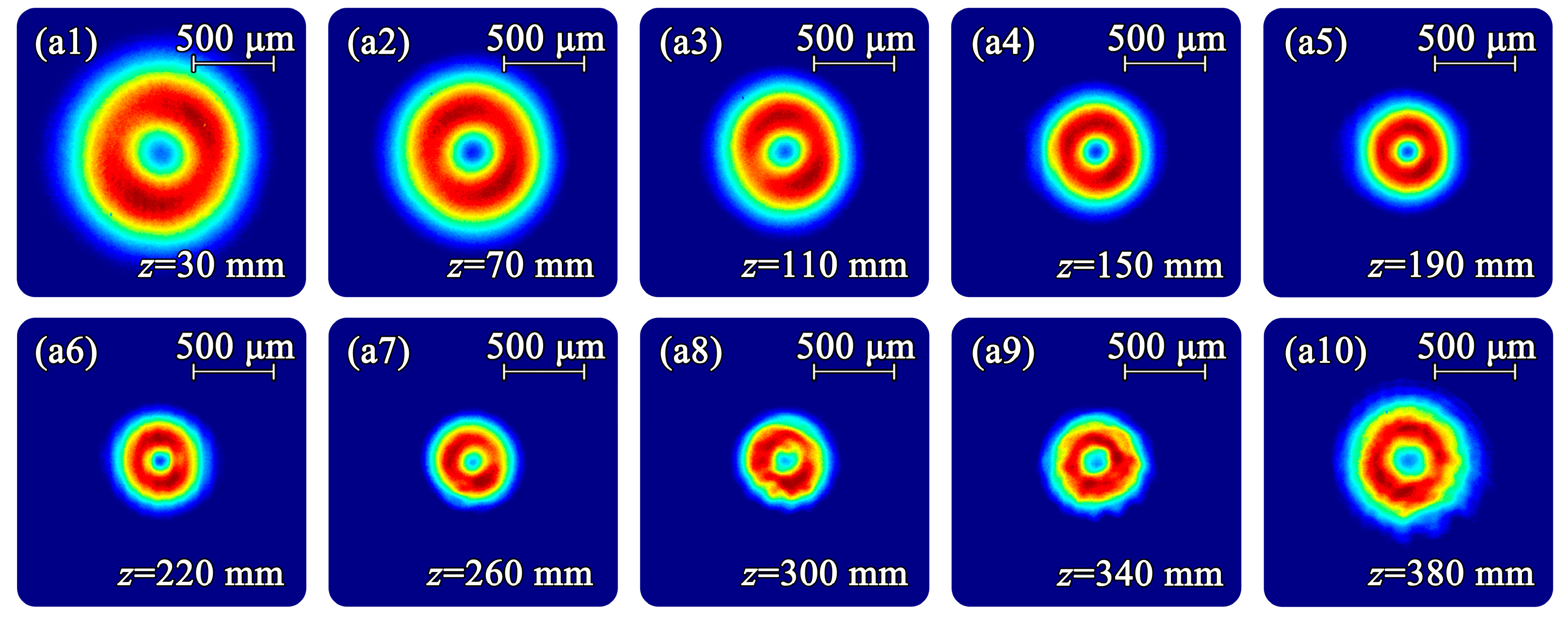
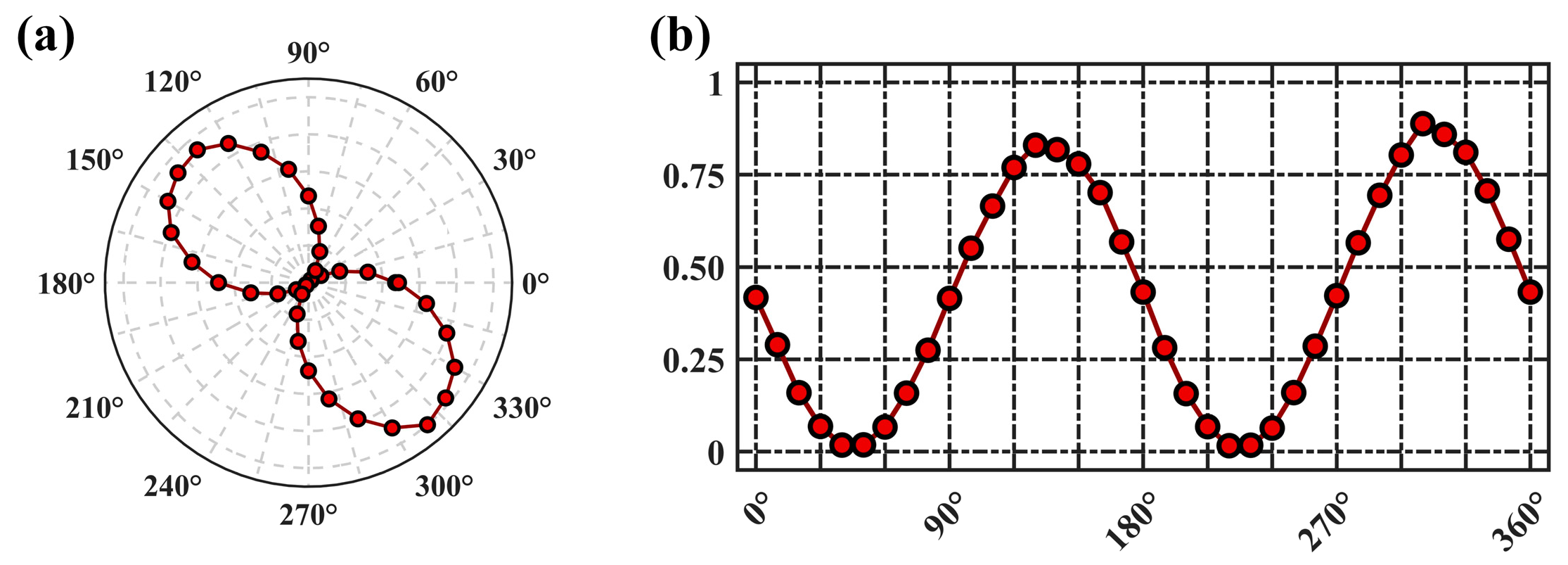
4. Experimental Results and Discussion
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Allen, L.; Beijersbergen, M.W.; Spreeuw, R.J.C.; Woerdman, J.P. Orbital angular momentum of light and the transformation of Laguerre-Gaussian laser modes. Phys. Rev. A 1992, 45, 8185–8189. [Google Scholar] [CrossRef]
- Lavery, M.P.J.; Speirits, F.C.; Barnett, S.M.; Padagett, M.J. Detection of a spinning object using light’s orbital angular momentum. Science 2013, 341, 537–540. [Google Scholar] [CrossRef]
- Bozinovic, N.; Yue, Y.; Ren, Y.; Tur, M.; Kristensen, P.; Huang, H.; Willner, A.E.; Ramachandran, S. Terabit-scale orbital angular momentum mode division multiplexing in fibers. Science 2013, 340, 1545–1548. [Google Scholar] [CrossRef]
- Wang, B.; Shi, J.; Zhang, T.; Xu, X.; Cao, Y.; Li, X. Improved lateral resolution with an annular vortex depletion in STED microscopy. Opt. Lett. 2017, 42, 4885–4888. [Google Scholar] [CrossRef]
- Graffitti, F.; D’Ambrosio, V.; Proietti, M.; Ho, J.; Piccirillo, B.; De Lisio, C.; Marrucci, L.; Fedrizzi, A. Hyperentanglement in structured quantum light. Phys. Rev. Res. 2020, 2, 043350. [Google Scholar] [CrossRef]
- Cheng, T.-Y.; Wang, W.-Y.; Li, J.-S.; Guo, J.-X.; Liu, S.; Lü, J.-Q. Rotational Doppler effect in vortex light and its applications for detection of the rotational motion. Photonics 2022, 9, 441. [Google Scholar] [CrossRef]
- Toyoda, K.; Miyamoto, K.; Aoki, N.; Morita, R.; Omatsu, T. Using optical vortex to control the chirality of twisted metal nanostructures. Nano Lett. 2012, 12, 3645–3649. [Google Scholar] [CrossRef] [PubMed]
- Aleksanyan, A.; Kravets, N.; Brasselet, E. Multiple-star system adaptive vortex coronagraphy using a liquid crystal light valve. Phys. Rev. Lett. 2017, 118, 203902. [Google Scholar] [CrossRef] [PubMed]
- Jeffries, G.D.; Edgar, J.S.; Zhao, Y.; Shelby, J.P.; Fong, C.; Chiu, D.T. Using polarization-shaped optical vortex traps for single-cell nanosurgery. Nano Lett. 2007, 7, 415–420. [Google Scholar] [CrossRef]
- Yang, F.F.; Li, H.; Liu, H.G.; Chen, X.F. Highly efficient nonlinear vortex beam generation by using a compact nonlinear fork grating. Opt. Lett. 2023, 48, 6376–6379. [Google Scholar] [CrossRef]
- Soskin, M.; Vasnetsov, M.; Pas’ko, V.; Plutenko, D. Optical vortex generated with an asymmetric forked grating. J. Opt. 2020, 22, 104001. [Google Scholar] [CrossRef]
- Marrucci, L.; Manzo, C.; Paparo, D. Optical spin-to-orbital angular momentum conversion in inhomogeneous anisotropic media. Phys. Rev. Lett. 2006, 96, 163905. [Google Scholar] [CrossRef]
- Ling, X.H.; Luo, H.L.; Guan, F.X.; Zhou, X.X.; Luo, H.L.; Zhou, L. Vortex generation in the spin-orbit interaction of a light beam propagation inside a uniaxial medium: Origin and efficiency. Opt. Express 2020, 28, 27258–27267. [Google Scholar] [CrossRef]
- Beijersbergen, M.W.; Allen, L.; Van der Veen, H.E.L.O.; Woerdman, J.P. Astigmatic laser mode converters and transfer of orbital angular momentum. Opt. Commun. 1993, 96, 123–132. [Google Scholar] [CrossRef]
- Shen, D.H.; He, T.; Yu, X.B.; Zhao, D.M. Mode conversion and transfer of orbital angular momentum between Hermite-Gaussian and Laguerre-Gaussian beams. IEEE. Photonics J. 2022, 14, 6510506. [Google Scholar] [CrossRef]
- Ma, H.T.; Hu, H.J.; Xie, W.K.; Xu, X.J. Study on the generation of a vortex laser beam by using phase-only liquid crystal spatial light modulator. Opt. Eng. 2013, 52, 091721. [Google Scholar] [CrossRef]
- Li, R.; Ren, Y.; Liu, T.; Wang, C.; Liu, Z.; Zhao, J.; Sun, R.; Wang, Z. Generating large topological charge Laguerre-Gaussian beam based on 4 k phase-only spatial light modulator. Chin. Opt. Lett. 2022, 20, 120501. [Google Scholar] [CrossRef]
- Pinnell, J.; Rodríguez-Fajardo, V.; Forbes, A. Probing the limits of orbital angular momentum generation and detection with spatial light modulators. J. Opt. 2021, 23, 015602. [Google Scholar] [CrossRef]
- Ren, Y.X.; Li, M.; Huang, K.; Wu, J.G.; Gao, H.F.; Wang, Z.Q.; Li, Y.M. Experimental generation of Laguerre-Gaussian beam using digital micromirror device. Appl. Opt. 2010, 49, 1838–1844. [Google Scholar] [CrossRef]
- Beijersbergen, M.W.; Coerwinkel, R.P.C.; Kristensen, M.; Woerdman, J.P. Helical-wavefront laser beams produced with a spiral phaseplate. Opt. Commun. 1994, 112, 321–327. [Google Scholar] [CrossRef]
- Zhou, Z.H.; Li, P.; Ma, J.B.; Zhang, S.R.; Gu, Y.Z. Generation and detection of optical vortices with multiple cascaded spiral phase plates. Photonics 2022, 9, 354. [Google Scholar] [CrossRef]
- Rafayelyan, M.; Brasselet, E. Laguerre-Gaussian modal q-plates. Opt. Lett. 2017, 42, 1966–1969. [Google Scholar] [CrossRef] [PubMed]
- Huang, K.; Liu, H.; Garcia-Vidal, F.J.; Hong, M.H.; Luk’yanchuk, B.; Teng, J.; Qiu, C.W. Ultrahigh-capacity non-periodic photon sieves operating in visible light. Nat. Commun. 2015, 6, 7059. [Google Scholar] [CrossRef]
- Ahmed, H.; Kim, H.; Zhang, Y.B.; Intaravanne, Y.; Jang, J.; Rho, J.; Chen, S.Q.; Chen, X.Z. Optical metasurfaces for generating and manipulating optical vortex beams. Nanophotonics 2022, 11, 941–956. [Google Scholar] [CrossRef]
- Chen, Y.F.; Lan, Y.P.; Wang, S.C. Generation of Laguerre-Gaussian modes in fiber-coupled laser diode end-pumped lasers. Appl. Phys. B 2001, 72, 167–170. [Google Scholar] [CrossRef]
- Chen, Y.F.; Lan, Y.P. Dynamics of the Laguerre Gaussian TEM0,l mode in a solid state laser. Phys. Rev. A 2001, 63, 063807. [Google Scholar] [CrossRef]
- Fang, Z.Q.; Yao, Y.; Xia, K.G.; Li, J.L. Simple Nd:YAG laser generated vector and vortex beam. Chin. Opt. Lett. 2015, 13, 031405. [Google Scholar] [CrossRef][Green Version]
- Fang, Z.Q.; Xia, K.G.; Yao, Y.; Li, J.L. Radially polarized LG01-mode Nd:YAG laser with annular pumping. Appl. Phys. B 2014, 117, 219–224. [Google Scholar] [CrossRef]
- Fang, Z.Q.; Xia, K.G.; Yao, Y.; Li, J.L. Radially polarized and passively Q-switched Nd:YAG laser under annular-shaped pumping. IEEE. J. Sel. Top. Quant. 2014, 21, 337–342. [Google Scholar] [CrossRef]
- Bisson, J.F.; Senatsky, Y.; Ueda, K.I. Generation of Laguerre-Gaussian modes in Nd:YAG laser using diffractive optical pumping. Laser Phys. Lett. 2005, 2, 327. [Google Scholar] [CrossRef]
- Kim, J.W.; Mackenzie, J.I.; Hayes, J.R.; Clarkson, W.A. High power Er:YAG laser with radially-polarized Laguerre-Gaussian (LG01) mode output. Opt. Express 2011, 19, 14526–14531. [Google Scholar] [CrossRef] [PubMed]
- Kim, J.W. High-power laser operation of the first-order Laguerre-Gaussian (LG) mode in a diode-laser-pumped Nd:YAG laser. J. Korean Phys. Soc. 2012, 61, 739–743. [Google Scholar] [CrossRef]
- Kim, D.J.; Kim, J.W.; Clarkson, W.A. Q-switched Nd:YAG optical vortex lasers. Opt. Express 2013, 21, 29449–29454. [Google Scholar] [CrossRef] [PubMed]
- Kim, J.W.; Clarkson, W.A. Selective generation of Laguerre–Gaussian (LG0n) mode output in a diode-laser pumped Nd:YAG laser. Opt. Commun. 2013, 296, 109–112. [Google Scholar] [CrossRef]
- Lin, D.; Daniel, J.M.O.; Clarkson, W.A. Controlling the handedness of directly excited Laguerre-Gaussian modes in a solid-state laser. Opt. Lett. 2014, 39, 3903–3906. [Google Scholar] [CrossRef]
- Kim, D.J.; Kim, J.W. Direct generation of an optical vortex beam in a single frequency Nd:YVO4 laser. Opt. Lett. 2015, 40, 399–402. [Google Scholar] [CrossRef]
- Dietrich, T.; Rumpel, M.; Graf, T.; Ahmed, M.A. Investigations on ring-shaped pumping distributions for the generation of beams with radial polarization in an Yb:YAG thin-disk laser. Opt. Express 2015, 23, 26651–26659. [Google Scholar] [CrossRef]
- Lu, J.L.; Lin, H.; Zhang, G.; Li, B.; Zhang, L.; Lin, Z.; Chen, Y.; Petrov, V.; Chen, W. Direct generation of an optical vortex beam from a diode-pumped Yb:MgWO4 laser. Laser Phys. Lett. 2017, 14, 085878. [Google Scholar] [CrossRef]
- Zhao, Y.; Liu, Q.; Zhou, W.; Shen, D. ~1 mJ pulsed vortex laser at 1645 nm with well-defined helicity. Opt. Express 2016, 24, 15596–15602. [Google Scholar] [CrossRef]
- Liu, Q.; Zhao, Y.; Zhou, W.; Shen, D. Vortex operation in Er:LuYAG crystal laser at ~1.6 μm. Opt. Mater. 2017, 71, 31–34. [Google Scholar] [CrossRef]
- He, H.S.; Chen, Z.; Dong, J. Direct generation of vector vortex beams with switchable radial and azimuthal polarizations in a monolithic Nd:YAG microchip laser. Appl. Phys. Express 2017, 10, 052701. [Google Scholar] [CrossRef]
- He, H.S.; Chen, Z.; Li, H.B.; Dong, J. Low-threshold, nanosecond, high-repetition-rate vortex pulses with controllable helicity generated in Cr, Nd:YAG self-Q-switched microchip laser. Laser. Phys. 2018, 28, 055802. [Google Scholar] [CrossRef]
- Chen, D.M.; Wang, X.C.; He, H.S.; Dong, J. Vector vortices with tunable polarization states directly generated in a microchip laser. Appl. Phys. Express 2019, 12, 052012. [Google Scholar] [CrossRef]
- Chen, D.M.; Cai, S.; Dong, J. Highly efficient Yb: YAG microchip laser for direct generation of radially polarized vector vortices. Eng. Res. Express 2020, 2, 045035. [Google Scholar] [CrossRef]
- Li, J.L.; Yao, Y.; Yu, J.J.; Xia, K.G.; Zhou, C.H. Efficient vortex laser with annular pumping formed by circle Dammann grating. IEEE Photonic Technol. Lett. 2015, 28, 473–476. [Google Scholar] [CrossRef]
- Xu, Y.; Han, X.H.; Li, G.Y.; Liu, J.Y.; Xia, K.G.; Li, J.L. Vortex and LG01-mode Nd:YAG laser involving a circular Dammann grating. Opt. Eng. 2016, 55, 056101. [Google Scholar] [CrossRef]
- Li, G.Y.; Xia, K.G.; Wang, Z.Y.; Shen, H.; Shirakawa, A.; Ueda, K.I.; Li, J.L. Conical refraction, for annular pumping of an efficient vortex Nd:YAG laser. Laser Phys. Lett. 2017, 14, 075001. [Google Scholar] [CrossRef]
- Li, K.; Tang, K.F.; Lin, D.; Wang, J.; Li, B.X.; Liao, W.B.; Lin, Z.L.; Zhang, G. Direct generation of optical vortex beams with tunable topological charges up to 18th using an axicon. Opt. Laser Technol. 2021, 143, 107339. [Google Scholar] [CrossRef]
- Liu, J.; Gu, J.; Huang, L.; Zhang, C.X.; Bai, Z.Y.; Fan, D.Y. Mid-infrared vortex array generation with a tunable singularity in an Er:YAP laser. Appl. Phys. Lett. 2023, 123, 021110. [Google Scholar] [CrossRef]
- Fan, L.; Wang, L.M.; Sun, R.; Fan, H.B.; Zhu, J. High-power and efficient vortex Nd: YVO4 laser using annular pumping. Laser Phys. 2023, 33, 115002. [Google Scholar] [CrossRef]
- Liu, J.; Duan, Y.M.; Mao, W.J.; Jin, X.X.; Li, Z.H.; Zhu, H.Y. An axicon-based annular pump acousto-optic Q-switched Nd: GdVO4 self-Raman vortex laser. Crystals 2023, 13, 1484. [Google Scholar] [CrossRef]
- Zhang, Z.H.; Liu, J.; Duan, Y.M.; Zhang, Y.C.; Jin, X.X.; Li, Z.H.; Zhu, H.Y. Robust high-order petal-mode laser with tunable topological pumped by an axicon-based annular beam. Appl. Phys. Lett. 2024, 124, 151102. [Google Scholar] [CrossRef]
- Huang, X.; Xu, B.; Cui, S.; Xu, H.; Cai, Z.; Chen, L. Direct generation of vortex laser by rotating induced off-axis pumping. IEEE J. Sel. Top. Quant. 2018, 24, 1601606. [Google Scholar] [CrossRef]
- Lin, G.P.; Cao, Y.Q.; Ji, R.R.; Hou, C.F.; Lu, Z.H. Direct generation of a narrow-linewidth Laguerre–Gaussian vortex laser in a monolithic nonplanar oscillator. Opt. Lett. 2018, 43, 4164. [Google Scholar] [CrossRef] [PubMed]
- Luo, S.Y.; Cai, Z.P.; Sheng, C.X.; Li, L.; Chen, Q. 604-nm high-order vortex beams directly generated from a Pr:YLF laser with a cavity-loss-induced gain switching mechanism. Opt. Laser Technol. 2020, 127, 106185. [Google Scholar] [CrossRef]
- Lin, X.; Feng, Q.; Zhu, Y.; Ji, S.; Xiao, B.; Xu, H.; Li, W.; Cai, Z. Diode-pumped wavelength-switchable visible Pr3+:YLF laser and vortex laser around 670 nm. Opto-Electron. Adv. 2021, 4, 210006. [Google Scholar] [CrossRef]
- Li, Q.; Xu, M.M.; Hu, M.; Li, H.Z.; Liu, C.; Ji, Y.Y.; Bi, M.H.; Zhou, X.F.; Ye, Z.B.; Liu, C. Direct generation of vortex beams from an off-axis pumped all-solid-state laser. Opt. Quant. Electron. 2024, 56, 699. [Google Scholar] [CrossRef]
- Okida, M.; Omatsu, T.; Itoh, M.; Yatagai, T. Direct generation of high power Laguerre-Gaussian output from a diode-pumped Nd: YVO4 1.3-μm bounce laser. Opt. Express 2007, 15, 7616–7622. [Google Scholar] [CrossRef]
- Okida, M.; Hayashi, Y.; Omatsu, T.; Hamazaki, J.; Morita, R. Characterization of 1.06 μm optical vortex laser based on a side-pumped Nd: GdVO4 bounce oscillator. Appl. Phys. B 2009, 95, 69–73. [Google Scholar] [CrossRef]
- Chard, P.; Shardlow, P.C.; Damzen, M.J. High-power non-astigmatic TEM00 and vortex mode generation in a compact bounce laser design. Appl. Phys. B 2009, 97, 275. [Google Scholar] [CrossRef]
- Zhao, Y.; Wang, Z.; Yu, H.; Zhuang, S.; Zhang, H.; Xu, X.; Xu, J.; Wang, J. Direct generation of optical vortex pulses. Appl. Phys. Lett. 2012, 101, 031113. [Google Scholar] [CrossRef]
- Yao, Y.; Xia, K.; Kang, M.; Fang, Z.; Li, J. Transverse mode transition and LG01-mode generation in an end-pumped Nd: YVO4 laser. Chin. Opt. Lett. 2013, 11, 121406. [Google Scholar] [CrossRef]
- Ding, Y.; Xu, M.; Zhao, Y.; Yu, H.; Zhang, H.; Wang, Z.; Wang, J. Thermally driven continuous-wave and pulsed optical vortex. Opt. Lett. 2014, 39, 2366–2369. [Google Scholar] [CrossRef] [PubMed][Green Version]
- Wang, S.; Zhang, S.; Qiao, H.; Li, P.; Hao, M.; Yang, H.; Xie, J.; Feng, G.; Zhou, S. Direct generation of vortex beams from a double-end polarized pumped Yb:KYW laser. Opt. Express 2018, 26, 26925–26932. [Google Scholar] [CrossRef]
- Zhang, W.Y.; Tong, L.Y.; Yuan, Y.; Chen, C.D.; Cai, Y.J.; Zhao, L.N. Self-Q-switched Tm: YAP vortex laser by thermal-lensing effect. Infrared. Phys. Technol. 2022, 123, 104197. [Google Scholar] [CrossRef]
- Zhang, Z.L.; Gui, K.; Zhao, C.M.; Zhang, H.Y.; Xing, Y.X. Direct generation of vortex beam with a dual-polarization microchip laser. IEEE Photonic Technol. Lett. 2019, 31, 1221–1224. [Google Scholar] [CrossRef]
- Lin, X.J.; Cui, S.W.; Ji, S.H.; Tian, Q.Y.; Zhu, Y.; Li, W.S.; Xu, H.Y.; Cai, Z.P. LD-pumped high-power high-efficiency orange vortex Pr3+:YLF lasers. Opt. Laser Technol. 2021, 133, 106571. [Google Scholar] [CrossRef]
- Yonezawa, K.; Kozawa, Y.; Sato, S. Generation of a radially polarized laser beam by use of the birefringence of a c-cut Nd:YVO4 crystal. Opt. Lett. 2006, 31, 2151–2153. [Google Scholar] [CrossRef]
- Ito, A.; Kozawa, Y.; Sato, S. Selective oscillation of radially and azimuthally polarized laser beam induced by thermal birefringence and lensing. J. Opt. Soc. Am. B 2009, 26, 708–712. [Google Scholar] [CrossRef]
- Kim, D.J.; Kim, J.W. High-power TEM00 and Laguerre-Gaussian mode generation in double resonator configuration. Appl. Phys. B 2015, 121, 401–405. [Google Scholar] [CrossRef]
- Kim, D.J.; Mackenzie, J.I.; Kim, J.W. Adaptable beam profiles from a dual-cavity Nd:YAG laser. Opt. Lett. 2016, 41, 1740–1743. [Google Scholar] [CrossRef] [PubMed]
- Kim, D.J.; Kim, J.W. Dual-cavity Nd:YAG laser with Laguerre-Gaussian (LG0n) mode output. Opt. Commun. 2017, 383, 26–30. [Google Scholar] [CrossRef]
- Kerridge-Johns, W.R.; Damzen, M.J. Vortex laser from anti-resonant ring coupled cavities. Opt. Express 2018, 26, 32839–32846. [Google Scholar] [CrossRef] [PubMed]
- Munj, A.H.; Kerridge-Johns, W.R. Unidirectional ring vortex laser using a wedge-plate shearing interferometer. Opt. Express 2023, 31, 4954–4963. [Google Scholar] [CrossRef] [PubMed]
- Yan, R.P.; Li, M.M.; Li, X.D.; Zhao, C.; Zhou, Y.P.; Jiang, Y.G. Vortex laser generation and chirality control in a LD end pumped Nd:YVO4 laser. Optik 2021, 236, 166669. [Google Scholar] [CrossRef]
- Ito, A.; Kozawa, Y.; Sato, S. Generation of hollow scalar and vector beams using a spot-defect mirror. J. Opt. Soc. Am. A 2010, 27, 2072–2077. [Google Scholar] [CrossRef]
- Tan, S.W.; Zhou, C.H.; Shirakakwa, A.; Ueda, K.I.; Li, J.L. Vortex Ti: Sapphire laser by using an intracavity spot-defect spatial filter. Opt. Laser Technol. 2017, 96, 76–80. [Google Scholar] [CrossRef]
- Qiao, Z.; Xie, G.Q.; Wu, Y.H.; Yuan, P.; Ma, J.G.; Qian, L.J.; Fan, D.Y. Generation high-charge optical vortices directly from laser up to 288th order. Laser Photonics Rev. 2018, 12, 1800019. [Google Scholar] [CrossRef]
- Chen, H.; Li, X.W.; Cui, Y.F.; Zhang, B.Y.; Chang, X.Y.; Qi, Y.Y.; Ding, J.; Yan, B.Z.; Wang, Y.L.; Lu, Z.W.; et al. Generation of tunable vortex beams from a side-pumped Nd:YAG laser utilizing spot defect mirrors. Opt. Commun. 2024, 563, 130587. [Google Scholar] [CrossRef]
- Harris, M.; Hill, C.A.; Tapster, P.R.; Vaughan, J.M. Laser modes with helical wave fronts. Phys. Rev. A 1994, 49, 3119. [Google Scholar] [CrossRef]
- Hu, A.J.; Lei, J.; Chen, P.F.; Wang, Y.; Li, S.M. Numerical investigation on the generation of high-order Laguerre–Gaussian beams in end-pumped solid-state lasers by introducing loss control. Appl. Opt. 2014, 53, 7845–7853. [Google Scholar] [CrossRef]
- Oron, R.; Danziger, Y.; Davidson, N.; Friesem, A.A.; Hasman, E. Laser mode discrimination with intra-cavity spiral phase elements. Opt. Commun. 1999, 169, 115–121. [Google Scholar] [CrossRef]
- Oron, R.; Davidson, N.; Friesem, A.A.; Hasman, E. Efficient formation of pure helical laser beams. Opt. Commun. 2000, 182, 205–208. [Google Scholar] [CrossRef]
- Yang, T.L.; Yang, J.; Li, X.P.; Wang, H.; Zhang, Z.Z.; Wang, Y.P.; Wang, X.J. High power nanosecond optical vortex laser oscillation in mode-selection slab resonator. Appl. Phys. B 2024, 130, 92. [Google Scholar] [CrossRef]
- Ngcobo, S.; Litvin, I.; Burger, L.; Forbes, A. A digital laser for on-demand laser modes. Nat. Commun. 2013, 4, 2289. [Google Scholar] [CrossRef]
- Naidoo, D.; Roux, F.S.; Dudley, A.; Litvin, I.; Piccirillo, B.; Marrucci, L.; Forbes, A. Controlled generation of higher-order Poincaré sphere beams from a laser. Nat. Photonics 2016, 10, 327–332. [Google Scholar] [CrossRef]
- Zhou, W.; Bao, Y.S.; Xu, H.W.; Liu, J.; Cai, Y.; Xu, S.X.; Fan, D.Y. Highly efficient solid-state vortex laser in a robust and simple configuration. Opt. Express 2024, 32, 24156–24165. [Google Scholar] [CrossRef]
- Wei, D.Z.; Cheng, Y.; Ni, R.; Zhang, Y.; Hu, X.P.; Zhu, S.N.; Xiao, M. Generating controllable Laguerre-Gaussian laser modes through intracavity spin-orbital angular momentum conversion of light. Phys. Rev. Appl. 2019, 11, 014038. [Google Scholar] [CrossRef]
- Sroor, H.; Huang, Y.W.; Sephton, B.; Naidoo, D.; Vallés, A.; Ginis, V.; Qiu, C.W.; Ambrosio, A.; Capasso, F.; Forbes, A. High-purity orbital angular momentum states from a visible metasurface laser. Nat. Photonics 2020, 14, 498–503. [Google Scholar] [CrossRef]
- Tao, X.; Liang, Y.; Zhang, S.R.; Li, Y.Q.; Guo, M.H.; Li, P. Generation of Perfect Vortex Beams with Complete Control over the Ring Radius and Ring Width. Photonics 2023, 10, 1382. [Google Scholar] [CrossRef]
- Litvin, I.A.; Ngcobo, S.; Naidoo, D.; Ait-Ameur, K.; Forbes, A. Doughnut laser beam as an incoherent superposition of two petal beams. Opt. Lett. 2014, 39, 704–707. [Google Scholar] [CrossRef] [PubMed]
- Kubodera, K.; Otsuka, K. Single-transverse-mode LiNdP4O12 slab waveguide laser. J. Appl. Phys. 1979, 50, 653. [Google Scholar] [CrossRef]
- McDonagh, L.; Wallenstein, R.; Knappe, R.; Nebel, A. High-efficiency 60 W TEM00 Nd:YVO4 oscillator pumped at 888 nm. Opt. Lett. 2006, 31, 3297–3299. [Google Scholar] [CrossRef] [PubMed]
- Ma, J.; Li, P.; Zhou, Z.; Gu, Y. Characteristics of fork-shaped fringes formed by off-axis interference of two vortex beams. J. Opt. Soc. Am. A 2021, 38, 115–123. [Google Scholar] [CrossRef]


| lc (m) | σ (m2) | τf (s) | α1 (cm−1) | α2 (cm−1) | ηt |
| 5 × 10−3 | 15.6 × 10−23 | 90 × 10−6 | 8.8 | 2.4 | 100% |
| ηp | w0 (mm) | T | L (mm) | δ1 (solid line) | δ2 (dashed line) |
| 75.94% | 0.83 | 1.50% | 20.00 | 5.50% | 6.90% |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Guo, M.; Tao, X.; Li, Y.; Zhang, S.; Wu, Z.; Gu, Y.; Li, P. A Watt-Level, High-Quality LG0,±1 Vortex Beam made from a Nd:YVO4 Laser Pumped by an Annular Beam. Photonics 2024, 11, 843. https://doi.org/10.3390/photonics11090843
Guo M, Tao X, Li Y, Zhang S, Wu Z, Gu Y, Li P. A Watt-Level, High-Quality LG0,±1 Vortex Beam made from a Nd:YVO4 Laser Pumped by an Annular Beam. Photonics. 2024; 11(9):843. https://doi.org/10.3390/photonics11090843
Chicago/Turabian StyleGuo, Minghao, Xin Tao, Yueqing Li, Shirui Zhang, Zhenkun Wu, Yuzong Gu, and Peng Li. 2024. "A Watt-Level, High-Quality LG0,±1 Vortex Beam made from a Nd:YVO4 Laser Pumped by an Annular Beam" Photonics 11, no. 9: 843. https://doi.org/10.3390/photonics11090843
APA StyleGuo, M., Tao, X., Li, Y., Zhang, S., Wu, Z., Gu, Y., & Li, P. (2024). A Watt-Level, High-Quality LG0,±1 Vortex Beam made from a Nd:YVO4 Laser Pumped by an Annular Beam. Photonics, 11(9), 843. https://doi.org/10.3390/photonics11090843





