Abstract
We experimentally demonstrate a scheme for generating massively parallel and real-time physical random bits (PRBs) by using weak-resonant-cavity Fabry-Perot laser diodes (WRC-FPLDs) with optical feedback. By using external optical feedback to modify the nonlinear dynamic behavior of the longitudinal modes in WRC-FPLDs, the chaotic behavior of each channel can be induced under suitable feedback strength. By filtering these longitudinal modes, a real-time PRBs at 10 Gbits/s can be generated by using field programmable gate array (FPGA) board for the real-time post-processing of a single-channel chaotic signal. Considering the presence of up to 70 longitudinal modes within a broad spectral range exceeding 40 nm, each of these modes can be used to extract chaotic time sequences for random number generation. Therefore, our PRB generation scheme has the potential to achieve a data throughput of over 700 Gbits/s.
1. Introduction
Random numbers exhibit properties such as a uniform distribution, unpredictability, and uniqueness, and they are suitable for applications like secure communication, encryption, and copyright protection in multimedia [1,2,3]. Based on their generation methods, random numbers can be classified into pseudo-random numbers and physical random numbers. Pseudo-random numbers are typically generated by deterministic algorithms, known for their advantages in simplicity, efficiency, and good statistical characteristics [4,5]. However, their deterministic essence can lead to issues such as predictability and periodicity. To overcome the aforementioned shortcomings, physical random numbers are generated based on entropy sources extracted from various non-deterministic random phenomena occurring in the real world. Considering that semiconductor lasers under external perturbations can easily generate chaotic laser signals with a wide bandwidth and high-intensity fluctuations, they are highly suitable as entropy sources for generating physical random bits (PRBs). Hence, related PRBs generation schemes have become a research hotspot, and the fast PRBs generated show great potential applications in advancing fields such as computer science, information security, and optical communication [6,7,8,9,10,11,12,13,14,15,16,17,18,19,20,21,22]. In 2010, Kanter et al. demonstrated the generation of 300 Gbits/s random bits by utilizing high derivatives and least significant bit (LSB) extraction via a post-processing approach [9]. In 2015, Sakuraba et al. obtained 1.2 Tbits/s random bits via a 35.2 GHz standard bandwidth chaotic signal generated through three cascaded laser diodes [10]. The utilization of PRBs not only enhances the security and reliability of digital systems but also drives the innovation in emerging technologies that rely on high-quality random number generation.
One of the critical performance metrics for random numbers is their generation rate. Increasing the bandwidth of entropy sources is an effective way to boost the speed of random number generation. Entropy sources based on chaotic laser diodes have achieved bandwidths exceeding 50 GHz [23]. However, related schemes that rely on a single entropy source face the limitations imposed by hardware bottlenecks. Therefore, researchers have explored some parallel generation approaches using dual or multiple paths to overcome these constraints. For instance, our research team previously proposed to obtain two parallel streams of 10 Gbps PRBs from mutually coupled semiconductor laser systems [24]. Building upon this foundation, an interleaving operation merged the two sets of PRB streams, obtaining a PRB rate of 1.12 Tbits/s [25]. Recently, significant progress, including using chaotic optical frequency combs from Si3N4 micro-rings for massive parallel PRB generation [26,27,28] and leveraging wavelength-division multiplexing for scalability, have been achieved by scholars worldwide in this field. However, fabricating microcavities with a high Q-factor [29] typically involves numerous additional manufacturing steps, thereby amplifying both complexity and the cost of the production process. To enhance parallel chaotic generation while managing costs, an optical feedback mechanism modifies the nonlinear dynamics of WRC-FPLDs, enabling large-scale parallel chaotic generation in a straightforward experimental setup [30,31,32]. This method not only supports real-time PRB generation by using chaotic lasers and multi-quantization technology but also validates its feasibility through experimental verification.
By utilizing an optical feedback mechanism to perturb WRC-FPLDs under specific parameters, chaotic signals across multiple comb channels can be achieved, each serving as an entropy source. Real-time processing involves sampling and quantizing with an 8 bit Analog-to-Digital Converter (ADC) at 2.5 GHz, utilizing a field-programmable gate array (FPGA) board; the lower four effective bits are extracted and subjected to real-time processing on the chip [33,34,35,36,37,38], achieving single-channel chaotic signal PRBs at 10 Gbits/s. It instantiated a chaotic comb with 70 chaotic comb lines, demonstrating the potential to achieve a throughput of up to 700 Gbits/s in large-scale parallel real-time PRB generation. This work lays foundational groundwork for cost-effective, high-quality, high-speed real-time PRB production, marking a significant stride forward in the fields of modern computing and communications.
2. Experimental Setup
The experimental setup involves generating a chaotic comb using a WRC-FPLD coupled with FPGA boards to achieve parallel real-time PRBs under optical feedback, as depicted in Figure 1a. The WRC-FPLD is driven by a precise current source controller (ILX Lightware, LDC-3724C, Newport, Bozeman, MT, USA) to regulate bias current. Temperature control is crucial, maintaining the laser diode at a stable 17.03 °C to ensure a consistent chaotic comb amplitude and constant output power. Light emitted from the WRC-FPLD passes through a 30:70 fiber coupler with 1 × 2 ports. The 30% part output from FC1 passes through a 50:50 optical fiber coupler with a 2 × 2 port configuration, with FC2 connected to a variable attenuator and a 1 km optical fiber, forming a closed-loop feedback to the WRC-FPLD. In addition, an optical power meter (PM, Thorlabs PM100D, Newton, MA, USA) is utilized to detect the feedback power. The 70% output from FC1 passes through a polarization controller (PC), an optical isolator (ISO), and an erbium-doped fiber amplifier (EDFA, FIPHENE BML01-EDFA, FIPHENE, Shanghai, China). The amplified chaotic light is utilized as a chaotic entropy source via a demultiplexer, and then the optical chaotic comb is demultiplexed into a different-wavelength single-channel chaotic comb, which is further converted into electrical signals by a photodetector (PD). Two ADCs with a 1.25 GHz sampling frequency quantize the entropy signal into initial bit sequences. Subsequently, FPGA processes the sequences through self-delayed XOR operations, retaining the 4 least significant bits for real-time PRB outputs. Figure 1b shows the output spectrum of the WRC-FPLD at the state of free-running, which is monitored by an optical spectrum analyzer (Ando AQ6317C, Yokogawa, Tokyo, Japan, with a minimum resolution bandwidth of 0.02 nm). The output spectral range exceeds 40 nm, while the longitudinal mode interval is about 0.58 nm, determined by the active region length of the utilized WRC-FPLD. The output spectrum contains 70 comb lines in the wavelength region spanning 40 nm, indicating that WRC-FPLD has the potential to provide enough carrier channels. Figure 1c depicts the output spectrum of the WRC-FPLD under feedback condition. Compared to its free-running state, the WRC-FPLD with feedback shows a reduction in output spectrum power amplitude while exhibiting noticeable widening. Within a 40 nm bandwidth, 70 chaotic comb teeth exhibit high signal-to-noise ratios, making them suitable candidates for an effective entropy source and real-time PRB generation. These findings underscore the potential of WRC-FPLDs to utilize feedback mechanisms as a scalable parallel chaotic entropy source, facilitating cost-effective and compact integration strategies.
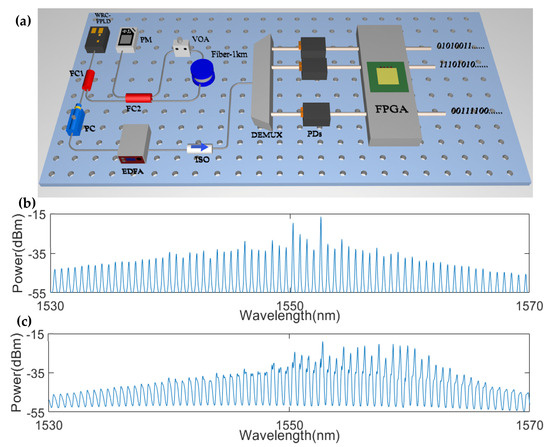
Figure 1.
(a) Experimental setup for real-time PRB generator. WRC-FPLD: weak-resonant-cavity Fabry-Perot laser diode; FC: fiber coupler; PM: power meter; VOA: variable optical attenuator; PC: polarization controller; EDFA: erbium-doped optical fiber amplifier; ISO: optical isolator; DEMUX: demultiplexer; PDs: photodetectors; FPGA: field-programmable gate array. (b) Output spectrum of the laser at free-running. (c) Output spectrum of the laser with feedback.
3. Analysis of Chaotic Characteristics of Chaotic Combs
To thoroughly analyze the chaotic characteristics of each comb tooth, we selectively filtered comb teeth at different wavelengths from the chaotic combs for detailed examination. Figure 2 illustrates our findings, presenting the results of spectral analysis, time sequences representation, autocorrelation curves, and frequency spectra to evaluate the chaotic signal quality. Figure 2(a1)–(a4) display the spectral characteristics of comb teeth at wavelengths of 1539.5 nm, 1545.2 nm, 1556.8 nm, and 1561.5 nm. Each spectrum exhibits significant broadening, indicative of chaotic behavior. Corresponding time sequences in Figure 2(b1)–(b4) show highly disordered amplitude fluctuations. The amplitude of the time sequences fluctuates rapidly and vigorously, reflecting the chaotic nature. Figure 2c shows the autocorrelation curves derived from the time sequence data shown in Figure 2b. We observe distinct peaks in the autocorrelation curve, indicating weak periodic components in the chaotic signal. This characteristic degrades the randomness of generated PRBs. In post-processing, we only retain the lower 4 bits of the data as valid data. By discarding the upper 4 bits and combining other subsequent treatments such as XOR operation and bits reversal to eliminate the influence of delay characteristics in the chaotic signal, qualified PRBs can be obtained. Figure 2(d1)–(d4) depict corresponding power spectra. Under an optical feedback power of about −14 dB, the chaotic comb exhibits broad-radio-frequency noise with an effective bandwidth of up to 7.5 GHz, indicating robust chaotic dynamics. As a result, the theoretical maximum rate of the generated PRB for the channel can arrive at 120 Gb/s when adopting FPGA onboard ADCs with an 8 bit vertical resolution. Additionally, through inspecting other chaotic comb teeth, the results show that all the chaotic comb teeth possess similar effective bandwidths.

Figure 2.
Optical spectrum (a), corresponding time sequences (b), autocorrelation of time sequences (c), and power spectrum (d) of a single chaotic comb with a central wavelength of 1539.5 nm (the first row, (a1−d1)), 1545.2 nm (the second row, (a2−d2)), 1556.8 nm (the third row, (a3−d3)), and 1561.5 nm (the fourth row, (a4−d4)).
4. PRB Extraction and Evaluation
The experimentally generated chaotic comb is passed through a filter, and the individual comb teeth at various wavelengths are directed to photodetectors to convert the optical signal into chaotic electrical signal. The single-channel chaotic signal undergoes sampling and quantization by onboard 8 bit ADCs, yielding multiple effective bits of random data. The ADCs operate with a clock signal of 1.25 GHz configured in dual-channel mode, where one ADC receives an in-phase clock and the other receives an inverted clock. In this case, an interleaved sampling rate of 2.5 Gbits/s can be achieved. During this experiment, Verilog Hardware Description Language (HDL) is used to drive the FPGA board, and then data input can be realized from integrating ADCs. Verilog HDL processes and analyzes sampled data within the FPGA to enable monitoring and controlling functionalities. Figure 3a showcases quantized signal sampling by ADCs. For enhancing data processing efficiency, ADCs sample a chaotic signal in parallel and convert serialized data into 8-channel parallel streams. From this diagram, one can see that each channel signal exhibits chaotic behavior. Figure 3b further provides a detailed discrete-time sequence diagram of corresponding 8 bit parallel signal from the initial three sets of data of Figure 3a.

Figure 3.
(a) Eight parallel discrete data sampled by ADCs. (b) Corresponding detailed graph from the initial three sets of data of (a).
Figure 4 presents a detailed depiction of the real-time post-processing evolution of PRBs and the corresponding time sequences. Real-time sampling results can be obtained from onboard ADCs across eight channels, where the hexadecimal format is presented to strictly correspond with the experimental data. The eight-channel discrete data undergo conversion from a parallel to a serial format via a serial-to-parallel converter. Next, the data are transmitted to the FPGA board and subsequently split into two paths. For one path, after following a 312-clock cycle delay, the data undergo a bit reversal operation from high to low. Simultaneously, for the other path, the data are stored as initial data in dedicated registers. Following an additional 1-clock cycle delay, an XOR operation is performed between the initial data and the delayed reversed data. By retaining only the four least significant bits (LSBs), final random sequences can be formed. Figure 4a demonstrates the successful execution of the FPGA board driven by the Verilog HDL program through the Quartus II integrated circuit (IC) design software suite. This process enables the acquisition of specific real-time data, which are presented in an enlarged view for clarity. Figure 4b displays the time sequences of the original data, while Figure 4c shows the results after the delay reversal process. Subsequently, Figure 4d presents the outcome following XOR processing. Finally, Figure 4e depicts the truncated 4-LSBs data based on Figure 4d. Here, the time sequences within the dash frames in Figure 4b–e are utilized for obtaining serial_data, reverse_data, XOR_data, and 4LSB_data in Figure 4a, respectively.

Figure 4.
(a) Detailed data for real-time sampling and real-time post-processing. (b) Time sequences of series–parallel conversion. (c) Reversed time sequences after a delay of 312 clock cycles on the basis of (b). (d) Time sequences of XOR. (e) Time sequences of 4-LSBs on the basis of (d).
Figure 5a depicts the probability distribution of the initial chaotic data. From this diagram, the probability of raw sampling data has a non-uniform distribution. The probability distribution graph reveals the asymmetry in the distribution function, which leads to an imbalance in the proportions of “0” and “1” and then diminishes the randomness of the random numbers. After extracting the lower 4 bits using FPGA and performing self-delayed XOR processing, the resulting normal distribution is depicted in Figure 5b. From this diagram, one can observe that, following 4-LSBs post-processing, the generated bit sequences contain different bit patterns with equal frequencies. In Figure 5c, a two-dimensional graph is generated from the first one million data points organized in a 1000 × 1000 format, where “0” and “1” correspond to white and black, respectively. The binary image appears to be disordered and lacks any discernible regular textural patterns.
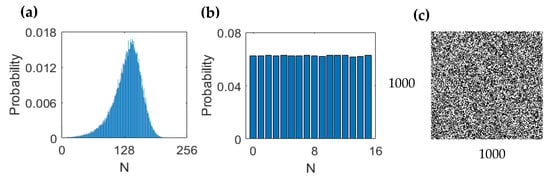
Figure 5.
(a) The histogram distribution of the initial data. (b) Histograms of the distribution of the extracted 4-LSBs. (c) Two-dimensional graph generated by the first 1 M points in the bit sequences under 4-LSBs processing in the form of 1000 × 1000, where bits “1” and bits “0” are converted into white and black dots, respectively.
The triple standard deviation test is used to assess the randomness of a long sequences of bits. This test typically involves two aspects: testing for statistical bias and testing for serial autocorrelation coefficients. Figure 6a,b illustrate the variation of the statistical bias with the sequence length N and the serial autocorrelation coefficient Ck for N = 1 Gbits in the 4-LSBs case [39]. The red curve in Figure 6a,b represents the standard curve of the statistical deviation. By comparing both the sequence bias and the autocorrelation coefficient, we assess whether the statistical properties of random bit sequences satisfy the criteria for true random bits based on the triple standard deviation (where 3σ = 1.5N−0.5 in Figure 6a, 3σ = 3 N−0.5 in Figure 6b, N = 1 Gbits) criterion. The 1 Gbits sequences passed both the statistical bias test and the serial autocorrelation coefficient test, with values below the triple standard deviation range. The statistical bias test indicates minimal difference between the sequence mean and the theoretical mean, while the serial autocorrelation coefficient test shows a very weak correlation between consecutive observations. Furthermore, with a sequence length of 1 Gbits, this large sample size both ensures the accuracy of the analysis and enhances the representativeness and stability of the data. The temporal waveforms and eye diagrams of random bits from the experiment, depicted in Figure 6c,d, exhibit a clearly defined structure. Specifically, the eye diagrams show well-formed openings, indicating robust signal integrity, and the intervals between the intersections on the eye diagrams are equal to the width of a specific code type.

Figure 6.
(a) Variation of statistical bias b with sample size N. (b) First 200 serial autocorrelation coefficients for the binary sequences. (c) 4−LSBs temporal waveforms. (d) Eye diagrams of random bits.
To ensure the reliability of the findings and mitigate individual specificity, the data was subjected to a randomness assessment on real-time PRBs sequences generated by randomly selecting 10 chaotic combs. Figure 7 illustrates the NIST test results for 10 specific comb teeth at wavelengths of 1539 nm, 1542 nm, 1545 nm, 1555 nm, 1556 nm, and 1557 nm, 1561 nm, 1562 nm, 1563 nm and 1564 nm. Notably, all 10 chaotic combs successfully pass the 15 NIST tests at 4-LSBs, confirming the validity of the findings while minimizing biases from inadequate sample sizes. Therefore, it is predictable that the 70 chaotic comb teeth generated in the experiment could potentially serve as independent chaotic entropy. Furthermore, appropriate optimization and refinement of the experimental parameters can enhance the signal-to-noise ratio and generate a greater number of usable comb lines.

Figure 7.
Results of NIST tests for bit sequences generated by the entropy source of the chaotic comb lines in 1539 nm, 1542 nm, 1545 nm, 1555 nm, 1556 nm, 1557 nm, 1561 nm, 1562 nm, 1563 nm, and 1564 nm under 4-LSBs processing, where a set of 1000 sequences of 1 M bits is used for evaluation.
5. Conclusions
In summary, we validated a massive parallel real-time PRB generation scheme by using chaotic entropy sources extracted from optical feedback WRC-FPLD. Initially, we investigated the influence of optical feedback on the nonlinear dynamic characteristics of longitudinal modes of the WRC-FPLD. These perturbations alter the nonlinear dynamic state of the longitudinal modes, inducing chaotic behavior and enabling the generation of massively parallel chaotic sources. Next, after selecting four appropriate comb lines and thoroughly analyzing their dynamic behaviors, each comb line was induced into a chaotic state. A single-channel chaotic signal was sampled vertically and quantized by using two 8 bit ADCs, and a PRB generation rate of 10 Gbits/s single channel was achieved by real-time post-processing via FPGA. Furthermore, we explored the feasibility of a massively multi-channel random-bit output scheme. By randomly selecting 10 channels, each channel generated 10 Gbits/s real-time PRB sequences, while the outputs of each channel passed the NIST SP 800-22 tests. In this work, the laser could generate over 70 chaotic carrier channels, covering a wavelength range exceeding 40 nm. These channels have the potential to serve as reliable sources of chaotic entropy. Using only one comb and one FPGA board, our method shows a significant improvement over most PRB generators reported previously and possesses a potential real-time PRB generation rate of up to 700 Gbits/s. This pioneering research presents a more effective solution for high-throughput and cost-effective ultrafast real-time PRB generation.
Author Contributions
Conceptualization, Y.W. and G.X.; methodology, Y.W.; validation, Y.W., G.X. and J.W.; formal analysis, Y.W., J.W. and X.T.; investigation, Y.W.; resources, Z.W.; data curation, Y.W.; writing—original draft preparation, Y.W.; writing—review and editing, Y.W.; visualization, Y.W.; supervision, G.X.; project administration, Z.W.; funding acquisition, Z.W. and G.X. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by the National Natural Science Foundation of China (62335015, 61875167) and the Chongqing Natural Science Foundation (CSTB2022NSCQ-MSX0313, CSTB2024NSCQ-LZX0033).
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
The original contributions presented in the study are included in the article, and further inquiries can be directed to the corresponding author.
Conflicts of Interest
The authors declare no conflicts of interest.
References
- Vicente, R.; Mirasso, C.-R.; Fischer, I. Simultaneous bidirectional message transmission in a chaos-based communication scheme. Opt. Lett. 2007, 32, 403–405. [Google Scholar] [CrossRef] [PubMed]
- Sciamanna, M.; Shore, K.-A. Physics and applications of laser diode chaos. Nat. Photonics 2015, 9, 151–162. [Google Scholar] [CrossRef]
- Li, P.; Li, Z.; Halang, W.-A.; Chen, G. A stream cipher based on a spatiotemporal chaotic system. Chaos Solitons Fractals 2007, 32, 1867–1876. [Google Scholar] [CrossRef]
- Blum, L.; Blum, M.; Shub, M. A simple unpredictable pseudo-random number generator. SIAM J. Comput. 1986, 15, 364–383. [Google Scholar] [CrossRef]
- Eichenaur, B.-J.; Lehn, J.; Topuzoglu, A. A nonlinera congruential pseudo-random number generator with power of two modulus. Math. Comput. 1998, 51, 757–759. [Google Scholar] [CrossRef]
- Uchida, A.; Amano, K.; Inoue, K.; Hirano, M.; Naito, S.; Someya, H.; Oowada, I.; Kurashige, T.; Shiki, M.; Yoshimori, S.; et al. Fast physical random bit generation with chaotic semiconductor lasers. Nat. Photonics 2008, 2, 728–732. [Google Scholar] [CrossRef]
- Reidler, I.; Aviad, Y.; Rosenbluh, M.; Kanter, I. Ultrahigh-speed random number generation based on a chaotic semiconductor laser. Phys. Rev. Lett. 2009, 103, 024102. [Google Scholar] [CrossRef]
- Hirano, K.; Yamazaki, T.; Morikatsu, S.; Okumura, H.; Aida, H.; Uchida, A.; Yoshimori, S.; Yoshimura, K.; Harayama, T.; Davis, P. Fast random bit generation with bandwidth-enhanced chaos in semiconductor lasers. Opt. Express 2010, 18, 5512–5524. [Google Scholar] [CrossRef] [PubMed]
- Kanter, I.; Aviad, Y.; Reidler, I.; Cohen, E.; Rosenbluh, M. An optical ultrafast random bit generator. Nat. Photonics 2010, 4, 58–61. [Google Scholar] [CrossRef]
- Sakuraba, R.; Iwakawa, K.; Kanno, K.; Uchida, A. Tb/s physical random bit generation with bandwidth-enhanced chaos in three-cascaded semiconductor lasers. Opt. Express 2015, 23, 1470–1490. [Google Scholar] [CrossRef]
- Zhang, L.; Pan, B.; Chen, G.; Guo, L.; Lu, D.; Zhao, L.; Wang, W. 640-Gbit/s fast physical random number generation using a broadband chaotic semiconductor laser. Sci. Rep. 2017, 7, 45900. [Google Scholar] [CrossRef]
- Li, P.; Wang, Y.-C.; Zhang, J.-Z. All-optical fast random number generator. Opt. Express 2010, 18, 20360–20369. [Google Scholar] [CrossRef] [PubMed]
- Li, X.-Z.; Chan, S.-C. Heterodyne random bit generation using an optically injected semiconductor laser in chaos. IEEE J. Quantum Electron. 2013, 49, 829–838. [Google Scholar] [CrossRef]
- Takahashi, R.; Akizawa, Y.; Uchida, A.; Harayama, T.; Tsuzuki, K.; Sunada, S.; Arai, K.; Yoshimura, K.; Davis, P. Fast physical random bit generation with photonic integrated circuits with different external cavity lengths for chaos generation. Opt. Express 2014, 22, 11727–11740. [Google Scholar] [CrossRef]
- Ran, C.; Tang, X.; Wu, Z.-M.; Xia, G.-Q. Dual-channel physical random bits generation by a master-slave vertical-cavity surface-emitting lasers chaotic system. Laser Phys. 2018, 28, 126202. [Google Scholar] [CrossRef]
- Li, X.-Z.; Chan, S.-C. Random bit generation using an optically injected semiconductor laser in chaos with oversampling. Opt. Lett. 2012, 37, 2163–2165. [Google Scholar] [CrossRef] [PubMed]
- Shi, B.; Luo, C.; Flores, J.-G.-F.; Lo, G.; Kwong, D.-L.; Wu, J.; Wong, C.-W. Gbps physical random bit generation based on the mesoscopic chaos of a silicon photonics crystal microcavity. Opt. Express 2020, 28, 36685–36695. [Google Scholar] [CrossRef] [PubMed]
- Ge, Z.; Xiao, T.; Hao, T.; Li, W.; Li, M. Tb/s fast random bit generation based on a broadband random optoelectronic oscillator. IEEE Photonics Technol. Lett. 2021, 33, 1223–1226. [Google Scholar] [CrossRef]
- Virte, M.; Mercier, E.; Thienpont, H.; Panajotov, K.; Sciamanna, M. Physical random bit generation from chaotic solitary laser diode. Opt. Express 2014, 22, 17271–17280. [Google Scholar] [CrossRef]
- Oliver, N.; Soriano, M.-C.; Sukow, D.-W.; Fischer, I. Dynamics of a semiconductor laser with polarization-rotated feedback and its utilization for random bit generation. Opt. Lett. 2011, 36, 4632–4634. [Google Scholar] [CrossRef]
- Akizawa, Y.; Yamazaki, T.; Uchida, A.; Harayama, T.; Sunada, S.; Arai, K.; Yoshimura, K.; Davis, P. Fast random number generation with bandwidth-enhanced chaotic semiconductor lasers at 8 × 50 Gb/s. IEEE Photonics Technol. Lett. 2012, 24, 1042–1044. [Google Scholar] [CrossRef]
- Argyris, A.; Deligiannidis, S.; Pikasis, E.; Bogris, A.; Syvridis, D. Implementation of 140 Gb/s true random bit generator based on a chaotic photonic integrated circuit. Opt. Express 2010, 18, 18763–18768. [Google Scholar] [CrossRef]
- Qiao, L.-J.; Lv, T.-S.; Xu, Y.; Zhang, M.-J.; Wang, T.; Zhou, R.-K.; Wang, Q.; Xu, H.-C. Generation of flat wideband chaos based on mutual injection of semiconductor lasers. Opt. Lett. 2019, 44, 5394–5397. [Google Scholar] [CrossRef]
- Wu, J.-G.; Tang, X.; Wu, Z.-M.; Xia, G.-Q.; Feng, G.-Y. Parallel generation of 10 Gbits/s physical random number streams using chaotic semiconductor lasers. Laser Phys. 2012, 22, 1476–1480. [Google Scholar] [CrossRef]
- Tang, X.; Wu, Z.-M.; Wu, J.-G.; Deng, T.; Chen, J.J.; Fan, L.; Zhong, Q.-Z.; Xia, G.-Q. Tbits/s physical random bit generation based on mutually coupled semiconductor laser chaotic entropy source. Opt. Express 2015, 23, 33130–33141. [Google Scholar] [CrossRef]
- Ji, X.-C.; Yao, X.-W.; Klenner, A.; Gan, Y.; Gaeta, A.-L.; Hendon, C.-P.; Lipson, M. Chip-based frequency comb sources for optical coherence tomography. Opt. Express 2019, 27, 19896–19905. [Google Scholar] [CrossRef] [PubMed]
- Marchand, P.-J.; Riemensberger, J.; Skehan, J.-C.; Ho, J.-J.; Pfeiffer, M.-H.-P.; Liu, J.-Q.; Hauger, C.; Lasser, T.; Kippenberg, T.-J. Soliton microcomb based spectral domain optical coherence tomography. Nat. Commun. 2021, 12, 427. [Google Scholar] [CrossRef] [PubMed]
- Shen, B.-T.; Shu, H.-W.; Xie, W.-Q.; Chen, R.-X.; Liu, Z.; Ge, Z.-F.; Zhang, X.-G.; Wang, Y.-M.; Zhang, Y.-H.; Cheng, B.-W.; et al. Harnessing microcomb-based parallel chaos for random number generation and optical decision making. Nat. Commun. 2023, 14, 4590. [Google Scholar] [CrossRef] [PubMed]
- Xiao, Z.-Y.; Li, T.; Cai, T.; Zhang, H.; Huang, Y.; Li, C.; Yao, B.; Wu, K.; Chen, J. Near-zero-dispersion soliton and broadband modulational instability Kerr microcombs in anomalous dispersion. Light Sci. Appl. 2023, 12, 33. [Google Scholar] [CrossRef]
- Hu, C.-X.; Xia, G.-Q.; Jiang, Z.-F.; Yue, D.-Z.; Yang, W.-Y.; Lin, G.-R.; Wu, Z.-M. Simultaneous Generation of Multi-Channel Broadband Chaotic Signals Based on Two Unidirectionally Coupled WRC-FPLDs. IEEE Photonics J. 2020, 12, 1504008. [Google Scholar] [CrossRef]
- Tang, X.; Xia, G.-Q.; Ran, C.; Deng, T.; Lin, X.-D.; Fan, L.; Gao, Z.-Y.; Lin, G.-R.; Wu, Z.-M. Fast Physical Random Bit Generation Based on a Broadband Chaotic Entropy Source Originated from a Filtered Feedback WRC-FPLD. IEEE Photonics J. 2019, 11, 7800710. [Google Scholar] [CrossRef]
- Yin, Z.-S.; Wang, F.; Deng, T.; Hu, D.-W.; Xia, G.-Q.; Wu, Z.-M. Multi-channel chaotic signal generation using a weak resonant cavity Fabry–Perot laser diode subject to self-phase-modulated feedback. Laser Phys. Lett. 2023, 20, 115802. [Google Scholar] [CrossRef]
- Wang, L.-S.; Zhao, T.; Wang, D.-M.; Wu, D.-Y.; Zhou, L.; Wu, J.; Liu, X.-Y.; Wang, Y.-C. Real-Time 14-Gbps Physical Random Bit Generator Based on Time-Interleaved Sampling of Broadband White Chaos. IEEE Photonics J. 2017, 9, 7201412. [Google Scholar] [CrossRef]
- Lin, Y.; Wang, F.; Liu, B. Random number generators for large-scale parallel Monte Carlo simulations on FPGA. J. Comput. Phys. 2018, 360, 93–103. [Google Scholar] [CrossRef]
- Yang, J.; Liu, J.-N.; Su, Q.; Li, Z.-Y.; Fan, F.; Xu, B.-J.; Guo, H. 5.4 Gbps real time quantum random number generator with simple implementation. Opt. Express 2016, 24, 27475–27481. [Google Scholar] [CrossRef] [PubMed]
- Zhang, X.-G.; Nie, Y.-Q.; Zhou, H.-Y.; Liang, H.; Ma, X.-F.; Zhang, J.; Pan, J.-W. Fully integrated 3.2 Gbps quantum random number generator with real-time extraction. Rev. Sci. Instrum. 2016, 87, 076102. [Google Scholar] [CrossRef]
- Xu, Y.-P.; Lu, P.; Mihailov, S.; Bao, X.-Y. Real-time physical random bit generation at Gbps based on random fiber lasers. Opt. Lett. 2017, 42, 4796–4799. [Google Scholar] [CrossRef] [PubMed]
- Ugagin, K.; Terashime, Y.; Iwakawa, K.; Uchida, A.; Harayama, T.; Yoshimura, K.; Inubushi, M. Real-time fast physical random number generator with a photonic integrated circuit. Opt. Express 2017, 25, 6511–6523. [Google Scholar] [CrossRef]
- Li, N.; Kim, B.; Chizhevsky, V.-N.; Locquet, A.; Bloch, M.; Citrin, D.-S.; Pan, W. Two approaches for ultrafast random bit generation based on the chaotic dynamics of a semiconductor laser. Opt. Express 2014, 22, 6634–6646. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).