Improving the Performances of Optical Tweezers by Using Simple Binary Diffractive Optics
Abstract
1. Introduction
- (a)
- The trap is illuminated by a rectified LGp0 beam [4]. Let us recall that a radial Laguerre–Gauss LGp0 beam is made up of a central peak surrounded by p rings alternately positive and negative. The beam rectification is obtained by inserting a binary diffractive optical element made up of concentric dephasing zones making all the rings to be positive. The longitudinal force is improved by a factor ranging from (p + 1) to (p + 2). In contrast, the radial force is not improved.
- (b)
- (c)
- The third possibility is to introduce a primary or secondary spherical aberration on the path of the incident LGp0 beam. This allows for increasing several times both the longitudinal and transverse trapping effect for a given incident power [3] especially if the spherical aberration is negative.
2. Optical Tweezers Illuminated by a Beam Subject to Spherical Aberration
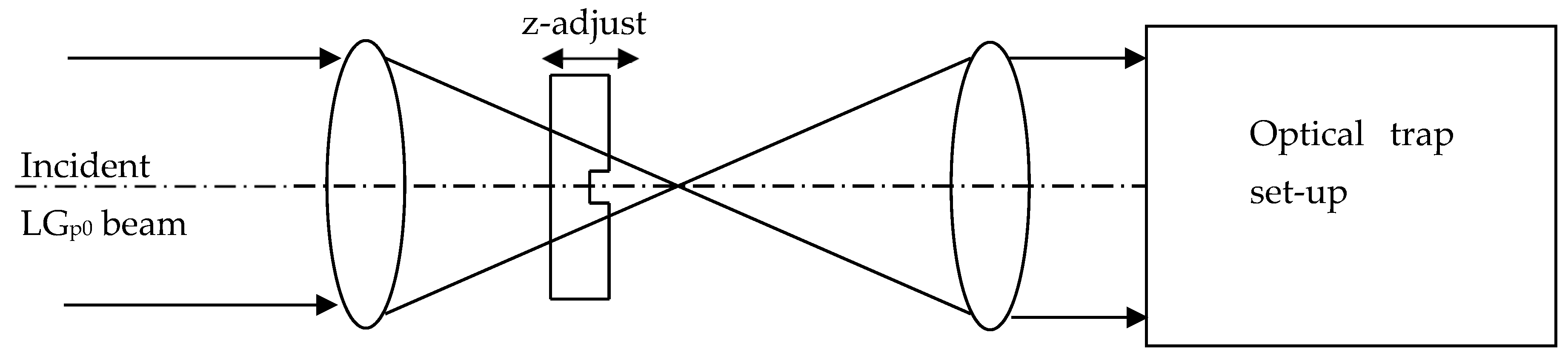
3. Restructuring the Laser Beam Illuminating the Tweezers
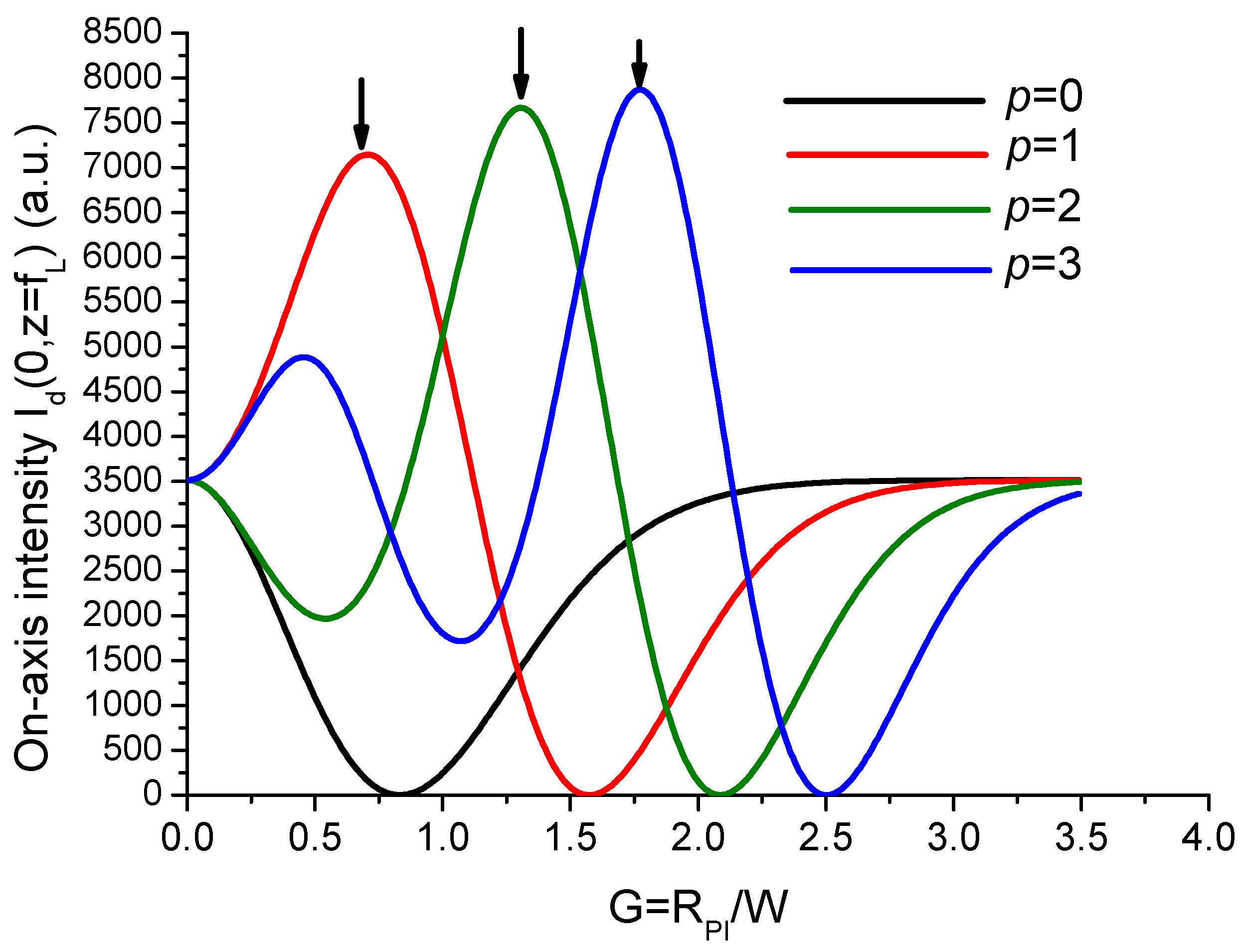
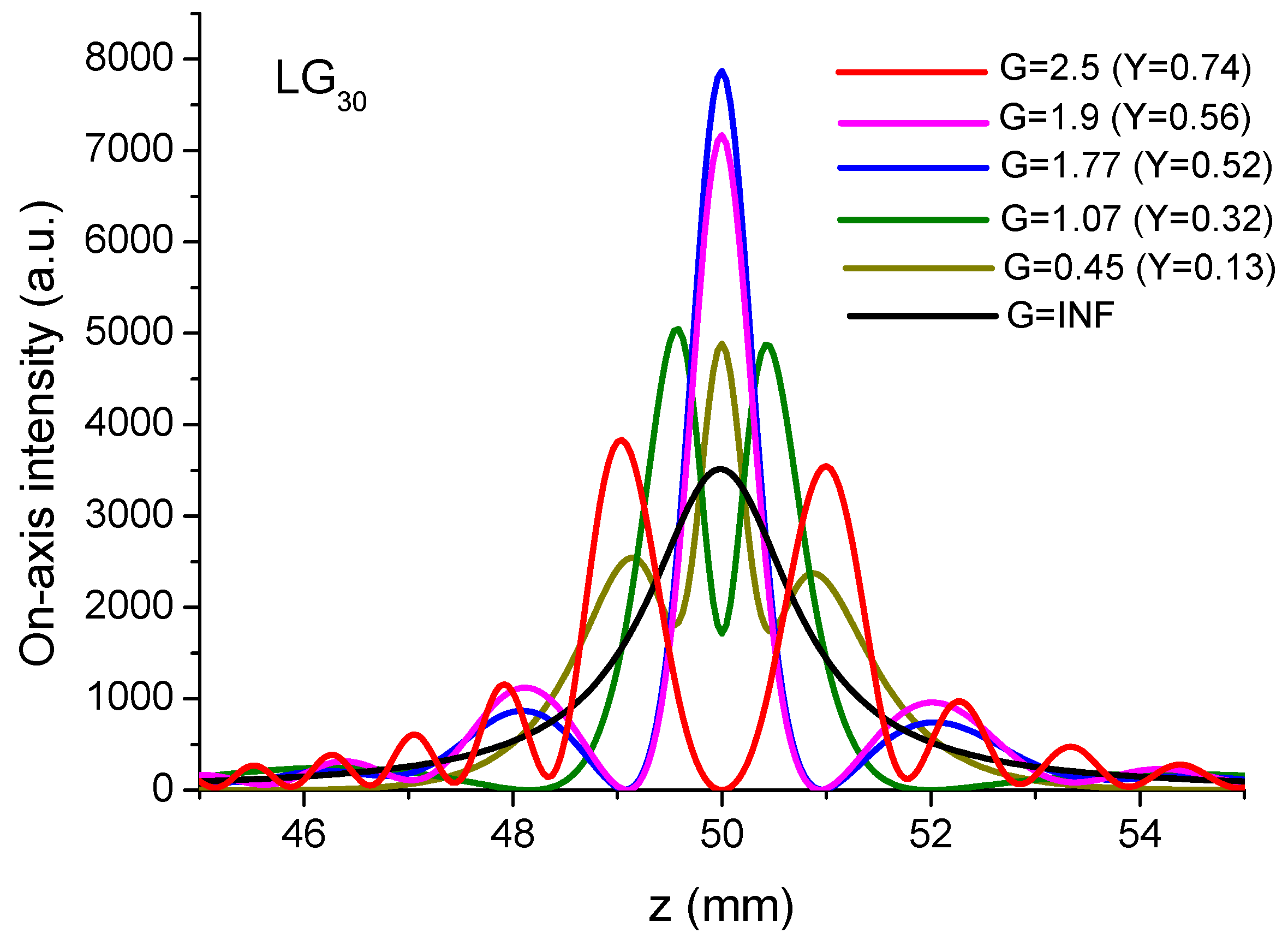
- P = 1 → max → G = 0.7 (zero of intensity)
- zero → G = 0.84
- p = 2 → min > 0 → G = 0.54 (1st zero)
- max → G = 1.31 (2nd zero)
- zero → G = 2.08
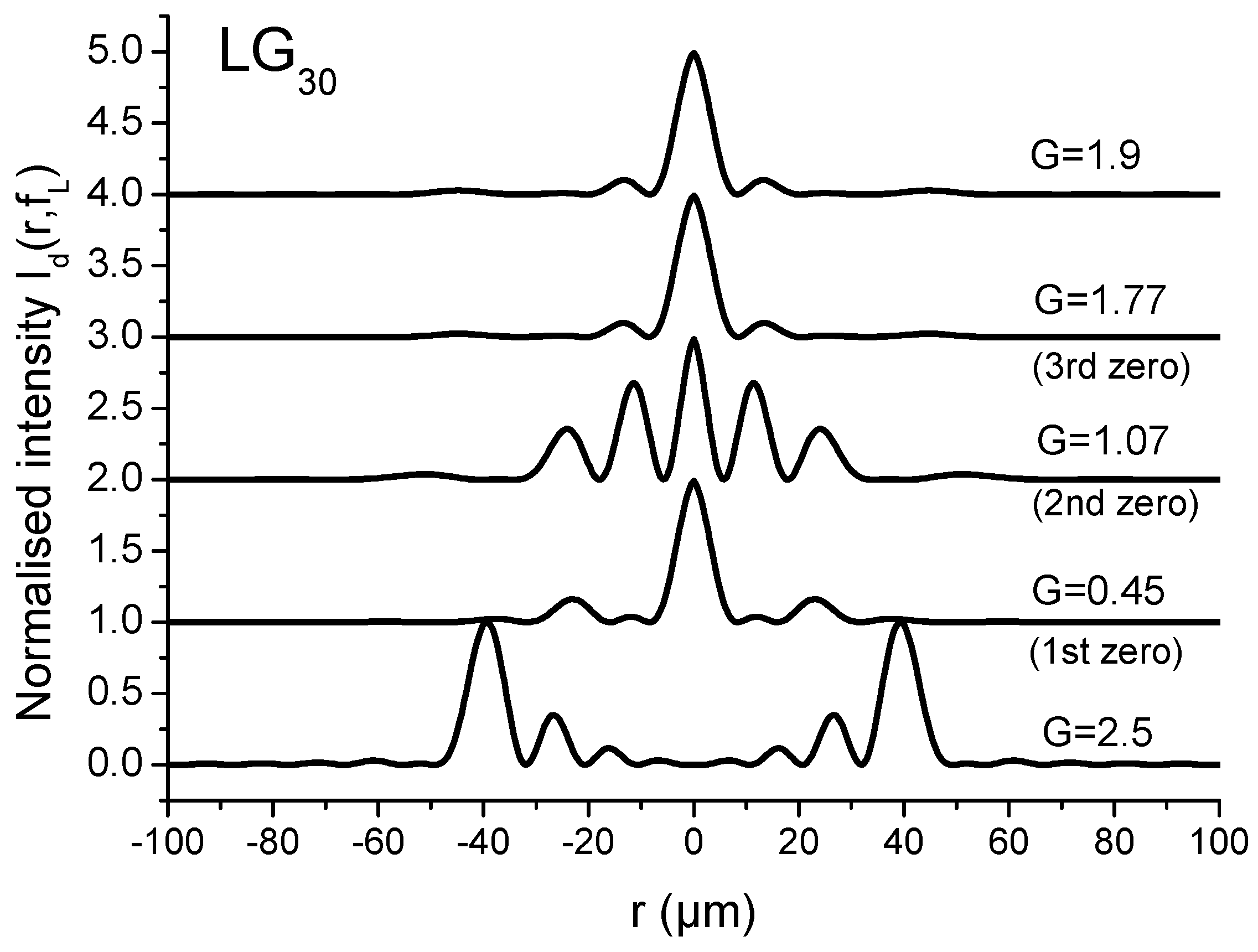
- p = 3 → max1 → G = 0.45 (1st zero)
- min > 0 → G = 1.06 (2nd zero)
- max2 → G = 1.77 (3rd zero)
- zero → G = 2.5
| p | Values of Ratio ρ/W for the Zeros of Intensity of LGp0 Mode | ||
|---|---|---|---|
| 1 | 0.707106 | ||
| 2 | 0.541195 | 1.306562 | |
| 3 | 0.455946 | 1.071046 | 1.773407 |
- (i)
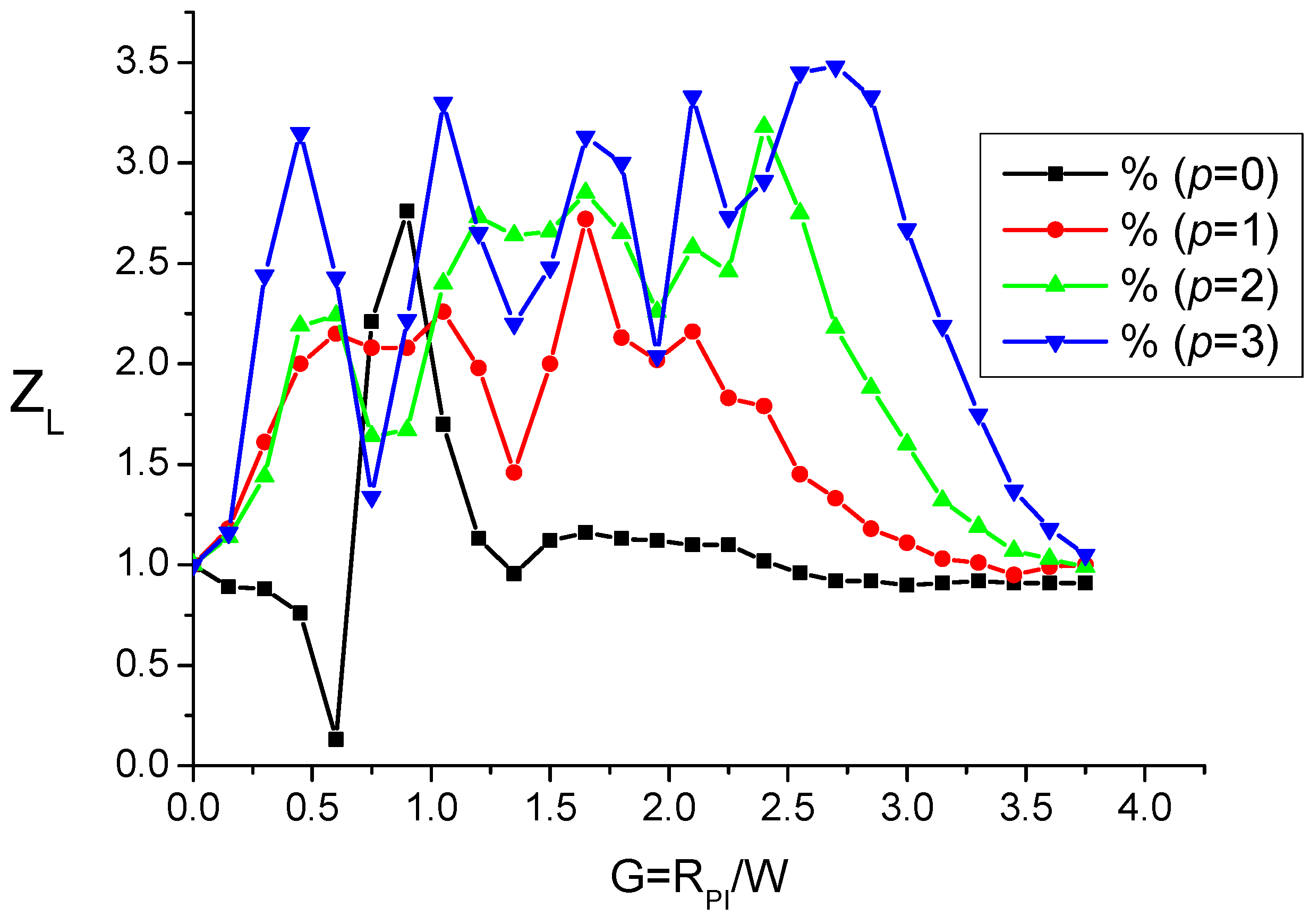
- For p = 0, it is seen that the performance of the tweezers is reduced since while it is boosted to about 2.5 for , for which the focused Gaussian beam is an optical bottle beam, as seen above, well adapted for trapping particles with lower refractive indexes than the surrounding medium.
- (ii)
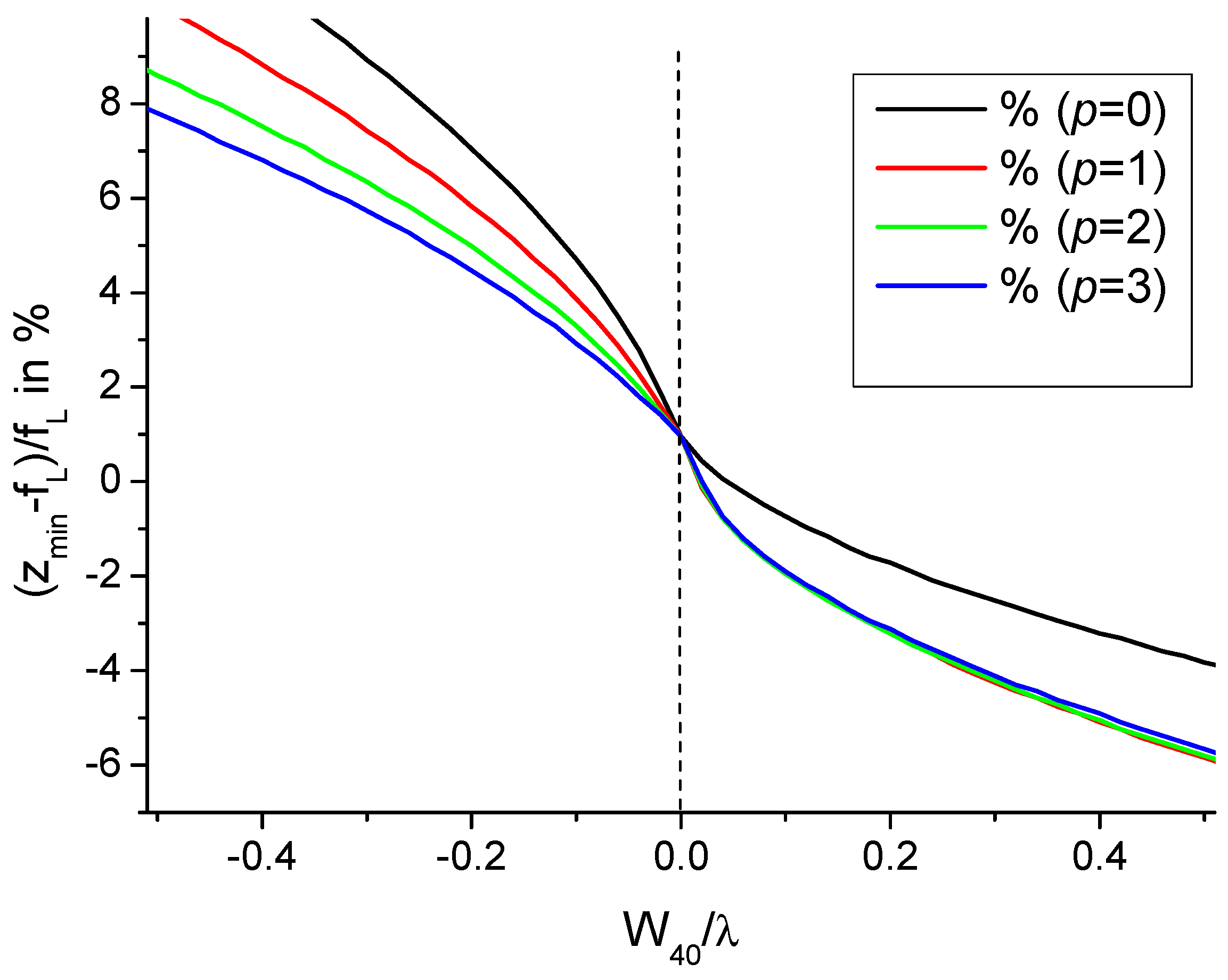
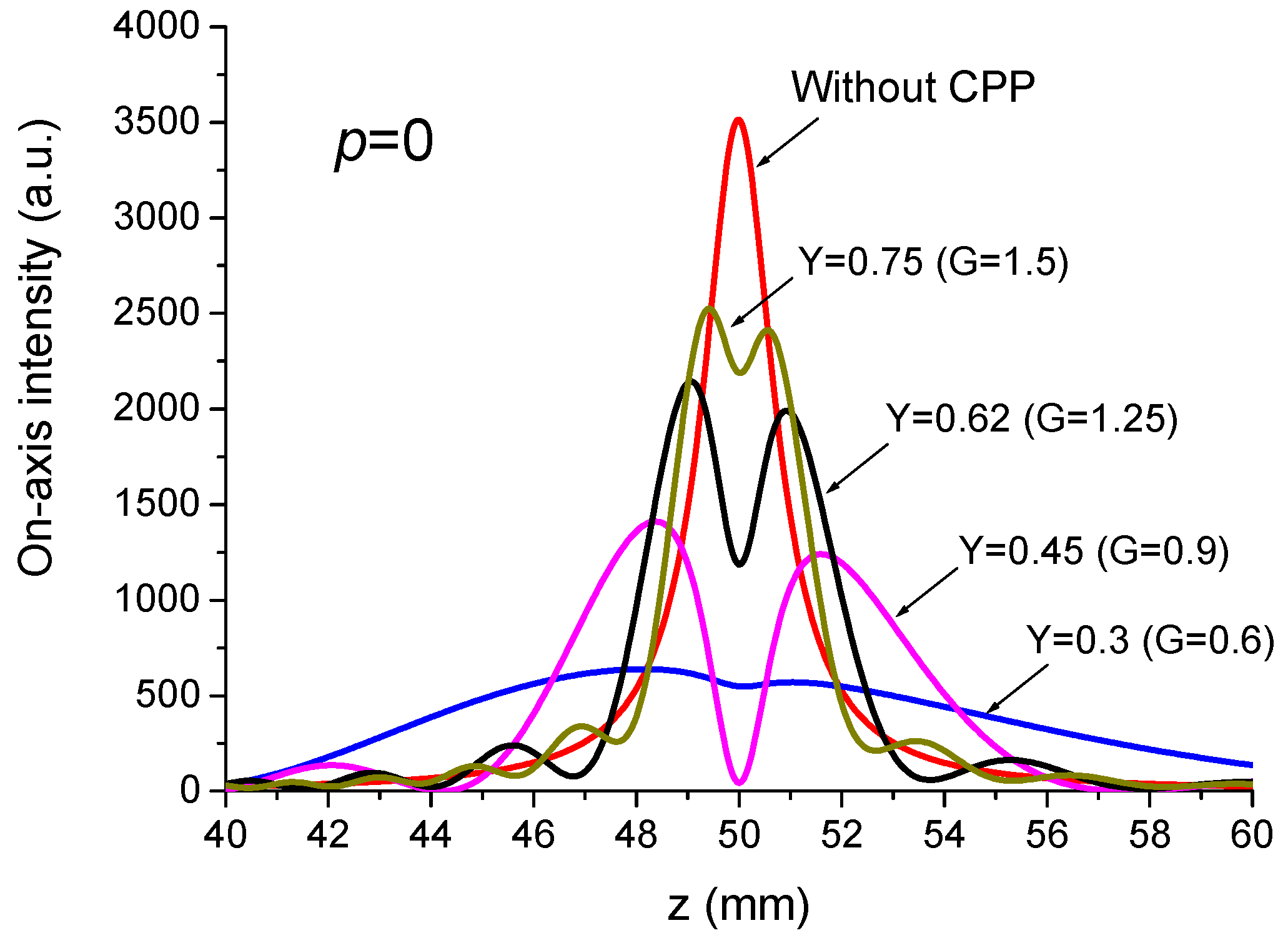
- For , it is seen that can reach a value in the range of 2.5 to 3.2 for particular values of ratio . By taking into account the plots in Figure 9, the improved values of can correspond to the situation of a single-lobed beam or of an OBB depending on the value of ratio . Consequently, it is necessary to envisage a possible adjusting of parameter G. This cannot be reasonably achieved by varying because the device is obtained from the etching of a piece of glass. Reasonably, we have to envisage the variation in parameter W for adjusting the value of the ratio for a given CPP as shown in Figure 13. Note that, by a simple longitudinal displacement, the CPP could allow to move from single-lobed-tweezers to OBB-tweezers while keeping, for instance, a Gaussian illumination.
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
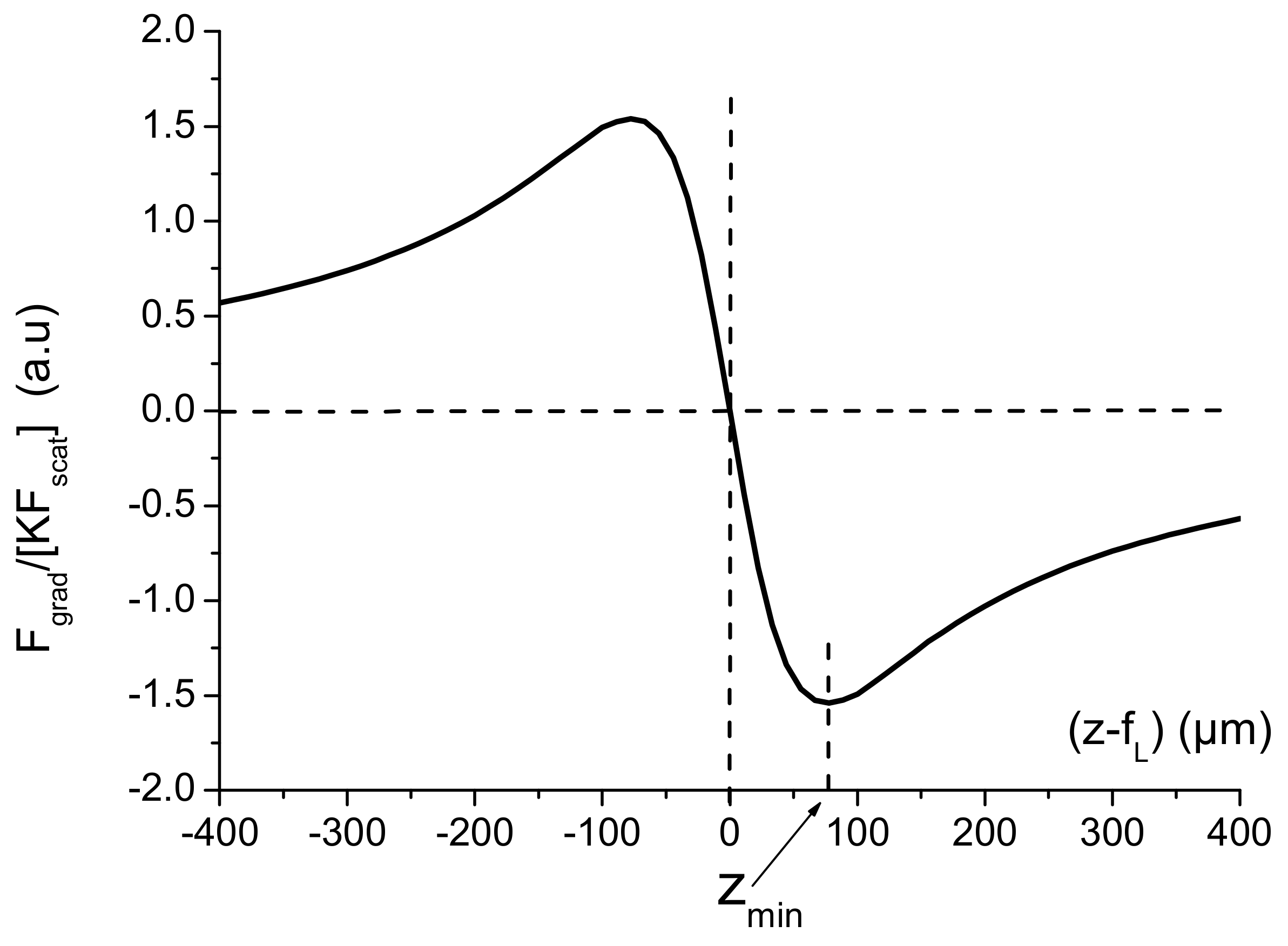
Appendix A. The Basics of Optical Tweezers

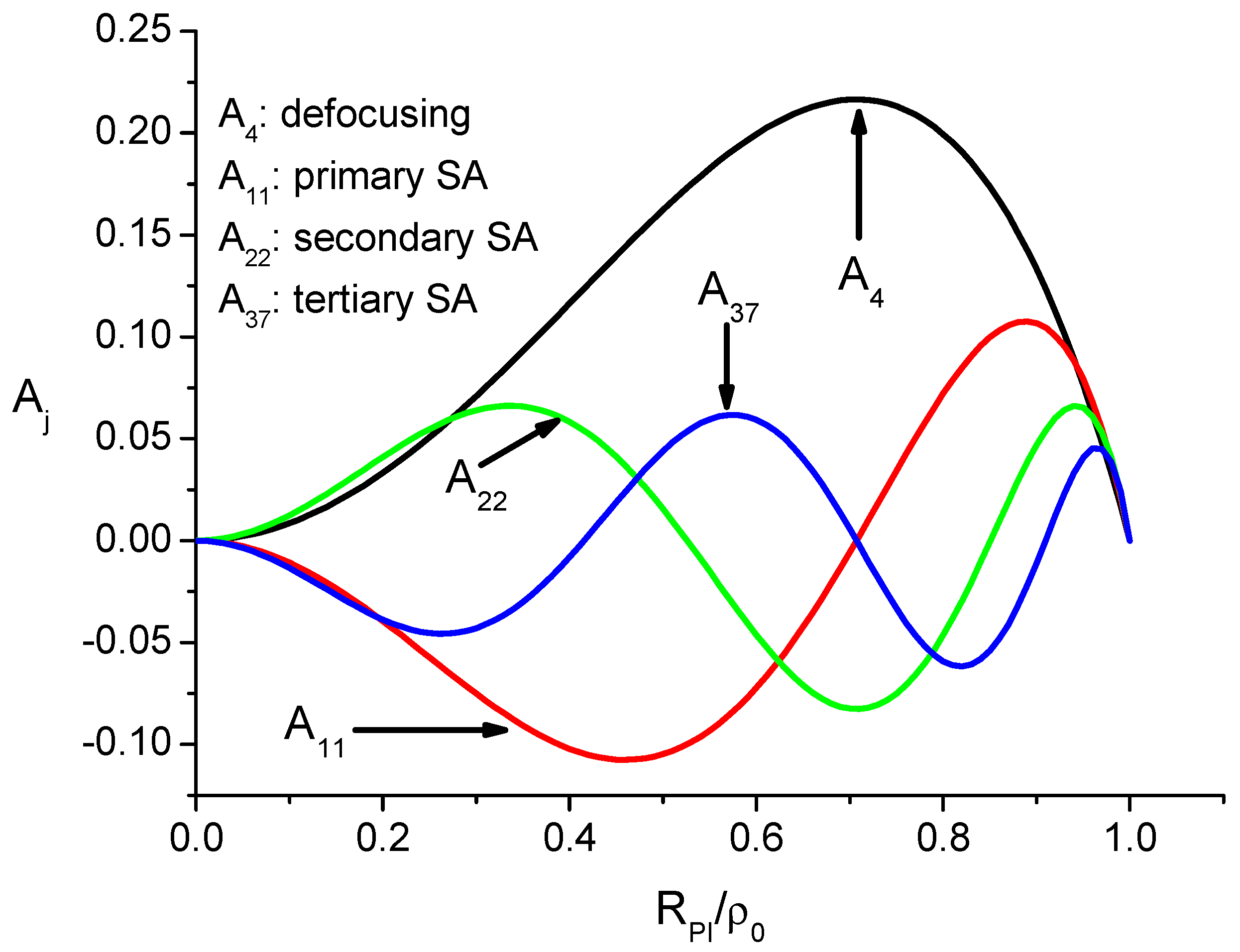
Appendix B. The Aberration Coefficients of the Circular Phase Plate
| J | Type of aberration | |
| 4 | Defocus | |
| 11 | Primary spherical | |
| 22 | Secondary spherical | |
| 37 | Tertiary spherical |

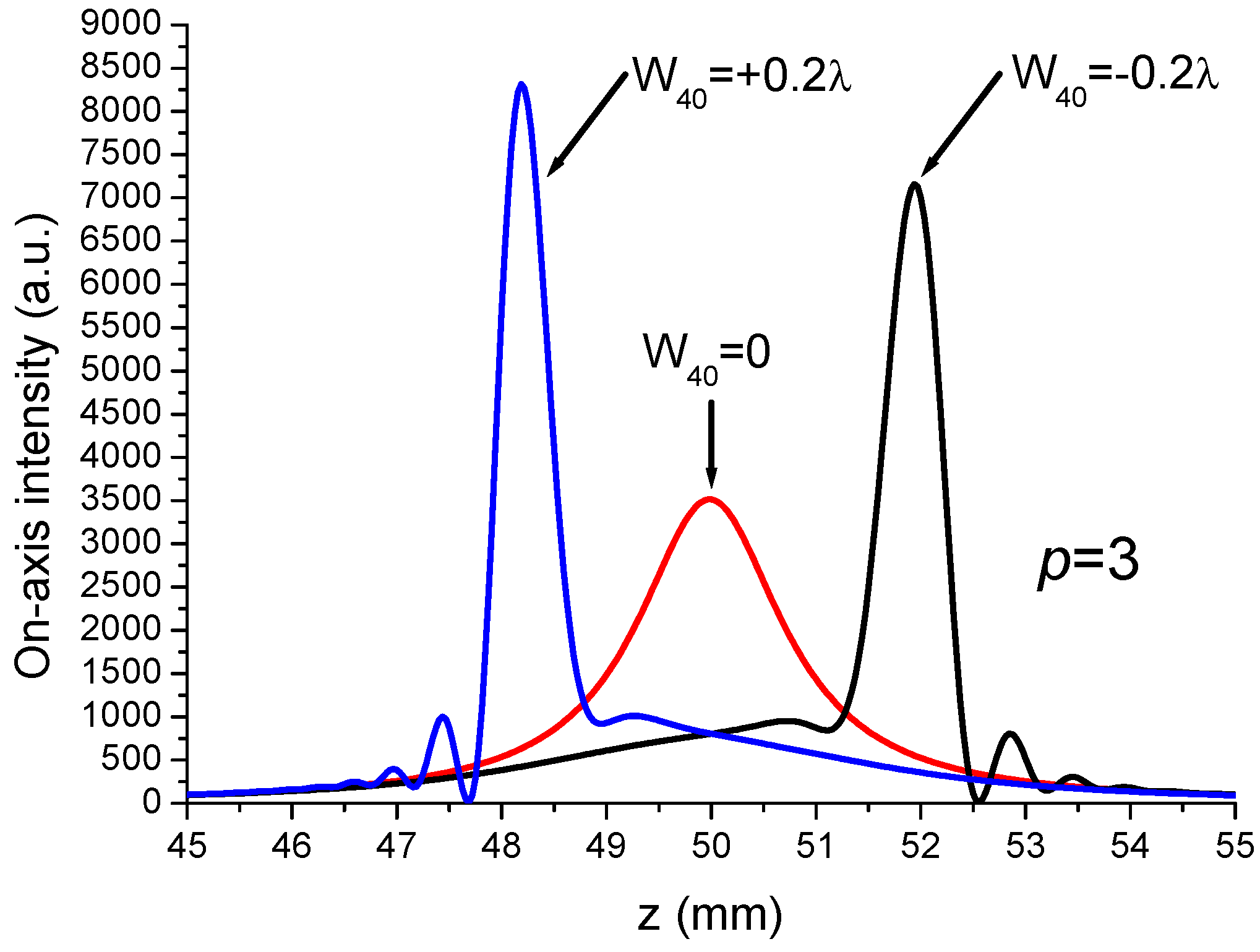
References
- Yoshida, A.; Asakura, T. Propagation and focusing of Gaussian laser beams beyond conventional diffraction limit. Opt. Commun. 1996, 123, 694–704. [Google Scholar] [CrossRef]
- Pu, J.; Zhang, H. Intensity distribution of Gaussian beams focused by a lens with spherical aberration. Opt. Commun. 1998, 151, 331–338. [Google Scholar] [CrossRef]
- Ait-Ameur, K.; Hasnaoui, A. Improving the longitudinal and radial forces of optical tweezers: A numerical study. Opt. Commun. 2024, 551, 130033. [Google Scholar] [CrossRef]
- Haddadi, S.; Ait-Ameur, K. Improvement of optical trapping effect by structuring the illuminating laser beam. Optik 2022, 25, 168439. [Google Scholar] [CrossRef]
- Quang, Q.H.; Doan, T.T.; Thanh, V.D.; Xuan, K.B.; Nguyen, L.L.; Manh, T.N. Nonlinear microscope objective using thin layer of organic dye for optical tweezers. Eur. Phys. J. D 2020, 74, 52. [Google Scholar] [CrossRef]
- Haddadi, S.; Ait-Ameur, K. Optical tweezers based on nonlinear focusing. Appl. Phys. B 2023, 129, 38. [Google Scholar] [CrossRef]
- Chai, H.S.; Wang, L.G. Improvement of optical trapping effect by using the focused high-order Laguerre-Gaussian beams. Micron 2012, 43, 887–892. [Google Scholar] [CrossRef] [PubMed]
- Neuman, K.; Block, S. Optical trapping. Rev. Sci. Instrum. 2004, 75, 2787–2809. [Google Scholar] [CrossRef] [PubMed]
- Ashkin, A. Acceleration and trapping of particles by radiation pressure. Phys. Rev. Lett. 1970, 24, 156–159. [Google Scholar] [CrossRef]
- Ashkin, A.; Dziedzic, J.M. Optical levitation by radiation pressure. Appl. Phys. Lett. 1971, 19, 282–285. [Google Scholar] [CrossRef]
- Harada, Y.; Asakura, T. Radiation forces on a dielectric sphere in the Rayleigh scattering regime. Opt. Commun. 1996, 124, 529–541. [Google Scholar] [CrossRef]
- Lang, M.J.; Block, S.M. Resource letter: LBOT-1: Laser-based optical tweezers. Am. J. Phys. 2003, 71, 201–215. [Google Scholar] [CrossRef]
- Dienerowitz, M.; Mazilu, M.; Dholakia, K. Optical manipulation of nanoparticles: A review. J. Nanophotonics 2008, 2, 021875. [Google Scholar] [CrossRef]
- Ota, T.; Sugiura, T.; Kawata, S.; Booth, M.J.; Neil, M.A.; Juskaitis, R.; Wilson, T. Enhancement of laser trapping force by spherical aberration correction using a deformable mirror. Jpn. J. Appl. Phys. 2003, 42, L701–L703. [Google Scholar] [CrossRef]
- Escobar, I.; Saavedra, G.; Martinez-Corral, M.; Lancis, J. Reduction of the spherical aberration effect in high-numerical-aperture optical scanning instruments. JOSA A 2006, 23, 3150–3155. [Google Scholar] [CrossRef]
- Nader, S.; Reihani, S.; Oddershede, L.B. Optimising immersion media refractive index improves optical trapping by compensating spherical aberrations. Opt. Lett. 2007, 32, 1998–2000. [Google Scholar]
- Zhong, M.C.; Wang, Z.Q.; Li, Y.M. Aberration compensation for optical trapping of cells within living mice. Appl. Opt. 2017, 56, 1972–1976. [Google Scholar] [CrossRef] [PubMed]
- Snyder, K.; Grier, D.G. Aberration compensation for enhanced holographic particle characterization. Opt. Express 2023, 31, 35200–35207. [Google Scholar] [CrossRef]
- Mafusire, C.; Forbes, A. Mean focal length of an aberrated lens. JOSA A 2011, 28, 1403–1409. [Google Scholar] [CrossRef]
- Bouzid, O.; Haddadi, S.; Fromager, M.; Cagniot, E.; Ferria, K.; Forbes, A.; Ait-Ameur, K. Focusing anomalies with binary diffractive optical elements. Appl. Opt. 2017, 56, 9735–9741. [Google Scholar] [CrossRef]
- Itoh, H.; Matsumoto, N.; Inoue, T. Spherical aberration correction suitable for a wavefront controller. Opt. Express 2009, 17, 14367–14373. [Google Scholar] [CrossRef]
- Theofanidou, E.; Wilson, L.; Hossack, W.J.; Arlt, J. Spherical aberration correction for optical tweezers. Opt. Commun. 2004, 236, 145–150. [Google Scholar] [CrossRef]
- Siegman, A.E. Analysis of laser beam quality degradation caused by quartic phase aberrations. Appl. Opt. 1993, 32, 5893–5901. [Google Scholar] [CrossRef]
- Mahajan, V.N. Zernike-Gauss polynomials and optical aberrations of systems with Gaussian pupils. Appl. Opt. 1995, 34, 8057–8059. [Google Scholar] [CrossRef]
- Mahajan, V.N. Zernike circle polynomials and optical aberrations of system with circular pupils. Appl. Opt. 1994, 33, 8121–8123. [Google Scholar] [CrossRef]
- Bourouis, R.; Ait-Ameur, K.; Ladjouze, H. Optimization of the Gaussian beam flattening using a phase plate. J. Mod. Opt. 1997, 44, 1417–1427. [Google Scholar] [CrossRef]
- Chaloupka, J.; Meyerhofer, D. Characterization of a tunable, single-beam ponderative-optical trap. JOSA B 2000, 17, 713–722. [Google Scholar] [CrossRef]
- Gahagan, K.T.; Swartzlander, G.A. Trapping of low-index microparticles in an optical vortex. JOSA B 1998, 15, 524–534. [Google Scholar] [CrossRef]
- Haddadi, S.; Fromager, M.; Louhibi, D.; Hasnaoui, A.; Harfouche, A.; Cagniot, E.; Ait-Ameur, K. Improving the intensity of a focused laser beam. In Proceedings of the SPIE LASE, Laser Resonators, Microresonators, and Beam Control XVII, San Francisco, CA, USA, 7–12 February 2015; Volume 9343, p. 93431R. [Google Scholar]
- Ait-Ameur, K. The advantages and disadvantages of using structured high-order but single Laguerre-Gauss LGp0 laser beams. Photonics 2024, 11, 217. [Google Scholar]
- Yang, Y.; Ren, Y.X.; Chen, M.; Arita, Y.; Rosales-Guzman, C. Optical trapping with structured light: A review. Adv. Photonics 2021, 3, 034001. [Google Scholar] [CrossRef]
- Forbes, A. Structured light from lasers. Las. Photon. Rev. 2019, 13, 1970043. [Google Scholar] [CrossRef]
- Forbes, A.; Oliveira, M.; Dennis, M.R. Structured Light. Nat. Photonics 2021, 15, 253–262. [Google Scholar] [CrossRef]
- Auyeung, R.C.Y.; Kim, H.; Mathews, S.; Piqué, A. Laser forward transfer using structured light. Opt. Express 2015, 23, 422–430. [Google Scholar] [CrossRef]
- Otte, E.; Denz, C. Optical trapping gets structure: Structured light for advanced optical manipulation. Appl. Phys. Rev. 2020, 7, 04108. [Google Scholar] [CrossRef]
- Häfner, T.; Strauβ, J.; Roider, C.; Heberle, J.; Schmidt, M. Tailored laser beam shaping for efficient and accurate microstructuring. Appl. Phys. A 2018, 124, 111. [Google Scholar] [CrossRef]
- Benstiti, A.; Bencheikh, A.; Ferria, K.; Chabou, S.; Boumeddine, O.C. Gaussian laser beam structuring using acousto-optic effect: A parametric characterization. Appl. Phys. B 2022, 128, 141. [Google Scholar] [CrossRef]
- Ando, T.; Ohtake, Y.; Matsumoto, N.; Inove, T.; Fukuchi, N. Mode purities of Laguerre-Gaussian beams generated via complex-amplitude modulation using phase-only spatial light modulators. Opt. Lett. 2009, 34, 34–36. [Google Scholar] [CrossRef] [PubMed]
- Huang, B.; Li, Q.; Yang, L.; Zhao, C.; Wen, S. Controlled higher-order transverse mode conversion from a fiber laser by polarization manipulation. J. Opt. 2018, 20, 024016. [Google Scholar] [CrossRef]
- Hu, A.; Lei, J.; Chen, P.; Wang, Y.; Li, S. Numerical investigation on the generation of high-order Laguerre-Gaussian beams in end-pumped solid-state lasers by introducing loss control. Appl. Opt. 2014, 53, 7845–7853. [Google Scholar] [CrossRef]
- Ishaaya, A.A.; Davidson, N.; Friesem, A.A. Very high-order pure Laguerre-Gaussian mode selection in a passive Q-switched Nd:YAG laser. Opt. Express 2005, 13, 4952–4962. [Google Scholar] [CrossRef]
- Huang, Y.J.; Chiang, P.Y.; Liang, H.C.; Su, K.W.; Chen, Y.F. High power Q-switched laser with high-order Laguerre-Gaussian modes: Application for extra-cavity harmonic generations. Appl. Phys. B 2011, 105, 385–390. [Google Scholar] [CrossRef]
- Dong, J.; Bai, S.C.; Liu, S.H.; Ueda, K.I.; Kaminskii, A.A. A high repetition rate passively Q-switched microchip laser for controllable transverse laser modes. J. Opt. 2016, 18, 055205. [Google Scholar] [CrossRef]
- Machavariani, G. Effect of phase imperfections on higher-mode selection with intracavity phase elements. Appl. Opt. 2004, 43, 6328–6333. [Google Scholar] [CrossRef] [PubMed]
- Senatsky, Y.; Bisson, J.-F.; Li, J.; Shirakawa, A. Laguerre-Gaussian modes selection in diode-pumped solid-state lasers. Opt. Rev. 2012, 19, 201–221. [Google Scholar] [CrossRef]
- Ashkin, A.; Dziedzic, J.M.; Bjorkholm, J.E.; Chu, S. Observation of a single-beam gradient force optical trap for dielectric particles. Opt. Lett. 1986, 11, 288–290. [Google Scholar] [CrossRef]


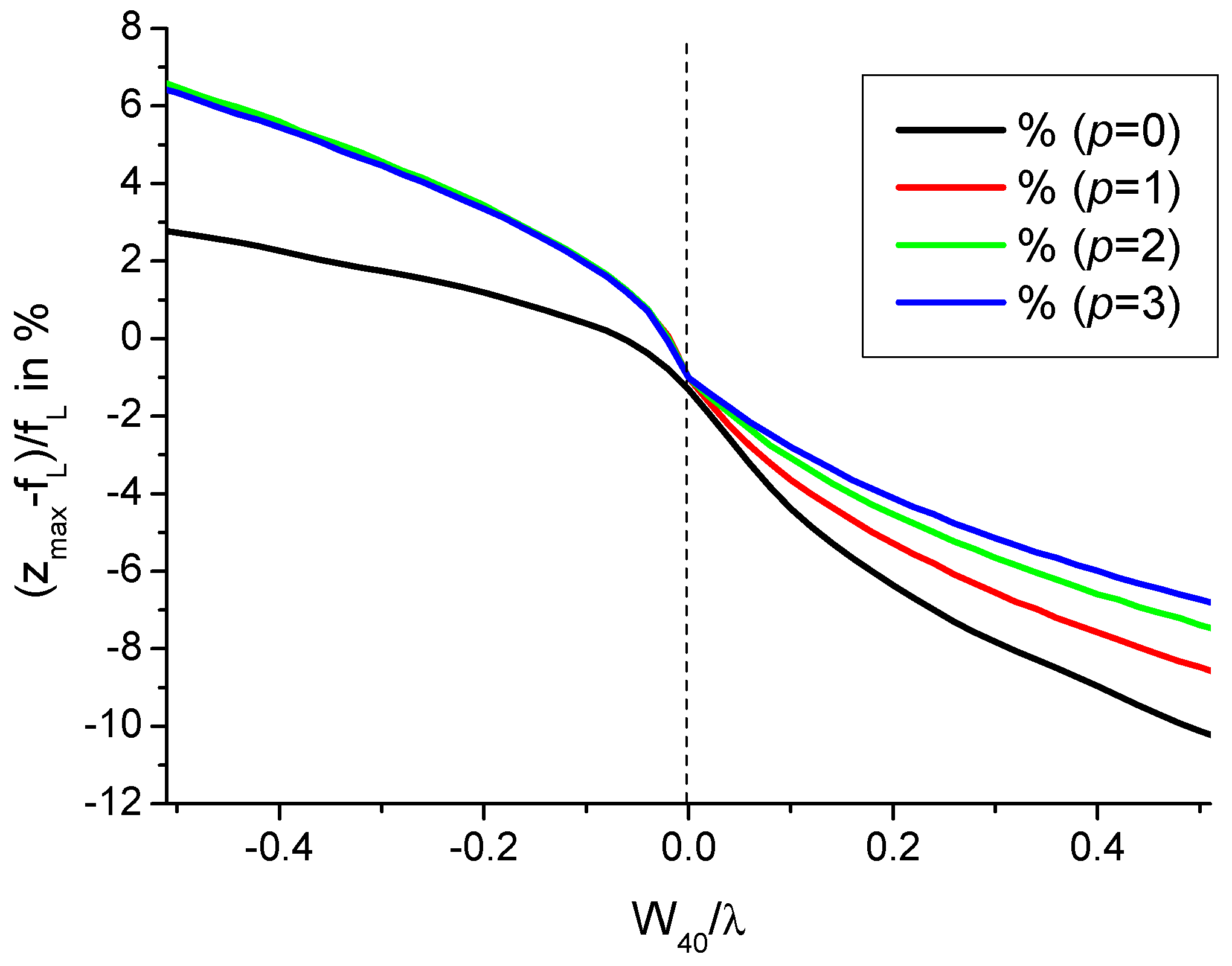


| p | 0 | 1 | 2 | 3 |
|---|---|---|---|---|
| 2 W | 2.55 W | 3 W | 3.35 W |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Aït-Ameur, K.; Hasnaoui, A. Improving the Performances of Optical Tweezers by Using Simple Binary Diffractive Optics. Photonics 2024, 11, 744. https://doi.org/10.3390/photonics11080744
Aït-Ameur K, Hasnaoui A. Improving the Performances of Optical Tweezers by Using Simple Binary Diffractive Optics. Photonics. 2024; 11(8):744. https://doi.org/10.3390/photonics11080744
Chicago/Turabian StyleAït-Ameur, Kamel, and Abdelkrim Hasnaoui. 2024. "Improving the Performances of Optical Tweezers by Using Simple Binary Diffractive Optics" Photonics 11, no. 8: 744. https://doi.org/10.3390/photonics11080744
APA StyleAït-Ameur, K., & Hasnaoui, A. (2024). Improving the Performances of Optical Tweezers by Using Simple Binary Diffractive Optics. Photonics, 11(8), 744. https://doi.org/10.3390/photonics11080744





