Abstract
A new vibration-based mechanism of optical frequency/wavelength sweeping in fiber lasers induced by optical path length modulation of a laser cavity section is proposed. The mechanism is implemented for an erbium-doped fiber ring laser with a saturable absorber. Without the vibrations, the laser generates a single longitudinal mode (SLM) radiation. We show experimentally for the first time that mechanical vibrations of the laser cavity section can lead to mode dynamics in both frequency and time domains. The possibility of obtaining various mode dynamics, such as vibration-induced sweeping in a wavelength range of up to 2.2 nm or SLM generation with periodic mode hopping between two fixed longitudinal modes depending on the pump wavelength, is experimentally shown. In this vibration-based approach, the interval between changes in the laser cavity modes has good stability, because it directly relates to the vibration period.
1. Introduction
The development of lasers is an important task due to their high practical value in various areas of human activity. One of their important characteristics is the possibility to tune the optical frequency/lasing wavelength. Such lasers are called tunable. To implement this possibility, various electrically or manually controlled spectral selectors, such as tunable fiber Bragg gratings (FBGs), bulk diffraction gratings or interference filters, are used in most cases. However, these optical elements are quite expensive. One of the alternatives is to use physical effects of lasing mode competition. For example, the spatial hole burning (SHB) effect is associated with inhomogeneous gain saturation along the fiber length under the influence of a narrowband standing wave radiation formed in the laser cavity. These inhomogeneities have a period equal to half of the wavelength and are also associated with populational inhomogeneities called dynamic population gratings (DPGs). Unlike conventional static FBGs, DPGs have a relatively short lifetime (from fractions of to a dozen milliseconds) associated with finite lifetime of the upper laser level. It is known that a typical spectral width of periodic structures decreases when their length increases. In fiber lasers, DPGs are formed along the entire length of the active fiber, which can be up to units or even several tens of meters. Therefore, DPGs have high spectral selectivity down to several MHz. As a result, DPGs can play the role of fine spectral selectors allowing selection of individual longitudinal modes of the laser cavity. Note that DPG can be formed in both absorbing and amplifying media. In the former case, DPG leads to stabilization of single-frequency lasing and, in the latter case, to the initiation of a jump in the generated mode and tuning the laser frequency [1]. A regular sequence of generated mode hops is called a self-induced wavelength/optical frequency sweeping effect (self-sweeping effect for short). The development of fiber self-sweeping lasers is described in detail in reviews [1,2]. In addition to these reviews and references therein, we would like to add [3] published in 2005, one of the earliest works on self-sweeping fiber lasers which mentioned an observation of lasing line drift at a constant rate in one direction with rapid jump back. This behavior is typical for ordinary self-sweeping lasers. The authors observed the self-sweeping effect in a ring laser based on ytterbium-doped photonic crystal fiber.
The operation of a typical self-sweeping laser is described as the generation of a sequence of pulses, each of which consists of a few longitudinal modes of the cavity. In a limiting case, single-mode pulses can be generated. In this case, the laser radiation consists of the so-called “mode pulses”. The mode composition of each pulse, as well as the frequency difference between neighboring pulses, is determined by the properties of the DPG formed by the previous pulses. In the case of a large number of pulses, the process of mode hopping looks like tuning the laser wavelength. Some self-sweeping fiber lasers generating the mode pulses mentioned above have a number of advantages, such as a wide tuning range (up to 26 nm in [4]), the capability to generate single-frequency radiation with linewidth less than 1 MHz at each pulse [5], and discreteness of laser frequency change. However, such lasers also have some drawbacks. Although successive pulses are discrete in the frequency domain, they exhibit noticeable irregularity in the time domain (i.e., repetition rate and/or pulse duration). It may be assumed that this irregularity results from the influence of random uncontrolled processes (for example, thermal fluctuations or sound vibrations) on laser generation. As a result, this drawback complicates the use of such lasers in a number of applications [1]. One of the solutions requires the direct measurement of intensity dynamics with high sampling rate and to use these data for further processing (see, for example, [6]). High sampling rate and a long duration of a single sweeping scan (up to several tens of seconds) result in large data sets which require significant computing resources for mathematical processing. Moreover, implementation of this approach in a practical device also requires some individual adjustments of the measurement unit parameters based on the laser pulses characteristics (duration, duty cycle, etc.).
In this work, we propose a technique to stabilize the mode-hopping period in an SLM fiber laser by influencing a cavity element periodically. The technique is aimed at mode-hopping control by using optical path oscillations in the laser cavity element. To demonstrate the method, we use an erbium-doped fiber (EDF) ring laser with continuous-wave (CW) intensity dynamics [5]. We experimentally show for the first time that mechanical vibrations of a section of a passive fiber in such lasers can result in regular modal dynamics in both frequency and time domains. The mechanism of vibration-induced sweeping is based on small oscillations in the spectrum position of a composite reflector formed by an amplifying fiber loop mirror and a DPG, which occur because of slight modulation of the optical path length. At that, sweeping is absent without vibrations, but vibration-induced oscillations of the spectral position of the DPG-based selector initiate the mode-hopping process. In this approach, the time period of the mode hops is locked to the vibration period. In addition, experiments show that the mode dynamics in the EDF laser is sensitive to the pump wavelength. When the laser is pumped with short-wave radiation (1548 nm, which is characterized by strong absorption in the active medium), each mode hop is characterized by a successive decrease in the optical frequency by one free spectral range (FSR) of the laser cavity. In this case, linear wavelength sweeping is observed over a long time interval in an upward direction. When the laser is pumped with longer wavelength radiation (1564 nm, which is characterized by lower absorption), the direction of the frequency hop changes after every mode hop. In this case, long-term optical frequency dynamics look like optical frequency stabilization.
We believe that the results of our research are useful not only for the development of self-sweeping lasers [1,2] but also for the ones generating single longitudinal mode (SLM) radiation [7]. It is well known that one of the undesirable effects in SLM lasers is mode hopping which in most cases is uncontrollable [8]. The proposed method allows control of the mode-hopping process with external vibration. So, our research gives information about mode hopping, which can be useful for stable SLM generation.
2. Experiment
The scheme of the vibration-induced sweeping Er-doped fiber (EDF) laser based on polarization-maintaining (PM) components is shown in Figure 1. A similar scheme was proposed in our previous work [5]. To describe the laser operation, it is convenient to divide the laser cavity structure into linear and ring parts which are separated from each other by the central coupler with a coupling ratio of 20/80. The ring part is an amplifying fiber loop mirror (AFLM) which includes the central coupler, a reflective wavelength division multiplexer (RWDM), PM Er-doped fiber (EDF-1) and a polarizing fiber (PZF). PM EDF-1 (IXF-EDF-HD-PM, iXblue Photonics, Besançon, France), 9.6 m long with high core absorption of about 83 dB/m at 1530 nm wavelength, is used as the gain medium. To obtain lasing in the L-band telecom spectral range, a sufficiently long highly erbium-doped EDF-1 fiber is used. The PM EDF-1 is pumped with a tunable laser source based on the master oscillator power amplifier (MOPA) configuration. We use a homemade cladding-pumped erbium-doped fiber amplifier. The amplifier includes a multimode diode, a pump and signal combiner, 2 m of erbium-doped fiber, two optical isolators and a coupler (the latter was used to control the power at the output of the amplifier). It is worth noting that frequency sweeping is not related to the amplifier, because an isolator has been added to the amplifier output. The tunable master oscillator seed radiation generated by a laser diode can be tuned from 1530 to 1565 nm. Only two pump wavelengths—1548 and 1564 nm—are used in the experiments. These two characteristic wavelengths have significantly different EDF absorption, which considerably influences the EDF laser output parameters. The power of the seed radiation can be increased at maximum to about 1 W in an additional PM EDF amplifier. The pump radiation was coupled to the PM EDF-1 through a reflective port of a 1540/1610 RWDM (LightComm, Shenzhen, China). PZF (HB1550Z, Fibercore, Southampton, UK), 2.3 m long, which was used to select one of polarization states. The radiation passed through the PZF and entered the central coupler. The linear part of the cavity consists of another 1.4 m long active PM EDF, PM EDF-2, (ER35-7-PM-Coractive, Québec, QC, Canada), with reduced core absorption of about 24 dB/m at a wavelength of 1530 nm and a fiber loop mirror (FLM). The FLM reflectance of ~90% was limited by internal excess losses in the 50/50 PM fiber coupler used here. An optical isolator is used at the laser output to eliminate the influence of unwanted reflections from measuring instruments on the laser generation dynamics.
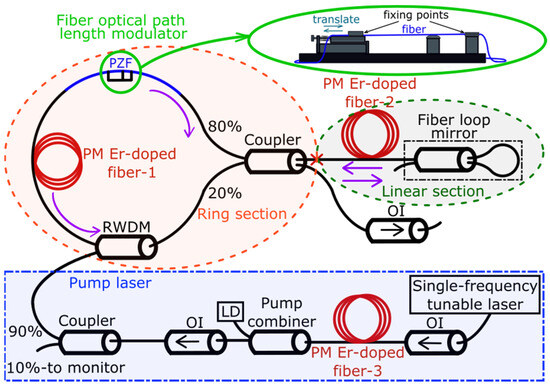
Figure 1.
The scheme of the ring EDF laser. Pink and black arrows indicate direction of generated radiation propagation in the laser and through optical isolators (OI-1, OI-2, OI-3), respectively.
Compared to our previous laser [5], the following changes were made: (1) the reflectance of FLM was increased from ~80 to ~90% by replacing the coupler, (2) the coupling ratio of the central coupler was decreased from 30/70 to 20/80, (3) the length of PZF was increased from 0.8 m to 2.3 m, (4) the length of PM EDF-2 was slightly decreased from 1.8 m to 1.4 m. These changes are aimed at improving the output parameters of the EDF laser (increasing the output power, as well as increasing the ratio of the SLM lasing duration and switching time between the generated modes).
Long-term spectral dynamics were analyzed using a wavelength meter (WS6-200, Angstrom/HighFinesse, Novosibirsk, Russia/Tübingen, Germany), allowing us to make up to 1000 measurements per second. The process of changing the generated frequency was recorded using the heterodyning method [9]. The output radiation of the EDF laser was mixed with the radiation of the reference single-frequency laser (TSL770, Santec, Komaki, Japan) in a fiber coupler. The intensity dynamics of generated radiation and the dynamics of heterodyne signals were measured with fast photodetectors and recorded with a digital oscilloscope (DS6104, Rigol, Suzhou, China) with 1 GHz bandwidth. The beat signal was further analyzed with fast Fourier transform in the frequency range from 100 to 500 MHz.
Taking into account previous works [1,5], we expected self-sweeping operation with long mode pulses. In such a laser, the linear part is used for rough frequency selection, and the ring part is used for switching to the next laser cavity longitudinal mode during the self-sweeping process. However, the results show that the described fiber laser generates stable radiation in a single longitudinal mode (SLM) regime of about 1608 nm in wavelength without any self-sweeping operation. At the same time, it was found that sweeping wavelength dynamics can be observed with the abovementioned wavelength meter when a mechanical strain is applied to the section of the laser cavity passive fiber. We used a micro-translation stage (MTS) to create a controllable strain in the section of the passive fiber. A section of PZF about 24 cm long was used as the passive fiber for certainty only (similar results presented below can be obtained with other passive fibers in the ring part of the cavity). We will call a mechanical setup for stretching the fiber the fiber optical path length modulator (FOPLM). A sketch of the FOPLM is shown in the inset to Figure 1. It has a relatively complicated construction. For example, the fiber has an additional support between fixing points. As is shown later, the system is a mechanical cavity similar to an oscillating string. The FOPLM allowed us to observe transition between the SLM stabilization and the wavelength sweeping regimes and back to the stabilization by adjusting the strain of the passive fiber. Let us describe in more detail the influence of the strains on the laser operating regime at different pump wavelengths.
3. Results
3.1. Pumping at 1548 nm Wavelength
First, we carried out measurements not applying any tension to the abovementioned section of the PZF installed inside FOPLM. The laser generates the stabilized SLM radiation with a wavelength of about 1607.8 nm (demonstrated in Figure 2a) with an output power of 4.5 mW. The SLM lasing is confirmed with wavelength monitoring, as well as with the absence of any fast-intensity modulation observed at the laser output. The generation wavelength can be changed in the range from 1607 to 1609 nm by influencing the cavity elements, for example, by creating tension on part of the active or passive fibers.
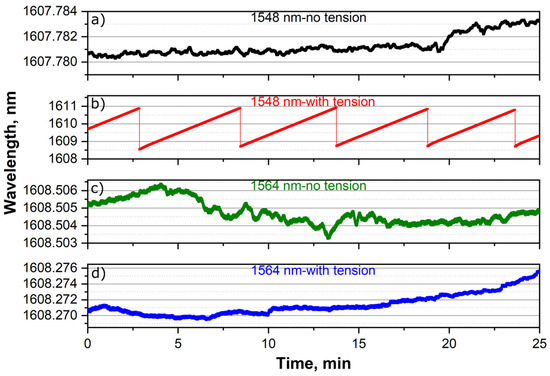
Figure 2.
Lasing wavelength dynamics measured at pumping wavelength of 1548 nm (a) without tension and (b) with tension and at a pump wavelength of 1564 nm (c) without tension and (d) with tension.
The appearance of fast-intensity modulation could be observed when we stretched the section of the PZF installed in FOPLM. One should note that the generated power was not affected considerably by the stretching. Typical dependence of the output power on the pump is shown in Figure 3 by blue squares and circles. Hysteresis in the output power is typical near the lasing threshold for such lasers with saturable absorbers. As the pump power increases (blue circles), laser generation begins at the upper pump power threshold of ~450 mW. In this case, the output power level increases abruptly to 5.3 mW. The output power increases linearly with the pump up to ~7.3 mW at pump power of 490 mW. The output power reduces linearly down to ~1.5 mW (see blue squares in Figure 3) with reducing the pump to the lower threshold of ~400 mW. The generation wavelength sweeping was observed in the laser in the hysteresis region. The largest sweeping range of 2.2 nm was observed at the output power of 4.5 mW (see Figure 2b). In this case the sweeping rate was 7 pm/s.
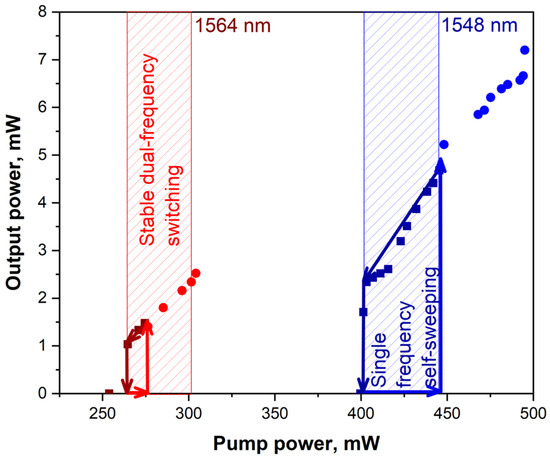
Figure 3.
Dependence of the output power on pump power for representative tension settings at pump wavelength of 1564 and 1548 nm shown by red and blue symbols, respectively. The direction of the arrows corresponds to the direction of power change.
The typical intensity dynamics measured with a digital oscilloscope (CW signal with periodical bursts) is presented in Figure 4a. A heterodyne signal was also measured synchronously. The result of the heterodyning signal processing is presented in Figure 4b. Comparison of Figure 4a,b shows that periods of CW lasing with a duration of ~10 ms correspond to SLM radiation. At the same time, the intensity burst corresponds to moments of mode hopping. In this case, the value of the optical frequency jump corresponds to one free spectral range (FSR) of the cavity of ~10 MHz. It can be seen that hopping occurs in one direction, which indicates sweeping of optical frequency. Also, compared to our previous work [5], the stability of the duration of single-frequency generation has been improved. The SLM duration varies from the generation of one longitudinal mode to another by approximately 10%, and in [5] the duration fluctuated by approximately two times. The full sweeping range of 2.2 nm (demonstrated in Figure 2b) corresponds to ~3100 regular mode hops.
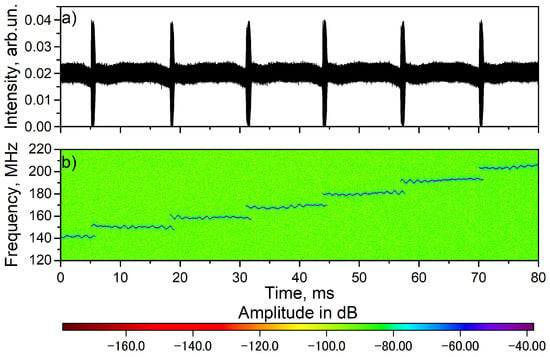
Figure 4.
(a) Intensity dynamics and (b) spectrogram of a heterodyne signal for laser pumped at wavelength of 1548 nm.
3.2. Pump Wavelength of 1564 nm
Similar experiments were carried out for another pump wavelength of 1564 nm. In this case the laser also generates stabilized SLM at about a 1608.6 nm (demonstrated in Figure 2c) wavelength measured at the output power of 1.5 mW not applying any tension with the FOPLM. The pump dependence of the output power also has the hysteresis character (red circles and squares in Figure 3 for increasing and decreasing the pump, respectively). In this case both thresholds decreased significantly—from 450 to 275 mW and from 400 to 262 mW for upper and lower thresholds, respectively. The pump has lower absorption, and population inversion is more uniform (with lower maximum inversion value) along the active fiber length as compared with pumping at shorter wavelengths. Reduction of maximum population inversion values results in lower excited state absorption losses which are important for EDF lasers. Reduction of the losses leads in turn to reduction of the pump thresholds. In contrast to the case of shorter pump wavelength, where sweeping operation was demonstrated under tension, stabilization of lasing wavelength is observed in this case at pump powers ranging from 265 to 300 mW. A typical example of the lasing wavelength stabilization at about 1608 nm is shown in Figure 2d, measured at the output power of 1.5 mW. The results show that the generation wavelength practically does not change for the pump wavelength of 1564 nm. However, in contrast to the regime of SLM stabilization, characteristic bursts in intensity dynamics are observed (see Figure 5a). The results of heterodyne signal processing shown in Figure 5b demonstrate that each intensity burst corresponds to a mode hopping by the same value in a forward or backward direction, and each new jump alternates its direction. Thus, the regular change in the direction of the jump leads to the absence of a significant change in wavelength even during a large period of time of ~25 min (see Figure 2d). It should be noted that small-scale kilohertz temporal modulation of optical frequency (with its amplitude up to a few megahertz) observed in Figure 4b and Figure 5b is associated with the operation of the stabilization circuit of the heterodyne laser. It can also be noted that the bursts appeared approximately two times more frequently than at the other pump wavelength of 1548 nm (the repetition period is close to 6 ms instead of 12 ms).
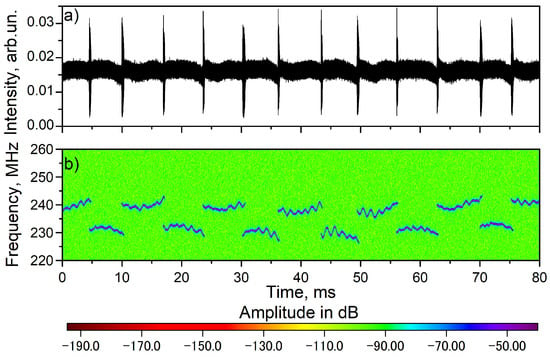
Figure 5.
(a) Intensity dynamics and (b) spectrogram of a heterodyne signal for laser pumped at wavelength of 1564 nm.
4. Discussion
Thus, our research demonstrates that, without tension of the PZF, the laser operates in the SLM regime, regardless of the pump wavelength. Tension of the PZF results in regular dynamics in both intensity and optical frequency. Moreover, the use of a short-wavelength pump with high absorption in the active fiber leads to a gradual decrease in the optical frequency by a fixed value, and the use of longer-wavelength pumping leads to periodic optical frequency hops with alternating direction after each new hop, but also by the same fixed frequency hop value (see Figure 4b and Figure 5b, respectively). This behavior of the optical frequency measured as long-term wavelength dynamics looks like either wavelength self-sweeping or wavelength stabilization (Figure 2b,d, respectively).
We think that our FOPLM do not change optical fiber length from one static value to another by changing the position of the translation stage, but it behaves like an ordinary guitar string. The main result of the tension change is associated with shifting position of the vibration resonance in the FOPLM. The FOPLM is a mechanical cavity with tunable eigenfrequencies. So, tension of the fiber inside the FOPLM changes the resonant frequency but does not create oscillations in the cavity. During the experiments, it was discovered that vibrations were produced by a power supply used for an EDF amplifier in the MOPA pump laser and located on the same table with other parts of the fiber laser cavity. It has been experimentally confirmed that vibration isolation of the power supply suppresses the laser frequency dynamics. Thus, the periodicity of the optical frequency change is determined by the mechanical resonance in the power supply, and the tension of the PZF placed inside the FOPLM only shifts the position of the mechanical resonance closer to or further from the frequency of the driving force (vibration frequency of the power supply). Since we did not control the vibration frequency of the power supply (because it is determined by its design), we could only control the amplitude of the vibrations (fiber optical path length modulations) with PZF stretching (moving FOPLM resonance closer to or further from the vibration frequency). As a result the frequency of the mode hops in the experiments also turned out to be fixed (the average period of mode hops was ~12.6 ms).
One should note that oscillations of the PZF length also led to a corresponding modulation of the fiber laser cavity length. The result of the latter modulation can be noted in Figure 4b and Figure 5b, where, besides kilohertz modulation associated with operation of the stabilization circuit of the heterodyne laser, additional slow modulation can be noted with a period of ~13 ms. To make these slow modulations in Figure 4b and Figure 5b more obvious, we reconstructed the temporal dependence of the lasing beat frequency in terms of the single cavity mode oscillations in Figure 6a,c, respectively. Let us consider the reconstruction using Figure 6c. The black curve shows the original beat signal presented in Figure 5b. The blue curve is generated from the black one by adding one FSR value of the laser cavity (~10 MHz) to the beat frequencies whose values are below 235 MHz. Thus, the blue curve shows slow temporal oscillations of frequency of a single longitudinal cavity mode, confirming the modulation of the laser cavity length. Fitting of the blue curve by a sinusoidal function is shown by a red one, which demonstrates good periodicity of the mode oscillations. A similar procedure was applied to the beat frequency signal measured at shorter wavelength (1548 nm) pumping shown in Figure 4b. Multiples of FSR values were subtracted from the beat signal to reconstruct temporal dynamics of frequency of a single longitudinal cavity mode in this case. Modulation of the cavity mode frequency is also noticeable in Figure 6b (zoomed-in view of the red and blue curves shown in Figure 6a), but it is partially hidden due to the presence of an additional slow frequency drift. The period of this slow modulation is equal to the mode-hopping period in Figure 4b and is twice as large as the mode-hopping period in Figure 5b. Thus, these results confirm our hypothesis that optical frequency hops in the laser are synchronized with modulation of the laser cavity length.
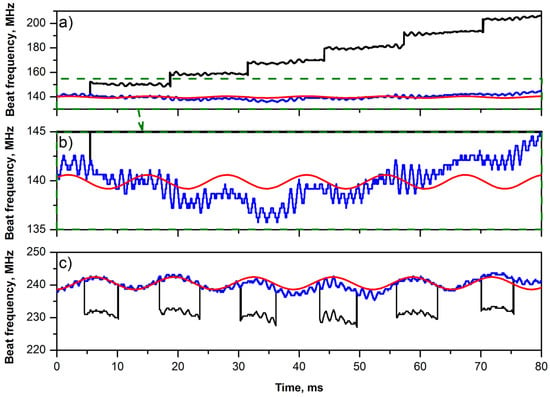
Figure 6.
Beat frequency temporal dependence for laser pumped at wavelength of 1548 nm, (a) full view and (b) zoomed-in view for the red and blue curves, (c) for laser pumped at wavelength of 1564 nm.
As mentioned in the Introduction, the DPGs are formed during the laser generation in the EDF of the amplifying fiber loop mirror (AFLM). The presence of a spectral reflector (in particular, DPG) inside the AFLM should lead to the appearance of some spectral structures in the reflection of the AFLM. For example, the reflection/transmission spectra of a fiber loop mirror (FLM) with inserted FBG were studied in [10]. It was shown there that the presence of the FBG leads to the appearance of such additional structures in the reflection spectrum of the FLM. The total width of the structures is equal to the width of the FBG reflection spectrum. This spectral structure has deep modulation. The modulation period decreases with displacement (mismatch) between the geometrical center of the FBG and the FLM center. Positions of local maxima of the spectral modulation are highly sensitive (at the level of fractions of a wavelength) to changes in the value of the displacement between the centers. Similar spectral features can be expected for the reflection spectra of AFLM, in which the FBG is replaced by a DPG. However, the problem ceases to be stationary due to oscillations of the optical path. Small oscillations (of the order of fractions of a wavelength) in the position of the nodes and antinodes of the standing wave in the AFLM relative to the positions of the minima and maxima of the dynamic grating change the gain of the generated signal. In addition, the positions of the maxima of the AFLM reflection spectrum also begin to oscillate (to change spectral position). As a result, one can expect that these spectral shifts will result in the optical frequency hops.
Let us consider qualitatively the effect of such AFLM reflectance spectrum position oscillations on the laser frequency dynamics. For simplicity, let us assume that the AFLM reflectance spectrum is described by a Gaussian function and that the zero mode (lasing mode, which records DPG and produces this resonance structure) has the highest reflection as compared to neighboring ones (green line in Figure 7a). First, let us also assume that the spectrum is centered at the optical frequency of the lasing mode. In this case, the laser will generate in the SLM regime. Let the position of the spectrum oscillate harmoniously in time. Red and blue curves (see Figure 7a) show extreme positions of the spectrum shifted in opposite directions, and the double-sided arrow indicates the region of oscillations of the reflection maximum. If the amplitude of the reflection spectrum position oscillations is smaller than half of the cavity free spectral range (FSR), then the laser will continue lasing in the SLM regime. At larger reflection maximum shifts, another laser cavity longitudinal mode having larger reflectance will accumulate in the cavity faster and the laser will start to oscillate at this new mode. The maximum displacement of about ⅔ of FSR is shown in Figure 7a as such an example. In this case, the laser will hop a mode with either increasing or decreasing number at the extreme positions of the AFLM spectrum (for blue and red lines in Figure 7a, respectively). This case corresponds to experiments with long-wavelength pumping (Figure 5), where the AFLM reflection spectrum begins to move in the opposite direction after each mode hop and a new mode hop takes place at the opposite extreme position in the backward direction again.
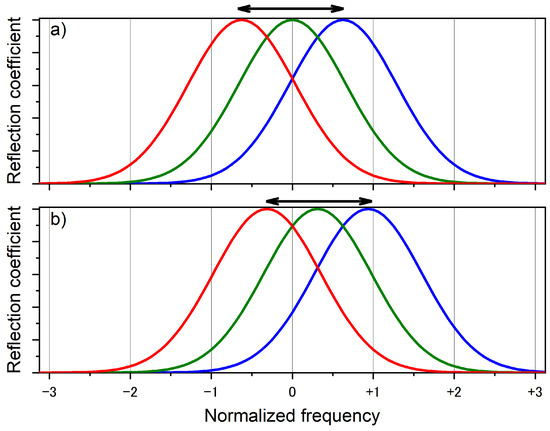
Figure 7.
Qualitative evolution of reflectance spectrum (a) without and (b) with initial spectral shift.
Let us consider now a slightly different case, when the AFLM reflection spectrum is initially shifted from optical frequency of lasing mode. As an example, the green line in Figure 7b corresponding to the reflection spectrum recorded by lasing mode is shifted by ⅓ FSR. The laser will operate in the SLM generation regime without AFLM reflection spectrum oscillations. Let us add some small oscillations of the AFLM reflection spectrum position. In this case the conditions for a mode hopping will be achieved only for the direction corresponding to the initial shift of the AFLM reflection spectrum (blue line in Figure 7b). When the spectrum shifts in the opposite direction (red line in Figure 7b), the reflectance for the zero mode will remain larger than for the others. This case corresponds to the short-wavelength pumping (Figure 4). Taking this qualitative picture of the vibration-induced mode hopping into account, one can conclude that the larger the initial frequency shift, the smaller the oscillation of the reflection spectrum position required for the hop to the neighboring mode.
Note that in conventional self-sweeping lasers it is assumed that the value of the shift is large enough and there is no need for oscillation of an optical frequency selector position for the mode hopping to occur. In this case, the repetition rate of the mode hops is determined by the recording speed of the DPGs. One should also note the following: (1) the qualitative picture of the mode hops presented above (Figure 7) implies that the DPG recording (re-recording) time should be long enough, as compared with the AFLM optical path length modulation period. (2) The possibility of controlling the moment of the mode hops in conventional self-sweeping lasers by changing the AFLM length requires additional research.
Let us return to the temporal characteristics of the laser again. It is important to compare a ratio between the lifetime of the DPG (τ ≈ 10 ms in erbium) and the period of the optical path oscillations T (i.e., the period of the AFLM reflection spectrum oscillations). On the one hand, the period T should not be too long compared to the lifetime τ, so that the position of the DPG in the amplifying fiber does not have time to be re-recorded, when the position of nodes and antinodes in a generated standing wave slowly changes by the FOPLM. On the other hand, the period T should not be too short, because the DPG requires time for formation after each new mode hop. For example, the problem of suppression of DPG formation in ruby lasers was discussed in the 1970s [11,12]. The authors proposed to quickly change the optical path lengths on both sides of the ruby laser active medium in antiphase, so that the DPG would not have time to be recorded. In our case, the period of the optical path modulation (mode hops) in the laser (T ≈ 13.2 ms) is comparable to the upper laser level lifetime in erbium τ ≈ 10 ms (i.e., T ≈ τ). Therefore, it was possible both to record highly selective DPGs and to shift the positions of the nodes and antinodes of a standing wave in the AFLM relative to the maxima and minima of the DPG when changing the optical path length in the AFLM. Thus, such a time ratio allowed us to experimentally demonstrate the transition from optical frequency stabilization to vibration-induced sweeping when we applied FOPLM to the AFLM in the erbium-doped fiber ring laser.
Another important result demonstrated experimentally in our work is the dependence of the vibration-induced sweeping process on the pump wavelength. This fact was observed previously in self-sweeping lasers. For example, self-sweeping with fixed normal sweeping direction [4] or with variable sweeping direction (as well as with wavelength stopping) depending on pump power [13] is observed for thulium-doped fiber lasers pumped at wavelengths of 1540 or 1570 nm, respectively. The authors associated the self-sweeping direction change with the presence of unpumped regions in the long gain fiber with strong pump absorption resulting in nonuniform distribution of the population inversion along the gain fiber length. The length of the amplifying part of the gain fiber increases with the pump and the self-sweeping direction becomes the same as for pumping at a lower absorption wavelength of 1540 nm. One should also note that self-sweeping in the reverse direction was also observed in ytterbium-doped fiber lasers [14,15].
5. Conclusions
The main mechanism responsible for self-sweeping operation is considered to be the creation of dynamic gain/absorption and refractive index gratings [1]. In the approach considered earlier, each new generated mode recorded its selector with a minimum loss/maximum gain shifted in a certain direction from the generating frequency, which led to a sequential change in generated modes with tuning in this direction. In this work, we propose and experimentally demonstrate a new mechanism for wavelength sweeping operation, in which the presence of asymmetry in the transmission/reflection spectrum of one of the narrow selectors and small oscillations of its spectral position will be accompanied by mode hops in the direction of the transmission/reflection spectrum shift. This mechanism results in vibration-induced sweeping when the spectral asymmetry is too small to start generation at a new frequency and self-sweeping is absent without vibrations. Vibration-induced oscillations of the spectral position of the DPG-based selector can help initiate the mode-hopping process. We used an AFLM as an example of such a spectral selector and an FOPLM based on a passive fiber to produce oscillations of the AFLM reflection spectrum maximum. In this case, a change in the generated mode initiates the process of recording the selector at a new frequency, like in conventional self-sweeping lasers. Finally, this vibration-induced sweeping results in improved stability at the optical frequency hop repetition rate. The rate fluctuations are ~10% that exceed previously known results from self-sweeping lasers without optical path modulation.
The implemented optical path modulation system is relatively simple and was only used to demonstrate the effect, but it is not very convenient for practical applications. The most optimal solution, which allows one to control both the amplitude and frequency of forced oscillations, is the use of piezoelectric crystals. It is expected that further research will be carried out using piezocrystals to optimize the laser output characteristics in terms of mode change repetition rate and its stability.
Author Contributions
Conceptualization, E.K.K., I.A.L. and S.I.K.; methodology, E.K.K. and S.I.K.; validation, E.K.K., I.A.L. and S.I.K.; investigation, E.K.K.; data curation, E.K.K.; writing—original draft preparation, E.K.K.; writing—review and editing, E.K.K., I.A.L. and S.I.K.; funding acquisition, I.A.L. and S.I.K. All authors have read and agreed to the published version of the manuscript.
Funding
This work was carried out as a part of the state assignment, state registration N. 1021062912374-2-1.3.6.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
The original contributions presented in the study are included in the article, further inquiries can be directed to the corresponding authors.
Acknowledgments
The equipment of the Center for Collective Use “High Resolution Spectroscopy of Gases and Condensed Matters” at the Institute of Automation and Electrometry was used in this work.
Conflicts of Interest
The authors declare no conflicts of interest.
References
- Poddubrovskii, N.R.; Drobyshev, R.V.; Lobach, I.A.; Kablukov, S.I. Fiber lasers based on dynamic population gratings in rare-earth-doped optical fibers. Photonics 2022, 9, 613. [Google Scholar] [CrossRef]
- Zuo, Z.; Wang, K.; Chen, H.; Lu, B.; Bai, J. Recent progress and development trend of self-sweeping fiber laser. Front. Phys. 2021, 9, 809049. [Google Scholar] [CrossRef]
- Abitan, H.; Bohr, H.; Pedersen, C.F. Fiber ring laser with a feedback mirror. Appl. Opt. 2005, 44, 7802–7805. [Google Scholar] [CrossRef]
- Budarnykh, A.E.; Vladimirskaya, A.D.; Lobach, I.A.; Kablukov, S.I. Broad-range self-sweeping single-frequency linearly polarized Tm-doped fiber laser. Opt. Lett. 2018, 43, 5307–5310. [Google Scholar] [CrossRef]
- Kashirina, E.K.; Lobach, I.A.; Kablukov, S.I. Single-Frequency Continuous-Wave Self-Sweeping Fiber Laser Based on Separated Gain and Absorption Dynamics Gratings. Photonics 2023, 10, 843. [Google Scholar] [CrossRef]
- Smolyaninov, N.N.; Tkachenko, A.Y.; Lobach, I.A.; Kablukov, S.I. A module for processing optical signals from devices based on a self-sweeping fiber laser. Instrum. Exp. Tech. 2021, 64, 241–247. [Google Scholar] [CrossRef]
- Yang, Z.; Li, C.; Xu, S.; Yang, C. Single-Frequency Fiber Lasers; Springer: Singapore, 2019. [Google Scholar] [CrossRef]
- Ma, M.; Hu, Z.; Xu, P.; Wang, W.; Hu, Y. Detecting mode hopping in single-longitudinal-mode fiber ring lasers based on an unbalanced fiber Michelson interferometer. Appl. Opt. 2012, 51, 7420–7425. [Google Scholar] [CrossRef] [PubMed]
- Protopopov, V.V. Laser Heterodyning; Springer: Berlin/Heidelberg, Germany, 2009; Volume 149. [Google Scholar]
- Shu, X.; Yu, L.; Zhao, D.; Zhang, L.; Sugden, K.; Bennion, I. Transmission characteristics of Sagnac interferometers based on fiber Bragg gratings. J. Opt. Soc. Am. B 2002, 19, 2770–2780. [Google Scholar] [CrossRef]
- Folin, K.G.; Antsiferov, V.V. Generation Kinetics, Radiation Spectrum, and Directivity of a Ruby Laser with a Spatially Homogeneous Inverted Population. Sov. J. Exp. Theor. Phys. 1969, 28, 65. [Google Scholar]
- Antsiferov, V.V.; Pivtsov, V.S.; Ugozhaev, V.D.; Folin, K.G. Spike structure of the emission of solid-state lasers. J. Quantum Electron. 1973, 3, 211–215. [Google Scholar] [CrossRef]
- Budarnykh, A.E.; Lobach, I.A.; Kablukov, S.I. Self-sweeping Tm-doped fiber laser with wavelength stopping. Laser Phys. Lett. 2019, 16, 025108. [Google Scholar] [CrossRef]
- Navratil, P.; Peterka, P.; Honzatko, P.; Kubecek, V. Reverse spontaneous laser line sweeping in ytterbium fiber laser. Laser Phys. Lett. 2017, 14, 035102. [Google Scholar] [CrossRef]
- Huang, X.; Lu, C.; Zuo, Z.; Chen, H.; Lu, B.; Bai, J. Self-sweeping regimes control in a bi-directional Yb-doped ring fiber laser. Opt. Laser Technol. 2024, 168, 109943. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).