Abstract
The terahertz (THz) region of the electromagnetic spectrum, spanning from 0.1 to 10 THz, offers unique opportunities for imaging, spectroscopy, and communication applications. However, the potential of THz technologies has been limited by the availability of efficient and versatile THz emitters. Spintronic THz emitters (STEs), leveraging the ultrafast dynamics of electron spins in magnetic materials, have emerged as a promising solution to this challenge. STEs offer significant advantages, including broad bandwidth, high power output, and room-temperature operation, positioning them at the forefront of THz technology development. Despite these advances, understanding the operational principles and improving the performance of STEs remain areas of active research. This review focuses on the theoretical models that describe the behavior of STEs, aiming to provide a comprehensive overview of the underlying physics and suggest directions for future enhancements. Through a detailed examination of these models, the review seeks to clarify the basics of the physics driving STE performance and highlight innovative strategies for their optimization and application expansion.
1. Introduction
The terahertz (THz) region of the electromagnetic spectrum, typically defined as frequencies from 0.1 to 10 THz, lies between the microwave and infrared light. This segment of the spectrum has long been recognized for its potential across a broad range of applications, including, but not limited to, non-destructive testing, medical imaging, and high-speed communication systems [1,2,3,4,5]. However, the exploitation of THz waves has been historically constrained by the lack of effective and versatile THz emitters [6].
THz emitters are pivotal in bridging this technological gap, offering unique advantages that are indispensable for applications that require penetrating non-conductive materials without the ionizing effects of X-rays [1,7]. The capability of THz radiation to provide detailed spectral information enhances its application in the chemical, biological, and material sciences, where traditional techniques fall short [1].
Among the various approaches to THz generation, spintronic THz emitters (STEs) have gained significant attention. These devices utilize spintronics, a branch of physics focused on the natural spin of electrons and their related magnetic moments, alongside the basic electronic charge. Employing rapid spin dynamics and magnetic heterostructures, STEs effectively and quickly transform magnetic energy into terahertz (THz) radiation [8,9,10,11].
The interest in STEs originates primarily from their robust performance characteristics, which include broad spectral bandwidth and high peak power output, alongside the practical advantage of room-temperature operation and ease of integration into semiconductor devices [12,13,14,15].
Despite these advantages, current STEs typically achieve power levels in the range of microwatts to milliwatts [12], which may be insufficient for certain applications that demand higher power for signal penetration or imaging resolution [3]. Additionally, while tunability across a broad spectrum has been demonstrated, fine-tuning specific frequencies with high precision remains challenging [13]. These limitations highlight the need for advancements in both efficiency and tunability. Enhancing the efficiency of STEs involves optimizing the spin conversion processes and material properties to maximize THz emission. Improving tunability requires developing methods to precisely control the spectral characteristics of the emitted THz radiation, such as by engineering the magnetic heterostructures or utilizing external fields.
A clear understanding of the fundamental physical principles that govern STEs is essential to these advancements. This includes not only the spintronic phenomena but also the geometrical characteristics that can significantly influence device performance. Theoretical models and simulations are indispensable tools in this endeavor, providing insights that are essential for the iterative design and optimization of these complex systems.
This review aims to explore the theoretical frameworks that describe spintronic THz emitters. By reviewing these models, we seek to show the foundational physics that supports STE operations and to highlight promising directions for future research and development. We will discuss how theoretical models can address the current challenges in efficiency and tunability, ultimately contributing to the realization of more effective and versatile THz emitters.
2. Basic Background of Spintronic THz Emitters
2.1. THz Time-Domain Spectroscopy Introduction
Terahertz time-domain spectroscopy (THz-TDS) is a cutting-edge spectroscopic technique that measures the properties of materials in the terahertz frequency range. This technique exploits the unique interactions of THz radiation with various materials to extract information about their electronic, photonic, and vibronic properties, which are often inaccessible to other forms of spectroscopy [1].
At the core of THz-TDS is the generation and detection of short pulses of terahertz radiation. The process begins with a femtosecond laser, which emits ultrashort light pulses. These pulses are used to excite a suitable THz emitter, typically a photoconductive antenna or a nonlinear crystal, which in turn generates THz pulses. The emitted THz radiation is then directed towards the sample under investigation. As the THz pulse interacts with the sample, it undergoes absorption and phase shifts, which are dependent on the material’s properties. After passing through the sample, the pulse is detected in a manner that captures both its amplitude and phase. This detection usually involves an electro-optic crystal where the THz pulse and a synchronized optical gating pulse come together. The interaction between the THz pulse and the gating pulse in the crystal produces a change in the polarization of the gating pulse, which can be measured to determine the THz field strength and phase at each point in time [1,3,8,16]. A typical and basic experimental setup is shown in Figure 1.
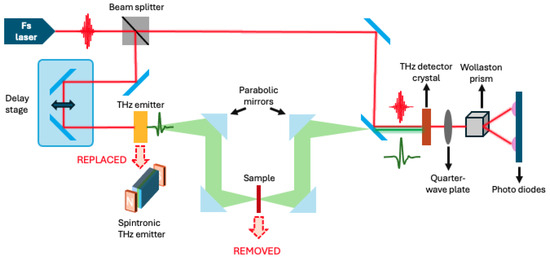
Figure 1.
A typical THz-TDS experimental setup. Overall experimental configuration for spintronic THz emission closely resembles that of THz-TDS. In STE setups, the conventional THz emitter is replaced by the spintronic THz emitter, and the sample typically studied in THz-TDS is omitted.
By analyzing these time-domain data, one can convert them into frequency-domain spectra through the Fourier transform, providing rich details about the material’s response across the THz range. THz-TDS is particularly valuable for studying semiconductors, superconductors, biological tissues, and various other materials, making it a versatile tool in both scientific research and industrial applications [1,3,5].
The study into spintronic terahertz (THz) emitters has been greatly enhanced by advancements in THz time-domain spectroscopy (THz-TDS). This technique has proven crucial in identifying and analyzing the rapid electron dynamics and spin phenomena within spintronic materials. THz-TDS measures the electric field of the emitted THz waves as a function of time, providing a direct insight into the dynamics of the charge carriers and the efficiency of the spin-to-charge conversion processes that are central to the operation of these emitters. This spectroscopic approach has enabled a deeper understanding of the complex mechanisms that facilitate THz generation, laying the groundwork for the development and optimization of efficient spintronic THz sources [1,11,16].
2.2. Basic Structure and Operation of STEs
In spintronic terahertz emitter (STE) technology, devices are typically constructed using a combination of ferromagnetic (FM) and non-magnetic (NM) layers. The operational principle begins with the application of a femtosecond laser pulse, which rapidly heats the metallic layers, thereby driving the entire system into a non-equilibrium condition. This intense laser pulse specifically targets the electrons in the ferromagnetic layer, causing a significant number of them to transition energetically from the valence band to the conduction band. This electron excitation elevates them above the Fermi level, altering both their band velocity and scattering rates [12,13].
The different transport properties between spin-up and spin-down electrons play a crucial role in the system. Specifically, in ferromagnetic metals, majority-spin (spin-up) electrons generally have a significantly longer lifetime than minority-spin (spin-down) electrons. This difference results in a pronounced imbalance in the populations of spin-up and spin-down electrons, leading to the generation of a net spin-polarized current. While the charge component of the current may be screened in metallic FM/NM structures, the spin-polarized current carries an imbalance in electron spin orientations through the material, contributing to the observed phenomena [9,12,17,18,19,20,21,22].
After the generation of the spin-polarized current, it will diffuse from the FM layer into the adjoining NM layer. In the NM layer, strong spin–orbit coupling (SOC) allows for the conversion of this spin current into a charge current through the inverse spin Hall effect (ISHE). Here, the spin-polarized electrons experience a force due to the SOC, leading them to scatter in directions dependent on their spin orientation, which will be eventually observed as a transverse charge current. This charge current will then be generated in a picosecond timescale to produce a THz wave. This THz wave will then propagate through the whole multilayer system and be detected [8,12,13,23,24]. A schematic layout of a typical bilayer spintronic THz emitter can be seen in Figure 2.
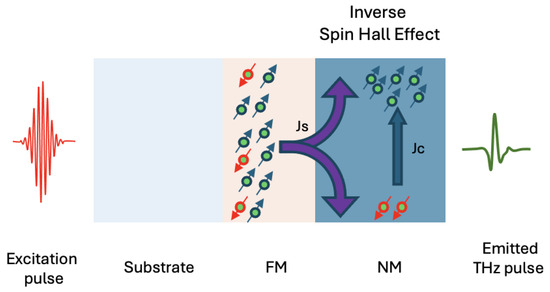
Figure 2.
A typical bilayer spintronic THz emitter. is the spin current and is the charge current.
In spintronic terahertz (THz) emitters, the inverse spin Hall effect (ISHE) is the primary mechanism for converting spin currents into transverse charge currents, which are essential for generating THz radiation. ISHE operates across the bulk of materials, where symmetry allows for the generation of a charge current perpendicular to both the spin polarization direction and the spin current direction. This effect is fundamental to the design and operation of spintronic THz emitters due to its robustness and the straightforward nature of its integration into device architectures [8].
Besides ISHE, other phenomena such as the inverse Rashba–Edelstein effect (IREE) [25] and the anomalous Hall effect (AHE) [26,27,28] also contribute to the functionality of spintronic devices, though they are less commonly associated with the primary THz emission mechanism. Figure 3 provides a visual comparison of ISHE, IREE, and AHE, emphasizing their distinct operational contexts within the STEs.
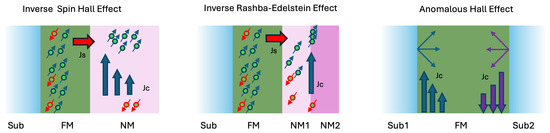
Figure 3.
An intuitive description of how ISHE, IREE, and AHE act in THz emission.
IREE occurs primarily at interfaces where inversion symmetry is disrupted, such as between ferromagnetic (FM) and non-magnetic (NM) layers, or in materials that inherently lack inversion symmetry in their bulk. This effect involves the conversion of a spin current into a charge current through mechanisms related to Rashba spin–orbit coupling, which are highly relevant in structures like Ag/Bi interfaces, topological insulators, two-dimensional electron gases (2DEGs), and transition metal dichalcogenides (2DTMDCs) [8,9].
In addition, the anomalous Hall effect (AHE) is a basic spintronic charge-to-charge-current conversion phenomenon [29]. The AHE results from intrinsic spin–orbit coupling and magnetization in single-layer ferromagnetic materials, and generates a transverse voltage as a charge current passes through the material [26,27,28,29]. While the AHE can influence the performance of spintronic devices under specific conditions, its impact on THz emitters is typically secondary compared with ISHE.
The integration of these effects—ISHE, IREE, and AHE—into spintronic THz emitters offers potential pathways to enhance device performance and manipulate spin currents more effectively [26,27,28]. This integration highlights the diverse operational domains of these effects and underscores their potential impacts on the efficiency and functionality of spintronic devices.
3. THz Generation in the STE: Physical Phenomena
In this section, we dissect the complex THz emission process into three basic sequential stages: (1) femtosecond (fs) laser-induced excitation and the creation of a spin-polarized current, (2) the transformation of spin current into a charge current, and (3) the subsequent emission of THz waves. Each stage will be thoroughly discussed in the subsequent sections, providing a detailed analysis of the mechanisms driving the THz wave generation.
3.1. Spin Current Generation
The ultrafast demagnetization phenomenon induced by femtosecond laser in magnetic materials has attracted great attention from many researchers since its discovery [30]. In the overall spin current generation process in spintronic THz emitters (STEs), it is widely accepted that ultrafast spin transport is driven by the ultrafast demagnetization mechanism [31,32].
When a femtosecond laser pulse impinges on a ferromagnetic (FM) layer, it rapidly elevates the energy state of the electrons, creating non-equilibrium conditions within the material. This intense, short-duration pulse induces ultrafast demagnetization by significantly disturbing the magnetic order. Specifically, the laser pulse excites electrons from the d-band to the sp-band, leading to a temporary reduction in the net magnetization of the ferromagnetic.
The process of ultrafast demagnetization is central to the subsequent spin dynamics. By disrupting the magnetic order, the laser pulse enables the excitation of spin-polarized electrons. These electrons exhibit energy-dependent lifetimes differing between the spin majority and minority carriers. As a result, this differential in electron lifetimes facilitates a rapid flow of spin-polarized electrons, injecting a highly polarized spin current into the nonmagnetic (NM) metallic layer of the heterostructure [17].
The generation of this spin-polarized current is characterized by superdiffusive transport, where spin-polarized electrons migrate from regions of higher excitation to regions of lesser excitation. The direction of this migration depends on the relative temperatures of the ferromagnetic (FM) and non-magnetic (NM) layers. This behavior can be likened to an ultrafast spin Seebeck effect. In typical materials like nickel (Ni), mobile majority-spin electrons can be up to 90% spin-polarized, while for iron (Fe), the polarization can reach approximately 65% [19]. However, it is important to note that a higher degree of spin polarization does not directly correlate with a higher spin current in FM/NM systems. The magnitude of the spin current depends on several factors, including the spin-dependent scattering mechanisms and the specific material properties of the FM and NM layers. These dynamics are critical for understanding the efficient injection and propagation of spin currents within the heterostructure. The superdiffusive spin transport, driven by laser-induced heating, not only serves as an ultrafast analog to the spin Seebeck effect [33,34,35] but also produces longitudinal spin currents that are significantly larger in magnitude, albeit transiently existing on the order of a few hundred femtoseconds [17,19].
3.2. Charge Current Generation
After understanding the basics of how the spin current is generated and then injected into the neighboring layers, to develop a deeper understanding of spintronic THz emitters, one must delve into the mechanisms of the generation of the charge current from the spin current, where, in an STE, the inverse spin Hall effect (ISHE) plays a significant role. To understand the ISHE, we first review the spin Hall effect (SHE). The SHE manifests in materials with significant spin–orbit coupling, such as platinum or tungsten. The effect can be quantified by the following equation [35]:
where is the spin current, is the spin Hall angle, is the charge current, and is the spin polarization vector. This phenomenon arises as electrons with opposite spins are deflected in opposite directions due to the intrinsic spin–orbit interactions within the material, creating a spin accumulation on the edges of the material.
Conversely, ISHE converts an existing spin current back into a charge current, which is essential for detecting spin currents. This conversion is described by the following [35]:
People also commonly write it as follows [13]:
to directly show that, in an STE, the spin current generates a perpendicular effective charge current relative to both itself and the axis of magnetization.
In this context, ISHE is critical as it enables the generation of an electrical signal from a spin current, which can be utilized in various technological applications. This effect not only demonstrates the conversion of spin to charge but also highlights the interplay between electrical and magnetic properties in spintronics, emphasizing their importance in advanced computing and storage systems. These phenomena underscore the fundamental role that SHE and ISHE play in the operation of spintronic THz emitters.
3.3. THz Emission
After the generation of the charge current, we will proceed to the following THz emission process, which is easy to capture. Whatever the effect of charge current generation is, the central part is the production of this charge current. Only when the charge current is generated can we further achieve the THz emission. This is straightforward when integrated with the Maxwell equations—specifically, Faraday’s law of induction and Ampère’s circuital law; the electrical signal generated by the spin-to-charge conversion effects of a spintronic THz emitter can be mathematically described as follows:
where E denotes the electric field, B the magnetic field, the vacuum permittivity, and the vacuum permeability [8,11].
4. THz Outcoupling from the STE: Geometry Influence
After exploring the fundamentals of the spintronic terahertz (THz) emission process, we will review how the overall geometric configuration influences THz emission. This section shifts focus from the general physical mechanisms to more detailed processes involved.
As previously discussed, the overall process can be segmented into three main stages. We will follow the general logic of these stages to comprehensively understand the macroscopic aspects of the THz emission in STEs. A more detailed overview of the process is shown in Figure 4.
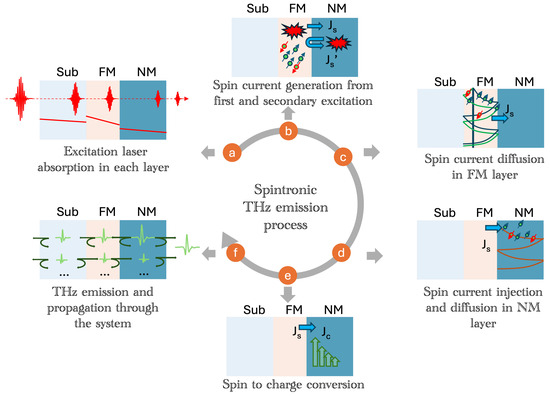
Figure 4.
An overview of the whole spintronic THz emission process.
We will follow these separated stages and explain the overall THz outcoupling from an STE.
4.1. Pump Laser Influence
In spintronic THz emitters, the generation of terahertz (THz) emission follows a sequence of critical stages, initiated by the excitation of the system with an optical pump laser (process (a) in Figure 4). This pump laser plays a significant role, as it drives the system into an out-of-equilibrium state, enabling the subsequent THz emission processes.
The initial effect of the pump laser is to generate a spin current () within the ferromagnetic (FM) layer (process (b) in Figure 4). The magnitude of this spin current, which directly influences the generated charge current (), is dependent on the amount of pump laser energy absorbed by the FM layer [12,36,37,38]. This relationship can be summarized and represented mathematically as follows:
where denotes the absorption of pump laser energy in the FM layer. Various models that describe THz emission in spintronic devices consider this factor crucial, and a detailed discussion of these models will follow in subsequent sections.
The absorption term has been calculated by considering the multiple reflections within all metal layers. Only a portion of the total absorbed power actively contributes to the generation of the THz signal. This contributing fraction is inversely proportional to the combined thicknesses of the metal layers [12,36,38,39]. Thus, people also use the following:
where A is the total absorption of the system, is the incident pump laser fluence, and and are the thicknesses of the NM layer and FM layer, respectively, to describe the total spin current.
Recently, another method is used to specifically calculate the absorption in one single layer in a multilayer system. This method integrates the transfer matrix method with the Poynting theorem to precisely calculate the energy absorption within individual FM layers, enhancing the accuracy of the models used in describing these systems according to Equation (6) [40,41]. The absorption for a specific layer can be expressed as follows:
where represents the initial energy input into the system, denotes the energy dissipated within the layer, quantifies the energy per unit area crossing a surface at position , and d is the thickness of the layer. This method is not only limited to calculating the absorption in the FM layer; it can be used to decouple the absorption of the laser in any specific layer and, therefore, apply to special calculations when the absorption in the other specific layers is needed [41]. The method also allows for the calculation of a detailed pump laser energy distribution profile within the layer, which is important for understanding the dynamics of energy absorption and spin generation. This distribution is defined by the derivative of energy per unit area with respect to the depth within the layer, as follows:
This detailed energy profile facilitates the computation of a geometrically dependent spin generation efficiency profile, which is critical for calculating the total spin population within the emitter, which can be expressed as follows [40]:
where is the spin generation efficiency profile along the FM layer, z refers to the local axis of the layer, and d is the thickness of the FM layer.
In addition to the models previously discussed, considerable attention has been directed towards understanding how the wavelength of the pump laser influences THz emission from spintronic devices. The influence of pump laser wavelength on THz emission remains a contentious topic, with varied experimental results reported.
In exploring the impact of pump laser wavelength on THz emission, researchers have reported divergent findings based on various experimental setups. Some studies suggest that the THz emission amplitude is independent of the pump wavelength. For instance, Papaioannou et al. (2018) demonstrated that an optimized spintronic THz emitter Fe/Pt grown on a MgO substrate generates similar THz radiation when excited by ultrafast laser pulses at either 800 nm or 1550 nm [42]. Similarly, Herapath et al. (2019) found no significant variation in THz generation efficiency across a range of wavelengths from 900 to 1500 nm in thin-film W/CoFeB/Pt emitters [43].
However, other studies highlight a dependency of THz emission on the wavelength. Adam et al. (2019) observed that excitation with highly energetic blue light significantly enhances THz emission in Ta/NiFe/Pt layers compared with infrared light, suggesting wavelength-dependent dynamics [44]. Moreover, Magusara et al. (2022) reported optimal THz generation from an Fe/Pt bilayer on a MgO substrate in the 1200 to 1800 nm wavelength range, with a pronounced reduction in efficiency beyond 2500 nm, indicating a threshold pump photon energy of about 0.35 eV required for effective emission [45]. These latter findings align with theoretical predictions that suggest that the THz emission is influenced by the wavelength-dependent absorption properties of the materials involved, as different dielectric constants at various wavelengths can affect the overall excitation laser absorption and thus influence the THz emission [40].
4.2. Spin Diffusion Influence
Apart from the absorption of the pump laser energy in the layers that will influence the total THz emission, the geometry of the spin diffusion in the material and across the interfaces is also going to influence the overall THz emission (processes (c) and (d) in Figure 4). A general model used for describing the spatial spin current density in the NM layer can be expressed as follows [12]:
where is the density of the spin current injected into the NM layer; and are the thicknesses of the FM layer and the NM layer, respectively; is the spin current relaxation length; and . More generally, the total spin current generation over the whole NM layer can then be integrated into the following:
where is the spin-current generation density per pump-pulse excitation density, is the spin-current transmission amplitude across the FM/NM interface, and is the spin-current relaxation length in the NM layer.
Yang et al. also developed a more general spatial model for spin current inside the NM layer and considering the multiple spin reflections and transmission probabilities at each interface as follows [40]:
where is the spin diffusion length inside the NM model; d is the thickness of the NM layer; and refer to the probabilities for a spin to be transmitted over the right and the left interfaces of the NM layer respectively; ; d is the thickness of the NM layer; and , . Using this model, by considering the spin reflections at the interfaces of the layers, the model was able to show a better description of the THz emission curve, where a second derivative appears at low thicknesses of NM [25,39].
Apart from the general spin diffusion model often considered in the NM layer, synonymous with spin current relaxation, the spin diffusion happening in the FM layer is also significant. After the generated spins reach the interfaces, they will be partially transmitted (injected) into the NM layer and partially reflected. This process is also considered important in describing the following THz emission. A general model describing this spin diffusion process is also developed by considering the multiple reflections at each interface. This model is referred to as the spin generation efficiency profile function [40], as follows:
where d is the thickness of the FM layer, , , , , and denotes the number of spins crossing the right and left interfaces of the FM layer, respectively. These efficiency profiles serve as critical tools for quantifying the total spin current injected into the NM layer, which is used in the calculation in Equation (9), advancing our understanding of spin transport dynamics.
4.3. THz Absorption Influence
Having understood how the pump laser absorption and subsequent spin diffusion processes unfold in both the NM and FM layers, another crucial aspect in understanding THz outcoupling is the absorption of the generated THz in the STE. One significant consideration in this process is the conversion of charge current to an electric field (process (e) in Figure 4), often described by the following equations [8,12,36,39]:
where
Here, e represents the elementary charge of an electron; signifies the impedance of free space; and denote the refractive indices of air and substrate, respectively; and stands for the local conductivity of the metal layer in the THz frequency. Upon considering the charge-to-field conversion, to provide a more accurate depiction of THz field decay across different layer thicknesses (process (f) in Figure 4), some studies incorporate a term describing THz attenuation [39], as follows:
where denotes the effective inverse attenuation coefficient of THz radiation in the metal layers.
Another comprehensive approach to encompass all the aforementioned influences is to employ a modified transfer matrix method, often referred to as the transfer matrix method with source (TMMS) [24]. This method initiates from the Maxwell equations with a source current term and proceeds to a general transfer matrix solution that incorporates a 3D charge current term, as follows:
Here, signifies the overall transfer matrix of the entire STE system, with the labels ‘0’ and ‘∞’ representing the leftmost and rightmost air layers, respectively; represents the amplitude of the emitted radiation towards the right side of the multilayer; and represents the amplitude towards the left. and denote the field generated by charge currents propagating in different directions.
The 3D charge current term directly encompasses both a temporal and a spatial profile of the charge current generated within the NM layer. The temporal profile is often described with the following [40]:
where a represents the rise time of the charge current, b is the time of the switching off of the charge current, h refers to an approximate peak value of the current, and is the time position of the temporal profile. Another type of temporal profile can be constructed as the time derivative of Equation (20). The shapes of these temporal profiles are often observed in different works [13,14,24,40,41]. The spatial profile can be readily considered as an exponential decay or, more precisely, can be directly inserted as Equation (13) (considered the spin reflections at the NM interfaces) if more accurate results are required. Given that the charge current generation is directly embedded in the TMMS, the charge-to-field conversion and the subsequent THz absorption are automatically included in the calculations using the TMMS. This makes THz outcoupling calculation flexible and accurate using TMMS by adjusting the thickness, dielectric constants, and sequence of the materials accordingly.
5. Discussion and Comparison of the General Models
5.1. Typical Bilayer Structures of an STE
After comprehensively going through the impact of each stage of the emission process on the overall THz emission, a model can be derived by including all the pertinent effects discussed earlier. One typical model is the following [8,12]:
In this context, the terms from the first to the last correspond to distinct stages of the model outlined in the previous sections: absorption of the pump pulse, generation of spin current, conversion of spin to charge current, and conversion of charge current to the electric field. The elements share the same physical meaning in the above Equations (7), (12) and (17). Here, refers to the spin Hall angle in the NM layer.
Another typical general model focuses more on stressing that when the thickness of the NM layer exceeds the spin diffusion length, the transient charge current exists only in the NM layer. The overall model expressed as follows [39]:
where the first term is the spin Hall angle, the second term is the fraction of the absorption of the excitation laser, the third term shows the spin current diffusion in FM to the NM interface ( is a critical thickness below which no spin current reaches the NM layer and above which the spin polarization saturates with a constant ), the fourth and fifth terms together are the spin accumulation in the NM layer, and the last term is the decay of the THz radiation along the propagation in the system. Here, is the excitation laser power absorbed. The physical meaning of the element shares the same with Equations (17) and (18). For a more detailed explanation and the derivation of these terms, we refer readers to the original article [39]. Additionally, we have provided a summary Table 1 at the end of the section that outlines the physical meanings and significance of each term in Equation (22) and other relevant equations. This table aims to aid readers in understanding the contributions of each component in the model.

Table 1.
A summary table of the general models.
Another general model considers more by taking into account the spin loss coefficient, which describes the injection efficiency of the spin current at the interface, as follows [36]:
where is the spin injection efficiency, is the pump energy absorption, and is the spin Hall angle of NM.
Although the discussed models are applicable to variations in both the ferromagnetic (FM) and the non-magnetic (NM) layer thicknesses, they primarily concentrate on the impact of the NM layer thickness on the overall terahertz (THz) emission. However, simplified models exist that distinctly separate the influences of NM and FM layer thicknesses on the THz emission characteristics, as exemplified in a study by Zhou et al. [25] as follows:
and
In the given equations, and represent the electrical conductivities of the ferromagnetic (FM) and non-magnetic (NM) layers, respectively. The elements and denote the spin diffusion lengths in the FM and NM layers. Additionally, and describe the decay constants for the excitation laser intensity at the FM/NM interfaces, dependent on the thicknesses of the FM and NM layers, respectively. The first term in the models represents the shunting effect. The second term describes the spin diffusion processes, detailing how spin information propagates through each layer. Finally, the third term models the decay of the excitation laser intensity within the system, providing insights into the interaction between the laser and the material layers.
A summary table of the general models that mainly focus on the FM excitation influence on the overall THz emission is shown below. The table shows the general meaning of each term in the models.
Different from the above-mentioned models, the TMMS model [24,40,46], by incorporating all relevant effects in each term and by inserting the appropriate spatial and temporal profiles, can automatically simulate the entire process with the correct material parameters input at the start. It can also help calculate or estimate the charge or spin current profiles generated in the system based on the experimentally measured THz time-domain profiles.
5.2. Secondary Enhancement to the THz Emission
Apart from the above widely accepted models, recently, a new model came out stressing the importance of the secondary enhancement to the overall THz emission in typical spintronic THz emission processes; this model was developed mainly based on the TMMS [24] model introduced above as follows [41] (Figure 4 process (b)):
This model embedded all the effects stressed above and, at the same time, separated the THz emission contribution of the whole STE into three parts. This model shows that the excitation of the FM layer in the initial stage contributes to not only THz emission but also the excitation of the NM layer. When the NM layer is excited, it generates hot electrons that subsequently travel back to the FM layer, acting as a secondary excitation source. This secondary excitation enhances the total spin current generation in the FM layer, thereby enhancing the THz emission. The first two terms of this model describe the general THz emission resulting from the excitation of the FM layer. The first term captures the contribution to terahertz radiation from the FM to NM superdiffusion process, while the second term accounts for the contribution from minor processes, excluding the influence of the NM layer. Subsequently, the third term delineates the enhancement process, illustrating the relationship between the FM and NM layers in facilitating THz emission. Here, d refers to the thickness of the NM layer, refers to the spin diffusion length in the NM layer, refers to the THz emission amplitude from the NM layer, is the THz emission amplitude from the FM layer, is the excitation laser absorption in the FM layer, is the absorption of the excitation laser in the NM layer, and is the amount of energy from NM diffuse to FM after the excitation ( is the energy diffusion length in NM), and , , are the scaling parameters.
In this model, which is based on the TMMS framework [24,40], several factors can be manually incorporated into the calculation process to enhance flexibility and accuracy, which have covered all the processes mentioned in Figure 4. These factors include the spatial profile of the spin current in the ferromagnetic (FM) layer, the absorption of the excitation laser in each layer, and its interaction with the spin current profile in the FM layer (Equations (8), (10), and (15) to Equation (14)). Additionally, the model considers the spin current spatial profile in the non-magnetic (NM) layer, accounting for multiple reflections from the left and right interfaces (Equation (13)), as well as the reflection and transmission efficiency of spins at these interfaces.
5.3. AHE-Based THz Emission
In addition to the models describing THz emission from the ISHE discussed previously, the AHE may also play a significant role in the THz emission observed in an STE [26,28]. The AHE predominantly occurs within the FM layers. Zhang et al. reported a robust correlation between experimental data and the thickness dependence predicted by their model, thereby supporting the hypothesis that the AHE in single FM layers can contribute to THz emission. The model is shown in their study as follows [27]:
In the model, d represents the thickness of the FM layer, F indicates the fluence, and is the AHE angle. The term describes the FM layer’s absorbance. The reflection coefficients at the interfaces are denoted as and . The symbol refers to the non-equilibrium electron mean free path, and signifies the decay length of terahertz (THz) emission within the FM layer. The variable is used for the average electron velocity, and quantifies the saturation magnetization. The refractive indices of air and the substrate are represented as and , respectively. is defined as the impedance of free space. Furthermore, and are calculated as and , respectively.
5.4. Extension of Bilayer Samples
The majority of the models previously discussed mainly focused on describing terahertz (THz) emission from typical bilayer samples, generally configured as Sub/FM/NM or Sub/NM/FM, or single-layer samples with the AHE dominating the emission. In efforts to enhance THz emission in spintronic terahertz emitters (STEs), several studies have explored the use of more complex layer structures. Notably, configurations such as trilayers () [12] and stacked bilayers () or stacked trilayers () have been investigated [47,48]. These more complicated systems are not fully described by most existing models. However, the transfer matrix method with source model (TMMS) developed by Yang et al., which extends the traditional transfer matrix method (TMM) by incorporating spin current diffusion and generation spatial profiles, offers a robust framework. This model is designed to be directly applicable to structures involving trilayers and potentially more complex multilayer assemblies. It achieves this function through the incorporation of adjustable parameters for the initial number of layers when defining the system’s geometry [24,40,49].
5.5. THz Bandwidth Study
In addition to optimizing the amplitude of the spintronic terahertz emitter (STE), advancing the bandwidth capabilities of STEs represents a pivotal research direction. The bandwidth of the emitted terahertz (THz) wave is primarily influenced by the temporal dynamics of the charge current, as THz wave emission is directly derived from these currents [46,50]. Consequently, the temporal profile of the charge current, as well as the time delay between the initiation of the charge current and the subsequent THz emission, is a critical factor. Investigating these temporal aspects of both spin and charge currents offers valuable insights into potential optimizations of the STE. A novel approach using the perturbative transfer matrix method (PTMM) [46] has been proposed to address these temporal delays. This model facilitates a deeper understanding of the interaction between laser excitation and THz emission, providing a useful analytical tool for future research in this domain.
6. THz Detection at the Detector: Response Functions
Following the emission of the terahertz (THz) wave from the spintronic THz emitter (STE), the detection process must be meticulously analyzed. This process generally encompasses two principal stages: (1) the propagation of the THz signal from the emitter to the detector and (2) the signal’s propagation within the detector itself. These stages collectively form a comprehensive response function, denoted as , which can be described as follows [13]:
where accounts for the propagation of the THz pulse from the sample to the detector, including aspects such as focusing, and represents the electro-optic detection response function of the detection crystal utilized.
Consequently, the final signal detected can be represented by the following:
where is the frequency domain representation of the THz field immediately following emission from the STE. Understanding this relationship is crucial when quantifying the exact profiles of charge or spin currents. However, for studies focusing on relative comparisons of THz emission amplitudes across different samples, without delving into detailed charge or spin current profiles, the overall response function may be disregarded.
7. Conclusions and Future Outlook
In summary, this review has explored the diverse theoretical frameworks underlying the performance of spintronic terahertz (THz) emitters, highlighting their operational principles and the physical phenomena responsible for THz generation. From the introduction of THz time-domain spectroscopy to the intricate design and operation of spintronic THz emitters (STEs), we have delineated the critical components and experimental setups commonly employed in this field.
The theoretical models discussed provide a profound understanding of the mechanisms of THz generation within STEs, including the generation of spin and charge currents and their subsequent conversion into THz radiation. These models are essential for predicting and optimizing the performance characteristics of STEs, offering insights into the influence of various physical factors such as spin diffusion and THz absorption.
Moreover, we have considered how the geometry of the emitter and the characteristics of the pump laser significantly affect the efficiency of THz outcoupling. Each aspect in geometrical configuration, from the sequence of the layers to the thickness of the layers, plays a pivotal role in the emitter’s overall functionality and efficiency by affecting the excitation laser propagation and THz propagation in the system.
The ongoing development and refinement of theoretical models are crucial for advancing our understanding and enhancing the technological applications of spintronic THz emitters. As research progresses, these models will continue to evolve, potentially leading to new paradigms in the application of THz technology in communications, imaging, and beyond. The insights gained from these theoretical explorations not only deepen our comprehension of fundamental physical processes but also drive innovations in THz science and technology.
Author Contributions
Conceptualization, Y.Y.; writing—original draft preparation, Y.Y.; writing—review and editing, Y.Y. and S.D.F.; supervision, M.B.; project administration, M.B.; funding acquisition, M.B. All authors have read and agreed to the published version of the manuscript.
Funding
This work was supported by the Singaporean Ministry of Education AcRF Tier 2 Programme “Dynamical characterization of the spin-to-charge conversion mechanisms in 2D heterostructures” (Grant No. MOE-T2EP50222-0014).
Data Availability Statement
Data are contained within the article.
Acknowledgments
The authors express their gratitude to all colleagues whose contributions have enriched the content of this review paper.
Conflicts of Interest
The authors declare no conflicts of interest.
Correction Statement
This article has been republished with a minor correction to the Funding statement. This change does not affect the scientific content of the article.
References
- Neu, J.; Schmuttenmaer, C.A. Tutorial: An introduction to terahertz time domain spectroscopy (THz-TDS). J. Appl. Phys. 2018, 124, 231101. [Google Scholar] [CrossRef]
- Smith, R.M.; Arnold, M.A. Terahertz time-domain spectroscopy of solid samples: Principles, applications, and challenges. Appl. Spectrosc. Rev. 2011, 46, 636–679. [Google Scholar] [CrossRef]
- Tonouchi, M. Cutting-edge terahertz technology. Nat. Photonics 2007, 1, 97–105. [Google Scholar] [CrossRef]
- Federici, J.; Moeller, L. Review of terahertz and subterahertz wireless communications. J. Appl. Phys. 2010, 107, 111101. [Google Scholar] [CrossRef]
- Ferguson, B.; Zhang, X.C. Materials for terahertz science and technology. Nat. Mater. 2002, 1, 26–33. [Google Scholar] [CrossRef] [PubMed]
- Wang, Q.; Chen, Y.; Mao, J.; Yang, F.; Wang, N. Metasurface-assisted terahertz sensing. Sensors 2023, 23, 5902. [Google Scholar] [CrossRef] [PubMed]
- Kemp, M.C.; Taday, P.; Cole, B.E.; Cluff, J.; Fitzgerald, A.J.; Tribe, W.R. Security applications of terahertz technology. In Proceedings of the Terahertz for Military and Security Applications, SPIE, Orlando, FL, USA, 21 April 2003; Volume 5070, pp. 44–52. [Google Scholar]
- Seifert, T.S.; Cheng, L.; Wei, Z.; Kampfrath, T.; Qi, J. Spintronic sources of ultrashort terahertz electromagnetic pulses. Appl. Phys. Lett. 2022, 120, 180401. [Google Scholar] [CrossRef]
- Cheng, L.; Li, Z.; Zhao, D.; Chia, E.E. Studying spin–charge conversion using terahertz pulses. Appl. Mater. 2021, 9, 070902. [Google Scholar] [CrossRef]
- Walowski, J.; Münzenberg, M. Perspective: Ultrafast magnetism and THz spintronics. J. Appl. Phys. 2016, 120, 140901. [Google Scholar] [CrossRef]
- Huisman, T.J.; Rasing, T. THz emission spectroscopy for THz spintronics. J. Phys. Soc. Jpn. 2017, 86, 011009. [Google Scholar] [CrossRef]
- Seifert, T.; Jaiswal, S.; Martens, U.; Hannegan, J.; Braun, L.; Maldonado, P.; Freimuth, F.; Kronenberg, A.; Henrizi, J.; Radu, I.; et al. Efficient metallic spintronic emitters of ultrabroadband terahertz radiation. Nat. Photonics 2016, 10, 483–488. [Google Scholar] [CrossRef]
- Kampfrath, T.; Battiato, M.; Maldonado, P.; Eilers, G.; Nötzold, J.; Mährlein, S.; Zbarsky, V.; Freimuth, F.; Mokrousov, Y.; Blügel, S.; et al. Terahertz spin current pulses controlled by magnetic heterostructures. Nat. Nanotechnol. 2013, 8, 256–260. [Google Scholar] [CrossRef] [PubMed]
- Liu, J.; Lee, K.; Yang, Y.; Li, Z.; Sharma, R.; Xi, L.; Salim, T.; Boothroyd, C.; Lam, Y.M.; Yang, H.; et al. Spintronic terahertz emitters in silicon-based heterostructures. Phys. Rev. Appl. 2022, 18, 034056. [Google Scholar] [CrossRef]
- Cheng, L.; Wang, X.; Yang, W.; Chai, J.; Yang, M.; Chen, M.; Wu, Y.; Chen, X.; Chi, D.; Goh, K.E.J.; et al. Far out-of-equilibrium spin populations trigger giant spin injection into atomically thin MoS2. Nat. Phys. 2019, 15, 347–351. [Google Scholar] [CrossRef]
- Wu, W.; Yaw Ameyaw, C.; Doty, M.F.; Jungfleisch, M.B. Principles of spintronic THz emitters. J. Appl. Phys. 2021, 130, 091101. [Google Scholar] [CrossRef]
- Battiato, M.; Carva, K.; Oppeneer, P.M. Superdiffusive Spin Transport as a Mechanism of Ultrafast Demagnetization. Phys. Rev. Lett. 2010, 105, 027203. [Google Scholar] [CrossRef] [PubMed]
- Choi, G.M.; Min, B.C.; Lee, K.J.; Cahill, D.G. Spin current generated by thermally driven ultrafast demagnetization. Nat. Commun. 2014, 5, 4334. [Google Scholar] [CrossRef] [PubMed]
- Battiato, M.; Carva, K.; Oppeneer, P.M. Theory of laser-induced ultrafast superdiffusive spin transport in layered heterostructures. Phys. Rev. B 2012, 86, 024404. [Google Scholar] [CrossRef]
- Kirilyuk, A.; Kimel, A.V.; Rasing, T. Ultrafast optical manipulation of magnetic order. Rev. Mod. Phys. 2010, 82, 2731–2784. [Google Scholar] [CrossRef]
- Rudolf, D.; La-O-Vorakiat, C.; Battiato, M.; Adam, R.; Shaw, J.M.; Turgut, E.; Maldonado, P.; Mathias, S.; Grychtol, P.; Nembach, H.T.; et al. Ultrafast magnetization enhancement in metallic multilayers driven by superdiffusive spin current. Nat. Commun. 2012, 3, 1037. [Google Scholar] [CrossRef] [PubMed]
- Zhang, G.P.; Hübner, W. Laser-Induced Ultrafast Demagnetization in Ferromagnetic Metals. Phys. Rev. Lett. 2000, 85, 3025–3028. [Google Scholar] [CrossRef] [PubMed]
- Eschenlohr, A.; Battiato, M.; Maldonado, P.; Pontius, N.; Kachel, T.; Holldack, K.; Mitzner, R.; Föhlisch, A.; Oppeneer, P.M.; Stamm, C. Ultrafast spin transport as key to femtosecond demagnetization. Nat. Mater. 2013, 12, 332–336. [Google Scholar] [CrossRef] [PubMed]
- Yang, Y.; Dal Forno, S.; Battiato, M. Transfer-matrix description of heterostructured spintronics terahertz emitters. Phys. Rev. B 2021, 104, 155437. [Google Scholar] [CrossRef]
- Zhou, C.; Liu, Y.; Wang, Z.; Ma, S.; Jia, M.W.; Wu, R.; Zhou, L.; Zhang, W.; Liu, M.; Wu, Y.; et al. Broadband terahertz generation via the interface inverse Rashba-Edelstein effect. Phys. Rev. Lett. 2018, 121, 086801. [Google Scholar] [CrossRef] [PubMed]
- Liu, Y.; Cheng, H.; Xu, Y.; Vallobra, P.; Eimer, S.; Zhang, X.; Wu, X.; Nie, T.; Zhao, W. Separation of emission mechanisms in spintronic terahertz emitters. Phys. Rev. B 2021, 104, 064419. [Google Scholar] [CrossRef]
- Zhang, Q.; Luo, Z.; Li, H.; Yang, Y.; Zhang, X.; Wu, Y. Terahertz emission from anomalous Hall effect in a single-layer ferromagnet. Phys. Rev. Appl. 2019, 12, 054027. [Google Scholar] [CrossRef]
- Mottamchetty, V.; Rani, P.; Brucas, R.; Rydberg, A.; Svedlindh, P.; Gupta, R. Direct evidence of terahertz emission arising from anomalous Hall effect. Sci. Rep. 2023, 13, 5988. [Google Scholar] [CrossRef] [PubMed]
- Seifert, T.S.; Martens, U.; Radu, F.; Ribow, M.; Berritta, M.; Nádvorník, L.; Starke, R.; Jungwirth, T.; Wolf, M.; Radu, I.; et al. Frequency-Independent Terahertz Anomalous Hall Effect in DyCo5, Co32Fe68, and Gd27Fe73 Thin Films from DC to 40 THz. Adv. Mater. 2021, 33, 2007398. [Google Scholar] [CrossRef] [PubMed]
- Beaurepaire, E.; Merle, J.C.; Daunois, A.; Bigot, J.Y. Ultrafast spin dynamics in ferromagnetic nickel. Phys. Rev. Lett. 1996, 76, 4250. [Google Scholar] [CrossRef] [PubMed]
- Gupta, R.; Cosco, F.; Malik, R.; Chen, X.; Saha, S.; Ghosh, A.; Pohlmann, T.; Mardegan, J.; Francoual, S.; Stefanuik, R.; et al. Element-resolved evidence of superdiffusive spin current arising from ultrafast demagnetization process. Phys. Rev. B 2023, 108, 064427. [Google Scholar] [CrossRef]
- Rouzegar, R.; Brandt, L.; Nádvorník, L.; Reiss, D.A.; Chekhov, A.L.; Gueckstock, O.; In, C.; Wolf, M.; Seifert, T.S.; Brouwer, P.W.; et al. Laser-induced terahertz spin transport in magnetic nanostructures arises from the same force as ultrafast demagnetization. Phys. Rev. B 2022, 106, 144427. [Google Scholar] [CrossRef]
- Seifert, T.S.; Jaiswal, S.; Barker, J.; Weber, S.T.; Razdolski, I.; Cramer, J.; Gueckstock, O.; Maehrlein, S.F.; Nadvornik, L.; Watanabe, S.; et al. Femtosecond formation dynamics of the spin Seebeck effect revealed by terahertz spectroscopy. Nat. Commun. 2018, 9, 2899. [Google Scholar] [CrossRef] [PubMed]
- Xiao, J.; Bauer, G.E.; Uchida, K.C.; Saitoh, E.; Maekawa, S. Theory of magnon-driven spin Seebeck effect. Phys. Rev. B 2010, 81, 214418. [Google Scholar] [CrossRef]
- Adachi, H.; Uchida, K.i.; Saitoh, E.; Maekawa, S. Theory of the spin Seebeck effect. Rep. Prog. Phys. 2013, 76, 036501. [Google Scholar] [CrossRef] [PubMed]
- Qiu, H.; Kato, K.; Hirota, K.; Sarukura, N.; Yoshimura, M.; Nakajima, M. Layer thickness dependence of the terahertz emission based on spin current in ferromagnetic heterostructures. Opt. Express 2018, 26, 15247–15254. [Google Scholar] [CrossRef] [PubMed]
- Sasaki, Y.; Suzuki, K.; Mizukami, S. Annealing effect on laser pulse-induced THz wave emission in Ta/CoFeB/MgO films. Appl. Phys. Lett. 2017, 111, 102401. [Google Scholar] [CrossRef]
- Seifert, T.S.; Tran, N.M.; Gueckstock, O.; Rouzegar, S.M.; Nadvornik, L.; Jaiswal, S.; Jakob, G.; Temnov, V.V.; Muenzenberg, M.; Wolf, M.; et al. Terahertz spectroscopy for all-optical spintronic characterization of the spin-Hall-effect metals Pt, W and Cu80Ir20. J. Phys. D Appl. Phys. 2018, 51, 364003. [Google Scholar] [CrossRef]
- Torosyan, G.; Keller, S.; Scheuer, L.; Beigang, R.; Papaioannou, E.T. Optimized spintronic terahertz emitters based on epitaxial grown Fe/Pt layer structures. Sci. Rep. 2018, 8, 1311. [Google Scholar] [CrossRef] [PubMed]
- Yang, Y.; Dal Forno, S.; Battiato, M. Modeling spintronic terahertz emitters as a function of spin generation and diffusion geometry. Phys. Rev. B 2023, 107, 144407. [Google Scholar] [CrossRef]
- Agarwal, P.; Yang, Y.; Medwal, R.; Asada, H.; Fukuma, Y.; Battiato, M.; Singh, R. Secondary spin current driven efficient THz spintronic emitters. Adv. Opt. Mater. 2023, 11, 2301027. [Google Scholar] [CrossRef]
- Papaioannou, E.T.; Torosyan, G.; Keller, S.; Scheuer, L.; Battiato, M.; Mag-Usara, V.K.; L’huillier, J.; Tani, M.; Beigang, R. Efficient terahertz generation using Fe/Pt spintronic emitters pumped at different wavelengths. IEEE Trans. Magnet. 2018, 54, 9100205. [Google Scholar] [CrossRef]
- Herapath, R.I.; Hornett, S.M.; Seifert, T.; Jakob, G.; Kläui, M.; Bertolotti, J.; Kampfrath, T.; Hendry, E. Impact of pump wavelength on terahertz emission of a cavity-enhanced spintronic trilayer. Appl. Phys. Lett. 2019, 114, 041107. [Google Scholar] [CrossRef]
- Adam, R.; Chen, G.; Bürgler, D.E.; Shou, T.; Komissarov, I.; Heidtfeld, S.; Hardtdegen, H.; Mikulics, M.; Schneider, C.M.; Sobolewski, R. Magnetically and optically tunable terahertz radiation from Ta/NiFe/Pt spintronic nanolayers generated by femtosecond laser pulses. Appl. Phys. Lett. 2019, 114, 212405. [Google Scholar] [CrossRef]
- Mag-Usara, V.K.; Escaño, M.C.; Petoukhoff, C.E.; Torosyan, G.; Scheuer, L.; Madéo, J.; Afalla, J.; Talara, M.L.; Muldera, J.E.; Kitahara, H.; et al. Optimum excitation wavelength and photon energy threshold for spintronic terahertz emission from Fe/Pt bilayer. Iscience 2022, 25, 104615. [Google Scholar] [CrossRef] [PubMed]
- Yang, Y.; Dal Forno, S.; Battiato, M. Perturbative transfer matrix method for optical-pump terahertz-probe spectroscopy of ultrafast dynamics in spintronic terahertz emitters. Phys. Rev. B 2024, 109, 024425. [Google Scholar] [CrossRef]
- Feng, Z.; Yu, R.; Zhou, Y.; Lu, H.; Tan, W.; Deng, H.; Liu, Q.; Zhai, Z.; Zhu, L.; Cai, J.; et al. Highly efficient spintronic terahertz emitter enabled by metal–dielectric photonic crystal. Adv. Opt. Mater. 2018, 6, 1800965. [Google Scholar] [CrossRef]
- Yang, D.; Liang, J.; Zhou, C.; Sun, L.; Zheng, R.; Luo, S.; Wu, Y.; Qi, J. Powerful and Tunable THz Emitters Based on the Fe/Pt Magnetic Heterostructure. Adv. Opt. Mater. 2016, 4, 1944–1949. [Google Scholar] [CrossRef]
- Yang, Y.; Dal Forno, S.; Battiato, M. Removal of Spectral Distortion Due to Echo for Ultrashort THz Pulses Propagating Through Multilayer Structures with Thick Substrate. J. Infrared Millim. Terahertz Waves 2021, 42, 1142–1152. [Google Scholar] [CrossRef]
- Wang, X.; Cheng, L.; Zhu, D.; Wu, Y.; Chen, M.; Wang, Y.; Zhao, D.; Boothroyd, C.B.; Lam, Y.M.; Zhu, J.X.; et al. Ultrafast spin-to-charge conversion at the surface of topological insulator thin films. Adv. Mater. 2018, 30, 1802356. [Google Scholar] [CrossRef] [PubMed]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).