Modelling and Analysis of Vector and Vector Vortex Beams Reflection for Optical Sensing
Abstract
1. Introduction
2. Methods
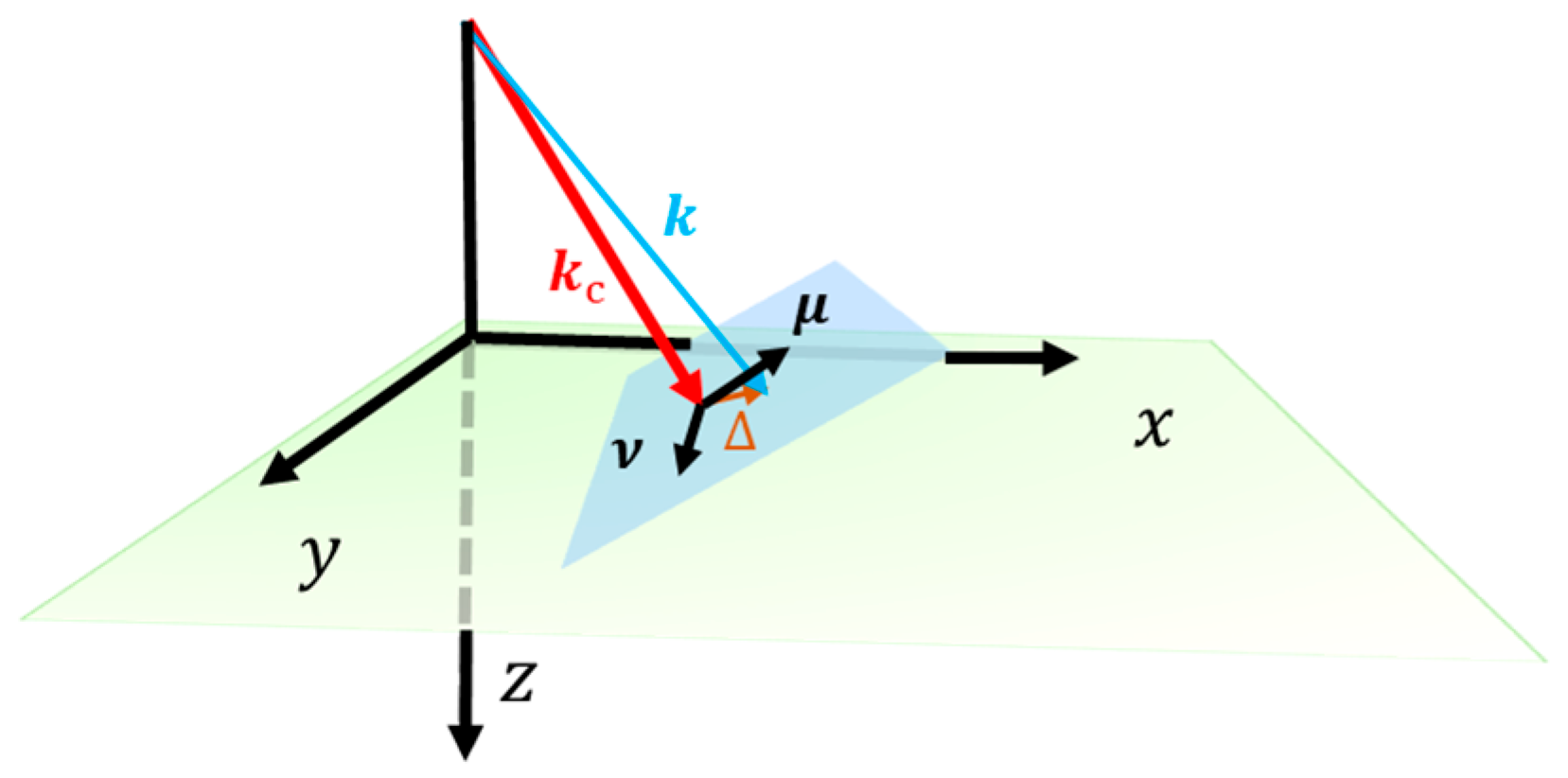
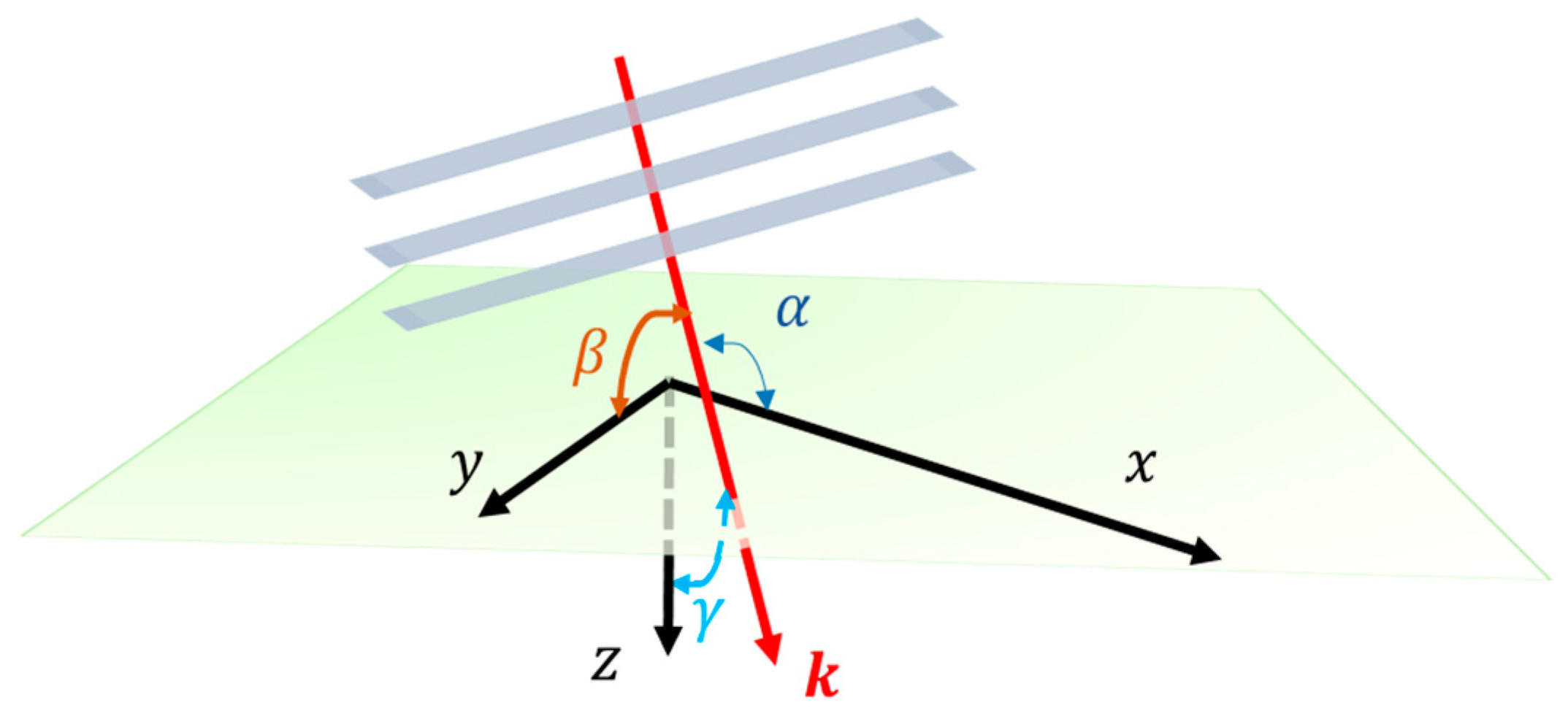
2.1. Expressions of a Well-Collimated Incident Beam
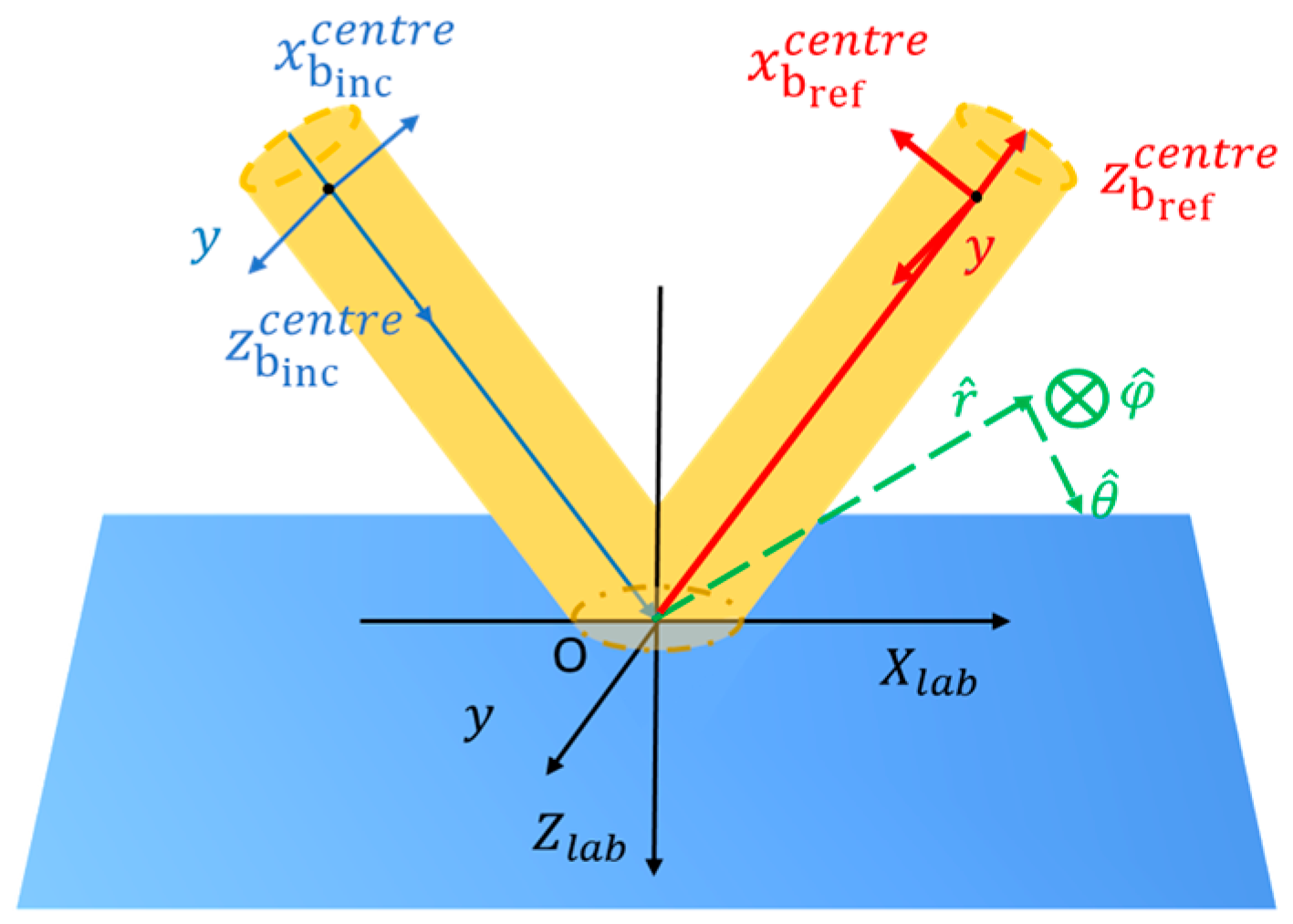
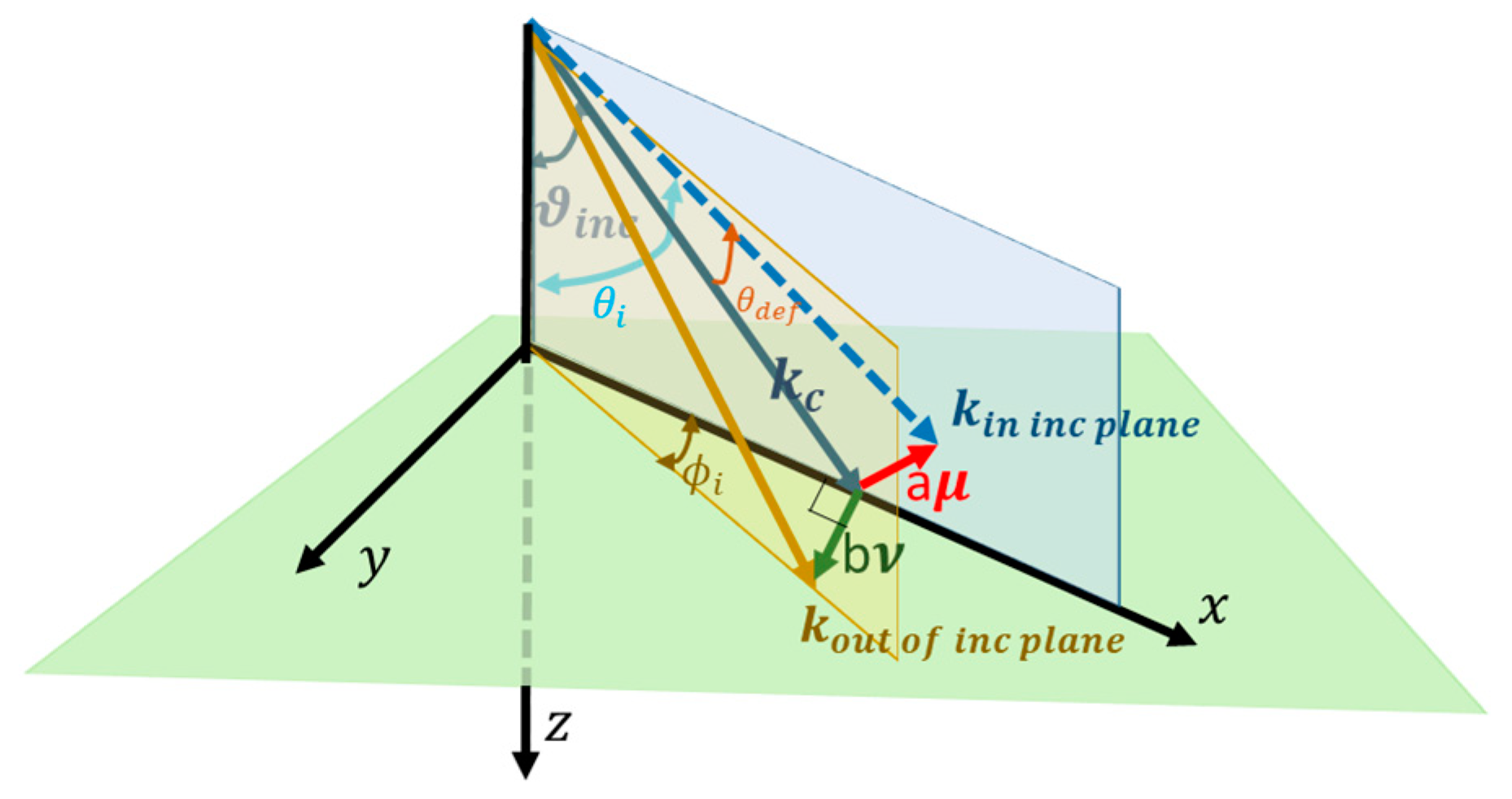
2.2. Frames of Reference and Coordinates in the Reflection Process of Light Beams
2.3. Calculation of Reflected Optical Fields on Dielectric Materials
3. Results
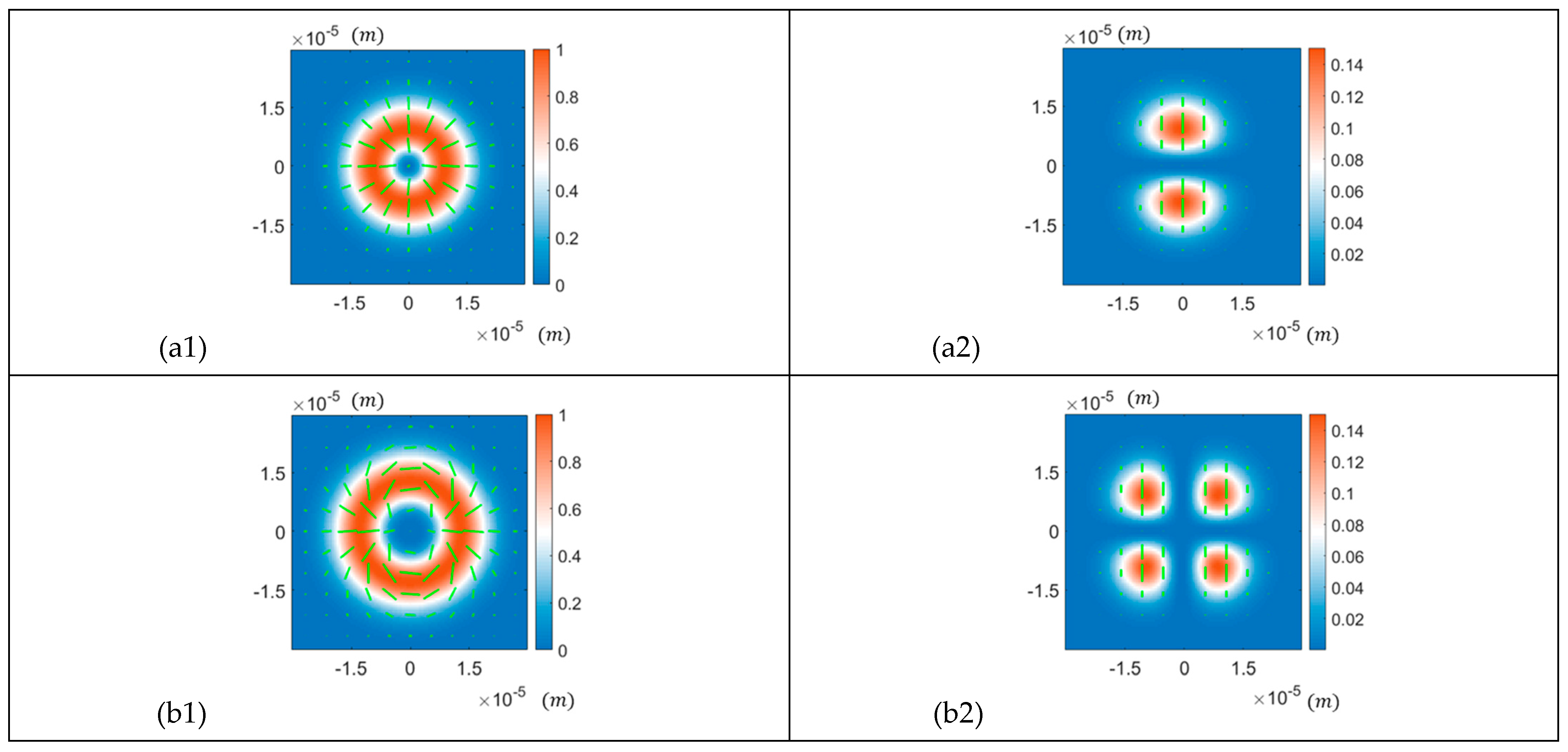
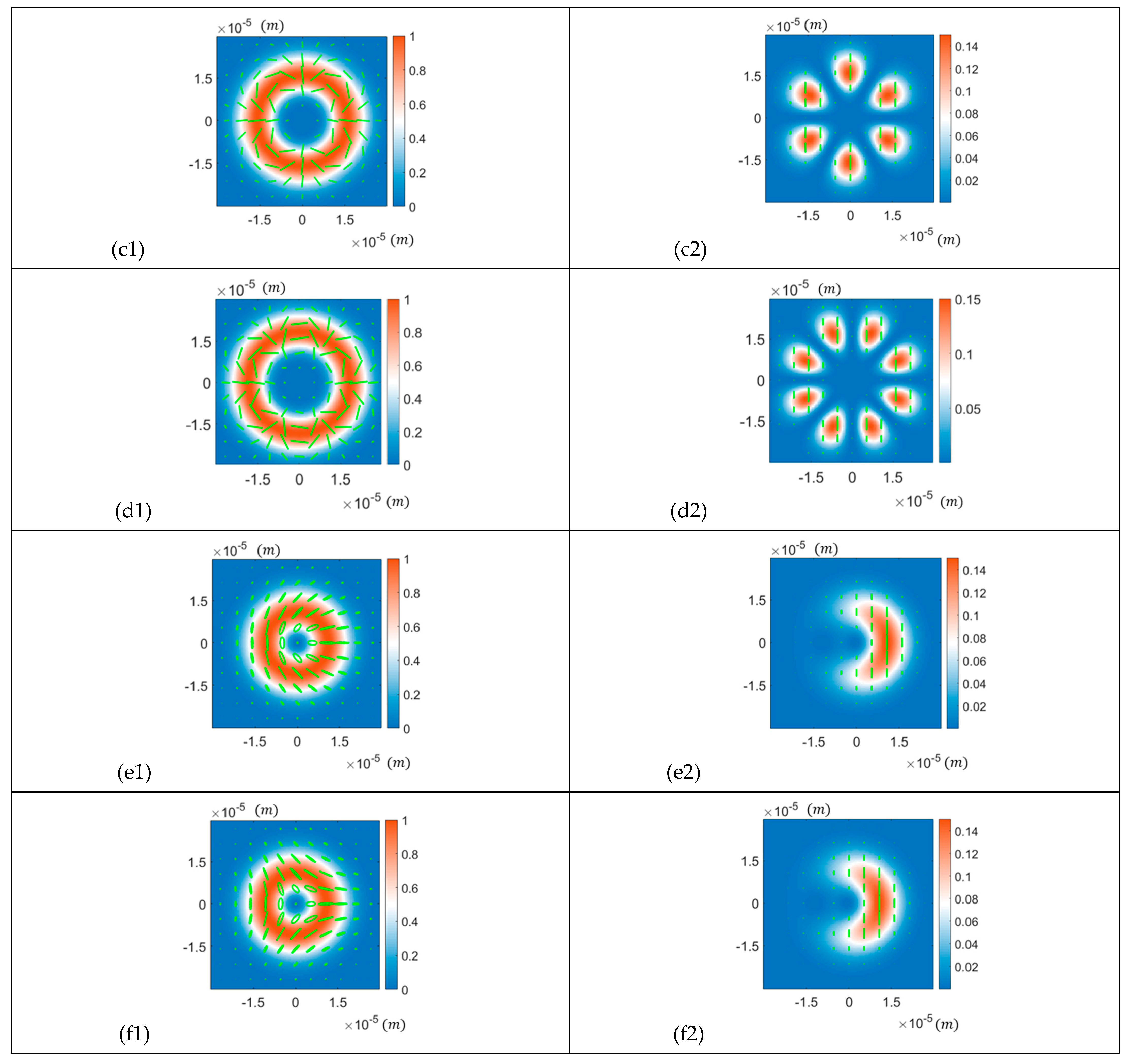
3.1. Intensity and Polarisation Distribution of the Incident Beam and of the Reflected Beam at the Brewster Angle
- Radially polarised beams ();
- Vector beam with hybrid polarisation states ();
- Vector beam with hybrid polarisation states ();
- Vector beam with hybrid polarisation states ();
- ‘Lemon’-polarised vortex beams (, );
- ‘Star’-polarised vortex beams (, ).
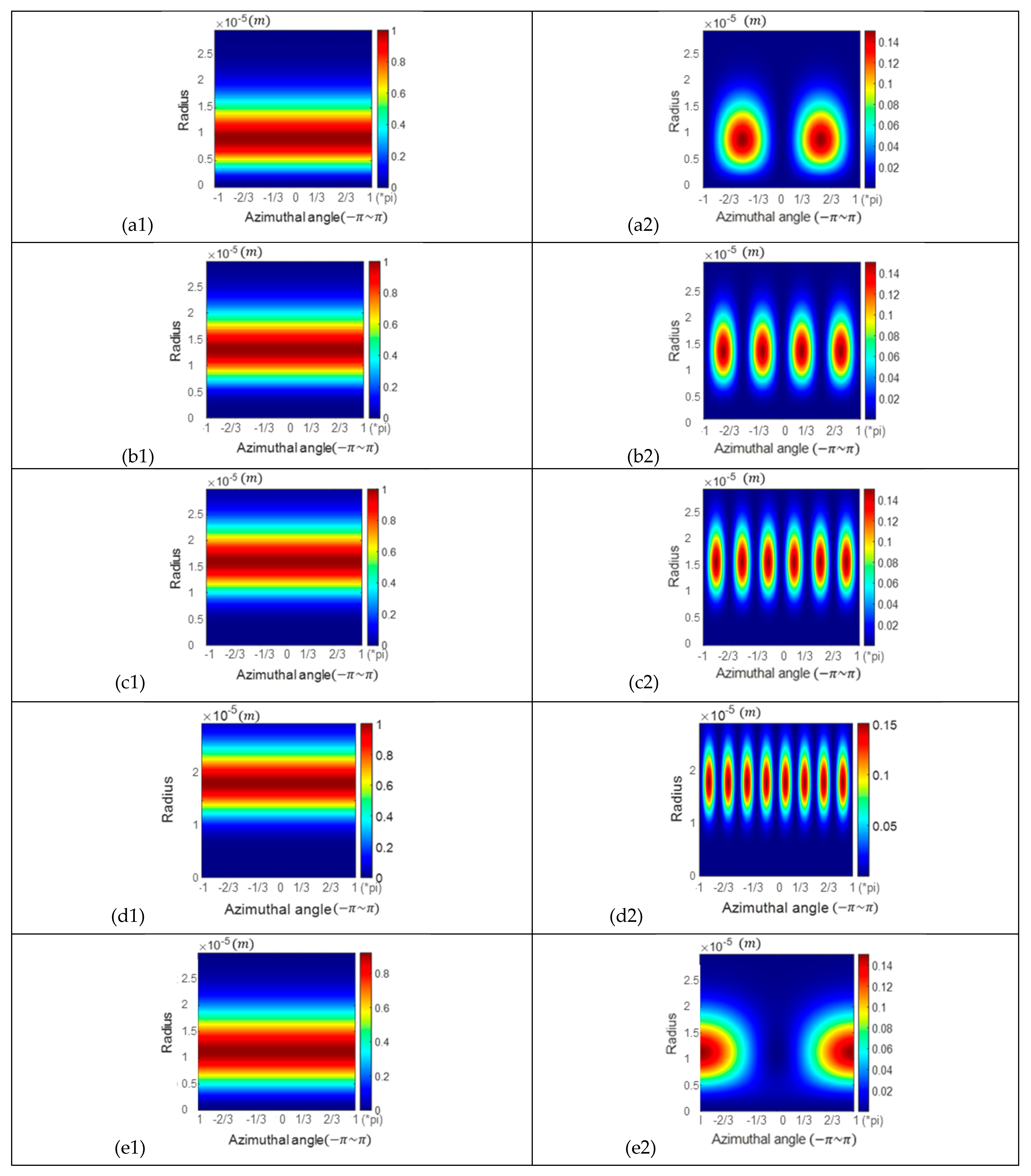
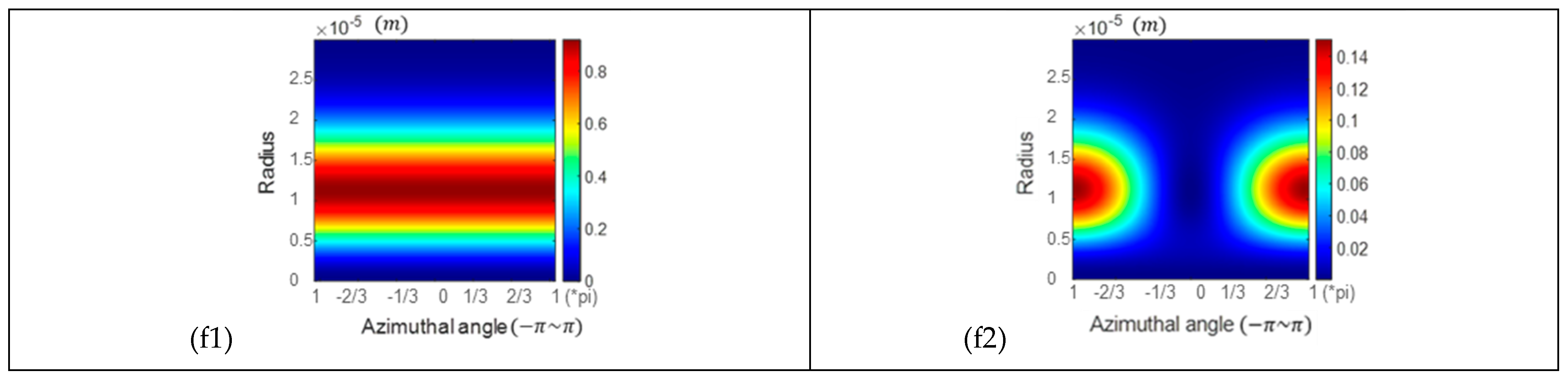
3.2. Intensity Distribution of the Incident Beam and the Optical Field Reflected at the Brewster Angle in Azimuthal and Radial Coordinates ()
4. Discussion
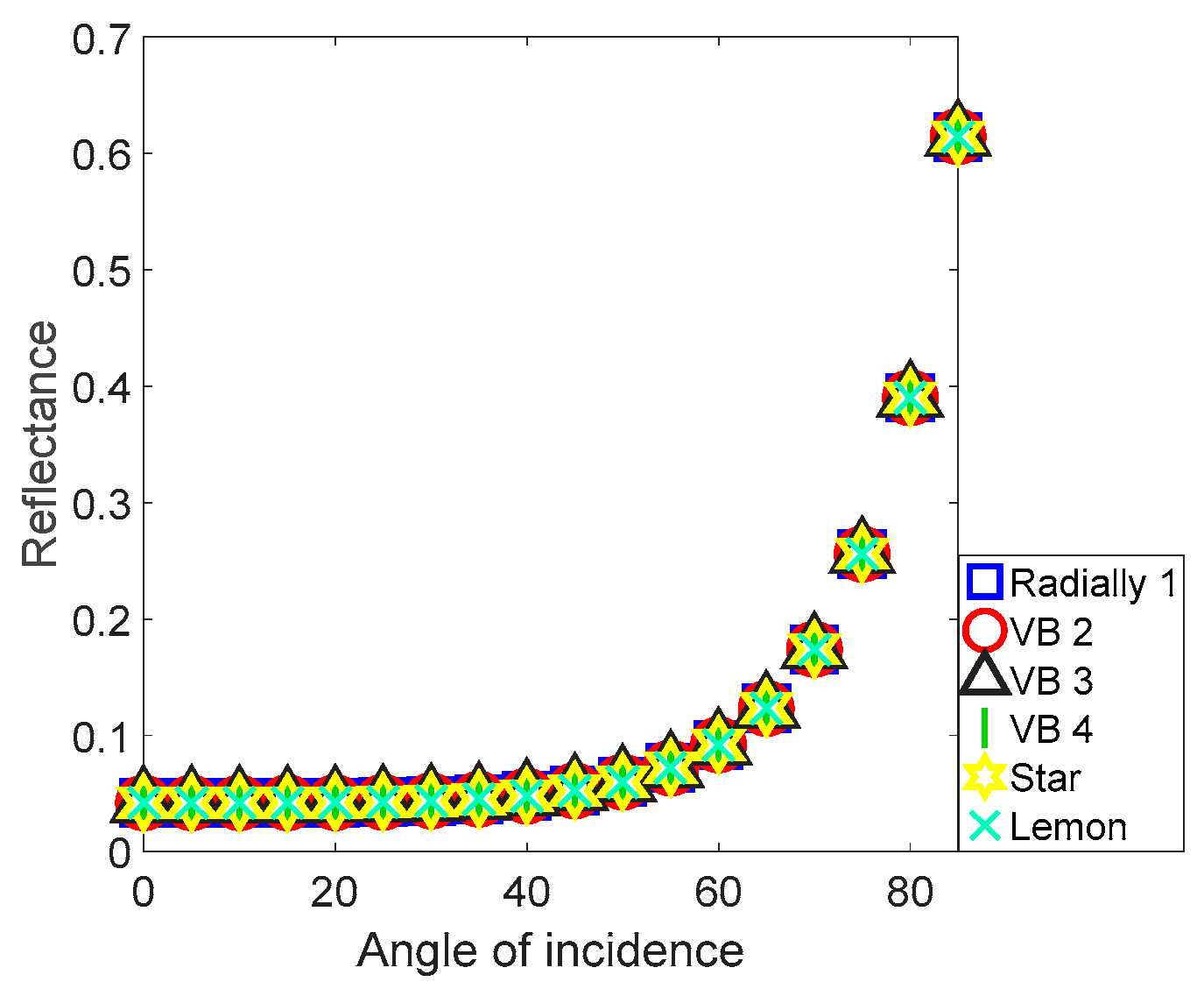
4.1. Reflectance Variation across Incident Angles from 1° to 85°
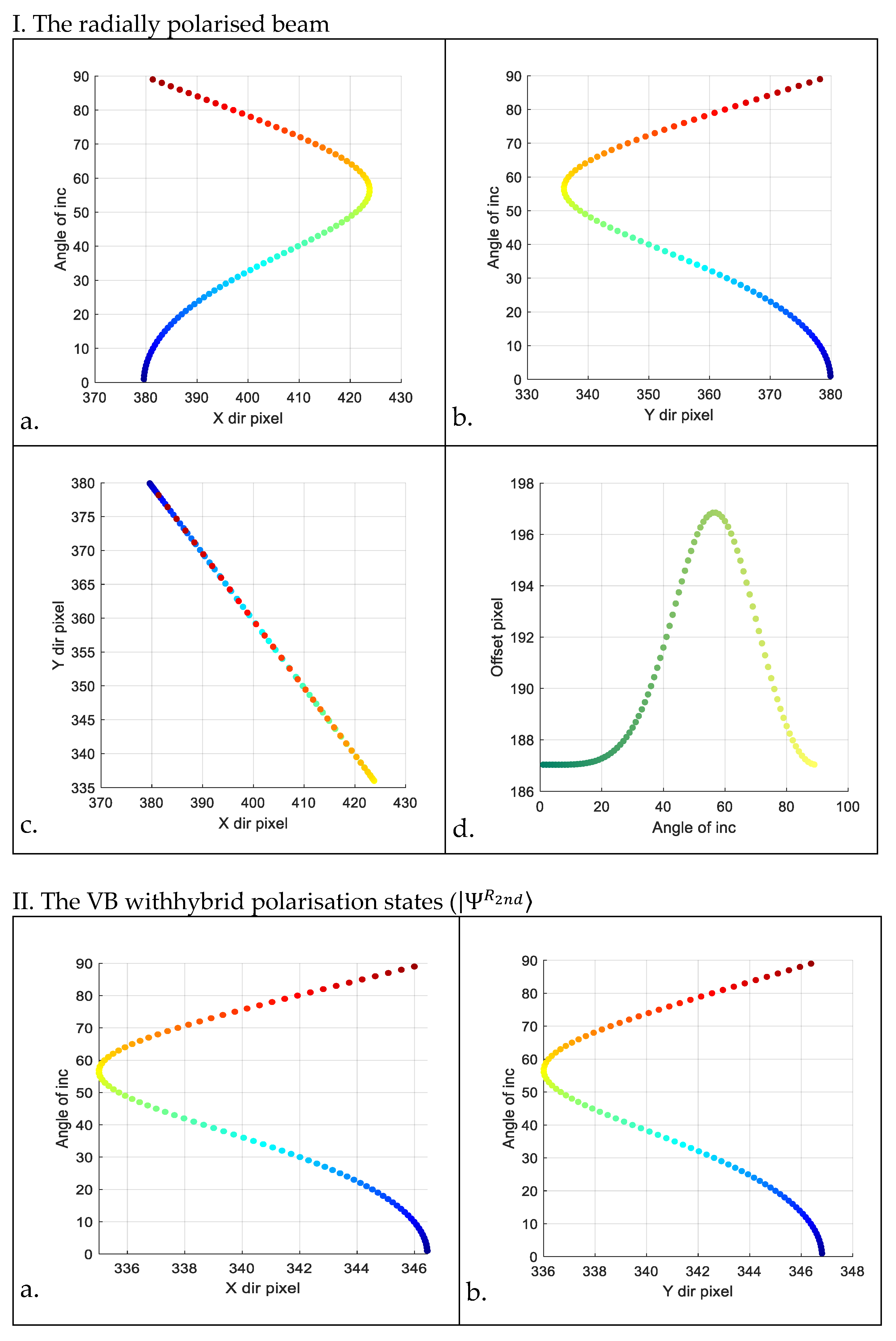
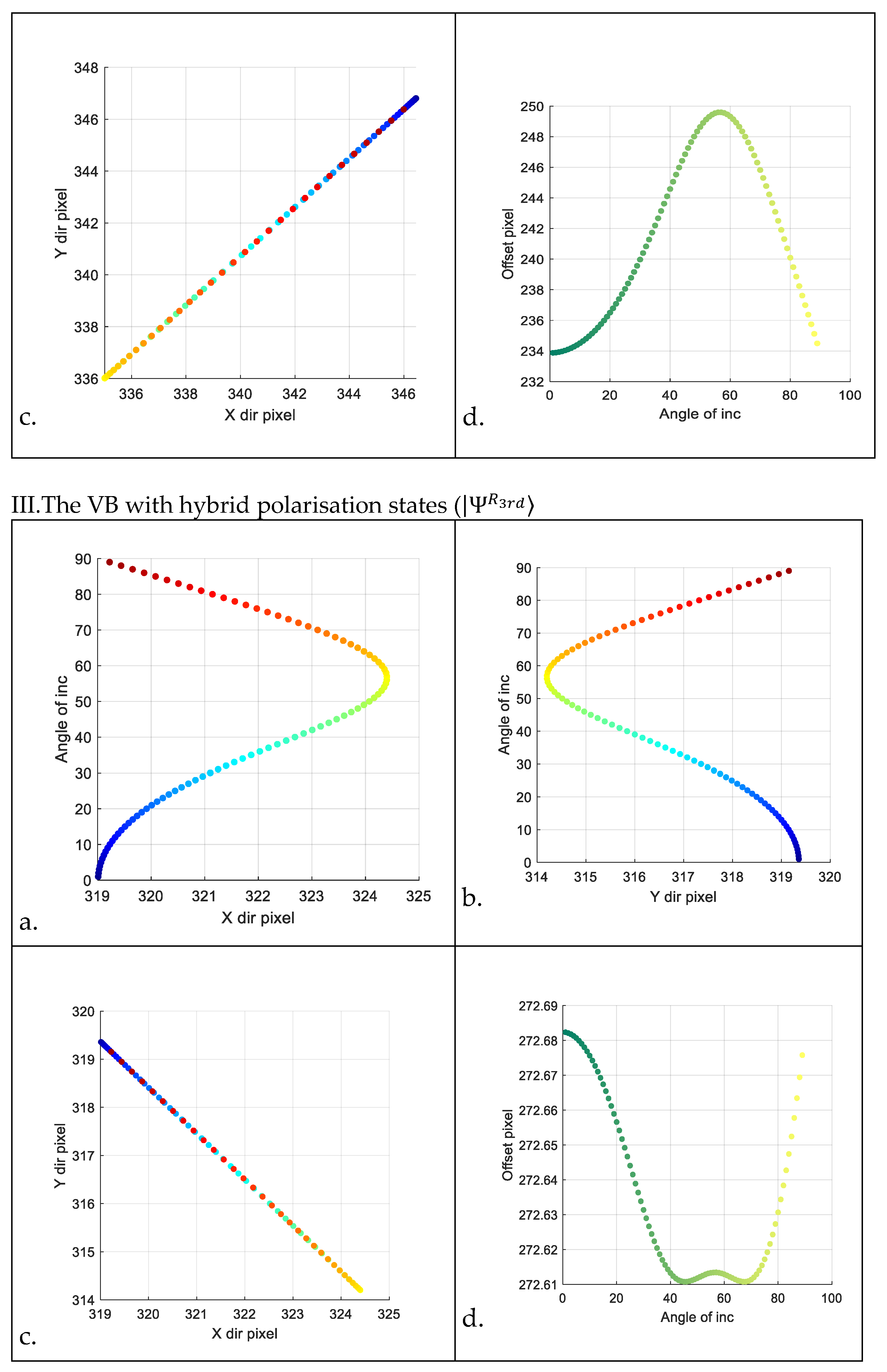
4.2. Shift in the Intensity Centroid of Reflected Beams across Incident Angles from 1° to 89°
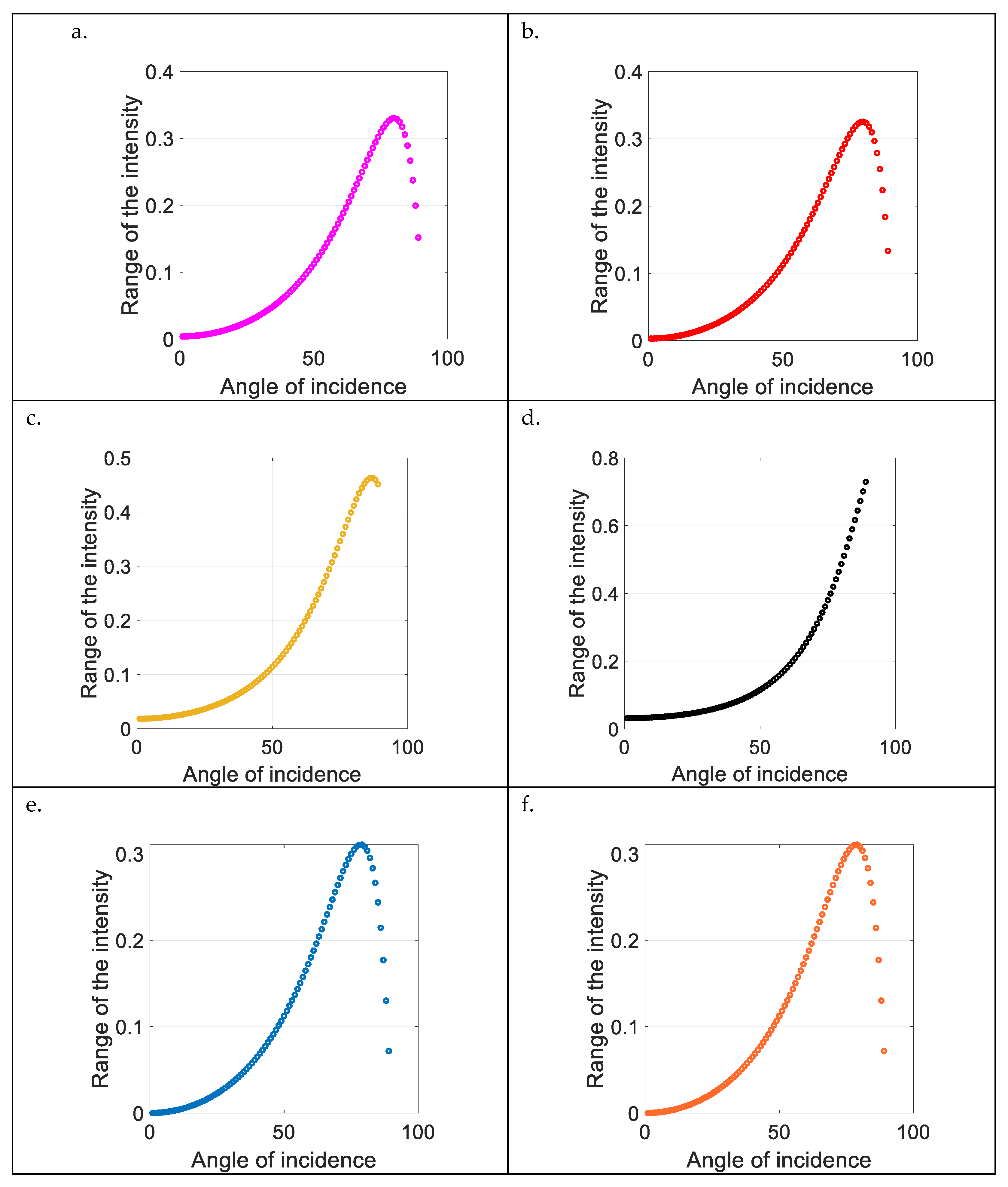
4.3. Range of the Intensity of the Reflected Fields in the () Coordinates
- Except for the VB with hybrid states of polarisation , the trend of the other five types of beams shows multivalued properties;
- Range of the intensity of the VB with hybrid states of polarisation is greater than that of other beams;
- For the four types of VBs, the higher the modulus of OAM carried by their eigenstates, the better the performance in deducing the incident angle from the intensity range;
- The trends shown in graphs (e) and (f) of the lemon’-polarised and ‘star’-polarised vortex beams are the same.
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Kolb, A.; Barth, E.; Koch, R.; Larsen, R. Time-of-flight cameras in computer graphics. Comput. Gr. Forum 2010, 29, 141–159. [Google Scholar] [CrossRef]
- Sarbolandi, H.; Plack, M.; Kolb, A. Pulse Based Time-of-Flight Range Sensing. Sensors 2018, 18, 1679. [Google Scholar] [CrossRef]
- Lange, R.; Seitz, P. Solid-state time-of-flight range camera. IEEE J. Quantum Electron. 2001, 37, 390–397. [Google Scholar] [CrossRef]
- Hansard, M.; Lee, S.; Choi, O.; Horaud, R.P. Time-of-Flight Cameras: Principles, Methods and Applications; Springer Science & Business Media: Berlin/Heidelberg, Germany, 2012. [Google Scholar]
- Uttam, D.; Culshaw, B. Precision time domain reflectometry in optical fiber systems using a frequency modulated continuous wave ranging technique. J. Light. Technol. 1985, 3, 971–977. [Google Scholar] [CrossRef]
- Wojtkiewicz, A.; Misiurewicz, J.; Nalecz, M.; Jedrzejewski, K.; Kulpa, K. Two-dimensional signal processing in FMCW radars. In Proceedings of the XXth National Conference on Circuit Theory and Electronic Networks; University of Mining and Metallurgy: Kolobrzeg, Poland, 1997; pp. 475–480. [Google Scholar]
- Elsayed, H.; Shaker, A. From Stationary to Mobile: Unleashing the Full Potential of Terrestrial LiDAR through Sensor Integration. Can. J. Remote Sens. 2023, 49, 2285778. [Google Scholar] [CrossRef]
- Guo, Q.; Su, Y.; Hu, T. LiDAR Principles, Processing and Applications in Forest Ecology; Elsevier Science: Amsterdam, The Netherlands, 2023. [Google Scholar]
- Wang, R. 3D building modeling using images and LiDAR: A review. Int. J. Image Data Fusion 2013, 4, 273–292. [Google Scholar] [CrossRef]
- Li, Y.; Zhao, L.; Chen, Y.; Zhang, N.; Fan, H.; Zhang, Z. 3D LiDAR and multi-technology collaboration for preservation of built heritage in China: A review. Int. J. Appl. Earth Obs. Geoinf. 2023, 116, 103156. [Google Scholar] [CrossRef]
- Li, Y.; Ibanez-Guzman, J. Lidar for autonomous driving: The principles, challenges, and trends for automotive lidar and perception systems. IEEE Signal Process. Mag. 2020, 37, 50–61. [Google Scholar] [CrossRef]
- Di Stefano, F.; Chiappini, S.; Gorreja, A.; Balestra, M.; Pierdicca, R. Mobile 3D scan LiDAR: A literature review. Geomat. Nat. Hazards Risk 2021, 12, 2387–2429. [Google Scholar] [CrossRef]
- Berezhnyy, I. A combined diffraction and geometrical optics approach for lidar overlap function computation. Opt. Lasers Eng. 2009, 47, 855–859. [Google Scholar] [CrossRef]
- Nape, I.; Singh, K.; Klug, A.; Buono, W.; Rosales-Guzman, C.; McWilliam, A.; Franke-Arnold, S.; Kritzinger, A.; Forbes, P.; Dudley, A.; et al. Revealing the invariance of vectorial structured light in complex media. Nat. Photonics 2022, 16, 538–546. [Google Scholar] [CrossRef]
- Yu, W.; Pi, H.; Taylor, M.; Yan, J. Geometric Representation of Vector Vortex Beams: The Total Angular Momentum-Conserving Poincaré Sphere and Its Braid Clusters. Photonics 2023, 10, 1276. [Google Scholar] [CrossRef]
- Cvijetic, N.; Milione, G.; Ip, E.; Wang, T. Detecting lateral motion using light’s orbital angular momentum. Sci. Rep. 2015, 5, 15422. [Google Scholar] [CrossRef]
- Fang, L.; Wan, Z.; Forbes, A.; Wang, J. Vectorial doppler metrology. Nat. Commun. 2021, 12, 4186. [Google Scholar] [CrossRef] [PubMed]
- Fu, S.; Guo, C.; Liu, G.; Li, Y.; Yin, H.; Li, Z.; Chen, Z. Spin-orbit optical Hall effect. Phys. Rev. Lett. 2019, 123, 243904. [Google Scholar] [CrossRef] [PubMed]
- Ahlawat, L.; Kishor, K.; Sinha, R.K. Photonic spin Hall effect-based ultra-sensitive refractive index sensor for haemoglobin sensing applications. Opt. Laser Technol. 2024, 170, 110183. [Google Scholar] [CrossRef]
- Bliokh, K.Y.; Nori, F. Relativistic hall effect. Phys. Rev. Lett. 2012, 108, 120403. [Google Scholar] [CrossRef] [PubMed]
- Jhajj, N.; Larkin, I.; Rosenthal, E.W.; Zahedpour, S.; Wahlstrand, J.K.; Milchberg, H.M. Spatiotemporal optical vortices. Phys. Rev. X 2016, 6, 031037. [Google Scholar] [CrossRef]
- Gui, G.; Brooks, N.J.; Kapteyn, H.C.; Murnane, M.M.; Liao, C.T. Second-harmonic generation and the conservation of spatiotemporal orbital angular momentum of light. Nat. Photonics 2021, 15, 608–613. [Google Scholar] [CrossRef]
- Gui, G.; Brooks, N.J.; Wang, B.; Kapteyn, H.C.; Murnane, M.M.; Liao, C.T. Single-frame characterization of ultrafast pulses with spatiotemporal orbital angular momentum. ACS Photonics 2022, 9, 2802–2808. [Google Scholar] [CrossRef] [PubMed]
- Mazanov, M.; Sugic, D.; Alonso, M.A.; Nori, F.; Bliokh, K.Y. Transverse shifts and time delays of spatiotemporal vortex pulses reflected and refracted at a planar interface. Nanophotonics 2022, 11, 737–744. [Google Scholar] [CrossRef]
- Hosten, O.; Kwiat, P. Observation of the spin Hall effect of light via weak measurements. Science 2008, 319, 787–790. [Google Scholar] [CrossRef] [PubMed]
- Bliokh, K.Y.; Bliokh, Y.P. Polarization, transverse shifts, and angular momentum conservation laws in partial reflection and refraction of an electromagnetic wave packet. Phys. Review. E Stat. Nonlinear Soft Matter Phys. 2006, 75, 066609. [Google Scholar] [CrossRef] [PubMed]
- Li, H.Y.; Wu, Z.S.; Shang, Q.C.; Bai, L.; Li, Z.J. Reflection and transmission of Laguerre Gaussian beam from uniaxial anisotropic multilayered media. Chin. Phys. B 2017, 26, 034204. [Google Scholar] [CrossRef]
- Zhen, W.; Wang, X.L.; Ding, J.; Wang, H.T. Controlling the symmetry of the photonic spin Hall effect by an optical vortex pair. Phys. Rev. A 2023, 108, 023514. [Google Scholar] [CrossRef]
- Ou, J.; Jiang, Y.; Zhang, J.; He, Y. Reflection of Laguerre–Gaussian beams carrying orbital angular momentum: A full Taylor expanded solution. J. Opt. Soc. Am. A 2013, 30, 2561–2571. [Google Scholar] [CrossRef]
- Andrews, D.L.; Babiker, M. (Eds.) The Angular Momentum of Light; Cambridge University Press: Cambridge, UK, 2012. [Google Scholar]
- Goodman, J.W. Introduction to Fourier Optics; Roberts and Company publishers: Greenwood Village, CO, USA, 2005. [Google Scholar]
- Paschotta, R. Article on Fourier Optics in the RP Photonics Encyclopedia. Available online: https://www.rp-photonics.com/fourier_optics.html (accessed on 29 July 2024).
- Zhang, J.; Huang, S.J.; Zhu, F.Q.; Shao, W.; Chen, M.S. Dimensional properties of Laguerre–Gaussian vortex beams. Appl. Opt. 2017, 56, 3556–3561. [Google Scholar] [CrossRef]
- Hall, D.G. Vector-beam solutions of Maxwell’s wave equation. Opt. Lett. 1996, 21, 9–11. [Google Scholar] [CrossRef] [PubMed]
- Galvez, E.J.; Khadka, S.; Schubert, W.H.; Nomoto, S. Poincaré-beam patterns produced by nonseparable superpositions of Laguerre–Gauss and polarization modes of light. Appl. Opt. 2012, 51, 2925–2934. [Google Scholar] [CrossRef]
- Fu, S.; Gao, C. Vector Beams and Vectorial Vortex Beams. In Optical Vortex Beams. Advances in Optics and Optoelectronics; Springer: Singapore, 2023. [Google Scholar] [CrossRef]
- Milione, G.; Sztul, H.I.; Nolan, D.A.; Alfano, R.R. Higher-order Poincaré sphere, Stokes parameters, and the angular momentum of light. Phys. Rev. Lett. 2011, 107, 053601. [Google Scholar] [CrossRef]
- Cardano, F.; Karimi, E.; Marrucci, L.; de Lisio, C.; Santamato, E. Generation and dynamics of optical beams with polarization singularities. Opt. Express 2013, 21, 8815–8820. [Google Scholar] [CrossRef] [PubMed]
- Rosales-Guzmán, C.; Ndagano, B.; Forbes, A. A review of complex vector light fields and their applications. J. Opt. 2018, 20, 123001. [Google Scholar] [CrossRef]
- Paschotta, R. Article on Brewster’s Angle in the RP Photonics Encyclopedia. Available online: https://www.rp-photonics.com/brewster_s_angle.html (accessed on 29 July 2024).
- Born, M.; Wolf, E. Principles of Optics: Electromagnetic Theory of Propagation, Interference and Diffraction of Light; Elsevier: Amsterdam, The Netherlands, 2013. [Google Scholar]




Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yu, W.; Yan, J. Modelling and Analysis of Vector and Vector Vortex Beams Reflection for Optical Sensing. Photonics 2024, 11, 729. https://doi.org/10.3390/photonics11080729
Yu W, Yan J. Modelling and Analysis of Vector and Vector Vortex Beams Reflection for Optical Sensing. Photonics. 2024; 11(8):729. https://doi.org/10.3390/photonics11080729
Chicago/Turabian StyleYu, Wangke, and Jize Yan. 2024. "Modelling and Analysis of Vector and Vector Vortex Beams Reflection for Optical Sensing" Photonics 11, no. 8: 729. https://doi.org/10.3390/photonics11080729
APA StyleYu, W., & Yan, J. (2024). Modelling and Analysis of Vector and Vector Vortex Beams Reflection for Optical Sensing. Photonics, 11(8), 729. https://doi.org/10.3390/photonics11080729




