Improved Structured Light Centerline Extraction Algorithm Based on Unilateral Tracing
Abstract
1. Introduction
2. Materials and Methods
2.1. Image Preprocessing
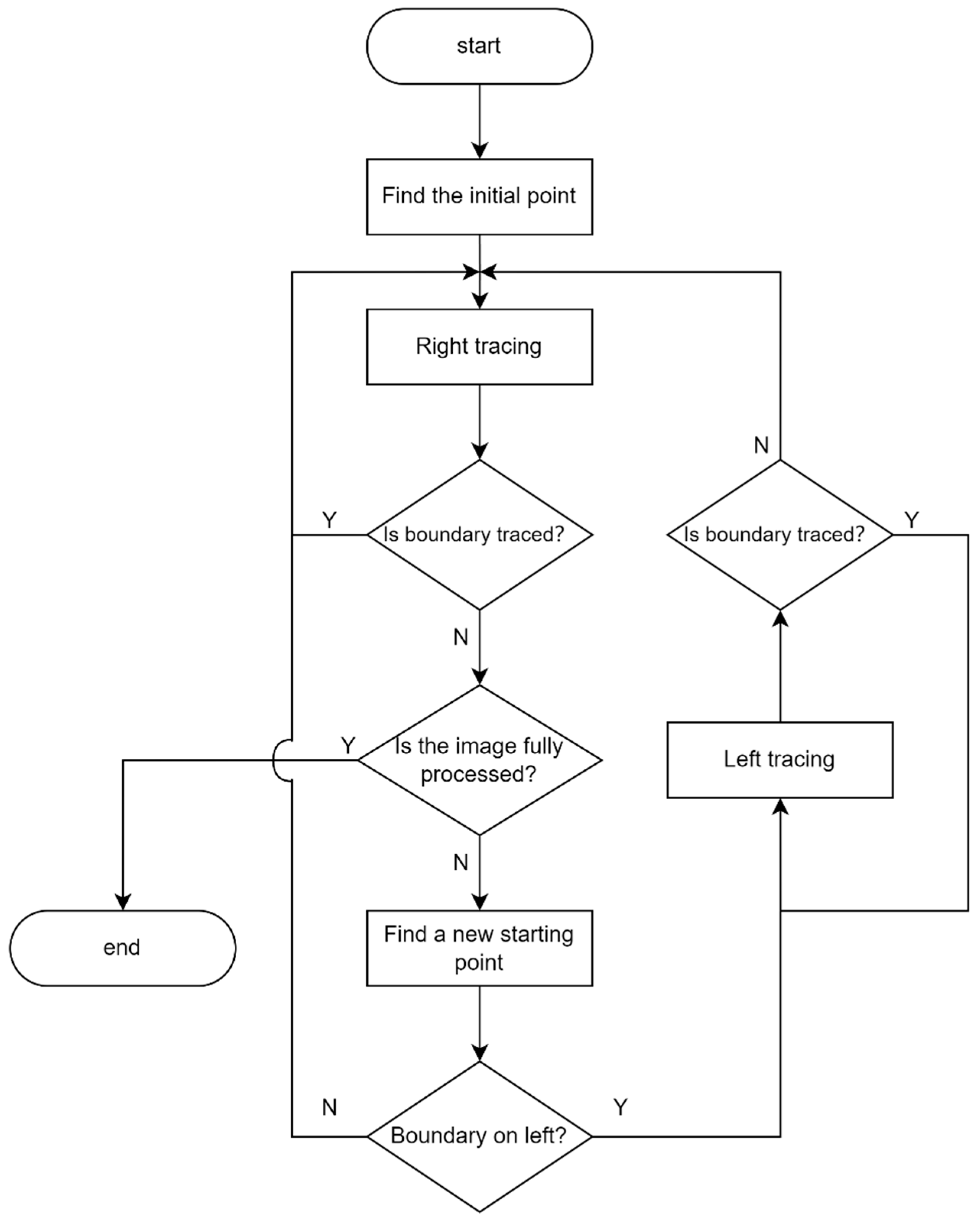
2.2. Improved Boundary-Tracing Algorithm
- (1)
- Traverse the image to find the first pixel point greater than a threshold value as the starting point.
- (2)
- Take the starting point as the current point and, starting from the pixel point with chain code value 0 (as shown in Figure 2), search clockwise for the next boundary point greater than the threshold value, then set the searched point as the current point.
- (3)
- When the chain code value of the current point is even, subtract 1 from the starting chain code value of the next boundary point search, which corresponds to a counterclockwise rotation of 45°; when it is odd, subtract 2 from the chain code value, corresponding to a counterclockwise rotation of 90°.
- (4)
- Repeat steps (2) and (3) until the next boundary point searched is the starting point, then end the boundary tracing.
- (1)
- Search for a pixel point with a grayscale value not equal to 0 from top to bottom and from left to right in the preprocessed image as the initial point, mark this point as , and set it as the current point.
- (2)
- Perform rightward boundary tracing from the current point, then set the traced boundary point as the new current point. When there is no pixel that meets the criteria, stop tracing and repeat step (1) to find a new initial point.
- (3)
- For the new initial point , check the left-side pixels. If there are pixels satisfying the boundary conditions among the three pixels to the left (u, v − 1), (u + 1, v − 1), (u + 2, v − 1), consider that there is also a laser stripe on the left side of the new initial point, mark this point as , and perform leftward boundary tracing from .
- (4)
- After tracing the upper boundary of the laser stripe to the left, perform rightward boundary tracing from .
- (5)
- Repeat steps (2), (3), and (4) until completing the upper boundary tracing of the laser stripe by traversing the columns of the image.
2.3. Initial Center Point Determination Based on the Gray-Level Centroid Method
2.4. Center Point Optimization Based on the Hessian Matrix
3. Results and Discussion
3.1. Line-Structured Light Center Point Extraction Experiment
3.2. Algorithm Accuracy and Efficiency Experiment
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Nguyen, T.T.; Slaughter, D.C.; Max, N.; Maloof, J.N.; Sinha, N. Structured Light-Based 3D Reconstruction System for Plants. Sensors 2015, 15, 18587–18612. [Google Scholar] [CrossRef] [PubMed]
- Cao, X.; Xie, W.; Ahmed, S.M.; Li, C.R. Defect detection method for rail surface based on line-structured light. Measurement 2020, 159, 107771. [Google Scholar] [CrossRef]
- Park, C.S.; Chang, M. Reverse engineering with a structured light system. Comput. Ind. Eng. 2009, 57, 1377–1384. [Google Scholar] [CrossRef]
- Lyvers, E.P.; Mitchell, O.R.; Akey, M.L.; Reeves, A.P. Subpixel measurements using a moment-based edge operator. IEEE Trans. Pattern Anal. Mach. Intell. 1989, 11, 1293–1309. [Google Scholar] [CrossRef]
- Jiang, C.; Li, W.-L.; Wu, A.; Yu, W.-Y. A novel centerline extraction algorithm for a laser stripe applied for turbine blade inspection. Meas. Sci. Technol. 2020, 31, 095403. [Google Scholar] [CrossRef]
- Li, Y.; Zhou, J.; Huang, F.; Liu, L. Sub-Pixel Extraction of Laser Stripe Center Using an Improved Gray-Gravity Method †. Sensors 2017, 17, 814. [Google Scholar] [CrossRef]
- Baumgartner, A.; Steger, C.; Mayer, H.; Eckstein, W.; Ebner, H. Automatic road extraction based on multi-scale, grouping, and context. Photogramm. Eng. Remote Sens. 1999, 65, 777–786. [Google Scholar]
- Su, X.Q.; Xiong, X.M. High-speed method for extracting center of line structured light. J. Comput. Appl. 2016, 36, 238–242. [Google Scholar]
- Xia, X.; Fu, S.P.; Xia, R.B.; Zhao, J.B.; Hou, W.G. Extraction algorithm of line structured light center based on improved gray gravity method. Laser J. 2024, 45, 75–79. [Google Scholar]
- Zhou, X.M.; Wang, H.; Li, L.J.; Zheng, S.C.; Fu, J.J.; Tian, Q.H. Line laser center extraction method based on the improved thinning method. Laser J. 2023, 44, 70–74. [Google Scholar]
- Ye, C.; Feng, W.; Wang, Q.; Wang, C.; Pan, B.; Xie, Y.; Hu, Y.; Chen, J. Laser stripe segmentation and centerline extraction based on 3D scanning imaging. Appl. Opt. 2022, 61, 5409–5418. [Google Scholar] [CrossRef]
- Wang, R.J.; Huang, M.M.; Ma, L.D. Research on Center Extraction Algorithm of Line Structured Light Based on Unilateral Tracking and Midpoint Prediction. Chin. J. Lasers 2024, 51, 108–118. [Google Scholar]
- Li, W.; Peng, G.; Gao, X.; Ding, C. Fast Extraction Algorithm for Line Laser Strip Centers. Chin. J. Lasers 2020, 47, 192–199. [Google Scholar]
- Wu, Y.B.; Chen, D.L.; Yang, C.; He, W.; Sun, X.J. Multi-Line Structured Light Center Extraction Based on Improved Steger Algorithm. Appl. Laser 2023, 43, 188–195. [Google Scholar]
- Izadpanahkakhk, M.; Razavi, S.M.; Taghipour-Gorjikolaie, M.; Zahiri, S.H.; Uncini, A. Deep Region of Interest and Feature Extraction Models for Palmprint Verification Using Convolutional Neural Networks Transfer Learning. Appl. Sci. 2018, 8, 1210. [Google Scholar] [CrossRef]
- Yu, J. Based on Gaussian filter to improve the effect of the images in Gaussian noise and pepper noise. J. Phys. Conf. Ser. 2023, 2580, 012062. [Google Scholar] [CrossRef]
- Seo, J.; Chae, S.; Shim, J.; Kim, D.; Cheong, C.; Han, T.-D. Fast Contour-Tracing Algorithm Based on a Pixel-Following Method for Image Sensors. Sensors 2016, 16, 353. [Google Scholar] [CrossRef] [PubMed]
- Liu, J.; Liu, L.H. Laser Stripe Center Extraction Based on Hessian Matrix and Regional Growth. Laser Optoelectron. 2019, 56, 113–118. [Google Scholar]
- Zhang, T.Y.; Sun, C.Y. A fast parallel algorithm for thinning digital patterns. CACM 1984, 27, 236–239. [Google Scholar] [CrossRef]
- Zhang, J.; Lu, Y.H.; Liang, L.P.; Zhao, C.Y. Optimization Method of Adaptive Center Extraction of Linear Structured Light Stripe. Appl. Laser 2019, 39, 28–1034. [Google Scholar]









| Algorithm | Grayscale Centroid | Steger | Improved Thinning Method | Proposed Algorithm |
|---|---|---|---|---|
| RMSE (pixels) | 0.307 | 0.286 | 0.304 | 0.180 |
| Algorithm | Grayscale Centroid | Steger | Improved Thinning Method | Proposed Algorithm |
|---|---|---|---|---|
| Runtime (s) | 0.492 | 4.97 | 3.05 | 0.111 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Huang, Y.; Kang, W.; Lu, Z. Improved Structured Light Centerline Extraction Algorithm Based on Unilateral Tracing. Photonics 2024, 11, 723. https://doi.org/10.3390/photonics11080723
Huang Y, Kang W, Lu Z. Improved Structured Light Centerline Extraction Algorithm Based on Unilateral Tracing. Photonics. 2024; 11(8):723. https://doi.org/10.3390/photonics11080723
Chicago/Turabian StyleHuang, Yu, Wenjing Kang, and Zhengang Lu. 2024. "Improved Structured Light Centerline Extraction Algorithm Based on Unilateral Tracing" Photonics 11, no. 8: 723. https://doi.org/10.3390/photonics11080723
APA StyleHuang, Y., Kang, W., & Lu, Z. (2024). Improved Structured Light Centerline Extraction Algorithm Based on Unilateral Tracing. Photonics, 11(8), 723. https://doi.org/10.3390/photonics11080723






