Unraveling the Dominant Size Effect in Polydisperse Solutions and Maximal Electric Field Enhancement of Gold Nanoparticles
Abstract
1. Introduction
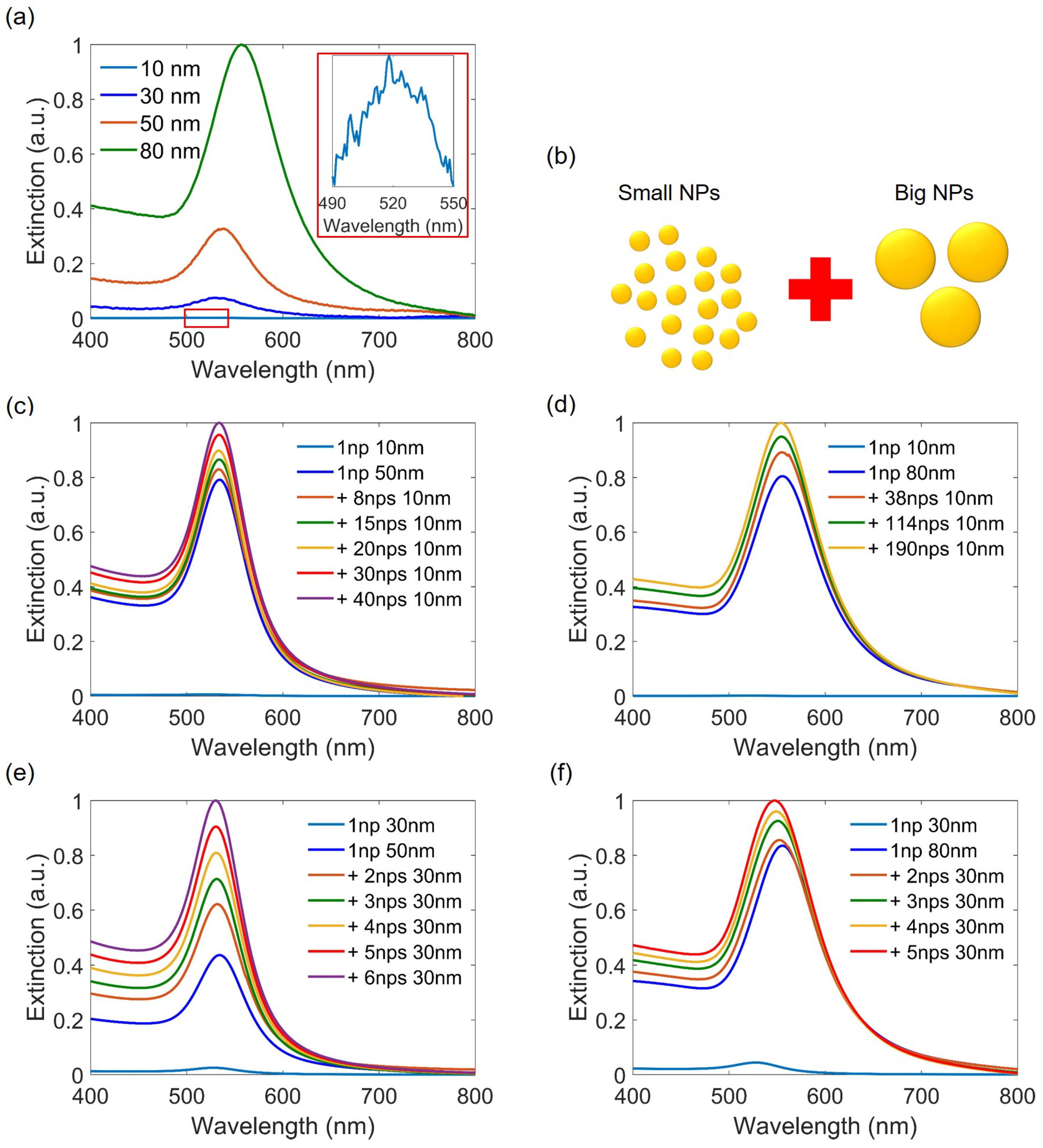
2. Experimental Study of Polydisperse Au NPs
3. Numerical Investigation of Polydisperse Au NPs
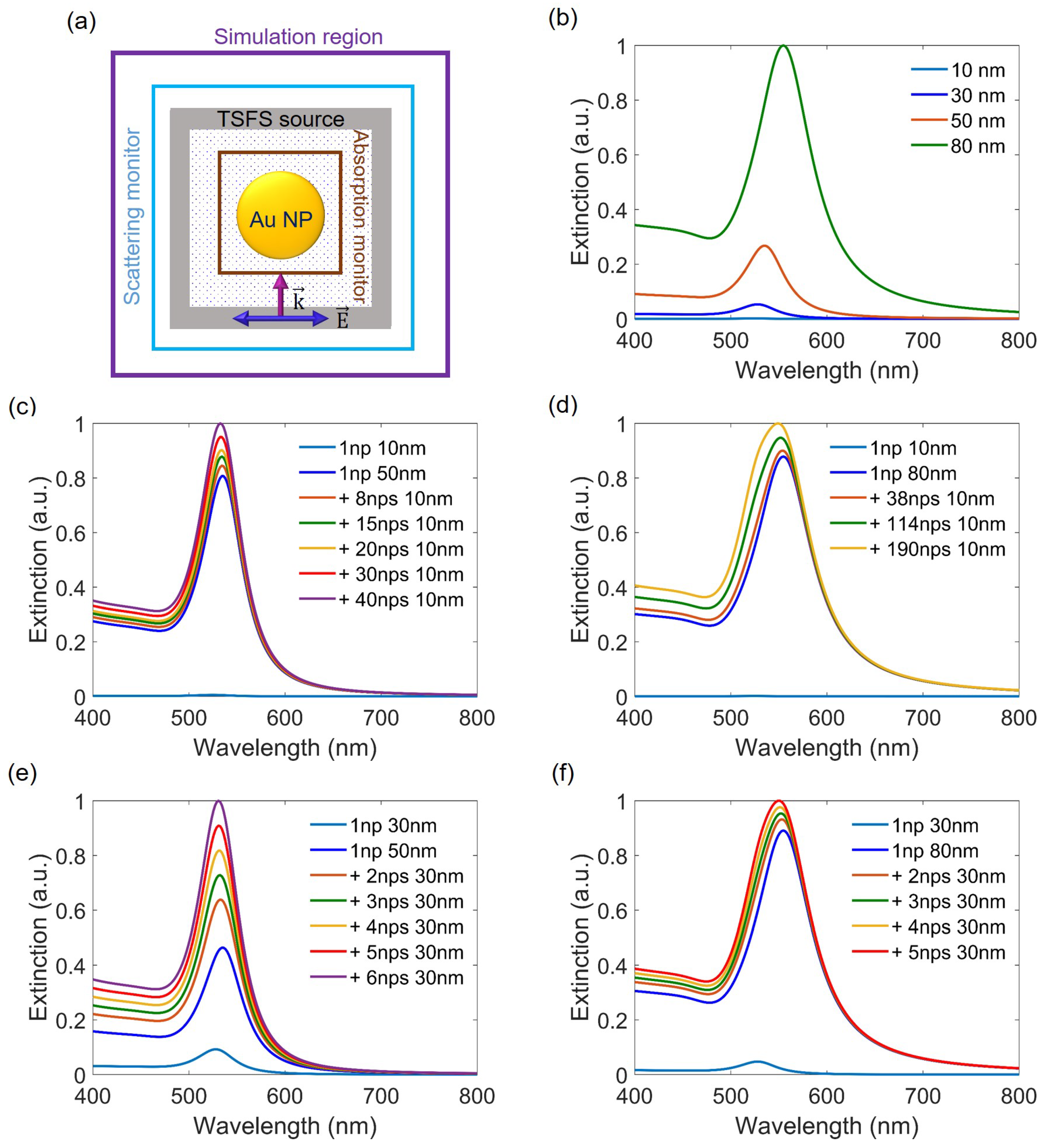
3.1. Simulation Model
3.2. Simulation Results
3.2.1. Optical Properties of Spherical Au NPs
3.2.2. Optical Properties of Spherical Au NPs Mixed with Ellipsoidal Au NPs
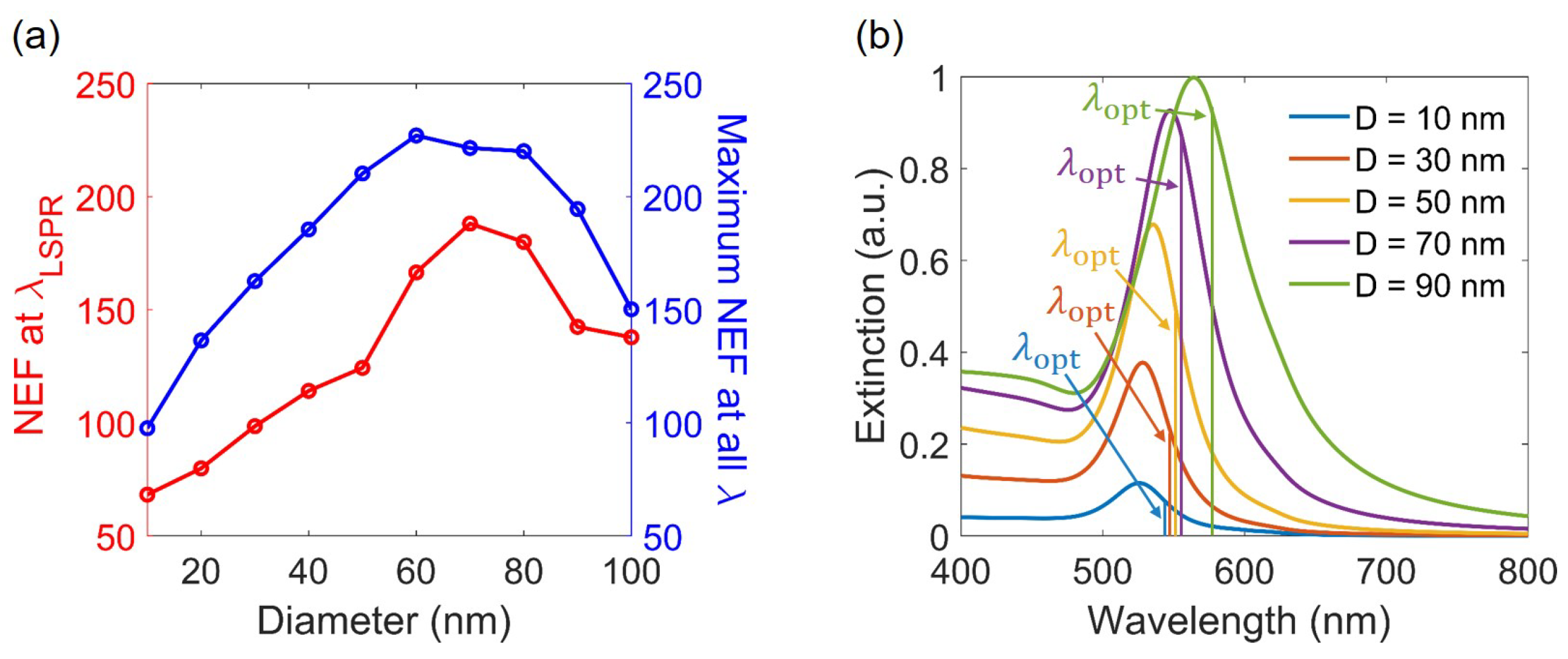
4. Numerical Investigation of NEF Enhancement of Single Spherical Au NP
4.1. Local Electric Field at Resonant Wavelength
4.2. Maximal Local Electric Field at All Wavelengths
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Schmid, G. Nanoparticles: From Theory to Application; John Wiley & Sons: Hoboken, NJ, USA, 2011. [Google Scholar]
- Schmid, G.; Corain, B. Nanoparticulated gold: Syntheses, structures, electronics, and reactivities. Eur. J. Inorg. Chem. 2003, 2003, 3081–3098. [Google Scholar] [CrossRef]
- Abdelhalim, M.A.K.; Mady, M.M.; Ghannam, M.M. Physical properties of different gold nanoparticles: Ultraviolet-visible and fluorescence measurements. J. Nanomed. Nanotechnol. 2012, 3, 178–194. [Google Scholar] [CrossRef]
- Rodrigues, T.S.; da Silva, A.G.; Camargo, P.H. Nanocatalysis by noble metal nanoparticles: Controlled synthesis for the optimization and understanding of activities. J. Mater. Chem. A 2019, 7, 5857–5874. [Google Scholar] [CrossRef]
- Mahmoud, M.A.; O’Neil, D.; El-Sayed, M.A. Hollow and solid metallic nanoparticles in sensing and in nanocatalysis. Chem. Mater. 2014, 26, 44–58. [Google Scholar] [CrossRef]
- Astruc, D. Introduction: Nanoparticles in catalysis. Chem. Rev 2020, 120, 461–463. [Google Scholar] [CrossRef]
- Mubeen, S.; Lee, J.; Lee, W.r.; Singh, N.; Stucky, G.D.; Moskovits, M. On the plasmonic photovoltaic. ACS Nano 2014, 8, 6066–6073. [Google Scholar] [CrossRef] [PubMed]
- Luo, Q.; Zhang, C.; Deng, X.; Zhu, H.; Li, Z.; Wang, Z.; Chen, X.; Huang, S. Plasmonic effects of metallic nanoparticles on enhancing performance of perovskite solar cells. ACS Appl. Mater. Interfaces 2017, 9, 34821–34832. [Google Scholar] [CrossRef] [PubMed]
- Huang, X.; Jain, P.K.; El-Sayed, I.H.; El-Sayed, M.A. Plasmonic photothermal therapy (PPTT) using gold nanoparticles. Lasers Med. Sci. 2008, 23, 217–228. [Google Scholar] [CrossRef]
- Doria, G.; Conde, J.; Veigas, B.; Giestas, L.; Almeida, C.; Assunção, M.; Rosa, J.; Baptista, P.V. Noble metal nanoparticles for biosensing applications. Sensors 2012, 12, 1657–1687. [Google Scholar] [CrossRef]
- Wang, J. Electrochemical biosensing based on noble metal nanoparticles. Microchim. Acta 2012, 177, 245–270. [Google Scholar] [CrossRef]
- Chandrakala, V.; Aruna, V.; Angajala, G. Review on metal nanoparticles as nanocarriers: Current challenges and perspectives in drug delivery systems. Emergent Mater. 2022, 5, 1593–1615. [Google Scholar] [CrossRef]
- Desai, N.; Momin, M.; Khan, T.; Gharat, S.; Ningthoujam, R.S.; Omri, A. Metallic nanoparticles as drug delivery system for the treatment of cancer. Expert Opin. Drug Deliv. 2021, 18, 1261–1290. [Google Scholar] [CrossRef] [PubMed]
- Enrichi, F.; Quandt, A.; Righini, G.C. Plasmonic enhanced solar cells: Summary of possible strategies and recent results. Renew. Sustain. Energy Rev. 2018, 82, 2433–2439. [Google Scholar] [CrossRef]
- Chatterjee, D.K.; Diagaradjane, P.; Krishnan, S. Nanoparticle-mediated hyperthermia in cancer therapy. Ther. Deliv. 2011, 2, 1001–1014. [Google Scholar] [CrossRef]
- Yaraki, M.T.; Tan, Y.N. Metal nanoparticles-enhanced biosensors: Synthesis, design and applications in fluorescence enhancement and surface-enhanced Raman scattering. Chem. Asian J. 2020, 15, 3180–3208. [Google Scholar] [CrossRef]
- Bek, A.; Jansen, R.; Ringler, M.; Mayilo, S.; Klar, T.A.; Feldmann, J. Fluorescence enhancement in hot spots of AFM-designed gold nanoparticle sandwiches. Nano Lett. 2008, 8, 485–490. [Google Scholar] [CrossRef]
- Wang, Z.; Meng, X.; Kildishev, A.V.; Boltasseva, A.; Shalaev, V.M. Nanolasers enabled by metallic nanoparticles: From spasers to random lasers. Laser Photonics Rev. 2017, 11, 1700212. [Google Scholar] [CrossRef]
- Long, L.; He, D.; Bao, W.; Feng, M.; Zhang, P.; Zhang, D.; Chen, S. Localized surface plasmon resonance improved lasing performance of Ag nanoparticles/organic dye random laser. J. Alloys Compd. 2017, 693, 876–881. [Google Scholar] [CrossRef]
- Grand, J.; Auguié, B.; Le Ru, E. Combined extinction and absorption UV–vis spectroscopy reveals shape imperfections of metallic nanoparticles. Anal. Chem. 2019, 91, 14639–14648. [Google Scholar] [CrossRef]
- Amendola, V.; Meneghetti, M. Size evaluation of gold nanoparticles by UV- vis spectroscopy. J. Phys. Chem. C 2009, 113, 4277–4285. [Google Scholar] [CrossRef]
- Gaikwad, A.V.; Verschuren, P.; Eiser, E.; Rothenberg, G. A simple method for measuring the size of metal nanoclusters in solution. J. Phys. Chem. B 2006, 110, 17437–17443. [Google Scholar] [CrossRef] [PubMed]
- Njoki, P.N.; Lim, I.I.S.; Mott, D.; Park, H.Y.; Khan, B.; Mishra, S.; Sujakumar, R.; Luo, J.; Zhong, C.J. Size correlation of optical and spectroscopic properties for gold nanoparticles. J. Phys. Chem. C 2007, 111, 14664–14669. [Google Scholar] [CrossRef]
- Tomaszewska, E.; Soliwoda, K.; Kadziola, K.; Tkacz-Szczesna, B.; Celichowski, G.; Cichomski, M.; Szmaja, W.; Grobelny, J. Detection limits of DLS and UV-Vis spectroscopy in characterization of polydisperse nanoparticles colloids. J. Nanomater. 2013, 2013, 313081. [Google Scholar] [CrossRef]
- Michaels, A.M.; Jiang, n.; Brus, L. Ag nanocrystal junctions as the site for surface-enhanced Raman scattering of single rhodamine 6G molecules. J. Phys. Chem. B 2000, 104, 11965–11971. [Google Scholar] [CrossRef]
- Schatz, G.C.; Young, M.A.; Van Duyne, R.P. Surface-Enhanced Raman Scattering: Physics and Applications; Springer: Berlin, Germany, 2006; Volume 103. [Google Scholar]
- Liu, Z.; Hou, W.; Pavaskar, P.; Aykol, M.; Cronin, S.B. Plasmon resonant enhancement of photocatalytic water splitting under visible illumination. Nano Lett. 2011, 11, 1111–1116. [Google Scholar] [CrossRef] [PubMed]
- Butet, J.; Brevet, P.F.; Martin, O.J. Optical second harmonic generation in plasmonic nanostructures: From fundamental principles to advanced applications. ACS Nano 2015, 9, 10545–10562. [Google Scholar] [CrossRef] [PubMed]
- Liu, T.M.; Tai, S.P.; Yu, C.H.; Wen, Y.C.; Chu, S.W.; Chen, L.J.; Prasad, M.R.; Lin, K.J.; Sun, C.K. Measuring plasmon-resonance enhanced third-harmonic χ (3) of Ag nanoparticles. Appl. Phys. Lett. 2006, 89, 043122. [Google Scholar] [CrossRef]
- Ma, W.; Yao, J.; Yang, H.; Liu, J.; Li, F.; Hilton, J.; Lin, Q. Effects of vertex truncation of polyhedral nanostructures on localized surface plasmon resonance. Opt. Express 2009, 17, 14967–14976. [Google Scholar] [CrossRef] [PubMed]
- Khlebtsov, B.N.; Burov, A.M.; Zarkov, S.V.; Khlebtsov, N.G. Surface-enhanced Raman scattering from Au nanorods, nanotriangles, and nanostars with tuned plasmon resonances. Phys. Chem. Chem. Phys. 2023, 25, 30903–30913. [Google Scholar] [CrossRef]
- Slablab, A.; Le Xuan, L.; Zielinski, M.; De Wilde, Y.; Jacques, V.; Chauvat, D.; Roch, J.F. Second-harmonic generation from coupled plasmon modes in a single dimer of gold nanospheres. Opt. Express 2012, 20, 220–227. [Google Scholar] [CrossRef]
- Huang, Y.; Ma, L.; Hou, M.; Li, J.; Xie, Z.; Zhang, Z. Hybridized plasmon modes and near-field enhancement of metallic nanoparticle-dimer on a mirror. Sci. Rep. 2016, 6, 30011. [Google Scholar] [CrossRef]
- Messinger, B.J.; Von Raben, K.U.; Chang, R.K.; Barber, P.W. Local fields at the surface of noble-metal microspheres. Phys. Rev. B 1981, 24, 649. [Google Scholar] [CrossRef]
- Zuloaga, J.; Nordlander, P. On the energy shift between near-field and far-field peak intensities in localized plasmon systems. Nano Lett. 2011, 11, 1280–1283. [Google Scholar] [CrossRef]
- Hong, S.; Li, X. Optimal size of gold nanoparticles for surface-enhanced Raman spectroscopy under different conditions. J. Nanomater. 2013, 2013, 790323. [Google Scholar] [CrossRef]
- Deeb, C.; Zhou, X.; Plain, J.; Wiederrecht, G.P.; Bachelot, R.; Russell, M.; Jain, P.K. Size dependence of the plasmonic near-field measured via single-nanoparticle photoimaging. J. Phys. Chem. C 2013, 117, 10669–10676. [Google Scholar] [CrossRef]
- Mansour, Y.; Battie, Y.; En Naciri, A.; Chaoui, N. Determination of the size distribution of metallic colloids from extinction spectroscopy. Nanomaterials 2021, 11, 2872. [Google Scholar] [CrossRef]
- Klinavičius, T.; Khinevich, N.; Tamulevičienė, A.; Vidal, L.; Tamulevičius, S.; Tamulevičius, T. Deep Learning Methods for Colloidal Silver Nanoparticle Concentration and Size Distribution Determination from UV–Vis Extinction Spectra. J. Phys. Chem. C 2024, 128, 9662–9675. [Google Scholar] [CrossRef]
- Liang, C.C.; Liao, M.Y.; Chen, W.Y.; Cheng, T.C.; Chang, W.H.; Lin, C.H. Plasmonic metallic nanostructures by direct nanoimprinting of gold nanoparticles. Opt. Express 2011, 19, 4768–4776. [Google Scholar] [CrossRef]
- Zhao, J.; Pinchuk, A.O.; McMahon, J.M.; Li, S.; Ausman, L.K.; Atkinson, A.L.; Schatz, G.C. Methods for describing the electromagnetic properties of silver and gold nanoparticles. Acc. Chem. Res. 2008, 41, 1710–1720. [Google Scholar] [CrossRef] [PubMed]
- Iqbal, M.; Usanase, G.; Oulmi, K.; Aberkane, F.; Bendaikha, T.; Fessi, H.; Zine, N.; Agusti, G.; Errachid, E.S.; Elaissari, A. Preparation of gold nanoparticles and determination of their particles size via different methods. Mater. Res. Bull. 2016, 79, 97–104. [Google Scholar] [CrossRef]
- Fu, Q.; Sun, W. Mie theory for light scattering by a spherical particle in an absorbing medium. Appl. Opt. 2001, 40, 1354–1361. [Google Scholar] [CrossRef] [PubMed]
- Wrigglesworth, E.G.; Johnston, J.H. Mie theory and the dichroic effect for spherical gold nanoparticles: An experimental approach. Nanoscale Adv. 2021, 3, 3530–3536. [Google Scholar] [CrossRef] [PubMed]
- Haynes, W.M. CRC Handbook of Chemistry and Physics; CRC press: Boca Raton, FL, USA, 2014. [Google Scholar]
- Kim, D.K.; Hwang, Y.J.; Yoon, C.; Yoon, H.O.; Chang, K.S.; Lee, G.; Lee, S.; Yi, G.R. Experimental approach to the fundamental limit of the extinction coefficients of ultra-smooth and highly spherical gold nanoparticles. Phys. Chem. Chem. Phys. 2015, 17, 20786–20794. [Google Scholar] [CrossRef] [PubMed]
- Shafiqa, A.; Abdul Aziz, A.; Mehrdel, B. Nanoparticle optical properties: Size dependence of a single gold spherical nanoparticle. J. Phys. Conf. Ser. 2018, 1083, 012040. [Google Scholar] [CrossRef]
- Montaño-Priede, J.L.; Pal, U. Estimating near electric field of polyhedral gold nanoparticles for plasmon-enhanced spectroscopies. J. Phys. Chem. C 2019, 123, 11833–11839. [Google Scholar] [CrossRef]
- Choi, K.W.; Zhong, X.L.; Li, Z.Y.; Im, S.H.; Park, O.O. Robust synthesis of gold rhombic dodecahedra with well-controlled sizes and their optical properties. CrystEngComm 2013, 15, 252–258. [Google Scholar] [CrossRef]
- Kelly, K.L.; Coronado, E.; Zhao, L.L.; Schatz, G.C. The optical properties of metal nanoparticles: The influence of size, shape, and dielectric environment. J. Phys. Chem. B 2003, 107, 668–677. [Google Scholar] [CrossRef]
- Cheng, L.; Zhu, G.; Liu, G.; Zhu, L. FDTD simulation of the optical properties for gold nanoparticles. Mater. Res. Express 2020, 7, 125009. [Google Scholar] [CrossRef]

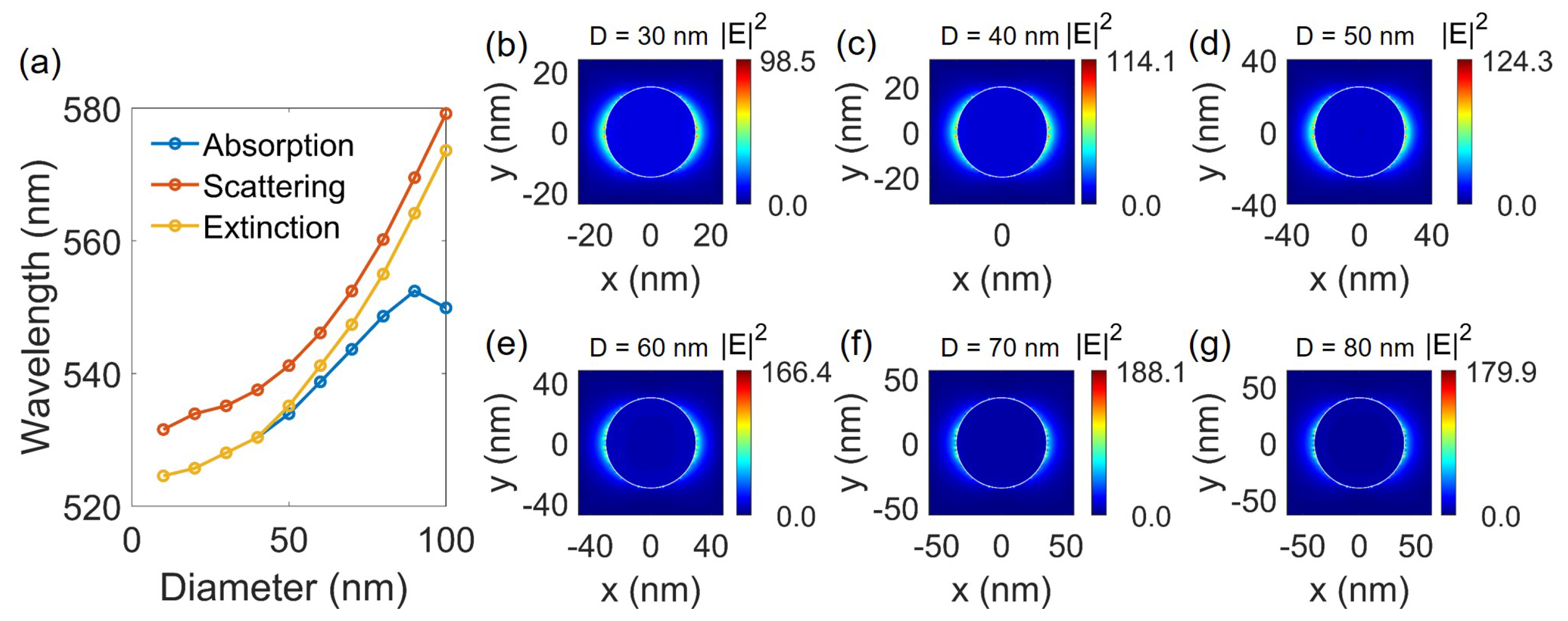
| NPs Size (nm) | (nm)/ (a.u.) | (nm)/ (a.u.) | / |
|---|---|---|---|
| 10 | 524.6/68.2 | 527/97.6 | 1.43 |
| 20 | 525.7/79.8 | 529/136.4 | 1.71 |
| 30 | 528/98.5 | 549.9/162.6 | 1.65 |
| 40 | 530.4/114.1 | 551.1/185.5 | 1.63 |
| 50 | 535.1/124.3 | 552.42/210.2 | 1.69 |
| 60 | 541.2/166.4 | 553.7/227 | 1.36 |
| 70 | 547.4/188.1 | 556.3/221.5 | 1.18 |
| 80 | 555/179.9 | 575/220.1 | 1.22 |
| 90 | 564.2/142.4 | 577.8/194.5 | 1.37 |
| 100 | 573.6/137.8 | 580.6/150.2 | 1.09 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Pham, Q.T.; Ngo, G.L.; Nguyen, C.T.; Ledoux-Rak, I.; Lai, N.D. Unraveling the Dominant Size Effect in Polydisperse Solutions and Maximal Electric Field Enhancement of Gold Nanoparticles. Photonics 2024, 11, 691. https://doi.org/10.3390/photonics11080691
Pham QT, Ngo GL, Nguyen CT, Ledoux-Rak I, Lai ND. Unraveling the Dominant Size Effect in Polydisperse Solutions and Maximal Electric Field Enhancement of Gold Nanoparticles. Photonics. 2024; 11(8):691. https://doi.org/10.3390/photonics11080691
Chicago/Turabian StylePham, Quang Truong, Gia Long Ngo, Chi Thanh Nguyen, Isabelle Ledoux-Rak, and Ngoc Diep Lai. 2024. "Unraveling the Dominant Size Effect in Polydisperse Solutions and Maximal Electric Field Enhancement of Gold Nanoparticles" Photonics 11, no. 8: 691. https://doi.org/10.3390/photonics11080691
APA StylePham, Q. T., Ngo, G. L., Nguyen, C. T., Ledoux-Rak, I., & Lai, N. D. (2024). Unraveling the Dominant Size Effect in Polydisperse Solutions and Maximal Electric Field Enhancement of Gold Nanoparticles. Photonics, 11(8), 691. https://doi.org/10.3390/photonics11080691





