Characterising Spatio-Temporal Coupling of Tightly Focused Femtosecond Laser Pulses in Micro-Structured Dispersive Materials ^†

Abstract

A 2D numerical model based on the finite-difference time-domain (FDTD) method had been developed to investigate the correspondence between the spatio-temporal aspects and intensity evolution of a focused laser beam after the propagation through micro-structured dispersive materials under the pulse duration variation in the few-cycle regime. In parallel with the laser field intensification investigations, a spatio-temporal analysis of the electromagnetic field in the focal point is elaborated as a function of the relative spatial extension of the pulse in order to provide a complex description of this approach. The numerical computations indicate that shorter and more intense pulses may be obtained in well-defined conditions. Also, the major contribution played by the input laser beam profile, numerical aperture, and the dispersive material features in the intensity enhancement process in the focal point is pointed out. The present approach can be used as a versatile method for field intensification in various ultra-short and ultra-intense few-cycle laser pulse experiments.

1. Introduction

In the last decade, the field of high-power lasers has rapidly expanded due to the actual quests in terms of laser–matter interaction in strong fields. Many aspects of this modern approach have been improved, providing efficient methods able to reach ultra-high intensities necessary for various domains of research and for a wide range of applications such as fundamental physics, life science, laser fusion, material science, photo-nuclear physics, exawatt–zetawatts radiation, many-body interactions in quantum electrodynamics, gamma radiation emission, and many others [1,2,3,4,5,6,7,8,9,10]. The development of such laser sources stimulated the elaboration of advanced tools to optimise laser beam profiles and design custom fields [11,12]. One of the actual limits in the shaping of ultra-short and ultra-intense laser beams is the control of their spatio-temporal features in a coupled way. Recent studies [11,13] emphasise that spatio-temporal coupling (STC) is mostly detrimental for ultra-short and ultra-intense laser pulse applications due to its destructive influence on the laser field intensity and pulse duration. In this direction, previous research concerning the spatio-temporal coupling has already demonstrated the interdependence of temporal and spatial coordinates manifested by the ultra-short laser pulses, assuming that the temporal properties of the pulse are not the same for every spatial position [14,15]. Analysing the spatio-temporal aspects of few-cycle laser pulses in a lambda cubed regime represents a main point of interest for experiments in the field of ultra-short and ultra-intense laser–matter interaction (e.g., intensity enhancement, vacuum birefringence studies, polarisation and boiling of the vacuum experiments, astrophysics, Compton scattering, repetitive neutron generation, proton acceleration at energies in the range of hundreds of MeV, or high energy photon–photon scattering) [16,17,18,19,20,21].

Considering the previously elaborated studies in the field of spatio-temporal (S-T) coupling of focused ultra-short laser pulses in high-power laser fields [22,23], in the lambda cube regime [24] and S-T analogy in the presence of piston error [25], the aim of the present work is to investigate the correspondence between the spatio-temporal discrepancy and intensity behaviour of ultra-short femtosecond laser pulses focalised inside micro-structured dispersive materials in the presence of pulse duration variation in the few-cycle regime. The S-T analysis is performed by a 2D numerical model based on the finite-difference time-domain (FDTD) method, which rigorously solves Maxwell’s equations by first discretising these relations by central differences in time and space and then numerically solving these equations by the software algorithm. The FDTD method offers a complex description of the evolution of the electromagnetic field in the vicinity of the focal point, and it does not exhibit any approximations or theoretical restrictions. The numerical results are explained in correspondence with the Rayleigh range, and they provide an extension of the results regarding the S-T disparity of focused ultra-short laser pulses in predefined conditions.

This numerical approach aims to make a significant contribution to the field of focal intensity experiments at petawatt laser facilities. It may provide essential aspects for higher intensity generation beyond the actual spatial and temporal limits employing tightly focused laser pulses, which could be broadly applicable for various high-power laser–matter interaction experiments planned at laser facilities in ultra-intense regimes.

2. Theoretical Approach

A 2D FDTD numerical model was developed in order to investigate the spatio-temporal aspects of the laser field evolution in the focal region after the propagation through dispersive media by using the FullWAVE package of the commercial software RSoft Photonics, version 8.1.0.0.3 [26]. This simulation engine offers the possibility to provide scalable physical scenarios for various dimensions. The FullWAVE package has several advanced computation options by extending the basic FDTD method. Thus, this numerical model is capable of including various material effects and decreasing simulation time. Also, this complex algorithm permits the non-linear and dispersive materials to be easily defined in the software interface. In this way, a complex S-T representation of the laser field evolution could be provided in the vicinity of the focal point considering four distinct propagation media under the pulse duration variation in the range of 2–10 temporal cycles denoted by L. This numerical study was exclusively focused on the spatio-temporal aspects of electromagnetic field propagation in arbitrary geometries. Specific non-linear processes such as self-phase modulation, filamentation, or ionisation are envisaged to be individually investigated in future work.

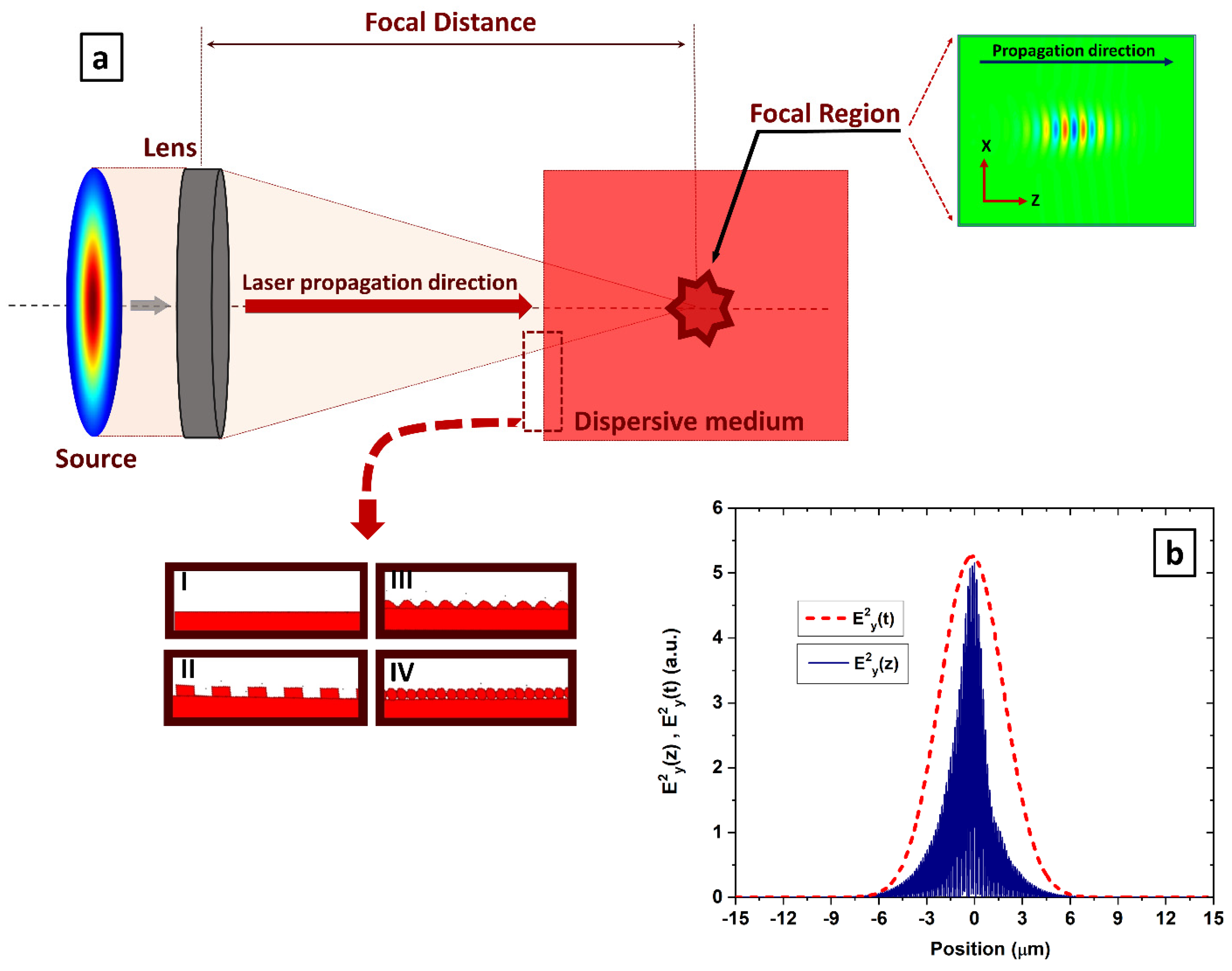
The sketch of the focused laser beam propagation system is depicted in Figure 1. Taking into account the fact that in RSoft, the standard unit of length is measured in microns, the proposed scalable design includes both a Gaussian and a flat-top laser source having two different diameters D of 30 µm and 90 µm, with the corresponding f-number of 2.5 and 0.8, respectively, central wavelength λ of 800 nm, and linear s-polarisation. The laser beam propagates along the symmetry axis, and for modelling simplicity, instead of using an off-axis parabolic mirror, which is commonly used in ultra-intense laser–matter interaction experiments, an optical lens with a diameter of 100 µm and a focal length of 75 µm was used to focus the laser pulse in four media: air, PMMA, HfO₂, and TiO₂ with the corresponding refractive indices n_PMMA = 1.49, n_HfO2 = 1.89, and n_TiO2 = 2.52 considered. As depicted in the first inset illustration of Figure 1a, the laser incident surface of the dispersive material is configured in different structured profiles at the micrometre scale: no-structure (I), step (II), sine (III), and one-layer spheres (IV). These profiles are considered the most efficient ones from the laser intensification point of view in accordance with the initial spatial distribution study of the laser field in the focal region and the previous investigations elaborated in this research direction [27,28]. Thus, the present numerical study was designed by assuming the optimum conditions related in [27]. Consequently, both step and sine micro-structured profiles have been considered to have a height of 1 µm and a pitch of 2 µm, while the microspheres of the one-layer spheres profile have both the height and the pitch equal to 1 µm.

The present work tackles two research directions as follows:

• Electromagnetic pulse intensity evolution in the focal region inside micro-structured dispersive materials is investigated both for Gaussian and flat-top laser source profiles in the presence of pulse duration variation;
• A complex analysis of the S-T coupling of the laser beam in a well-defined area around the focal point at different moments of time is performed considering the optimum geometrical parameters previously investigated.

For these, numerical computations of the spatio-temporal characteristics of the laser field evolution in the focal area were performed to determine the moments of time when the highest intensity values were obtained. These numerical results could lead to an analytical correspondence between the laser field intensity evolution and the S-T coupling of the electromagnetic field in the focal region. To elaborate on an S-T description of the laser field, a contrastive analysis similar to [25] employing new input data obtained in the present conditions is performed, assuming that S-T aspects are not equivalent [24,25]. In accordance with this numerical analysis, the spatial extension of the laser pulse may be significantly shorter than the one obtained from the analytical Minkowski relation (s = c∙τ, where s represents the spatial extension of the laser pulse, c is the speed of light, and τ is the pulse duration) as it is shown in Figure 1b for the particular case of non-structured TiO₂ material with Gaussian laser pulse durations of τ = 2L and f# = 2.5. The spatial laser field analysis is based on the distribution of the electromagnetic field in the focal area inside micro-structured materials at a given moment of time when the maximum field is reached. In the second inset of Figure 1a, the spatial distribution is depicted by using false colour-coded plots in order to illustrate the positive and negative values of the field (red and blue colours, respectively) and zero field, which is symbolised by the green colour. The temporal aspects of the electromagnetic field behaviour for different pulse durations and numerical apertures are investigated in the vicinity of the waist of the focused beams by plotting the temporal evolution envelope of the electromagnetic field E_y² (t) by transforming the temporal axis into a spatial one using the Minkowski space relation. An extended study concerning the disparity between the spatial and temporal extent of the pulse is related in [24]. The numerical results concerning the S-T coupling of the ultra-short laser pulses obtained in this work show that the S-T discrepancy possesses a key role in the intensity enhancement process.

This numerical analysis had the aim to contribute to a better description of the S-T equivalence of the laser pulses in the few-cycle regime by conducting a well-defined method to investigate the evolution of the laser intensity in the focal region inside micro-structured dispersive materials.

3. Numerical Results and Discussions

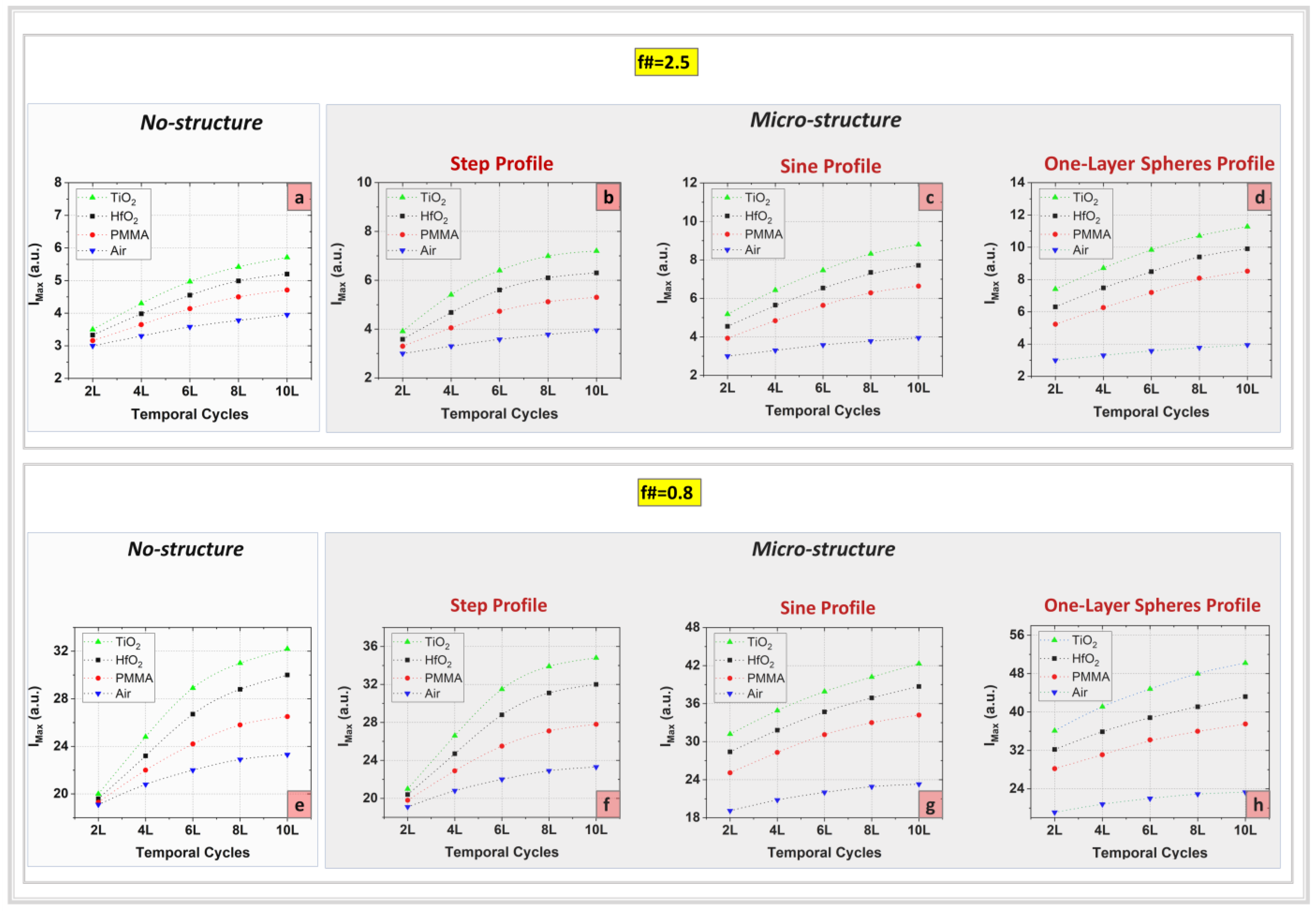
The S-T evolution of the laser field has been numerically investigated in the vicinity of the focal region under the pulse duration variation in the few-cycle regime in order to determine the specific moments of time when the highest intensity values are registered. First, a complex analysis of the behaviour of the electromagnetic field intensity has been performed after the propagation of a Gaussian laser beam through the dispersive materials previously mentioned in a well-defined area around the focal point for two different numerical apertures denoted by f# being equal to 2.5 and 0.8, respectively (Figure 2a–h).

On the basis of my laser dispersive media interaction sketch depicted in Figure 1, the corresponding highest values of the laser intensity both for non-structured (Figure 2a,e) and micro-structured dispersive materials (Figure 2b–d,f–h) have been determined. These plots are computed by using the data provided by the temporal monitors positioned in well-defined points from the focal area, where the highest fields are registered. By comparing these two cases, one can observe in Figure 2 a slightly different evolution of the upper-intensity values registered under the pulse duration variation for each micro-structured profile of the dispersive materials. The highest intensity values are obtained for the profile of the one-layer spheres for all the pulse durations and for all three dispersive materials considered (HfO₂, PMMA, and TiO₂). As illustrated in Figure 2a–h, the intensity at 10 cycles pulse duration, which corresponds to 26 fs both for f# equal to 2.5 and 0.8, respectively, has registered a considerable increase compared to the resulting laser intensity values in the few-cycle regime. Moreover, compared to the no-structure profile case, about two times higher intensity values for the case of each micro-structured profile were obtained for both numerical aperture values considered. Also, it can be noticed that the maximum intensity values computed for each profile correspond to the TiO₂ dispersive material for both f-number values.

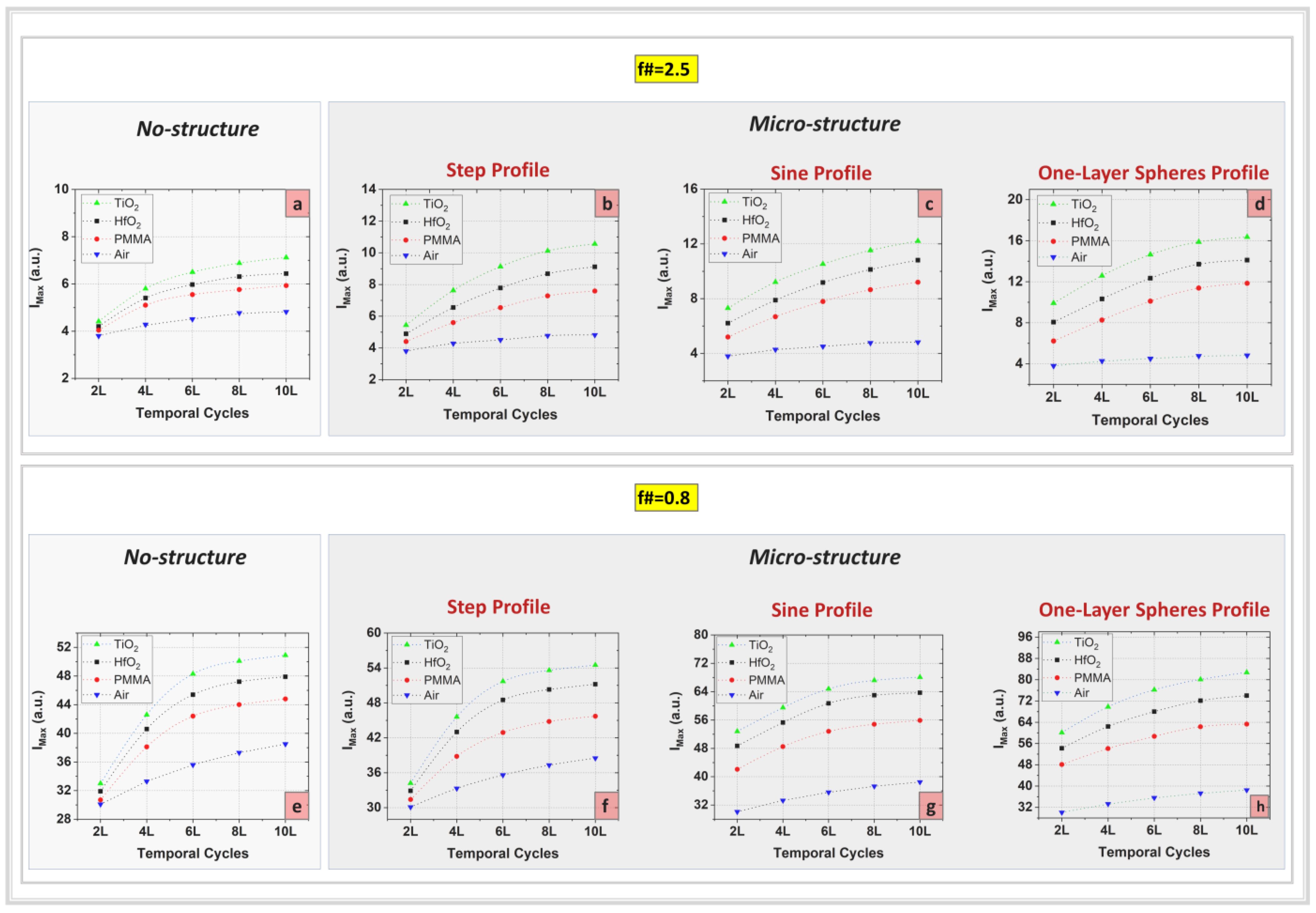
Comparing the case of the Gaussian beam (Figure 2) with the case of the flat-top beam profile (Figure 3), a similar behaviour of the laser intensity in the presence of pulse duration variation is noticeable in the same range previously mentioned using similar input parameters for all dispersive materials profiles. Also, it can be observed that, for an equal emitted energy value, the laser field intensity registered in the focal point for a laser source beam diameter equal to 90 µm is considerably higher than that of 30 µm due to the great influence of the laser source numerical aperture on the paraxial and peripheral rays direction after the propagation through the lens. Moreover, in both cases of flat-top and Gaussian laser sources, the resulting intensity values increase with the refractive index of the dispersive media, which is of particular interest in the context of the laser intensity enhancement process. Thus, the highest field intensity values were obtained for the TiO₂ dispersive medium, which possesses the highest corresponding refractive index value. In this direction, additional numerical computations concerning the spatial distribution evolution of the laser field and monotonical increase of the resulting intensity values with a refractive index for a wide variety of dispersive materials are envisaged to be particularly investigated in future work focusing on the influence of the material’s atomic structure characteristics.

This study denotes a significant increase in the laser intensities of about three times higher values obtained for the case of the flat-top beam source by using micro-structured material profiles for both f-number values considered. These plots clearly show that in the frame of the laser–matter interaction process, laser intensity enhancement depends on specific geometrical features, and it can be achieved in certain conditions, taking into account the actual requirements in ultra-intense laser experiments. As a general remark, these numerical results reveal that the material refractive index and micro-structured profile impose a major contribution to the laser field intensification, and this effect depends particularly on the input laser beam profile and the geometric parameters of the laser–matter interaction setup. These numerical computations show that the higher intensity values obtained in the case of a one-layer microspheres profile compared to the other two micro-structured profiles (step and sine) may emerge from the behaviour of the microspheres as an array of near-field lenses which focuses the incident beam into multiple spots, thereby inducing the laser field enhancement during the propagation through the dispersive media which is of great interest in the actual ultra-intense laser experiments. Considering the previous studies related to the S-T description of the ultra-short pulse evolution in the focal area [24,25], the S-T analogy of the laser field in focus has been investigated in two cases: f# = 2.5 and f# = 0.8 under the pulse duration variation down to the few-cycle regime in both cases of flat-top and Gaussian laser sources.

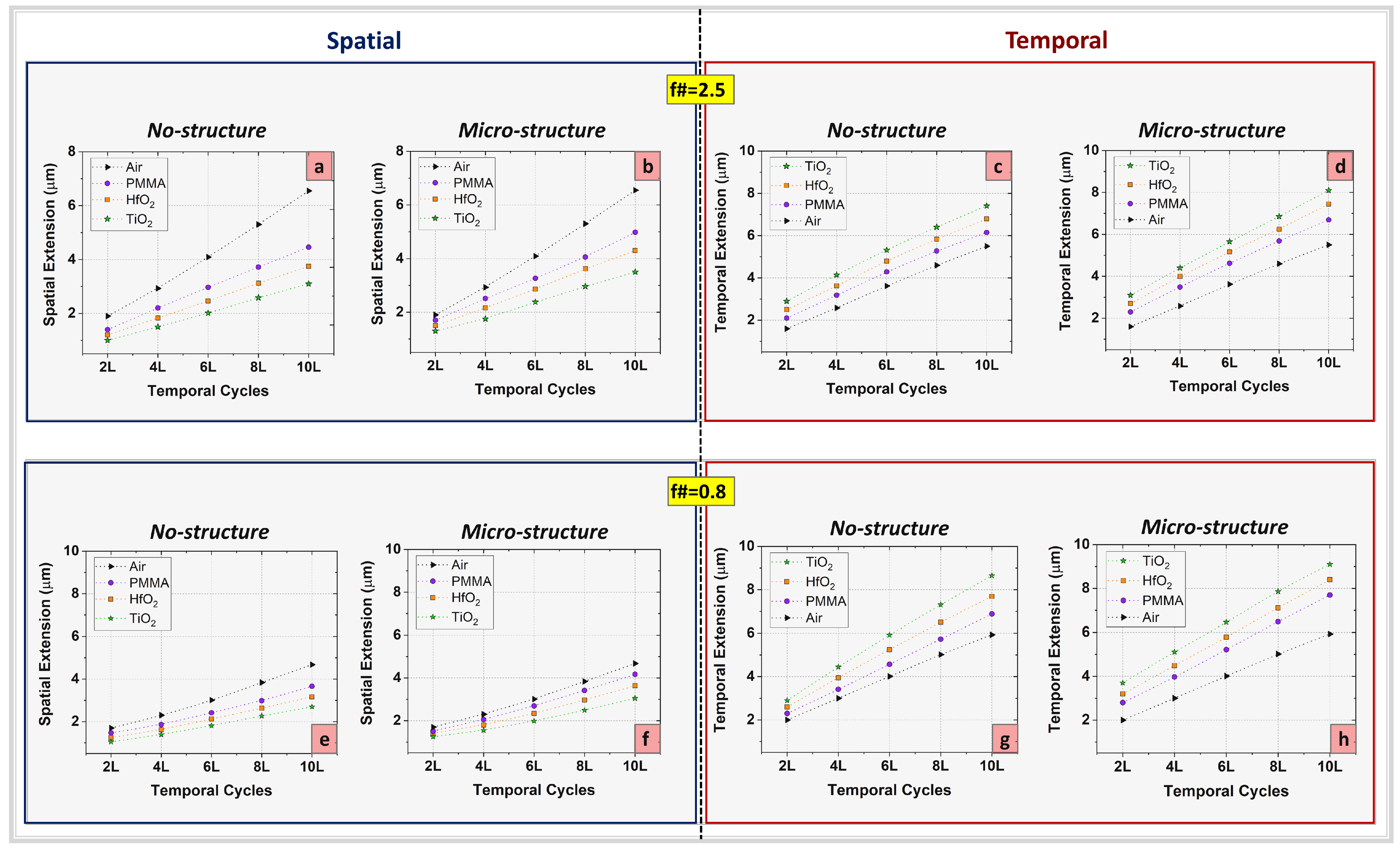
The temporal evolution of the ultra-short laser pulse for different values of τ is analysed in the vicinity of the focal point, considering the data registered by the time monitors placed along the propagation axis. In order to plot the envelope of the temporal evolution of the electromagnetic field Ey² (t), the temporal axis is transformed into a spatial one using the Minkowski relation and the spatial extension of the laser field is considered along the propagation axis. These computations are performed in units of c·τ, taking into consideration that 1 µm corresponds to 3.33 fs. This S-T equivalence study implies the same geometrical features of the laser–matter interaction setup and similar conditions previously considered in the intensity evolution approach. The S-T analogy investigation had been performed for all three dispersive media previously considered in the case of non-structured and 1D microsphere layer profiles. Compared to the other two profiles of the micro-structured materials (sine and step), the 1D microspheres layer profile had been found in the previous section of this work to be the most efficient one in terms of laser intensification in certain conditions.

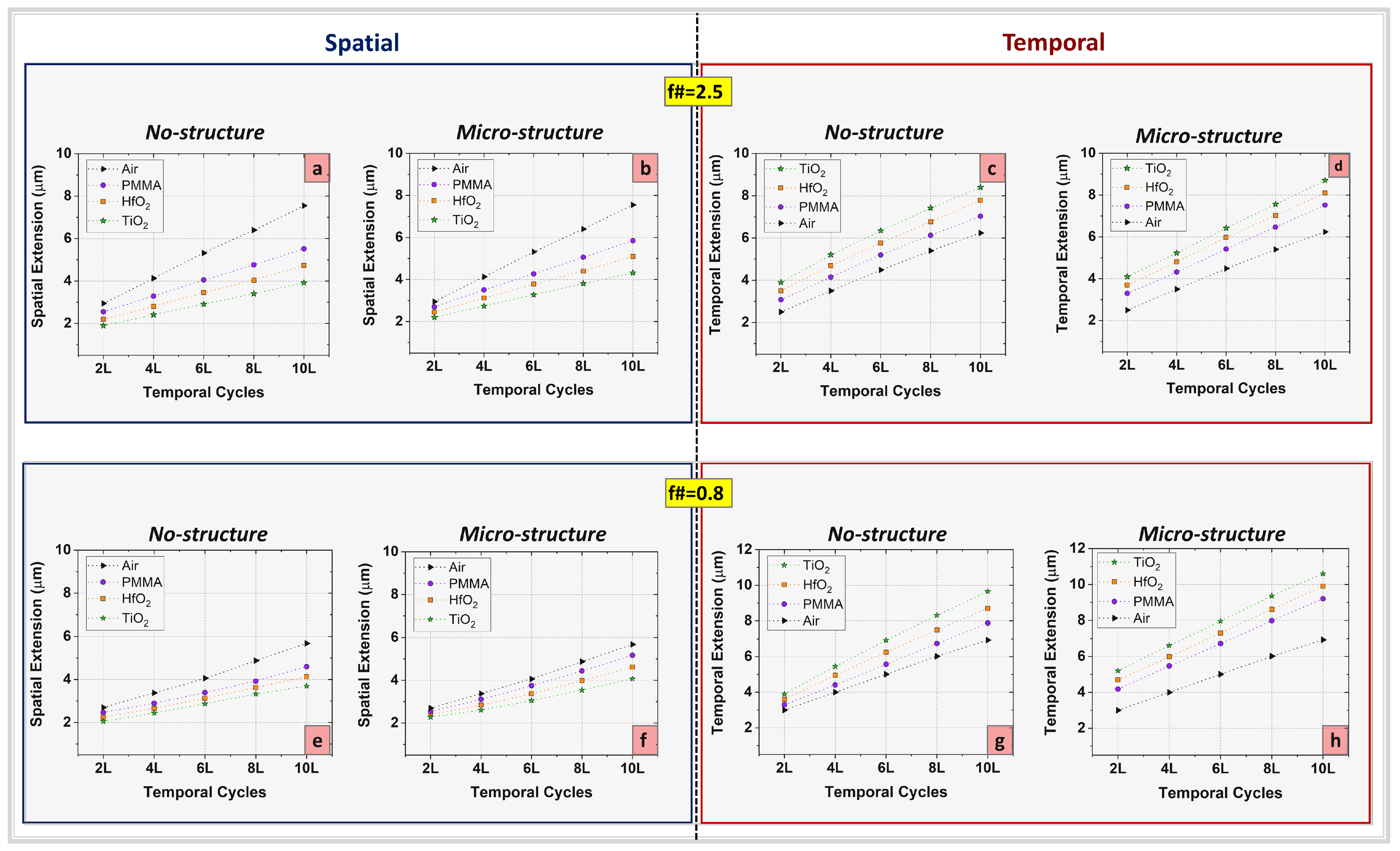
One can observe in Figure 4 the behaviour of the spatial and temporal FWHM values for the case of Gaussian incident laser source for both f-numbers previously considered. As depicted in the reddish side of Figure 4, the highest temporal extension values have been obtained for the TiO₂ dispersive material both for non-structured and micro-structured profiles. Moreover, over two times higher temporal extension values were obtained at 10 cycles of pulse duration for all four media considered compared to the two temporal cycle cases.

As a general overview of Figure 4, the FWHM of the temporal and spatial envelopes of the Gaussian laser pulse exhibits a considerable increase as a function of the pulse duration variation for both f-numbers considered. From a spatial point of view, the FWHM values registered for the micro-structured profile are slightly higher than the numerical values computed for the non-structured profile for both f# values. The numerical computations reveal that the highest ratio between the spatial and temporal FWHM values has been registered in the case of TiO₂ both for non-structured and micro-structured profiles at the duration of 10 temporal cycles pulse duration corresponding to 26 fs. This aspect may be explained in accordance with the material’s features imposing a linear dependence between the S-T ratio and the refractive index of the dispersive media. Thus, a conceptual explanation of these numerical results may emerge from the fact that the highest intensities and S-T ratio values have been obtained for the case of the dispersive material with the highest refractive index (n_TiO2 = 2.51). These results prove that the S-T analogy of ultra-short and ultra-intense laser beams during the propagation through dispersive media exhibits a rigorous dependence on the media refractive index.

Meanwhile, a complementary study of S-T analogy is elaborated in the case of a flat-top incident laser source by maintaining similar conditions imposed in the Gaussian laser source study regarding the dispersive materials, micro-structured profile, and f-numbers values, with respect to the geometrical features of the laser–matter interaction setup. By comparing the case of the flat-top beam profile (Figure 5) with the Gaussian one (Figure 4), it was observed that the EM pulse FWHM values obtained for both f# were considered to present a similar behaviour as a function of pulse duration variation. It can also be observed that the EM pulse FWHM values obtained for the case of flat-top beam profile when f# = 2.5 present a slight increase for all investigated cases. Comparing the maximum spatial FWHM values computed for these two types of laser sources when f# = 0.8, a consistent decrease of the spatial extensions obtained for the case of flat-top beam profile was noticed for all pulse durations considered. These results prove that the input laser beam profile plays an essential role in the spatio-temporal dynamics in the few-cycle regime.

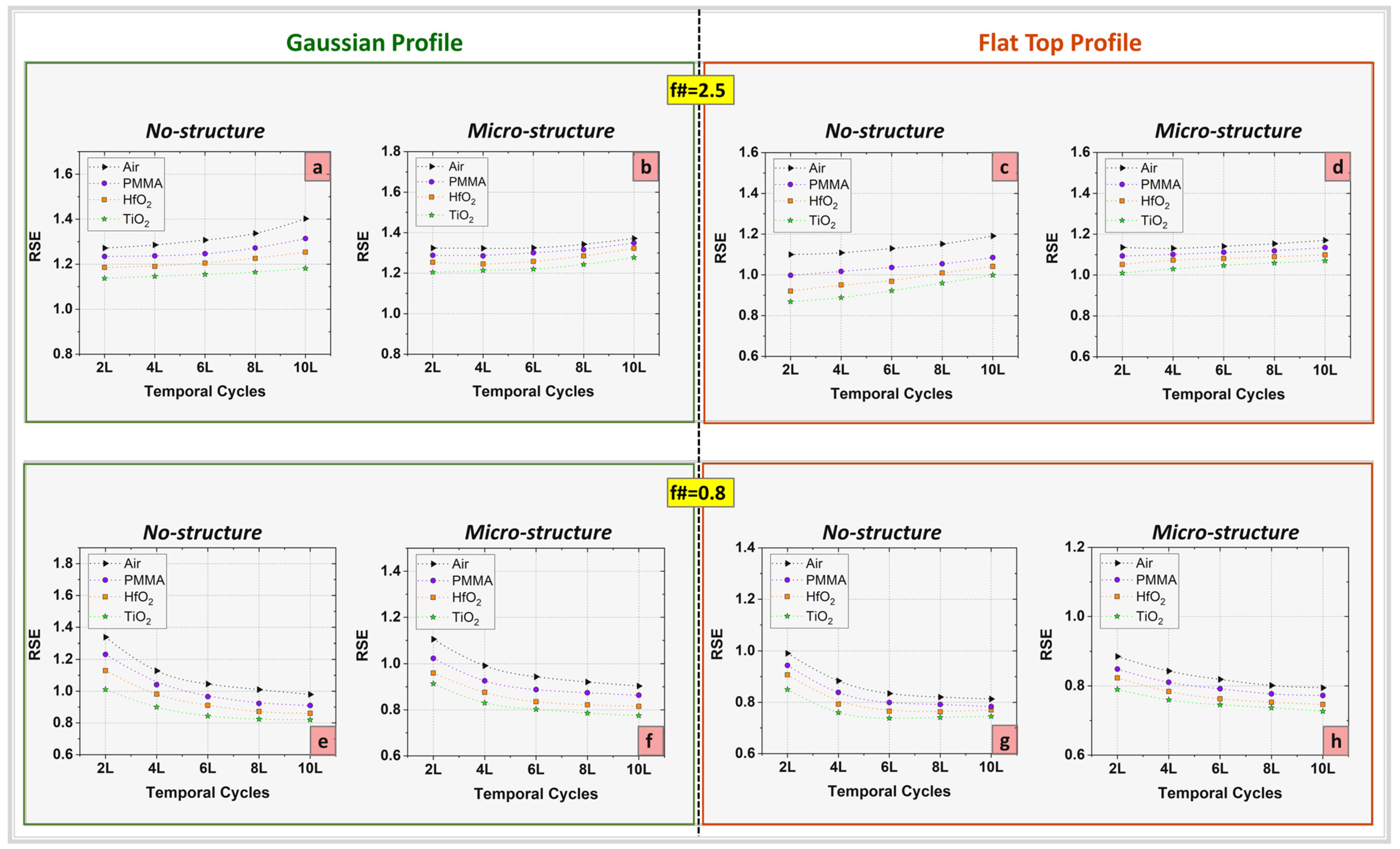
In order to investigate this disparity between the spatial and temporal extent of the focused ultra-short laser pulses, the present numerical approach used the relative spatial extension (RSE) of the pulse comprehensively described in [24]. The S-T analogy implementation permitted the determination of the numerical values RSE according to the relation u = n·s_FWHM/(c·τ_FWHM), where n represents the media refractive index, s_FWHM is the full width at half maximum of the spatial extension envelope of the focused laser pulse, and τ_FWHM denotes the temporal duration of the pulse determined in the focal point. The quantification of RSE for both Gaussian and flat-top source profiles under pulse duration variation is depicted in Figure 6. Comparing these two cases, one can observe that RSE behaves in the same way, registering slightly higher values for micro-structured material when f# = 2.5 (Figure 6b,d) and lower values when f# = 0.8 (Figure 6f,h). Also, it is noticeable that for f# = 2.5, the relative spatial extension of the electromagnetic pulse behaves in the opposite way, as in the case when f# = 0.8, by alternating the purposed materials. Thereby, RSE is lightly increasing with the pulse duration for the case of f# = 2.5 (Figure 6a–d), while for f# = 0.8, it encounters a considerable decrease for all cases considered in terms of input laser source and material profiles (Figure 6e–h). In correspondence with the intensity study presented earlier in this work, this spatio-temporal analysis shows that for high f#, both RSE and intensity values exhibit an increase for all cases considered, while for lower f#, the intensities present a similar increase, but the RSE significantly decreases with respect to the pulse duration variation.

As a generic outcome, this numerical approach demonstrates that the spatial extent of the focused ultra-short laser pulse depends on the Rayleigh range and is shorter than the temporal one for all investigated cases. Also, it is shown that more intense pulses may be obtained in well-defined conditions.

4. Conclusions

A numerical model based on the FDTD method is elaborated to investigate the correspondence between the spatio-temporal aspects and intensity evolution of a focused laser beam after the propagation through dispersive media under the pulse duration variation down to the few-cycle regime. First, it is shown that the input laser beam profile, numerical aperture, and dispersive material features play an essential role in the laser field intensification process in the focal point. According to the S-T overview of the focused laser beam numerically modelled in correspondence with the extension of the Rayleigh range, my numerical computations show that shorter and more intense pulses may be obtained in predefined conditions. This numerical approach may bring significant contributions to the laser field intensity enhancement highly required in various ultra-short and ultra-intense laser pulse experiments down to the few-cycle regime.