Abstract
Metasurfaces can flexibly manipulate electromagnetic waves by engineering subwavelength structures, which have attracted enormous attention in holography, cloaking, and functional multiplexing. For structures with n-fold (n > 2) rotational symmetry, they have been utilized to realize broadband and high-efficiency wavefront manipulation with generalized Pancharatnam–Berry phase, whereas spin-selective wavefront manipulation is still a challenge limited by their symmetrical spin–orbit interactions. Here, we demonstrate the spin-selective wavefront manipulations with generalized Pancharatnam–Berry phase in the range of 560–660 nm with a metal–insulator–metal metasurface consisting of the chiral C3 logarithmic spiral nanostructures. As a proof of concept, two deflectors and a bifocal metalens are designed. This configuration may provide a platform for various applications in polarimetry, polarization-selective images, and nonlinear optical responses.
1. Introduction
Metasurfaces could flexibly manipulate the properties of the electromagnetic wave by periodically arranging the subwavelength structures [1,2]. Benefitting from exotic electromagnetic properties, metasurfaces have been exploited to realize the spin-Hall effect [3], anomalous refraction [4], invisibility cloaking [5], electrostatic steering of thermal emission [6], and spin-selective wavefront manipulations [7,8,9,10]. Among them, geometric metasurfaces with the Pancharatnam–Berry (PB) phase have attracted enormous attention for wavefront manipulations by rotating the elements [11,12,13]. However, limited by the symmetrical spin–orbit interactions for two opposite spins (i.e., the incident right and left circularly polarized (RCP and LCP) beams are split into opposite directions.), spin-switchable functionalities are difficult to implement [14,15,16]. Although such a limitation is broken by combining the PB phase with the propagation phase, the phase properties of broadband and robust are destroyed [7,17,18]. An alternative approach is utilizing 3D or planar chiral nanostructures to design a geometric metasurface, but it commonly suffers from fabrication complexity or weak chiral response [19,20,21].
Planar structures with n-fold (n > 2) rotational symmetry, such as the swastika and the array of nanoslit meta-atoms, are commonly used to enhance the chiral response benefitting from stronger electromagnetic field interactions [22,23,24]. Moreover, a more general form of geometric phase was first found in nonlinear optics by utilizing these structures [25,26]. Since the nonlinear harmonic waves with different helicity can obtain phases of (m − 1)σθ and (m + 1)σθ (m represents the order of harmonic generation) for circularly polarized fundamental wave illumination, spin-selective wavefront manipulations have been realized [27,28]. Nevertheless, the realization of broadband wavefront manipulation is impeded, because these structures are usually recognized as isotropic without geometric phase response in linear optics and possess strong resonance leading to chiral response in a narrowband [22,29]. Recently, the generalized PB phase has been proposed, exploiting multi-fold rotational symmetry structures. Different from the previous relation of geometric phases Φ ≈ 2σθ (the σ = ±1 indicates the incident LCP and RCP, respectively, and θ is the rotation angle of the C2 nanostructures), it is expressed as multiple times the rotation angle [30,31,32,33]. Moreover, the broadband and high-efficiency wavefront manipulations have been demonstrated [34]. However, they can only realize symmetrical spin–orbit interactions, and thus, broadband spin-selective wavefront manipulations are still a great challenge with high-fold rotational symmetry nanostructures.
Here, we propose a metal–insulator–metal (MIM) metasurface that can achieve broadband spin-selective wavefront manipulations with the generalized PB phase. Benefiting from strong electric field interactions between adjacent elements, the designed C3 logarithmic spiral nanostructures exhibit chiral response and broadband wavefront manipulation capabilities, simultaneously. By interleaving the C3 nanostructure and its axisymmetric structures, two independent phase profiles are generated for spin-selective wavefront manipulations. The broadband deflectors and a spin-dependent bifocal metalens are designed as a demonstration in the wavelength range of 560–660 nm. This broadband spin-selective wavefront manipulation configuration may be found in many potential applications in multichannel vectorial holograms, polarization detection, and others requiring broadband spin-selective wavefront manipulation.
2. Concept and Design
To achieve broadband spin-selective wavefront manipulation with the generalized PB phase, a MIM configuration is used (this configuration could reduce the fabrication burden and possesses higher efficiency [11,34]). The C3 logarithmic spiral (LS) element is illustrated in Figure 1a. Affected by the lattice coupling effect, the n-fold rotational symmetry meta-atom can obtain the generalized PB phase that can be expressed as (in the square lattice) [30]:
where the principal axis rotation direction decides the sign ±. When the lattice changes to hexagonal, it will obtain a more complex expression. Such a planar structure consists of the top gold (Au) element, the insulator layer titanium dioxide (TiO2) film, and the bottom Au ground plane (the refractive indexes of TiO2 and Au are from the Palik’s Handbook [35]). The bottom Au ground plane serves as a mirror, which can maximally reflect incident light. The chiral response and wavefront manipulation are mainly dependent on the Au element and TiO2 film. The white dotted line is used to construct this planar structure, which can be described as follows:
where C and Λ are the constant and truncated coefficient, respectively. The range of β is positive, and the dotted line is replicated with 120° intervals to construct the chiral C3 LS meta-atom.
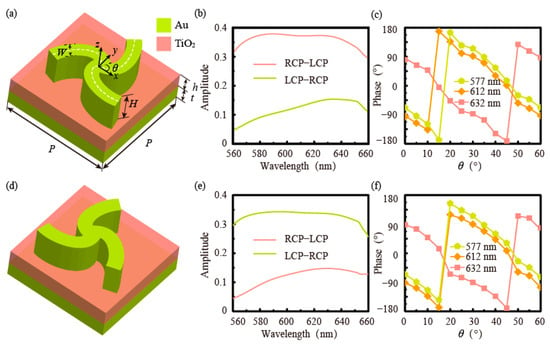
Figure 1.
Schematic and simulated results of the LS and ALS structures. (a,d) Schematics of LS and ALS elements with C3 rotational symmetries with P = 500 nm, t = 500 nm, h = 500 nm, H = 290 nm, C = 10 nm, and Λ= 0.98. The cross-polarization reflection amplitude spectra under LCP and RCP light incidence in 560–660 nm for (b) LS and (e) ALS structure, respectively. The phase spectra of (c) LS structure for RCP incidence and (f) ALS structures for LCP incidence with a 5° interval at wavelengths of 577 nm, 612 nm, and 632 nm.
The LS element is designed aiming at 560–660 nm, and the corresponding simulated results (using the finite element method; for more details, see Supplementary Information S1) of reflected cross-polarized (the cross-polarization represents the incident LCP light is converted to the reflected RCP light [16,36]) amplitude and phase spectra are shown in Figure 1b,c. For LCP normal incidence along the z-direction, the average reflected amplitude of cross-polarization is about ∼0.11 because most of the power is straightforwardly reflected and absorbed. However, the high average reflectance of cross-polarization ∼0.36 allows for RCP excitation. Meanwhile, the phase shifts in Figure 1c cover the whole 2π range if θ (orientation angle) changes from 0° to 60° at the wavelength of 577 nm, 612 nm, and 632 nm, (these typical wavelengths have been widely found in the medical field and red laser), respectively, which agrees well with the theoretical expectation (6θ), according to Equation (1). By symmetrizing the LS structure in Figure 1a along its y-axis, another LS (named as ALS) structure is obtained as shown in Figure 1d. The cross-polarization component is suppressed under RCP illumination (the average reflection amplitude is lower than ∼0.11), but the average reflectance exceeds ∼0.33 for LCP incidence within the same broadband range. Affected by the structural chirality, the reflectance spectra between LS and ALS elements show apparent differences (Supplementary Information S2). Moreover, the phase shifts under LCP incidence can cover the 0–2π range when θ changes from 0° to 60° at 577 nm, 612 nm, and 632 nm, respectively, as shown in Figure 1f. Such results also agree well with the theoretical expectation (6θ) according to Equation (1), demonstrating the generation of the generalized PB phase. The generalized PB phase can be obtained in the whole wavelength range of 560–660 nm as shown in Figure S2 (Supplementary Materials), which is not exactly multiple times of θ [30]. By changing the materials and sizes of elements, the performances of the LS and ALS structures may be further improved.
Figure 2b,d illustrate the instantaneous electric and magnetic field distributions to reveal the physical mechanism of spin-selective wavefront manipulations corresponding to side views of LS (in Figure 2a) and ALS (in Figure 2d) structures, respectively, underlying the different responses of different structures for two spin states. In Figure 2b (left), the electric intensity of two LS structures under LCP incidence is stronger than that of RCP at a resonant wavelength of 577 nm, which may originate from strong near-field interaction between adjacent meta-atoms (red dashed line), leading to large absorption or reflection [37]. The magnetic field distribution in Figure 2b (right) indicates that the magnetic intensity is approximately the same for LCP and RCP incidence, and thus, the influence of the magnetic field on the performance of the LS structure is relatively small. Due to the chiral LS structure without mirror symmetry, the cut plane depicts slicing a single arm of the ALS structure in Figure 2c (Supplementary Information S2). The electric intensity for LCP illumination is weaker than that of RCP for the ALS element in Figure 2d (left), while the magnetic intensity seems unchanged for LCP and RCP incidence. Corresponding contour maps are shown in Figure S3 (Supplementary Information S4). Therefore, the different responses of LS and ALS structures are mainly induced by electric field interaction for two spin states.
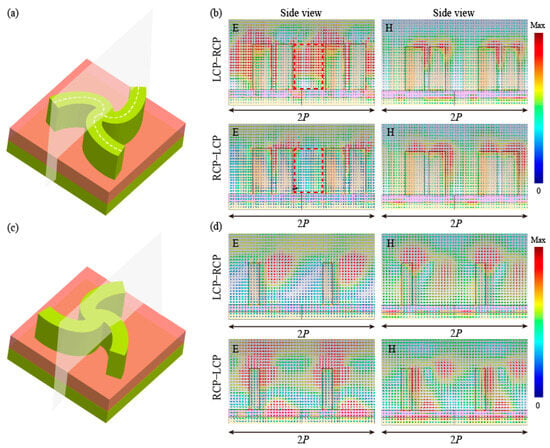
Figure 2.
Three-dimensional views and distributions of instantaneous electric and magnetic field. (a,c) Three-dimensional views of LS and ALS elements. (b,d) Side views of instantaneous electric and magnetic field distributions for LCP and RCP illumination at 577 nm.
3. Spin-Selective Metadevices
To verify the asymmetric characteristics of the designed scheme, two separate deflectors are designed, whose deflection angles are calculated by the following [1,38]:
here, λ is the wavelength, and Γ presents the period of the deflector. By periodically arranging the LS structure with a phase interval of π/16, a deflector is designed, and its top view in the xoy plane is schematically shown in Figure 3a (top). Figure 3a (bottom) depicts corresponding normalized far-field distributions at three wavelengths. Different from the metasurface with the symmetric photonic spin-Hall effect that converts different circularly polarized light to different directions with the opposite deflection angle, such a deflector simultaneously achieves wavefront manipulation and polarization filtering. The simulated deflection angles are −4.2°, −4.5°, and −4.6° at 577 nm, 612 nm, and 632 nm under RCP incidence, respectively, which are basically consistent with theoretical expectations in Equation (3). The average deflection efficiency (diffraction efficiency, defined as the ratio of the reflected power for a specific angle to the total reflected power [39,40]) reaches ∼20.4% from 560 nm to 660 nm in Figure 3b, but it is lower than ∼6.3% for LCP illumination. Another deflector is obtained by arranging the ALS structure with the same incremental rotation angle (in Figure 3a) at the top of Figure 3c. The power is mainly deflected to +1st-order with deflection angles 4.1°, 4.3°, and 4.5° at 577 nm, 612 nm, and 632 nm for LCP, respectively. Moreover, the average diffraction efficiency exceeds ∼24.5% in 560–660 nm in Figure 3d, but most of the power vanishes (the average diffraction efficiency is lower than ∼6.9%) under RCP illumination. Therefore, this scheme can be used to design broadband spin-selective wavefront manipulation metadevices.
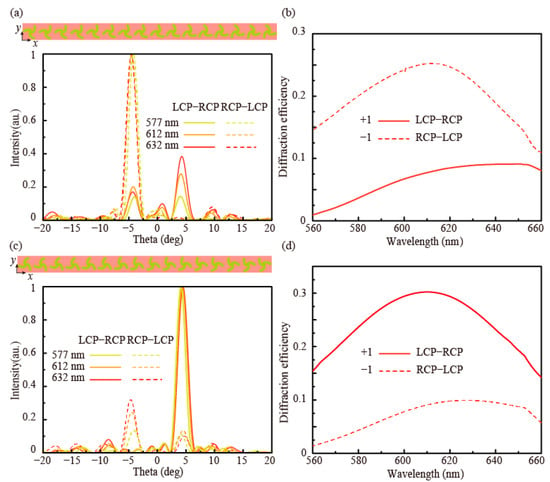
Figure 3.
Element arrangement and simulated results: Top views of two metadevices comprising (a) LS and (c) ALS structures and their normalized far-field intensity distributions for LCP and RCP illumination. (b,d) Diffraction efficiencies of deflectors as a function of the wavelength.
To further demonstrate spin-selective functionality, a bifocal metalens in Figure 4 has been designed, and the phase distributions are given by [41,42]:
where λ = 577 nm is the central wavelength, and a indicates focal shift. f is the focal length.
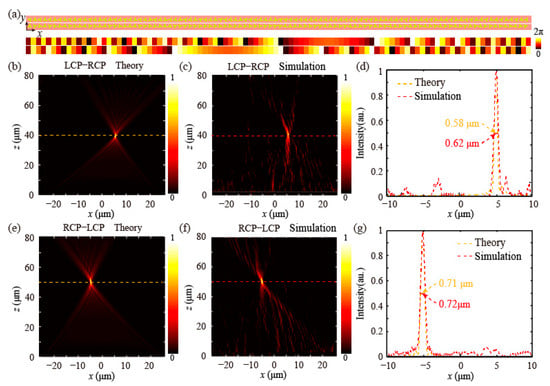
Figure 4.
Demonstrations of spin-selective wavefront manipulations with a bifocal metalens. (a) The top view of the bifocal metalens and its phase distributions. The theoretical (b) and simulated (c) intensities for LCP incidence (a1 = 5 μm, f1 = 40 μm). (d,g) The normalized sectional intensity curves. The theoretical (e) and simulated (f) intensities for RCP incidence (a2 = −5 μm and f2 = 50 μm).
Figure 4a illustrates the vertical view of the bifocal metalens (composed of LS and ALS elements in different regions) and its phase distribution. For LCP incidence, the intensity distributions (theory and simulation results) on the z = f1 plane are displayed in Figure 4b,c, whose normalized sectional intensity curves are plotted in Figure 4d. Here, the theoretical results are obtained by vectorial angular spectrum theory, and the simulated results are calculated by the finite integration method [43,44,45] (for more details, see Supplementary Information S1). The full-width at half-maximum (FWHM) in simulation is ∼0.62 μm, which approaches the theoretical calculation (∼0.58 μm). This difference may be attributed to the perfect assumption of amplitude and phase in theoretical calculation. Both theoretical and simulated results are close to the diffraction limit (1.22λ/2NA = 0.563 μm, NA = 0.625 is the numerical aperture) [46,47]. Moreover, the simulated focusing efficiency (the definition sees Refs. [48,49]) reaches ∼6.57%. However, the incident RCP light is focused on different positions, and corresponding intensity distributions on the z = f2 plane are exhibited in Figure 4e,f. The theoretical intensity distribution in Figure 4e agrees well with the simulated result in Figure 4f. The simulated focusing efficiency is up to ∼29.73%. Their normalized intensities in Figure 4g reveal that the simulated FWHM of ∼0.72 μm approximatively approaches the theoretical calculation of ∼0.71 μm, and both of them reach the diffraction limit (0.704, NA = 0.5). These results demonstrate that such a metadevice can achieve spin-selective wavefront manipulations with the generalized PB phase. Furthermore, a thorough explanation of the data has been shown in Supplementary Information S5.
4. Conclusions
In summary, a platform of MIM metasurface is proposed to achieve broadband spin-selective wavefront manipulations with the generalized PB phase. Since the electric field interaction between adjacent elements can be enhanced, the designed C3 logarithmic spiral nanostructures show the chiral response. To verify the proposed method, two broadband deflectors in the range of 560–660 nm are designed to verify the asymmetric characteristics. In addition, a spin-dependent bifocal metalens (with a maximum efficiency of ∼29.73%) that can focus the incident LCP and RCP light on different positions is proposed. This work may be extensively applied in chiroptical spectroscopy, polarimetry, and polarization-selective images.
Supplementary Materials
The following supporting information can be downloaded at: https://www.mdpi.com/article/10.3390/photonics11080690/s1, Figure S1: Schematic of positions of LS and ALS elements; Figure S2: The simulated phase shifts at 560–660 nm; Figure S3: 3D views and instantaneous electric and magnetic field distributions. Supplementary Information S1: Simulation methodology; Supplementary Information S2: The positions of LS and ALS structures; Simulation methodology; Supplementary Information S3: Phase shifts in the broadband wavelength range; Supplementary Information S4: The contour images of the two structures; Supplementary Information S5: Data explanation.
Author Contributions
Conceptualization and methodology, S.G. and J.C.; investigation, T.Z. (Tingting Zhang), X.M., Z.W., H.G. and G.Y.; writing—original draft preparation, F.B., J.C. and T.Z. (Tianci Zhao); funding acquisition, J.C. and S.G. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by the Natural Science Foundation of Inner Mongolia of China under Grant RZ2400001611, Inner Mongolia Autonomous Region High level Talent Introduction and Research Support Program Grant DC2400002157, the Scientific Research Project of Inner Mongolia University of Technology under Grant BS2021033, the Basic Scientific Research Business Expenses Project for Universities Directly Affiliated with Inner Mongolia Autonomous Region Grant JY20220214, and Doctoral Research Start up Fund of Inner Mongolia University of Technology Grant DC2300001263.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
The data presented in this study are available on request from the corresponding author.
Conflicts of Interest
The authors declare no conflicts of interest.
References
- Yu, N.; Genevet, P.; Kats, M.A.; Aieta, F.; Tetienne, J.P.; Capasso, F.; Gaburro, Z. Light propagation with phase discontinuities: Generalized laws of reflection and refraction. Science 2011, 334, 333–337. [Google Scholar] [CrossRef]
- Zaidi, A.; Rubin, N.A.; Meretska, M.L.; Li, L.W.; Dorrah, A.H.; Park, J.S.; Capasso, F. Metasurface-enabled single-shot and complete mueller matrix imaging. Nat. Photonics 2024, 18, 704–712. [Google Scholar] [CrossRef]
- Kim, M.; Lee, D.; Yang, Y.; Kim, Y.; Rho, J. Reaching the highest efficiency of spin hall effect of light in the near-infrared using all-dielectric metasurfaces. Nat. Commun. 2022, 13, 2036. [Google Scholar] [CrossRef] [PubMed]
- Sell, D.; Yang, J.; Wang, E.W.; Phan, T.; Doshay, S.; Fan, J.A. Ultra-high-efficiency anomalous refraction with dielectric metasurfaces. ACS Photonics 2018, 5, 2402–2407. [Google Scholar] [CrossRef]
- Xu, H.X.; Hu, G.; Wang, Y.; Wang, C.; Wang, M.; Wang, S.; Huang, Y.; Genevet, P.; Huang, W.; Qiu, C.-W. Polarization-insensitive 3d conformal-skin metasurface cloak. Light Sci. Appl. 2021, 10, 75. [Google Scholar] [CrossRef] [PubMed]
- Siegel, J.; Kim, S.; Fortman, M.; Wan, C.; Kats, M.A.; Hon, P.W.C.; Sweatlock, L.; Jang, M.S.; Brar, V.W. Electrostatic steering of thermal emission with active metasurface control of delocalized modes. Nat. Commun. 2024, 15, 3376. [Google Scholar] [CrossRef] [PubMed]
- Chen, Y.; Yang, X.; Gao, J. Spin-controlled wavefront shaping with plasmonic chiral geometric metasurfaces. Light Sci. Appl. 2018, 7, 84. [Google Scholar] [CrossRef]
- Huang, Y.; Xiao, T.; Xie, Z.; Zheng, J.; Su, Y.; Chen, W.; Liu, K.; Tang, M.; Müller-Buschbaum, P.; Li, L. Single-layered reflective metasurface achieving simultaneous spin-selective perfect absorption and efficient wavefront manipulation. Adv. Opt. Mater. 2021, 9, 2001663. [Google Scholar] [CrossRef]
- Li, T.; Chen, Y.; Fu, B.; Liu, M.; Wang, J.; Gao, H.; Wang, S.; Zhu, S. Spin-selective trifunctional metasurfaces for deforming versatile nondiffractive beams along the optical trajectory. Laser Photonics Rev. 2024, 2024, 2301372. [Google Scholar] [CrossRef]
- Huang, Y.; Xiao, T.; Chen, S.; Xie, Z.; Zheng, J.; Zhu, J.; Su, Y.; Chen, W.; Liu, K.; Tang, M.; et al. All-optical controlled-not logic gate achieving directional asymmetric transmission based on metasurface doublet. Opto-Electron. Adv. 2023, 6, 220073. [Google Scholar] [CrossRef]
- Zheng, G.; Mühlenbernd, H.; Kenney, M.; Li, G.; Zentgraf, T.; Zhang, S. Metasurface holograms reaching 80% efficiency. Nat. Nanotechnol. 2015, 10, 308–312. [Google Scholar] [CrossRef]
- Ming, Y.; Intaravanne, Y.; Ahmed, H.; Kenney, M.; Lu, Y.Q.; Chen, X. Creating composite vortex beams with a single geometric metasurface. Adv. Mater. 2022, 34, 2109714. [Google Scholar] [CrossRef] [PubMed]
- Fang, B.; Shu, F.; Wang, Z.; Ji, J.; Jin, Z.; Hong, Z.; Shen, C.; Cheng, Q.; Li, T. On-chip non-uniform geometric metasurface for multi-channel wavefront manipulations. Opt. Lett. 2023, 48, 3119–3122. [Google Scholar] [CrossRef]
- Gou, Y.; Ma, H.F.; Wu, L.W.; Wang, Z.X.; Xu, P.; Cui, T.J. Broadband spin-selective wavefront manipulations based on pancharatnam–berry coding metasurfaces. ACS Omega 2021, 6, 30019–30026. [Google Scholar] [CrossRef] [PubMed]
- Xiao, S.; Wang, J.; Liu, F.; Zhang, S.; Yin, X.; Li, J. Spin-dependent optics with metasurfaces. Nanophotonics 2017, 6, 215–234. [Google Scholar] [CrossRef]
- Zhang, M.; Pu, M.; Zhang, F.; Guo, Y.; He, Q.; Ma, X.; Huang, Y.; Li, X.; Yu, H.; Luo, X. Plasmonic metasurfaces for switchable photonic spin–orbit interactions based on phase change materials. Adv. Sci. 2018, 5, 1800835. [Google Scholar] [CrossRef] [PubMed]
- Balthasar Mueller, J.P.; Rubin, N.A.; Devlin, R.C.; Groever, B.; Capasso, F. Metasurface polarization optics: Independent phase control of arbitrary orthogonal states of polarization. Phys. Rev. Lett. 2017, 118, 113901. [Google Scholar] [CrossRef]
- Zhang, F.; Guo, Y.; Pu, M.; Li, X.; Ma, X.; Luo, X. Metasurfaces enabled by asymmetric photonic spin-orbit interactions. Opto-Electron. Eng. 2020, 47, 200366. [Google Scholar]
- Wu, X.; Feng, Y.; Zhang, C.; Liu, H.L. Three-dimensional chiral metasurfaces for circular-polarized anomalous beam steering. Opt. Lett. 2022, 47, 1794–1797. [Google Scholar] [CrossRef]
- He, C.; Sun, T.; Guo, J.; Cao, M.; Xia, J.; Hu, J.; Yan, Y.; Wang, C. Chiral metalens of circular polarization dichroism with helical surface arrays in mid-infrared region. Adv. Opt. Mater. 2019, 7, 1901129. [Google Scholar] [CrossRef]
- Ma, Z.; Li, Y.; Li, Y.; Gong, Y.; Maier, S.A.; Hong, M. All-dielectric planar chiral metasurface with gradient geometric phase. Opt. Express 2018, 26, 6067–6078. [Google Scholar] [CrossRef]
- Zhu, A.Y.; Chen, W.T.; Zaidi, A.; Huang, Y.W.; Khorasaninejad, M.; Sanjeev, V.; Qiu, C.W.; Capasso, F. Giant intrinsic chiro-optical activity in planar dielectric nanostructures. Light Sci. Appl. 2018, 7, 17158. [Google Scholar] [CrossRef] [PubMed]
- Kim, D.; Yu, J.; Hwang, I.; Park, S.; Demmerle, F.; Boehm, G.; Amann, M.C.; Belkin, M.A.; Lee, J. Giant nonlinear circular dichroism from intersubband polaritonic metasurfaces. Nano Lett. 2020, 20, 8032–8039. [Google Scholar] [CrossRef]
- Faraz, F.; Li, Z.; Zhang, Z.; Rehman Abbasi, T.U.; Wang, X.; Rukhlenko, I.D.; Zhu, W. High-efficiency geometric phase metasurface with multifold rotationally symmetric resonators. ACS Appl. Opt. Mater. 2023, 1, 173–178. [Google Scholar] [CrossRef]
- Liu, B.; Sain, B.; Reineke, B.; Zhao, R.; Meier, C.; Huang, L.; Jiang, Y.; Zentgraf, T. Nonlinear wavefront control by geometric-phase dielectric metasurfaces: Influence of mode field and rotational symmetry. Adv. Opt. Mater. 2020, 8, 1902050. [Google Scholar] [CrossRef]
- Liu, B.; Geromel, R.; Su, Z.; Guo, K.; Wang, Y.; Guo, Z.; Huang, L.; Zentgraf, T. Nonlinear dielectric geometric-phase metasurface with simultaneous structure and lattice symmetry design. ACS Photonics 2023, 10, 4357–4366. [Google Scholar] [CrossRef]
- Li, G.; Chen, S.; Pholchai, N.; Reineke, B.; Wong, P.W.H.; Pun Edwin, Y.B.; Cheah, K.W.; Zentgraf, T.; Zhang, S. Continuous control of the nonlinearity phase for harmonic generations. Nat. Mater. 2015, 14, 607–612. [Google Scholar] [CrossRef]
- Chen, S.; Li, G.; Zeuner, F.; Wong, W.H.; Pun, E.Y.B.; Zentgraf, T.; Cheah, K.W.; Zhang, S. Symmetry-selective third-harmonic generation from plasmonic metacrystals. Phys. Rev. Lett. 2014, 113, 033901. [Google Scholar] [CrossRef] [PubMed]
- Li, G.; Zhang, S.; Zentgraf, T. Nonlinear photonic metasurfaces. Nat. Rev. Mater. 2017, 2, 17010. [Google Scholar]
- Xie, X.; Pu, M.B.; Jin, J.J.; Xu, M.; Guo, Y.; Li, X.; Gao, P.; Ma, X.; Luo, X. Generalized pancharatnam-berry phase in rotationally symmetric meta-atoms. Phys. Rev. Lett. 2021, 126, 183902. [Google Scholar] [CrossRef] [PubMed]
- Yuan, Y.; Zhang, K.; Ratni, B.; Song, Q.; Ding, X.; Wu, Q.; Burokur, S.N.; Genevet, P. Independent phase modulation for quadruplex polarization channels enabled by chirality-assisted geometric-phase metasurfaces. Nat. Commun. 2020, 11, 4186. [Google Scholar] [CrossRef]
- Song, Q.; Baroni, A.; Sawant, R.; Ni, P.; Brandli, V.; Chenot, S.; Vézian, S.; Damilano, B.; de Mierry, P.; Khadir, S.; et al. Ptychography retrieval of fully polarized holograms from geometric-phase metasurfaces. Nat. Commun. 2020, 11, 2651. [Google Scholar] [CrossRef] [PubMed]
- Deng, Q.; Yang, J.; Lan, X.; Zhang, W.; Cui, H.; Xie, Z.; Li, L.; Huang, Y. Investigations of generalized pancharatnam-berry phase in all-dielectric metasurfaces. Results Phys. 2023, 51, 106730. [Google Scholar] [CrossRef]
- Cai, J.; Zhang, F.; Pu, M.; Chen, Y.; Guo, Y.; Xie, T.; Feng, X.; Ma, X.; Li, X.; Yu, H.; et al. All-metallic high-efficiency generalized pancharatnam–berry phase metasurface with chiral meta-atoms. Nanophotonics 2022, 11, 1961–1968. [Google Scholar] [CrossRef]
- Palik, E.D. Handbook of Optical Constants of Solids; Boston Academic Press: Boston, MA, USA, 1991; pp. 286–395. [Google Scholar]
- Zhang, F.; Xie, X.; Pu, M.; Guo, Y.; Ma, X.; Li, X.; Luo, J.; He, Q.; Yu, H.; Luo, X. Multistate switching of photonic angular momentum coupling in phase-change metadevices. Adv. Mater. 2020, 32, 1908194. [Google Scholar] [CrossRef] [PubMed]
- Wang, L.; Guo, X.; Zhang, Y.; Zhou, X.; Yuan, L.; Zhang, P.; Liang, S.; Lan, F.; Zeng, H.; Zhang, T.; et al. Enhanced thz eit resonance based on the coupled electric field dropping effect within the undulated meta-surface. Nanophotonics 2019, 8, 1071–1078. [Google Scholar] [CrossRef]
- Xu, Z.; Ni, C.; Cheng, Y.; Dong, L.; Wu, L. Photo-excited metasurface for tunable terahertz reflective circular polarization conversion and anomalous beam deflection at two frequencies independently. Nanomaterials 2023, 13, 1846. [Google Scholar] [CrossRef]
- Asadchy, V.S.; Albooyeh, M.; Tcvetkova, S.N.; Díaz-Rubio, A.; Ra’di, Y.; Tretyakov, S.A. Perfect control of reflection and refraction using spatially dispersive metasurfaces. Phys. Rev. B 2016, 94, 075142. [Google Scholar] [CrossRef]
- Cai, J.; Yu, H. Full-space wavefront manipulation enabled by asymmetric photonic spin-orbit interactions. Opt. Express 2023, 31, 1409–1419. [Google Scholar] [CrossRef]
- Zhang, Z.; Luo, J.; Song, M.; Yu, H. Polarization filtering and phase controlling metasurfaces based on a metal-insulator-metal grating. Plasmonics 2017, 12, 1797–1803. [Google Scholar] [CrossRef]
- Zhao, M.; Chen, M.K.; Zhuang, Z.P.; Zhang, Y.; Chen, A.; Chen, Q.; Liu, W.; Wang, J.; Chen, Z.M.; Wang, B.; et al. Phase characterisation of metalenses. Light Sci. Appl. 2021, 10, 52. [Google Scholar] [CrossRef] [PubMed]
- Luo, X. Catenary Optics; Springer: Berlin/Heidelberg, Germany, 2019; pp. 377–419. [Google Scholar]
- Pu, M.; Li, X.; Ma, X.; Wang, Y.; Zhao, Z.; Wang, C.; Hu, C.; Gao, P.; Huang, C.; Ren, H.; et al. Catenary optics for achromatic generation of perfect optical angular momentum. Sci. Adv. 2015, 1, e1500396. [Google Scholar] [CrossRef] [PubMed]
- Cai, J.; Zhang, F.; Pu, M.; Xie, T.; Feng, X.; Yu, H.; Luo, X. Broadband and high-efficiency photonic spin-hall effect with all-metallic metasurfaces. Opt. Express 2022, 30, 14938–14947. [Google Scholar] [CrossRef]
- Paniagua-Domínguez, R.; Yu, Y.F.; Khaidarov, E.; Choi, S.; Leong, V.; Bakker, R.M.; Liang, X.; Fu, Y.H.; Valuckas, V.; Krivitsky, L.A.; et al. A metalens with a near-unity numerical aperture. Nano Lett. 2018, 18, 2124–2132. [Google Scholar] [CrossRef]
- Qiao, M.; Yan, J.; Jiang, L. Direction controllable nano-patterning of titanium by ultrafast laser for surface coloring and optical encryption. Adv. Opt. Mater. 2022, 10, 2101673. [Google Scholar] [CrossRef]
- Zhuang, Z.P.; Chen, R.; Fan, Z.B.; Pang, X.N.; Dong, J.W. High focusing efficiency in subdiffraction focusing metalens. Nanophotonics 2019, 8, 1279–1289. [Google Scholar] [CrossRef]
- Cai, J.; Zhang, F.; Zhang, M.; Ou, Y.; Yu, H. Simultaneous polarization filtering and wavefront shaping enabled by localized polarization-selective interference. Sci. Rep. 2020, 10, 14477. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).