2. Materials and Methods
Our processing setup was based on an oscillator–regenerative amplifier system, Carbide (Light Conversion). This laser system works at a wavelength of ~1030 nm (λ), providing pulses of ~200 fs (τ) duration with an M2 of ~1.1. The repetition rate can be varied up to ~3.2 MHz. The output beam from the laser system was delivered into a complex train of scanner subsystems, including a fast-z-scanner (not used in this work) and a rotational r-ɵ-z-scanner (self-made) at a working distance of ~6 mm. The optical system had a numerical aperture (NA) of ~0.5 and focused the laser to a beam waist of about 2 µm.
For this work, a 2D trajectory, which was calculated in a microcontroller, was scanned by the floating r-ɵ-z-scanner and rastered by the laser pulses. Single-depth planar cuts were computed for a fixed nominal z-position of 1284 µm (corresponding to the target focus).
The cuts were generated as circles starting on the center, focused at the nominally intended depth (z-position), and increasing their radial distance using the r-ɵ-z-scanner. The distance between the spots on the pathway and the distance between tracks could be arbitrarily chosen in the controlling software, but both were fixed to 3 µm.
We used a positioning system to find the anterior surface of flat poly(methyl methacrylate) (PMMA) samples of 3 mm thickness (test material not part of the laser system), which was then used as a reference point for further processing. This was measured with a confocal setup (measurement system not part of the laser system); it was focused, and the reflection from the material was detected with a photodiode connected to a monomode fiber. The laser focus was on the anterior surface of the PMMA, when the signal of the photodiode was maximal. The resolution of this confocal system at that point merely depended on the NA of the focusing optics and on the aberrations within the system. The axial resolution of the setup was ~1 µm. Further signal peaks (lower in amplitude) facilitated the determination of the z-position of each cut (producing at least scattering), given the presence of a layered system.
The z-position of the anterior surface of the PMMA and those z-positions of the cut were confocally determined by shifting the focusing optics in the z-direction; refraction was not taken into account, but the refractive index of the PMMA for 1030 nm (1.4811) was accounted for [
8].
The LIOB threshold of the used setup was experimentally determined by observing the cavitation bubble pattern of the same 3 × 3 µm spaced scan for increasing energies in ~1 nJ steps, as the lowest pulse energy for which a homogeneous cavitation bubble pattern was observed. This threshold depended primarily on the laser and optical train characteristics. The empirically determined LIOB threshold (~56 nJ) for this setup on the PMMA is, however, compatible with the theoretical estimates determining the threshold [
9]:
where E
Th is the pulse energy threshold for LIOB, k is a scaling constant, τ is the pulse duration, m is the multiphoton order, M
2 is the beam, and NA is the numerical aperture of the system.
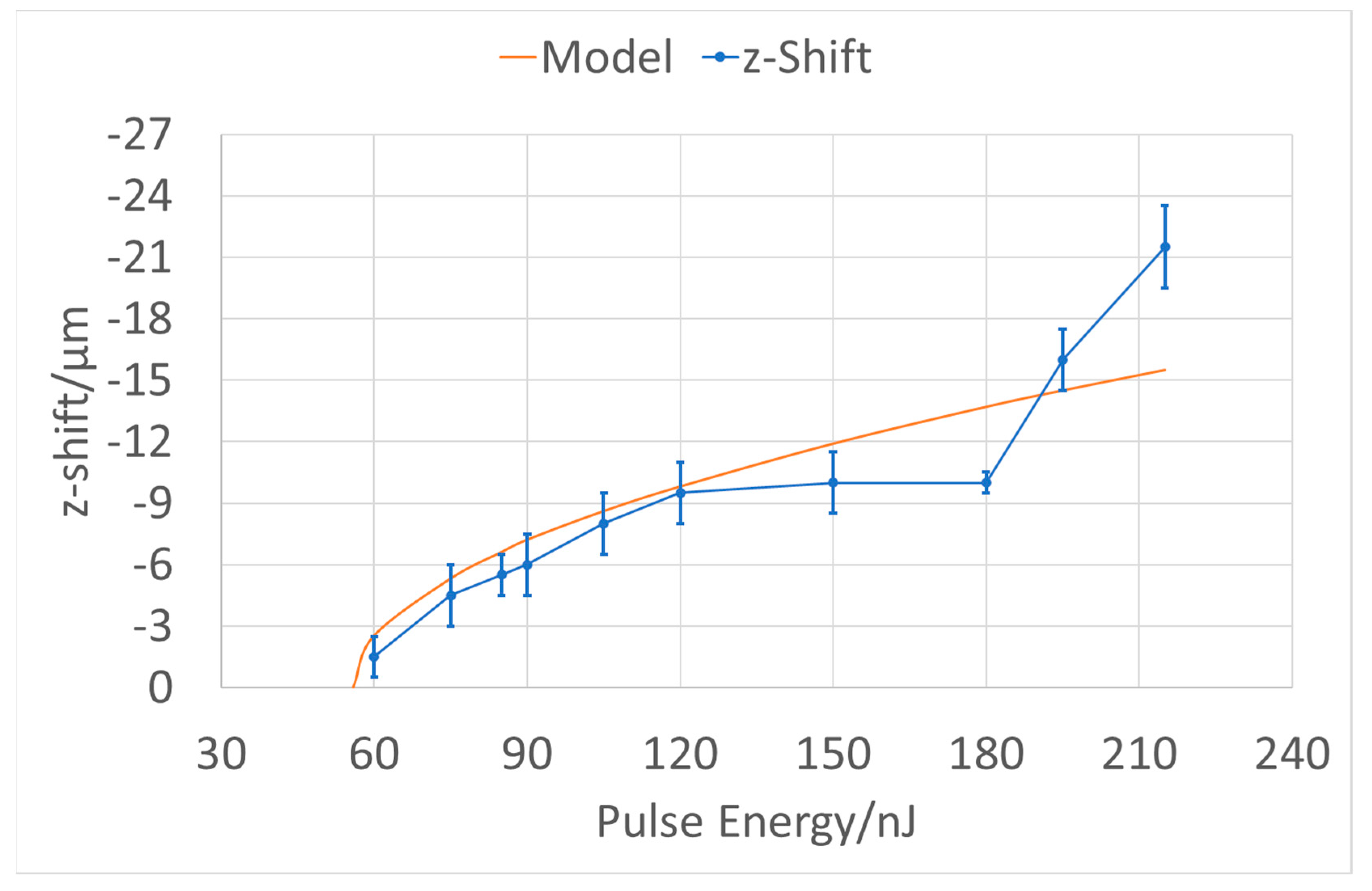
For these cutting experiments, the (single-pulse) energy of the laser was varied between 60 nJ and 215 nJ. Different energy levels (for the same spot spacings, i.e., different doses) running from 1.07 × (~60 nJ) to 3.8 × (~215 nJ) for the laser-induced optical breakdown (LIOB) threshold (~56 nJ) were used to perform flat cuts within the PMMA at the same nominal focus position. The z-locations of the effective cut and the anterior surface of the PMMA were confocally determined. The difference (PMMA_surface—Cut_layer) was used as an estimate for the effective shift in the z-position of the cut.
In more detail:
Spot spacings were fixed to 3 × 3 µm.
PMMA was positioned as follows: confocal was measured for the anterior surface 3 times, averaged, and set as the PMMA anterior height (reference null z-position). The target cut depth (z-position) in the PMMA was set to 1284 µm, in all cases.
The cut was flat, parallel to the nominal flat PMMA surface.
Immediately after the cut was performed, the confocal signal was measured from the cut.
The actual LIOBth of the used system was 56 nJ.
The following energies were used: 60 nJ (1.07× LIOBth), 75 nJ (1.34× LIOBth), 85 nJ (1.52× LIOBth), 90 nJ (1.61× LIOBth), 105 nJ (1.88× LIOBth), 120 nJ (2.14× LIOBth), 150 nJ (2.68× LIOBth), 180 nJ (3.21× LIOBth), 195 nJ (3.48× LIOBth), and 215 nJ (3.84× LIOBth).
For each energy value, 3 independent cuts were performed by positioning the same PMMA plate, but to a “fresh, undamaged” location.
Three measurements of the cut at various positions were performed to estimate the z-position of the cut.
For the error bars, the standard deviations calculated from 9 measurements were considered.
The confocal measurement from the cut was asynchronous from the angle to increase the contrast ratio of the peak and average signals, because using 3 × 3 µm for very low energies, the adjacent pulses may not always overlap, so one needs to average many photodiode signals staying at the same position.
The difference (PMMA_surface—Cut_layer) was used as a surrogate for the effective shift in the z-position of the cut.
Comparison to Pre-Existing Models
As introduced earlier, Docchio et al. [
1] studied plasma induced in liquids by nanosecond Nd:YAG laser pulses and its spatio-temporal dynamics to develop a moving LIOB model, which subsequently lead to a refined optical breakdown model in dielectrics [
2]. In this work, we compared our experimental measurements to the predictions provided by the models. Specifically, we assumed that the position of the cut (along the propagation axis) corresponds to the maximum extent of the breakdown region (with respect to the nominal focus position towards the laser source). This equates to the following:
where z
max is the maximum extent of the breakdown region (in our case assumed to represent the effective position of the cut), z
R is the Rayleigh length (approximately 9 µm in our setup), and β is the ratio of pulse energy to the breakdown threshold of a material (approximately 56 nJ for PMMA in our setup).
This model (directly providing the shift, as the maximum extent of the breakdown region) was compared to the measured values (difference between the actual and nominal z-position). The analysis is based on the comparison of the actual measurements to the theoretical models (for providing an explanation).
4. Discussion
The moving breakdown model of Docchio et al. [
1] described the laser–tissue interaction of nanosecond laser pulses in an aqueous medium. For ultrashort laser pulses in the low picosecond and femtosecond regimes, the theoretical predictions by the model contradicted the experimental observations [
10].
The basis of both moving breakdown models seems intuitive, and according to them, the breakdown may occur out of focus (in front of the focus) once the threshold is exceeded. The extent of the breakdown region (along the propagation axis, i.e., z-axis) can be determined by observing the portion of intensity above the threshold value. This moving breakdown prediction has been experimentally confirmed for long pulses [
1].
It should be noted that the model does not account for plasma shielding effects, i.e., the absorption by the plasma.
For ultrashort laser pulses (shorter than the picosecond regime), the small spatial extent of the pulse leads to a different time- and position-dependent breakdown due to the finite propagation speed of the laser pulses. In that ultrashort pulse regime, breakdown starts in front of the focus and then further propagates toward the focus [
2]; this is different from the previous simple moving breakdown model (valid for ns regime) in which the breakdown process starts in focus and only the extent of the breakdown region includes positions up the beam path. Noack and Vogel [
10] presented a rate equation model to predict the breakdown threshold of water by applying a time-dependent laser intensity from which lower breakdown predictions are obtained for femtosecond pulses. Such ultrashort laser pulses no longer fill the focal volume completely, and models must account for the propagation of the pulse.
As shown in previous work [
2], breakdown is initiated closer to the laser source, contrary to the previous moving breakdown model [
1] for which the breakdown begins at focus (and propagates upstream). Since the pulse propagation in the medium is ignored, the earlier moving breakdown model predicts an identical result, irrespective of the actual pulse duration.
Unfortunately, no closed-form expression for the time-dependent breakdown position has been reported, so we have used numerical procedures to determine it.
The amount of z-shift (backwards towards the laser source) is related to the Rayleigh length of the beam in focus. This means that (beyond the pulse energy above the threshold) parameters affecting the Rayleigh length (mainly NA and wavelength, but also M2 or Strehl Ratio) will also directly affect the amount of z-shift (for the same pulse energy), whereas parameters that do not affect the Rayleigh length (e.g., pulse duration) may only indirectly affect the amount of z-shift (due to effects in the LIOB threshold).
In the ultrashort pulse regime (shorter than picoseconds), breakdown occurs in front of the focus, yet (in the absence of plasma shielding) the intensity continues to increase as the pulse propagates to the focus position (due to the reduction in beam diameter), which may partially offset the intensity decreases caused by plasma absorption.
The revised moving breakdown model well matches the phenomenological observations described in this work, at least for the regime below 2.7× LIOBth (~150 nJ in our setup).
By applying the revised moving breakdown model for short pulses, one can obtain position-dependent breakdown onsets, which in turn can be used to better control the laser focus to reach the user-desired z-position of the actual cut.
A refined moving breakdown model for ultrafast laser–material interactions that includes pulse propagation in the focal volume may help to improve the accuracy and precision of cuts performed using a femtosecond system for corneal LVC.
The results of a previous clinical study [
3] suggest that a lower laser energy setting in SMILE may result in deeper cuts; conversely (as in our work), a higher laser energy setting may lead to shallower cuts.
According to the clinical [
4,
5] and theoretical [
6,
7] literature, the actual cap thickness seems relevant to the clinical success of lenticule extraction. This reinforces the need for achieving accurate and predictable cap thicknesses (i.e., creating the cut at the predefined depth) in LVC.
Thicker caps may be associated with the induction of aberrations, and changes in corneal stiffness [
4], as well as the dioptric adjustment of spherical equivalent correction according to cap thickness, which may be required to obtain similar refractive outcomes in myopic SMILE procedures [
5].
Both of these effects can be explained optically and mechanically. The axial gradient index of the refraction structure of the stroma layer [
6] models a reduced optical effect for deeper cuts, whereas mechanical models also predict stronger undercorrections for thicker caps [
7].
These previous studies [
3,
4,
5,
6,
7], along with the previous models for moving optical breakdown [
1,
2], justify the laboratory work presented here.
In an attempt to minimize the impact of energy in the actual depth location of femtosecond cuts, an inspection of Equation (2) may provide some insights. Since the shift is linear with the Rayleigh length, reducing the Rayleigh length will diminish the effect (z-shift). This can be accomplished by reducing the wavelength (usually involving an in-depth redesign of the product) or reducing the minimum beam waist. In an alternative view, the Rayleigh length (i.e., the z-shift) can be reduced by increasing the NA (which usually involves less redesigning of the product compared to reducing the wavelength).
Further inspecting Equation (2), reducing β also diminishes the z-shift, and since β is the ratio of pulse energy to the breakdown threshold, reducing β implies working with energies close to the breakdown threshold. Previous studies [
11,
12] have already recommended working close to the breakdown threshold [
11] or establishing an optimum corridor for β from 1.5 to 3.15 [
12], whereas newer studies [
13] refined the optimum corridor for β from 1.4 to 2.0. This means that the associated shift would be restricted to 0.63× to 1.47× the Rayleigh length.
However, the implications of Equation (2) are intrinsically complex, since (e.g., according to Equation (1)) [
9] the wavelength and NA are both involved in the LIOB threshold, such that reducing the Rayleigh length (to diminish the z-shift effect) will reduce the LIOB threshold, which in turn would increase β. This should be resolved by reducing the laser energy in order to keep β in its optimum corridor [
11,
12,
13].
Since Equation (2) is governed by the square root of β − 1, higher energies would be associated with larger z-shifts, yet the effect of energy fluctuations (both absolute and relative) would have less effect (lower variance in z-shifts) for higher energies.
Since the moving breakdown model is on a per-pulse basis, the average energy of the train of pulses would determine the average z-shift, whereas the energy variations (within a treatment) would result in a wobbling of the z-shift.
During ultrashort pulse laser ablation, an intense laser beam focused within the tissue produces optical breakdown followed by plasma formation. The expansion of the plasma results in the creation of a cavitation bubble and its subsequent implosion [
14]. Spatially arranged pulses lead to coalescent bubbles that merge, resulting in a cleavage plane in the tissue. The one-dimensional bubble size is proportional to the cubic root of the laser pulse energy exceeding the threshold [
12]. In other words, the bubble volume is linearly proportional to the laser pulse energy exceeding the threshold. Pulse energies that are too low might induce uncut areas (so-called “black spots”), leading to increased surgical manipulation during dissection, and resulting in postoperative corneal edema and prolonged healing [
15]; however, pulse energies that are too high (or cumulative doses) would result in the formation of larger cavitation bubbles severing the tissue (the so-called “opaque bubble layer”) and lead to local tissue distortion [
16].
The shift determined in this work is primarily of the same importance for single- (flap, pockets, rings) or two-layer (lenticule) procedures, because the shift predicted by the moving LIOB model and the measured z-shifts would be approximately the same, irrespective of the desired cutting depth.
Earlier data [
3] showed that the cap was thicker in eyes treated with lower pulse energies and also after considering the postoperative thickening of the corneal epithelium as a covariate. This is in good agreement with the findings observed here for PMMA and with the predictions provided by the refined moving LIOB model for ultrashort laser pulses [
2].
Alternative hypotheses include self-focusing, previously suggested as the main non-linear effect contributing to the axial deviation of the focus [
17], which occurs when the interpulse time is shorter than the thermal diffusion time. The refractive index of the tissue changes locally due to the increase in temperature and shifts the focus position from the position predicted by linear Gaussian beam optics [
17]; the authors of the study showed that the deviation in the cutting depth depended considerably on the laser pulse energy.
Plasma shielding and non-linear self-focusing might be evaluated with different pulse durations.
However, in the first approach, the plasma length and the z-position at which the Gaussian propagation of the incoming (converging) beam reaches the LIOB energy density may be the simplest explanation. This is “merely” a geometric approach and does not require “advanced” laser–tissue interactions.
Further, the points reasonably well resemble the model estimates (though the measured points resemble a two-regime curve). For the tested parameters, the results suggest a 0.11 µm shift per nJ of pulse energy or ~1 µm shift per 9 nJ change in pulse energy.
Looking at the figure, two overlapping regimes seem to be suggested, or the error bars may produce that impression. It could well be that the plasma dominates (soft saturating curve up to 2.75× Eth ~160 nJ) for energies close to the threshold, and the mechanical bubble (photodisruption) dominates (steep curve above 2.75× Eth ~160 nJ) only for energies well above the threshold.
One may hypothesize that the mismatch between attempted and achieved z-positions of the cut may be different in lenticule thickness (a different z-shift for each cutting layer) and thus may affect the refractive outcomes in lenticule extraction and that the use of lower pulse energy may produce better refractive outcomes. This has been reported before [
18], but the authors could not confirm whether this observation was a result of the z-shift (refined moving LIOB model for ultrashort pulses) [
2]. However, thinner-than-planned lenticules have been reported recently, even for low pulse energy systems [
19].
Moreover, the deviations are expected to vary between different energy settings, and the exact underlying mechanisms of this observation are currently not confirmed.
Our analyses only used single-pulse energy as a variational parameter. By changing the pulse energy while keeping the repetition rate and spacings constant, not only would the single-pulse energy be varied, but the laser average power and treatment dose would also be varied. Alternatively, or as an extension, one could envision comparisons in which the single-pulse energy is kept constant and spacings are changed, as well as comparisons in which the single-pulse energy is varied along with spacings to preserve the treatment dose.
The underlying assumption is that the moving LIOB model is still based on the laser–tissue interaction of single pulses, and no cumulative effects are accounted for. However, Saerchen et al. also reported step-like changes in the cutting depth for extremely overlapping pulses [
20] (which is not the case in our setting).
However, the high repetition rate used for the experiment in this study may have caused effective heat accumulation in the material, which may have melted the material, manifesting the thermal effect. As a result, the processed area may have been increased and the depth reduced.
The compensation for the observed shift in z-direction (very well matched to the moving LIOB model) can be easily compensated for by offsetting the model predictions. An even simpler approach is based on the fact that the range of energies provided by commercial systems is limited (and ideally constrained to the range 1.4× LIOBTh to 3.15× LIOBTh) [
12]; specifically, using linear correlations between the model predictions and allowed pulse energy ranges would facilitate its statistical compensation. This may in turn improve the accuracy and precision of laser cuts for different pulse energies.