Nonlinear Dynamics of Silicon-Based Epitaxial Quantum Dot Lasers under Optical Injection
Abstract
1. Introduction
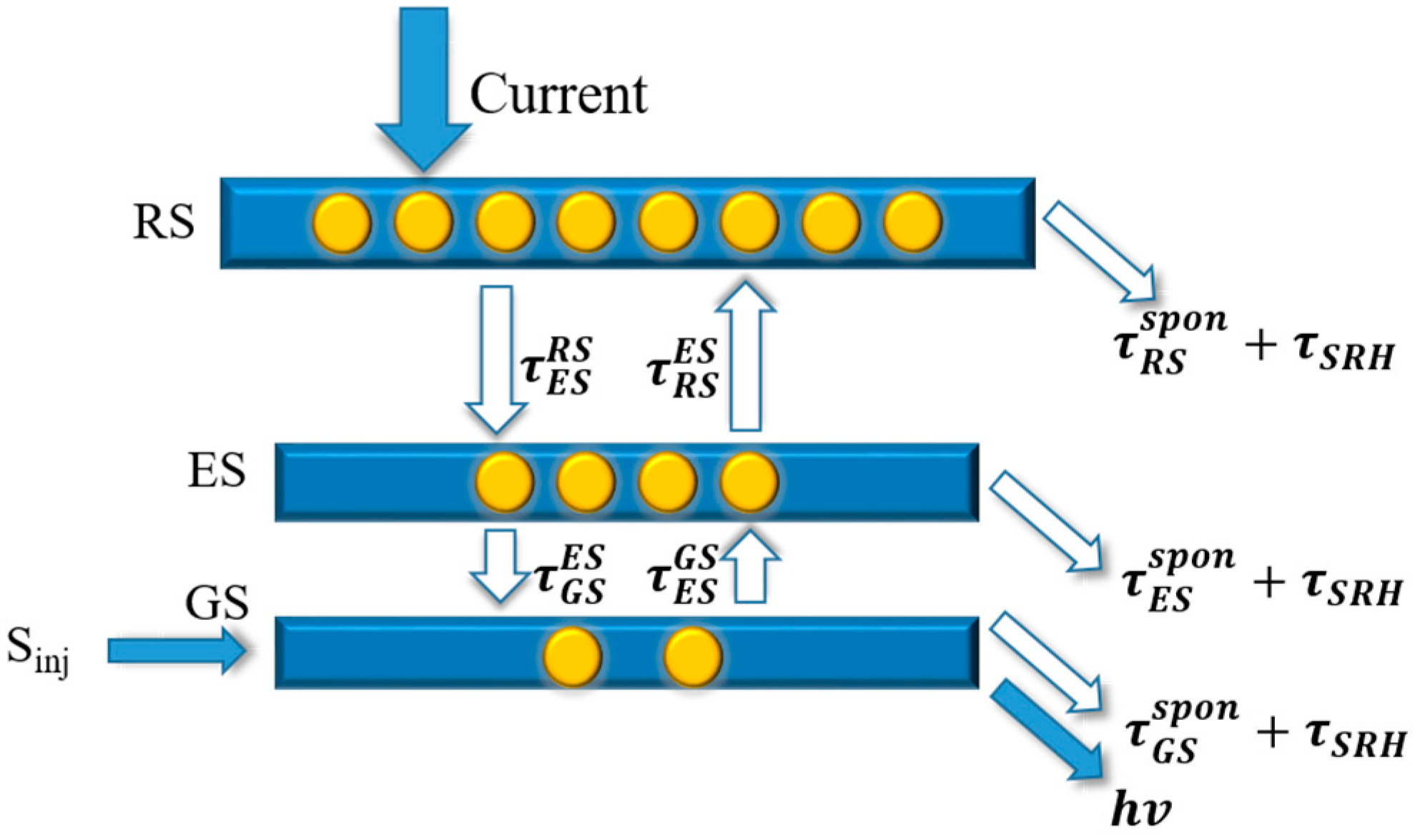
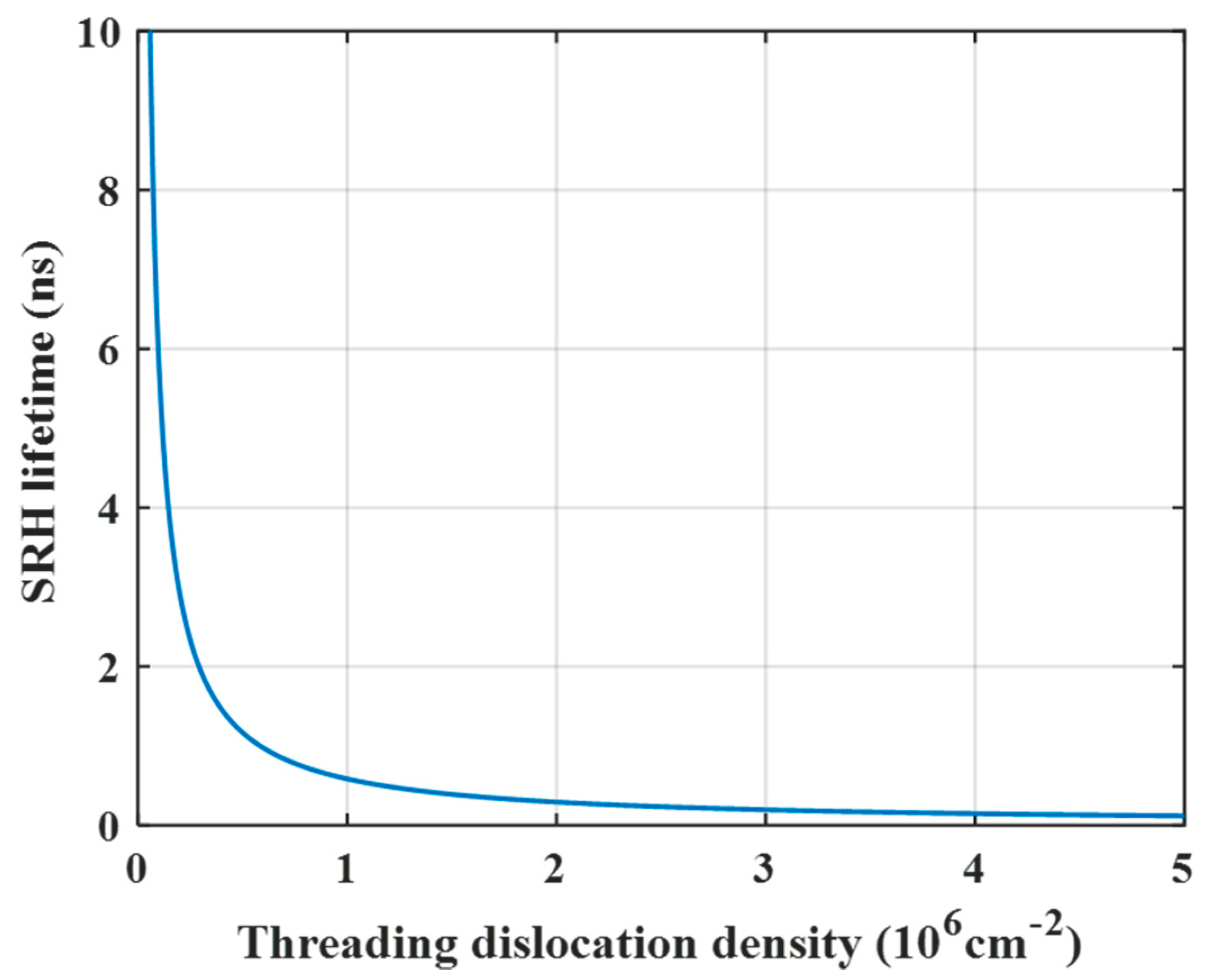
2. Theoretical Model
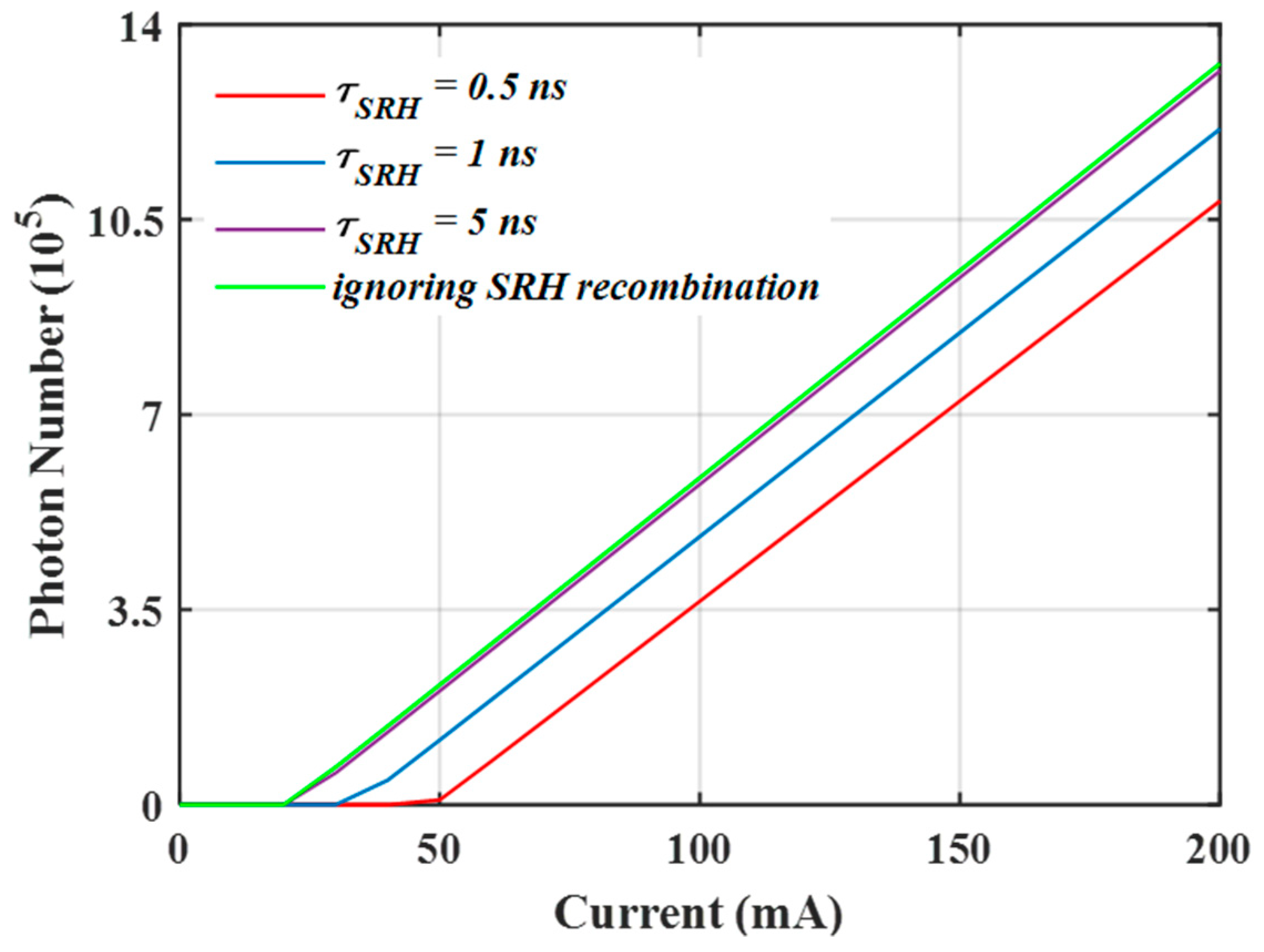
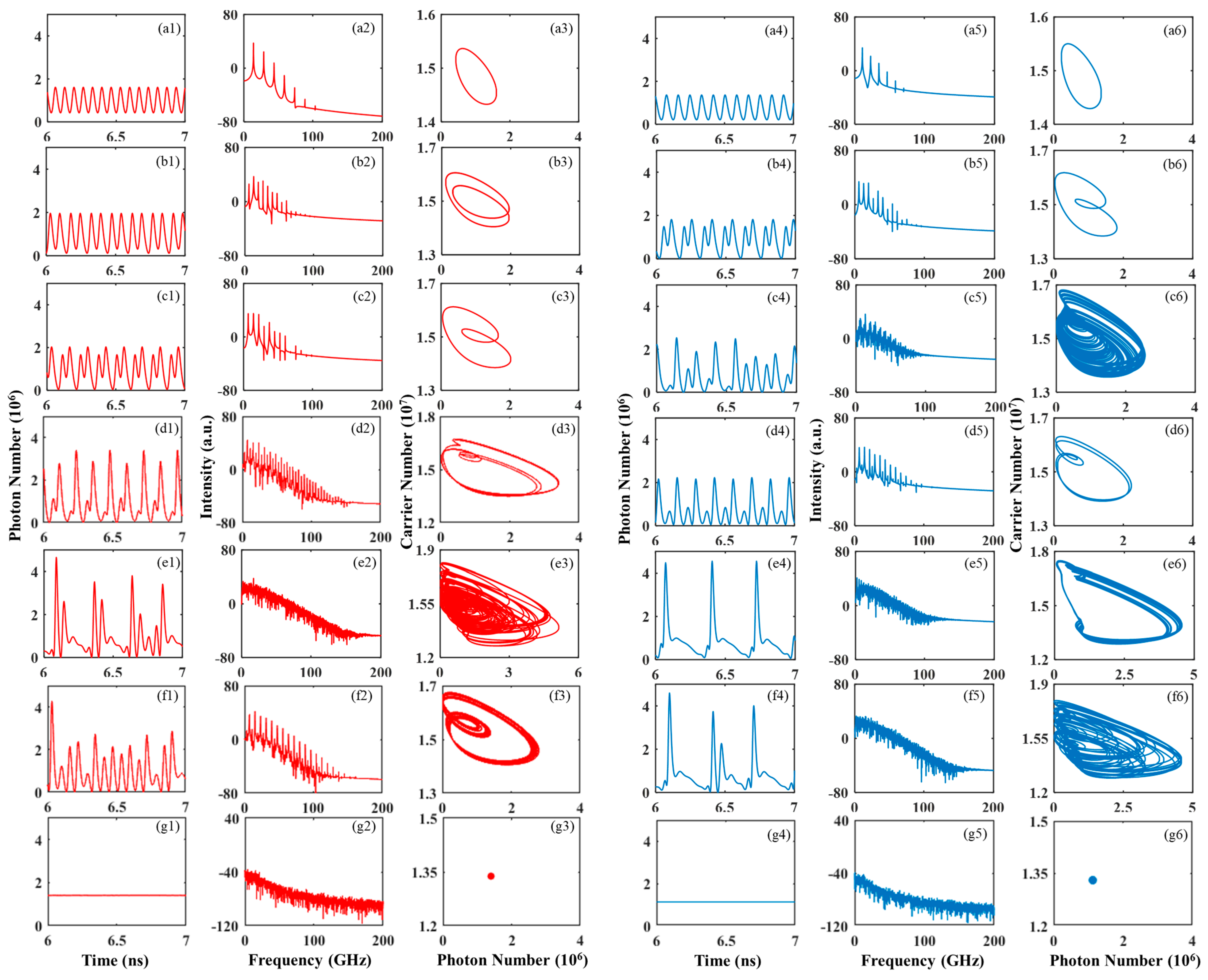
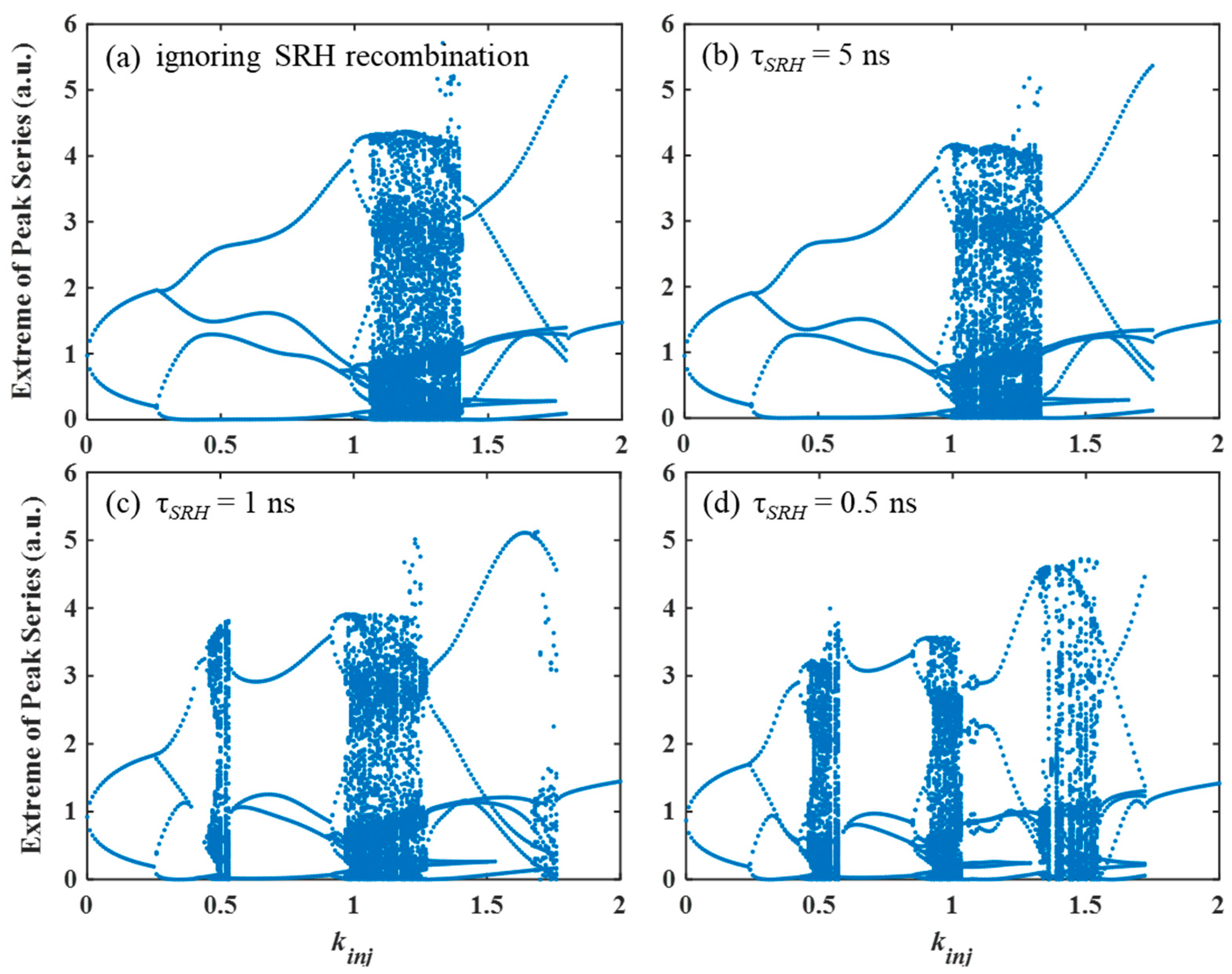
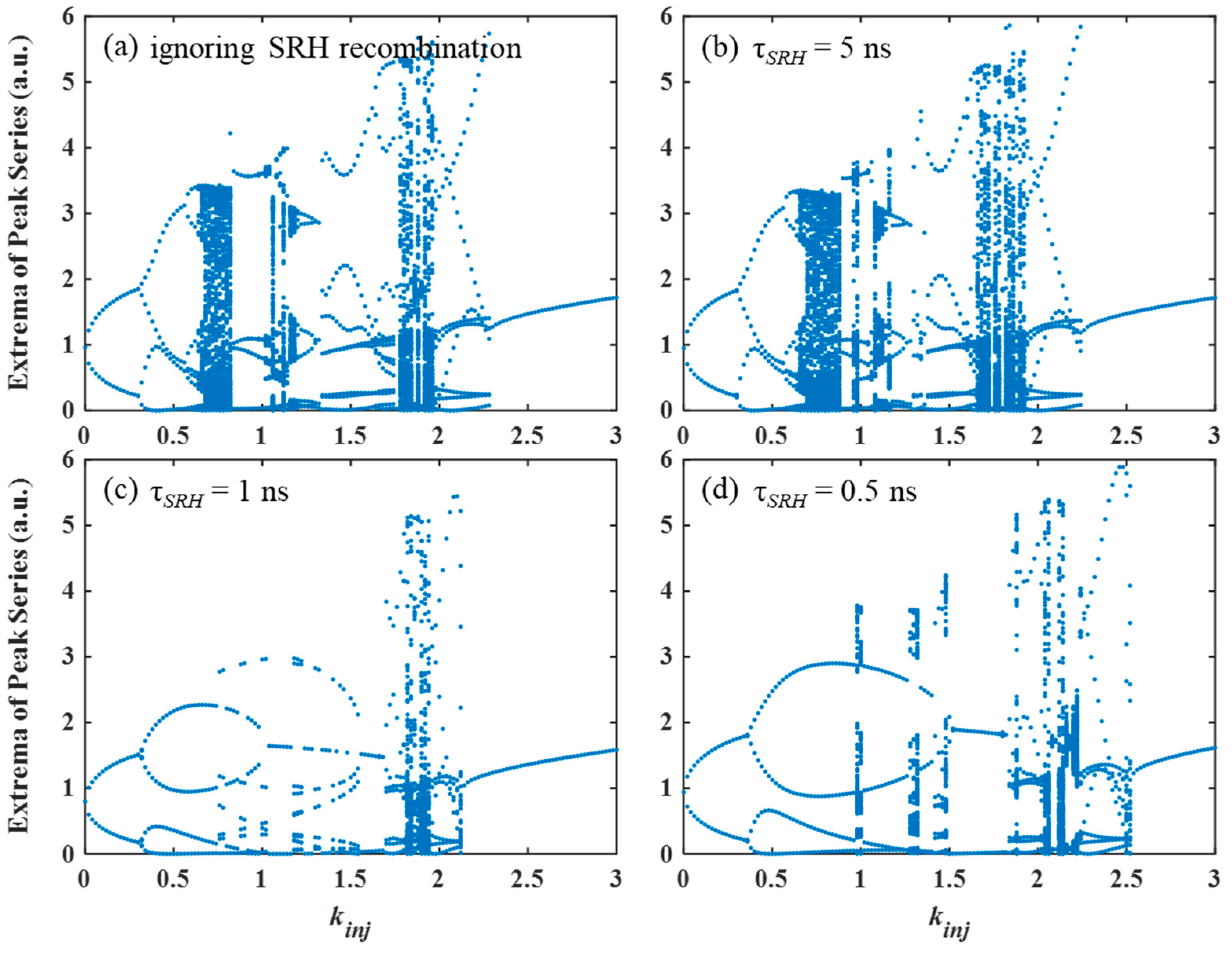
3. Results and Discussion
4. Conclusions
Author Contributions
Funding
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Lin, F.Y.; Tu, S.Y.; Huang, C.C.; Chang, S.M. Nonlinear dynamics of semiconductor lasers under repetitive optical pulse injection. IEEE J. Sel. Top. Quantum Electron. 2009, 15, 604–611. [Google Scholar] [CrossRef]
- Ohtsubo, J. Feedback induced instability and chaos in semiconductor lasers and their applications. Opt. Rev. 1999, 6, 1–15. [Google Scholar] [CrossRef]
- Abarbanel, H.D.I.; Kennel, M.B.; Illing, L.; Tang, S.; Chen, H.F.; Liu, J.M. Synchronization and communication using semiconductor lasers with optoelectronic feedback. IEEE J. Quantum Electron. 2001, 37, 1301–1311. [Google Scholar] [CrossRef]
- Jiang, N.; Xue, C.P.; Lv, Y.X.; Qiu, K. Physically enhanced secure wavelength division multiplexing chaos communication using multimode semiconductor lasers. Nonlinear Dyn. 2016, 86, 1937–1949. [Google Scholar] [CrossRef]
- Chang, D.; Zhong, Z.Q.; Valle, A.; Jin, W.; Jiang, S.; Tang, J.M.; Hong, Y.H. Microwave photonic signal generation in an optically injected discrete mode semiconductor laser. Photonics 2022, 9, 171. [Google Scholar] [CrossRef]
- Cui, C.; Fu, X.; Chan, S.C. Double-locked semiconductor laser for radio-over-fiber uplink transmission. Opt. Lett. 2009, 34, 3821–3823. [Google Scholar] [CrossRef]
- Romain, M.N.; Guy, V.; Jan, D.; Guy, V.S. Reducing the phase sensitivity of laser-based optical reservoir computing systems. Opt. Express 2016, 24, 1238–1252. [Google Scholar]
- Kawaguchi, Y.; Okuma, T.; Kanno, K.; Uchida, A. Entropy rate of chaos in an optically injected semiconductor laser for physical random number generation. Opt. Express 2021, 29, 2442–2457. [Google Scholar] [CrossRef]
- Zhang, L.; Pan, B.; Chen, G.; Guo, L.; Lu, D.; Zhao, L.; Wang, W. 640-Gbit/s fast physical random number generation using a broadband chaotic semiconductor laser. Sci. Rep. 2017, 7, 45900. [Google Scholar] [CrossRef] [PubMed]
- Bimberg, D.; Pohl, U.W. Quantum dots: Promises and accomplishments. Mater. Today 2011, 14, 388–397. [Google Scholar] [CrossRef]
- Liu, A.Y.; Komljenovic, T.; Davenport, M.L.; Gossard, A.C.; Bowers, J.E. Reflection sensitivity of 1.3 μm quantum dot lasers epitaxially grown on silicon. Opt. Express 2017, 25, 9535–9543. [Google Scholar] [CrossRef] [PubMed]
- Jin, Z.Y.; Huang, H.M.; Zhou, Y.G.; Zhao, S.Y.; Ding, S.H.; Wang, C.; Yao, Y.; Xu, X.C.; Grillot, F.; Duan, J.N. Reflection sensitivity of dual-state quantum dot lasers. Photonics Res. 2023, 11, 1713–1722. [Google Scholar] [CrossRef]
- Nishi, K.; Takemasa, K.; Sugawara, M.; Arakawa, Y. Development of quantum dot lasers for data-com and silicon photonics applications. IEEE J. Sel. Top. Quantum Electron. 2017, 23, 1–7. [Google Scholar] [CrossRef]
- Duan, J.N.; Zhou, Y.; Dong, B.Z.; Huang, H.M.; Norman, J.C.; Jung, D.; Zhang, Z.; Wang, C.; Bowers, J.E.; Grillot, F. Effect of p-doping on the intensity noise of epitaxial quantum dot lasers on silicon. Opt. Lett. 2020, 45, 4887–4890. [Google Scholar] [CrossRef] [PubMed]
- Ukhanov, A.A.; Stintz, A.; Eliseev, P.G.; Malloy, K.J. Comparison of the carrier induced refractive index, gain, and linewidth enhancement factor in quantum dot and quantum well lasers. Appl. Phys. Lett. 2004, 84, 1058–1060. [Google Scholar] [CrossRef]
- Ukhanov, A.A.; Wang, R.H.; Rotter, T.J.; Stintz, A.; Lester, L.F.; Eliseev, P.G.; Malloy, K.J. Orientation dependence of the optical properties in InAs quantum-dash lasers on InP. Appl. Phys. Lett. 2002, 81, 981–983. [Google Scholar] [CrossRef]
- Norman, J.C.; Jung, D.; Zhang, Z.; Wan, Y.; Liu, S.; Shang, C.; Herrick, R.W.; Chow, W.W.; Gossard, A.C.; Bowers, J.E. A review of high-performance quantum dot lasers on silicon. IEEE J. Quantum Electron. 2019, 55, 1–11. [Google Scholar] [CrossRef]
- Zheng, Y.F.; Xia, G.Q.; Lin, X.D.; Wang, Q.Q.; Wang, H.; Jiang, C.; Chen, H.; Wu, Z.M. Experimental investigation on the mode characteristics of an excited-state quantum dot laser under concave mirror optical feedback. Photonics 2023, 10, 166. [Google Scholar] [CrossRef]
- Yang, J.; Tang, M.; Chen, S.; Liu, H. From past to future: On-chip laser sources for photonic integrated circuits. Light Sci. Appl. 2023, 12, 16. [Google Scholar] [CrossRef]
- Tang, M.C.; Park, J.; Wang, Z.C.; Chen, S.; Jurczak, P.; Seeds, A.; Liu, H.Y. Integration of III-V lasers on Si for Si photonics. Prog. Quantum Electron. 2019, 66, 1–18. [Google Scholar] [CrossRef]
- Wan, Y.T.; Xiang, C.; Guo, J.; Koscica, R.; Kennedy, M.J.; Selvidge, J.; Zhang, Z.; Chang, L.; Xie, W.Q.; Huang, D.; et al. High speed evanescent quantum-dot lasers on Si. Laser Photonics Rev. 2021, 15, 2100057. [Google Scholar] [CrossRef]
- Wei, W.Q.; Huang, J.Z.; Ji, Z.T.; Han, D.; Yang, B.; Chen, J.J.; Qin, J.L.; Cui, Y.O.; Wang, Z.H.; Wang, T.; et al. Reliable InAs quantum dot lasers grown on patterned Si (001) substrate with embedded hollow structures assisted thermal stress relaxation. J. Phys. D Appl. Phys. 2022, 55, 40. [Google Scholar] [CrossRef]
- Liu, A.Y.; Chong, Z.; Norman, J.; Snyder, A.; Lubyshev, D.; Fastenau, J.M.; Liu, A.W.K.; Gossard, A.C.; Bowers, J.E. High performance continuous wave 1.3 µm quantum dot lasers on silicon. Appl. Phys. Lett. 2014, 104, 041104. [Google Scholar] [CrossRef]
- Liu, A.Y.; Bowers, J. Photonic integration with epitaxial III–V on silicon. IEEE J. Sel. Top. Quantum Electron. 2018, 24, 1–12. [Google Scholar] [CrossRef]
- Wei, W.Q.; Feng, Q.; Guo, J.J.; Guo, M.C.; Wang, J.H.; Wang, Z.H.; Wang, T.; Zhang, J.J. InAs/GaAs quantum dot narrow ridge lasers epitaxially grown on SOI substrates for silicon photonic integration. Opt. Express 2022, 28, 26555–26563. [Google Scholar] [CrossRef] [PubMed]
- Shang, C.; Wan, Y.T.; Norman, J.; Collins, N.; MacFarlane, I.; Dumont, M.; Liu, S.T.; Li, Q. Low-Threshold epitaxially grown 1.3-μm InAs quantum dot lasers on patterned (001) Si. IEEE J. Sel. Top. Quantum Electron. 2019, 25, 1–7. [Google Scholar] [CrossRef]
- Chen, S.; Li, W.; Wu, J.; Jiang, Q.; Tang, M.C.; Shutts, S.; Elliott, S.N.; Sobiesierski, A.; Seeds, A.J.; Ross, I.; et al. Electrically pumped continuous-wave III–V quantum dot lasers on silicon. Nat. Photonics 2016, 10, 307–311. [Google Scholar] [CrossRef]
- Zhao, S.Y.; Grillot, F. Effect of Shockley-Read-Hall recombination on the static and dynamical characteristics of epitaxial quantum-dot lasers on silicon. Phys. Rev. A 2021, 103, 9. [Google Scholar] [CrossRef]
- Chu, Q.; Zhao, S.Y.; Wang, J.W.; Sun, Y.X.; Yao, Y.; Xu, X.C.; Grillot, F.; Duan, J.N. Optical noise characteristics of injection-locked epitaxial quantum dot lasers on silicon. Opt. Express 2023, 31, 25177–25190. [Google Scholar] [CrossRef]
- Andre, C.; Boeckl, J.; Wilt, D.; Pitera, A.; Lee, M.L.; Fitzgerald, E.; Keyes, B.; Ringel, S. Impact of dislocations on minority carrier electron and hole lifetimes in GaAs grown on metamorphic SiGe substrates. Appl. Phys. Lett. 2004, 84, 3447–3449. [Google Scholar] [CrossRef]
- Saldutti, M.; Tibaldi, A.; Cappelluti, F.; Gioannini, M. Impact of carrier transport on the performance of QD lasers on silicon: A drift-diffusion approach. Photonics Res. 2020, 8, 1388–1397. [Google Scholar] [CrossRef]
- Duan, J.; Wang, X.G.; Zhou, Y.G.; Wang, C.; Grillot, F. Carrier-noise-enhanced relative intensity noise of quantum dot lasers. IEEE J. Quantum Electron. 2018, 54, 1–7. [Google Scholar] [CrossRef]
- Wang, C.; Zhuang, J.P.; Grillot, F.; Chan, S.C. Contribution of off-resonant states to the phase noise of quantum dot lasers. Opt. Express 2016, 24, 29872–29881. [Google Scholar] [CrossRef] [PubMed]
- Jiang, Z.F.; Wu, Z.M.; Jayaprasath, E.; Yang, W.Y.; Hu, C.X.; Xia, G.Q. Nonlinear dynamics of exclusive excited-state emission quantum dot lasers under optical injection. Photonics 2019, 6, 58. [Google Scholar] [CrossRef]

Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Fang, R.; Xia, G.-Q.; Zheng, Y.-F.; Wang, Q.-Q.; Wu, Z.-M. Nonlinear Dynamics of Silicon-Based Epitaxial Quantum Dot Lasers under Optical Injection. Photonics 2024, 11, 684. https://doi.org/10.3390/photonics11080684
Fang R, Xia G-Q, Zheng Y-F, Wang Q-Q, Wu Z-M. Nonlinear Dynamics of Silicon-Based Epitaxial Quantum Dot Lasers under Optical Injection. Photonics. 2024; 11(8):684. https://doi.org/10.3390/photonics11080684
Chicago/Turabian StyleFang, Ruilin, Guang-Qiong Xia, Yan-Fei Zheng, Qing-Qing Wang, and Zheng-Mao Wu. 2024. "Nonlinear Dynamics of Silicon-Based Epitaxial Quantum Dot Lasers under Optical Injection" Photonics 11, no. 8: 684. https://doi.org/10.3390/photonics11080684
APA StyleFang, R., Xia, G.-Q., Zheng, Y.-F., Wang, Q.-Q., & Wu, Z.-M. (2024). Nonlinear Dynamics of Silicon-Based Epitaxial Quantum Dot Lasers under Optical Injection. Photonics, 11(8), 684. https://doi.org/10.3390/photonics11080684





