Abstract
Optical rogue waves are a nonlinear phenomenon that offers a unique opportunity to gain fundamental insights into wave interaction and behavior, and the evolution of complex systems. Optical systems serve as a suitable testbed for the well-controlled investigation of this natural phenomenon, which cannot be easily studied in an ocean environment. Additionally, such systems offer practical applications in telecommunications and optical signal processing, making this topic a vital area of research. Fiber lasers are considered the best candidates for demonstrating and investigating the emergence of optical rogue waves. In particular, they offer significant advantages in nonlinear dynamics due to faster field evolution and a higher number of events that can be recorded within a relatively short time. In this paper, we present the development mechanisms of optical rogue wave events. It was found that multimode vector instability, pulse–pulse interaction, and soliton rain are the main nonlinear dynamics leading to the formation of optical rogue wave events.
1. Introduction
Due to the similarities between the propagation of waves in the ocean and optics, optical systems have received much attention over the last decade for studying the dynamics of rogue waves. This has opened up opportunities to study this natural phenomenon using optical testbed experiments in well-controlled investigations, which are conducted much more easily than using ocean waves. In addition, rogue waves in optical systems have an advantage in practical applications such as in telecommunications, optical signal processing, and high-power localized laser systems. Therefore, it is necessary to develop a detailed understanding of the underlying optical rogue wave (ORW) mechanisms.
In an optical system, the nonlinear dynamics are suitably versatile and highly efficient theoretical frameworks that can be successfully used for developing an understanding the basic features of ORWs’ emergence [1,2,3,4], and a nonlinear Schrödinger Equation (NLSE) is often used to model these phenomena [5,6,7]. This has also stimulated research in diverse areas of nonlinear optics to study ORWs in different optical systems, including nonlinearly driven cavities [8], parametric amplifiers [9], optically injected semiconductor lasers [10], titanium–sapphire lasers [11], and fiber lasers [12,13]. It was found that fiber laser systems offer great advantages in studying these nonlinear dynamics that are related to much faster field evolution, and hence, a high number of events can be recorded in a relatively short time. Therefore, extensive studies of ORW formation have been performed experimentally and theoretically on fiber lasers, including supercontinuum fiber lasers [14,15,16,17,18,19], Raman fiber amplifiers and lasers [20,21], fiber Brillouin lasers [22], and mode-locked fiber laser [12,13,23,24,25,26,27]. Among them, mode-locked fiber lasers are considered the best system for describing the emergence of ROWs. The main reason for ORWs’ appearance in these lasers is modulation instability, which is a nonlinear process where a CW or a steady-state solution becomes unstable due to perturbations, leading to the growth of sidebands and the eventual formation of ORWs. It was found that the gain level of active media and dissipative systems in the fiber laser also play a main role in driving various instabilities in ORW formation, such as Q-switching instability pulsating regimes [1], bunched chaotic multiple pulsing interaction [28], multiple soliton collisions [29], and the interaction with dispersive waves [30] which have been identified as a key mechanisms in the formation of RWs in fiber lasers. Solitons and breathers also play roles in the dynamics leading to ORW formation. However, in a mode-locked fiber laser, the ORW formation mechanisms are nonlinear multiple-pulse interactions and dispersion–nonlinearity balance. The multiple pulses, or dissipative solitons, can interact either weakly or strongly. The weak interaction processes are amplified by an active medium due to the endless recirculation of pulses in the cavity. This kind of interaction of multiple pulses can occur through their tails, or through dispersive waves (soliton rain), leading to a bunch of pulses that have a time shorter than the cavity round trip time [20,31,32,33]. Whereas strong interactions are affected by the cavity parameters, controlling these parameters can allow us to explore various pulsation behaviors like breathers. Also, ORW events as intermittent regimes have been studied experimentally in all-normal-dispersion passive mode-locked, fiber lasers [34,35,36,37]. Therefore, passive mode-locked laser operation with multiple pulses per cavity round trip is considered to be a preferred method for ORW mechanism investigations. Furthermore, the outcomes show that optical systems have become an excellent playground for studies of RWs not only due to their similarity to oceanic RWs, as studied in the NLSE but, indeed, more generally for the study of large and statistically defined events.
Despite the fact that there has been considerable effort focused towards understanding the physical mechanisms behind the emergence of ORW events, the complete picture still remains uncertain and unclear. This is because these waves appear from nowhere and disappear without a trace, as well as having a statistical probability distribution function (PDF) that is completely different from that found regularly in normal waves. Continued study in this area promises to reveal deeper insights into the behavior of extreme events in optical systems and beyond. Thus, it is necessary to build a testbed experiment that can exploit such events in analogue physical systems where well-controlled experiments can be set up, producing large data sets as well as allowing fast analysis of the data.
In this paper, we developed a testbed experiment of a vector testbed fiber laser system which takes into account the laser’s dynamic instabilities, particularly natural vector instability (polarization), for exploring ORW events in a well-controlled environment. This could help us to study as many ORW event mechanisms as possible. This means that rather than conducting one experiment to study only one or two events, we conduct fiber laser experiments that can observe most of the RW events. Therefore, the outcomes of this testbed experimental study could be beneficial for predicting and controlling the appearance of RWs in optical systems. In addition, understanding the physics behind RWs’ emergence is not only important to prevent this particular system from hazardous effects, but it can also provide a promising method for localized (time/space or both time and space) high-power laser generation.
2. Testbed Experimental Setup
The testbed fiber laser system was a unidirectional ring cavity oscillator, as illustrated in Figure 1. The laser cavity contained a 1 m long erbium-doped fiber (EDF) which was used as an active medium and had an absorption of 80 dB/m and a second-order dispersion (β2) of +59 ps2/km at 1550 nm. A fiber-pigtailed 980 nm laser diode was used to pump the EDF through a 980/1550 WDM. A polarization-insensitive isolator with 51 dB attenuation was used to ensure unidirectional operation of the ring cavity. The intra-cavity birefringence was controlled by PC1, while PC2 was used to control the SOP of a pump laser diode. PC1 and PC2, as well as the pump power, enabled high flexibility in the generation and control of the nonlinear dynamics of this laser. A 70:30 output coupler (OC) was used to output 30% of the cavity light. The rest of the cavity as SMF with a β2 of −22 ps2/km; we investigated the dynamics at different cavity lengths (615 m and 11.3 m). The laser output was detected using a 50 GHz fast photodetector (Finisar XPDV2320R; Walnut Creek, CA, USA) and recorded using an 80 GHz sampling oscilloscope (Agilent DSOX93204A; Santa Clara, CA, USA). The oscilloscope traces were recorded for 26 ms with an effective resolution of 12.5 ps per point and with an amplitude resolution of 8 bits. To analyze the results using the spatiotemporal dynamics, the 26 ms oscilloscope traces were split into segments. The length of each segment was equal to one round trip. Then, these segments were processed as a matrix, which provided the intensity evolution through many round trips.
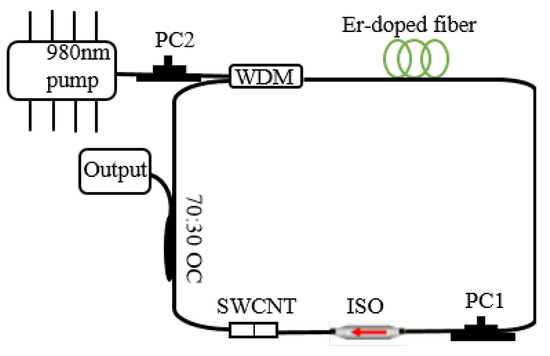
Figure 1.
The experimental setup. WDM: wavelength division multiplexing; PC: polarization controller; ISO: optical isolator; CNT: carbon nanotube SA; and OC: output coupler.
3. Results and Discussion
Using a long cavity length (615 m), we observed several new types of low-threshold vector resonance multimode instability [26]. Multimode instability inherits some features of modulation and multi-pulsing regimes in the form of the spatial modulation of the two orthogonal states of polarization (SOP) with a period equal to the beat length, and so leads to different levels of coherent coupling (synchronization) depending on the birefringence strength. We have shown that by tuning the interaction of two orthogonal SOPs of the laser cavity, we obtain polarization instability as a feature of MI, leading to the emergence of slow and fast ORWs, as shown in Figure 2 [38,39].
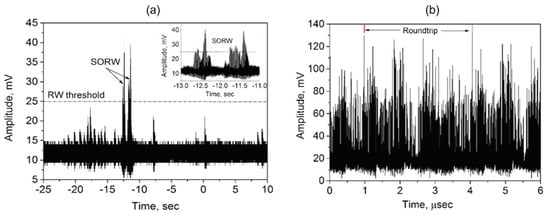
Figure 2.
(a) SORW event; (b) FORW event that emerged in our testbed fiber laser.
The regimes of slow and fast ORWs were classified based on their characteristic lifetime, which was calculated from the decay of the autocorrelation function (AF) of Figure 2. In this experiment, the SORW is observed to occur over a long time scale, as illustrated in Figure 2a, where the events have a lifetime of many seconds, whereas FORW in Figure 2b is observed to have a short time (sub-round trip time) where the event lifetime is in a ms or µs scale. Hence, the characteristic times of the SORW and FORW are 1.39 ms and 0.59 ms for slow ORW and fast ORW, respectively (the round trip time is 3.0773 µs). The spatiotemporal intensity evolution of the fast ORW show that the events are in two groups [36]. The first group of patterns are the common patterns that are observed over most of the polarization space with a relatively high likelihood. These common patterns can be classified into three kinds of fast ORW (lonely, twins and three sisters), as shown in Figure 3a–c. The second group of patterns are rare patterns; inside of this group, two mechanisms of pulse–pulse interaction were considered: the collision (the cross pattern) and the resonance interaction (the accelerated pattern), as shown in Figure 3d,e. This group of patterns have a relatively low likelihood. The switching between the regimes of interest can be adjusted simply by changing the birefringence in the cavity at a pump power of 18.4 mW.
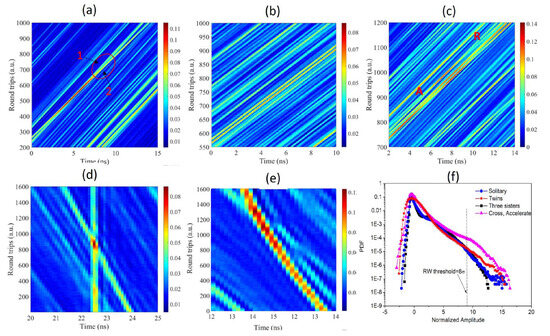
Figure 3.
Two-dimensional spatiotemporal evolution of (a) a lonely fast ORW; (b) a twin fast ORW; (c) a three-sisters fast ORW; (d) cross-pulsing fast ORWs; (e) accelerated ORWs; and (f) PDF of the fast ORW regimes.
In lonely fast ORWs (Figure 3a), it is clear that the ORWs emerged due to the pulse–pulse interactions, and they oscillated during ~200 round trips or ~600 µs (the red-colored); after that, the events lost energy to an event with less amplitude (the yellow-colored top in the front and back views) over 152 µs. Then, the pulse became unstable over 80 round trips (~240 µs) and, finally, for a short period of uncertainty, it split into two different pulses. The estimated likelihood of the pattern as the ratio between the number of observations of this pattern and the number of observations of the lonely ORW patterns has a high value of 0.6.
A parallel twin fast ORWs pattern was observed in the form of a two-pulse soliton molecule with a longer lifetime (333 round trips ~1 ms). This kind of pattern appeared either close to the main pulse or close to a high sub-harmonic pulse in the case of a multi-pulsing regime. The extremely long lifetime of the twin patterns can probably be explained by periodic amplification of the pattern in each round trip; that is to say, the pattern could not appear between pulses because the energy of the system was depleted and was not enough to amplify the pulse above the RW threshold. The likelihood of this pattern was ~0.3.
In the case of chaotic multi-pulsing during round-trip propagation, three consecutive fast ORW events emerged (Figure 3c). The lifetime of this pattern was about 75 round trips (~225 µs) and the period of oscillations of the pattern was similar to the period observed in the case of the twin pattern. The likelihood of this pattern was low (~0.1).
Also, when the laser operated with multiple pulses per cavity round trip, it was found that some pulses could propagate at different group velocities, leading to pulse–pulse collision and the formation of fast ORW events, as illustrated in Figure 3c. This pattern was formed only due to the collision of two pulses without any interference between them, and the integration of the oscilloscope traces revealed that the intensity of the peak was just the sum of the intensities of the two pulses. There was no sign of energy exchange due to the very high difference in the pulse speeds (~100 m/s). This high speed difference allowed the pulses to collide with each other and form fast ORWs with an event lifetime of about 10 round trips, a lifetime duration of 30 µs, and a likelihood of extremely low (<0.01).
In the collision patterns, it was found that the speed of the event can accelerate over time, as illustrated in Figure 3f. This acceleration was due intrinsic nonlinearities in both the active and the passive fibers. It accelerated by ~20 km/s2 and then decelerated gradually over approximately 600 round trips (~1.8 ms). The probability distribution function (PDF) of the fast ORW is shown in Figure 3e; it has a strongly asymmetric shape and large deviation from a Gaussian distribution with a long tail more than 8 σ from the mean, confirming the ORW criteria. Table 1 presents the lifetime, likelihood and formation mechanisms of the ORW patterns in the long-cavity fiber laser.

Table 1.
The observed RW patterns’ lifetimes, likelihoods and mechanisms.
In the short mode-locked cavity laser (~13 m), the main reasons for ORW emergence were soliton fission and soliton rain. Unlike the fundamental and harmonics mode-locked regime [40,41], soliton rain appeared when the laser operated in the partially mode-locked regime with the pre-existing CW components [32,33]. Under certain circumstances, the main pulses split into many pulses that occupied the whole laser cavity due to the soliton fission in the main pulse, as shown in Figure 4a, or they dissipated in the form of soliton breathing [42]. The spatiotemporal intensity measurements also showed that the interaction processes between solitons inside the main pulse can be clearly captured, and it was found that nonlinear soliton fission accounts for optical ORW generation. Many interactions in the main solitons around 47.5 ns confirm that the soliton fission ejected many solitons pulses in the form of soliton rain. The interaction between the solitons inside the main pulse is quasi-elastic collision when the temporal and frequency separation between two solitons is small. Also, it was found that the soliton fission regimes are affected by the pulse polarization evolution in the cavity, as shown in Figure 4b, where polarization control plays a big role in the direction of soliton rain formation and distribution. It seems that the soliton pulses break up due to the CW features into many pulses that propagate uniformly after controlling the cavity birefringence and pump power. These nonlinear localized dynamics are formed due to the balance in the nonlinear system through energy exchange with the environment in the presence of nonlinearity, dispersion, gain, and loss, which can be controlled by both the pump power and PC1. So, their existence and stability depend on the energy balance, which can manifest conditions for self-organization.
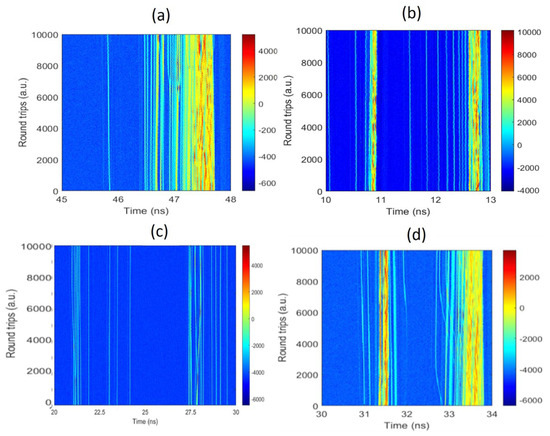
Figure 4.
The spatiotemporal intensity evolution of (a) soliton fission; (b) soliton rain formation and distribution; (c) soliton rain interactions; and (d) soliton rain acceleration.
The ejected pulses from the main soliton are distributed within the round trip in the form of soliton rain. So, soliton rain is formed in the laser cavity due to the interaction between three elements: the CW noisy background, the drift of small soliton pulses and the condensed phase. So, the CW components consist of a fluctuating noisy background that forms soliton rain around the cavity and leads to the formation of small pulses, like the way droplets form in a vapor cloud. When these small pulses are amplified, they drift toward the main pulses (condensed phase) with a variable relative velocity. So, the distribution of bound soliton rain inside the cavity (Figure 4c) became very heavy and chaotic, making the pulses travel at various group velocities, and, hence, they have a very high probability of interacting with each other and initiating ORW events. Moreover, the energy dissipation of solitons is visible during the interaction processes. Some amount of the soliton’s energy is transferred to dispersive waves. Consequently, soliton rain can also be accelerated because of the multiple interactions between the solitons and dispersive waves (Figure 4d). Soliton acceleration occurs due to the propagation of the small pulses formed in the laser cavity with a low constant speed in the order of 10 m/s due to inhomogeneous background levels, and this leads to collisions with the condensed soliton phase, while the condensed phase is a bunch of several tens of solitons which aggregate close to the main pulse. Importantly, the fraction of the weakly coherent background can be gradually varied by tuning the cavity parameters, and it was found that the observed soliton rain drifting can be controlled by both the intra-cavity birefringence (PC1) and the pump power.
4. Conclusions
We demonstrated that fiber lasers are an advisable tool for studying the physics behind the emergence of the RWs. We show that in the long-cavity fiber laser, ORW emerged in the slow and fast ORW pattens due to the multimode instability that inherits some features of multi-pulsing regimes in the form of the spatial modulation of the two orthogonal states of polarization. Fast ORW events have a lifetime duration shorter than the AF decay time, and events emerged as a result of pulse–pulse interactions and nonlinear pulses dynamics. Meanwhile, slow ORW events have a lifetime duration significantly longer than the decay time of the AF and are the result of polarization hopping between different attractors due to incoherent coupling from polarization instability.
In the short-cavity fiber laser, the ORW emerged as a results of soliton fission and soliton rain. Spatiotemporal intensity evolution confirmed the soliton fission and soliton interaction signatures for ORW formation. Both soliton fission and soliton rain are processes whereby there exists a complex self-organized intermediate regime in the order of many soliton pulses aggregated in a condensed soliton phase, which constitutes the CW. When the fluctuations in the CW exceed a certain level, these small amounts of soliton rain are formed, whereby a droplet is formed from a vapor cloud and then drifts towards a soliton cluster with a high probability to interact with other pulses or overlapping through their tails, forming ORW events.
Author Contributions
Conceptualization, H.J.K. and S.V.S.; methodology, H.J.K. and S.V.S.; validation, H.J.K. and S.V.S.; formal analysis, H.J.K. and S.V.S.; investigation, H.J.K. and S.V.S.; data curation, H.J.K. and S.V.S.; writing—original draft preparation, H.J.K.; writing—review and editing, H.J.K. and S.V.S.; visualization, H.J.K. and S.V.S.; supervision, S.V.S. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by the Leverhulme Trust, grant “HARVEST (RPG-2023-073)”, and “EPSRC project EP/W002868/1”.
Data Availability Statement
Data are available on request.
Conflicts of Interest
The authors declare no conflicts of interest.
References
- Garrett, C.; Gemmrich, J. Rogue waves. Phys. Today 2009, 62, 62–63. [Google Scholar] [CrossRef]
- Hammani, K.; Finot, C.; Kibler, B.; Millot, G. Soliton generation and rogue-wave-like behavior through fourth-order scalar modulation instability. IEEE. Photonics J. 2009, 1, 205–212. [Google Scholar] [CrossRef]
- Arecchi, F.; Bortolozzo, U.; Montina, A.; Residori, S. Granularity and inhomogeneity are the joint generators of optical rogue waves. Phys. Rev. Lett. 2011, 106, 153901. [Google Scholar] [CrossRef]
- Onorato, M.; Residori, S.; Bortolozzo, U.; Montina, A.; Arecchi, F. Rogue waves and their generating mechanisms in different physical contexts. Phys. Rep. 2013, 528, 47–89. [Google Scholar] [CrossRef]
- Baronio, F.; Degasperis, A.; Conforti, M.; Wabnitz, S. Solutions of the vector nonlinear Schrödinger equations: Evidence for deterministic rogue waves. Phys. Rev. Lett. 2012, 109, 044102. [Google Scholar] [CrossRef] [PubMed]
- Zhao, L.-C.; Liu, J. Rogue-wave solutions of a three-component coupled nonlinear Schrödinger equation. Phys. Rev. E 2013, 87, 013201. [Google Scholar] [CrossRef] [PubMed]
- Guo, B.-L.; Ling, L.-M. Rogue wave, breathers and bright-dark-rogue solutions for the coupled Schrödinger equations. Chin. Phys. Lett. 2011, 28, 110202. [Google Scholar] [CrossRef]
- Montina, A.; Bortolozzo, U.; Residori, S.; Arecchi, F. Non-Gaussian statistics and extreme waves in a nonlinear optical cavity. Phys. Rev. Lett. 2009, 103, 173901. [Google Scholar] [CrossRef]
- Hammani, K.; Finot, C.; Millot, G. Emergence of extreme events in fiber-based parametric processes driven by a partially incoherent pump wave. Opt. Lett. 2009, 34, 1138–1140. [Google Scholar] [CrossRef]
- Bonatto, C.; Feyereisen, M.; Barland, S.; Giudici, M.; Masoller, C.; Leite, J.R.R.; Tredicce, J.R. Deterministic optical rogue waves. Phys. Rev. Lett. 2011, 107, 053901. [Google Scholar] [CrossRef] [PubMed]
- Kovalsky, M.G.; Hnilo, A.A.; Tredicce, J.R. Extreme events in the Ti: Sapphire laser. Opt. Lett. 2011, 36, 4449–4451. [Google Scholar] [CrossRef]
- Grelu, P.; Akhmediev, N. Dissipative solitons for mode-locked lasers. Nat. Photonics 2012, 6, 84. [Google Scholar] [CrossRef]
- Xu, C.; Wise, F. Recent advances in fiber lasers for nonlinear microscopy. Nat. Photonics 2013, 7, 875–882. [Google Scholar] [CrossRef] [PubMed]
- Solli, D.; Ropers, C.; Koonath, P.; Jalali, B. Optical rogue waves. Nature 2007, 450, 1054. [Google Scholar] [CrossRef]
- Solli, D.; Ropers, C.; Jalali, B. Active control of rogue waves for stimulated supercontinuum generation. Phys. Rev. Lett. 2008, 101, 233902. [Google Scholar] [CrossRef] [PubMed]
- Lafargue, C.; Bolger, J.; Genty, G.; Dias, F.; Dudley, J.; Eggleton, B. Direct detection of optical rogue wave energy statistics in supercontinuum generation. Electron. Lett. 2009, 45, 217–219. [Google Scholar] [CrossRef]
- Dudley, J.M.; Genty, G.; Dias, F.; Kibler, B.; Akhmediev, N. Modulation instability, Akhmediev Breathers and continuous wave supercontinuum generation. Opt. Express 2009, 17, 21497–21508. [Google Scholar] [CrossRef] [PubMed]
- Kibler, B.; Finot, C.; Dudley, J.M. Soliton and rogue wave statistics in supercontinuum generation in photonic crystal fiber with two zero dispersion wavelengths. Eur. Phys. J. Spec. Top. 2009, 173, 289–295. [Google Scholar] [CrossRef]
- Dudley, J.M.; Genty, G.; Eggleton, B.J. Harnessing and control of optical rogue waves in supercontinuum generation. Opt. Express 2008, 16, 3644–3651. [Google Scholar] [CrossRef]
- Hammani, K.; Finot, C.; Dudley, J.M.; Millot, G. Optical rogue-wave-like extreme value fluctuations in fiber Raman amplifiers. Opt. Express 2008, 16, 16467–16474. [Google Scholar] [CrossRef]
- Tarasov, N.; Sugavanam, S.; Churkin, D. Spatio-temporal generation regimes in quasi-CW Raman fiber lasers. Opt. Express 2015, 23, 24189–24194. [Google Scholar] [CrossRef]
- Hanzard, P.-H.; Talbi, M.; Mallek, D.; Kellou, A.; Leblond, H.; Sanchez, F. Brillouin scattering-induced rogue waves in self-pulsing fiber lasers. Sci. Rep. 2017, 7, 45868. [Google Scholar] [CrossRef] [PubMed]
- Soto-Crespo, J.; Grelu, P.; Akhmediev, N. Dissipative rogue waves: Extreme pulses generated by passively mode-locked lasers. Phys. Rev. E 2011, 84, 016604. [Google Scholar] [CrossRef]
- Zaviyalov, A.; Egorov, O.; Iliew, R.; Lederer, F. Rogue waves in mode-locked fiber lasers. Phys. Rev. A 2012, 85, 013828. [Google Scholar] [CrossRef]
- Finot, C.; Hammani, K.; Fatome, J.; Dudley, J.M.; Millot, G. Selection of extreme events generated in Raman fiber amplifiers through spectral offset filtering. IEEE J. Quantum Electron. 2010, 46, 205–213. [Google Scholar] [CrossRef]
- Sergeyev, S.V.; Kbashi, H.J.; Tarasov, N.; Loiko, Y.; Kolpakov, S.A. Vector-Resonance-Multimode Instability. Phys. Rev. Lett. 2017, 118, 033904. [Google Scholar] [CrossRef] [PubMed]
- Kolpakov, S.A.; Kbashi, H.J.; Sergeyev, S.V. Dynamics of vector rogue waves in a fiber laser with a ring cavity. Optica 2016, 3, 870–875. [Google Scholar] [CrossRef]
- Lecaplain, C.; Grelu, P.; Soto-Crespo, J.; Akhmediev, N. Dissipative rogue waves generated by chaotic pulse bunching in a mode-locked laser. Phys. Rev. Lett. 2012, 108, 233901. [Google Scholar] [CrossRef] [PubMed]
- Akhmediev, N.; Soto-Crespo, J.; Ankiewicz, A. Could rogue waves be used as efficient weapons against enemy ships? Eur. Phys. J. Spec. Top. 2010, 185, 259–266. [Google Scholar] [CrossRef]
- Demircan, A.; Amiranashvili, S.; Brée, C.; Mahnke, C.; Mitschke, F.; Steinmeyer, G. Rogue wave formation by accelerated solitons at an optical event horizon. Appl. Phys. B 2014, 115, 343–354. [Google Scholar] [CrossRef]
- Chouli, S.; Grelu, P. Soliton rains in a fiber laser: An experimental study. Phys. Rev. A 2010, 81, 063829. [Google Scholar] [CrossRef]
- Kbashi, H.J.; Sergeyev, S.V.; Al-Araimi, M.; Tarasov, N.; Rozhin, A. Vector soliton rain. Laser Phys. Lett. 2019, 16, 035103. [Google Scholar] [CrossRef]
- Sergeyev, S.V.; Eliwa, M.; Kbashi, H.J. Polarization attractors driven by vector soliton rain. Opt. Express 2022, 30, 35663–35670. [Google Scholar] [CrossRef]
- Runge, A.F.; Aguergaray, C.; Broderick, N.G.; Erkintalo, M. Raman rogue waves in a partially mode-locked fiber laser. Opt. Lett. 2014, 39, 319–322. [Google Scholar] [CrossRef]
- Liu, Z.W.; Zhang, S.M.; Wise, F.W. Rogue waves in a normal-dispersion fiber laser. Opt. Lett. 2015, 40, 1366–1369. [Google Scholar] [CrossRef]
- Teğin, U.; Wang, P.; Wang, L.V. Real-time observation of optical rogue waves in spatiotemporally mode-locked fiber lasers. Commun. Phys. 2023, 6, 60. [Google Scholar] [CrossRef]
- Laprel, C.; Billet, C.; Meng, F.; Ryczkowski, P.; Sylvestre, T.; Finot, C.; Genty, G.; Dudley, J.M. Real-time characterization of spectral instabilities in a modelocked fibre laser exhibiting soliton similariton dynamics. Sci. Rep. 2019, 9, 13950. [Google Scholar] [CrossRef]
- Kolpakov, S.; Kbashi, H.J.; Sergeyev, S.V. Slow optical rogue waves in a unidirectional fiber laser. In CLEO: QELS_Fundamental Science; Optica Publishing Group: Washington, DC, USA, 2016; JW2A-56. [Google Scholar]
- Kbashi, H.J.; Kolpakov, S.A.; Sergeyev, S.V. Fast and slow optical rogue waves in the fiber laser. Front. Phys. 2022, 10, 1048508. [Google Scholar] [CrossRef]
- Kbashi, H.J.; Sergeyev, S.V.; Al-Araimi, M.; Rozhin, A.; Korobko, D.; Fotiadi, A. High-frequency vector harmonic mode locking driven by acoustic resonances. Opt. Lett. 2019, 44, 5112–5115. [Google Scholar] [CrossRef]
- Kbashi, H.J.; Sharma, V.; Sergeyev, S.V. Phase-stable millimeter-wave generation using switchable dual-wavelength fiber laser. Opt. Lasers Eng. 2021, 137, 106390. [Google Scholar] [CrossRef]
- Kbashi, H.J.; Zajnulina, M.; Martinez, A.G.; Sergeyev, S.V. Mulitiscale spatiotemporal structures in mode-locked fiber lasers. Laser Phys. Lett. 2020, 17, 035103. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).