Birefringence and Anisotropy of the Losses Due to Two-Photon Absorption of Femtosecond Pulses in Crystals
Abstract
1. Introduction
2. Materials and Methods
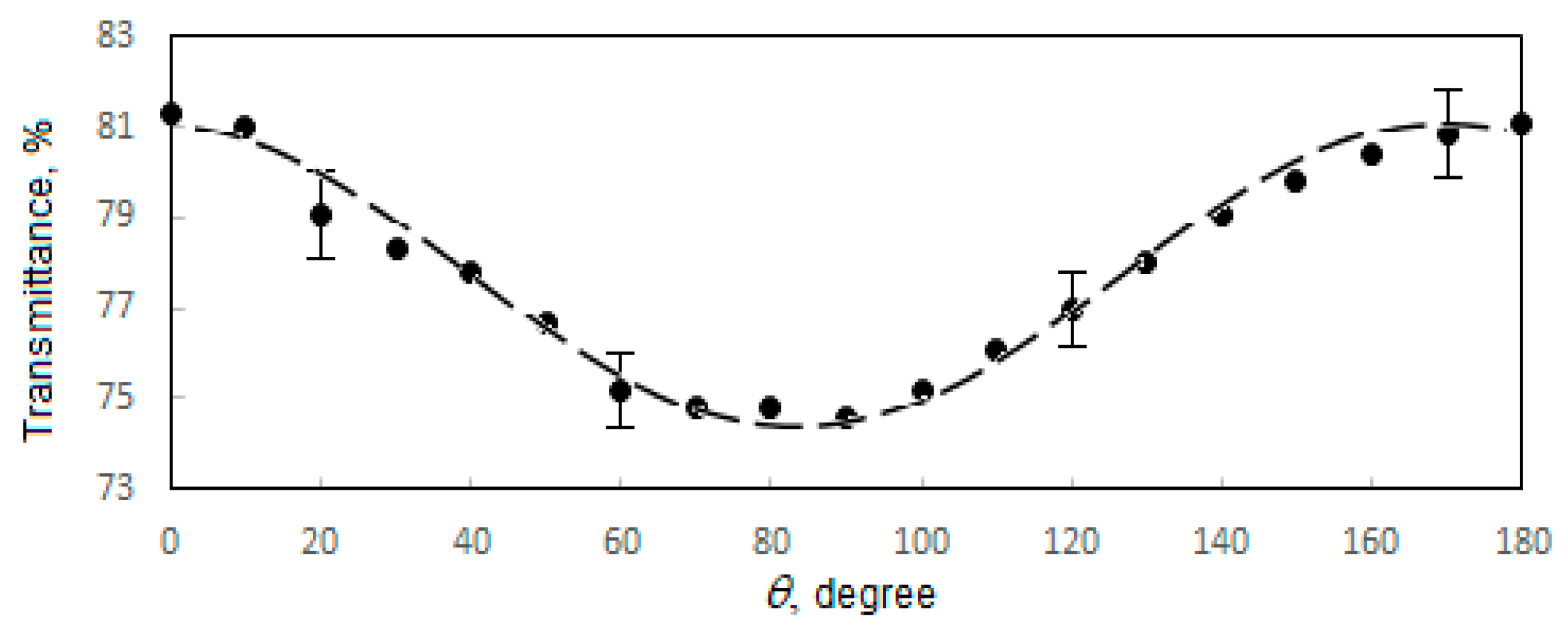
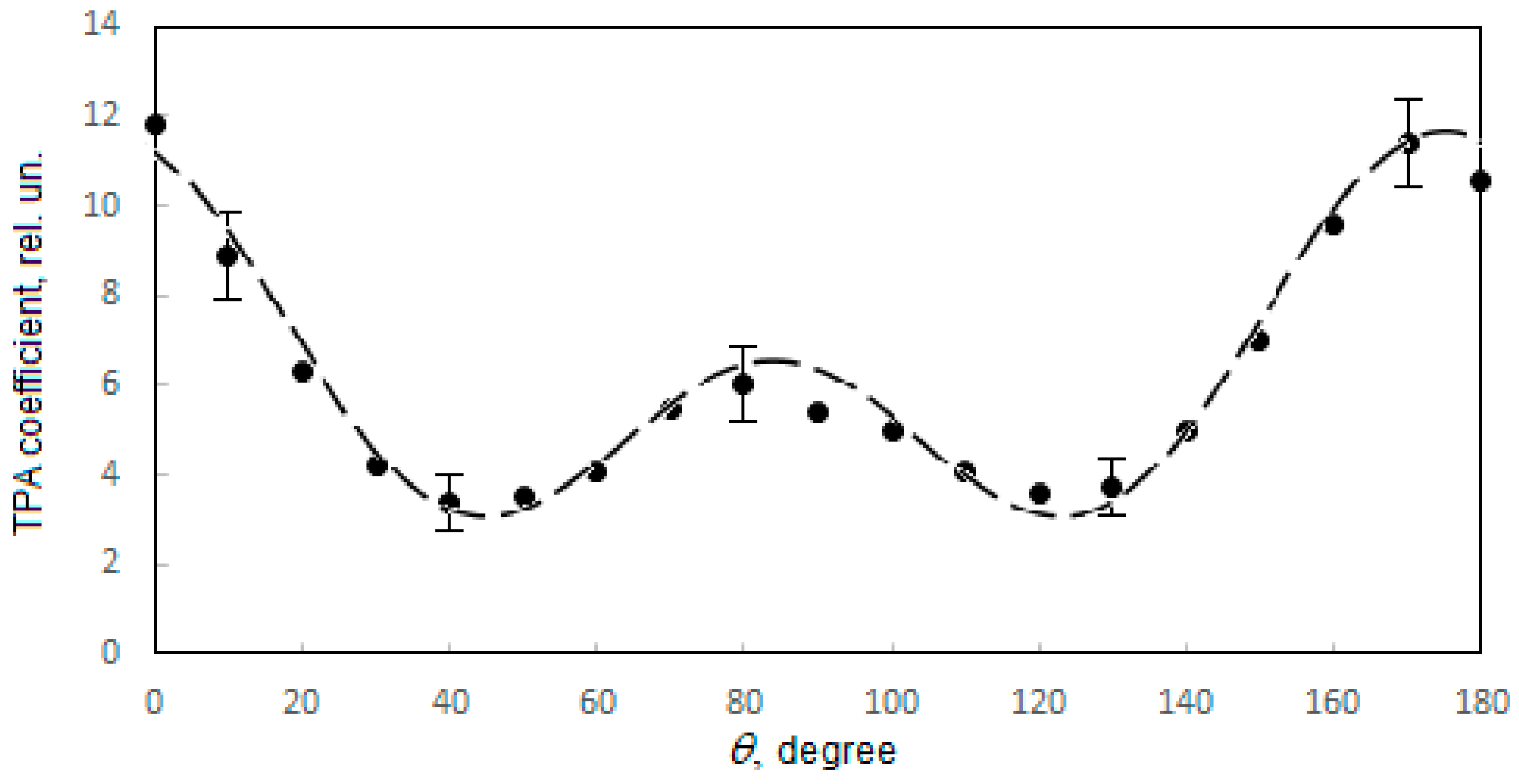
3. Results and Discussion
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Van Stryland, E.W.; Wu, Y.Y.; Hagan, D.J.; Soileau, M.J.; Mansour, K. Optical limiting with semiconductors. J. Opt. Soc. Am. B 1988, 5, 1980–1989. [Google Scholar]
- DeLong, K.W.; Stegeman, G.I. Two-photon absorption as a limitation to all-optical waveguide switching in semiconductors. Appl. Phys. Lett. 1990, 57, 2063–2064. [Google Scholar]
- Lukanin, V.I.; Chunaev, D.S.; Karasik, A.Y. Two-photon absorption of high-power picosecond pulses in PbWO4, ZnWO4, PbMoO4, and CaMoO4 crystals. J. Exp. Theor. Phys. 2011, 113, 412–421. [Google Scholar]
- Kinyaevskiy, I.O.; Kovalev, V.I.; Koribut, A.V.; Dunaeva, E.E.; Semin, N.S.; Ionin, A.A. Stimulated Raman scattering of 0.3-ps 515 nm laser pulses in Ca3(VO4)2 and Ca0.27Sr0.3(VO4)2. Opt. Spectr. 2023, 131, 195–198. [Google Scholar]
- Shen, Y.R. The Principles of Nonlinear Optics; J. Wiley & Sons: New York, NY, USA, 1984. [Google Scholar]
- Basov, N.G.; Grasiuk, A.Z.; Efimkov, V.F.; Zubarev, I.G.; Katulin, V.A.; Popov, Y.M. Semiconductor Lasers Using Optical Pumping. J. Phys. Soc. Japan 1966, 21, 277–282. [Google Scholar]
- Bepko, S.J. Anisotropy of two-photon absorption in GaAs and CdTe. Phys. Rev. B 1975, 12, 669–672. [Google Scholar]
- DeSalvo, R.; Sheik-Bahae, M.; Said, A.A.; Hagan, D.J.; Van Stryland, E.W. Z-scan measurements of the anisotropy of nonlinear refraction and absorption in crystals. Opt. Lett. 1993, 18, 194–196. [Google Scholar]
- Dvorak, M.D.; Schroeder, W.A.; Anderson, D.R.; Smirl, A.L.; Wherrett, B.S. Measurement of the anisotropy of two-photon absorption coefficients in zincblende semiconductors. IEEE J. Quantum Electron. 1994, 30, 256–268. [Google Scholar]
- Kinyaevskiy, I.O.; Kovalev, V.I.; Semin, N.S.; Danilov, P.A.; Kudryashov, S.I.; Koribut, A.V.; Dunaeva, E.E. Two-Photon Absorption in Ca3(VO4)2 and Ca2.7Sr0.3(VO4)2 Crystals. Photonics 2023, 10, 466. [Google Scholar]
- Frank, M.; Smetanin, S.N.; Jelínek, M.; Vyhlídal, D.; Ivleva, L.I.; Dunaeva, E.E.; Voronina, I.S.; Tereshchenko, D.P.; Shukshin, V.E.; Zverev, P.G.; et al. Stimulated Raman scattering in yttrium, gadolinium, and calcium orthovanadate crystals with single and combined frequency shifts under synchronous picosecond pumping for sub-picosecond or multi-wavelength generation around 1.2 μm. Crystals 2020, 10, 871. [Google Scholar]
- Bechthold, P.S.; Liebertz, J.; Deserno, U. Linear and nonlinear optical properties of Ca3(VO4)2. Opt. Commun. 1978, 27, 393–398. [Google Scholar]
- Danishevskii, A.M.; Ivchenko, E.A.; Kochegarov, S.F.; Stepanova, M.I. Dependence of two-photon absorption coefficient on light polarization in cubic-symmetry semiconductors. Sov. Phys. JETP Lett. 1972, 16, 440–443. [Google Scholar]
- Bloembergen, N. Nonlinear Optics; W.A. Benjamin, Inc.: New York, NY, USA, 1965. [Google Scholar]
- Jha, S.; Bloembergen, N. Nonlinear Optical Susceptibilities in Group-IV and III-V Semiconductors. Phys. Rev. 1968, 171, 891–898. [Google Scholar]
- Pask, H.M. The design and operation of solid-state Raman lasers. Prog. Quantum Electron. 2003, 27, 3–56. [Google Scholar]
- Basiev, T.T.; Osiko, V.V. New materials for SRS lasers. Russ. Chem. Rev. 2006, 75, 847–862. [Google Scholar]

Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Kovalev, V.; Krasin, G. Birefringence and Anisotropy of the Losses Due to Two-Photon Absorption of Femtosecond Pulses in Crystals. Photonics 2024, 11, 683. https://doi.org/10.3390/photonics11070683
Kovalev V, Krasin G. Birefringence and Anisotropy of the Losses Due to Two-Photon Absorption of Femtosecond Pulses in Crystals. Photonics. 2024; 11(7):683. https://doi.org/10.3390/photonics11070683
Chicago/Turabian StyleKovalev, Valeri, and George Krasin. 2024. "Birefringence and Anisotropy of the Losses Due to Two-Photon Absorption of Femtosecond Pulses in Crystals" Photonics 11, no. 7: 683. https://doi.org/10.3390/photonics11070683
APA StyleKovalev, V., & Krasin, G. (2024). Birefringence and Anisotropy of the Losses Due to Two-Photon Absorption of Femtosecond Pulses in Crystals. Photonics, 11(7), 683. https://doi.org/10.3390/photonics11070683





