Polarized-Speckle Deviation Imaging through Scattering Media under Strong Background Light Interference

Abstract

A crucial challenge faced by noninvasive imaging through strongly scattering media is overcoming background light interference. Polarization-based anti-scattering methods can eliminate background light interference, but fail to utilize speckle images that do not contain unscattered object light for object reconstruction. Although speckle correlation imaging (SCI) methods can utilize speckle images for object reconstruction, it is difficult to achieve stable high-quality reconstruction and overcome background light interference using these methods. In this study, we propose a polarized-speckle deviation imaging (PSDI) method to overcome background light interference and achieve high-quality imaging through strongly scattering media. PSDI utilizes the bispectrum and autocorrelation of polarized speckle image deviations to reconstruct the Fourier phase and amplitude spectra of the object image, respectively. Experimental results show that when the background light is polarized and unpolarized, PSDI can achieve stable high-fidelity reconstruction of a polarized object when the signal-to-background ratio (SBR) is lower than −7 dB and −9 dB, respectively. PSDI bridges the gap between imaging with strongly scattered light and overcoming strong background light interference, and is expected to find widespread applications in fields such as biomedical imaging, astronomical observation, underwater imaging, and remote sensing.

1. Introduction

In fields such as biomedical imaging, astronomical observation, underwater imaging, and remote sensing, overcoming the optical scattering effects of media to obtain high-quality optical images of objects has always been a key research topic. Polarization provides rich information as a fundamental dimension of a light field. Polarization-based anti-scattering imaging methods have made significant progress in areas such as imaging through haze and underwater imaging. Schechner et al., established a classic polarization-difference dehazing imaging model based on the polarization difference between unscattered object light and atmospheric scattered light [1]. The scattered light includes both the object and background light. Fang et al., further considered the polarization characteristics of object light, establishing a more practical dehazing imaging model [2]. Liang et al., introduced the polarization orientation angle of haze-scattered light into the imaging model to enhance the model’s color preservation capability [3]. Hu et al., proposed a polarimetric image recovery method using circularly polarized light for active illumination, proving more effective than methods based on linear polarization [4]. Essentially, these methods utilize the differences in polarization characteristics between scattered light and unscattered object light to eliminate the effects of haze scattering in the image. Schechner et al., established a classic physical model for underwater passive polarization imaging based on the polarization difference between unscattered object light and scattering interference light [5]. Liu et al., further proposed an active polarization-based anti-scattering imaging technique that can minimize scattering effects in turbid water [6]. Liu et al., proposed a polarization imaging model that can correct color deviations caused by water absorption [7]. Contrary to conventional wisdom, Li et al., used the polarization difference to suppress the object signal to estimate the polarization and intensity information of backward scattered light, and then enhance underwater images [8]. Cai et al., proposed a fusion algorithm based on compressed sensing for intensity and polarization images, which significantly enhances degraded underwater images [9]. Similar to imaging through haze, the essence of these underwater imaging methods is to utilize the polarization difference between unscattered object light and scattered light to separate them, aiming to enhance the unscattered object light in the degraded image. Although polarization has been widely used in anti-scattering imaging, these anti-scattering imaging methods face significant challenges in scenarios with strong scattering where there is no unscattered object light.

When objects are hidden behind strongly scattering media, all object photons undergo multiple random scattering events and no longer maintain ballistic propagation characteristics. In this case, traditional imaging methods can only extract images formed by the interference of scattered light, known as speckle images, and cannot directly observe information about the object [10]. Bertolotti et al., and Katz et al., in a counterintuitive approach using strongly scattered object light, proposed the speckle correlation imaging (SCI) method, which allows the reconstruction of the object image from the speckle [10,11]. First, they reconstructed the Fourier amplitude spectrum of the object image (referred to as the object amplitude spectrum) through the autocorrelation of the speckle image. Then, they combined the amplitude spectrum with an iterative phase-retrieval (IPR) algorithm [12] to reconstruct the Fourier phase spectrum of the object image (referred to as the object phase spectrum). Finally, they obtained the object image by performing an inverse Fourier transform on the reconstructed object Fourier spectrum. The physical basis of SCI is the optical memory effect (OME) [13,14,15] of the scattering medium, which is a linear space-invariant system when the angle of light incidence is within a certain range. SCI can achieve noninvasive imaging without knowing the scattering characteristics of the medium and has significant application potential, hence it has attracted widespread attention in recent years. Extensive research has further expanded SCI, including breaking through the limitations of the field of view and reconstructing multiple objects [16,17,18,19,20], tracking and reconstructing moving objects [21,22,23,24,25], and overcoming interference caused by broadband visible light illumination [26,27,28]. However, the implementation of classic SCI requires a darkroom environment where only object light exists, which is difficult to satisfy in industrial and outdoor environments with pervasive background light. Therefore, it is imperative to study how to achieve noninvasive imaging through strongly scattering media under the interference of background light.

Researchers have proposed several methods to improve the SCI to overcome the interference of background light. Li et al., reconstructed a high-precision object amplitude spectrum from speckle images disturbed by background light, using a background fitting based on Zernike polynomials and low-rank sparse decomposition [29]. Zhou et al., further achieved around-corner imaging under background light interference by combining Zernike polynomial fitting with the SCI [30]. Ma et al., utilized the Plug-and-Play (PnP) algorithm and the generalized alternating projection (GAP) optimization framework in the phase spectrum reconstruction process of SCI, effectively overcoming the interference of background light [31]. Niu et al., eliminated the influence of background light on speckle images based on principal component analysis and reconstructed several other objects by moving one object [32]. Shui et al., modulated the object light and used the principle of the lock-in amplifier to obtain object speckle images free from the interference of background light [33]. Although the above methods can overcome the interference of background light, they still face inherent shortcomings of IPR during the reconstruction of the object phase spectrum: (i) its reliance on the object amplitude spectrum makes it susceptible to noise interference, and the phase spectrum reconstruction accuracy is limited by the accuracy of the amplitude spectrum reconstruction; (ii) it requires extensive iterative calculations with different initial guesses of the phase spectrum to select a satisfactory solution, making the reconstruction process uncertain and the quality unstable. Bispectral analysis can overcome the shortcomings of IPR but is not suitable for scenarios with background light interference [34,35]. Reconstruction networks based on deep learning technology can avoid using IPR to reconstruct the object [36,37,38,39,40,41,42]. To overcome background light interference, Zheng et al., built an end-to-end deep neural network [43], while Zhang et al., designed a spatial-frequency dual-domain deep neural network using the frequency-domain features of speckles [44]. However, current deep-learning-based methods still have poor generalization capabilities for unknown scenes. That is, when there is a significant difference between the scattering scene corresponding to the reconstruction and the scattering scene corresponding to the network training, the quality of the reconstruction will significantly decrease. Furthermore, because data collection is required for network training, deep learning-based methods cannot achieve noninvasive imaging. Therefore, there is an urgent need for a method that can achieve high-quality noninvasive imaging of objects hidden behind strongly scattering media under background light interference.

In this study, we propose a polarized-speckle deviation imaging method (PSDI) that overcomes the interference from strong background light in imaging through strongly scattering media. Initially, we expanded the recursive-driven bispectral imaging method (ReDBI) that we previously proposed [35], transitioning from the use of unpolarized to polarized speckle images, thereby developing a polarization-based ReDBI method (p-ReDBI). The p-ReDBI inherits the advantages of the ReDBI, featuring an independent, high-precision, and stable reconstruction process of the object phase spectrum. Subsequently, we demonstrated that although p-ReDBI cannot be directly used when background light is present, the interference from background light on p-ReDBI can be mitigated by exploiting the polarization difference between the object and background light. Building on these foundations, we discovered that by replacing the polarized speckle images used in p-ReDBI with their deviations, it is possible to eliminate the interference of the background light during object reconstruction. We used the bispectrum and autocorrelation of the polarized speckle image deviation to reconstruct the object phase spectrum and object amplitude spectrum, respectively, thus deriving the PSDI method. Similar to p-ReDBI, PSDI avoids the drawbacks of IPR inherent in SCI-based methods. Unlike traditional polarization-based anti-scattering imaging methods, PSDI directly utilizes speckles formed by strongly scattered light for object reconstruction, making it applicable in scenarios where there is no unscattered object light. Moreover, in the experimental demonstration of PSDI, we conducted polarization object reconstruction under both polarized and unpolarized strong background light interference. The detector recorded scattered light both with and without an analyzing polarizer, thereby obtaining polarized and unpolarized speckle images. We implemented object reconstruction through ReDBI, p-ReDBI, and PSDI and conducted a comparative analysis of the reconstruction quality.

2. Principles

The concept of the PSDI is described in Figure 1. Figure 1a shows a scenario of imaging with strongly scattered light under strong background light interference. Consider an object with polarization properties placed behind a strongly scattering medium. The size of the object is within the range of the optical memory effect of the scattering medium. The object light is incident on a dynamic medium and is strongly scattered. After propagating through free space, it passes through a linear polarizer and ultimately reaches the surface of a detector that is not equipped with an imaging lens, where it is captured as a speckle image. Consistent with the classical SCI method, we set the integration time of a speckle image to be shorter than the decorrelation time of the medium. As changes in the medium can be neglected within this decorrelation time, such a setting ensures that high-frequency information of the object is preserved in the speckle image [11,35]. The scattering medium is considered an imperfect optical imaging element, and together with the linear polarizer and detector, forms a polarized speckle imaging system. It is assumed that the system’s transformation of the polarization object light is insensitive to the polarization state of the object light and can be represented by a point spread function [45].

When there is no background light interference in the scattering scene, the speckle image captured at an analyzer angle $\theta$ using the linear polarizer is denoted as

$$\begin{array}{c}\hfill s(\mathbf{x};\theta )=h\left(\mathbf{x}\right)\otimes g(\mathbf{x};\theta )\end{array}$$

(1)

where $\mathbf{x}$ represents the two-dimensional spatial position vector on the plane of the detector surface; s denotes the speckle image; h denotes the point spread function of the speckle imaging system; g denotes the ideal image of the object on the detector plane after the polarization analysis. The Fourier spectrum of the speckle image under no-interference conditions is represented as

$$\begin{array}{c}\hfill \mathcal{S}(\mathbf{f};\theta )=\mathcal{H}\left(\mathbf{f}\right)\mathcal{G}(\mathbf{f};\theta )\end{array}$$

(2)

where $\mathbf{f}$ represents the two-dimensional spatial frequency vector corresponding to $\mathbf{x}$; $\mathcal{S}$ denotes the Fourier spectrum of the speckle image; $\mathcal{H}$ represents the optical transfer function (OTF) of the speckle imaging system; $\mathcal{G}$ refers to the Fourier spectrum of g, which is commonly referred to as the object spectrum. With $\varphi$ as the Fourier phase, $\mathcal{S}$ and $\mathcal{G}$ can be expressed as

$$\begin{array}{cc}\hfill & \mathcal{S}(\mathbf{f};\theta )=\left|\mathcal{S}(\mathbf{f};\theta )\right|exp\left[j{\varphi }_{\mathcal{S}}(\mathbf{f};\theta )\right]\hfill \\ \hfill & \mathcal{G}(\mathbf{f};\theta )=\left|\mathcal{G}(\mathbf{f};\theta )\right|exp\left[j{\varphi }_{\mathcal{G}}(\mathbf{f};\theta )\right]\hfill \end{array}$$

(3)

where ${\varphi }_{\mathcal{S}}(\mathbf{f};\theta )$ and $\left|\mathcal{S}\right(\mathbf{f};\theta \left)\right|$ are the phase and amplitude spectra of the polarized speckle image, respectively, and ${\varphi }_{\mathcal{G}}(\mathbf{f};\theta )$ and $\left|\mathcal{G}\right(\mathbf{f};\theta \left)\right|$ are those of the object. To achieve noninvasive imaging of the object when the OTF of the system is unknown, it is necessary to directly reconstruct both the phase and amplitude spectra of the object from the speckle images.

2.1. Principle of Polarization-Based Recursive-Driven Bispectrum Imaging (p-ReDBI) in the Absence of Background Light Interference

Our previously proposed ReDBI method is capable of reconstructing objects from unpolarized speckle images with high precision and stability in dynamic scattering scenes without background light interference [35]. Here, we extend the ReDBI method to develop the p-ReDBI method, which enables the utilization of polarized speckle images for reconstruction. The bispectrum of the speckle image at the analyzer angle $\theta$, in the absence of background light interference, is defined as follows:

$$\begin{array}{c}\hfill \mathcal{B}\left({\mathbf{f}}_1,{\mathbf{f}}_2;\theta \right)=\mathcal{S}\left({\mathbf{f}}_1;\theta \right)\mathcal{S}\left({\mathbf{f}}_2;\theta \right){\mathcal{S}}^{*}\left({\mathbf{f}}_1+{\mathbf{f}}_2;\theta \right)\end{array}$$

(4)

Assuming that changes in the scattering medium only alter its microscopic details without affecting its macroscopic statistical properties, a series of speckle images are continuously captured at intervals greater than the decorrelation time of the medium with the analyzer angle kept constant. The ensemble average of the bispectra of these speckle images is

$$\begin{array}{cc}\hfill 〈\mathcal{B}\left({\mathbf{f}}_1,{\mathbf{f}}_2;\theta \right)〉=& \left|\mathcal{G}\left({\mathbf{f}}_1;\theta \right)∥\mathcal{G}\left({\mathbf{f}}_2;\theta \right)∥\mathcal{G}\left({\mathbf{f}}_1+{\mathbf{f}}_2;\theta \right)\right|\hfill \\ \hfill & \times exp\left\{j\left[{\varphi }_{\mathcal{G}}\left({\mathbf{f}}_1;\theta \right)+{\varphi }_{\mathcal{G}}\left({\mathbf{f}}_2;\theta \right)-{\varphi }_{\mathcal{G}}\left({\mathbf{f}}_1+{\mathbf{f}}_2;\theta \right)\right]\right\}\hfill \\ \hfill & \times 〈\mathcal{H}\left({\mathbf{f}}_1\right)\mathcal{H}\left({\mathbf{f}}_2\right){\mathcal{H}}^{*}\left({\mathbf{f}}_1+{\mathbf{f}}_2\right)〉\hfill \end{array}$$

(5)

where the brackets $\langle \cdots \rangle$ represent an ensemble average over these speckle images, and $〈\mathcal{H}\left({\mathbf{f}}_1\right)\mathcal{H}\left({\mathbf{f}}_2\right){\mathcal{H}}^{*}\left({\mathbf{f}}_1+{\mathbf{f}}_2\right)〉$ is termed as the bispectrum transfer function and has been demonstrated to be real in our previous study [35]. Thus, according to Equation (5), it can be derived that

$$\begin{array}{c}\hfill exp\left[j{\varphi }_{\langle \mathcal{B}\rangle }\left({\mathbf{f}}_1,{\mathbf{f}}_2;\theta \right)\right]=exp\left\{j\left[{\varphi }_{\mathcal{G}}\left({\mathbf{f}}_1;\theta \right)+{\varphi }_{\mathcal{G}}\left({\mathbf{f}}_2;\theta \right)-{\varphi }_{\mathcal{G}}\left({\mathbf{f}}_1+{\mathbf{f}}_2;\theta \right)\right]\right\}\end{array}$$

(6)

where ${\varphi }_{\langle \mathcal{B}\rangle }\left({\mathbf{f}}_1,{\mathbf{f}}_2;\theta \right)$ represents the phase of $〈\mathcal{B}\left({\mathbf{f}}_1,{\mathbf{f}}_2;\theta \right)〉$. Furthermore, it can be obtained that

$$\begin{array}{c}\hfill exp\left[j{\varphi }_{\mathcal{G}}\left({\mathbf{f}}_1+{\mathbf{f}}_2;\theta \right)\right]=exp\left[j{\varphi }_{\mathcal{G}}\left({\mathbf{f}}_1;\theta \right)\right]exp\left[j{\varphi }_{\mathcal{G}}\left({\mathbf{f}}_2;\theta \right)\right]exp\left[-j{\varphi }_{\langle \mathcal{B}\rangle }\left({\mathbf{f}}_1,{\mathbf{f}}_2;\theta \right)\right]\end{array}$$

(7)

The above equation indicates that when the analyzer angle $\theta$ remains constant, the unit amplitude phasor $exp\left[j{\varphi }_{\mathcal{G}}\left({\mathbf{f}}_1+{\mathbf{f}}_2\right)\right]$ of the object spectrum at $\left({\mathbf{f}}_1+{\mathbf{f}}_2\right)$ can be reconstructed based on the unit amplitude phasor $exp\left[j{\varphi }_{\mathcal{G}}\left({\mathbf{f}}_1\right)\right]$ of the object spectrum at ${\mathbf{f}}_1$, the unit amplitude phasor $exp\left[j{\varphi }_{\mathcal{G}}\left({\mathbf{f}}_2\right)\right]$ at ${\mathbf{f}}_2$, and the unit amplitude phasor $exp\left[j{\varphi }_{\langle \mathcal{B}\rangle }\left({\mathbf{f}}_1,{\mathbf{f}}_2\right)\right]$ of the ensemble average of the bispectra of the speckle images at $\left({\mathbf{f}}_1,{\mathbf{f}}_2\right)$. This constitutes the recursive reconstruction principle of the unit amplitude phasor $exp\left[j{\varphi }_{\mathcal{G}}\left(\mathbf{f}\right)\right]$ of the object spectrum, or the object phase spectrum ${\varphi }_{\mathcal{G}}\left(\mathbf{f}\right)$. The recursion is initialized by the assumption of ${\varphi }_{\mathcal{G}}\left(\right|\mathbf{f}|\equiv 1)=0$, which will only cause the object translation in the reconstructed image and not lose the object’s structural features [46,47].

In the absence of background light interference, the object amplitude spectrum can be reconstructed through the autocorrelations of the speckle images. By calculating the ensemble average of the autocorrelations of the speckle images and utilizing the convolution theorem, it can be derived that [10,11]

$$\begin{array}{cc}\hfill \langle s(\mathbf{x};\theta )★s(\mathbf{x};\theta )\rangle & =\langle \left[h\right(\mathbf{x})\otimes g(\mathbf{x};\theta \left)\right]★\left[h\right(\mathbf{x})\otimes g(\mathbf{x};\theta \left)\right]\rangle \hfill \\ \hfill & =\langle \left[h\right(\mathbf{x})★h(\mathbf{x}\left)\right]\otimes \left[g\right(\mathbf{x};\theta )★g(\mathbf{x};\theta \left)\right]\rangle \hfill \end{array}$$

(8)

where ★ represents the autocorrelation operator. Because the autocorrelation of the point spread function of the speckle imaging system $\left[h\right(\mathbf{x})★h(\mathbf{x}\left)\right]$ is essentially regarded as the autocorrelation of broadband noise and is a sharply peaked function [11], the ensemble average of the speckle image autocorrelations can be expressed as the autocorrelation of the object superimposed with a constant background term B, that is

$$\begin{array}{c}\hfill \langle s(\mathbf{x};\theta )★s(\mathbf{x};\theta )\rangle =g(\mathbf{x};\theta )★g(\mathbf{x};\theta )+B\end{array}$$

(9)

The autocorrelation of the speckle image is obtained by performing the inverse Fourier transform of the energy spectrum of the speckle image. Hence, it follows that

$$\begin{array}{c}\hfill \langle s(\mathbf{x};\theta )★s(\mathbf{x};\theta )\rangle =〈{\mathcal{F}}^{-1}\left\{\mathcal{F}{\left[s(\mathbf{x};\theta )\right]}^2\right\}〉\end{array}$$

(10)

The central part of the ensemble average of the speckle image autocorrelations is extracted using a rectangular window to serve as an estimate of the object’s autocorrelation. According to the Wiener-Khinchin theorem, the power spectrum of the object is the magnitude of the Fourier transform of its autocorrelation. The amplitude spectrum of the object is the square root of its power spectrum. Therefore, the reconstruction of the object amplitude spectrum is carried out according to

$$\begin{array}{c}\hfill \left|\mathcal{G}(\mathbf{f};\theta )\right|=\sqrt{\left|\mathcal{F}\right\{W\left(\mathbf{x}\right)[\langle s(\mathbf{x};\theta )★s(\mathbf{x};\theta )\rangle ]\left\}\right|}\end{array}$$

(11)

where $W\left(\mathbf{x}\right)$ is the rectangular window.

Therefore, in the absence of background light interference, the phase and amplitude spectra of the polarized object can be reconstructed using Equations (7) and (11), respectively. This is the principle of p-ReDBI. In p-ReDBI, the process of reconstructing the phase spectrum based on polarized images is deterministic and does not depend on the object’s amplitude spectrum.

2.2. The Impact of Background Light Interference on p-ReDBI

When background light interference is present, the polarized speckle images captured by the detector cannot be directly represented by Equation (1). Assuming that the background light is constant over time, after the background light and object light enter the scattering medium together, the polarized speckle images captured by the detector are given by

$$\begin{array}{c}\hfill s_i(\mathbf{x};\theta )=h\left(\mathbf{x}\right)\otimes g(\mathbf{x};\theta )+i(\mathbf{x};\theta )\end{array}$$

(12)

where $i(\mathbf{x};\theta )$ represents the background light interference term at the analyzer angle $\theta$. The Fourier spectrum of the polarized speckle image under background light interference is

$$\begin{array}{c}\hfill {\mathcal{S}}_i(\mathbf{f};\theta )=\mathcal{H}\left(\mathbf{f}\right)\mathcal{G}(\mathbf{f};\theta )+\mathcal{F}\left[i(\mathbf{x};\theta )\right]=\mathcal{H}\left(\mathbf{f}\right)\mathcal{G}(\mathbf{f};\theta )+I(\mathbf{f};\theta )\end{array}$$

(13)

where $I(\mathbf{f};\theta )$ represents the Fourier spectrum of the background light interference term. Therefore, the bispectrum of the polarized speckle image under the background light interference is

$$\begin{array}{cc}\hfill {\mathcal{B}}_i\left({\mathbf{f}}_1,{\mathbf{f}}_2;\theta \right)& ={\mathcal{S}}_i\left({\mathbf{f}}_1;\theta \right){\mathcal{S}}_i\left({\mathbf{f}}_2;\theta \right){\mathcal{S}}_i^{*}\left({\mathbf{f}}_1+{\mathbf{f}}_2;\theta \right)\hfill \\ \hfill & =\left[\mathcal{H}\left({\mathbf{f}}_1\right)\mathcal{G}\left({\mathbf{f}}_1;\theta \right)+I\left({\mathbf{f}}_1;\theta \right)\right]\times \left[\mathcal{H}\left({\mathbf{f}}_2\right)\mathcal{G}\left({\mathbf{f}}_2;\theta \right)+I\left({\mathbf{f}}_2;\theta \right)\right]\times \hfill \\ \hfill & \left[{\mathcal{H}}^{*}\left({\mathbf{f}}_1+{\mathbf{f}}_2\right){\mathcal{G}}^{*}\left({\mathbf{f}}_1+{\mathbf{f}}_2;\theta \right)+I^{*}\left({\mathbf{f}}_1+{\mathbf{f}}_2;\theta \right)\right]\hfill \end{array}$$

(14)

Comparing the form of the above equation with that of Equation (5) reveals that there is no relationship similar to Equation (6) under the interference of background light. Therefore, it is impossible to use the ensemble average of the bispectrum of speckle images as in Equation (7) to reconstruct the object phase spectrum when background light interference is present.

Moreover, the autocorrelation representation of the polarized speckle images under the interference of background light is

$$\begin{array}{c}\hfill s_i(\mathbf{x};\theta )★s_i(\mathbf{x};\theta )=[h\left(\mathbf{x}\right)\otimes g(\mathbf{x};\theta )+i(\mathbf{x};\theta )]★[h\left(\mathbf{x}\right)\otimes g(\mathbf{x};\theta )+i(\mathbf{x};\theta )]\end{array}$$

(15)

As the object light and background light are uncorrelated, $h\left(\mathbf{x}\right)\otimes g(\mathbf{x};\theta )$ and $i(\mathbf{x};\theta )$ are uncorrelated. The above equation can be further approximated as

$$\begin{array}{c}\hfill s_i(\mathbf{x};\theta )★s_i(\mathbf{x};\theta )\approx [h\left(\mathbf{x}\right)\otimes g(\mathbf{x};\theta )]★[h\left(\mathbf{x}\right)\otimes g(\mathbf{x};\theta )]+[i(\mathbf{x};\theta )★i(\mathbf{x};\theta )]\end{array}$$

(16)

From Equation (16), it can be seen that when the background light interference is present, the autocorrelation of the speckle image not only contains the autocorrelation of the speckles generated by the object light but also includes the autocorrelation of the background light. Under this condition, the autocorrelation of the speckle images cannot be approximated as the autocorrelation of the object. Therefore, the p-ReDBI method cannot be directly applied to scattering scenarios with background light.

It is worth noting that when there is a significant difference in the polarization direction between the object light and the background light, the ratios of energy between the object light and the background light in the polarized speckle images collected at different analyzer angles also vary. Therefore, by utilizing the polarization diversity of the scattering scene, the analyzer angle can be adjusted to increase the proportion of the object light energy in the speckle images, and subsequent reconstruction can be executed by p-ReDBI after mitigating the interference from the background light. This method is particularly suitable when the background light is nearly linearly polarized. In this situation, the background light in the polarized speckle image at a certain analyzer angle will be almost eliminated.

2.3. Principle of Polarized-Speckle Deviation Imaging (PSDI) for Overcoming Background Light Interference

However, when the background light is not linearly polarized, it is impossible to eliminate the interference of the background light based on the polarization direction difference between the background light and object light. The capability of p-ReDBI to resist interference from the background light is limited. In this subsection, we will further investigate the method of imaging through strongly scattering media that can overcome the interference of the background light without being affected by the polarization state of the background light.

Under the interference of the background light, the ensemble average of the speckle images collected at the analyzer angle $\theta$ is expressed as

$$\begin{array}{cc}\hfill 〈s_i(\mathbf{x};\theta )〉& =\langle h\left(\mathbf{x}\right)*g(\mathbf{x};\theta )+i(\mathbf{x};\theta )\rangle \hfill \\ \hfill & =\langle h\left(\mathbf{x}\right)\rangle *g(\mathbf{x};\theta )+i(\mathbf{x};\theta )\hfill \end{array}$$

(17)

The difference between the polarized speckle image and its ensemble average, or the deviation of the polarized speckle image, is expressed as

$$\begin{array}{c}\hfill s^{\prime }(\mathbf{x};\theta )=s_i(\mathbf{x};\theta )-〈s_i(\mathbf{x};\theta )〉=[h\left(\mathbf{x}\right)-\langle h\left(\mathbf{x}\right)\rangle ]\otimes g(\mathbf{x};\theta )\end{array}$$

(18)

The Fourier transform of the deviation of the polarized speckle image is

$$\begin{array}{cc}\hfill {\mathcal{S}}^{\prime }(\mathbf{f};\theta )& =\mathcal{F}\left[s^{\prime }(\mathbf{x};\theta )\right]=\{\mathcal{H}\left(\mathbf{f}\right)-\mathcal{F}\left[\langle h\left(\mathbf{x}\right)\rangle \right]\}\mathcal{G}(\mathbf{f};\theta )\hfill \\ \hfill & =\left[\mathcal{H}\right(\mathbf{f})-\langle \mathcal{H}(\mathbf{f})\rangle ]\mathcal{G}(\mathbf{f};\theta )\hfill \end{array}$$

(19)

Next, we will evaluate the value of the ensemble average of the point spread function $\langle h\left(\mathbf{x}\right)\rangle$. $\langle h\left(\mathbf{x}\right)\rangle$ can be viewed as the distribution of photon numbers at different positions on the image plane, after numerous photons from a point light source have undergone multiple independent random scattering events. This distribution also reflects the probability that photons from the point source reach different positions. The position vector of any photon arriving at the image plane is determined by the superposition of the displacements among many independent scattering events experienced by the photon. Consequently, based on the central limit theorem, $\langle h\left(\mathbf{x}\right)\rangle$ can be approximated as a Gaussian function.

Furthermore, we evaluate the Fourier transform, $\langle \mathcal{H}\left(\mathbf{f}\right)\rangle$, of $\langle h\left(\mathbf{x}\right)\rangle$. The Fourier transform of a Gaussian function remains a Gaussian function. For the following Gaussian function with a standard deviation $\sigma$,

$$\begin{array}{c}\hfill k\left(x\right)={\displaystyle \frac{1}{\sqrt{2\pi }\sigma }}exp\left({\displaystyle \frac{-x^2}{2{\sigma }^2}}\right)\end{array}$$

(20)

the Fourier transform of this Gaussian function can be calculated as

$$\begin{array}{c}\hfill \mathcal{K}\left(\mu \right)=\mathcal{F}\left[k\left(x\right)\right]=exp\left[{\displaystyle \frac{-{\mu }^2}{1/\left(2{\pi }^2{\sigma }^2\right)}}\right]\end{array}$$

(21)

According to the above equation, the Fourier transform of a Gaussian function with a standard deviation of $\sigma$ is another Gaussian function with a standard deviation of $1/\left(2\pi \sigma \right)$. This implies that the larger the standard deviation of the original Gaussian function, or the more dispersed its distribution, the smaller the standard deviation of the resulting Gaussian function from the Fourier transform, leading to a more concentrated distribution. Compared to an ideal imaging lens, the value of $\langle h\left(\mathbf{x}\right)\rangle$ of a strongly scattering medium is considerably more dispersed. Correspondingly, the value of $\langle \mathcal{H}\left(\mathbf{f}\right)\rangle$ is highly concentrated and occurs only near the zero-frequency vector. Therefore, $\langle \mathcal{H}\left(\mathbf{f}\right)\rangle$ of a strongly scattering medium can be reasonably approximated as a Dirac delta function.

Referring to the definition of the bispectrum of the polarized speckle image, when the analyzer angle is $\theta$, the bispectrum of the deviation of the polarized speckle image is defined as

$$\begin{array}{c}\hfill {\mathcal{B}}^{\prime }\left({\mathbf{f}}_1,{\mathbf{f}}_2;\theta \right)={\mathcal{S}}^{\prime }\left({\mathbf{f}}_1;\theta \right){\mathcal{S}}^{\prime }\left({\mathbf{f}}_2;\theta \right){\mathcal{S}}^{\prime *}\left({\mathbf{f}}_1+{\mathbf{f}}_2;\theta \right)\end{array}$$

(22)

Substituting Equation (19) into the above equation and then taking the ensemble average of a series of speckle images yields

$$\begin{array}{cc}\hfill 〈{\mathcal{B}}^{\prime }\left({\mathbf{f}}_1,{\mathbf{f}}_2;\theta \right)〉=& \left|\mathcal{G}\left({\mathbf{f}}_1;\theta \right)∥\mathcal{G}\left({\mathbf{f}}_2;\theta \right)∥\mathcal{G}\left({\mathbf{f}}_1+{\mathbf{f}}_2;\theta \right)\right|\times \hfill \\ \hfill & exp\left\{j\left[{\varphi }_{\mathcal{G}}\left({\mathbf{f}}_1;\theta \right)+{\varphi }_{\mathcal{G}}\left({\mathbf{f}}_2;\theta \right)-{\varphi }_{\mathcal{G}}\left({\mathbf{f}}_1+{\mathbf{f}}_2;\theta \right)\right]\right\}\times \hfill \\ \hfill & 〈\left[\mathcal{H}\left({\mathbf{f}}_1\right)-〈\mathcal{H}\left({\mathbf{f}}_1\right)〉\right]\left[\mathcal{H}\left({\mathbf{f}}_2\right)-〈\mathcal{H}\left({\mathbf{f}}_2\right)〉\right]\left[{\mathcal{H}}^{*}\left({\mathbf{f}}_1+{\mathbf{f}}_2\right)-〈{\mathcal{H}}^{*}\left({\mathbf{f}}_1+{\mathbf{f}}_2\right)〉\right]〉\hfill \end{array}$$

(23)

Let

$$\begin{array}{c}\hfill {\mathcal{H}}^{\prime }\left(\mathbf{f}\right)=\mathcal{H}\left(\mathbf{f}\right)-\langle \mathcal{H}\left(\mathbf{f}\right)\rangle \end{array}$$

(24)

we can obtain

$$\begin{array}{cc}\hfill & 〈{\mathcal{H}}^{\prime }\left({\mathbf{f}}_1\right){\mathcal{H}}^{\prime }\left({\mathbf{f}}_2\right){\mathcal{H}}^{\prime *}\left({\mathbf{f}}_1+{\mathbf{f}}_2\right)〉\hfill \\ \hfill =& 〈\left[\mathcal{H}\left({\mathbf{f}}_1\right)-〈\mathcal{H}\left({\mathbf{f}}_1\right)〉\right]\left[\mathcal{H}\left({\mathbf{f}}_2\right)-〈\mathcal{H}\left({\mathbf{f}}_2\right)〉\right]\left[{\mathcal{H}}^{*}\left({\mathbf{f}}_1+{\mathbf{f}}_2\right)-〈{\mathcal{H}}^{*}\left({\mathbf{f}}_1+{\mathbf{f}}_2\right)〉\right]〉\hfill \end{array}$$

(25)

Expanding Equation (25) and considering that $\langle \mathcal{H}\left(\mathbf{f}\right)\rangle$ is approximately a Dirac delta function, it can be concluded that as long as ${\mathbf{f}}_1+{\mathbf{f}}_2\ne 0$ is satisfied, $〈{\mathcal{H}}^{\prime }\left({\mathbf{f}}_1\right){\mathcal{H}}^{\prime }\left({\mathbf{f}}_2\right){\mathcal{H}}^{\prime *}\left({\mathbf{f}}_1+{\mathbf{f}}_2\right)〉$ takes real values. Thus, when ${\mathbf{f}}_1+{\mathbf{f}}_2\ne 0$, according to Equation (23), we obtain

$$\begin{array}{c}\hfill exp\left[j{\varphi }_{\mathcal{G}}\left({\mathbf{f}}_1+{\mathbf{f}}_2;\theta \right)\right]=exp\left[j{\varphi }_{\mathcal{G}}\left({\mathbf{f}}_1;\theta \right)\right]exp\left[j{\varphi }_{\mathcal{G}}\left({\mathbf{f}}_2;\theta \right)\right]exp\left[-j{\varphi }_{〈{\mathcal{B}}^{\prime }〉}\left({\mathbf{f}}_1,{\mathbf{f}}_2;\theta \right)\right]\end{array}$$

(26)

where ${\varphi }_{〈{\mathcal{B}}^{\prime }〉}\left({\mathbf{f}}_1,{\mathbf{f}}_2;\theta \right)$ represents the phase of $〈{\mathcal{B}}^{\prime }\left({\mathbf{f}}_1,{\mathbf{f}}_2;\theta \right)〉$. The above equation has the same form as Equation (7). Therefore, when interference from background light exists, the bispectrum of the deviation of the speckle image can be utilized to eliminate the interference and recursively reconstruct the object phase spectrum. The flow of this recursive reconstruction is the same as that of the p-ReDBI. It is noteworthy that in the derivation of Equation (26), we only considered the existence of background light, but whether it is polarized or not has not garnered attention. In other words, the principle of object phase spectrum reconstruction depicted in Equation (26) is still applicable even when the background light is not linearly polarized.

Next, we explore whether the autocorrelation of the polarized speckle image deviation can also be used to reconstruct the object amplitude spectrum when background light interference is present. The ensemble average of the autocorrelation of the polarized speckle image deviation at the analyzer angle $\theta$ is

$$\begin{array}{c}\hfill 〈s^{\prime }(\mathbf{x};\theta )★s^{\prime }(\mathbf{x};\theta )〉=\langle \{[h\left(\mathbf{x}\right)-\langle h\left(\mathbf{x}\right)\rangle ]★[h\left(\mathbf{x}\right)-\langle h\left(\mathbf{x}\right)\rangle ]\}\otimes [g(\mathbf{x};\theta )★g(\mathbf{x};\theta )]\rangle \end{array}$$

(27)

$h\left(\mathbf{x}\right)$ can essentially be considered broadband noise [11]. $\langle h\left(\mathbf{x}\right)\rangle$, when transformed into the frequency domain, only retains value at surprisingly low frequencies. Consequently, $\left[h\right(\mathbf{x})-\langle h(\mathbf{x})\rangle ]$ can be deemed broadband noise, with its autocorrelation being a sharply peaked function. This means that similar to the case without background light interference, the ensemble average of the autocorrelation of the speckle image deviation can also be represented as the overlay of object autocorrelation on a constant background term. Therefore, under the interference of background light, the speckle image in Equation (11) can be replaced by the deviation of the speckle image to reconstruct the object amplitude spectrum, that is,

$$\begin{array}{c}\hfill \left|\mathcal{G}(\mathbf{f};\theta )\right|=\sqrt{\left|\mathcal{F}\left\{W\left(\mathbf{x}\right)\left[〈s^{\prime }(\mathbf{x};\theta )★s^{\prime }(\mathbf{x};\theta )〉\right]\right\}\right|}\end{array}$$

(28)

The mechanism for object phase spectrum reconstruction depicted in Equation (26), in conjunction with the mechanism for object amplitude spectrum reconstruction depicted in Equation (28), collectively constitutes the core of the PSDI method. The implementation flowchart of PSDI is shown in Figure 1b. The object reconstruction algorithm of PSDI is summarized in Algorithm 1.

Algorithm 1: Object reconstruction algorithm in PSDI method

Input: Polarized speckle images $s_i(\mathbf{x};\theta )$, rectangular window $W\left(\mathbf{x}\right)$, initial conditions of object phase spectrum reconstruction ${\varphi }_{\mathcal{G}}\left(\right|\mathbf{f}|\equiv 1)=0$ and ${\varphi }_{\mathcal{G}}(\mathbf{f}\equiv 0)=0$  Output: Reconstructed object image $g(\mathbf{x};\theta )$  1 $s^{\prime }(\mathbf{x};\theta )\leftarrow s_i(\mathbf{x};\theta )-〈s_i(\mathbf{x};\theta )〉$;   // $\phantom{(}$Deviation of the polarized speckle image$\phantom{(}$  2 ${\mathcal{S}}^{\prime }(\mathbf{f};\theta )\leftarrow \mathcal{F}\left[s^{\prime }(\mathbf{x};\theta )\right]$  3 ${\mathcal{B}}^{\prime }\left({\mathbf{f}}_1,{\mathbf{f}}_2;\theta \right)\leftarrow {\mathcal{S}}^{\prime }\left({\mathbf{f}}_1;\theta \right){\mathcal{S}}^{\prime }\left({\mathbf{f}}_2;\theta \right){\mathcal{S}}^{\prime *}\left({\mathbf{f}}_1+{\mathbf{f}}_2;\theta \right)$  4 $exp\left[j{\varphi }_{〈{\mathcal{B}}^{\prime }〉}\left({\mathbf{f}}_1,{\mathbf{f}}_2;\theta \right)\right]\leftarrow 〈{\mathcal{B}}^{\prime }\left({\mathbf{f}}_1,{\mathbf{f}}_2;\theta \right)〉/\left|〈{\mathcal{B}}^{\prime }\left({\mathbf{f}}_1,{\mathbf{f}}_2;\theta \right)〉\right|$  5 $exp\left[j{\varphi }_{\mathcal{G}}\left({\mathbf{f}}_1+{\mathbf{f}}_2;\theta \right)\right]\leftarrow exp\left[j{\varphi }_{\mathcal{G}}\left({\mathbf{f}}_1;\theta \right)\right]exp\left[j{\varphi }_{\mathcal{G}}\left({\mathbf{f}}_2;\theta \right)\right]exp\left[-j{\varphi }_{〈{\mathcal{B}}^{\prime }〉}\left({\mathbf{f}}_1,{\mathbf{f}}_2;\theta \right)\right]$   // $\phantom{(}$Reconstruct the object phase spectrum$\phantom{(}$  6 $R^{\prime }(\mathbf{x};\theta )\leftarrow 〈s^{\prime }(\mathbf{x};\theta )★s^{\prime }(\mathbf{x};\theta )〉$  6 $\left|\mathcal{G}(\mathbf{f};\theta )\right|\leftarrow \sqrt{\left|\mathcal{F}\left\{W\left(\mathbf{x}\right)〈R^{\prime }(\mathbf{x};\theta )〉\right\}\right|}$;   // $\phantom{(}$Reconstruct the object amplitude spectrum$\phantom{(}$  8 $\mathcal{G}(\mathbf{f};\theta )\leftarrow \left|\mathcal{G}(\mathbf{f};\theta )\right|exp\left[j{\varphi }_{\mathcal{G}}(\mathbf{f};\theta )\right]$;   // $\phantom{(}$Reconstruct the object spectrum$\phantom{(}$  9 $g(\mathbf{x};\theta )\leftarrow {\mathcal{F}}^{-1}\left[\mathcal{G}(\mathbf{f};\theta )\right]$ 10 return

3. Experiments and Results

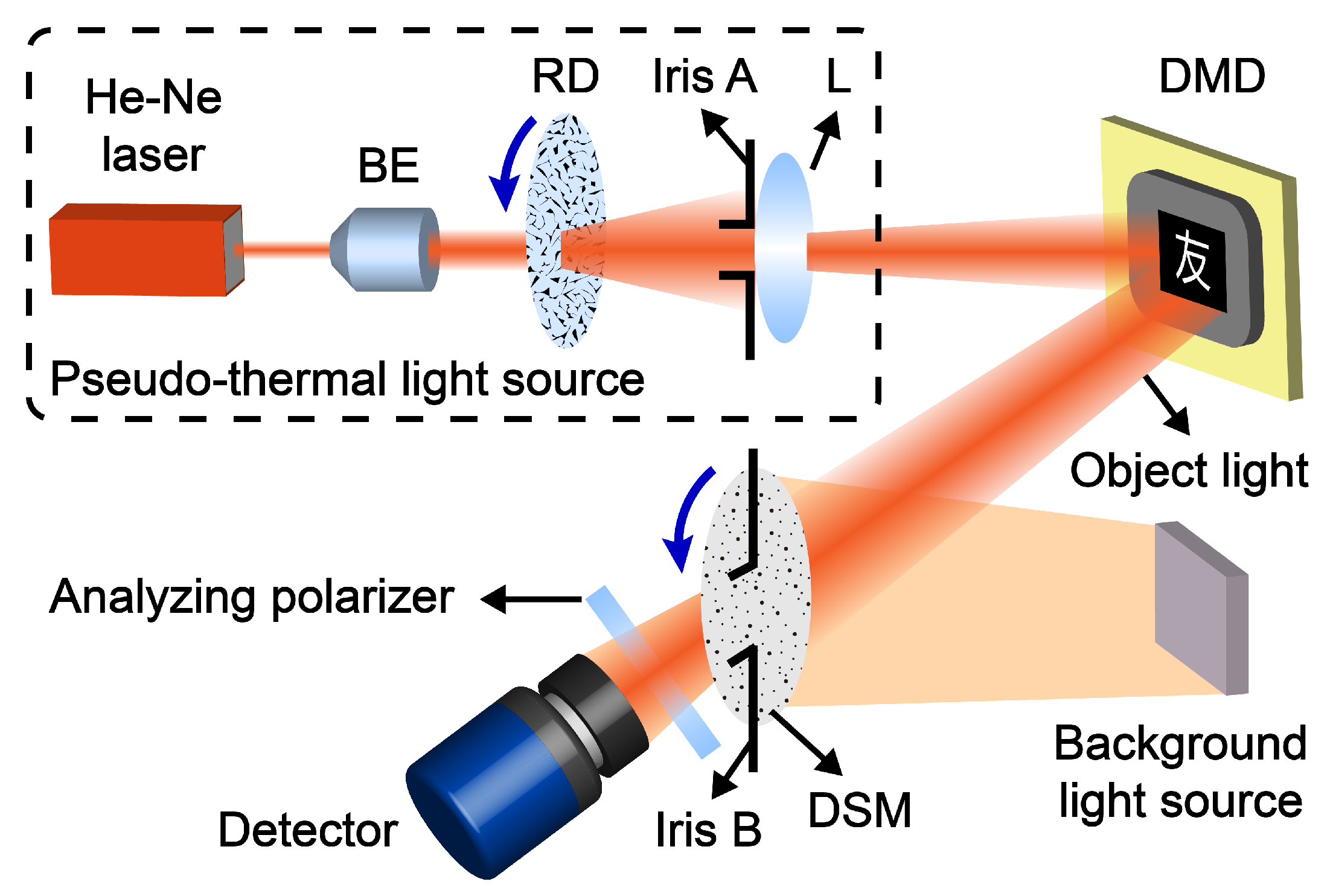
To demonstrate the validity of our PSDI method, we constructed an experimental system as shown in Figure 2. The beam from the He-Ne laser (Edmund 1125P, 5 mW, 632.8 nm) was expanded and then incident on a high-speed rotating diffuser to generate pseudo-thermal light. Subsequently, the pseudo-thermal light passed through an aperture and a convex lens to adjust the beam diameter and then illuminated the object pattern loaded on a digital micromirror device (DMD, Texas Instrument, DLP5500, Dallas, TX, USA). After leaving the surface of the DMD, the generated object light was incident on a rotating ground glass (Bobang Quartz, 220 grit). This ground glass served as a dynamic strongly scattering medium, and its decorrelation time can be adjusted by changing the rotation speed. Given that the He-Ne laser used in this study emits light with a fixed linear polarization direction, the resulting object light was partially polarized. The background light was incident on the scattering medium along with the object light. In the experiment, a 24-inch LCD monitor displaying a pure white image was used as the polarized background light source, while a fluorescent lamp served as the unpolarized background light source. After passing through the medium, the forward scattered object light and background light together traversed an aperture (with a diameter of 2 mm) immediately adjacent to the medium. Subsequently, the scattered light passed through a rotatable linear polarizer, which acted as an analyzer, and finally reached the surface of the detector where it was captured as speckle images. The analyzer can be optionally included or removed depending on whether polarized speckle images were being collected. The exposure time of a speckle image was 0.5 s. The distance between the object and the ground glass was approximately 29 cm. The distance between the ground glass and the detector surface was approximately 14 cm.

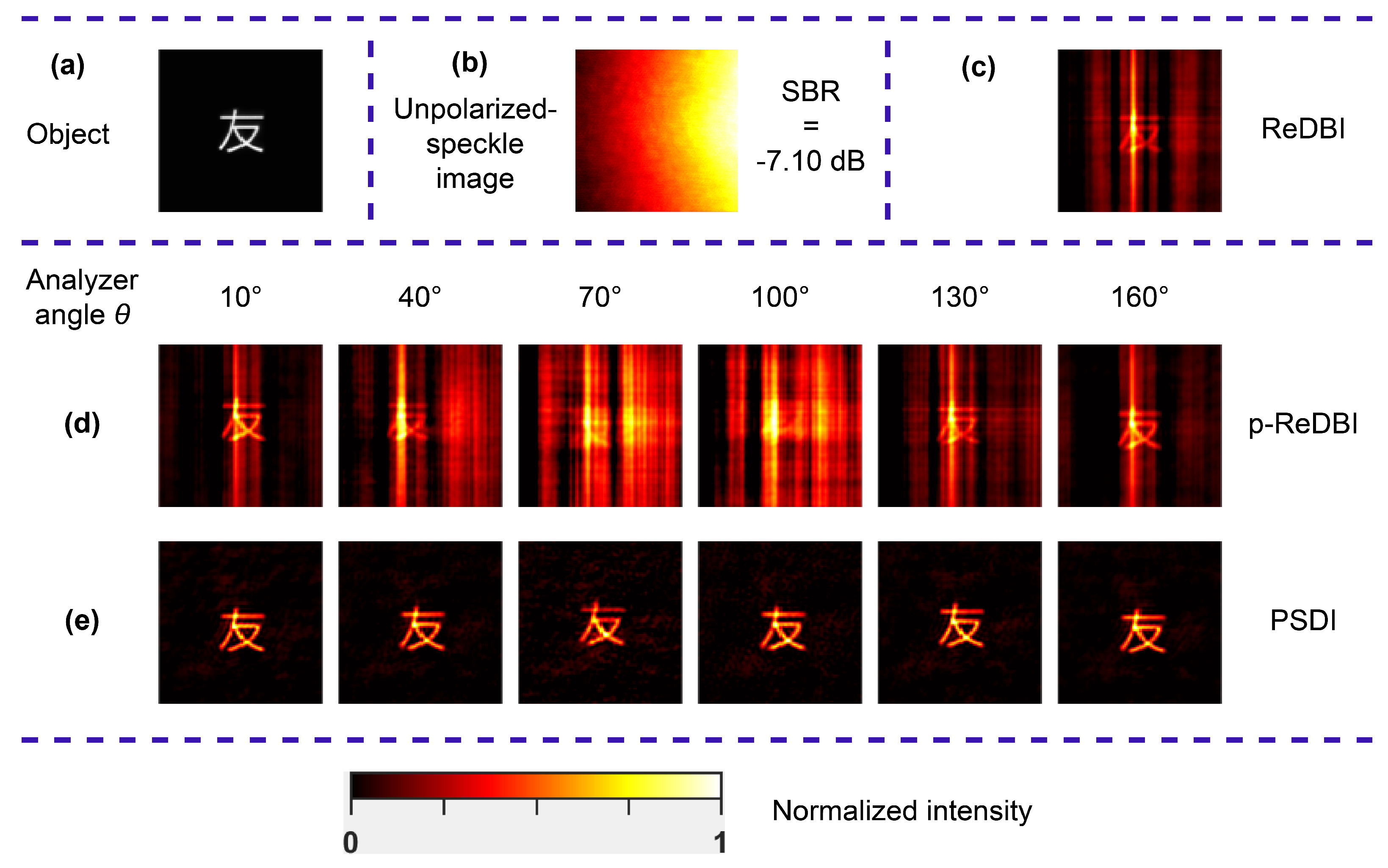
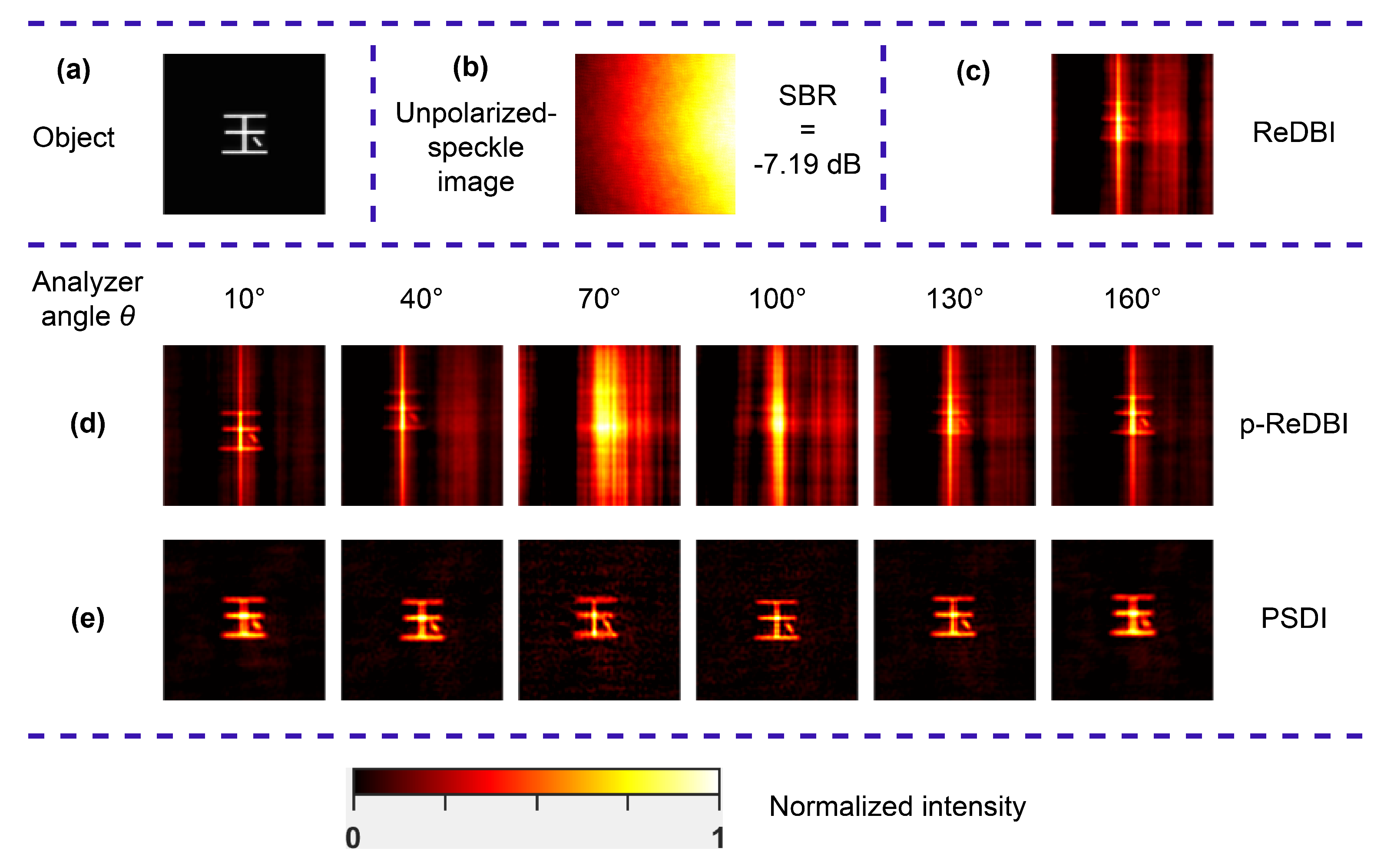
First, we conducted experiments to reconstruct polarization objects under the interference of polarized strong background light. Chinese character objects “友” and “玉” were sequentially loaded onto the DMD, with each object having a vertical length of 0.65 mm. In the absence of the scattering medium, background light, and the analyzer, the detector captured the original object images of “友” and “玉” through an imaging lens, as depicted in Figure 3a and Figure 4a, respectively. Subsequently, the imaging lens was removed, the scattering medium was introduced, and the LCD screen used as the background light source was turned on and set to the maximum brightness. The speckle images captured for the two objects are shown in Figure 3b and Figure 4b, respectively. In the speckle images, the portion of light from the object was considered as the signal, while the portion from the background light was considered as the background interference. The signal-to-background ratio (SBR) of the speckle image was determined by the following processes: (i) retaining the object light and removing the background light source, the average value of the difference between each pixel’s response on the detector and the average dark current noise was taken as the signal intensity $I_{\mathrm{sig}}$; (ii) retaining the background light and removing the object light, the average value of each pixel’s response on the detector was taken as the background intensity $I_{\mathrm{back}}$; (iii) for the speckle images captured with both object light and background light, their SBR was noted as $10{log}_{10}\left(I_{\mathrm{sig}}/I_{\mathrm{back}}\right)$. Without the analyzer, the measured average SBR of the speckle images for the object “友” was −7.10 dB, and for the object “玉,” it was −7.19 dB. The intensity of the background light was significantly greater than that of the object light. We captured 50 frames of speckle images continuously for the reconstruction. The reconstruction results obtained using ReDBI are shown in Figure 3c and Figure 4c. As can be observed, the features of the object “友” could be minimally identified, but the features of the object “玉” were almost unrecognizable, and significant background noise was present in the reconstruction results.

To reconstruct the objects utilizing the polarization properties of scattered light, we introduced an analyzer in front of the detector to collect polarized speckle images. After rotating the analyzer to different angles, we observed that the total response of the detector pixels reached a minimum at an analyzer angle of 10° and a maximum at 100°. This indicates that the polarization direction of the background light, which has a much greater intensity than that of the object light, is around 100°. The decorrelation time of the medium was set to one minute. At six different analyzer angles—10°, 40°, 70°, 100°, 130°, and 160°—we collected 50 frames of speckle images at each angle for object reconstruction. The time interval for collecting each speckle image was set longer than the decorrelation time of the medium. The reconstruction results from the speckle images at these six angles using p-ReDBI are shown in Figure 3d and Figure 4d. It is evident that at the analyzer angle of 10°, the quality of object reconstruction is higher than that at other angles and is also higher than that achieved with ReDBI. However, significant background noise remains in the reconstructed images. This is because, in our experiments, both the object light and background light are partially polarized. As a result, regardless of the analyzer angle at which the scattered light is analyzed, the detector still captures scattered light containing background light. The p-ReDBI method merely reduces the proportion of background light in the scattered light by selecting an appropriate analyzer angle; however, it does not further eliminate the interference of background light in the speckle images. At angles around 100°, object features were unrecognizable in the reconstructed images, and the quality was even worse than that of ReDBI. This phenomenon occurs because at an analyzer angle around 10°, the ratio of object to background light intensities in the scattered light after polarization analysis is significantly higher than before, whereas, at angles near 100°, this ratio is lower after polarization analysis than before. Therefore, utilizing the polarization difference between the object and background light and selecting an appropriate analyzer angle to enhance the proportion of object light in the scattered light after polarization analysis improves the quality of object reconstruction. Furthermore, we utilized PSDI to reconstruct the objects with the speckle images captured at different analyzer angles. The reconstruction results are presented in Figure 3e and Figure 4e. It is evident that PSDI reconstructs high-quality object images at all analyzer angles. In other words, PSDI nearly completely eliminates background light interference during the reconstruction process through the bispectrum and autocorrelation of speckle deviation. Thus, PSDI enables high-quality feature reconstruction of polarization objects under strong polarized background light interference.

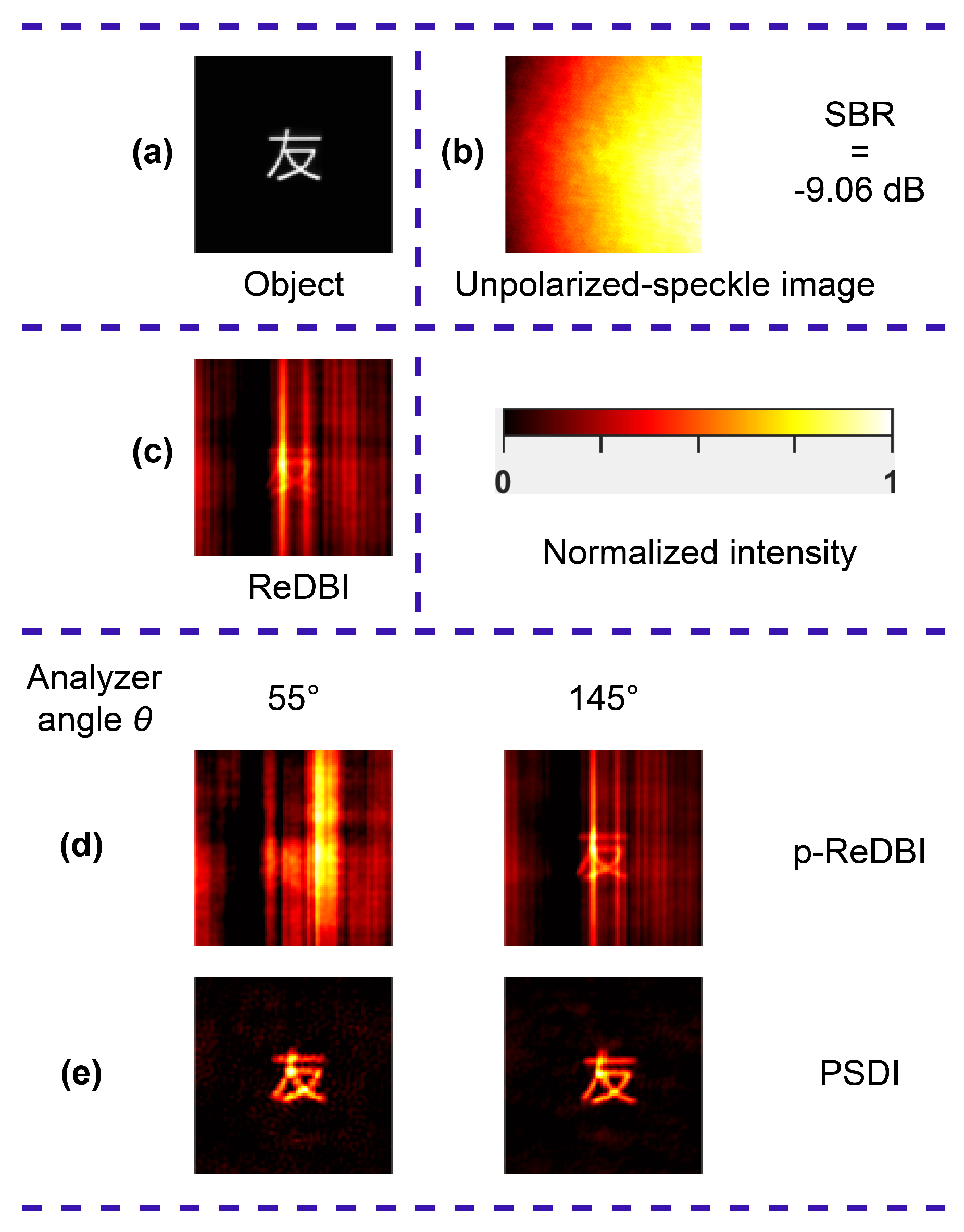
Second, we conducted experiments to reconstruct a polarization object under strong unpolarized background light interference. The object for reconstruction was the Chinese character “友”, with a vertical length of 0.65 mm. The decorrelation time of the medium was set to 20 s. With no scattering medium, background light, or analyzer, the detector captured the original object image through an imaging lens, as shown in Figure 5a. Subsequently, the imaging lens was removed, the scattering medium was introduced, and a fluorescent lamp serving as the background light source was turned on. The captured speckle image is shown in Figure 5b, with the average SBR measured at −9.06 dB. After continuously collecting 50 frames of unpolarized speckle images, the object image reconstructed using ReDBI is displayed in Figure 5c. It is evident from the reconstructed image that the object features are nearly indistinguishable. Next, the analyzer was placed in front of the detector to capture polarized speckle images. After rotating the analyzer to different angles, we observed that the total response of the detector pixels reached a minimum at an analyzer angle of 55° and a maximum at 145°. Subsequently, 50 speckle images were captured for each analyzer angle. The object images reconstructed using p-ReDBI are shown in Figure 5d. At the analyzer angle of 55°, where the intensity of the scattered light after polarization analysis was at its lowest, it was impossible to reconstruct object features from the speckle images; however, at the analyzer angle of 145°, where the scattered light’s intensity was the highest, it was possible to reconstruct a few object features from the polarized speckle images, though significant background noise was evident in the reconstructed image. Furthermore, we utilized speckle images from these two analyzer angles for object reconstruction via PSDI, and the results are shown in Figure 5e. PSDI successfully reconstructed the object features at both analyzer angles. Compared with the original object image, the reconstructed Chinese characters exhibit thicker lines. The primary source of this reconstruction error stems from the approximations made in deriving the principles of PSDI’s object phase spectrum and amplitude spectrum reconstruction (Equations (26) and (28)). Despite this error, PSDI demonstrates a powerful capability to reconstruct high-quality structural features of polarization objects even under strong unpolarized background light interference.

4. Discussion and Conclusions

A significant challenge faced by noninvasive methods of imaging through strongly scattering media is overcoming the interference from background light. Polarization-based anti-scattering imaging methods can utilize the polarization difference between object light and background light to eliminate the interference of background light; however, these methods cannot reconstruct objects using speckle images that do not contain unscattered object light. Some SCI-based techniques can mitigate the background light interference during the object reconstruction with speckle images. However, the reconstruction quality and stability of these techniques are significantly constrained by the IPR mechanism used to reconstruct the object phase spectrum. Although the ReDBI method proposed in our previous study [35] can overcome the shortcomings of IPR to achieve higher-quality and more stable noninvasive imaging through strongly scattering media, it is not suitable for scattering scenarios with background light interference. In this study, we propose a novel PSDI method to overcome the interference of background light and achieve high-quality imaging through strongly scattering media. In scenarios with dynamic scattering media, PSDI utilizes the bispectrum and autocorrelation of the polarized-speckle deviation to reconstruct the Fourier phase and amplitude spectra of the object image, thereby eliminating the interference of background light. Moreover, PSDI possesses a deterministic phase spectrum reconstruction process that does not rely on the object amplitude spectrum, thereby avoiding the shortcomings of the IPR mechanism in SCI-based techniques.

In the experimental validation, we constructed a scattering scene composed of a polarized object, a dynamic strongly scattering medium, and background light. The background light could switch between unpolarized and polarized states and was significantly more intense than the object light. When the background light was polarized, the average SBR of the speckle images was less than −7 dB. When the background light was unpolarized, the average SBR was −9.06 dB. We conducted object reconstruction using the ReDBI, p-ReDBI, and PSDI. The results indicated that ReDBI, which utilizes the bispectrum and autocorrelation of unpolarized speckle images for reconstruction, was almost incapable of reconstructing object features. Therefore, when background light interference is present, it is not feasible to directly reconstruct the object’s phase and amplitude spectra separately from the bispectrum and autocorrelation of the speckle image. p-ReDBI, which uses the bispectrum and autocorrelation of polarized speckle images, was able to reconstruct some object features under certain analyzing polarizer angles when the object light and background light had different polarization directions. At these analyzer angles, compared to before the polarization analysis, the proportion of object light in the scattered light increases while the background light is reduced. The reconstruction quality of the p-ReDBI improved with a higher proportion of object light present in the polarized scattered light after polarization detection. However, because the influence of background light cannot be completely eliminated by polarization analysis alone, the reconstruction results of the p-ReDBI method exhibit significant blurring and noise, and sometimes even fail to reconstruct the object features. Unlike ReDBI and p-ReDBI, the PSDI method proposed in this study can reconstruct high-quality object images, regardless of the analyzing polarizer angles under which the speckle images were captured. The reconstruction results confirm that irrespective of whether the background light is polarized or unpolarized, PSDI can completely eliminate background light interference through the bispectrum and autocorrelation of speckle deviation, thereby reconstructing the phase spectrum and amplitude spectrum of the hidden object with high quality. PSDI demonstrates a powerful capability to overcome background light interference, as well as the ability to reconstruct the object with high fidelity.

Although PSDI exhibits exciting performance, it is important to note that it faces certain limitations during implementation. First, PSDI requires the acquisition of an ensemble average set of speckle image deviation, thus necessitating that the scattering medium be dynamic. Because the media in real scattering scenarios such as biological tissues, atmosphere, and water bodies are typically dynamic, this requirement of PSDI can be easily met in practical applications. Additionally, PSDI requires that the background light remains stable and unchanged during the acquisition of speckle images. This condition is also easily achieved in many scenarios, such as those with a background of sunlight and skylight, which can be considered stable over certain periods. Third, during the recursive phase spectrum reconstruction in PSDI, reconstruction errors occurring at lower frequencies typically build up and carry over to the reconstruction at higher frequencies. To achieve higher-quality reconstruction in scenarios with significant scattering disturbances, the recursive reconstruction can be reformulated as an optimization problem. The optimization aims to minimize the mismatch between the Fourier phase of the unknown object and the known phase of the speckle spectrum autocorrelation.

It is promising that the limits of PSDI performance have not yet been explored in this study. Confined by the maximum power of the background light sources, we only demonstrated the reconstruction results of the PSDI under the lowest SBR achievable with the current experimental setup. PSDI can achieve high-quality object reconstruction even under lower SBRs. Testing the limit of SBR requires the use of more suitable experimental devices. Furthermore, PSDI can be used for noninvasive imaging through strongly scattering media, as it does not require the determination of the light scattering properties of the medium or access to the opposite side of the medium. Noninvasive imaging methods using speckle images, such as PSDI, do not require reference information and can be directly applied even when the medium changes, demonstrating a strong potential for various applications. For example, in multimode fibers, light signals propagate in multiple modes, and the interference between these modes results in the formation of speckle patterns that are similar to those encountered in imaging through scattering media [48,49]. Reconstructing the original information carried by light as it propagates through multimode fibers is crucial for optical communication and medical endoscopic imaging. Therefore, all noninvasive methods of imaging through scattering media, including the PSDI method, are expected to find applications in fiber optic imaging. For instance, they can be used to develop flexible endoscopes that leverage their adaptability to medium changes. In conclusion, PSDI bridges the gap between imaging with strongly scattered light and overcoming strong background light interference, and is expected to find widespread applications in fields such as biomedical imaging, astronomical observation, underwater imaging, and remote sensing.