Automatic Defect Detection Instrument for Spherical Surfaces of Optical Elements
Abstract
1. Introduction
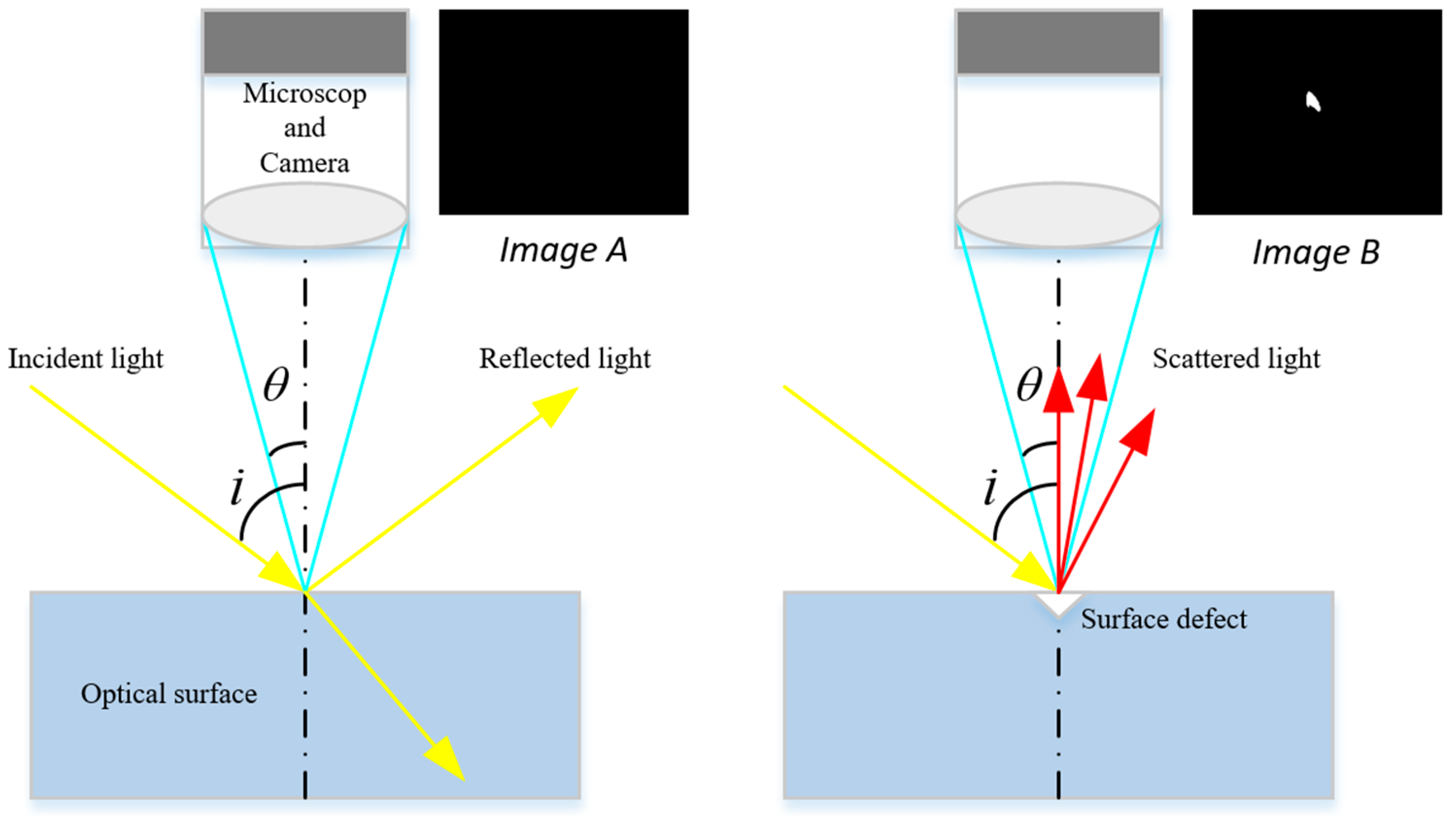
2. Dark-Field Scattering Microscopy Imaging
3. Overall Program Design
4. Theoretical Calculation
4.1. Spherical Surface Parameters
4.2. Calculation of Scanning Time
4.3. Calculation of Scanning-Path
5. Platform Construction
5.1. Imaging System
5.2. Motion Scanning System
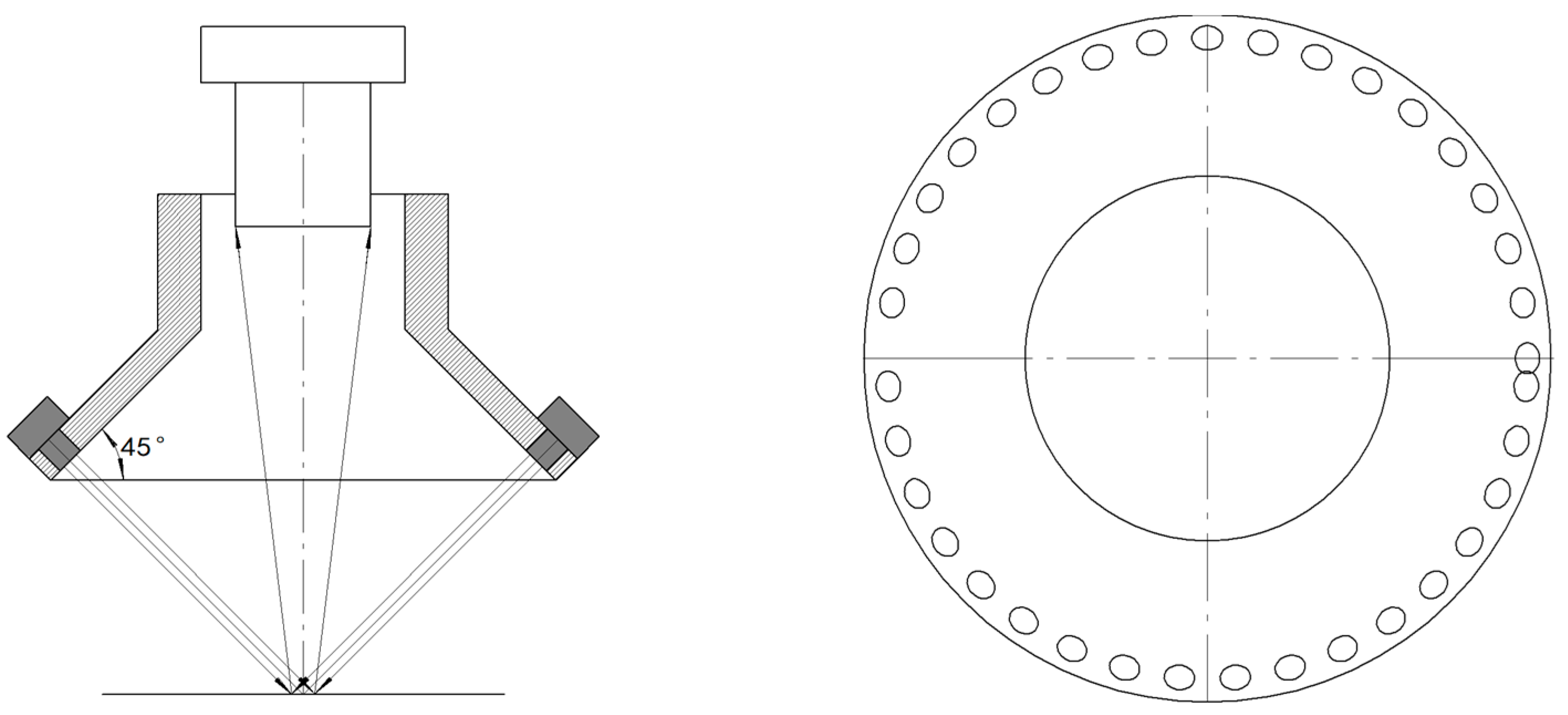
5.3. Multi-Angle-Channel Illumination System
5.4. System Integration
6. Experiment
6.1. Defect Resolution Capability
6.2. Image of Weak Scratch
6.3. The Defect Detection Process and Experiment
7. Discussion
8. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Fournier, J.; Grua, P.; Neauport, J.; Fargin, E.; Jubera, V.; Talaga, D.; DelGuerzo, A.; Raffy, G.; Jouannigot, S. Temperature dependence of luminescence for different surface flaws in high purity silica glass. Opt. Mater. Express 2013, 3, 1–10. [Google Scholar] [CrossRef]
- Zhao, Y.; Shao, J.; Liu, X.; Li, D. Tracking and understanding laser damage events in optics. High Power Laser Part. Beams 2022, 34, 011004-1–011004-12. [Google Scholar]
- Wang, L. Optical system of extreme ultraviolet lithography. Chin. J. Opt. Appl. Opt. 2010, 3, 453–461. (In Chinese) [Google Scholar]
- Ma, B.; Li, L.; Chang, J.; Du, B. Refractive Projection Lens for 90nm Resolution Lithography. Acta Opt. Sin. 2009, 29, 453–461. (In Chinese) [Google Scholar]
- Baker, L.R. Inspection of Surface Flaws by Comparator Microscopy. Appl. Opt. 1988, 27, 4620–4625. [Google Scholar] [CrossRef]
- Li, M.; Hou, X.; Zhao, W.; Wang, H.; Li, M.; Hu, X.; Zhao, Y.; Zhou, Y. Current situation and development trend of aspheric optical surface defect detection technology. Infrared Laser Eng. 2022, 51, 20220457-1–20220457-20. (In Chinese) [Google Scholar]
- Trivedia, V.; Joglekara, M.; Mahajan, S. Digital holographic imaging of refractive index distributions for defect detection. Opt. Laser Technol. 2019, 111, 439–446. [Google Scholar] [CrossRef]
- Falldorf, C.; Agour, M.; Kopylow, C.V. RB Bergmann. Phase retrieval for optical inspection of technical components. J. Opt. 2012, 14, 065701. [Google Scholar] [CrossRef]
- Zhou, H.; Hussain, M.M.R.; Banerjee, P.P. A review of the dual-wavelength technique for phase imaging and 3D topography. Light Adv. Manuf. 2022, 3, 314–334. [Google Scholar] [CrossRef]
- Khorin, P.A.; Volotovskiy, S.G.; Khonina, S.N. Optical detection of values of separate aberrations using a multi-channel filter matched with phase Zernike functions. Comput. Opt. 2021, 45, 525–534. (In Russian) [Google Scholar] [CrossRef]
- Khonina, S.N.; Khorin, P.A.; Serafimovich, P.G. Analysis of the wavefront aberrations based on neural networks processing of the interferograms with a conical reference beam. Appl. Phys. B 2022, 128, 60. [Google Scholar] [CrossRef]
- Khorin, P.A.; Dzyuba, A.P.; Chernykh, A.V. Neural Network-Assisted Interferogram Analysis Using Cylindrical and Flat Reference Beams. Appl. Sci. 2023, 13, 4831. [Google Scholar] [CrossRef]
- Choi, W.J.; Ryu, S.Y.; Kim, J.K.; Kim, J.Y.; Kim, D.U.; Chang, K.S. Fast mapping of absorbing defects in optical materials by full-field photothermal reflectance microscopy. Opt. Lett. 2013, 38, 4907–4910. [Google Scholar] [CrossRef]
- Sun, G.; Zhou, Z. Application of laser ultrasonic technique for non-contact detection of drilling-induced delamination in aeronautical composite components. Opt. Int. J. Light Electron Opt. 2014, 125, 3608–3611. [Google Scholar] [CrossRef]
- Lu, R.; Wu, A.; Zhang, T.; Wang, Y. Review on automated optical (visual) inspection and its applications in defect detection. Acta Opt. Sin. 2018, 38, 0815002. [Google Scholar]
- Lu, M.; Wang, Z.; Gao, P.; Guo, J. Defect detection and current situation of optical components. Opt. Instrum. 2020, 42, 88–94. [Google Scholar]
- Zhang, Z.; Xian, T.; Xu, D.; Feng, Z. Surface flaws detection algorithms for large aperture optical element. In Proceedings of the International Conference on Advanced Mechatronic Systems, Beijing, China, 22–24 August 2015. [Google Scholar]
- GB/T 41805-2022; Yang, Y.Y.; Cao, P.; Li, G.; Yang, L.M.; Liu, X. Methodology for the Quantitative Inspection of the Defect on Optics Surface—Microscopic Scattering Dark-Field Imaging. State Administration for Market Regulation, National Standardization Management Committee: Beijing, China, 2023.
- Zhang, Y.; Yang, Y.; Li, C.; Wu, F.; Chai, H.; Yan, K.; Zhou, L.; Li, Y.; Liu, D.; Bai, J.; et al. Defects evaluation system for spherical optical surfaces based on microscopic scattering dark-field imaging method. Appl. Opt. 2016, 55, 6162–6171. [Google Scholar] [CrossRef]
- Chen, X.; Li, J.; Sui, Y. A new stitching method for dark-field surface defects inspection based on simplified target-tracking and path correction. Sensors 2020, 20, 448. [Google Scholar] [CrossRef]
- Guo, S.; Lv, X.; Lu, Y. Research on defect detection of large-aperture multi-faceted optical components. In Proceedings of the SPIE of Applied Optics and Photonics, Beijing, China, 18 December 2023. [Google Scholar]
- Cao, P.; Yang, Y.; Li, C. Alignment methods for micron-scale surface defects automatic evaluation of large-aperture fine optics. Chin. Opt. Lett. 2015, 13, 041102. [Google Scholar]
- Tao, X.; Zhang, Z.T.; Zhang, F.; Xu, D. A Novel and Effective Surface Flaw Inspection Instrument for Large-Aperture Optical Elements. IEEE Trans. Instrum. Meas. 2015, 64, 2530–2540. [Google Scholar]
- Yin, Z.; Liu, H.; Zhao, L. Efficient and precise detection for surface flaws on large-aperture optics based on machine vision and machine learning. Opt. Laser Technol. 2023, 159, 109011. [Google Scholar] [CrossRef]
- Rosati, G.; Boschetti, G.; Biondi, A.; Rossi, A. Real-time defect detection on highly reflective curved surfaces. Opt. Lasers Eng. 2009, 47, 379–384. [Google Scholar] [CrossRef]
- Dong, J. Line-scanning laser scattering system for fast defect inspection of a large aperture surface. Appl. Opt. 2017, 56, 7089–7098. [Google Scholar] [CrossRef]









| Multimodal | Curve Face or Planar (C/P) | Sub Aperture Size (mm) | Scanning Method (Line/Area Scan) | Experiment Data | ||||
|---|---|---|---|---|---|---|---|---|
| Aperture | R/D | Min Defect Size (µm) | Time (min) | |||||
| Ours | Yes | C | 35 | A | Φ200 mm | 1 | 2 | 15 |
| Paper [21] | Yes | C | 6.6 × 4.4 | A | Φ150 mm | N | 0.5 | N |
| Paper [22] | No | P | 2.3 × 2.3 | A | 320 × 320 | N | N | N |
| Paper [23] | Yes | P | N | L | 810 × 460 | N | N | 6 |
| Paper [24] | No | P | 50 × 50 | A | 430 × 430 | N | 10 | 6 |
| Paper [25] | No | C | N | A | N | N | N | N |
| Paper [26] | No | P | N | L | 810 × 450 | N | 0.5 | 14 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Shi, Y.; Zhang, M.; Li, M. Automatic Defect Detection Instrument for Spherical Surfaces of Optical Elements. Photonics 2024, 11, 681. https://doi.org/10.3390/photonics11070681
Shi Y, Zhang M, Li M. Automatic Defect Detection Instrument for Spherical Surfaces of Optical Elements. Photonics. 2024; 11(7):681. https://doi.org/10.3390/photonics11070681
Chicago/Turabian StyleShi, Yali, Mei Zhang, and Mingwei Li. 2024. "Automatic Defect Detection Instrument for Spherical Surfaces of Optical Elements" Photonics 11, no. 7: 681. https://doi.org/10.3390/photonics11070681
APA StyleShi, Y., Zhang, M., & Li, M. (2024). Automatic Defect Detection Instrument for Spherical Surfaces of Optical Elements. Photonics, 11(7), 681. https://doi.org/10.3390/photonics11070681




