Symmetry-Engineered Dual Plasmon-Induced Transparency via Triple Bright Modes in Graphene Metasurfaces
Abstract
1. Introduction
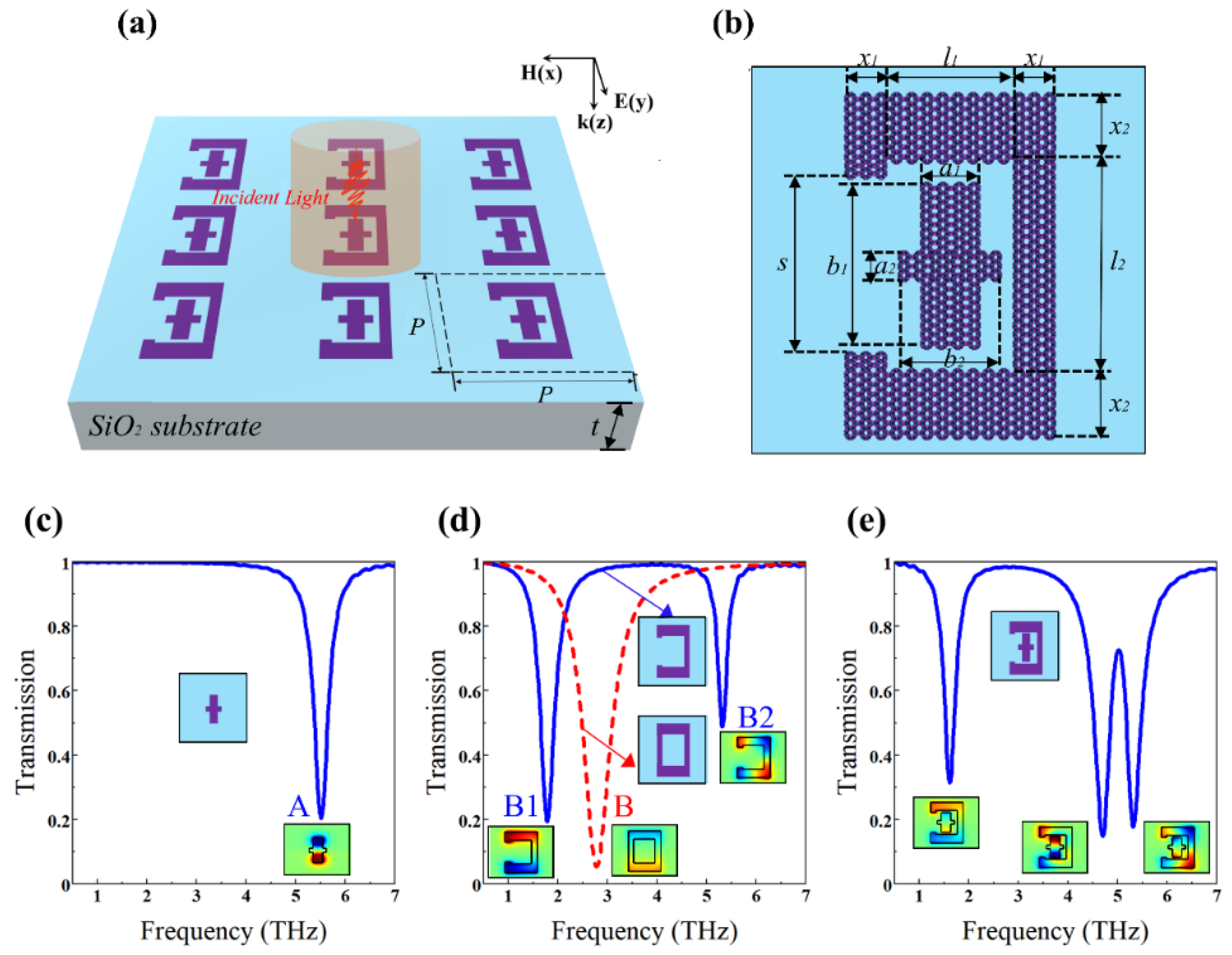
2. Structure and Method
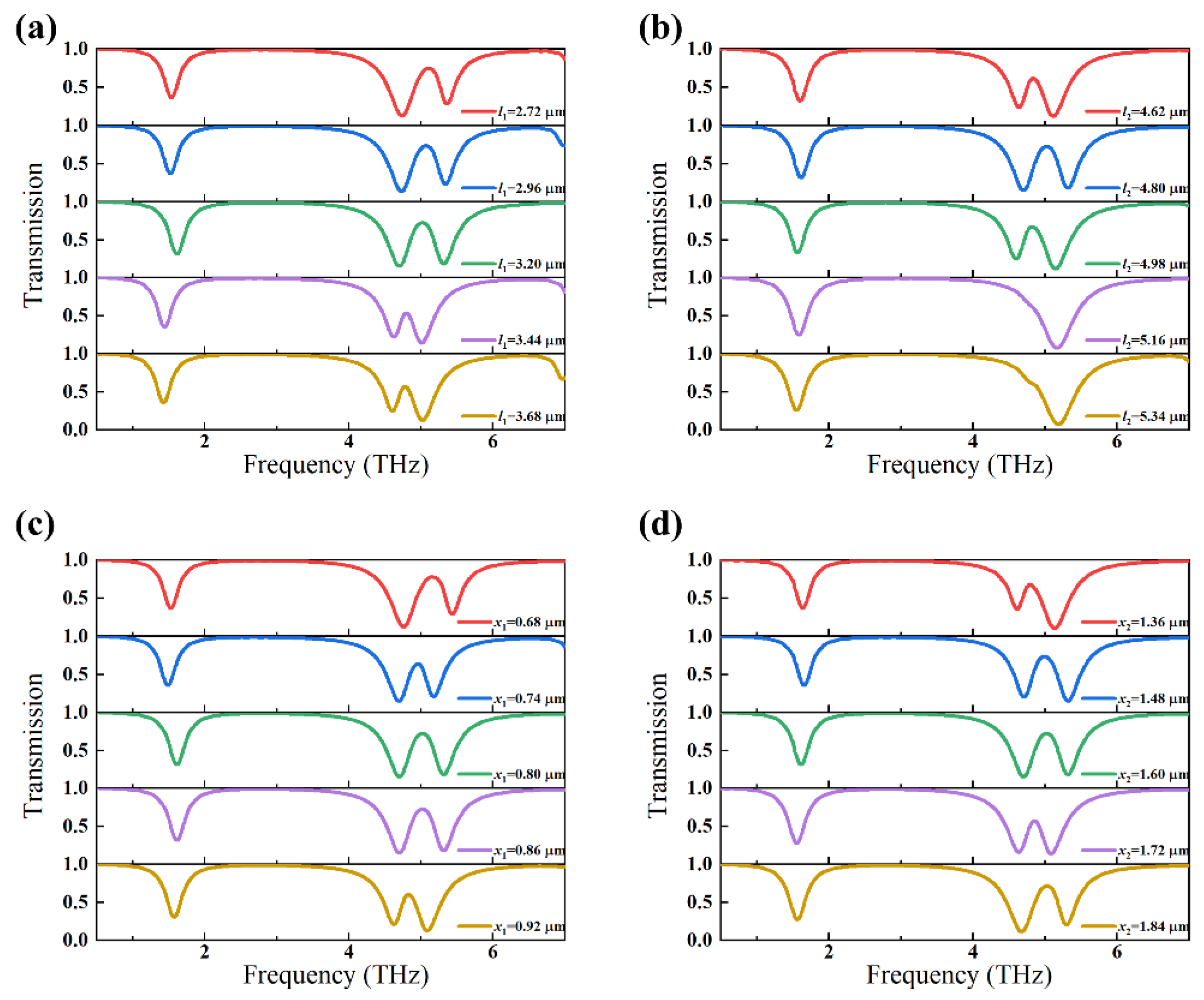
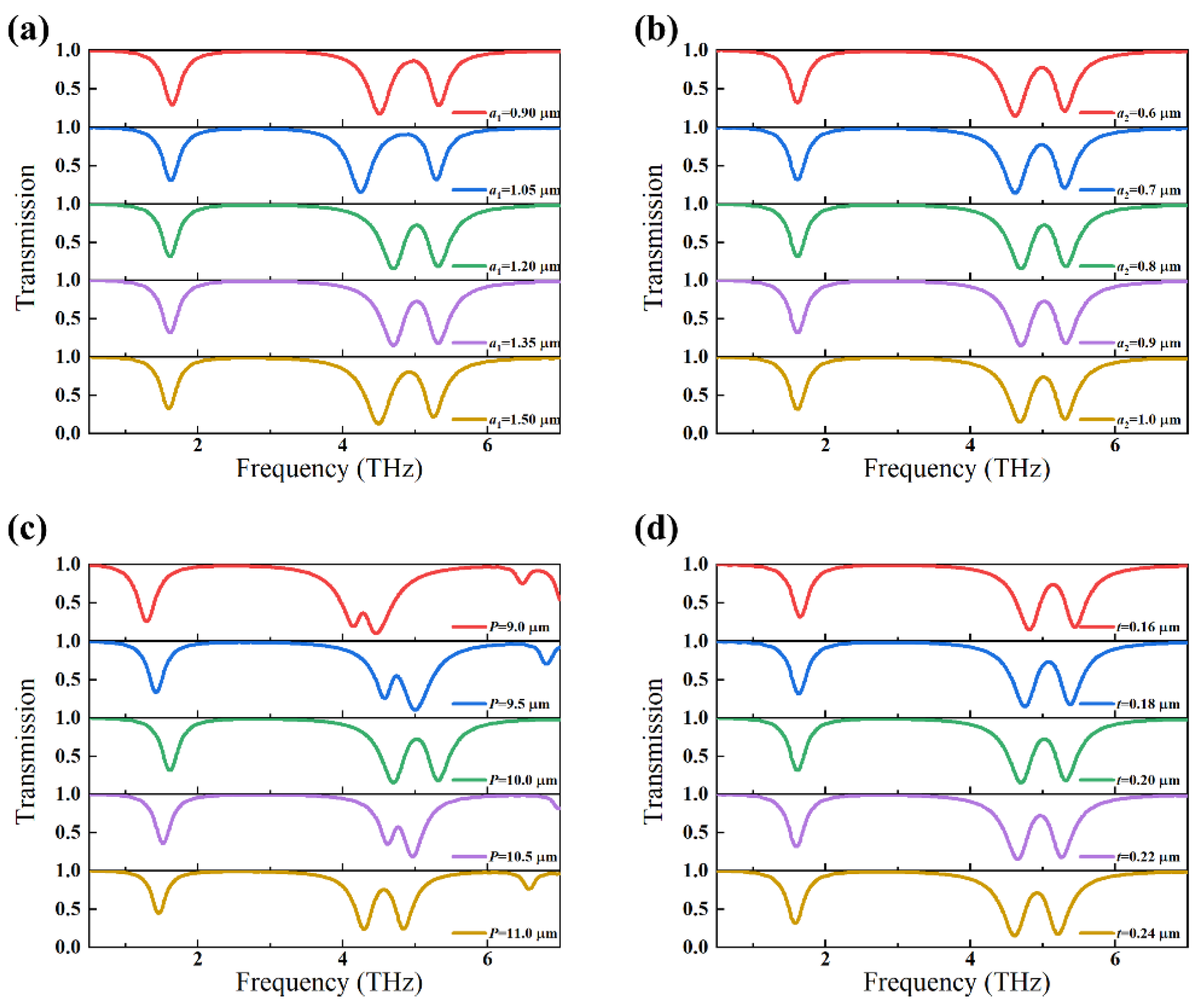
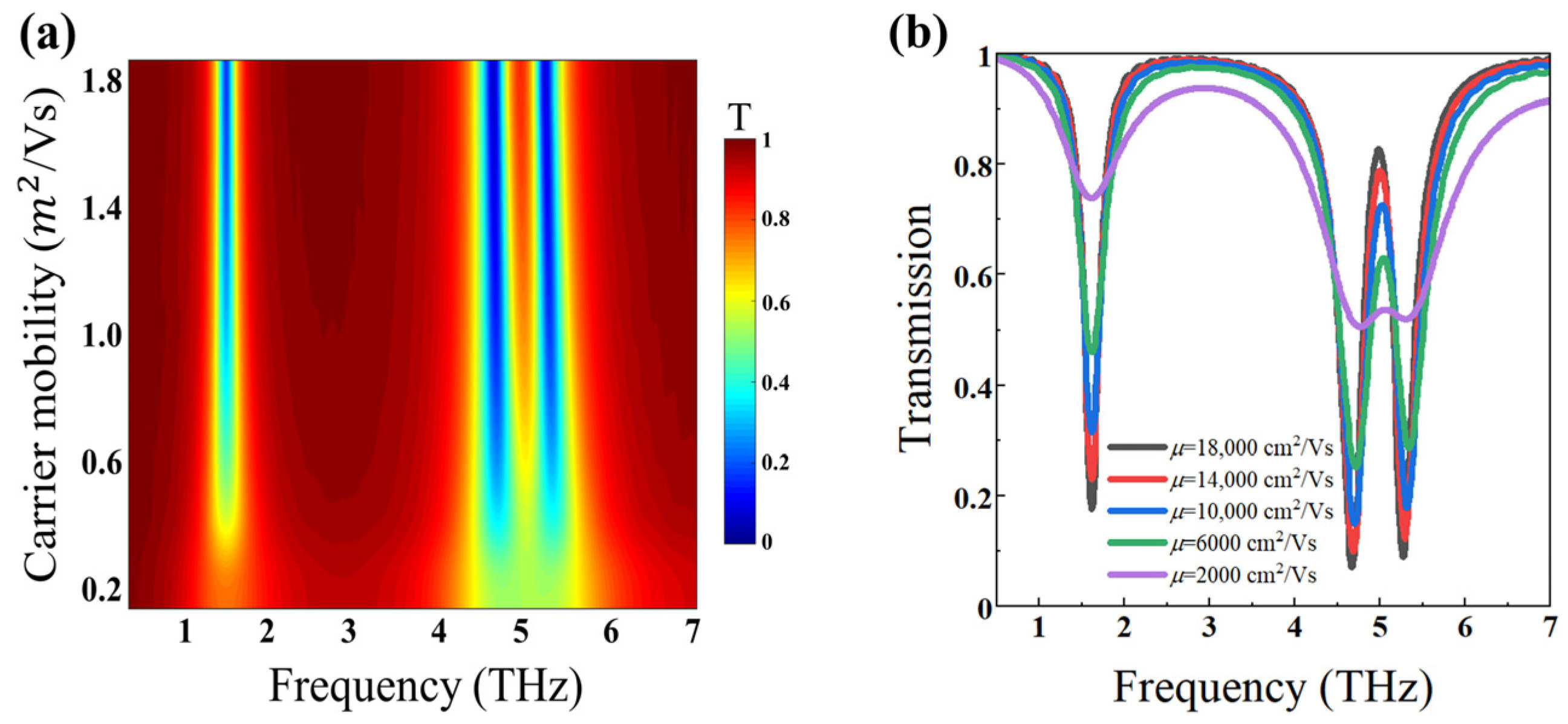
3. Results and Discussion
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Yang, Y.; Kravchenko, I.I.; Briggs, D.P.; Valentine, J. All-dielectric metasurface analogue of electromagnetically induced transparency. Nat. Commun. 2014, 5, 5753. [Google Scholar] [CrossRef] [PubMed]
- Hu, Y.; Jiang, T.; Sun, H.; Tong, M.; You, J.; Zheng, X.; Xu, Z.; Cheng, X. Ultrafast frequency shift of electromagnetically induced transparency in terahertz metaphotonic devices. Laser Photonics Rev. 2020, 14, 1900338. [Google Scholar] [CrossRef]
- Wang, C.; Jiang, X.; Zhao, G.; Zhang, M.; Hsu, C.W.; Peng, B.; Stone, A.D.; Jiang, L.; Yang, L. Electromagnetically induced transparency at a chiral exceptional point. Nat. Phys. 2020, 16, 334–340. [Google Scholar] [CrossRef]
- Zhang, S.; Genov, D.A.; Wang, Y.; Liu, M.; Zhang, X. Plasmon-induced transparency in metamaterials. Phys. Rev. Lett. 2008, 101, 047401. [Google Scholar] [CrossRef] [PubMed]
- Niu, X.; Hu, X.; Yan, Q.; Zhu, J.; Cheng, H.; Huang, Y.; Lu, C.; Fu, Y.; Gong, Q. Plasmon-induced transparency effect for ultracompact on-chip devices. Nanophotonics 2019, 8, 1125–1149. [Google Scholar] [CrossRef]
- Xiong, C.X.; Xu, H.; Zhao, M.Z.; Zhang, B.H.; Liu, C.; Zeng, B.; Wu, K.; Ruan, B.X.; Li, M.; Li, H.J. Triple plasmon-induced transparency and outstanding slow-light in quasi-continuous monolayer graphene structure. Sci. China Phys. Mech. Astron. 2020, 64, 224211. [Google Scholar] [CrossRef]
- Luo, P.; Wei, W.; Lan, G.; Wei, X.; Meng, L.; Liu, Y.; Yi, J.; Han, G. Dynamical manipulation of a dual-polarization plasmon-induced transparency employing an anisotropic graphene-black phosphorus heterostructure. Opt. Express 2021, 29, 29690–29703. [Google Scholar] [CrossRef] [PubMed]
- Ge, J.H.; You, C.; Feng, H.; Li, X.; Wang, M.; Dong, L.; Veronis, G.; Yun, M. Tunable dual plasmon-induced transparency based on a monolayer graphene metamaterial and its terahertz sensing performance. Opt. Express 2020, 28, 31781–31795. [Google Scholar] [CrossRef] [PubMed]
- Liu, Y.; Weng, X.; Wang, M.; Li, W.; Ma, S.; Zhang, L.; Zhou, P.; Deng, L. Full control of Fano spectral profile with GST-based metamaterial. ACS Photonics 2022, 9, 888–894. [Google Scholar] [CrossRef]
- Chong, M.Z.; Zhao, J.; Yin, L.Z.; Han, F.Y.; Zhang, C.Q.; Liu, P.K. Nonlinear modulation of terahertz waves based on a MAPbI3/Gold/Si hybrid plasmon-induced transparency (PIT) metasurface. Opt. Mater. 2022, 129, 112554. [Google Scholar] [CrossRef]
- Zhang, B.; Li, H.; Xu, H.; Zhao, M.; Xiong, C.; Liu, C.; Wu, K. Absorption and slow-light analysis based on tunable plasmon-induced transparency in patterned graphene metamaterial. Opt. Express 2019, 27, 3598–3608. [Google Scholar] [CrossRef] [PubMed]
- He, Z.; Li, Z.; Li, C.; Xue, W.; Cui, W. Ultra-high sensitivity sensing based on ultraviolet plasmonic enhancements in semiconductor triangular prism meta-antenna systems. Opt. Express 2019, 28, 17595–17610. [Google Scholar] [CrossRef] [PubMed]
- Ono, M.; Hata, M.; Tsunekawa, M.; Nozaki, K.; Sumikura, H.; Chiba, H.; Notomi, M. Ultrafast and energy-efficient all-optical switching with graphene-loaded deep-subwavelength plasmonic waveguides. Nat. Photonics 2020, 14, 37–43. [Google Scholar] [CrossRef]
- Pitchappa, P.; Manjappa, M.; Ho, C.P.; Singh, R.; Singh, N.; Lee, C. Active control of electromagnetically induced transparency analog in terahertz MEMS metamaterial. Adv. Opt. Mater. 2016, 4, 541–547. [Google Scholar] [CrossRef]
- Mao, L.; Li, Y.; Li, G.; Zhang, S.; Cao, T. Reversible switching of electromagnetically induced transparency in phase change metasurfaces. Adv. Photonics 2020, 2, 056004. [Google Scholar] [CrossRef]
- Paul, S.; Ray, M. Plasmonic switching and bistability at telecom wavelength using the subwavelength nonlinear cavity coupled to a dielectric waveguide: A theoretical approach. J. Appl. Phys. 2016, 120, 203102. [Google Scholar] [CrossRef]
- Zhang, Z.; Yang, J.; He, X.; Han, Y.; Huang, J.; Chen, D. Tunable plasmon-induced transparency and slow light in terahertz chipscale semiconductor plasmonic waveguides. J. Phys. D Appl. Phys. 2020, 53, 315101. [Google Scholar] [CrossRef]
- Xia, S.; Zhai, X.; Wang, L.; Wen, S. Plasmonically induced transparency in in-plane isotropic and anisotropic 2D materials. Opt. Express 2020, 28, 7980–8002. [Google Scholar] [CrossRef]
- Sang, T.; Dereshgi, S.A.; Hadibrata, W.; Tanriover, I.; Aydin, K. Highly efficient light absorption of monolayer graphene by quasi-bound state in the continuum. Nanomaterials 2021, 11, 484. [Google Scholar] [CrossRef]
- Jin, R.; Huang, L.; Zhou, C.; Guo, J.; Fu, Z.; Chen, J.; Wang, J.; Li, X.; Yu, F.; Chen, J.; et al. Toroidal dipole BIC-driven highly robust perfect absorption with a graphene-loaded metasurface. Nano Lett. 2023, 23, 9105–9113. [Google Scholar] [CrossRef]
- Liu, Z.; Xie, Y.; Luo, X.; Zhou, F.; Cheng, Z.; Yi, Z. Dynamically adjustable high-Q quasi-bound state in the continuum based on Si gratings and graphene hybrid system. Opt. Laser Technol. 2024, 177, 111106. [Google Scholar] [CrossRef]
- He, Z.; Cui, W.; Ren, X.; Li, C.; Li, Z.; Xue, W.; Zhang, B.; Zhao, R. Ultra-high sensitivity sensing based on tunable plasmon-induced transparency in graphene metamaterials in terahertz. Opt. Mater. 2020, 108, 110221. [Google Scholar] [CrossRef]
- Liu, Z.; Gao, E.; Zhang, Z.; Li, H.; Xu, H.; Zhang, X.; Luo, X.; Zhou, F. Dual-mode on-to-off modulation of plasmon-induced transparency and coupling effect in patterned graphene-based terahertz metasurface. Nanoscale Res. Lett. 2020, 15, 1. [Google Scholar] [CrossRef] [PubMed]
- He, X.; Liu, F.; Lin, F.; Shi, W. Graphene patterns supported terahertz tunable plasmon induced transparency. Opt. Express 2018, 26, 9931–9944. [Google Scholar] [CrossRef]
- Fan, C.; Ren, P.; Jia, W.; Jia, Y.; Wang, J. Tunable plasmon induced transparency in patterned graphene metamaterial with different carrier mobility. Superlattices Microstruct. 2019, 136, 106295. [Google Scholar] [CrossRef]
- Zheng, S.; Zhao, Q.; Peng, L.; Jiang, X. Tunable plasmon induced transparency with high transmittance in a two-layer graphene structure. Results Phys. 2021, 23, 104040. [Google Scholar] [CrossRef]
- Tang, B.; Guo, Z.; Jin, G. Polarization-controlled and symmetry-dependent multiple plasmon-induced transparency in graphene-based metasurfaces. Opt. Express 2022, 30, 35554–35566. [Google Scholar] [CrossRef] [PubMed]
- Wu, T.; Wang, G.; Jia, Y.; Shao, Y.; Chen, C.; Han, J.; Gao, Y.; Gao, Y. Dual-spectral plasmon-induced transparent terahertz metamaterial with independently tunable amplitude and frequency. Nanomaterials 2021, 11, 2876. [Google Scholar] [CrossRef] [PubMed]
- Xu, H.; Zhao, M.; Zheng, M.; Xiong, C.; Zhang, B.; Peng, Y.; Li, H. Dual plasmon-induced transparency and slow light effect in monolayer graphene structure with rectangular defects. J. Phys. D Appl. Phys. 2018, 52, 025104. [Google Scholar] [CrossRef]
- Gao, E.; Liu, Z.; Li, H.; Xu, H.; Zhang, Z.; Luo, X.; Xiong, C.; Liu, C.; Zhang, B.; Zhou, F. Dynamically tunable dual plasmon-induced transparency and absorption based on a single-layer patterned graphene metamaterial. Opt. Express 2019, 27, 13884–13894. [Google Scholar] [CrossRef]
- Li, M.; Li, H.; Xu, H.; Xiong, C.; Zhao, M.; Liu, C.; Ruan, B.; Zhang, B.; Wu, K. Dual-frequency on-off modulation and slow light analysis based on dual plasmon-induced transparency in terahertz patterned graphene metamaterial. New J. Phys. 2020, 22, 103030. [Google Scholar] [CrossRef]
- Cui, W.; Li, C.; Ma, H.; Xu, H.; Yi, Z.; Ren, X.; Cao, X.; He, Z.; Liu, Z. Excellent sensing based on dual-plasmon induced transparency in graphene metasurface. Phys. E Low-Dimens. Syst. Nanostruct. 2021, 134, 114850. [Google Scholar] [CrossRef]
- Li, G.; Sang, T.; Qi, H.; Wang, X.; Yin, X.; Wang, Y.; Hu, L. Flexible control of absorption enhancement of circularly polarized light via square graphene disks. OSA Contin. 2020, 3, 1999–2009. [Google Scholar] [CrossRef]
- Horng, J.; Chen, C.F.; Geng, B.; Girit, C.; Zhang, Y.; Hao, Z.; Bechtel, H.A.; Martin, M.; Zettl, A.; Crommie, M.F.; et al. Drude conductivity of Dirac fermions in graphene. Phys. Rev. B 2011, 83, 165113. [Google Scholar] [CrossRef]
- Deng, G.; Song, X.; Dereshgi, S.A.; Xu, H.; Aydin, K. Tunable multi-wavelength absorption in mid-IR region based on a hybrid patterned graphene-hBN structure. Opt. Express 2019, 27, 23576–23584. [Google Scholar] [CrossRef] [PubMed]
- Corrigan, T.D.; Kolb, P.W.; Sushkov, A.B.; Drew, H.D.; Schmadel, D.C.; Phaneuf, R.J. Optical plasmonic resonances in split-ring resonator structures: An improved LC model. Opt. Express 2008, 16, 19850–19864. [Google Scholar] [CrossRef] [PubMed]
- Papasimakis, N.; Fedotov, V.A.; Savinov, V.; Raybould, T.A.; Zheludev, N.I. Electromagnetic toroidal excitations in matter and free space. Nat. Mater. 2016, 15, 263–271. [Google Scholar] [CrossRef] [PubMed]
- Yahiaoui, R.; Manjappa, M.; Srivastava, Y.K.; Singh, R. Active control and switching of broadband electromagnetically induced transparency in symmetric metadevices. Appl. Phys. Lett. 2017, 111, 021101. [Google Scholar] [CrossRef]
- Wang, L.; Zhao, Z.; Du, M.; Qin, H.; Ako, R.T.; Sriram, S. Tuning symmetry-protected quasi bound state in the continuum using terahertz meta-atoms of rotational and reflectional symmetry. Opt. Express 2022, 30, 23631–23639. [Google Scholar] [CrossRef]
- Gong, C.; Zhan, M.; Yang, J.; Wang, Z.; Liu, H.; Zhao, Y.; Liu, W. Broadband terahertz metamaterial absorber based on sectional asymmetric structures. Sci. Rep. 2016, 6, 32466. [Google Scholar] [CrossRef]
- Sang, T.; Gao, J.; Wang, L.; Qi, H.; Yin, X.; Wang, Y. Numerical study of angle-insensitive and tunable dual-band THz absorber using periodic cross-shaped graphene arrays. Materials 2019, 12, 2063. [Google Scholar] [CrossRef] [PubMed]
- Xu, K.; Huang, J.; Wang, W. Broadband perfect optical absorption enabled by quasi-bound states in the continuum in graphene non-concentric rings. Phys. Chem. Chem. Phys. 2023, 25, 604–611. [Google Scholar] [CrossRef] [PubMed]
- Mi, Q.; Sang, T.; Pei, Y.; Yang, C.; Li, S.; Wang, Y.; Ma, B. High-quality-factor dual-band Fano resonances induced by dual bound states in the continuum using a planar nanohole slab. Nanoscale Res. Lett. 2021, 16, 150. [Google Scholar] [CrossRef]
- Vu, T.V.; Hieuc, N.V.; Phuc, H.V.; Hieu, N.N.; Bui, H.D.; Idrees, M.; Amin, B.; Nguyen, C.V. Graphene/WSeTe van der Waals heterostructure: Controllable electronic properties and Schottky barrier via interlayer coupling and electric field. Appl. Surf. Sci. 2020, 507, 145036. [Google Scholar] [CrossRef]
- Choi, M.S.; Nipane, A.; Kim, B.S.Y.; Ziffer, M.E.; Datta, I.; Borah, A.; Jung, Y.; Kim, B.; Rhodes, D.; Jindal, A.; et al. High carrier mobility in graphene doped using a monolayer of tungsten oxyselenide. Nat. Electron. 2021, 4, 731–739. [Google Scholar] [CrossRef]
- Zhu, A.; Bu, P.; Cheng, L.; Hu, C.; Mahapatra, R. High-sensitivity sensor based on diametrical graphene strip plasma-induced transparency. Photonics 2023, 10, 830. [Google Scholar] [CrossRef]
- Liu, Z.; Zhang, X.; Zhang, Z.; Gao, E.; Zhou, F.; Li, H.; Luo, X. Simultaneous switching at multiple frequencies and triple plasmon-induced transparency in multilayer patterned graphene-based terahertz metamaterial. New J. Phys. 2020, 22, 083006. [Google Scholar] [CrossRef]
- Zhang, X.; Liu, Z.; Zhang, Z.; Gao, E.; Zhou, F.; Luo, X.; Wang, J.; Wang, Y. Photoelectric switch and triple-mode frequency modulator based on dual-PIT in the multilayer patterned graphene metamaterial. J. Opt. Soc. Am. A 2020, 37, 1002–1007. [Google Scholar] [CrossRef]
- Yan, R.; Arezoomandan, S.; Sensale-Rodriguez, B.; Xing, H.G. Exceptional terahertz wave modulation in graphene enhanced by frequency selective surfaces. ACS Photonics 2016, 3, 315–323. [Google Scholar] [CrossRef]



| Ref. | Metasurface Structure | Modulation Mode | Modulation Degree (Max) | Insertion Loss (Min) |
|---|---|---|---|---|
| [47] | Multilayered graphene | Dual-frequency | 87.5% | <0.21 dB |
| [48] | Multilayered graphene | Single-frequency | 83.3% | <0.33 dB |
| [49] | Hybrid Metal–graphene | Single-frequency | >90% | <0.50 dB |
| This work | Single-layered graphene | Multiple- frequency | 89% | 0.19 dB |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Cao, Y.; Sang, T. Symmetry-Engineered Dual Plasmon-Induced Transparency via Triple Bright Modes in Graphene Metasurfaces. Photonics 2024, 11, 660. https://doi.org/10.3390/photonics11070660
Cao Y, Sang T. Symmetry-Engineered Dual Plasmon-Induced Transparency via Triple Bright Modes in Graphene Metasurfaces. Photonics. 2024; 11(7):660. https://doi.org/10.3390/photonics11070660
Chicago/Turabian StyleCao, Yanrui, and Tian Sang. 2024. "Symmetry-Engineered Dual Plasmon-Induced Transparency via Triple Bright Modes in Graphene Metasurfaces" Photonics 11, no. 7: 660. https://doi.org/10.3390/photonics11070660
APA StyleCao, Y., & Sang, T. (2024). Symmetry-Engineered Dual Plasmon-Induced Transparency via Triple Bright Modes in Graphene Metasurfaces. Photonics, 11(7), 660. https://doi.org/10.3390/photonics11070660





