Abstract
Polarization influences on the performance of multi-wavelength Brillouin Er3+-doped fiber laser are investigated by adjusting the polarization controller (PC) in the fiber loop mirror (FLM), where the linear laser cavity is composed of a fiber-tailed mirror and an FLM, and the stimulated Brillouin scattering (SBS) and the Er3+-doped fiber amplification (EDFA) simultaneously serve as the cavity gain. We realized 1–7 Brillouin laser lines by increasing the 980 nm pump power. For the first-order Brillouin laser, the signal–noise ratio (SNR) and optical intensity present a sinusoidal envelope; the conversion efficiency changes significantly from 0.56465 dBm/mw to 0.44975 dBm/mw by adjusting the ring’s angle in the PC; the first-order SBS thresholds are 20.4 mw, 36.1 mw and 28.5 mw at different angles θ2 = 36°, 276° and 300°, respectively; flatness between the two Brillouin lasers change obviously from 2.863 dB to 41.801 dB with different ring angles; the second-order Brillouin laser is suppressed and disappears finally at Δθ2 = −64° to −84° and 106°~136° angle variation. For the fifth-order Brillouin laser, the highest-order Brillouin laser line is seriously suppressed until it disappears at some angle variations similarly. The powers and wavelength stabilities for one-, three- and seven-wavelength Brillouin fiber lasers were measured in 1 h, and the obtained Er3+-doped multi-wavelength Brillouin fiber laser (MWBFL) worked stably during that time, but the stabilities become worse with higher SBS orders.
1. Introduction
Multi-wavelength Brillouin fiber lasers (MWBFLs) are very attractive in the world due to their wide application in photonics microwave generation [1,2], wavelength division multiplexing in optical fiber communication [3] and optical sensing [4,5,6]. To date, many kinds of optical schemes and gain methods have been reported to generate multi-wavelength Brillouin scattering lasers, such as EDFA [7,8], semiconductor optical amplifiers [9], dual-wavelength pumping [10], Lyot filter [11], Sagnac loop [7], bi-directional ring cavity [12], low SBS threshold photonic crystal fibers [13] and self-excited structures [11,14]. Among these approaches, the EDFA is an excellent gain medium candidate because it has a wide gain spectrum and large gain coefficient, and demonstrates a low-polarization-dependent gain spectrum. SBS in the fiber is also a kind of gain, but it is a kind of nonlinear gain with a narrow band. Simply, combining the SBS in the single-mode fiber (SMF) with EDFA gain in the laser cavity is a convenient scheme for the MWBFL. The cavity structure of the MWBFL works without any filter, only providing feedback oscillation, which is different from other multi-wavelength fiber lasers [15,16]. The SBS in fibers has a Lorentzian shape in essence, with a ~35 MHz narrow linewidth. It travels backward with the seed light in the laser cavity. By fixing two high-reflectivity components [6,17,18] at each end of the linear cavity, SBS stimulated by the amplified seed light in the SMF oscillates continuously in the laser cavity, and finally, a stable Brillouin laser output is formed.
As a high-reflective optical component, the FLM [19] is often used as wide-banded and linearly without any filtering effect in the MWBFL. In order to suppress the non-uniform characteristics of EDFA or gain competition in the laser, a PC is usually incorporated in the FLM to optimize the cavity loss and obtain the best laser performance [20,21] because the reflective coefficient of the FLM can be controlled by precisely adjusting the PC’s angle. The PC exists widely in the laser cavity [16,22,23,24,25,26] for its convenience to change the polarization state of oscillating light. Cheng et al. reported three [24], four [25] and six [16] kinds of output modes of multi-wavelength fiber laser (MWFL) by rotating the PC ring. Xiaoyi Bao et al. used a PC to select a particular wavelength for the laser output signal by suppressing the side modes [26]. However, researchers focus mainly on the laser output with a simple qualitative description of PC effects on the laser’s performance, without any quantitative analysis. There are no published papers to analyze the polarization effects on the MWBFL quantitatively that we know of. Additionally, different from the polarization burning hole (PBH) effect in the multi-wavelength fiber laser in references [16,24,25] where two comb-like filters must be well matched by adjusting the PC, the MWBFL works without any filtering component. In the MWBFL cavity, the FLM-inserting PC only provides the tunable reflectivity to satisfy the SBS threshold of every order. The reported work concentrated mainly on the number of Brillouin laser lines, OSNR of Brillouin spectrum and tunability [9,13], without discussing the polarization influence on the laser performance. However, Ibarra-Escamilla et al. reported that the modulation depth of an FLM strongly depends on polarization inside the loop through ring-angle rotation [27,28]. As a vital device in the laser cavity, the polarization effect on the FLM will consequently influence Brillouin laser performance. The PC changes the FLM’s reflectivity, consequently, the feedback in the Brillouin laser cavity also varies, which will cause the optical power to exceed or be less than the SBS threshold, which is to say, the threshold of each order Brillouin laser and the appearance of a higher-order Brillouin laser.
In this paper, the polarization influence on the MWBFL output performance is studied and analyzed in detail, for the first time that we know of in the MWBFL field, by adjusting the PC that is inserted into the Brillouin laser cavity to change the polarization state (SOP) of oscillating light. In our experiment, the output Brillouin laser numbers increase from 1 to 7 in the 1550 nm~1552 nm range with 980 nm pump power. Through rotating the angle of the middle ring in the PC, the last Brillouin laser line in the total laser numbers disappears at some angles or appears periodically by varying the PC angle; peak -values and conversion efficiency of the single-line Brillouin laser also change with the ring. For two Brillouin laser lines, the flatness is changed from 2.863 dB to 41.801 dB, and the fifth-order Brillouin laser line is suppressed seriously at some angle variations, −44° and −34°, both significantly influenced by the angle of the PC. The wavelength/intensity fluctuation is much more serious for the higher-order Brillouin laser than the lower-order Brillouin laser. All the above results could be used as references for the Er3+-doped MWBFL.
2. Experimental Setup
The scheme of Er3+-doped MWBFL is shown in Figure 1. In this configuration, a linear cavity is formed by a fiber-tailed mirror (provided by Mingchuang Optoelectronics Co., Ltd., Shenzhen, China) and a fiber loop mirror (FLM), which are set at both ends simultaneously. Reflection of the fiber-tailed mirror is 99%; and reflection of the fiber loop mirror is 92%. In order to measure the polarization characteristics of MWBFL, a 3-ring PC (provided by Hanyu Fiber Optic Communication Technology Company, Shanghai, China) is inserted into the FLM to vary the cavity loss and polarization state. The total cavity gain in the laser is provided by EDFA and SBS in the 20 Km single-mode fiber (SMF, SMF-28e, Corning Company, Corning, NY, USA). The pump laser is a distributed feedback laser (DFB, FITEL, FURUKAWA Solutions, Norcross, GA, USA) with 1 MHz linewidth @3 dB, optical intensity 48.1 mw, central wavelength 1550.974 nm, which serves as the seed pump light for SBS in SMF. When its intensity exceeds the SMF threshold, the SBS can be excited and then oscillate in the laser cavity. A 3-port circulator is used to direct light from 1st port to 2nd port before entering the linear cavity. The 2nd port is connected to the 10% arm of the 1:9 coupler. Then, the pump light is amplified enough by EDFA to stimulate the SBS in SMF. In the EDFA, the maximum power of 980 nm laser (provided by Hoya tech, Shenzhen, China) is 300 mw, and the Er3+-doped fiber (EDF, EDFC-980-HP, Coherent Corporation, Santa Clara, CA, USA) is 6 m whose doping concentration is 1500 ppm, NA is 0.23. The FLM is composed of a 1:1 coupler by connecting the two output arms and inserting a 3-ring PC. The PC in the loop is formed by three plates in series, as shown in Figure 1. When the optical power from EDFA exceeds the SBS threshold of 20 Km SMF, the first-order SBS will be excited and propagate backward through EDFA again and the 90% arm in the 1:9 coupler in the laser cavity. Then, the SBS oscillates in the linear cavity and forms the Brillouin laser output through the 10% arm of the 1:9 coupler and the 3rd port of the circulator. Consequently, if the laser power of first-order SBS is also higher than the 2-order SBS threshold, the 2nd Brillouin laser will be output simultaneously. Successively, higher-order SBS would be excited if the power transmitting in the linear cavity is larger than its threshold. The Brillouin laser output is measured by optical spectrum analyzer (OSA, 0.02 nm wavelength resolution, AQ 6370D, Yokogawa, Japan). In total, the laser line number of MWBFL is decided by the amplified coefficient of EDFA and the SBS threshold of long-distance SMF.
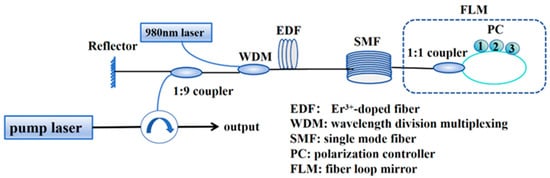
Figure 1.
The scheme of multi-wavelength Brillouin Er3+-doped fiber laser.
Adjusting the ring’s angle, the reflectivity and SOP of FLM are changed accordingly [28,29]. Especially in reference [28], the reflectivity characteristics of FLM inserting a PC have been modeled by using the equivalent optical path technique and simulated with the model. According to Equation (11) in this paper, the reflectivity of FLM R = cos2δ, where δ is the birefringence intensity of PC. In paper [29], the PC is regarded as a three-waveplate structure. The model of PC is quarter waveplate, half waveplate and quarter waveplate, in series. The reflectivity rate R = cos2θ, where θ is the angle of the half waveplate. Changing the PC state, the FLM behaves like a variable reflector. Though different models are applied to analyze the FLM reflectivity, the same mathematical results and simulation curves are obtained. That is to say, the PC provides continuously amplitude-tunable capability with rotating angles of the three rings. In this paper, we analyze the polarization influence on MWBFL with the three-waveplates model as demonstrated in reference [29]. If rings 1 and 3 are orientated optimally, the cavity loss is changed by rotating the middle 2nd ring, resulting in the optical intensity variation for different angles. Compared with the threshold of the high-order SBS, pump seed power would cause the appearance/disappearance of this-order Brillouin laser. Finally, the output number and flatness of MWBFL lines would decrease/increase with the angle rotation.
3. Experimental Results and Discussions
In the experiment, the performance of the Er3+-doped MWBFL is investigated in detail. By varying the power of the 980 nm laser in EDFA and adjusting the ring’s angle in the PC, the laser spectra, laser conversion efficiency for the first-order Brillouin laser, multi-wavelength flatness with different polarization states, and output stability are analyzed.
Precisely rotating angles of the three rings, the Brillouin laser power reaches its maximum when θ1 = 36°, θ2 = 36° and θ3 = 16°. Under this condition, by increasing the 980 nm pump power in EDFA, the optical spectra of the Brillouin fiber laser are shown in Figure 2a. With the 980 nm laser power increment, more Stokes waves are generated and eventually, a seven-wavelength Brillouin laser is obtained at 980 nm pump power 300 mw. As with the Brillouin pump, the power of the highest-order Stokes Brillouin light is lower than the threshold of next-order SBS, so the eighth-order Brillouin laser cannot be excited. The wavelength difference between two adjacent Brillouin laser lines is 0.088 nm, which corresponds to the Brillouin frequency shift in SMF. The number distribution of the Brillouin laser lines with the EDFA pump power is depicted in Figure 2b. The critical power for the number of the Brillouin laser is clearly demonstrated and derived from the laser spectra. However, the peak amplitude of every laser line changes significantly and causes the conversion or flatness deterioration.
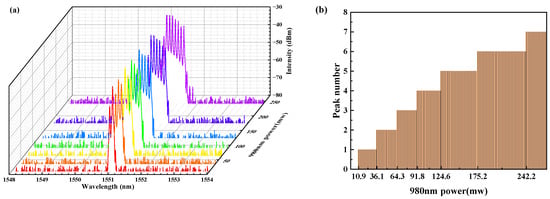
Figure 2.
(a) The output spectra and (b) the number distribution of the Brillouin laser with different 980 nm power.
When the three rings in the PC are at their optimized positions θ1 = 36°, θ2 = 36° and θ3 = 16° and the 980 nm pump power is 36.1 mw, the optical intensity of the first-Brillouin laser reaches its maximum seen from the optical spectrum. By changing the angle θ2 step at 30°, we obtain several optical spectra, as shown in Figure 3a, to analyze the polarization effect on the Brillouin laser. It is assumed that the angle θ2 = 36° is the original position. When ring 2 is rotated to the left, the angel variation is negative; when ring 2 is rotated to the right, the angel variation is positive; as shown in the coordinate axes. With θ2 angle variation from −144° to 168 °, the optical spectra keep one Stokes laser line. Their central wavelengths are a constant 1551.062 nm. The optical SNRs (OSNR) of the first-order Brillouin laser are distributed in Figure 3b, where a nearly 5 dB OSNR difference is caused by the middle-ring rotation. Similarly, the peak value varies with the θ2 angle as depicted in Figure 3b. It can be seen that the optical intensity is approaching symmetry with the original position, and the power distribution presents a sinusoidal envelope.
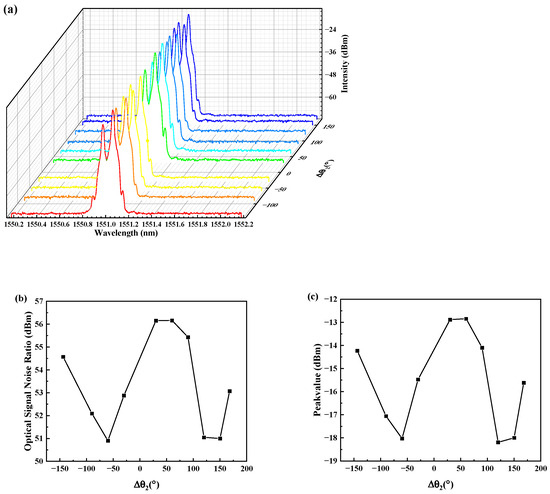
Figure 3.
First Brillouin wavelength: (a) spectra, (b) OSNR and (c) optical intensity with θ2 variation.
Rotating θ2 to three positions 276°, 36° and 300°, respectively, corresponding to angle variations 120°, 0° and 96°, the polarization states of the laser cavity and cavity loss are modulated by the PC simultaneously. The optical spectra show that the Brillouin lasers are −18.194 dBm, −12.881 dBm and −17.997 dBm. Then, we increase the 980 nm pump power at each θ2, respectively setting θ2 at the three angles. When θ2 = 36°, the conversion efficiency of the Brillouin laser is 0.56465 dBm/mw; when θ2 = 276°, the conversion efficiency is 0.44975 dBm/mw; when θ2 = 300°, the conversion efficiency is 0.53102 dBm/mw; as depicted in Figure 4. Obviously, at the oriented angle, the Brillouin laser has the highest efficiency, resulting from the lower cavity loss. It is worth noting that the optical intensities of θ2 = 276° and θ2 = 300° are less than that of θ2 = 36°. Because the laser cavity losses for the two angles are larger than the oriented angle, the Brillouin laser could be excited only by increasing the 980 nm pump power further. The excited powers for the three angles are 20.4 mw (for 36°), 36.1 mw (for 276°) and 28.5 mw (for 300°); and the cutoff powers are 36.1 mw (for 36°), 50.9 mw (for 276°) and 46 mw (for 300°). Comparing the situations of the minimum and maximum cavity loss, a 15.7 mw difference of 980 nm pump power is generated to stimulate the first-order Brillouin laser. Where 36.1 mw 980 nm pump power is the threshold for the θ2 = 276°, but it is almost the cutoff power for θ2 = 36°. So, the optical spectrum of the Brillouin laser will be different at the same 980 nm power at different PC angles. If the 980 nm power is increased further to exceed the cutoff power under the three conditions, the second Stokes would be excited and the single Brillouin laser line becomes two.
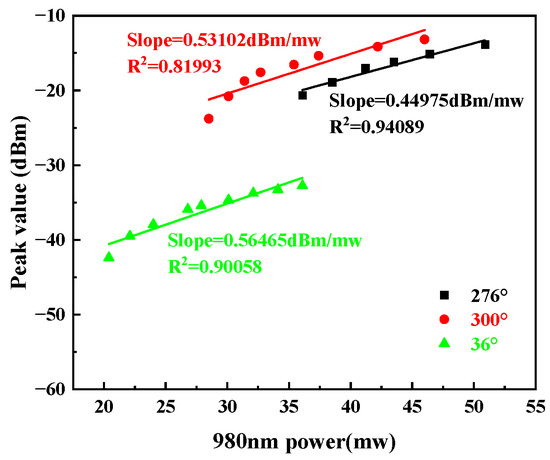
Figure 4.
The conversion efficiencies for different θ2.
To describe the linewidth of the Brillouin laser line, the homodyne spectrum method is applied and a Mach–Zender interferometer (MZI) is built as shown in Figure 5a. The optical signal from the BFL is launched into the MZI. A 30 Km delaying fiber is inserted in one of the MZI arms. The measurement signals through photodetector (PD) presented on an electrical spectrum analyzer (ESA) are fitted to the Lorentzian shape, as shown in Figure 5b. We firstly estimate the homodyne full-width @20 dB below the peak of the homodyne signal to reduce the measurement error, because the BFL spectrum is very narrow. The measured linewidth @20 dB is 62 kHz, so the obtained Lorentzian linewidth @3 dB is 3.1 kHz.
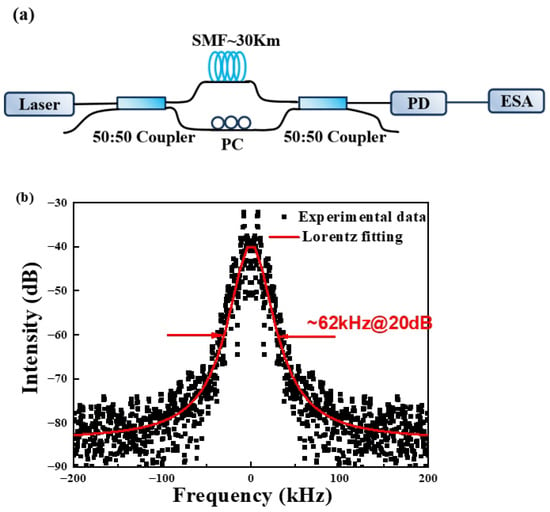
Figure 5.
(a) The laser bandwidth measurement setup; (b) the measurement of BFL linewidth by the homodyne spectrum method.
Setting the three rings in PC at the original positions θ1 = 36°, θ2 = 36° and θ3 = 16°, dual Brillouin laser wavelengths are generated continuously when the 980 nm pump power is from 36.1 mw to 64.3 mw, as shown in Figure 6. The peak values of the second-order Brillouin laser increased gradually with the 980 nm power. If the 980 nm power exceeds 64.3 mw, third-order stimulated Brillouin scattering in SMF will be excited. As seen from Figure 6, flatness (difference between peak values) between the two laser lines is improved and reaches best before the higher-order Brillouin laser generation. When the 980 nm laser power is 64.3 mw, the flatness is best at 4.94 dB. The two Brillouin lasers are so remarkably flat due to the optimization of the PC state. Under this power condition, we then changed the angle of ring 2, and the optical spectra and flatness analysis of the two Brillouin laser lines varied obviously, as shown in Figure 7a,b. The flatness between the two Brillouin lasers is between 2.863 dB and 41.801 dB. The angle variations are limited in the ranges −64° to −84° and 106°~136°, the flatness is more than 30 dB, and the second-order Brillouin laser is suppressed seriously until it disappears.
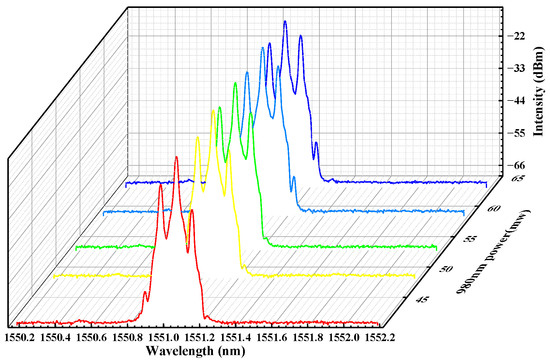
Figure 6.
The dual Brillouin wavelengths with EDFA.
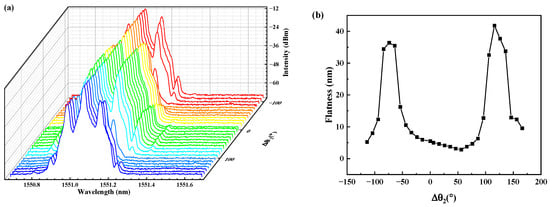
Figure 7.
The flatness between two Brillouin wavelengths changing with angle θ2: (a) the optical spectra; (b) the flatness analysis.
Polarization effects on five-wavelength Brillouin laser lines are also investigated based on the PC angle rotation. The three rings in the PC are still set at the original position, five Brillouin laser wavelengths exist when the 980 nm pump power is between 124.6 mw and 175.2 mw, as shown in Figure 8a. It is noted that the fifth-order Brillouin laser stands out firstly when the 980 nm pump power is 124.6 mw, then gradually increases with the increase in 980 nm pump power, and finally reaches the highest peak value when the 980 nm laser power is 175.2 mw. The distribution of the peak values of the fifth-order Brillouin laser is presented in Figure 8b, where the peak values increase with the 980 nm power. Flatness among all the five lines is also best when the 980 nm power is 175.2 mw. At this time, we adjust the ring angle θ2, then the numbers of the MWBFL and flatness of the five laser lines vary obviously in the optical spectra, as shown in Figure 9a. With the SOP change in the FLM, the highest-order Brillouin laser line is suppressed seriously at some angle variations, −44° and −34°, as shown in the inserted figure in Figure 9b, resulting from the increase in cavity loss of the PC. The flatness variation between the five Brillouin lasers with Δθ2 is depicted in Figure 9b. The best lasing output is achieved around the original angle Δθ2 = −4° (θ2 = 32°) and Δθ2 = 66° (θ2 = 330°), with the highest SNR 50.4 dB and flatness 7.5 dB. When the flatness of the fifth-order and first-order Brillouin laser is much more than 12.5 dB, it means that the exciting and oscillation condition of the fifth-order are not satisfied, and the fifth-order Brillouin laser is seriously deteriorated like the frontmost spectra in Figure 8a.
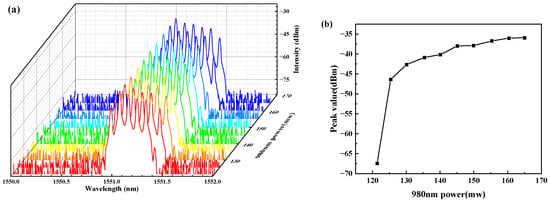
Figure 8.
(a) Fifth-order Brillouin laser spectra with EDFA; (b) peak-values distribution of the 5th-Brillouin laser.
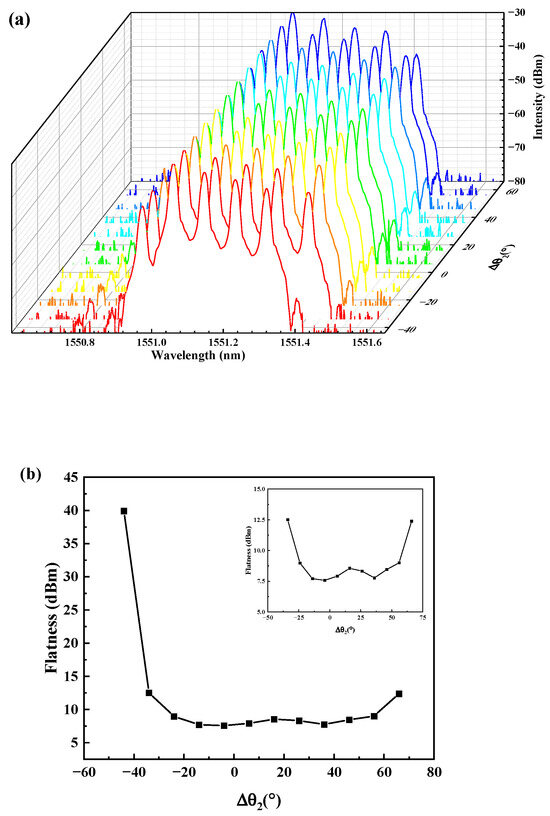
Figure 9.
(a) Five-wavelength Brillouin laser spectra with θ2 variation; (b) the flatness distribution at different θ2.
Stable working is vital for MWBFL engineering applications. The stability of the MWBFL laser in this paper is measured in detail. The one-wavelength, three-wavelength and seven-wavelength Brillouin laser lines are measured every 5 min in an hour, including their optical intensity fluctuations and wavelength stabilities. Power fluctuation and wavelength variation of first-order Brillouin stokes in the one-wavelength Brillouin laser in an hour are shown in Figure 10, where the three plates are in their original positions θ1 = 36°, θ2 = 36° and θ3 = 16°. The power fluctuation is between −40.019 dBm and −39.094 dBm, less than 1 dB. Meanwhile, the central-wavelength fluctuation of the first Brillouin laser in an hour is 0.02 nm, which is also the wavelength resolution of OSA. The above measurement results indicate that the Brillouin laser output has good stability over time. Similarly, the stabilities of the three-wavelength Brillouin laser are shown in Figure 11a,b, when the three rings in the PC are at the original angles and the 980 nm pump power is 69.3 mw. The first, second and third laser lines have 0.164 dBm, 0.368 dBm and 0.393 dBm power variation, and 0.00 nm, 0.04 nm and 0.00 nm wavelength fluctuation, respectively. Further, the stabilities of the seven-wavelength laser lines are shown in Figure 12a,b. Similarly, the 1st to 7th laser lines each have 0.19 dBm, 0.38 dBm, 0.618 dBm, 0.742 dBm, 0.962 dBm, 1.741 dBm and 4.565 dBm power variation, 0.00 nm, 0.04 nm, 0.00 nm, 0.00 nm, 0.04 nm, 0.04 nm and 0.04 nm wavelength fluctuation, respectively. Comparing all the curves in Figure 10 and Figure 11, we find that the stabilities of optical power and central wavelength become worse when the order of SBS is highest, i.e., the last Brillouin laser line in the whole wavelength range.
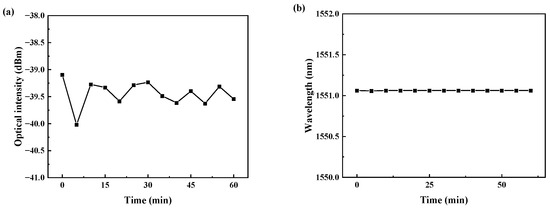
Figure 10.
Stability of 1-wavelength Brillouin laser line in an hour: (a) the optical intensities (b) the central wavelengths.
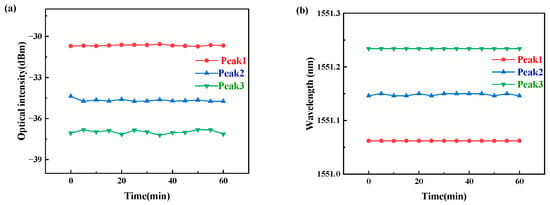
Figure 11.
Stabilities of 3-wavelength BFL in an hour: (a) the optical intensities (b) the central wavelengths.
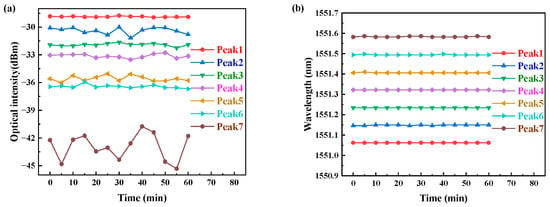
Figure 12.
Stabilities of 7-wavelength BFL in an hour: (a) the optical intensities (b) the central wavelengths.
4. Conclusions
The polarization effects on the linear-cavity Er3+-doped MWBFL are analyzed in this paper. By rotating the angle of the middle ring in the three-ring PC, the reflectivity and SOP of the FLM are changed, and the output performance of the MWBFL is influenced accordingly. We obtained 1- to 7-wavelength Brillouin lasers with the 980 nm pump power increasing to 311 mw. For the first Brillouin laser, its output powers change sinusoidally; the conversion efficiency changes from 0.56465 dBm/mw to 0.44975 dBm/mw with the angle variation Δθ2; and the SBS thresholds are 20.4 mw, 36.1 mw and 28.5 mw at different angles θ2 = 36°, 276° and 300°. The optical spectra of two-wavelength Brillouin laser lines are presented with increasing the 980 nm pump power, where the second-order SBS reaches a peak before the appearance of the next-order Brillouin light; flatness between the two Brillouin lasers change obviously from 2.863 dB to 41.801 dB with different ring angles; the second-order Brillouin laser is suppressed and disappears finally at −64° to −84° and 106°~136° angle variations. Meanwhile, the optical spectra of five-wavelength Brillouin laser lines are also presented, and flatness among all the five lines is best reached when the 980 nm power is 175 mw; if the ring angle θ2 is adjusted, then the numbers of the MWBFL and flatness of the five laser lines vary obviously in the optical spectra by adjusting the middle ring 2. The highest-order Brillouin laser line is seriously suppressed until it disappears at angle variations, −44° and −34°, resulting from the increase in cavity loss of the PC. The power and wavelength stabilities for the one-, three- and seven-wavelength MWBFLs are measured in 1 h, and the obtained Er3+-doped MWBFL worked stably during that time, but the stabilities become worse with higher SBS orders. The results of this experiment can provide references for the practical applications of multi-wavelength Brillouin fiber lasers.
Author Contributions
Conceptualization, Y.H.; methodology, Y.H. and K.Y.; software, W.L. and M.M.; validation, Y.H.; formal analysis, M.M. and Y.H.; investigation, M.M. and Y.H.; data curation, M.M.; writing—original draft preparation, Y.H. and M.M.; writing—review and editing, Y.H. and K.Y.; visualization, M.M. and W.L.; supervision, K.Y.; project administration, Y.H. and K.Y.; funding acquisition, Y.H. and K.Y. All authors have read and agreed to the published version of the manuscript.
Funding
This research is funded by the Science and Technology Research Project of Henan Province grant numbers 232102210175 and 242102211088, and the Young Backbone Teachers Program in University of Henan Province grant number 2021GGJS092.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
The original contributions presented in the study are included in the article, further inquiries can be directed to the corresponding authors.
Conflicts of Interest
The authors declare no conflicts of interest.
References
- Qi, H.; Zhou, X.; Zhang, Y.; Yang, G.; Bi, M.; Hu, M. Multi-wavelength Brillouin erbium-doped fiber laser with 40 GHz frequency shift interval assisted by Sagnac loop filter. Optoelectron. Lett. 2024, 20, 265–271. [Google Scholar] [CrossRef]
- Al-Mashhadani, M.K.S.; Al-Mashhadani, T.F.; Goktas, H.H. Broadly tunable 40 GHz Brillouin frequency spacing multiwavelength Brillouin-Erbium fiber laser for DWDM. Opt. Commun. 2019, 451, 116–123. [Google Scholar] [CrossRef]
- Ismail, A.; Al-Mansoori, M.H.; Abdullah, F.; Jamaludin, M.Z.; Al-Qartoubi, M.; Almamari, S.H.; Alkhaldi, H.S. Tunable C plus L bands triple frequency spacing multi-wavelength Brillouin-erbium fiber laser. Opt. Fiber Technol. 2021, 64, 102535. [Google Scholar] [CrossRef]
- Murray, J.B.; Cerjan, A.; Redding, B. Massively distributed fiber strain sensing using Brillouin lasing. Opt. Express 2022, 30, 25765–25773. [Google Scholar] [CrossRef] [PubMed]
- Liu, Y.; Shang, Y.; Yi, X.; Guo, R.; Zheng, Y. Triple Brillouin frequency spacing Brillouin fiber laser sensor for temperature measurement. Opt. Fiber Technol. 2020, 54, 102106. [Google Scholar] [CrossRef]
- Zhou, X.; Li, Z.; Ge, C.; Fan, B.; Wang, T. Multi-wavelength Brillouin erbium-doped fiber laser sensor with high tunable temperature sensing coefficient. Opt. Quant. Electron. 2019, 51, 14. [Google Scholar]
- Chen, L.; He, J.; Liu, Y. Flat multi-Wavelength Brillouin Erbium-doped fiber laser based on a Sagnac loop for high-sensitivity sensor. Sensors 2022, 22, 9017. [Google Scholar] [CrossRef] [PubMed]
- Mamdoohi, G.; Soltanian, M.R.K.; Légaré, F. Flatness enhancement of multi-wavelength Brillouin-Raman fiber laser with 10 GHz spacing utilizing Raman pump power distribution. Opt. Express 2023, 31, 26167–26177. [Google Scholar] [CrossRef] [PubMed]
- Zhang, Z.; Wu, J.; Xu, K.; Hong, X.; Lin, J. Tunable multiwavelength SOA fiber laser with ultra-narrow wavelength spacing based on nonlinear polarization rotation. Opt. Express 2009, 17, 17200–17205. [Google Scholar] [CrossRef]
- Zhu, K.; He, J.; Chang, K.; Xing, D.; Liu, Y.; Wang, Z. Tunable and narrow linewidth multi-wave length Brillouin-erbium fiber laser using dual-wavelength pumping. Optoelectron. Lett. 2022, 18, 0349–0353. [Google Scholar] [CrossRef]
- Zhao, Q.; Pei, L.; Wu, L.; Ning, T.; Zheng, J.; Li, J. Wide tuning range and high OSNR self-seeded multi-wavelength Brillouin-erbium fiber laser based on a Lyot filter. Appl. Opt. 2018, 57, 10474–10478. [Google Scholar] [CrossRef] [PubMed]
- Geng, X.; Jiang, Y.; Sun, M. A multi-wavelength Brillouin fiber laser of switchable frequency spacing based on a bi-directional ring cavity. Opt. Commun. 2022, 531, 129201. [Google Scholar] [CrossRef]
- Nasir, M.N.M.; Yusoff, Z.; Al-Mansoori, M.H.; Rashid, H.A.A.; Choudhury, P.K. Widely tunable multi-wavelength Brillouin erbium fiber laser utilizing low SBS threshold photonic crystal fiber. Opt. Express 2009, 17, 12829–12834. [Google Scholar] [CrossRef] [PubMed]
- Zou, H.; Shi, Y. A polarization sensitive self-excited multi-wavelength Brillouin-Erbium fiber laser without filtering devices. Opt. Laser Technol. 2024, 175, 110742. [Google Scholar] [CrossRef]
- Li, T.; Yan, F.; Wang, P.; Wang, X.; Suo, Y.; Zhou, H. Switchable multi-wavelength thulium-doped fiber laser using a two-taper fiber filter. Infrared Phys. Technol. 2022, 125, 104269. [Google Scholar] [CrossRef]
- Cheng, J. Dual-wavelength EDF laser outputing six kinds of different lasing lines. J. Optoelectron. Adv. M. 2023, 25, 10–13. [Google Scholar]
- Torres-Gonzalez, D.; Sierra-Hernandez, J.M.; Jauregui-Vazquez, D.; Reyes-Ayona, J.R.; Estudillo-Ayala, J.M.; Bianchetti, M.; Gallegos-Arellano, E.; Hernandez-Garcia, J.C.; Rojas-Laguna, R. An aluminum coated all-fiber mirror and a Mach-Zehnder interferometer for developing a switchable and tunable multi-wavelength laser. Opt. Commun. 2023, 537, 129397. [Google Scholar] [CrossRef]
- Zhang, Z.; Liu, F.; Guo, X.; Chen, T.; Han, L.; Zhang, W. Optimization of Dual-Wavelength linear cavity Er bium-Doped fiber laser based on pairs of fiber Bragg gratings. Opt. Fiber Technol. 2024, 83, 103675. [Google Scholar] [CrossRef]
- Mortimore, D.B. Fiber loop reflectors. J. Light. Technol. 1988, 6, 1216–1224. [Google Scholar] [CrossRef]
- Abu Hasan, N.N.; Sulaiman, A.H.; Abdullah, F.; Md Yusoff, N.; Ismail, A.; Jamaludin, M.Z. Polarization Effect on Dual and Quad Output Fiber Laser Based on Sagnac Loop Mirror Interferometer. Fiber Integr. Opt. 2024, 43, 1–13. [Google Scholar] [CrossRef]
- Liu, Y.; Guo, R.; Zhao, J.; Chen, P.; Gu, Y.; Ning, Y.; You, Y.; Chou, X. An EDFA-gain equalizer based on a Sagnac loop with an unpumped Erbium-doped Fiber. J. Light. Technol. 2021, 39, 4496–4502. [Google Scholar] [CrossRef]
- Zhao, Q.; Pei, L.; Ruan, Z.; Zheng, J.; Wang, J.; Tang, M.; Li, J.; Ning, T. Tunable and wavelength interval precisely controlled erbium-doped fiber laser by employing the fused taper technology. Chin. Opt. Lett. 2022, 20, 011402. [Google Scholar] [CrossRef]
- Zhang, W.Y.; Zheng, L.; Jiang, H.J.; Liu, N.N.; Yang, K.; Xian, T.H.; Zhan, L. Bright-dark pulse pair in a passively mode-locked fiber laser based on thulium-doped fiber. IEEE Photonics Technol. Lett. 2024, 36, 429–432. [Google Scholar] [CrossRef]
- Cheng, J.; Wang, T.; Chen, G. Triple-wavelength EDF laser based on phase-shifted fiber grating and 50 µm MMF. Laser Phys. 2021, 31, 095102. [Google Scholar] [CrossRef]
- Cheng, J.; Zheng, W.; Liu, Z.; Zhang, J.; Yan, P. Quadruple-wavelength EDF Laser based on Chirped fiber grating and 62.5 μm multimode fiber. J. Russ. Laser Res. 2021, 42, 190–195. [Google Scholar] [CrossRef]
- Yin, G.; Wang, X.; Bao, X. Effect of beam waists on performance of the tunable fiber laser based on in-line two-taper Mach–Zehnder interferometer filter. Appl. Opt. 2011, 50, 5714–5720. [Google Scholar] [CrossRef]
- Armas-Rivera, I.; Rodriguez-Morales, L.A.; Beltran-Perez, G.; Duran-Sanchez, M.; Andres, M.V.; Ibarra-Escamilla, B. Polarization properties of a fiber optic loop mirror. Opt. Laser Technol. 2021, 140, 107070. [Google Scholar] [CrossRef]
- Feng, S.; Mao, Q.; Shang, L.; Lit, J.W.Y. Reflectivity characteristics of the fiber loop mirror with a polarization controller. Opt. Commun. 2007, 277, 322–328. [Google Scholar] [CrossRef]
- Wei, L.; Xu, X.; Khattak, A.; Henley, B. Continuously tunable comb filter based on a high-birefringence fiber loop mirror with a polarization controller. J. Light. Technol. 2021, 39, 4800–4808. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).