Abstract
This study aimed to examine the mechanisms of the photoplethysmography (PPG) signal formation using Monte Carlo simulations of light transport in biological tissues and experimental observations. Based on a three-layer skin model in backscattering geometry, we sequentially simulated volumetric blood changes and the aggregation/disaggregation of erythrocytes in the dermal layer and estimated their contribution to the registered PPG signal. The calculations were conducted for two wavelengths: 525 nm and 810 nm. For green light, absorption predominates over scattering in the formation of a PPG signal, whereas, for near-infrared light, scattering prevails over absorption. This theoretical result was verified using the Modified Beer–Lambert law and clinical in vivo PPG data of seven healthy subjects. Changes in the size of the scatterers during erythrocyte aggregation and disaggregation can significantly contribute to the PPG signal at near-infrared light. Thus, for the green waveband, the classical volumetric model can be considered dominant in the PPG signal formation. In contrast, for the near-infrared range, both volumetric and aggregation effects must be considered as being approximately equal.
1. Introduction
Photoplethysmography (PPG) is a simple and widespread optical technique for assessing important cardiovascular parameters [1]. This method is based on illuminating a tissue with incoherent optical radiation in the visible or near-infrared range and recording a flux that has passed through or backscattered from the tissue [2]. The set of parameters measured by PPG include arterial oxygen saturation, pulse rate and its variability, blood pressure, pulse wave velocity, vascular stiffness, and microvascular blood flow [1,3]. However, today, there is no clear understanding of how the PPG signal is formed. Researchers are actively discussing this topic. Currently, there are three main factors (models) influencing the formation of the PPG signal [4]:
- Variations in the blood fraction (volume) inside the skin (volumetric model);
- The orientation, aggregation, and deformation of red blood cells (RBCs);
- The mechanical movements of capillaries in the superficial layers of the dermis and the compression of surrounding cellular tissues.
The volumetric model is classic and is widely used for describing the origin of the PPG signal. The model assumes that the intensity of the light backscattered by the skin changes due to variations (fluctuations) in the blood volume in the skin, affecting the optical properties of the medium [5]. It is believed that the volumetric variations mainly change the absorption coefficient of the medium, which leads to a change in the amplitude of the registered optical radiation. Thus, the PPG signal recorded by a photodetector is an amplitude-modulated signal due to the passage of pulse waves through blood vessels. The volumetric model has been repeatedly confirmed both theoretically and experimentally. For example, Moço et al. validated the model using Monte Carlo (MC) simulations and experimentally verified it using diffuse reflectance spectroscopy and videocapillaroscopy [6]. During an experiment on the nail fold of a finger, green light penetrated through the capillary loops and reached arterioles. Their investigation showed that the PPG signal was formed due to the light absorbance by dermal arterioles.
In the early 1980s, through experiments, several authors suggested that changes in the orientation of red blood cells (RBCs), depending on the cardiac cycle, are the main reason for the formation of the PPG wave [7]. This hypothesis is based on the electrophysiological characteristics, where at the end of diastole (i.e., low blood flow), the RBCs orient themselves randomly due to reduced shear stress. As blood flow increases, the red blood cells tend to align themselves along with the flow, and, during systole, the alignment is parallel to the direction of the flow [4]. The orientation of RBCs influences the overall attenuation of light by the tissue, which likely leads to the formation of a PPG signal. This hypothesis was confirmed experimentally in an in vitro model with tubes with moving blood [8]. Shvartsman and Fine also found a similar effect and confirmed that PPG signals can arise due to geometric changes in RBC aggregation [9]. They conducted an in vitro experiment using tubes containing a blood solution. They found the pulsating blood flow after administering high-molecular Dextran, which activates RBC aggregation. Later, they developed the scattering-driven PPG signal model [10]. The key point in their model was changing the size (dimension) of scatterers due to the RBC aggregation and the subsequent change in the scattering of the medium, which ultimately leads to the amplitude modulation of the registered optical flux. Thus, in contrast to the volumetric model, the orientation, aggregation, and deformation of the RBCs lead mainly to changes in the medium scattering. In addition, an in vitro study by Njoum and Kyriacou [11] demonstrated the influence of the shear rate and clot formation on the registered PPG signal.
Finally, the model of PPG signal formation in which the key point is the elastic deformation of the microvascular bed and superficial layers of the dermis was recently proposed [12]. The model states that the pulse fluctuations in transmural blood pressure deform the components of connective tissues of the dermis, leading to periodic changes in both scattering and absorption. These local changes in the optical properties are further registered by a photodetector as variations in the backscattered light power. However, not all experimental observations support this theory. This indicates the potential presence of other reasons for the signal formation.
Meanwhile, recent work by Chatterjee et al. [13], based on Monte Carlo simulations and experimental observations, showed that all of the above factors occur in PPG signal formation. The question is the contribution of each individual factor to the signal depending on different parameters of tissue illumination (wavelength, measurement method, etc.). It is possible that, under certain conditions, one factor will dominate, whereas others will be insignificant. The most common measurement method in PPG is the reflectance mode, in which a light source and a detector are located on the same side of the sensor [14]. This mode allows measurements to be taken at more locations on the body, as opposed to transmittance mode, which is only applicable to certain locations, such as the fingertip and earlobe. Typically, LEDs at wavelengths of 525 nm, 660 nm, 770 nm, 810 nm, 940 nm, etc., are used as light sources. The most commonly used detector is a silicon photodiode, but other detectors, such as photocells and phototransistors, are also used [14]. There is also a non-contact PPG imaging technique in which CCD and CMOS cameras are used as detectors [15].
Understanding the mechanisms of PPG signal formation is important for interpreting pulse oximetry data and the physiological indices of the pulse waveform [16,17]. This is also important when modeling the PPG waveform using various methods, such as the numerical MC approach [18]. For a deep understanding of the mechanisms underlying the origin of the PPG signal, a fundamental knowledge of the processes of absorption and scattering of light in tissue and their influence on the registered optical flux is required. Thus, the aim of our study is the numerical simulation of the absorption and scattering processes in tissues to evaluate volumetric and aggregation effects.
This study was conducted as follows: In the first stage, we quantified the contribution of absorption and scattering changes to the registered PPG signal using the Monte Carlo (MC) modeling of light propagation in tissues. In the second stage, we verified the simulation results using clinical data and the Modified Beer–Lambert law (MBLL). Finally, we simulated the process of aggregation and disaggregation of RBCs for near-infrared (NIR) light and compared their impact with the blood volumetric effect.
2. Materials and Methods
2.1. Optical Model of the Tissue
The MC simulations were based on a previously developed three-layer optical model of the skin in backscattering geometry [19,20]. The skin was presented with the following layers: epidermis, dermis, and subcutaneous tissue (see Figure 1). The epidermis was 0.2 mm thick, the dermis was 0.7 mm thick, and the subcutaneous tissue was semi-infinite [21]. The dermis and hypodermis of the skin are characterized by a level of blood volume (Vb), which can be considered as the relative total hemoglobin fraction (Hb and HbO2) in the diagnostic volume of tissue. The absorption coefficients of each layer were presented as a sum of the absorption coefficients of the constituent chromophores, taking into account their volume fractions [13,22,23,24]:
where λ is the wavelength; Vmel is the volume fraction of melanin in the epidermis; Vw and Vb are the volume fractions of water and blood in the appropriate layer, respectively; µa,mel, µa,w, µa,b, and µa,fat are the absorption coefficients of melanin, water, blood, and fat, respectively; and µa,baseline is the baseline absorption coefficient, which characterizes the absorption of connective tissue in the absence of other chromophores. The absorption coefficient of whole blood, in turn, was expressed through tissue oxygen saturation StO2 as follows [13]:
where µa,HbO2 and µa,Hb are the absorption coefficients of oxygenated and deoxygenated hemoglobin, respectively.
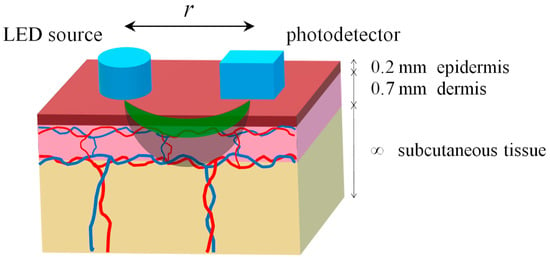
Figure 1.
Diagram of illumination and light propagation in the three-layer skin model. Green and gray colors conventionally indicate the areas of light penetration into the tissue for the green and NIR ranges, respectively.
The scattering coefficient of epidermal and subcutaneous tissue layers was determined by combining the Mie and Rayleigh theories [25]. Therefore, the scattering coefficient of the dermal layer was calculated as follows [26]:
where µs,t is the scattering coefficient of the bloodless dermis and µs,b is the scattering coefficient of whole blood. The scattering coefficient of the bloodless dermis, in turn, was also presented as a combination of Mie and Rayleigh scattering [22]:
where g is the anisotropy factor of the bloodless dermis.
2.2. Modeling of Variable Blood Volume
As known, the registered PPG signal consists of a slowly varying component (DC), which arises due to light absorption by immobile tissue structures, including an average blood volume level, and a variable component (AC), which is formed by arterial pulsations and blood flow. To simulate the AC component, it is enough to use two time points: diastole and systole. In order to unambiguously simulate the PPG signal recorded by a photodetector, it is necessary to model the propagation of photons in the medium for these two states. In diastole, there is a certain basic level of blood volume (Vb,0), and, in systole, an increment is added: Vb,0 + ΔVb. As the blood volume increases, the registered power of optical radiation decreases due to the stronger light absorption by blood. Thus, the signal in systole is less than the signal in diastole. As a rule, such a signal is inverted for more convenient perception and analysis.
In the first stage of this study, we numerically assessed the contribution of absorption and scattering variations to the total PPG signal. To accomplish this, we sequentially changed the optical properties of the dermis, since this layer makes the greatest contribution to signal formation [27]. In particular, first, we changed the absorption coefficient of the dermal layer by changing the Vb in (1). Then, we changed, in the same way, the scattering coefficient in (3). Finally, we changed the absorption and scattering together. The increase in the blood volume of the dermal layer relative to the baseline level (ΔVb/Vb,0) was 5%. This value is unknown in the literature and was selected due to a series of preliminary simulations. Thus, the values of the absorption and scattering coefficients of the second dermal layer were varied during the simulation. The absorption and scattering coefficients of the first and third layers were set to be constant.
2.3. Modeling of RBC Aggregation
To simulate the aggregation and disaggregation of RBCs, we determined the absorption and scattering coefficients of blood in the dermal layer as follows [10]:
where c(t) is the concentration of scatterers, σa(λ) is the absorption cross-section of RBCs, σs(λ) is the scattering cross-section of RBCs, and P = H·(1.4 − H) is the packing factor (H is the hematocrit value). The concentration of scatterers, in turn, can be defined as follows [10]:
where V is the volume of scatterers, V0 is the mean volume of one RBC, and NR is the number of RBCs in a rouleau. The absorption cross-section of RBCs depends on the tissue oxygen saturation in the following form [10]:
where σa,HbO2 and σa,Hb are the absorption cross-sections of oxygenated and deoxygenated hemoglobin, respectively.
Thus, by changing NR in (6), it is possible to simulate the change in the absorption and scattering of blood using Equation (5) and, thereby, the modulation of optical radiation backscattered from the tissue (which is the registered PPG signal). The average NR in one RBC aggregate for normal blood is 3 ± 2 [28], so we simulated the propagation of photons in the medium for a series of NR values (1, 2, 3, 4, and 5). During the aggregation and disaggregation of erythrocytes, the scattering cross-section also changes, but for simplicity, we assumed this parameter to be constant.
Considering Equations (5) and (6), we rewrote the expressions for the absorption and scattering coefficients of the dermal layer (1) and (3) into the following form:
Thus, the aggregation effect is now built into the volumetric model. If the size of the rouleaux does not change, then only variations in Vb remain, resulting in signal modulation. If NR changes over time, then two effects are present at once: aggregation and volumetric. The question is the contribution of each factor to the final registered signal. To answer this question, it is necessary to model these two effects separately.
2.4. Monte Carlo Simulation Parameters
In this work, we applied a numerical model based on the well-known principles of the MC simulation of photon transport in biological tissues and used a photon weighting technique [29]. To improve computation accuracy, a disk-detector geometry was used to compute backscattered fluxes [30]. A round source with a diameter of 1 mm and a 1 × 1 mm square detector was used to closely match the configuration of real PPG sensors. In the simulation, 109 photon packets were launched in the medium. The simulation result was the backscattered optical flux, computed relative to the incident flux illuminating the tissue. The calculations were conducted for two wavelengths, 525 nm and 810 nm, since the optical properties of the tissue at these wavelengths are very different. Using isosbestic points eliminates the dependence of the results on the blood oxygen saturation. We also varied the basic level of the dermal blood volume (Vb,0 = 0.05, 0.1, and 0.15 rel. units) and the source–detector distance (r). Green light is strongly absorbed by the medium, which does not allow the source and the detector to be moved far apart from each other since, at large distances, the registered flux is very weak. In our calculations, an acceptable signal level can be achieved up to approximately 5 mm for green light and 10 mm for NIR light. Thus, the source–detector separation was varied from 1 to 5 mm for 525 nm and from 1 to 10 mm for 810 nm. The simulations were performed in Matlab 2022 software (MathWorks, Portola Valley, CA, USA). As a final result, we calculated the AC/DC ratio of the PPG signal as follows [19]:
where Fluxdiast is the backscattered flux at the diastole and Fluxsyst is the backscattered flux at the systole.
The optical properties of the main chromophores included in skin layers were taken from known literature sources for MC simulation [22,31,32,33]. The tissue oxygen saturation was set at 75% when calculating the absorption coefficient of whole blood using Equation (2). The anisotropy factor and the refractive index were assumed to be 0.8 and 1.4, correspondingly, for all skin layers [34]. The optical and anatomical parameters of skin layers are presented in Table 1. The optical and anatomical properties of RBCs were taken from [35] (see Table 2).

Table 1.
Optical and anatomical parameters of the skin model layers used in MC modeling.

Table 2.
Optical and anatomical parameters of erythrocytes at a wavelength of 810 nm used to model the aggregation effect.
2.5. Modified Beer–Lambert Law Usage
To verify our MC results, we carried out an analytical assessment of blood volume changes (ΔVb) based on the Modified Beer–Lambert law (MBLL). Unlike the classical Beer–Lambert law, the modified version is suitable for the reflectance measurement mode, i.e., for our case. To apply the MBLL, we presented the skin as a single-layer homogeneous medium, the optical properties of which are equivalent to those of the dermal layer. The differential form of the MBLL, as revised by Kocsis, can be written as follows [36]:
where ΔA is the attenuation (optical density) change between two different states of the tissue (in our case, these are diastole and systole); L is the mean optical path length of the detected photons; K is the coefficient depending on the measurement geometry and optical properties of the medium; and µ′s = μs (1g) is the reduced scattering coefficient. In our study, the attenuation change is defined as follows:
where Idiast is the registered light intensity in diastole and Isyst is the light intensity in systole. The coefficient K can be determined based on the diffusion approximation for a homogeneous semi-infinite medium as follows [36]:
where
µa,0 and µ′s,0 are the initial values of the absorption and reduced scattering coefficients, i.e., at the moment of diastole. The increments in the absorption and scattering coefficients can be represented using Equations (1) and (3) in the following form:
Substituting (14) into (10), it is easy to determine the change in blood volume:
Equation (15) allows us to estimate the increase in blood volume separately, due to absorption if we use the first term in the denominator, scattering (the second term), and both processes together if we use both terms. The mean optical path length L can be estimated from the results of the MC simulations. ΔA can be measured experimentally using (11) during in vivo PPG examinations.
2.6. Clinical PPG Data Collection
To obtain the real optical density of skin (ΔA), we recorded raw PPG signals from healthy subjects using a previously developed perfusion measuring device operating in the PPG mode [37]. Various optical sensors operating at different wavelengths can be connected to the device. In this study, we used an optical sensor that included three green LEDs with a peak emission wavelength of 525 nm (BL-L324PGC, Betlux Electronics, Ningbo, China) and three near-infrared LEDs with a peak wavelength of 810 nm (IR-810-350C1, Power Light Systems, Berlin, Germany). The LEDs were arranged radially around the silicon photodiode (TEFD4300, Vishay, Malvern, Pennsylvania, USA) at a distance of 5 mm (see Figure 2a).
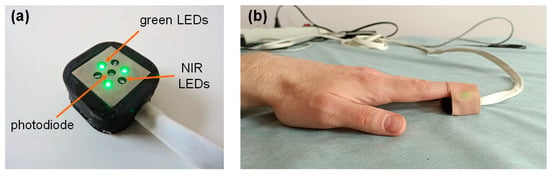
Figure 2.
The optical sensor used in this study (a); and attachment of the sensor to the subject’s fingertip during the measurements (b).
The measurements were carried out on seven healthy volunteers (five males and two females) without cardiovascular diseases. The average age of the subjects was 29 ± 7 years. The signals were recorded in a supine position at rest. The raw PPG signals at both wavelengths were recorded from the tip of the left index finger for 60 s with a sampling rate of 320 Hz and then stored on a computer for further processing (see Figure 2b). The recorded signals were processed in the LabView 2017 program (National Instruments, Austin, USA). Before calculating ΔA using Equation (11), the signals were preprocessed using a second-order low-pass Butterworth filter with a cutoff frequency of 10 Hz [38]. The experimental data were presented as the median [LQ, UQ], where LQ is the lower quartile and UQ is the upper quartile.
The clinical procedures were performed in accordance with the ethical principles of the Declaration of Helsinki and were approved by the Independent Ethics Committee of the Moscow Regional Research and Clinical Institute named after M.F. Vladimirsky (protocol no. 16, dated 15 December 2022). All participants gave their informed consent prior to their inclusion in this study.
3. Results
3.1. Contribution of Absorption and Scattering Variations to the PPG Signal
The results of the MC simulation in the form of the AC/DC ratio of the PPG signal formed by blood volume variations are presented in Figure 3. For the wavelength of 525 nm, a clear predominance of absorption in the signal formation was observed. In contrast, for the wavelength of 810 nm, the situation was exactly the opposite—scattering predominates over absorption. This relationship is observed uniformly for all source–detector distances (r). The AC/DC ratio increases with r for both wavelengths. Herewith, this dependence is more nonlinear for the 810 nm wavelength. This is a predictable result, since it has been confirmed experimentally in previous studies [19]. As for the dependence of the AC/DC ratio on the blood volume, a similar and expected result was also observed—AC/DC grows with an increasing Vb. This is explained by the fact that the larger the Vb, the smaller the DC component and, therefore, the larger the AC/DC ratio.
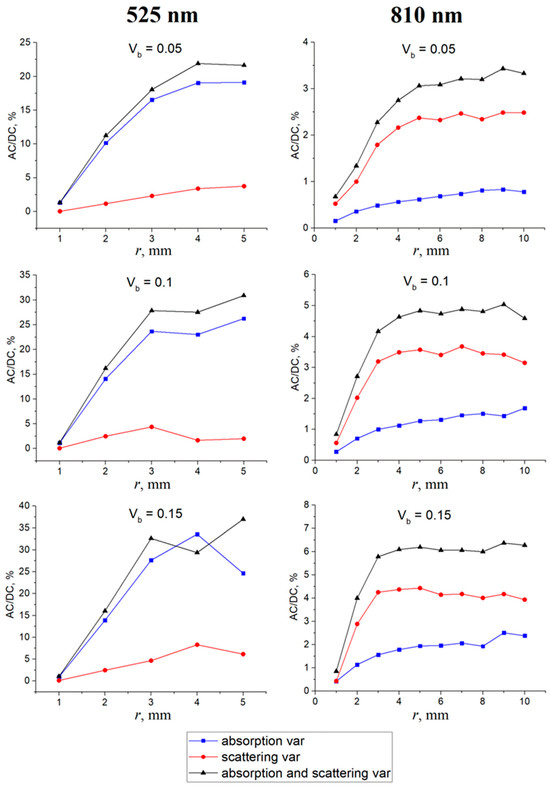
Figure 3.
AC/DC ratio of the PPG signal as a function of the source–detector distance (r) for different Vb values when changing the absorption of the medium (the blue curve), the scattering (the red curve), and the absorption and scattering simultaneously (the black curve). The results are shown for wavelengths of 525 nm (left) and 810 nm (right).
In order to numerically evaluate the contribution of each process (absorption and scattering) in signal formation, we divided the AC/DC values of the corresponding process by the AC/DC value of the total signal and averaged over all Vb and r levels. The total signal corresponds to a situation in which the absorption and scattering change together (the black curve in Figure 3). The results obtained are shown in Figure 4. For green light, the contributions of absorption and scattering to the total PPG signal were 88 ± 6% and 12 ± 5%. For NIR light, the contributions of absorption and scattering were 28 ± 5% and 72 ± 4%, respectively. Thus, green light is mainly modulated by absorption variations, which is consistent with the volumetric model. On the contrary, NIR light mainly changes due to variations in scattering.
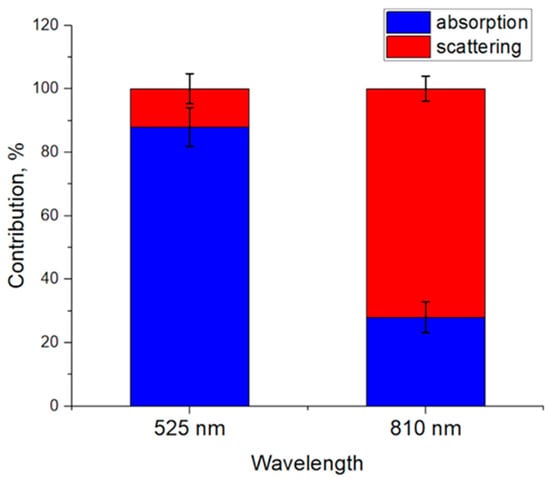
Figure 4.
Contribution of absorption and scattering variations to the PPG signal averaged over all Vb and r values. Data are presented as the average ± standard deviation.
3.2. Verification of MC Results Using Experimental Data and MBLL
To verify our theoretical results, we recorded the raw PPG signals from healthy subjects and numerically estimated the blood volume increments based on the MBLL. An example of the recorded signals at both wavelengths is presented in Figure 5a. The AC/DC ratio of the experimental signals was calculated for all subjects and was 5.65 [4.4, 9.27]% for green light and 1.55 [0.74, 2.51]% for NIR light (Figure 5b). The amplitude of the AC component mainly depends on the simulated increment of Vb in the dermal layer. In the simulation, we used an increment in the blood volume relative to the baseline (ΔVb/Vb,0) equal to 5%. As this value decreases, the AC/DC ratio also decreases. Thus, the AC/DC values simulated by MC converge to the experimental data at low Vb and ΔVb/Vb,0 values. At the same time, the relationship between the two wavelengths is also preserved.
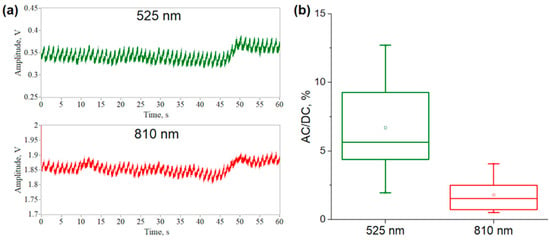
Figure 5.
An example of the recorded raw PPG signals at two wavelengths (a); and the calculated AC/DC ratio of signals for seven healthy subjects (b).
Next, we assessed the increment in blood volume based on real PPG signals using Equation (15) in three ways: only absorption, only scattering, and absorption and scattering together. The mean optical paths L for both wavelengths were calculated from the MC simulations at r = 5 mm. L was 1.07 cm for 525 nm and 1.59 cm for 810 nm. The obtained results are presented in Figure 6. It is logical to assume that an estimate based on absorption and scattering should give the most accurate result. As can be seen, such a calculation gives the same ΔVb value for the cases of green and NIR light. Hence, the calculation based only on scattering greatly overestimates the ΔVb value for green light. In contrast, an estimate based only on absorption is practically no different from the result based on absorption and scattering together. The exact opposite situation was obtained for NIR light. The absorption-based calculation overestimates the result, but the scattering-based estimate converges to the correct value.

Figure 6.
Estimates of the change in blood volume between diastole and systole, calculated using the MBLL and experimental data while taking into account only absorption of the medium (the blue boxes), only scattering (the red boxes), and absorption and scattering together (the black boxes).
The obtained result is consistent with the MC numerical data (see Figure 4). It confirms that the PPG signal at green light is modulated mainly due to variations in absorption, and, in the NIR range, due to changes in scattering. It is worth noting that this result is also consistent with our previous study [39], in which we analytically assessed the contribution of absorption and scattering to the PPG signal based on the MBLL. Thus, all these results of our numerical and analytical calculations agree with each other.
At this stage of our study, we simulated the change in scattering of the dermal layer due to variations in Vb according to the volumetric model. However, scattering can also be altered by other processes, for example, the aggregation and disaggregation of RBCs, which can lead to the same changes in the scattering coefficient. Thus, we have two hypotheses about the formation of a PPG signal in the NIR wavelength range: (1) the volumetric effect—due to changes in the concentration of scatterers in the diagnostic volume of tissue during the inflow and outflow of blood, and (2) due to the aggregation/disaggregation of erythrocytes. Therefore, the goal of the final stage of this study is to model RBC aggregation and compare it with the volumetric effect.
3.3. Modeling of the Aggregation Effect for NIR Light
At the final stage of this study, we simulated the formation of the PPG signal due to the aggregation and disaggregation of RBCs using Equations (5) and (6). In this case, the AC signal component is formed due to changes in the size of the aggregates during diastole and systole. We believe that, in diastole, RBCs aggregate due to a decrease in shear rate, and, in systole, they disaggregate due to the influx of a pressure wave. The results of the MC simulation of the aggregation and disaggregation of RBCs are shown in Figure 7. Figure 7a illustrates the dependence of the AC/DC ratio on the source–detector distance when the rouleau size (NR) changes from one to three cells. As can be seen, the main contribution to the signal formation comes from scattering variations, as well as from the volumetric effect (see Figure 3). Thus, this further confirms our result that the PPG signal at 810 nm is formed mainly by changes in scattering processes. It does not matter through what mechanism (volumetric or aggregation) these changes are formed.
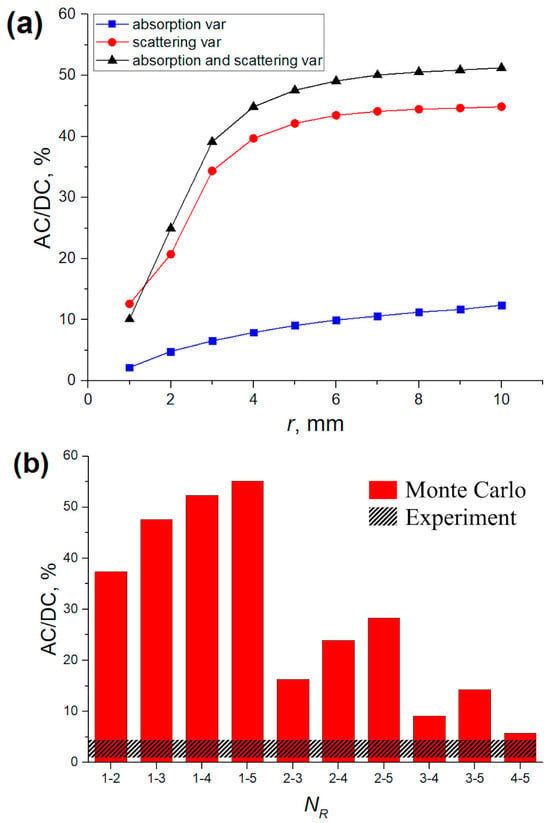
Figure 7.
AC/DC ratio of the PPG signal versus source–detector distance (r) when the number of erythrocytes in the rouleaux (NR) changes from one to three (a), and for different changes in NR at r = 5 mm (b). Calculations were performed for a wavelength of 810 nm at fixed Vb = 0.05 rel. units.
Figure 7b shows the AC/DC ratio for various options for changing NR during the aggregation/disaggregation of erythrocytes at a fixed source–detector distance (r = 5 mm, as in the experiment). The representation of NR through a hyphen shows a change in the rouleau size, which led to the formation of a variable PPG component. For example, NR = 25 means that the number of RBCs in the rouleaux changed from two to five during aggregation. The highest AC/DC ratio is observed when changing the rouleau size to one RBC. The experimental AC/DC ratio values are shown as the gray shaded area. This difference in numerical and experimental data is explained by the fact that not all RBCs in the blood form aggregates, but only a certain proportion. In the simulation, we assumed that all erythrocytes in the measured tissue volume formed rouleaux. We did not find in vivo data in the literature on what proportion of RBCs in the dermal layer of the skin form aggregates during the passage of a pulse wave in a normal state. Thus, a quantitative assessment of the influence of volumetric and aggregation effects on the PPG signal is currently very difficult. However, Figure 7 demonstrates the high sensitivity of the backscattered signal to the aggregation process.
Nevertheless, we can evaluate the sensitivity of the scattering of the medium to volumetric and aggregation changes. To accomplish this, it is necessary to differentiate the scattering coefficient of the dermal layer with respect to Vb and NR. After differentiation, we obtain the following:
It should be noted that the derivative of µs,derm with respect to NR depends on the blood volume. The simulated dependences of the derivatives of the scattering coefficient on NR are presented in Figure 8. The dependence of ∂µs,derm/∂Vb on NR was plotted for different values of the scattering cross-section (40, 60, 80 µm2), since it can vary depending on the shape and oxygenation of RBCs [35]. The hematocrit and average volume of RBCs are not very variable from subject to subject. The dependence of ∂µs,derm/∂NR on NR was plotted for different values of Vb (0.05, 0.15, and 0.3 rel. units).
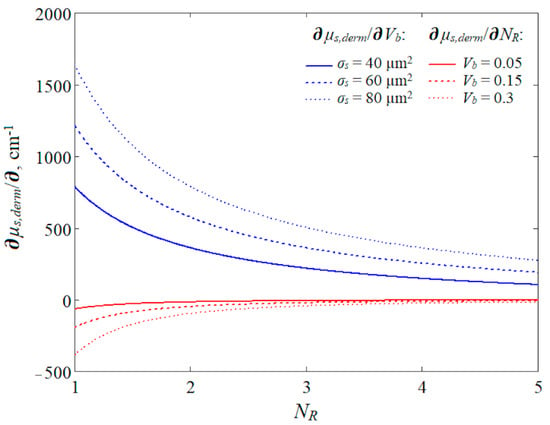
Figure 8.
Relationship between derivatives of the scattering coefficient of the dermal layer and the number of RBCs in aggregates (NR) at 810 nm. The derivative of the scattering coefficient with respect to the blood volume is shown by the blue lines and the derivative with respect to NR is shown by the red lines.
Figure 8 shows that the scattering coefficient is more sensitive to changes in the blood volume than the aggregation effect. However, the relationships were constructed for specific tissue optical properties and, thus, do not consider the intra- and inter-individual variability of optical properties. For example, the derivative with respect to Vb also depends on the scattering coefficient of the bloodless dermis (see Equation (16)). Thus, it cannot be stated unambiguously that the volumetric effect prevails over the aggregation one. In addition, Figure 8 reveals the opposing mechanisms of PPG signal formation for these two effects. Within the volumetric effect, the inflow of blood at systole causes an increase in the medium scattering as a whole since the scattering coefficient of blood is greater than that of the bloodless tissue. An increase in scattering leads to a decrease in the registered PPG signal. Within the aggregation effect, the disaggregation of erythrocytes occurs (a decrease in NR) at systole and increases the concentration of scatterers inside the blood. This also leads to a drop in the recorded signal. However, the magnitude of the aggregation effect depends on the average level of Vb, which is a completely logical and predictable result (see the red lines in Figure 8). Thus, in our opinion, the volumetric and aggregation effects are interdependent processes that should be considered together as approximately equal.
4. Discussion
In this study, we investigated the issue of the PPG signal origin, taking into account several fundamental optical processes of light interaction with biological tissues, namely, absorption and scattering. For the first time, we quantitatively assessed the contribution of absorption and scattering variations to the recorded PPG signal for two wavelength ranges: green and NIR. This is one of the advantages of our study; we did not find such data in the literature. The MC simulations were carried out for different baseline blood volume levels in the dermal layer of the skin. However, we did not study the dependence of the parameters of the registered signals on the melanin content in the skin. Melanin is known to strongly influence optical signals, especially in the green waveband [27]. In the modeling, we used a fixed melanin value in the epidermis equal to 0.05 rel. units, which is the average value for Caucasian people. Accordingly, we included only people with fair skin in the experiment. This can be considered a limitation of our study. We also simulated with MC the aggregation and disaggregation of RBCs applied to PPG for the first time and assessed its effect on the registered signal.
Based on theoretical and experimental investigation, we can conclude the applicability of signal formation models in PPG. Overall, our results are consistent with a study [6] that stated that the volumetric model is valid over the entire wavelength range from 450 to 1000 nm. However, our results show that in the NIR range, both volumetric and aggregation effects are mixed. There is a series of in vitro studies that have shown the effect of RBC aggregation on the PPG signal [9,11]. In particular, in a recent study by Rovas et al. [40], the authors quantified the effects of erythrocyte disorientation and aggregation using a silicone model of a radial artery. Their theoretical model based on pressure and flow rate yielded more accurate predictions than the model using pressure alone. These results indicate that flow rate-related RBC disorientation and aggregation significantly influence the PPG signal. Our results are in good agreement with this study.
It is worth noting that in vitro studies make it possible to separate the volumetric and aggregation effects, for example, by introducing substances that change RBC aggregation (Dextran, Poloxamer 188, and others). With in vivo measurements, this seems to be a more difficult task since the microvascular bed of skin is a complex and heterogeneous structure. For example, Fine and Kaminsky in their study [10] pinched the fingertip with a cuff and observed a difference in the shape of the oscillometric (volumetric) and PPG signals after applying a certain pressure, as well as the appearance of a time delay between them. This could potentially be used to separate these two effects and evaluate the aggregation process. Our further research will aim to achieve this separation for in vivo measurements.
5. Conclusions
Based on the MC simulation, it was found that for green light (525 nm), absorption predominates over scattering in the formation of the PPG signal. However, for NIR light (810 nm), scattering prevails over absorption. The obtained result clarifies the mechanism of PPG signal formation at different wavelength ranges. We can conclude that, for the green waveband, the classical volumetric model of the signal formation is fully valid, whereas for NIR light, the scattering-driven model is feasible [10]. Moreover, in the latter case, both volumetric and aggregation effects are responsible for signal formation.
Author Contributions
Conceptualization, D.G.L.; methodology, D.G.L. and D.A.R.; software, A.P.T.; validation, D.G.L.; formal analysis, D.G.L. and D.A.R.; investigation, D.G.L. and M.E.S.; data curation, D.G.L.; writing—original draft preparation, D.G.L. and M.E.S.; writing—review and editing, A.P.T. and D.A.R.; and project administration, D.G.L. and D.A.R. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Institutional Review Board Statement
This study was conducted in accordance with the Declaration of Helsinki and approved by the Independent Ethics Committee of Moscow Regional Research and Clinical Institute named after M.F. Vladimirsky (protocol no. 16, dated 15 December 2022).
Informed Consent Statement
Informed consent was obtained from all subjects involved in this study.
Data Availability Statement
Data can be made available on request.
Conflicts of Interest
The authors declare no conflicts of interest.
References
- Allen, J. Photoplethysmography and its application in clinical physiological measurement. Physiol. Meas. 2007, 28, R1–R39. [Google Scholar] [CrossRef] [PubMed]
- Kamal, A.A.R.; Harness, J.B.; Irving, G.; Mearns, A.J. Skin photoplethysmography—A review. Comput. Methods Programs Biomed. 1989, 28, 257–269. [Google Scholar] [CrossRef] [PubMed]
- Elgendi, M. On the analysis of fingertip photoplethysmogram signals. Curr. Cardiol. Rev. 2012, 8, 14–25. [Google Scholar] [CrossRef]
- Kyriacou, P.A.; Chatterjee, S. The origin of photoplethysmography. In Photoplethysmography; Allen, J., Kyriacou, P., Eds.; Academic Press: New York, NY, USA, 2022; pp. 17–43. [Google Scholar]
- Reisner, A.; Shaltis, P.A.; McCombie, D.; Asada, H.H.; Warner, D.S.; Warner, M.A. Utility of the photoplethysmogram in circulatory monitoring. J. Amer. Soc. Anesth. 2008, 108, 950–958. [Google Scholar] [CrossRef] [PubMed]
- Moço, A.V.; Stuijk, S.; de Haan, G. New insights into the origin of remote PPG signals in visible light and infrared. Sci. Rep. 2018, 8, 8501. [Google Scholar] [CrossRef]
- Nijboer, J.A.; Dorlas, J.C.; Mahieu, H.F. Photoelectric plethysmography-some fundamental aspects of the reflection and transmission methods. Clin. Phys. Physiol. Meas. 1981, 2, 205. [Google Scholar] [CrossRef]
- Lindberg, L.G.; Oberg, P.A. Optical properties of blood in motion. Opt. Exp. 1993, 32, 253–257. [Google Scholar] [CrossRef]
- Shvartsman, L.D.; Fine, I. Optical transmission of blood: Effect of erythrocyte aggregation. IEEE Trans. Biomed. Eng. 2003, 50, 1026–1033. [Google Scholar] [CrossRef]
- Fine, I.; Kaminsky, A. Scattering-driven PPG signal model. Biomed. Opt. Exp. 2022, 13, 2286–2298. [Google Scholar] [CrossRef]
- Njoum, H.; Kyriacou, P.A. Photoplethysmography for the Assessment of Haemorheology. Sci. Rep. 2017, 7, 1406. [Google Scholar] [CrossRef]
- Kamshilin, A.A.; Nippolainen, E.; Sidorov, I.S.; Vasilev, P.V.; Erofeev, N.P.; Podolian, N.P.; Romashko, R.V. A new look at the essence of the imaging photoplethysmography. Sci. Rep. 2015, 5, 10494. [Google Scholar] [CrossRef] [PubMed]
- Chatterjee, S.; Budidha, K.; Kyriacou, P. Investigating the origin of photoplethysmography using a multiwavelength Monte Carlo model. Physiol. Meas. 2020, 41, 084001. [Google Scholar] [CrossRef]
- Mejia-Mejia, E.; Allen, J.; Budidha, K.; El-Hajj, C.; Kyriacou, P.A.; Charlton, P.H. Photoplethysmography signal processing and synthesis. In Photoplethysmography; Academic Press: New York, NY, USA, 2022; pp. 69–146. [Google Scholar] [CrossRef]
- Merlo, S.; Bello, V.; Bodo, E.; Pizzurro, S. A VCSEL-Based NIR Transillumination System for Morpho-Functional Imaging. Sensors 2019, 19, 851. [Google Scholar] [CrossRef] [PubMed]
- Nitzan, M.; Ovadia-Blechman, Z. Physical and physiological interpretations of the PPG signal. In Photoplethysmography; Academic Press: New York, NY, USA, 2022; pp. 319–340. [Google Scholar] [CrossRef]
- Moscato, S.; Palmerini, L.; Palumbo, P.; Chiari, L. Quality Assessment and Morphological Analysis of Photoplethysmography in Daily Life. Front. Digit. Health 2022, 4, 912353. [Google Scholar] [CrossRef] [PubMed]
- Boonya-Ananta, T.; Rodriguez, A.J.; Ajmal, A.; Du Le, V.N.; Hansen, A.K.; Hutcheson, J.D.; Ramella-Roman, J.C. Synthetic photoplethysmography (PPG) of the radial artery through parallelized Monte Carlo and its correlation to body mass index (BMI). Sci. Rep. 2021, 11, 2570. [Google Scholar] [CrossRef] [PubMed]
- Lapitan, D.G.; Tarasov, A.P.; Rogatkin, D.A. Justification of the photoplethysmography sensor configuration by Monte Carlo modeling of the pulse waveform. J. Biomed. Photonics Eng. 2022, 8, 030306. [Google Scholar] [CrossRef]
- Lapitan, D.G.; Tarasov, A.P.; Rogatkin, D.A. Dependence of the registered blood flow in incoherent optical fluctuation flowmetry on the mean photon path length in a tissue. Photonics 2023, 10, 190. [Google Scholar] [CrossRef]
- Reuss, J.L. Multilayer modeling of reflectance pulse oximetry. IEEE Trans. Biomed. Eng. 2005, 52, 153–159. [Google Scholar] [CrossRef] [PubMed]
- Jacques, S.L. Skin Optics Summary. Oregon Medical Laser Center News. 1998. Available online: https://omlc.org/news/jan98/skinoptics.html (accessed on 23 November 2023).
- Saidi, I.S. Transcutaneous Optical Measurement of Hyperbilirubinemia in Neonates. PhD. Thesis, Rice University, Houston, TX, USA, 1992. [Google Scholar]
- Meglinski, I.V.; Matcher, S.J. Computer simulation of the skin reflectance spectra. Comput. Methods Programs Biomed. 2003, 70, 179–186. [Google Scholar] [CrossRef]
- Jacques, S.L. Optical properties of biological tissues: A review. Phys. Med. Biol. 2013, 58, R37–R61. [Google Scholar] [CrossRef]
- Cui, W.; Ostrander, L.E.; Lee, B.Y. In vivo reflectance of blood and tissue as a function of light wavelength. IEEE Trans. Biomed. Eng. 1990, 37, 632–639. [Google Scholar] [CrossRef] [PubMed]
- Chatterjee, S.; Kyriacou, P.A. Monte Carlo Analysis of Optical Interactions in Reflectance and Transmittance Finger Photoplethysmography. Sensors 2019, 19, 789. [Google Scholar] [CrossRef] [PubMed]
- Yeom, E.; Lee, S.J. Microfluidic-based speckle analysis for sensitive measurement of erythrocyte aggregation: A comparison of four methods for detection of elevated erythrocyte aggregation in diabetic rat blood. Biomicrofluidics 2015, 9, 024110. [Google Scholar] [CrossRef]
- Wang, L.; Jacques, S.L.; Zheng, L. MCML—Monte Carlo modeling of light transport in multi-layered tissues. Comput. Meth. Programs Biomed. 1995, 47, 131–146. [Google Scholar] [CrossRef]
- Tarasov, A.P. Acceleration of Monte Carlo simulation of light transport in tissues using disk-detector geometry in the backscattering problem. In Proceeding of the 2020 International Conference Laser Optics (ICLO), St. Petersburg, Russia, 2–6 November 2020; p. 1. [Google Scholar] [CrossRef]
- Bosschaart, N.; Edelman, G.J.; Aalders, M.C.; van Leeuwen, T.G.; Faber, D.J. A literature review and novel theoretical approach on the optical properties of whole blood. Lasers Med. Sci. 2014, 29, 453–479. [Google Scholar] [CrossRef] [PubMed]
- Hale, G.M.; Querry, M.R. Optical constants of water in the 200-nm to 200-m wavelength region. Appl. Opt. 1973, 12, 555–563. [Google Scholar] [CrossRef] [PubMed]
- Simpson, C.R.; Kohl, M.; Essenpreis, M.; Cope, M. Near-infrared optical properties of ex vivo human skin and subcutaneous tissues measured using the Monte Carlo inversion technique. Phys. Med. Biol. 1998, 43, 2465–2478. [Google Scholar] [CrossRef] [PubMed]
- Salomatina, E.; Jiang, B.; Novak, J.; Yaroslavsky, A.N. Optical properties of normal and cancerous human skin in the visible and near-infrared spectral range. J. Biomed. Opt. 2006, 11, 064026. [Google Scholar] [CrossRef]
- Bi, L.; Yang, P. Modeling of light scattering by biconcave and deformed red blood cells with the invariant imbedding T-matrix method. J. Biomed. Opt. 2013, 18, 055001. [Google Scholar] [CrossRef]
- Kocsis, L.; Herman, P.; Eke, A. The modified Beer–Lambert law revisited. Phys. Med. Biol. 2006, 51, N91. [Google Scholar] [CrossRef]
- Lapitan, D.G.; Rogatkin, D.A. Optical incoherent technique for noninvasive assessment of blood flow in tissues: Theoretical model and experimental study. J. Biophotonics 2021, 14, e202000459. [Google Scholar] [CrossRef] [PubMed]
- Lapitan, D.G.; Rogatkin, D.A.; Molchanova, E.A.; Tarasov, A.P. Estimation of phase distortions of the photoplethysmographic signal in digital IIR filtering. Sci. Rep. 2024, 14, 6546. [Google Scholar] [CrossRef] [PubMed]
- Lapitan, D.G.; Tarasov, A.P. Analytical assessment of the modulation depth of photoplethysmographic signal based on the modified Beer-Lambert law. In Proceedings of the 2019 IEEE 8th International Conference on Advanced Optoelectronics and Lasers (CAOL), Sozopol, Bulgaria, 6–8 September 2019; pp. 103–106. [Google Scholar] [CrossRef]
- Rovas, G.; Bikia, V.; Stergiopulos, N. Quantification of the Phenomena Affecting Reflective Arterial Photoplethysmography. Bioengineering 2023, 10, 460. [Google Scholar] [CrossRef] [PubMed]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).