Abstract
Purpose: To assess the possible impact of minor changes in fixation on wavefront measurements as a potential constraint in detecting subtle temporal variations in ocular wavefront error. Methods: Twelve healthy subjects with an average age of 36.3 ± 8.8 were instructed to put their heads in the aberrometer’s chin-rest and look at a fixation target that was embedded in the device. The fixation targets were readily observable to the participants without accommodation, thanks to the aberrometer’s Badal system. When each eye was staring at the target, its wavefront aberration was recorded three times and then averaged for further analysis. The averaged Zernike coefficients were rescaled to the smallest value of the maximum round pupil found among all eyes (4.41 mm), and this procedure was repeated for each target. Results: Alteration of the fixation targets caused changes to the Zernike coefficients of defocus (C(2,0)), vertical trefoil (C(3,–3)), vertical coma (C(3,–1)), horizontal coma (C(3,1)), oblique trefoil (C(3,3)), primary spherical aberration (C(4,0)), and secondary spherical aberration (C(6,0)), but the changes were not statistically significant. Nevertheless, an alteration in the target’s size and shape exhibited a significant correlation across all of the aforementioned coefficients in both eyes (p < 0.05). The total RMS of aberrations and the RMS of the spherical-like aberrations were both lowest while choosing the larger Maltese cross, and the bigger E-letter minimized the RMS of HOA and comatic aberrations. Conclusion: The aberrometric changes occur as a consequence of altering the fixational gaze and are within the range of the changes found after performing a near-vision task, so they might potentially act as a confounding factor when attempting to identify such small variations in the ocular wavefront. Using a smaller E-letter (5 arcmin) as an internal fixation target resulted in the least standard deviation of measurements, fixational stability, and higher accuracy in ocular wavefront measurements.
1. Introduction
Humans have the ability to fixate their eyes on a specific point for very long periods of time. However, the eyes still make small unconscious movements (microsaccades, tremor, and drift) even when they seem to be fixed on a visual target [1]. In many traditional vision tests, subjects are required to gaze at a specific target. For this reason, fixation targets play a crucial role in ensuring the accuracy, reliability, and standardization of eye examinations. Fixating might be problematic during experiments with prolonged periods of fixation [2]. The alteration in properties of the fixation target, such as color, brightness, and luminance has little impact on fixational eye movements [3], compared to the change in its size [4,5]. Among the properties, the shape of a fixation target is also modifiable in experiments. Thaler et al. [6] studied the effect of seven commonly used target shapes in their experiments.
To the best of the authors knowledge, the impact of an aberrometer’s fixation target size and shape on the ocular wavefront error has not yet been investigated. An aberrometer is a device used to assess the wavefront aberration of the eye in terms of Zernike polynomials. Like many ophthalmic devices, it also utilizes a fixation target, inside of which subjects should gaze while measuring their ocular wavefront. The change in the size and shape of the fixation target might cause small angle misalignments.
Undoubtedly, alignment is a fundamental aspect of optical systems, including aberrometers, and misalignment may affect the obtained results. Applegate et al. [7] emphasized that the measurement axis of the aberrometer must match the line of sight. Refractive surgery and designing contact lenses or intraocular lenses (IOLs) are affected by the aberrometric errors imposed by fixational eye movements. Padmanabhan et al. [8] conducted a study to evaluate the wavefront profiles and refractive outcomes of eyes in two groups: corrected eyes in which the applied ablation was decentered, and eyes where the applied ablation was centered. Their results demonstrated that the induced aberrations in the eyes that underwent decentered ablation were of a larger magnitude, and the visual acuity in these eyes was lower than in the well-centered ablated eyes. The extent of accommodation-induced lens decentration has been estimated using higher-order aberrations (HOA) by He and Applegate [9]. Fedtke et al. [10] showed that the decentered contact lenses resulted in the prevalence of third-order aberrations. Another study found an increase in wavefront aberrations and a decline in optical performance when IOLs experienced decentration and tilt [11]. McKelvie et al. [12] demonstrated that the tilt and decentration of intraocular lenses are among the elements that affect the higher-order aberrations. Achieving precise fixation, ensuring the adequate alignment of equipment, and properly determining the location of the pupil center are mentioned as crucial factors in reducing measurement variability and obtaining accurate measurements of higher-order wavefront error [13]. Mecê et al. [14] used a custom-built real-time Hartmann–Shack sensor to study the dynamics of ocular aberrations and conclude that fixational eye movements are unlikely to change the wavefront aberrations. Arines et al. [15] modeled two synthetic eyes that had distinct static aberrations and different amounts of HOA, with their movements following numerous trajectories. They reported that the estimated coefficients are affected by the fixational motions of eyes. Considering a simulated group of keratoconic wavefronts, Rio et al. [16] investigated the effect of misalignment on the image quality and found that when the misalignment was present, the mean root mean square (RMS) of HOA was in the levels reported in keratoconic patients who wear rigid gas permeable contact lenses.
The objective of this research was to examine how small random deviations in alignment when using larger fixation targets affect the wavefronts of the eye, as measured using a Shack–Hartmann aberrometer.
2. Methods
2.1. Materials
The IRX3 commercial Shack–Hartmann aberrometer (Imagine Eyes, Orsay, France) was used in this study to record the ocular wavefront (Figure 1). The Shack–Hartmann technique is the most often used wavefront-sensing method for assessing the optical quality of the eye [17]. In this procedure, when a subject is gazing at the fixating target that is placed inside the device, a laser beam is sent into the eye and it is reflected back from the fovea while its wavefront is aberrated due to the optics of the eye. Then, the beam is divided into multiple beams passing through an array of microlenslets, so beam spots can be recorded on a charge-coupled device. In order to determine the shape of the wavefront, one can compare the position of each spot to its non-distorted location; displacements in the x and y directions are related to the local derivative (slope) of the wavefront [18]. For the given pupil size, the device’s software can fit the observed wavefront and generate Zernike coefficients.

Figure 1.
IRX3 Shack–Hartmann aberrometer used in this study (Imagine Eyes, France).
Beside the original E-letter fixation target (10 arcmin in size, hereafter is called “E”) placed by the manufacturer inside the aberrometer, a smaller E-letter (5 arcmin, hereafter “e”), together with a bigger and a smaller Maltese cross (10 and 5 arcmin, hereafter is called “X” and “x”, respectively), were replaced as the fixation targets (as shown in Figure 2) in random order to find the effect of the fixation target’s shape and size on ocular aberrations.

Figure 2.
Different fixation targets used while measuring eyes aberrations: (a) bigger E-letter; (b) smaller E-letter; (c) bigger Maltese cross; (d) smaller Maltese cross.
2.2. Subjects and Experimental Conditions
The study group consisted of 12 healthy subjects with ages ranging from 26 to 50 years (mean 36.3 ± 8.8) who were asked to position their head in the chin-rest of the aberrometer and gaze on a fixation target inside the device. The refractive errors of the subjects were compensated with the help of the Badal system of the aberrometer, so they could observe the fixation targets clearly without wearing vision aids and without accommodation. The wavefront aberration of each eye was recorded in triplicate while looking at the target, and the mean of them was used for subsequent analysis. The aberrometric data obtained from the all eyes were rescaled to the smallest value of the maximum round pupil found among them (4.41 mm) for further analysis. This process was repeated for all of the targets and the ocular wavefronts were collected in terms of Zernike polynomials. The order of changing the fixation targets was random.
2.3. Statistical Analysis
For the data analysis, we utilized SPSS 25 statistical software (SPSS Inc., IBM Corporation, Endicott, NY, USA). To show the changes, we used Excel 2019 (Microsoft Corporation, Redmond, WA, USA). Due to the non-normal distributions of almost all the parameters, we used the Spearman correlation test to identify statistically significant correlation among parameters which were reported using a p-value, and Wilcoxon’s pairwise comparison was used to find statistically significant differences among the Zernike coefficients and some of the RMS data after fixation target alteration; in some of the RMS data that were following a normal distribution, a paired t-test was used to find a significant difference after fixation target change. The medians of the RMS data were plotted and compared as well. The standard deviations of all Zernike coefficients of the three measurements, which were taken for each eye, were aggregated to find the fixation target that results in a lower variability of wavefront error and better fixational stability.
3. Results
Zernike coefficients for the right and left eyes were not distributed normally and were not correlated in the majority of cases, so we considered both eyes in our study population. The analysis of these results showed that Zernike coefficients of defocus (C(2,0)), vertical trefoil (C(3,–3)), vertical coma (C(3,–1)), horizontal coma (C(3,1)), oblique trefoil (C(3,3)), primary spherical aberration (C(4,0)), and secondary spherical aberration (C(6,0)) changed after fixation target alteration.
The root mean squares of the following parameters were also estimated: all aberration coefficients (total RMS), higher-order aberrations (HOA-RMS), comatic aberrations, which included vertical and horizontal aberrations (Coma-RMS), and spherical-like aberration changes, which included primary and secondary spherical aberrations (Sph-RMS). The first three RMS data were distributed normally, so a paired t-test was applied to find statistically significant differences in the RMS values recorded while looking at different fixation points in all the eyes. The change in the Sph-RMS was investigated by the two-samples Wilcoxon test. None of these tests showed statistically significant differences in the pairs of the RMS values recorded when fixating at different fixational targets (p > 0.05).
3.1. Target’s Size Effect
The Wilcoxon’s pairwise comparison of the coefficients change after the target’s size alteration was not statistically significant in any of them for both eyes (p > 0.05), so the percentage of the coefficients’ rank change was reported (Table 1).

Table 1.
Zernike coefficients’ rank change due to the alteration in the size of fixation targets in the Wilcoxon signed-ranks test.
For instance, in Table 1, the C(2,0) rank in the Wilcoxon signed-ranks test increased only in 46% of all eyes when looking at the “E” target compared to looking at the “e” target; in other words, this means that its rank decreased in 54% of all eyes when shifting gaze from the “E” target to the “e” target (no tie found in the ranks). One can infer the rest likewise. This showed the high variability in coefficient changes due to the size of the fixation target.
These size-related changes were correlated among all of the above coefficients in both eyes (p < 0.05); for instance, the C(2,0) values obtained while gazing at the “X”/“E” target were correlated with the values obtained while gazing at the “x”/“e” target, showing the significant effect of the target size change.
Regarding the analysis of the RMS data, since the total RMS, the RMS of the HOA, and the RMS of comatic aberrations were normally distributed, their means were plotted to show their insignificant changes after fixation target alteration. For the RMS of the spherical-like aberrations, the median of it was plotted (Figure 3).
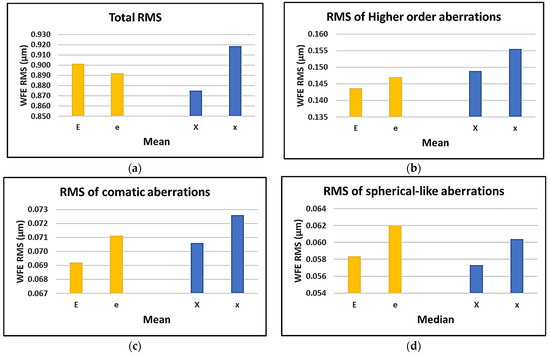
Figure 3.
Effect of target size on (a) mean of total RMS; (b) mean of HOA; (c) mean of comatic aberrations; (d) and median of spherical-like aberrations.
It can be seen that choosing the bigger Maltese cross gave the least total RMS of the aberrations and the lowest RMS of the spherical-like aberrations; however, the bigger E-letter yielded the lowest RMS of the HOA and the lowest RMS of the comatic aberrations. All the charts show that by shifting the gaze from the fixation target of “X” to “x”, an increase in the RMS values is expected. The same trend can be found when changing the gaze from the fixation target of “E” to “e”, except for the total RMS of the aberrations.
3.2. Target’s Shape Effect
In the Table 2, the percentage of rank change of the coefficients was provided, since none of the Wilcoxon’s pairwise comparisons of them after the target’s shape alteration for both eyes were statistically significant (p > 0.05).

Table 2.
Zernike coefficients’ rank change due to an alteration in the shape of the fixation targets in the Wilcoxon signed-ranks test.
Table 2 shows that just 58% of the eyes showed an increase in the C(3,−3) rank in the Wilcoxon signed-ranks test when looking at the “E” target compared to the “X” target. This indicates that 42% of the eyes showed a decrease in rank when shifting their gaze from the “E” target to the “X” target (there was no tie in the ranks). Thus, the shape of the fixation target exhibited a great amount of variability in the coefficient changes.
These shape-related changes were also correlated among all of the above coefficients in both eyes (p < 0.05). As an example, the correlation between the C(3,−3) values obtained while looking at the “X” and “x” targets and the values recorded when staring at the “E” and “e” targets suggests there is an influence from the change in target shape on the wavefront aberrations of eye.
Regarding the analysis of the RMS data, as mentioned, the means of the total RMS, RMS of the HOA, and the RMS of comatic aberrations were plotted to show their insignificant changes after fixation target alteration. For the RMS of spherical-like aberrations, the median of it was plotted (Figure 4).
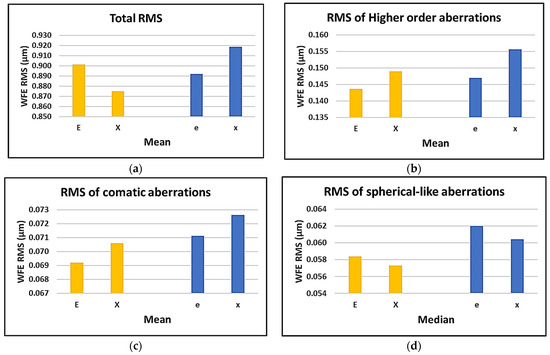
Figure 4.
Effect of target shape on (a) mean of total RMS; (b) mean of HOA; (c) mean of comatic aberrations; (d) and median of spherical-like aberrations.
Regarding the effect of target’s shape, variability was found in the result; it can be seen that by shifting the gaze from the fixation target of “E” and “e” to “X” and “x”, an increase in the RMS of comatic aberrations is expected. A decreasing trend can be found for the RMS of spherical aberrations when changing the gaze from the fixation target of “E”/“e” to “X”/“x”.
By aggregating the standard deviations (STD) of all Zernike coefficients recorded in three measurements per eye, it was also found that the smaller E-letter yielded less variability in the measurements (STDaggregated = 0.0065 μm).
4. Discussion
Aberrometers and other optical devices rely on alignment and any misalignment might compromise the accuracy of the readings. To the best of the author’s knowledge, no prior research has examined how the size and shape of the aberrometer’s fixation target affect the ocular wavefront error and this study aimed to evaluate these variables using a Shack–Hartman aberrometer.
Using a scanning laser ophthalmoscope, Culham et al. [19] were able to visualize the targets (single and multiple letters) on the fundus of normal- and low-vision patients, and digital photographs allowed them to compare the subject’s eye movement and fixational stability, estimated using the bivariate contour ellipse area (BCEA) norm. They reported that fixation in the normal group was influenced by the size of the target, but not by its shape. The ability to sustain consistent fixation varied among subjects, particularly among patients with limited vision. Bellmann et al. [20] used six central and pericentral fixation targets to study the fixation stability in healthy and age-related macular degenerated (AMD) patients. The BCEA was calculated for each target over a period of thirty seconds in order to quantify the fixation stability. The fixation stability for central fixation targets was noticeably greater and for pericentral targets was significantly smaller in healthy individuals. Patients with central vision loss have much less stable fixation, as shown by the BCEA values that are almost ten times greater in patients compared to normal participants. AMD patients had less fixational stability, as their BCEA values were almost ten times greater compared to normal participants. In another study involving young healthy subjects, Hirasawa et al. [21] used standard automated perimetry with three fixation targets (point, cross, and ring) to assess the correlation of fixation behavior, estimated by the BCEA parameter and threshold variations throughout all test points. They found that the BCEA grew notably as the size of the fixation target increased and recommended a small fixation target for the visual field test. Pirdankar and Das [22] investigated how the size and shape of the fixation target affect the stability of the ocular fixation in normal and strabismic monkeys. Cross, disk, a combination of disk and crosshair, and a % sign were the shapes used in their experiment. Their results showed that target size affects normal monkeys. A target size of 2° was the least steady, while a target size of 0.5° produced the most stable fixation. They also discovered that the strabismic monkeys’ responses to changes in target size and shape were significant and identical to those of normal monkeys as well. Additionally, they found that the bigger fixation targets such as the disk target, which resulted in the least central stimulation, yielded the highest BCEA scores.
Our results also show that when we aggregated the standard deviations of all Zernike coefficients of the three measurements which were taken for each eye, the smaller E-letter resulted in a lower variability of wavefront error. This is in agreement with the above reports, where smaller central fixation targets gave a better stability of ocular fixation, and shape did not impact the ocular aberrations. Nevertheless, there are further studies that have shown contradictory findings.
When Steinman [4] recorded the eye movements of two subjects using the contact lens method, he discovered that the bigger the fixation targets, the fewer the microsaccades. McCamy et al. [5] examined the effects of different parameters of the fixational target including its size on fixation stability. As the size of the circular fixation spot rose, they observed that the microsaccades rate decreased linearly. They conclude that the selection of the fixation target may influence the results of the experiment and suggested that researchers also include the size of their fixation targets in their reports. In a recent study by Watamaniuk et al. [23], three fixational targets were utilized: central target (single 0.2° gray dot), peripheral target (eight gray dots equally spaced to form a virtual circle), and a combination of both targets. They showed that the larger the peripheral fixation targets, the smaller the microsaccades, by an average of 46.3%. Additionally, they discovered that peripheral fixation targets had a considerable impact on reducing drift speed and consequently enhancing fixation stability. Meanwhile, there was no statistically significant difference between the average BCEA of the peripheral and central fixation targets. They suggested that the peripheral target is the most effective target to achieve a higher fixational stability of eyes during experiments. In their study, Thaler et al. [6] instructed participants to focus their attention on seven targets for a duration of 17 s in each session. The researchers analyzed spatial dispersion and the microsaccades rate to assess the stability of fixation. They discovered that only a target shape resembling a combination of a bull’s eye and a crosshair led to stable fixation. The conflicts in the literature might be attributed to differences in eye-tracking techniques and the size of the study population.
Meanwhile, the Wilcoxon signed-rank test that was applied on the recorded Zernike coefficients of C(2,0), C(3,–3), C(3,–1), C(3,1), C(3,3), C(4,0), and C(6,0) in our experiment did not show significant changes after fixation target alteration. Nevertheless, alterations in the size and shape of the fictional target exhibited statistically significant correlations across all of the coefficients in both eyes. When there is a significant correlation between two variables but the Wilcoxon signed-rank test is not significant, it may indicate that although there is an association between the variables, this association does not manifest as a consistent directional difference between the paired observations, i.e., the differences in the aberration coefficients which result from the alteration of fixational targets are not consistently in one direction. In the literature, the impact of the size and shape of an aberrometer’s fixation target on the wavefront aberration of the eye has not yet been explored; however, alterations in the size and shape of the fixation target may lead to small angle misalignment, and there are studies examining the impact of such misalignments on the ocular wavefront.
These studies, which examined the effect of misalignment of contact lenses, intraocular lenses, and vision correction procedures, have reported changes in ocular aberrations. According to research by Padmanabhan et al. [8], decentered keratorefractive ablation resulted in significant alterations in the tilt, oblique astigmatism, vertical coma, and spherical aberration. He and Applegate [9] estimated the influence of accommodation-induced lens decentration using vertical coma. The prevalence of third-order aberrations was also proved by Fedtke et al. [10] as a consequence of the decentered contact lenses. Lawu et al. [11] demonstrated that the decentration and tilt of IOLs resulted in an increase in wavefront aberrations, so that astigmatism, defocus, and coma were greatly influenced. According to research by McKelvie et al. [12], the HOA profiles of IOLs were significantly affected by decentration (22.7% of total variability between multivariate means) and tilt (5.7%).
Furthermore, two synthetic eyes with distinct static aberrations and varying amounts of HOA, of which their movements were following different trajectories, were modeled by Arines et al. [15] and the fixational movements of eyes were reported to impact the estimated Zernike coefficients. Nevertheless, Mecê et al. [14] used a custom-built Hartmann–Shack sensor to investigate the dynamics of eye aberrations in real-time and determined that the fixational eye movements are not expected to alter the wavefront aberrations. These results are consistent with our findings, as we found that the studied Zernike coefficients changed due to misalignment, but the change was not statistically significant.
Additionally, our analysis demonstrated that misalignment resulting from fixational targets size and shape change impacts the total RMS of aberrations, RMS of HOA, Sph-RMS, and Cma-RMS, although the impact was small and there was variability. These results are in agreement with Padmanabhan et al. [8], who reported a statistically significant change in the RMS of HOA between the participant groups who received normal or decentered keratorefractive ablation.
5. Conclusions
In conclusion, we showed that misalignments could potentially contribute to the unpredictable variations and impede the detection of subtle anatomical or physiological alterations in the human eye optics over a period of time. The alterations that occurred as a consequence of the fixation gaze changes are within the range of alterations observed after a near-vision task in our earlier work; hence, these changes might be a confounding factor while exploring the minor changes in the temporal wavefront error [24,25]. It is also found that using a smaller E-letter (5 arcmin) as the fixational target may give a lower variability of measurements and a higher fixational stability. Since small misalignments have minor effects on ocular aberrations, wavefront sensors could benefit from incorporating eye trackers to track and compensate for eye movements during the aberrometric measurements in order to reduce the variability between measurement sessions.
Author Contributions
Conceptualization, J.M.G.-M. and E.S.B.; methodology, J.M.G.-M. and E.S.B.; software, E.S.B. and J.M.G.-M.; validation, E.S.B. and J.M.G.-M.; formal analysis, E.S.B. and J.M.G.-M.; investigation, E.S.B. and J.M.G.-M.; resources, J.M.G.-M.; data curation, E.S.B. and J.M.G.-M.; writing—original draft preparation, E.S.B. and J.M.G.-M.; writing—review and editing, E.S.B., F.J.Á., and J.M.G.-M.; visualization, E.S.B. and J.M.G.-M.; supervision, J.M.G.-M.; project administration, J.M.G.-M.; funding acquisition, J.M.G.-M. All authors have read and agreed to the published version of the manuscript.
Funding
This research has received funding from the European Union’s Horizon 2020 research and innovation program under the Marie Skłodowska-Curie grant agreement No. 956720.
Institutional Review Board Statement
This study was conducted in accordance with the Declaration of Helsinki. The protocol of this study was approved by the ethical committee of CSIC (Instituto de Nanociencia y Materiales de Aragón—INMA) with an internal code of 010/202; by the Comité de Ética de la Investigación de la Comunidad de Aragón (CEICA) with reference PI21-074; and by the University of Minho Ethics Subcommittee for Life and Health Sciences CEICVS with the code 081-2022.
Informed Consent Statement
Informed consent was obtained from all subjects involved in this study.
Data Availability Statement
The data presented in this study are available on request from the corresponding author.
Conflicts of Interest
The authors declare no conflicts of interest.
References
- Alexander, R.G.; Martinez-Conde, S. Fixational Eye Movements. In Eye Movement Research; Klein, C., Ettinger, U., Eds.; Studies in Neuroscience, Psychology and Behavioral Economics; Springer: Cham, Switzerland, 2019; pp. 73–115. ISBN 978-3030-200831. [Google Scholar]
- Kowler, E. Eye Movements: The Past 25 Years. Vision Res. 2011, 51, 1457–1483. [Google Scholar] [CrossRef]
- Ukwade, M.T.; Bedell, H.E. Stability of Oculomotor Fixation as a Function of Target Contrast and Blur. Optom Vis. Sci. 1993, 70, 123–126. [Google Scholar] [CrossRef]
- Steinman, R.M. Effect of Target Size, Luminance, and Color on Monocular Fixation. J. Opt. Soc. Am. 1965, 55, 1158. [Google Scholar] [CrossRef]
- McCamy, M.B.; Najafian Jazi, A.; Otero-Millan, J.; Macknik, S.L.; Martinez-Conde, S. The Effects of Fixation Target Size and Luminance on Microsaccades and Square-Wave Jerks. PeerJ 2013, 1, e9. [Google Scholar] [CrossRef]
- Thaler, L.; Schütz, A.C.; Goodale, M.A.; Gegenfurtner, K.R. What Is the Best Fixation Target? The Effect of Target Shape on Stability of Fixational Eye Movements. Vis. Res. 2013, 76, 31–42. [Google Scholar] [CrossRef] [PubMed]
- Applegate, R.A.; Thibos, L.N.; Twa, M.D.; Sarver, E.J. Importance of Fixation, Pupil Center, and Reference Axis in Ocular Wavefront Sensing, Videokeratography, and Retinal Image Quality. J. Cataract. Refract. Surg. 2009, 35, 139–152. [Google Scholar] [CrossRef]
- Padmanabhan, P.; Mrochen, M.; Viswanathan, D.; Basuthkar, S. Wavefront Aberrations in Eyes with Decentered Ablations. J. Cataract. Refract. Surg. 2009, 35, 695–702. [Google Scholar] [CrossRef]
- He, L.; Applegate, R.A. Predicting Crystalline Lens Fall Caused by Accommodation from Changes in Wavefront Error. J. Cataract. Refract. Surg. 2011, 37, 1313–1322. [Google Scholar] [CrossRef][Green Version]
- Fedtke, C.; Ehrmann, K.; Thomas, V.; Bakaraju, R.C. Association between Multifocal Soft Contact Lens Decentration and Visual Performance. Clin. Optom. 2016, 8, 57–69. [Google Scholar] [CrossRef]
- Lawu, T.; Mukai, K.; Matsushima, H.; Senoo, T. Effects of Decentration and Tilt on the Optical Performance of 6 Aspheric Intraocular Lens Designs in a Model Eye. J. Cataract. Refract. Surg. 2019, 45, 662–668. [Google Scholar] [CrossRef]
- McKelvie, J.; McArdle, B.; McGhee, C. The Influence of Tilt, Decentration, and Pupil Size on the Higher-Order Aberration Profile of Aspheric Intraocular Lenses. Ophthalmology 2011, 118, 1724–1731. [Google Scholar] [CrossRef]
- Koenig, D.E.; Applegate, R.A.; Marsack, J.D.; Sarver, E.J.; Nguyen, L.C. Detecting Significant Change in Wavefront Error: How Long Does It Take? Clin. Exp. Optom. 2009, 92, 246–252. [Google Scholar] [CrossRef]
- Mecê, P.; Jarosz, J.; Conan, J.-M.; Petit, C.; Grieve, K.; Paques, M.; Meimon, S. Fixational Eye Movement: A Negligible Source of Dynamic Aberration. Biomed. Opt. Express 2018, 9, 717–727. [Google Scholar] [CrossRef] [PubMed]
- Arines, J.; Pailos, E.; Prado, P.; Bará, S. The Contribution of the Fixational Eye Movements to the Variability of the Measured Ocular Aberration. Ophthalmic Physiol. Opt. 2009, 29, 281–287. [Google Scholar] [CrossRef] [PubMed]
- Rio, D.; Rozema, J.J.; Hastings, G.D.; Marsack, J.D. The Impact of Misalignment on the Optical and Visual Image Quality of Template-Based Corrections in Keratoconus. Investig. Ophthalmol. Vis. Sci. 2018, 59, 5804. [Google Scholar]
- Rasouli, S.; Dashti, M.; Ramaprakash, A.N. An Adjustable, High Sensitivity, Wide Dynamic Range Two Channel Wave-Front Sensor Based on Moiré Deflectometry. Opt. Express 2010, 18, 23906–23913. [Google Scholar] [CrossRef] [PubMed]
- Shack, R.V. Production and Use of a Lenticular Hartmann Screen. Spring Meet. Opt. Soc. Am. 1971, 656, 1971. [Google Scholar]
- Culham, L.; Fitzke, F.; Timberlake, G.; Marshall, J. Assessment of Fixation Stability in Normal Subjects and Patients Using a Scanning Laser Ophthalmoscope. Clin. Vis. Sci. 1993, 8, 551–561. [Google Scholar]
- Bellmann, C.; Feely, M.; Crossland, M.D.; Kabanarou, S.A.; Rubin, G.S. Fixation Stability Using Central and Pericentral Fixation Targets in Patients with Age-Related Macular Degeneration. Ophthalmology 2004, 111, 2265–2270. [Google Scholar] [CrossRef]
- Hirasawa, K.; Okano, K.; Koshiji, R.; Funaki, W.; Shoji, N. Smaller Fixation Target Size Is Associated with More Stable Fixation and Less Variance in Threshold Sensitivity. PLoS ONE 2016, 11, e0165046. [Google Scholar] [CrossRef]
- Pirdankar, O.H.; Das, V.E. Influence of Target Parameters on Fixation Stability in Normal and Strabismic Monkeys. Invest. Ophthalmol. Vis. Sci. 2016, 57, 1087–1095. [Google Scholar] [CrossRef] [PubMed]
- Watamaniuk, S.N.J.; Badler, J.B.; Heinen, S.J. Peripheral Targets Attenuate Miniature Eye Movements during Fixation. Sci. Rep. 2023, 13, 7418. [Google Scholar] [CrossRef]
- Safarian Baloujeh, E.; González-Méijome, J.M. Wavefront Changes during a Sustained Reading Task in Presbyopic Eyes. Sensors 2024, 24, 3866. [Google Scholar] [CrossRef] [PubMed]
- Orduna-Hospital, E.; Safarian Baloujeh, E.; Navarro, R.; Sanchez-Cano, A. Optical and Motor Changes Associated with Lighting and near Vision Tasks in Electronic Devices. J. Eye Mov. Res. 2023, 16. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).