Efficient Direct Detection of Twin Single-Sideband Quadrature-Phase Shift Keying Using a Single Detector with Hierarchical Blind-Phase Search
Abstract
1. Introduction
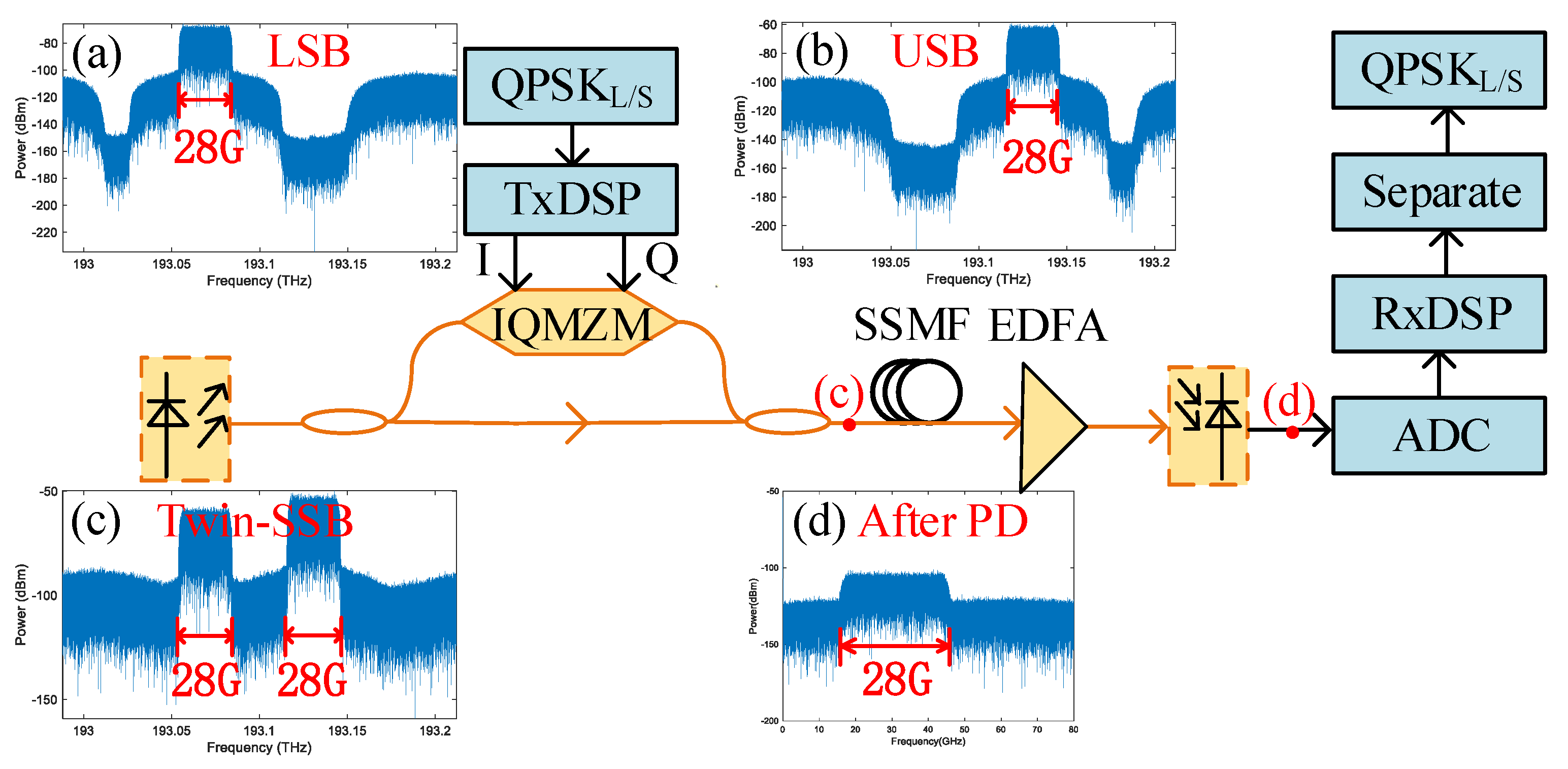
2. Operation Principle
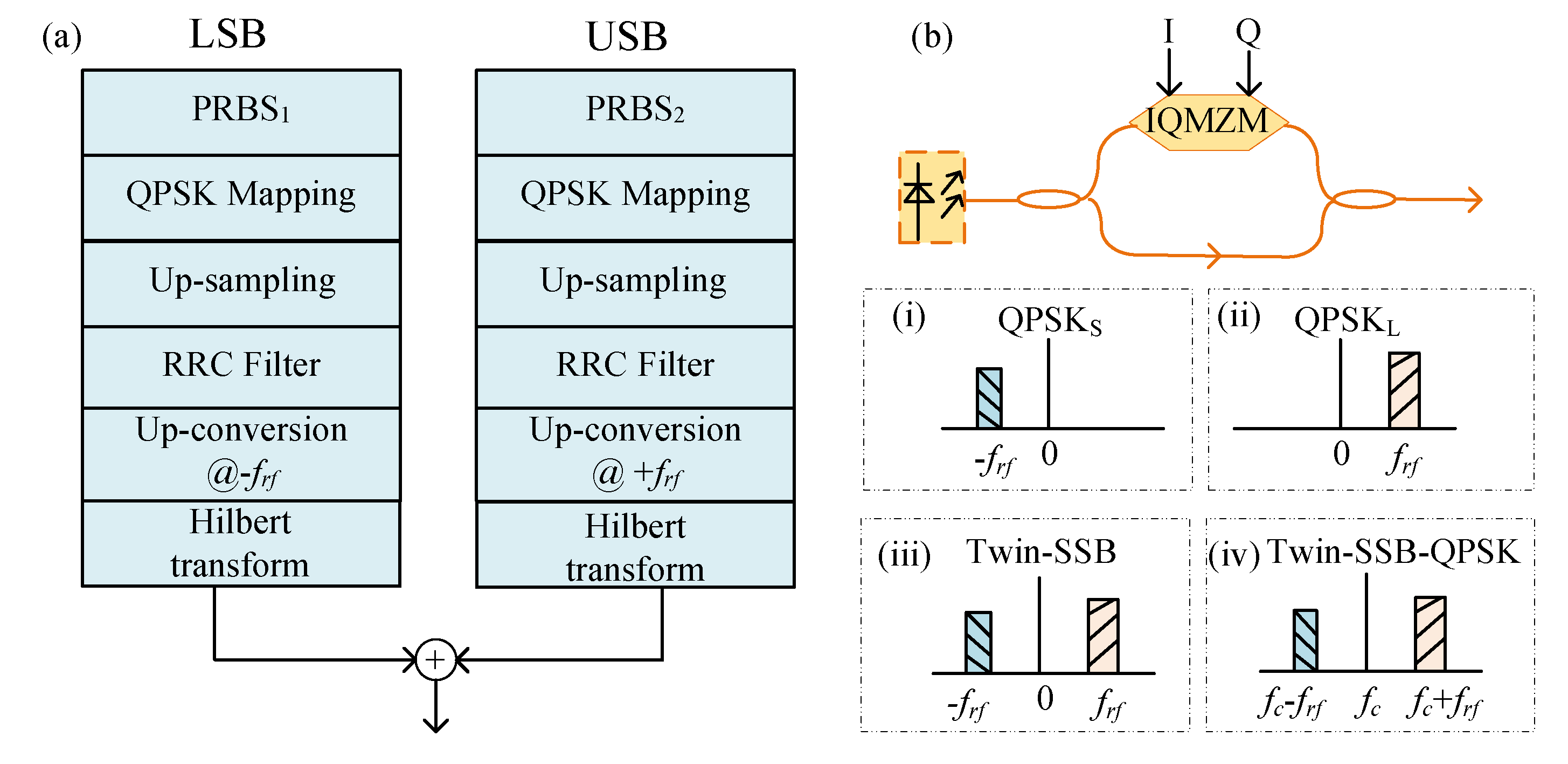
2.1. Twin-SSB-QPSK Transmitter
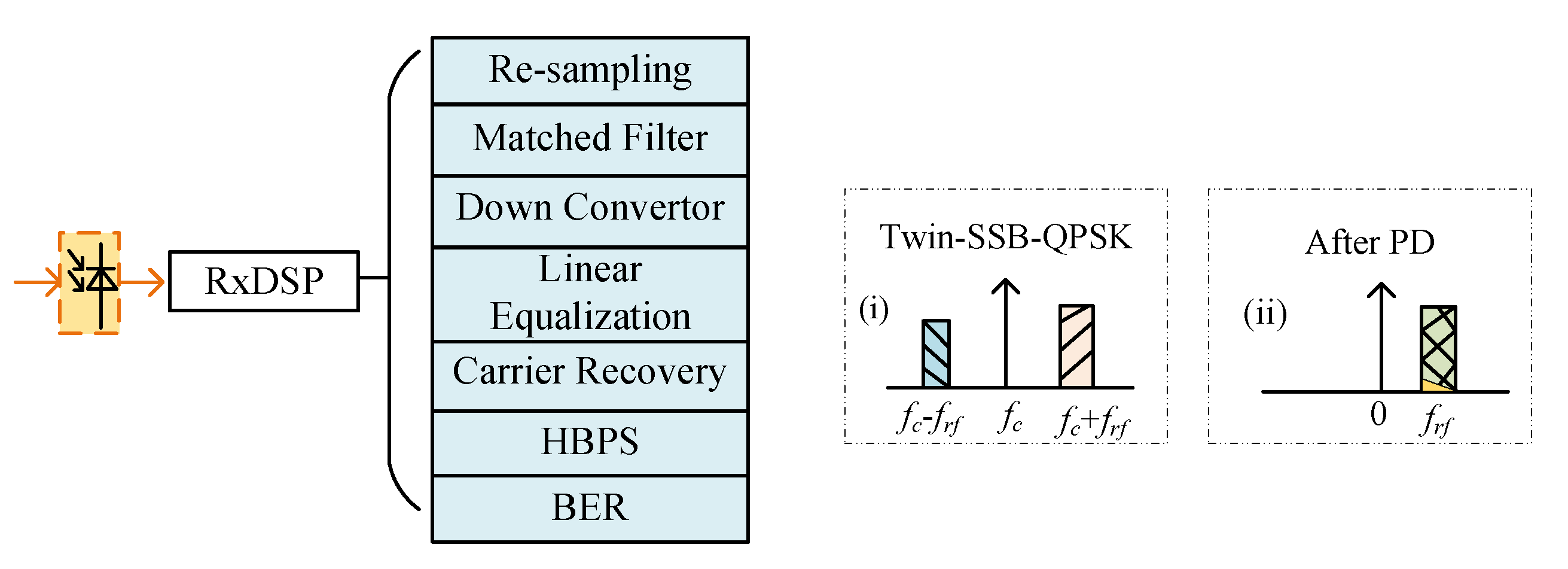
2.2. Proposed Twin-SSB Reception by Coherent Superposition
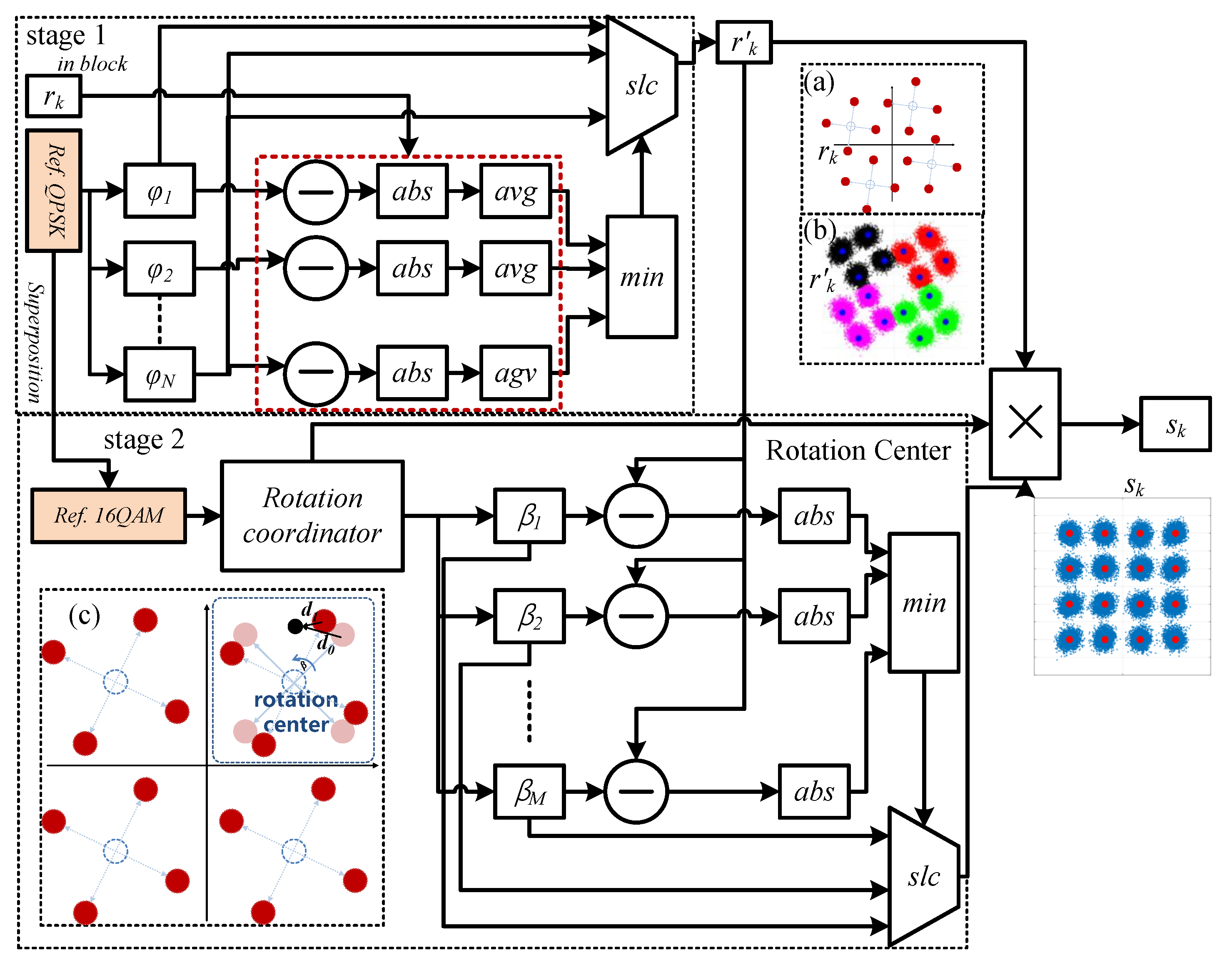
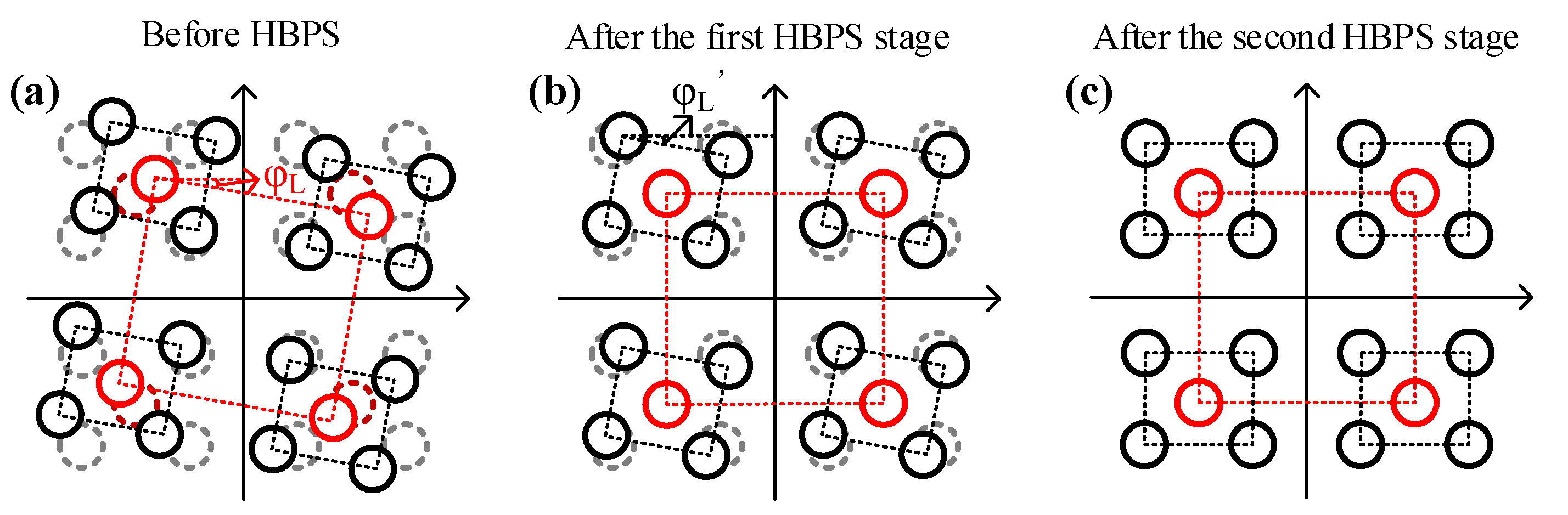
2.3. Phase Compensation Algorithm: HBPS
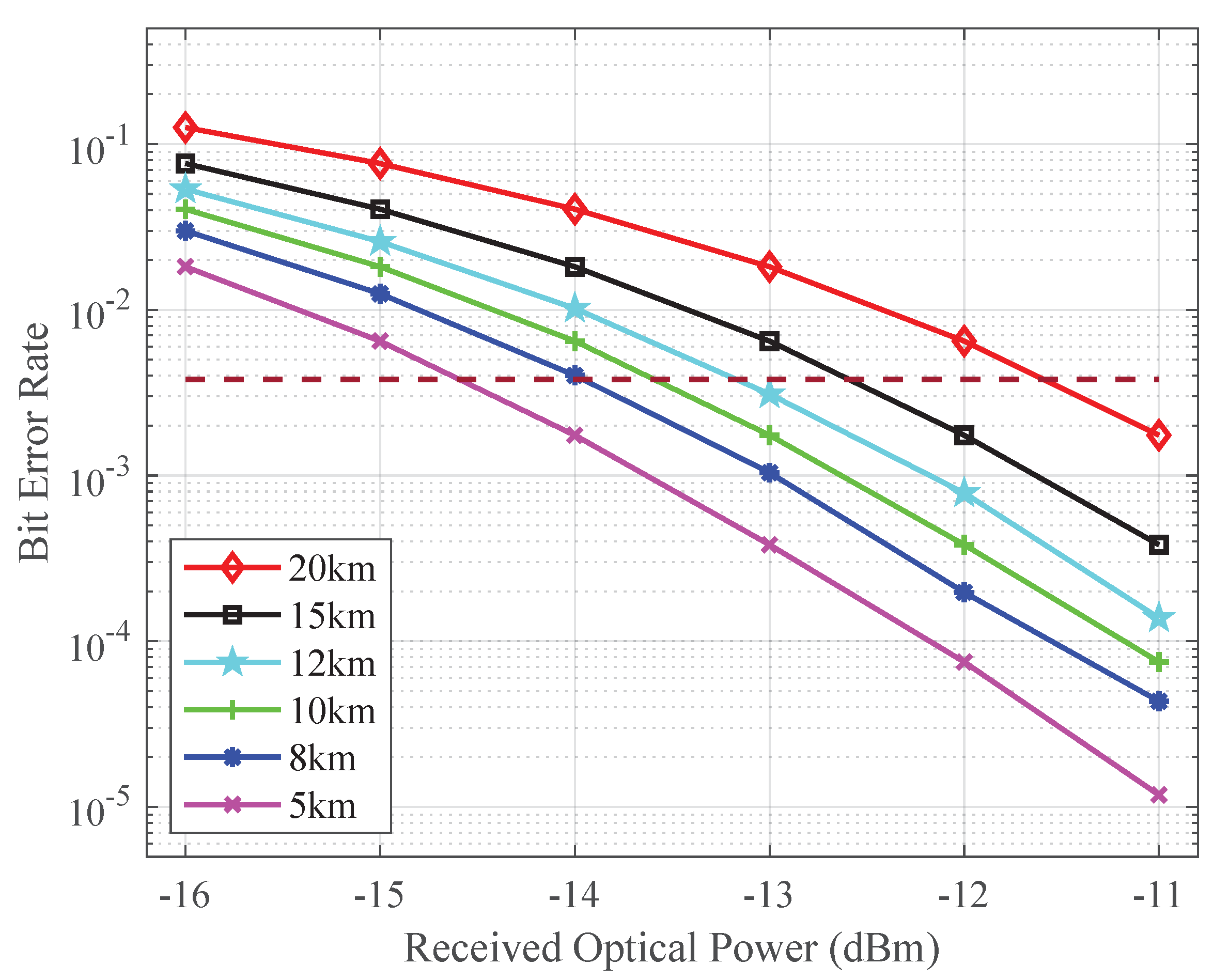
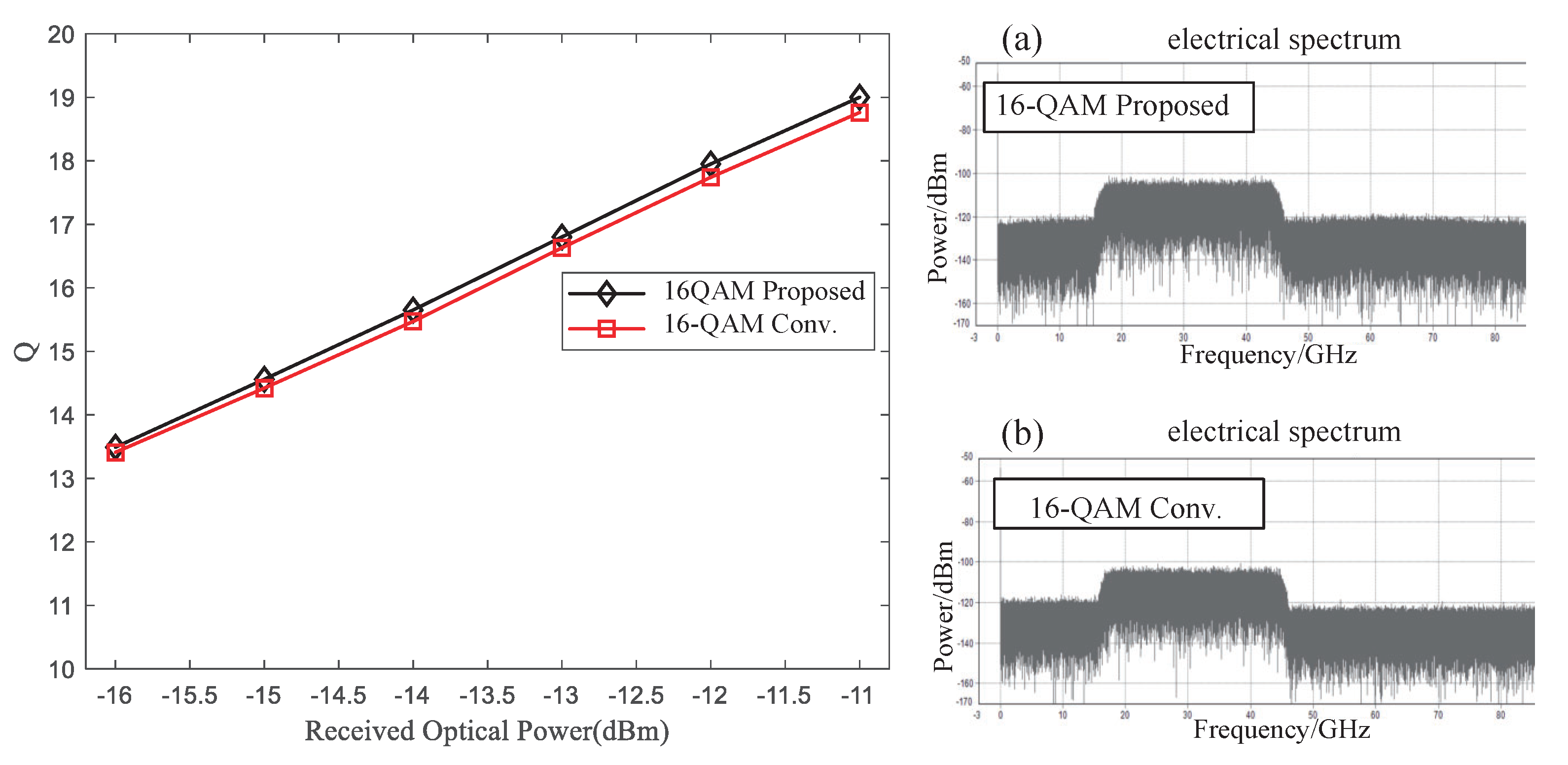
3. Experimental Verification
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Abbreviations
| 16-QAM | 16-ary quadrature amplitude modulation |
| ADC | analog-to-digital converter |
| BER | bit error ratio |
| BPS | blind-phase search |
| DSP | digital signal processing |
| HBPS | hierarchical blind-phase search |
| HD-FEC | hard-decision forward error correction |
| IQMZM | in-phase quadrature-phase Mach–Zehnder modulator |
| QPSK | quadrature-phase shift keying |
| PD | photodetector |
| PRBS | pseudo-random bit sequences |
| ROP | received optical power |
| RRC | root-raised cosine |
| SSMF | standard single-mode fiber |
| twin-SSB | twin single sideband |
| twin-SSB-QPSK | twin-SSB quadrature-phase shift keying |
References
- Beemkumar, N.; Sharma, S.K.; Sharma, R.; Prasad, S.; Kumar, D.; Marimuthu, J.; Gupta, P. Antenna Optical Communication Spectral Enhancement with Energy Analysis of Photovoltaic Cell Microgrid Environmental Application. Opt. Quant. Electron. 2023, 55, 770. [Google Scholar] [CrossRef]
- Guo, H. Experimental Demonstration of an Improved Control Design and Algorithm for Optical Communication Terminal with Disturbance. Optik 2022, 269, 169939. [Google Scholar] [CrossRef]
- Zhang, L.; Pang, X.; Jia, S.; Wang, S.; Yu, X. Beyond 100 Gb/s Optoelectronic Terahertz Communications: Key Technologies and Directions. IEEE Commun. Mag. 2020, 58, 34–40. [Google Scholar] [CrossRef]
- Kikuchi, N. Multilevel Signaling Technology for Increasing Transmission Capacity in High-Speed Short-Distance Optical Fiber Communication. IEICE Trans. Electron. 2019, 102, 316–323. [Google Scholar] [CrossRef]
- Yan, L.; Shi, L. Deep Fusion Technology of Optical Communication Channel Based on Multicarrier Modulation. Opt. Rev. 2019, 26, 537–548. [Google Scholar] [CrossRef]
- Gao, Y.; Shang, T.; Ma, L. Mobile Internet Big Data Technology-Based Echo Loss Measurement Method of Optical Communication System. Comput. Electr. Eng. 2022, 101, 108097. [Google Scholar] [CrossRef]
- Wei, X.; Yang, C.; Han, S. Prediction, Communication, and Computing Duration Optimization for VR Video Streaming. IEEE Trans. Commun. 2020, 69, 1947–1959. [Google Scholar] [CrossRef]
- Li, J.; An, S.; Su, Y. Zero-Guard Band Dual-SSB PAM4 Signal Transmission with Joint Equalization Scheme. Opt. Lett. 2020, 45, 6178–6181. [Google Scholar] [CrossRef] [PubMed]
- Lu, G.W.; Zhang, H.B.; Li, Z. Coherent Self-Superposition Aided SSB Nyquist 16QAM Synthesis from Twin-SSB Nyquist QPSK with Reduced DAC Resolution Requirement. In Proceedings of the 2020 Optical Fiber Communications Conference and Exhibition (OFC), San Diego, CA, USA, 8–12 March 2020; IEEE: Piscataway, NJ, USA, 2020; pp. 1–3. [Google Scholar] [CrossRef]
- Nakagawa, R.; Takanashi, Y.; Nakamura, M. Comparison of Twin-SSB Modulation Schemes. In Proceedings of the Next-Generation Optical Communication: Components, Sub-Systems, and Systems IX, San Francisco, CA, USA, 5–6 February 2020; SPIE: Bellingham, WA, USA, 2020; Volume 11309, pp. 114–121. [Google Scholar] [CrossRef]
- Chen, M.; Peng, M.; Zhou, H.; Zheng, Z.; Tang, X.; Maivan, L. Receiver Sensitivity Improvement in Spectrally-Efficient Guard-Band Twin-SSB-OFDM Using an Optical IQ Modulator. Opt. Commun. 2017, 405, 259–264. [Google Scholar] [CrossRef]
- Lu, G.W.; Zhang, H.B.; Li, Z. Synthesis of SSB Nyquist 16QAM from Twin-SSB QPSK via Optical Subcarrier Processing-Based Data Aggregation and Its Direct Detection with Hierarchical Blind Phase Search Algorithm. IEEE J. Sel. Top. Quantum Electron. 2020, 27, 1–8. [Google Scholar] [CrossRef]
- Lu, G.W.; Luís, R.S.; Mendinueta, J.M.D.; Sakamoto, T.; Yamamoto, N. Optical Subcarrier Processing for Nyquist SCM Signals via Coherent Spectrum Overlapping in Four-Wave Mixing with Coherent Multi-Tone Pump. Opt. Express 2018, 26, 1488–1496. [Google Scholar] [CrossRef] [PubMed]
- Zhou, Y.; Xiao, J.; Zhao, C.; Zuo, J.; Ming, J.; Zhao, L. Simplified Twin-Single-Sideband Direct Detection System Separating Left and Right Sideband Signals Using a Digital Signal Processing Algorithm Instead of Optical Bandpass Filters. Opt. Express 2022, 30, 619–628. [Google Scholar] [CrossRef] [PubMed]
- Zhao, L.; Guo, H.; Liu, Y.; Xiao, J.; Wu, T.; Song, S.; Guo, L. Independent Dual-Single-Sideband QPSK Signal Detection Based on a Single Photodetector. Opt. Express 2022, 30, 22946–22956. [Google Scholar] [CrossRef] [PubMed]
- Zhu, P.; Yoshida, Y.; Akahane, K.; Kitayama, K.i. High-speed reach-extended IM-DD system with low-complexity DSP for 6G fronthaul. J. Opt. Commun. Netw. 2024, 16, A24–A32. [Google Scholar] [CrossRef]
- Nsafoa-Yeboah, K.; Tchao, E.T.; Kommey, B.; Agbemenu, A.S.; Klogo, G.S.; Akrasi-Mensah, N.K. Flexible open network operating system architecture for implementing higher scalability using disaggregated software-defined optical networking. IET Netw. 2023, 13, 221–240. [Google Scholar] [CrossRef]



Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhang, H.; Liu, J.; Lu, G.-W.; Zhang, M.; Wan, F.; Cai, J.; Ling, W.; Hu, L. Efficient Direct Detection of Twin Single-Sideband Quadrature-Phase Shift Keying Using a Single Detector with Hierarchical Blind-Phase Search. Photonics 2024, 11, 624. https://doi.org/10.3390/photonics11070624
Zhang H, Liu J, Lu G-W, Zhang M, Wan F, Cai J, Ling W, Hu L. Efficient Direct Detection of Twin Single-Sideband Quadrature-Phase Shift Keying Using a Single Detector with Hierarchical Blind-Phase Search. Photonics. 2024; 11(7):624. https://doi.org/10.3390/photonics11070624
Chicago/Turabian StyleZhang, Hongbo, Jiao Liu, Guo-Wei Lu, Min Zhang, Feng Wan, Ju Cai, Weiwei Ling, and Liming Hu. 2024. "Efficient Direct Detection of Twin Single-Sideband Quadrature-Phase Shift Keying Using a Single Detector with Hierarchical Blind-Phase Search" Photonics 11, no. 7: 624. https://doi.org/10.3390/photonics11070624
APA StyleZhang, H., Liu, J., Lu, G.-W., Zhang, M., Wan, F., Cai, J., Ling, W., & Hu, L. (2024). Efficient Direct Detection of Twin Single-Sideband Quadrature-Phase Shift Keying Using a Single Detector with Hierarchical Blind-Phase Search. Photonics, 11(7), 624. https://doi.org/10.3390/photonics11070624




