Abstract
Photonic integrated circuits (PIC) devices are impacted by fabrication tolerances and therefore, prior knowledge of such variations could improve the PIC fabrication process and overall yield. This paper presents a method for predicting the fabrication impacts on a telecommunication optical digital to analog converter (oDAC)-based pulse amplitude modulator level four (PAM-4) transmitter as a case study where the certainty of this passive device is subjected to random variation. Our findings allow us to estimate the production yield in a fabrication scenario using the symbol error rate (SER) benchmark and this contributes to the study of the viability of oDAC PAM-4 transmitters to replace conventional electrical digital to analog converter (eDAC) PAM-4 transmitters.
1. Introduction
The intense demand for high-capacity networks, driven by novel applications such as 4K/8K video streaming, 5G mobile networks, the Internet of Things (IoTs), and cloud networking has put pressure on the need for an upgrade of bandwidth-limited optoelectronic components [1]. Hence, PIC pledge to unlock higher-capacity transceivers while minimizing their losses, footprint and power consumption. As PIC maturity continues to increase, leading to wide acceptability in industries and commercial applications, the complexity of PIC has also increased due to the large number of components on a single chip [2,3]. Examples with more than 1500 components on a single chip have been achieved and more are expected [2]. The success of PIC can be attributed to the possibility of the large-scale production of Silicon Photonics (SiP) at a reduced footprint, low component-to-component losses, low power consumption and low overall packaging cost [4]. This has allowed PIC to be used in application specific photonic integrated circuits (ASPIC), which play a role in data/telecommunications, medical applications and bio sensing and, even more recently, in transportation applications such as LIDAR [5,6]. Such application-specific designs require painstaking efforts, a long time and high cost to achieve results and their design cannot be transformed or used for other applications except the specific purposes they are designed for [7]. In some cases, the design may fail to meet the initial objective, which implies that the process has to be repeated and the cost of production will be increased [7].
Several factors are responsible for chip failure in SiP devices, often due to their small features of sub-micron size, which can lead to a significant performance mismatch between the supposed designed model and the actual device obtained after fabrication [8]. These factors can be categorized as fabrication variation, operational variation, system variation, random variation and high material index contrast [9,10]. Errors arising from these variations can constitute challenges in the overall chip performance, resulting in a reduced yield in mass productions of such PIC devices after fabrication. In addition, since light is highly sensitive to slight deviation, the inaccurate estimation of passive device properties such as the waveguide height, sidewall angle and width of directional coupler can adversely alter the path of the signal, leading to coupling mismatch [11,12]. Also, the device’s position in the die in mass production and the number of repeated runs of PIC devices in a given die can also slightly vary the behaviour of each of the devices in the entire die [9,13]. Such variations may result from ageing due to the wear and tear of lithography equipment, lithography exposure dose and chemical/mechanical polishing [9].
Several studies have been carried out in the past on the fabrication tolerances of PIC devices. L. Chrostowski et al. in [13] studied the linear correlation between similar components fabricated on the same chip and the variability in their wavelength mismatch. This study tried to establish how this variability can impact devices that are highly wavelength-dependent such as ring resonator modulators and optical filters in a wavelength division multiplexing (WDM) system. Therefore, several identical resonators on a 16 × 9 mm chip were fabricated. The results established a linear relationship between the resonator wavelength deviation and distance between two identical resonators on the chip with a maximum of a 4 nm wavelength mismatch between two resonators that are 1 nm apart. Similar work in [14] presented an analytical model to study the impact of wavelength mismatches among different devices on chips due to fabrication process variation on passive Silicon Photonic devices both at the component and device levels. The process variation that was modelled here depends on lithography imperfections resulting from resist age, sensitivity and thickness as well as other factors such as etching and exposure change. The model was evaluated by designing and fabricating a chip with several identical microresonators which are subjected to passive process variations and subsequently tested for system-level variation with a WDM-based SiP interconnect. The findings established a relationship between the optical signal-to-noise ratio of several WDM-based SiP interconnects modelled and the thickness and width variations of Silicon Photonics waveguides. Such models can also be used for other passive-based SiP devices. Other works in [15,16] also presented similar models to investigate and predict the performance of Silicon Photonic devices using the variability of passive device parameters. In both studies, several similar resonators were fabricated on a single chip and their manufacturing variabilities were studied. In [15], a Monte Carlo simulation approach was used to predict the device performance in relation to fabrication variabilities by measuring the spectral response of each device among several fabricated PICs on a 200 mm × 200 mm SiP wafer. Also, in [16], a device enhancement model was developed to improve the overall system performance of microresonators in optical interconnect networks by exploring different design waveguide parameters that can impact the performance and reliability at the device level. The model estimated the degree of the impact of the waveguide width and thickness variation on the resonant wavelength shift slop of the microresonators. The results, which presented a linear behaviour between the waveguide width/thickness and the wavelength shift slop, can be optimized to improve the optical signal to noise ratio (OSNR) of a WDM-based optical interconnect networks.
The task of characterizing the fabrication variation of PIC devices is highly challenging due to the cost and time required to carry out the process [15]. The advent of programmable photonics introduces a more robust generic template that can be exploited to implement a variety of functionality through software which can be used to optimize or predict chip performance before fabrication [17]. Just like we have field programmable gateway arrays (FPGA) in electronics, which can be reconfigured to meet specific use cases of customers, programmable photonics introduce such generic functionality known as field programmable photonic gateway arrays (FPPGA) for widespread PIC design in optical communications [18]. These FPPGAs are electronically reconfigurable basic elements that allow for the flexible configuration of a set of passive devices in order to mime several circuits without undergoing the long-term conventional fabrication circle [7,19,20]. Most FPPGA architectures are based on cascaded Mach Zehnder modulator (MZM) structures in various shapes and dimensions [21,22].
In this paper, a four-level pulse amplitude modulation (PAM-4) transmitter based on oDAC will be analysed using the hexagonal FPPGA mesh developed by iPronics [19,22]. This type of transmitter is an alternative design to replace a power-hungry and bandwidth-limited eDAC that is required in the conventional PAM-4 signal generation [23,24]. The oDAC devices are based on digital modulators and passive devices such as couplers and splitters [23]. Therefore, as a result of the light-interfering nature of such devices, precision is not guaranteed due to slight deviation during fabrication, which may result in performance degradation and a low yield [9,25]. The programmability and reconfigurability of iPronics’ FPPGA, as reported in [19,20], are applied to an oDAC PAM-4 transmitter in order to investigate its potential fabrication tolerances and predict its production yield, as a continuation of our work in [26].
Similar to the research work presented in [13,15], an FPPGA-based prediction model to study the impact of passive variation on PIC devices is developed and experimentally validated in an iPronics programmable grid with the following objectives.
- The design of a simple and efficient model for the emulation of fabrication imperfections and the non-conformity of any kind of passive devices and their implications in large-scale production. This enables us to estimate the possible yield from several runs after fabrication by mimicking different instances of the fabricated devices.
- The model is optimized to emulate an oDAC PAM-4 transmitter, which contributes to the study of the viability of an oDAC PAM-4 transmitter to replace conventional ones.
Furthermore, a Monte Carlo simulation of 1000 chips to mime an oDAC PAM-4 transmitter was carried out considering different splitter values due to fabrication errors. We then offline statistically estimated the SER performance of the devices, which we used to predict the failed and passed chips. Our aim is to demonstrate the potential of the methodology to evaluate the viability of a certain fabrication technique to meet the required yield.
2. Proposed Model
An oDAC PAM-4 transmitter is presented in Figure 1, where the signal from a continuous wave (CW) laser is split into the two arms of the device through an input coupler with input coupling factor and then recombined through an output coupler with output coupling factor . The non-return-to-zero (NRZ) electrical signals ( and ), which act as the most significant bit (MSB) and least significant bit (LSB), are applied to drive the modulators, as shown in Figure 1.
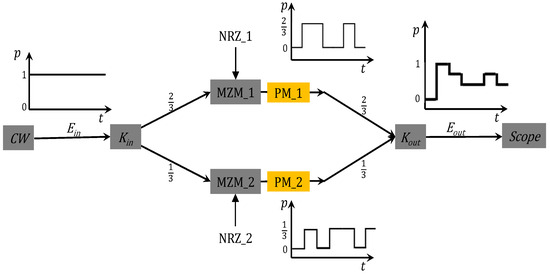
Figure 1.
Structure of an oDAC PAM-4 transmitter.
Due to the sensitive nature of interferometers, imprecision in the implementation of this type of device can reduce their performance during signal detection. For instance, eye diagrams at different values of are presented in Figure 2a–c. This is a challenge that requires further investigation.
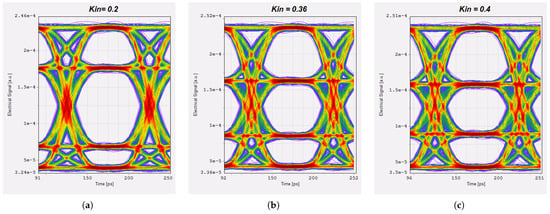
Figure 2.
Eye diagrams of an oDAC-PAM-4 signal: (a) = 0.2, (b) = 0.36, (c) = 0.4.
To model these effects, the FPPGA device developed by iPronics is used. The FPPGA comprises a set of MZMs or programmable unit core (PUC)s, which are hexagonally connected via a replicated geometric. Each PUC from the arrays is itself an MZM, as shown in Figure 3, which can be configured as a bar state with = 0, cross state with = 1, and as tunable with = any value between 0 and 1.
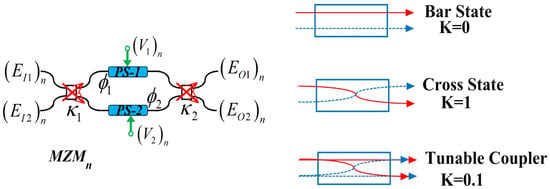
Figure 3.
PUC loaded with phase shifter and heater on both of its arms and its mode of implementation as the bar state, cross state and tunable coupler.
The mathematical expression of the output signal of a typical PUC/MZM, as shown in Figure 3, can be expressed as
where and are the applied voltages to tune the phase shifter (PS) in order to create and phase changes, and , PUC input and output coupling coefficients, , the half-wave voltage and .
A hexagonal array of the PUCs is shown in Figure 4a and it can be electrically tuned to provide functionalities such as filtering, optical interconnects and several other optical functionalities.
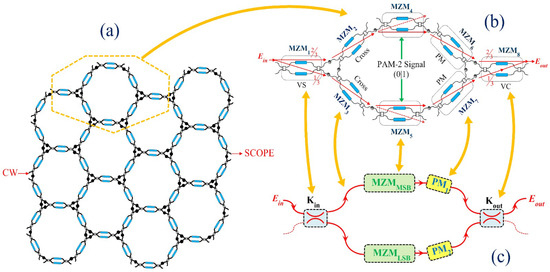
Figure 4.
Building blocks of programmable photonics: (a) mesh lattice with hexagonal cells, (b,c) oDAC-PAM-4 transmitter structure designed with the hexagonal cells. VS: variable splitter, PM: phase modulator, VC: variable combiner.
Furthermore, our proposed model, in Figure 4b,c, developed from the PUC arrays in Figure 4a, comprises two MZMs acting as amplitude modulator (AM) ( and ), which are arranged in parallel to form the two arms just as another major MZM circuit. Light from a CW laser can then be split into the two arms of the outer MZMs via an input optical splitter (which itself is an MZM) by setting its to 0.36, as recommended in [24].
In addition, phase modulator (PM)s mimed as and are placed immediately after each AM before the two signals are combined through an optical combiner with = 0.5. By coarse adjustment of the phase of either or , resulting in a phase adjustment, we can improve the PAM-4 to be equidistant.
To generate a PAM-4 signal using the proposed device, two NRZ digital signals are applied to drive the two AMs, where each driving implies a 1-bit modulation gate, as shown in Figure 4b,c. The constellation levels of the PAM-4 signal are set to following the oDAC design specification in [24].
Moreover, by making the input PUC ( in Figure 4b) that mimes a random variable with Gaussian distribution, which implies that = + , where is the fabrication variance, we can mime the fabrication tolerance of the device. So, a Monte Carlo simulation of the device is then carried out. For the sake of time, only 1000 device iterations are considered. At first, the simulation is conducted for a perfect passive coupling condition with the set to 0%. Then, is further varied from 2% to 12%. As expected, the coupling ratio of a passive device cannot surpass 1, so we opted to mime the effect of coupling resulting from the sinusoidal behaviour of the MZM leading to folded “1’s” and “0’s”.
A histogram of the Gaussian profile of the 1000 chips for a perfect passive coupler is presented in Figure 5a while the histograms of increased from 2 to 12% are presented in Figure 5a, Figure 5b and Figure 5c, respectively. No sign of imbalance is observed in Figure 5a, as expected, since no error is added in this case. This implies an emulation of a perfect fabrication scenario where the performance of passive device after fabrication is directly equivalent to the proposed design before fabrication. From the results in Figure 5b–d, remains unchanged despite increased since this level implies an absence of light. In addition, since rail to rail modulation is used, both and exhibit compression, as can be observed from the histograms. However, increased significantly impaired and due to overlapping, which may result in decision error. maintains improvement when compared with and . This is because has the highest signal-to-noise ratio since the highest signal power occurred at this level. Nevertheless, the impact of increased can be seen to cause to fold back towards .
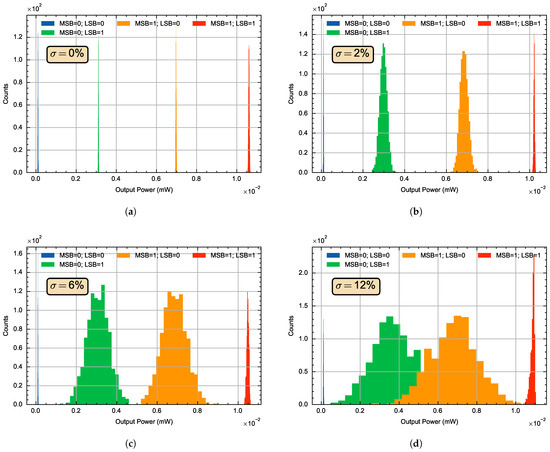
Figure 5.
Histograms of the Gaussian profile of 1000 oDAC device iterations for (a) 0%, (b) 2%, (c) 6%, (d) 12%.
Next, we have optimized to ensure the equidistance of the amplitude levels of our PAM-4 signal. As the maximum phase shift cannot exceed , the phases of both the PMs ( and ) are swept from 0 to radians. The variations in the amplitude levels of the oDAC-PAM-4 transmitter against the phase are obtained and presented in Figure 6a,b for and as in Figure 4c, showing the distribution of the signal amplitude against phase. The extinction ratio (ER) of the PAM-4 eyes against varying phases of and are also presented in Figure 6c,d, showing how phase variation impacts the signal’s ER. We have set the phase of to 2.4 radians for the further analysis that is conducted on the oDAC-PAM-4 transmitter in this study.
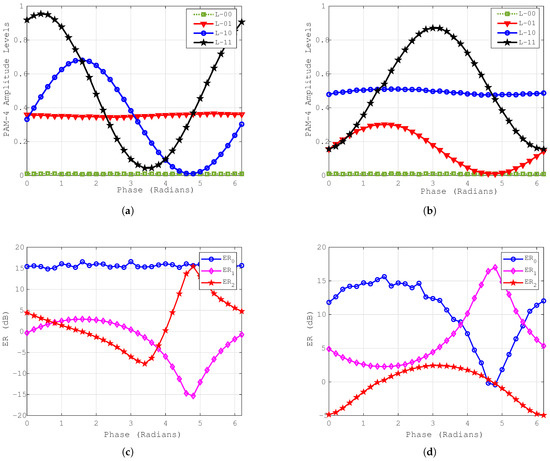
Figure 6.
PAM-4 signal amplitude levels and ER against varying phases of the PMs in Figure 4b when K = 0.36. (a) Amplitude levels against phase of the . (b) Amplitude levels against phase of the . (c) ER of the PAM-4 eyes against phase of . (d) ER of the PAM-4 eyes against phase of .
Data Extraction and Analysis
The procedure for data extraction and analysis is presented in Figure 7. Since the machine can be controlled using software, the process in Figure 7 follows repeated iterations to mime 1000 oDAC PAM-4 transmitters. Specifically, while varying the value of in the devices, the signal powers at the four levels of each of the 1000 emulated transmitters are extracted from the iPronics FPPGA machine through the power meter for offline processing.
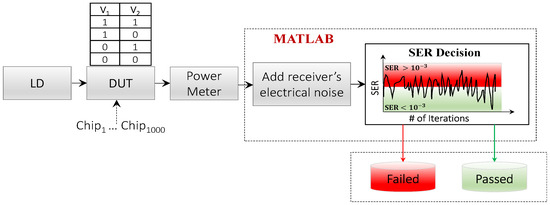
Figure 7.
Procedure for data extraction from the programmable device and offline processing for error analysis.
The obtained signal power levels are then processed offline as optical transmitted signals and detected through a PIN photodetector. A sketch of the decision circuit showing the waveform of the bit fluctuation across the four levels of the PAM-4 signal is presented in Figure A1 in Appendix A, where is the probability of deciding signal when signal is received and is the Gaussian pulse of the PAM-4 signal levels.
The generalized analytical expression for estimating the SER of a PAM-4 signal based on the schematic in Figure A1 is given by Equation (A2) in Appendix B.
Therefore, solving for all the in Figure A1, as presented in Equation (A2) using Equation (A4), we obtained Equation (A5) in Appendix C. By cancelling out some parameters in Equation (A5), we obtained the final equation to estimate the signal SER as Equation (A6).
The in Equations (A4)–(A6) is the receiver’s electrical noise, which is estimated as the sum of the thermal and short noise for a typical 10 GHz PIN receiver following the expression in [27] and it is assumed to be constant across the four PAM-4 levels. We have further assumed a typical detection of a 10 Gb/s signal at 1550 nm with a receiver sensitivity of dBm at SER = to adjust the receiver’s noise. In addition to this, the P2P power level of the signal from the machine is normalized to increase the impact of the signal noise before detection. An SER benchmark of is used to determine the failed or passed chips, as is clearly illustrated in Figure 7. Therefore, using Equation (A6) for SER calculation, all the 1000 mimed transmitters are analysed after detection. Signals detected with an SER above the threshold () are classified as having failed while those below the threshold are classified as having passed, as shown in Figure 7.
3. Results and Discussion
The graphs of the SER versus chip iteration when = 0 and when = 2% are presented in Figure 8a,b. With the light control as expected, the total 1000 iterated PICs passed the SER threshold, as shown in Figure 8a. When is increased to 2%, only 3 chips out of the 1000 mimed was seen to have failed while the rest passed the SER threshold we set, which implies a high tolerance due to decreased deviation from the coupling condition.
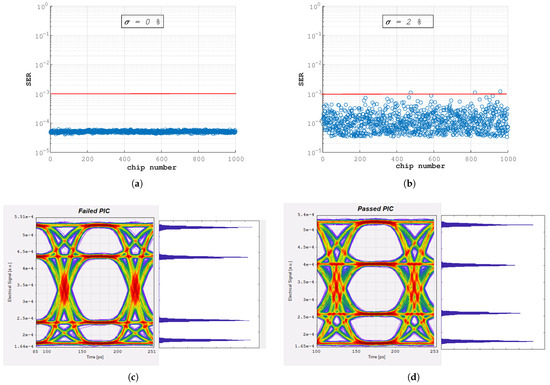
Figure 8.
SER versus the number of PIC mimed at = (a) 0%, (b) 2%, and eye diagram of one selected PIC from failed and passed categories when σn = 2%. (c) Failed PIC. (d) Passed PIC.
For further analysis of the results when = 2%, the PAM-4 amplitude levels of one PIC from the failed and passed categories are extracted and simulated to obtain the PAM-4 eye diagrams of the failed and passed PICs, as shown in Figure 8c,d. From the eye diagram of the failed PICs in Figure 8c, it can be observed that the amplitude levels of the signal are not equidistant, which results in error detection. Unlike the passed PIC with the eye diagram in Figure 8d, an improved equidistant signal level is observed and as such, detection is accomplished with less error at the receiver.
Moreover, by increasing the impact of from 6% to 12%, it is observed that the overlapping levels 10 and 01 increase. As a result of this, the numbers of failed PICs increase, which implies a low yield. Looking at the result of = 12% in Figure 9b, for instance, close to 50% of the PICs failed due to the high spread of levels 01 and 10, as clearly shown in the histogram in Figure 5d, which translates to a high loss in the production scenario.
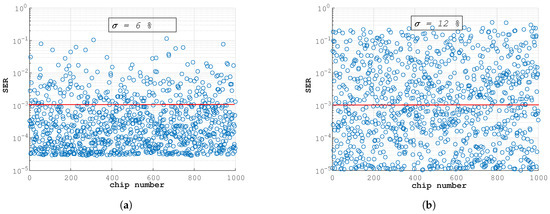
Figure 9.
SER versus the number of PIC mimed at = (a) 6%, (b) 12%.
In addition, the graph in Figure 10 summarizes the percentage of failed and passed chips against all instances of we have tested, which simplified our findings. The number of failed and passed PICs in each we have simulated, as plotted in Figure 8 and Figure 9, are obtained and estimated as a percentage of the total 1000 runs per . The linear behaviour of the number of both passed and failed chips in the figure can explain what would be expected in a fabrication scenario and this serves as a predictive template to analyse any passive device. Furthermore, the graph also reveals that such an oDAC-based PAM-4 transmitter is sensitive to component deviations resulting from passive variations. In comparison to the related works in [13,16], we have used the SER as a performance metric in this work, which translates to the linear behaviour in correlation with the passive variance. The median of the wavelength deviation in correlation with the distance between identical PIC devices within a wafer has been used in [13], which shows a linear relationship. These findings can also be compared with those in the work in [16], where an OSNR is used as a performance metric for wavelength mismatch. In the work, the waveguide width/thickness also exhibits a linear relationship with the wavelength shift slop, leading to variations in the output signal OSNR performance.
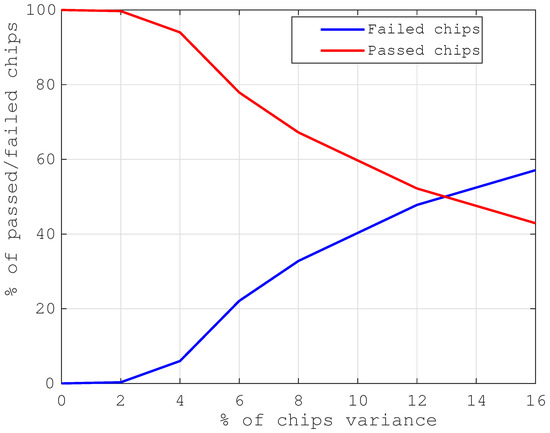
Figure 10.
Percentage of failed and passed chips at different passive variances.
4. Conclusions
In this paper, we have presented a hybrid model to study the effects of fabrication tolerance resulting from passive variation in PIC-based devices. Using the flexibility of FPPGA, an oDAC-based PAM-4 telecommunication transmitter was mimed with passive variances ranging from 0 to 12% while mimicking the production of 1000 oDAC-based PAM-4 transmitters. A Monte Carlo simulation of the device was carried out to predict the production yield at given instances of passive variation. While benchmarking the SER to , the number of failed and passed PICs have been determined at every instance of passive variance we have tested. Using the SER as a performance metric, the effect of passive variation and the SER gives a linear relationship in the number of failed and passed PICs of the oDAC-based PAM-4 transmitter after fabrication. These findings enable robust designs which consider critically the sensitive effect of passive variability on designed components and can be formulated into new design rules.
Author Contributions
A.E.A.: writing—original draft, visualization, conceptualization, methodology, investigation; A.T.: visualization, conceptualization, supervision, funding acquisition; M.L.: supervision, review; J.S.: investigation, software, methodology; T.C.: review, visualization, methodology, investigation; F.R.: software, review, visualization. All authors have read and agreed to the published version of the manuscript.
Funding
This work is supported by the European Regional Development Fund (FEDER), through the Competitiveness and Internationalization Operational Program (COMPETE 2020) of the Portugal 2020 framework [Project POWER with Nr. 070365 (POCI-01-0247-FEDER- 070365)]. The work is also supported by the European Commission through the HORIZON-JU-SNS-2022 FLEX-SCALE project with Grant Agreement number 101096909.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
The original contributions presented in the study are included in the article.
Conflicts of Interest
Authors Adebayo E. Abejide, João Santos, Francisco Rodrigues and António Teixeira are employed by PICAdvanced. Author Tanay Chattopadhyay was employed by the company the West Bengal Power Development Corporation Limited (WBPDCL). The remaining authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
Abbreviations
The following abbreviations are used in this manuscript:
| AM | amplitude modulator |
| ASPIC | application specific photonic integrated circuits |
| CW | continuous wave |
| eDAC | electrical digital to analog converter |
| ER | extinction ratio |
| FPGA | field programmable gateway arrays |
| FPPGA | field programmable photonic gateway arrays |
| IoTs | Internet of Things |
| input coupling factor | |
| output coupling factor | |
| LSB | least significant bit |
| NRZ | non-return-to-zero |
| MSB | most significant bit |
| MZM | Mach Zehnder modulator |
| oDAC | optical digital to analog converter |
| OSNR | optical signal to noise ratio |
| PAM-4 | pulse amplitude modulator level four |
| PAM-8 | pulse amplitude modulator level eight |
| PAM-16 | pulse amplitude modulator level sixteen |
| PIC | Photonic integrated circuits |
| PUC | programmable unit cell |
| PM | phase modulator |
| PS | phase shifter |
| PUC | programmable unit core |
| QAM | quadrature amplitude modulation |
| SER | symbol error rate |
| SiP | Silicon Photonics |
| WDM | wavelength division multiplexing |
Appendix A
Probability density of the four PAM levels is the combination of four Gaussian functions and can be written from a generalized Gaussian probability density function as [28,29]
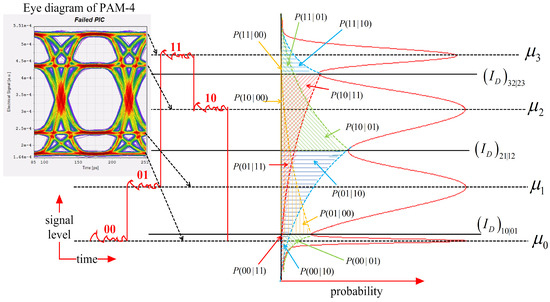
Figure A1.
PAM-4 signal waveform showing the signal levels and equivalent Gaussian probability densities of the four levels. Inset is an eye diagram of a simulated 10 Gbps hybrid PAM-4 signal.
Appendix B
This equation can be summarized as
where can be expressed as
where and are the mean and standard deviation of ith Gaussian level of the PAM-4 signal. is the probability of receiving signal level , which is equally as possible. In addition, depending on the noise contribution due to signal impairment, there is a probability that signal will constitute an error to symbol across the four Gaussian pulses in Figure A1. is the complimentary error function and is the threshold values of the signal level and . Whenever signal detection occurs above the threshold, a higher logical state is considered, and vice versa.
Appendix C
Some of the are cancelled out in Equation (A5), and the final expression to estimate the SER of the oDAC PAM-4 is given by
References
- Li, X.; Faruk, M.S.; Savory, S.J. Bidirectional symmetrical 100 Gb/s/λ coherent PON using a simplified ONU transceiver. IEEE Photonics Technol. Lett. 2022, 34, 838–841. [Google Scholar] [CrossRef]
- Smit, M.; Williams, K.; Tol, J.v.d. 1.3 Integration of Photonics and Electronics. In Proceedings of the 2019 IEEE International Solid- State Circuits Conference—(ISSCC), San Francisco, CA, USA, 17–21 February 2019; pp. 29–34. [Google Scholar] [CrossRef]
- Bogaerts, W.; Rahim, A. Programmable photonics: An opportunity for an accessible large-volume PIC ecosystem. IEEE J. Sel. Top. Quantum Electron. 2020, 26, 8302517. [Google Scholar] [CrossRef]
- Dai, D.; Bauters, J.; Bowers, J.E. Passive technologies for future large-scale photonic integrated circuits on silicon: Polarization handling, light non-reciprocity and loss reduction. Light. Sci. Appl. 2012, 1, e1. [Google Scholar] [CrossRef]
- Billah, M.R.; Blaicher, M.; Hoose, T.; Dietrich, P.I.; Marin-Palomo, P.; Lindenmann, N.; Nesic, A.; Hofmann, A.; Troppenz, U.; Moehrle, M.; et al. Hybrid integration of silicon photonics circuits and InP lasers by photonic wire bonding. Optica 2018, 5, 876–883. [Google Scholar] [CrossRef]
- Falconi, F.; Melo, S.; Scotti, F.; Malik, M.N.; Scaffardi, M.; Porzi, C.; Ansalone, L.; Ghelfi, P.; Bogoni, A. A Combined Radar & Lidar System Based on Integrated Photonics in Silicon-on-Insulator. J. Light. Technol. 2021, 39, 17–23. [Google Scholar] [CrossRef]
- Bogaerts, W. Tutorial Programmable Photonics. In Proceedings of the Optical Fiber Communication Conference (OFC), Washington, DC, USA, 6–11 June 2021; Optica Publishing Group: Washington, DC, USA, 2021; p. Tu1K.1. [Google Scholar] [CrossRef]
- Chrostowski, L.; Flueckiger, J.; Lin, C.; Hochberg, M.; Pond, J.; Klein, J.; Ferguson, J.; Cone, C. Design methodologies for silicon photonic integrated circuits. In Proceedings of the Smart Photonic and Optoelectronic Integrated Circuits XVI. SPIE, San Francisco, CA, USA, 1–6 February 2014; Volume 8989, pp. 83–97. [Google Scholar]
- Xing, Y.; Dong, J.; Khan, U.; Bogaerts, W. Capturing the effects of spatial process variations in silicon photonic circuits. ACS Photonics 2022, 10, 928–944. [Google Scholar] [CrossRef]
- Xing, Y.; Dong, J.; Dwivedi, S.; Khan, U.; Bogaerts, W. Accurate extraction of fabricated geometry using optical measurement. Photonics Res. 2018, 6, 1008–1020. [Google Scholar] [CrossRef]
- Cohen, R.A.; Amrani, O.; Ruschin, S. Improving the tolerances in high-performance silicon photonics modulators. Opt. Contin. 2022, 1, 934–948. [Google Scholar] [CrossRef]
- Bandyopadhyay, S.; Hamerly, R.; Englund, D. Hardware error correction for programmable photonics. Optica 2021, 8, 1247–1255. [Google Scholar] [CrossRef]
- Chrostowski, L.; Wang, X.; Flueckiger, J.; Wu, Y.; Wang, Y.; Fard, S.T. Impact of fabrication non-uniformity on chip-scale silicon photonic integrated circuits. In Proceedings of the Optical Fiber Communication Conference, San Francisco, CA, USA, 14 March 2014; Optica Publishing Group: Washington, DC, USA, 2014; p. Th2A-37. [Google Scholar]
- Nikdast, M.; Nicolescu, G.; Trajkovic, J.; Liboiron-Ladouceur, O. Chip-scale silicon photonic interconnects: A formal study on fabrication non-uniformity. J. Light. Technol. 2016, 34, 3682–3695. [Google Scholar] [CrossRef]
- Lu, Z.; Jhoja, J.; Klein, J.; Wang, X.; Liu, A.; Flueckiger, J.; Pond, J.; Chrostowski, L. Performance prediction for silicon photonics integrated circuits with layout-dependent correlated manufacturing variability. Opt. Express 2017, 25, 9712–9733. [Google Scholar] [CrossRef] [PubMed]
- Nikdast, M.; Nicolescu, G.; Trajkovic, J.; Liboiron-Ladouceur, O. DeEPeR: Enhancing performance and reliability in chip-scale optical interconnection networks. In Proceedings of the 2018 on Great Lakes Symposium on VLSI, Chicago, IL, USA, 23–25 May 2018; pp. 63–68. [Google Scholar]
- Fang, Z. Non-Volatile Programmable Photonics Based on Phase-Change Materials. Ph.D. Thesis, University of Washington, Washington, DC, USA, 2023. [Google Scholar]
- Zhuang, L.; Roeloffzen, C.G.; Hoekman, M.; Boller, K.J.; Lowery, A.J. Programmable photonic signal processor chip for radiofrequency applications. Optica 2015, 2, 854–859. [Google Scholar] [CrossRef]
- Pérez-López, D.; López, A.; DasMahapatra, P.; Capmany, J. Multipurpose self-configuration of programmable photonic circuits. Nat. Commun. 2020, 11, 6359. [Google Scholar] [CrossRef] [PubMed]
- Pérez, D.; Gasulla, I.; Crudgington, L.; Thomson, D.J.; Khokhar, A.Z.; Li, K.; Cao, W.; Mashanovich, G.Z.; Capmany, J. Multipurpose silicon photonics signal processor core. Nat. Commun. 2017, 8, 636. [Google Scholar] [CrossRef] [PubMed]
- Steinbrecher, G.R. Programmable Photonics for Quantum and Classical Information Processing. Ph.D. Thesis, Massachusetts Institute of Technology, Cambridge, MA, USA, 2019. [Google Scholar]
- Pérez, D.; Gasulla, I.; Capmany, J.; Soref, R.A. Reconfigurable lattice mesh designs for programmable photonic processors. Opt. Express 2016, 24, 12093–12106. [Google Scholar] [CrossRef] [PubMed]
- Nazarathy, M.; Tomkos, I. Accurate power-efficient format-scalable multi-parallel optical digital-to-analogue conversion. Photonics 2021, 8, 38. [Google Scholar] [CrossRef]
- Nazarathy, M.; Tomkos, I. Energy-efficient reconfigurable 4|16|64|256-QAM transmitter based on PAM2|4-driven optical DACs. IEEE Photonics Technol. Lett. 2022, 34, 1159–1162. [Google Scholar] [CrossRef]
- Zand, I.; Bogaerts, W. Effects of coupling and phase imperfections in programmable photonic hexagonal waveguide meshes. Photonics Res. 2020, 8, 211–218. [Google Scholar] [CrossRef]
- Lopes, G.; Abejide, A.E.; Santos, J.; Rodrigues, F.; Teixeira, A. Impact of Fabrication Tolerances on the Performance of Integrated Optics. In Proceedings of the 2023 IEEE Research and Applications of Photonics in Defense Conference (RAPID), Miramar Beach, FL, USA, 11–13 September 2023; pp. 1–2. [Google Scholar] [CrossRef]
- Agrawal, G.P. Fiber-Optic Communication Systems; John Wiley & Sons: New York, NY, USA, 2012. [Google Scholar]
- Jeruchim, C.M. Techniques for Estimating the Bit Error Rate in the Simulation of Digital Communication Systems. IEEE J. Sel. Areas Commun. 1984, SAC-2, 153–170. [Google Scholar] [CrossRef]
- Raza, A.; Zhong, K.; Ghafoor, S.; Iqbal, S.; Adeel, M.; Habib, S.; Butt Fasih, U.M.; Lu, C. SER estimation method for 56 GBaud PAM-4 transmission system. Chinease Opt. Lett. 2018, 16, 040604. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).