Polarization-Dependent Formation of Extremely Compressed Femtosecond Wave Packets and Supercontinuum Generation in Fused Silica
Abstract
1. Introduction
2. Materials and Methods
3. Results
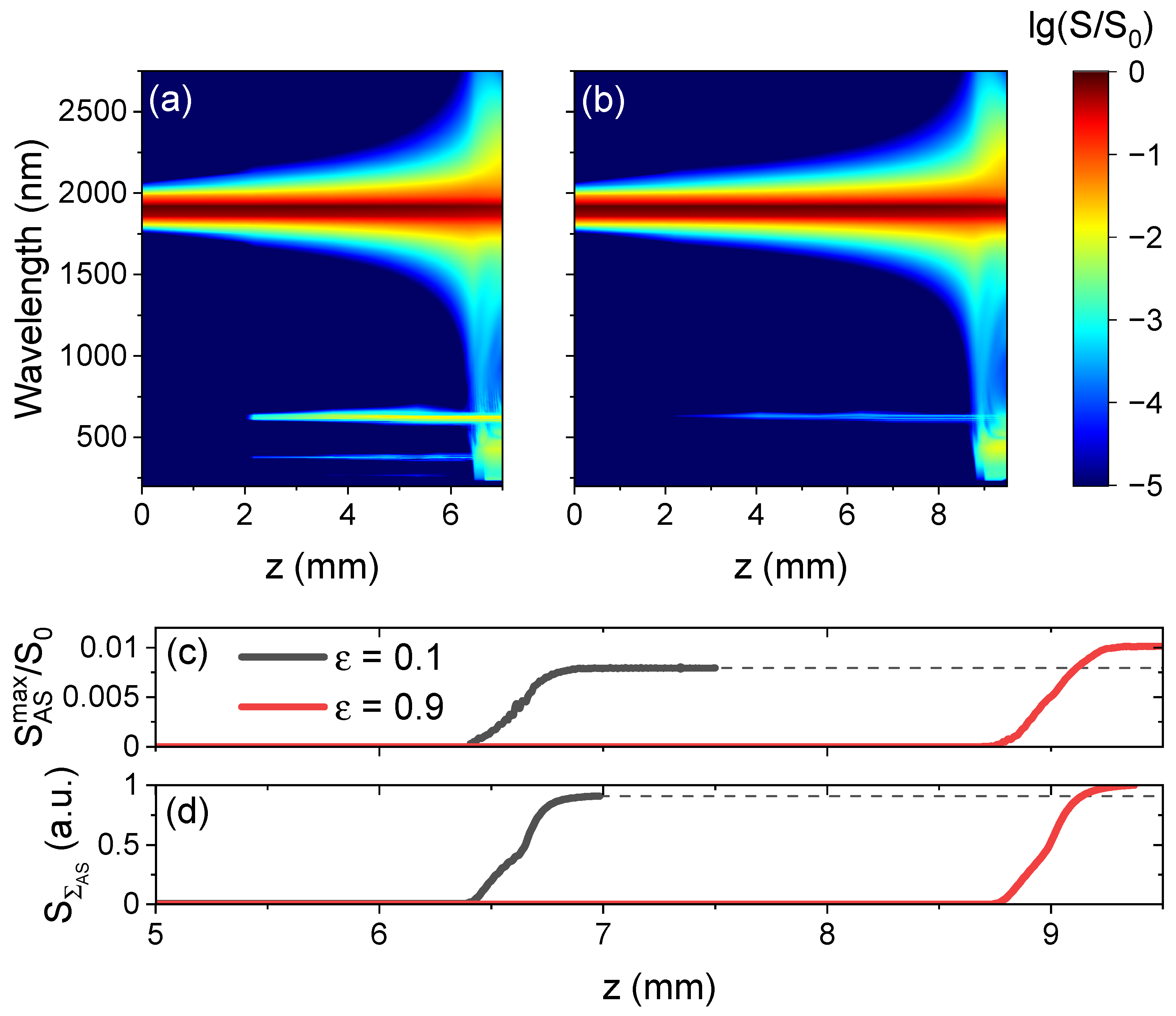
3.1. Polarization-Dependent Light Bullet Supercontinuum
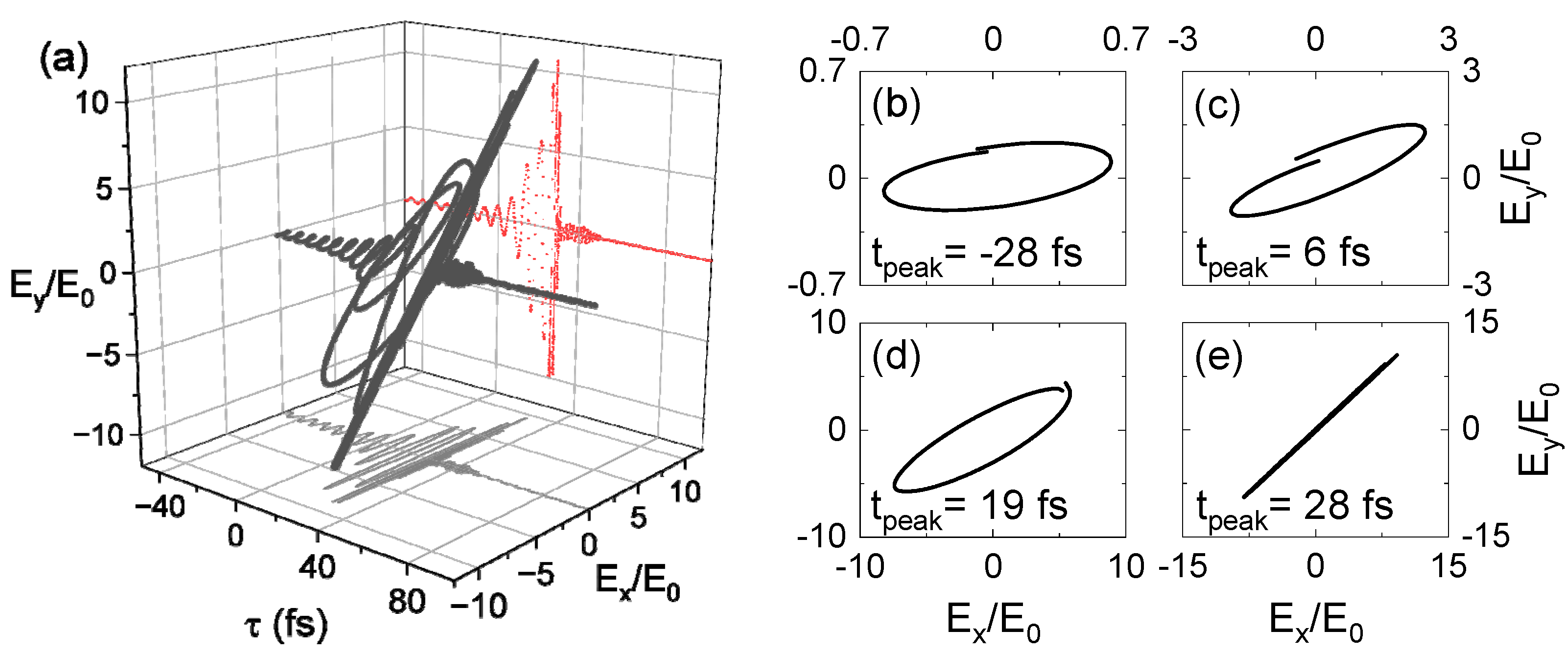
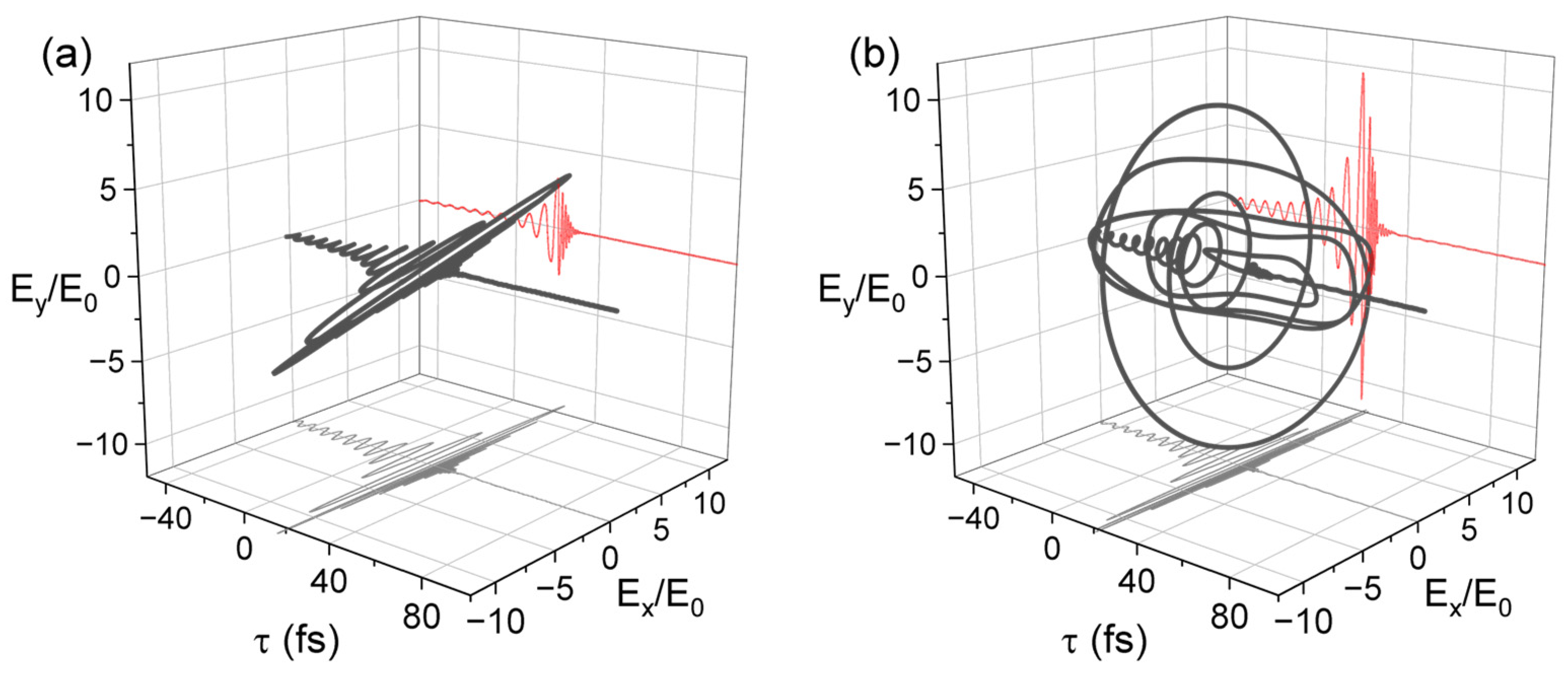
3.2. Dynamics of Polarization Parameters
4. Discussion
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Chin, S.L.; Hosseini, S.A.; Liu, W.; Luo, Q.; Théberge, F.; Aközbek, N.; Becker, A.; Kandidov, V.P.; Kosareva, O.G.; Schroeder, H. The Propagation of Powerful Femtosecond Laser Pulses in Opticalmedia: Physics, Applications, and New Challenges. Can. J. Phys. 2005, 83, 863–905. [Google Scholar] [CrossRef]
- Kandidov, V.P.; Shlenov, S.A.; Kosareva, O.G. Filamentation of High-Power Femtosecond Laser Radiation. Quantum Electron. 2009, 39, 205–228. [Google Scholar] [CrossRef]
- Bergé, L.; Skupin, S. Self-Channeling of Ultrashort Laser Pulses in Materials with Anomalous Dispersion. Phys. Rev. E 2005, 71, 065601. [Google Scholar] [CrossRef] [PubMed]
- Kandidov, V.P.; Zaloznaya, E.D.; Dormidonov, A.E.; Kompanets, V.O.; Chekalin, S.V. Light Bullets in Transparent Dielectrics. Quantum Electron. 2022, 52, 233–246. [Google Scholar] [CrossRef]
- Couairon, A.; Mysyrowicz, A. Femtosecond Filamentation in Transparent Media. Phys. Rep. 2007, 441, 47–189. [Google Scholar] [CrossRef]
- Minardi, S.; Eilenberger, F.; Kartashov, Y.V.; Szameit, A.; Röpke, U.; Kobelke, J.; Schuster, K.; Bartelt, H.; Nolte, S.; Torner, L.; et al. Three-Dimensional Light Bullets in Arrays of Waveguides. Phys. Rev. Lett. 2010, 105, 263901. [Google Scholar] [CrossRef]
- Faccio, D.; Averchi, A.; Lotti, A.; Kolesik, M.; Moloney, J.V.; Couairon, A.; Di Trapani, P. Generation and Control of Extreme Blueshifted Continuum Peaks in Optical Kerr Media. Phys. Rev. A 2008, 78, 033825. [Google Scholar] [CrossRef]
- Calabrese, C.; Stingel, A.M.; Shen, L.; Petersen, P.B. Ultrafast Continuum Mid-Infrared Spectroscopy: Probing the Entire Vibrational Spectrum in a Single Laser Shot with Femtosecond Time Resolution. Opt. Lett. OL 2012, 37, 2265–2267. [Google Scholar] [CrossRef]
- Auböck, G.; Consani, C.; Monni, R.; Cannizzo, A.; van Mourik, F.; Chergui, M. Femtosecond Pump/Supercontinuum-Probe Setup with 20 kHz Repetition Rate. Rev. Sci. Instrum. 2012, 83, 093105. [Google Scholar] [CrossRef]
- Dubietis, A.; Tamošauskas, G.; Šuminas, R.; Jukna, V.; Couairon, A. Ultrafast Supercontinuum Generation in Bulk Condensed Media. Lith. J. Phys. 2017, 57, 113–157. [Google Scholar] [CrossRef]
- Varela, O.; Zaïr, A.; Román, J.S.; Alonso, B.; Sola, I.J.; Prieto, C.; Roso, L. Above-Millijoule Super-Continuum Generation Using Polarisation Dependent Filamentation in Atoms and Molecules. Opt. Express OE 2009, 17, 3630–3639. [Google Scholar] [CrossRef]
- Rostami, S.; Chini, M.; Lim, K.; Palastro, J.P.; Durand, M.; Diels, J.-C.; Arissian, L.; Baudelet, M.; Richardson, M. Dramatic Enhancement of Supercontinuum Generation in Elliptically-Polarized Laser Filaments. Sci. Rep. 2016, 6, 20363. [Google Scholar] [CrossRef]
- Shen, Y.R. The Principles of Nonlinear Optics. Wiley: Hoboken, NJ, USA, 2003; ISBN 978-0-471-43080-3. [Google Scholar]
- Panov, N.A.; Shipilo, D.E.; Andreeva, V.A.; Kosareva, O.G.; Saletsky, A.M.; Xu, H.; Polynkin, P. Supercontinuum of a 3.9 − μ m Filament in Air: Formation of a Two-Octave Plateau and Nonlinearly Enhanced Linear Absorption. Phys. Rev. A 2016, 94, 041801. [Google Scholar] [CrossRef]
- Zukerstein, M.; Levy, Y. Enhancement of the Spectral Broadening Efficiency for Circular Polarization States in the High Absorption Regime for Gaussian and Doughnut-Shaped Beams in Fused Silica. Opt. Express 2023, 31, 16295. [Google Scholar] [CrossRef]
- Dormidonov, A.E.; Zaloznaya, E.D.; Kandidov, V.P.; Kompanets, V.O.; Chekalin, S.V. Formation of a Light Bullet in an Elliptically Polarized Pulse. JETP Lett. 2022, 115, 11–15. [Google Scholar] [CrossRef]
- Alonso, B.; Lopez-Quintas, I.; Holgado, W.; Drevinskas, R.; Kazansky, P.G.; Hernández-García, C.; Sola, Í.J. Complete Spatiotemporal and Polarization Characterization of Ultrafast Vector Beams. Commun. Phys. 2020, 3, 1–10. [Google Scholar] [CrossRef]
- Kolesik, M.; Moloney, J.V. Nonlinear Optical Pulse Propagation Simulation: From Maxwell’s to Unidirectional Equations. Phys. Rev. E 2004, 70, 036604. [Google Scholar] [CrossRef] [PubMed]
- Geints, I.Y.; Zaloznaya, E.D.; Dormidonov, A.E.; Kandidov, V.P. Influence of dispersion on dynamics of the anti-Stokes broadening of the femtosecond pulse spectrum during filamentation in fused silica. Mosc. Univ. Phys. Bull. 2023, 78, 489–495. [Google Scholar] [CrossRef]
- Keldysh, L.V. Ionization in the Field of a Strong Electromagnetic Wave. J. Exp. Theor. Phys. 1965, 20, 1307–1314. [Google Scholar]
- Bogatskaya, A.; Gulina, Y.; Smirnov, N.; Gritsenko, I.; Kudryashov, S.; Popov, A. An Experimental Study of Multiphoton Ionization in Fused Silica at IR and Visible Wavelengths. Photonics 2023, 10, 515. [Google Scholar] [CrossRef]
- Popov, V.S. Tunnel and Multiphoton Ionization of Atoms and Ions in a Strong Laser Field (Keldysh Theory). Physics-Uspekhi 2004, 47, 855. [Google Scholar] [CrossRef]
- Bosshard, C.; Gubler, U.; Kaatz, P.; Mazerant, W.; Meier, U. Non-Phase-Matched Optical Third-Harmonic Generation in Noncentrosymmetric Media: Cascaded Second-Order Contributions for the Calibration of Third-Order Nonlinearities. Phys. Rev. B 2000, 61, 10688–10701. [Google Scholar] [CrossRef]
- Brown, J.M.; Couairon, A.; Gaarde, M.B. Ab Initio Calculations of the Linear and Nonlinear Susceptibilities of N2, O2, and Air in Midinfrared Laser Pulses. Phys. Rev. A 2018, 97, 063421. [Google Scholar] [CrossRef]
- Vrublevskaya, N.R.; Shipilo, D.E.; Nikolaeva, I.A.; Panov, N.A.; Kosareva, O.G. Nonlinear Response of Diluted Gases to an Ultraviolet Femtosecond Pulse. JETP Lett. 2023, 117, 408–413. [Google Scholar] [CrossRef]
- Fedorov, V.Y.; Chanal, M.; Grojo, D.; Tzortzakis, S. Accessing Extreme Spatiotemporal Localization of High-Power Laser Radiation through Transformation Optics and Scalar Wave Equations. Phys. Rev. Lett. 2016, 117, 043902. [Google Scholar] [CrossRef] [PubMed]
- Marburger, J.H. Self-Focusing: Theory. Prog. Quantum Electron. 1975, 4, 35–110. [Google Scholar] [CrossRef]
- Zaloznaya, E.; Kompanets, V.; Dormidonov, A.; Geints, I.; Chekalin, S.; Kandidov, V. Short-Wavelength Cutoff of the Light Bullet Spectrum in Calcium Fluoride. Appl. Phys. B 2021, 127, 42. [Google Scholar] [CrossRef]
- Born, M.; Wolf, E. Principles of Optics. Electromagnetic Theory of Propagation, Interference and Diffraction of Light, 7th ed.; Cambridge University Press: Cambridge, UK, 1999; ISBN 978-1-139-64418-1. [Google Scholar]
- Gryaznov, G.A.; Makarov, V.A.; Perezhogin, I.A.; Potravkin, N.N. Modeling of Nonlinear Optical Activity in Propagation of Ultrashort Elliptically Polarized Laser Pulses. Phys. Rev. E 2014, 89, 013306. [Google Scholar] [CrossRef] [PubMed]
- Aközbek, N.; Iwasaki, A.; Becker, A.; Scalora, M.; Chin, S.L.; Bowden, C.M. Third-Harmonic Generation and Self-Channeling in Air Using High-Power Femtosecond Laser Pulses. Phys. Rev. Lett. 2002, 89, 143901. [Google Scholar] [CrossRef]
- Panov, N.A.; Kosareva, O.G.; Savelev-Trofimov, A.B.; Uryupina, D.S.; Perezhogin, I.A.; Makarov, V.A. Filamentation of Femtosecond Gaussian Pulses with Close-to-Linear or -Circular Elliptical Polarisation. Quantum Electron. 2011, 41, 160–162. [Google Scholar] [CrossRef]
- Kolesik, M.; Moloney, J.V.; Wright, E.M. Polarization Dynamics of Femtosecond Pulses Propagating in Air. Phys. Rev. E 2001, 64, 046607. [Google Scholar] [CrossRef] [PubMed]



Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Geints, I.; Kosareva, O. Polarization-Dependent Formation of Extremely Compressed Femtosecond Wave Packets and Supercontinuum Generation in Fused Silica. Photonics 2024, 11, 620. https://doi.org/10.3390/photonics11070620
Geints I, Kosareva O. Polarization-Dependent Formation of Extremely Compressed Femtosecond Wave Packets and Supercontinuum Generation in Fused Silica. Photonics. 2024; 11(7):620. https://doi.org/10.3390/photonics11070620
Chicago/Turabian StyleGeints, Ilia, and Olga Kosareva. 2024. "Polarization-Dependent Formation of Extremely Compressed Femtosecond Wave Packets and Supercontinuum Generation in Fused Silica" Photonics 11, no. 7: 620. https://doi.org/10.3390/photonics11070620
APA StyleGeints, I., & Kosareva, O. (2024). Polarization-Dependent Formation of Extremely Compressed Femtosecond Wave Packets and Supercontinuum Generation in Fused Silica. Photonics, 11(7), 620. https://doi.org/10.3390/photonics11070620





