Machine Learning in Short-Reach Optical Systems: A Comprehensive Survey
Abstract
1. Introduction
- We review existing deep learning (DL) models, providing a comprehensive understanding of their principles, characteristics, and hypothesis classes. This facilitates an in-depth exploration for researchers seeking supervised neural-network-based ML models suitable for their specific applications.
- We highlight the features and complexities of these models, elucidating recent developments in the field of DL. This information is valuable for researchers interested in delving deeper into research and staying abreast of current advancements.
- We discuss the current limitations and research gaps in the ongoing development of DL, addressing the challenges posed by these factors in real-world applications. Furthermore, we provide constructive insights regarding the selection of models and potential future directions.
- Given the challenge of high hardware complexity, we introduce model compression as a potential solution from the DL field. We present existing works that employ this approach within the optical communication field, aiming to inspire more researchers to pursue research in this domain.
2. Applications in Short-Reach Systems
3. DSP for Signal Equalization in Communication Systems
4. Traditional Sequential ML Methods
5. Advanced Sequential ML Methods
5.1. Distortion Model
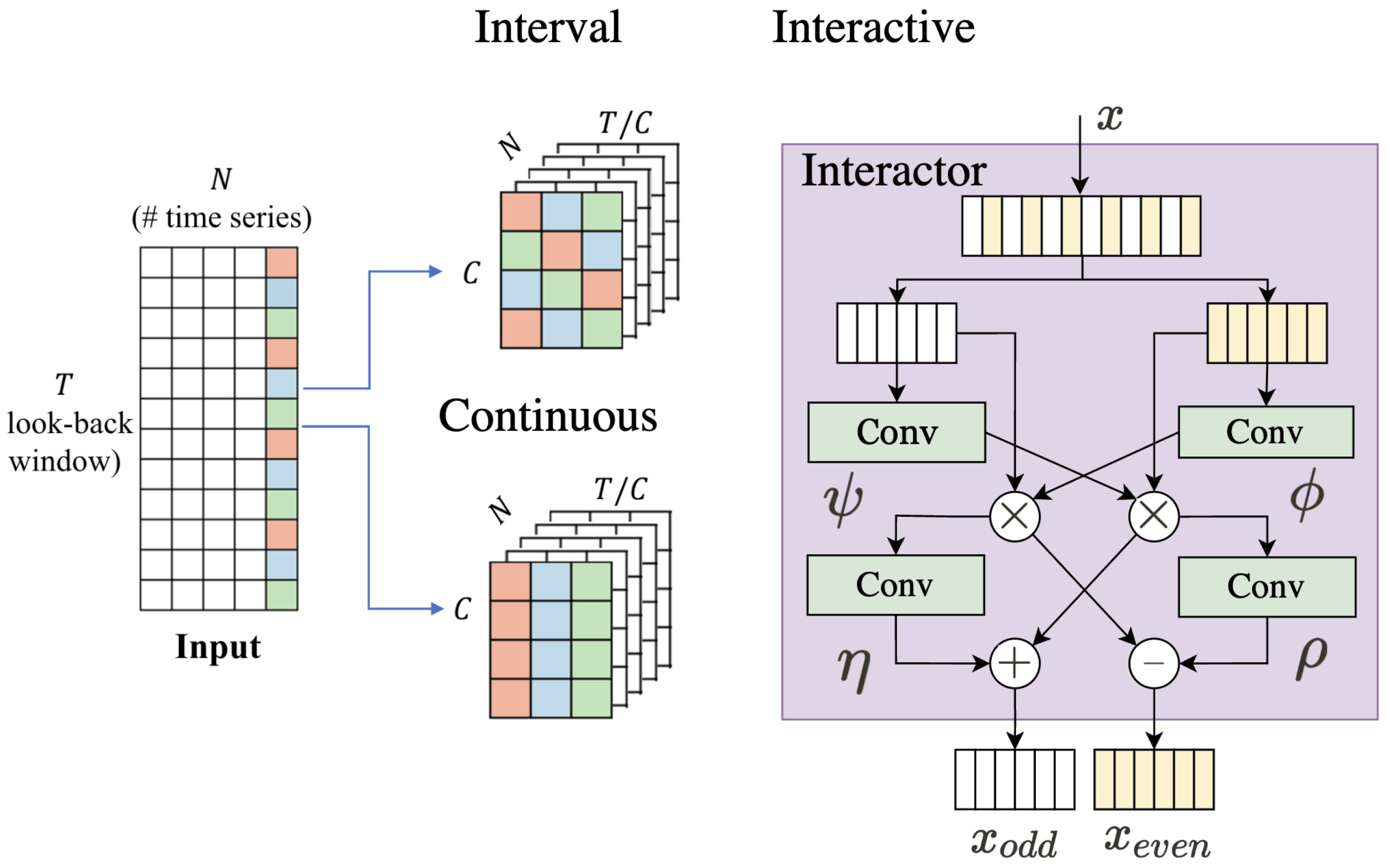
5.2. Temporal Convolution Neural Network
- CNNs can identify patterns regardless of their position within the input sequence. This property makes them well-suited for tasks where the position or timing of relevant features is not fixed, providing greater flexibility compared to LSTM.
- CNNs excel at capturing local patterns and extracting relevant features from the input sequence. This ability is particularly useful for tasks that require identifying and recognizing specific patterns or motifs within the data.
- Both CNNs and SCINet architectures typically have fewer parameters compared to LSTM models. This reduced parameter count can make training and inference more efficient, especially when working with limited computational resources or when dealing with large datasets.
5.3. Transformer-Based Network
5.4. Fourier Convolution Neural Network
6. Model Compression
7. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Durisi, G.; Koch, T.; Popovski, P. Toward massive, ultrareliable, and low-latency wireless communication with short packets. Proc. IEEE 2016, 104, 1711–1726. [Google Scholar] [CrossRef]
- Kapoor, R.; Porter, G.; Tewari, M.; Voelker, G.M.; Vahdat, A. Chronos: Predictable low latency for data center applications. In Proceedings of the Third ACM Symposium on Cloud Computing 2012, San Jose, CA, USA, 14–17 October 2012; pp. 1–14. [Google Scholar] [CrossRef]
- Xie, Y.; Wang, Y.; Kandeepan, S.; Wang, K. Machine learning applications for short reach optical communication. Photonics 2022, 9, 30. [Google Scholar] [CrossRef]
- Wu, Q.; Xu, Z.; Zhu, Y.; Zhang, Y.; Ji, H.; Yang, Y.; Qiao, G.; Liu, L.; Wang, S.; Liang, J.; et al. Machine Learning for Self-Coherent Detection Short-Reach Optical Communications. Photonics 2023, 10, 1001. [Google Scholar] [CrossRef]
- Ranzini, S.M.; Da, R.F.; Bülow, H.; Zibar, D. Tunable Optoelectronic Chromatic Dispersion Compensation Based on Machine Learning for Short-Reach Transmission. Appl. Sci. 2019, 9, 4332. [Google Scholar] [CrossRef]
- Che, D.; Hu, Q.; Shieh, W. Linearization of Direct Detection Optical Channels Using Self-Coherent Subsystems. J. Light. Technol. 2015, 34, 516–524. [Google Scholar] [CrossRef]
- Li, G.; Li, Z.; Ha, Y.; Hu, F.; Zhang, J.; Chi, N. Performance assessments of joint linear and nonlinear pre-equalization schemes in next generation IM/DD PON. J. Light. Technol. 2022, 40, 5478–5489. [Google Scholar] [CrossRef]
- Seb, S.J.; Gavioli, G.; Killey, R.I.; Bayvel, P. Electronic compensation of chromatic dispersion using a digital coherent receiver. Opt. Express 2007, 15, 2120–2126. [Google Scholar] [CrossRef]
- Fludger, C.R.; Duthel, T.; Van den Borne, D.; Schulien, C.; Schmidt, E.; Wuth, T.; Geyer, J.; De Man, E.; Khoe, G.; de Waardt, H. Coherent Equalization and POLMUX-RZ-DQPSK for Robust 100-GE Transmission. J. Light. Technol. 2008, 26, 64–72. [Google Scholar] [CrossRef]
- DeLange, O.E. Optical heterodyne detection. IEEE Spectrum 1968, 5, 77–85. [Google Scholar] [CrossRef]
- Kahn, J.M.; Barry, J.R. Wireless infrared communications. Proc. IEEE 1997, 85, 265–298. [Google Scholar] [CrossRef]
- Huang, L.; Xu, Y.; Jiang, W.; Xue, L.; Hu, W.; Yi, L. Performance and complexity analysis of conventional and deep learning equalizers for the high-speed IMDD PON. J. Light. Technol. 2022, 40, 4528–4538. [Google Scholar] [CrossRef]
- Kartalopoulos, S.V. Free Space Optical Networks for Ultra-Broad Band Services; IEEE: New York, NY, USA, 2011; Volume 256, ISBN 978-111-810-423-1. [Google Scholar]
- Tsiatmas, A.; Willems, F.M.J.; Baggen, C.P.M.J. Square root approximation to the Poisson channel. In Proceedings of the 2013 IEEE International Symposium on Information Theory (ISIT), Istanbul, Turkey, 7–13 July 2013; pp. 1695–1699. [Google Scholar] [CrossRef]
- Moser, S.M. Capacity results of an optical intensity channel with input-dependent Gaussian noise. IEEE Trans. Inf. Theory 2012, 58, 207–223. [Google Scholar] [CrossRef]
- Safari, M. Efficient optical wireless communication in the presence of signal-dependent noise. In Proceedings of the ICCW, London, UK, 8–12 June 2015; pp. 1387–1391. [Google Scholar] [CrossRef]
- Fadlullah, Z.M.; Fouda, M.M.; Kato, N.; Takeuchi, A.; Iwasaki, N.; Nozaki, Y. Toward intelligent machine-to-machine communications in smart grid. IEEE Commun. Mag. 2011, 49, 60–65. [Google Scholar] [CrossRef]
- Yi, L.; Li, P.; Liao, T.; Hu, W. 100 Gb/s/λ IM-DD PON Using 20G-Class Optical Devices by Machine Learning Based Equalization. In Proceedings of the 44th European Conference on Optical Communication, Roma, Italy, 23–27 September 2018; pp. 1–3. [Google Scholar] [CrossRef]
- Kaur, J.; Khan, M.A.; Iftikhar, M.; Imran, M.; Haq, Q.E.U. Machine learning techniques for 5G and beyond. IEEE Access 2021, 9, 23472–23488. [Google Scholar] [CrossRef]
- Simeone, O. A very brief introduction to machine learning with applications to communication systems. IEEE Trans. Cogn. Commun. Netw. 2018, 4, 648–664. [Google Scholar] [CrossRef]
- Rodrigues, T.K.; Suto, K.; Nishiyama, H.; Liu, J.; Kato, N. Machine learning meets computation and communication control in evolving edge and cloud: Challenges and future perspective. IEEE Commun. Surv. Tutor. 2019, 22, 38–67. [Google Scholar] [CrossRef]
- Zhang, Q.; Li, B.; Wu, R. A dynamic bandwidth allocation scheme for GPON based on traffic prediction. In Proceedings of the FSKD 2012: 9th International Conference on Fuzzy Systems and Knowledge Discovery, Chongqing, China, 29–31 May 2012; pp. 2043–2046. [Google Scholar] [CrossRef]
- Sarigiannidis, P.; Pliatsios, D.; Zygiridis, T.; Kantartzis, N. DAMA: A data mining forecasting DBA scheme for XG-PONs. In Proceedings of the 2016 5th International Conference on Modern Circuits and Systems Technologies (MOCAST), Thessaloniki, Greece, 12–14 May 2016; pp. 1–4. [Google Scholar] [CrossRef]
- Ruan, L.; Wong, E. Machine intelligence in allocating bandwidth to achieve low-latency performance. In Proceedings of the 2018 International Conference on Optical Network Design and Modeling (ONDM), Dublin, Ireland, 14–17 May 2018; pp. 226–229. [Google Scholar] [CrossRef]
- Yi, L.; Liao, T.; Huang, L.; Xue, L.; Li, P.; Hu, W. Machine Learning for 100 Gb/s/λ Passive Optical Network. J. Light. Technol. 2019, 37, 1621–1630. [Google Scholar] [CrossRef]
- Mikaeil, A.M.; Hu, W.; Hussain, S.B.; Sultan, A. Traffic-Estimation-Based Low-Latency XGS-PON Mobile Front-Haul for Small-Cell C-RAN Based on an Adaptive Learning Neural Network. Appl. Sci. 2018, 8, 1097. [Google Scholar] [CrossRef]
- Chen, T.; Guestrin, C. XGBoost, A Scalable Tree Boosting System. In Proceedings of the 22nd ACM SIGKDD (2016), International Conference on Knowledge Discovery and Data Mining, San Francisco, CA, USA, 13–17 August 2016; pp. 1–3. [Google Scholar] [CrossRef]
- Ye, C.; Zhang, D.; Hu, X.; Huang, X.; Feng, H.; Zhang, K. Recurrent Neural Network (RNN) Based End-to-End Nonlinear Management for Symmetrical 50Gbps NRZ PON with 29dB+ Loss Budget. In Proceedings of the 44th European Conference on Optical Communication, Roma, Italy, 23–27 September 2018; pp. 1–3. [Google Scholar] [CrossRef]
- Kanonakis, K.; Giacoumidis, E.; Tomkos, I. Physical-Layer-Aware MAC Schemes for Dynamic Subcarrier Assignment in OFDMA-PON Networks. J. Light. Technol. 2012, 30, 1915–1923. [Google Scholar] [CrossRef]
- Lim, W.; Kourtessis, P.; Senior, J.M.; Na, Y.; Allawi, Y.; Jeon, S.B.; Chung, H. Dynamic Bandwidth Allocation for OFDMA-PONs Using Hidden Markov Model. IEEE Access 2017, 5, 21016–21019. [Google Scholar] [CrossRef]
- Bi, M.; Xiao, S.; Wang, L. Joint subcarrier channel and time slots allocation algorithm in OFDMA passive optical networks. Opt. Commun. 2013, 287, 90–95. [Google Scholar] [CrossRef]
- Zhu, M.; Gu, J.; Chen, B.; Gu, P. Dynamic Subcarrier Assignment in OFDMA-PONs Based on Deep Reinforcement Learning. IEEE Photonics J. 2022, 14, 1–11. [Google Scholar] [CrossRef]
- Senoo, Y.; Asaka, K.; Kanai, T.; Sugawa, J.; Saito, H.; Tamai, H.; Minato, N.; Suzuki, K.I.; Otaka, A. Fairness-Aware Dynamic Sub-Carrier Allocation in Distance-Adaptive Modulation OFDMA-PON for Elastic Lambda Aggregation Networks. J. Opt. Commun. Netw. 2017, 9, 616–624. [Google Scholar] [CrossRef]
- Nakayama, Y.; Onodera, Y.; Nguyen, A.H.N.; Hara-Azumi, Y. Real-Time Resource Allocation in Passive Optical Network for Energy-Efficient Inference at GPU-Based Network Edge. IEEE Internet Things J. 2022, 9, 17348–17358. [Google Scholar] [CrossRef]
- Cabrera, A.; Almeida, F.; Castellanos-Nieves, D.; Oleksiak, A.; Blanco, V. Energy efficient power cap configurations through Pareto front analysis and machine learning categorization. Clust. Comput. 2023, 27, 3433–3449. [Google Scholar] [CrossRef]
- Chen, Z.; Wang, W.; Zou, D.; Ni, W.; Luo, D.; Li, F. Real-Valued Neural Network Nonlinear Equalization for Long-Reach PONs Based on SSB Modulation. IEEE Photonics Technol. Lett. 2022, 35, 167–170. [Google Scholar] [CrossRef]
- Xue, L.; Yi, L.; Lin, R.; Huang, L.; Chen, J. SOA pattern effect mitigation by neural network based pre-equalizer for 50G PON Opt. Opt. Express 2021, 29, 24714–24722. [Google Scholar] [CrossRef]
- Abdelli, K.; Tropschug, C.; Griesser, H.; Pachnicke, S. Fault Monitoring in Passive Optical Networks using Machine Learning Techniques. In Proceedings of the 23rd International Conference on Transparent Optical Networks, Bucharest, Romania, 2–6 July 2023; pp. 1–5. [Google Scholar] [CrossRef]
- Vela, A.P.; Shariati, B.; Ruiz, M.; Cugini, F.; Castro, A.; Lu, H.; Proietti, R.; Comellas, J.; Castoldi, P.; Yoo, S.J.B.; et al. Soft Failure Localization During Commissioning Testing and Lightpath Operation. J. Opt. Commun. Netw. 2018, 10, A27–A36. [Google Scholar] [CrossRef]
- Wang, Z.; Zhang, M.; Wang, D.; Song, C.; Liu, M.; Li, J.; Lou, L.; Liu, Z. Failure prediction using machine learning and time series in optical network. Opt. Express 2017, 25, 18553–18565. [Google Scholar] [CrossRef]
- Tufts, D.W. Nyquist’s Problem—The Joint Optimization of Transmitter and Receiver in Pulse Amplitude Modulation. Proc. IEEE 1965, 53, 248–259. [Google Scholar] [CrossRef]
- Munagala, R.L.; Vijay, U.K. A novel 3-tap adaptive feed forward equalizer for high speed wireline receivers. In Proceedings of the 2017 IEEE International Symposium on Circuits and Systems (ISCAS), Baltimore, MD, USA, 28–31 May 2017; pp. 1–4. [Google Scholar] [CrossRef]
- Williamson, D.; Kennedy, R.A.; Pulford, G.W. Block decision feedback equalization. IEEE Trans. Commun. 1992, 40, 255–264. [Google Scholar] [CrossRef]
- Forney, G.D. The Viterbi Algorithm: A Personal History. arXiv 2005, arXiv:cs/0504020. [Google Scholar]
- Du, L.B.; Lowery, A.J. Digital Signal Processing for Coherent Optical Communication Systems. IEEE J. Light. Technol. 2013, 31, 1547–1556. [Google Scholar]
- Malik, G.; Sappal, A.S. Adaptive Equalization Algorithms: An Overview. Int. J. Adv. Comput. Sci. Appl. 2011, 2. [Google Scholar] [CrossRef]
- Karanov, B.; Chagnon, M.; Thouin, F.; Eriksson, T.A.; Bülow, H.; Lavery, D.; Bayvel, P.; Schmalen, L. End-to-End Deep Learning of Optical Fiber Communications. J. Light. Technol. 2018, 36, 4843–4855. [Google Scholar] [CrossRef]
- Graves, A. Long Short-Term Memory. In Supervised Sequence Labelling with Recurrent Neural Networks; Springer: Berlin/Heidelberg, Germany, 2012; pp. 37–45. [Google Scholar] [CrossRef]
- Pascanu, R.; Gulcehre, C.; Cho, K.; Bengio, Y. How to Construct Deep Recurrent Neural Networks. arXiv 2013, arXiv:1312.6026. [Google Scholar]
- Jing, L.; Gulcehre, C.; Peurifoy, J.; Shen, Y.; Tegmark, M.; Soljacic, M.; Bengio, Y. Gated Orthogonal Recurrent Units: On Learning to Forget. Neural Comput. 2019, 31, 765–783. [Google Scholar] [CrossRef] [PubMed]
- Qin, X.; Yang, C.; Guo, H.; Gao, Y.; Zhou, Q.; Wang, X.; Wang, Z. Recurrent Neural Network Based Joint Equalization and Decoding Method for Trellis Coded Modulated Optical Communication System. J. Light. Technol. 2023, 41, 1734–1741. [Google Scholar] [CrossRef]
- Pascanu, R.; Mikolov, T.; Bengio, Y. On the difficulty of training recurrent neural networks. In Proceedings of the 2013 International Conference on Machine Learning (ICML), Atlanta, GA, USA, 16–21 June 2013; pp. 1310–1318. [Google Scholar] [CrossRef]
- Bengio, Y.; Simard, P.; Frasconi, P. Learning long-term dependencies with gradient descent is difficult. IEEE Trans. Neural Netw. 1994, 5, 157–166. [Google Scholar] [CrossRef]
- Hochreiter, S.; Schmidhuber, J. Long Short-Term Memory. Neural Comput. 1997, 9, 1735–1780. [Google Scholar] [CrossRef]
- Ling, P.; Li, M.; Guan, W. Channel-Attention-Enhanced LSTM Neural Network Decoder and Equalizer for RSE-Based Optical Camera Communications. Electronics 2022, 11, 1272. [Google Scholar] [CrossRef]
- Dey, R.; Salem, F.M. Gate-variants of Gated Recurrent Unit (GRU) neural networks. In Proceedings of the IEEE 60th International Midwest Symposium on Circuits and Systems (MWSCAS 2017), Boston, MA, USA, 6–9 August 2017; pp. 1597–1600. [Google Scholar] [CrossRef]
- Deligiannidis, S.; Mesaritakis, C.; Bogris, A. Performance and Complexity Analysis of Bi-Directional Recurrent Neural Network Models versus Volterra Nonlinear Equalizers in Digital Coherent Systems. J. Light. Technol. 2021, 39, 5791–5798. [Google Scholar] [CrossRef]
- Liu, X.; Wang, Y.; Wang, X.; Xu, H.; Li, C.; Xin, X. Bi-directional gated recurrent unit neural network based nonlinear equalizer for coherent optical communication system. Opt. Express 2021, 29, 5923–5933. [Google Scholar] [CrossRef] [PubMed]
- Wu, N.; Wang, X.; Lin, B.; Zhang, K. A CNN-Based End-to-End Learning Framework Toward Intelligent Communication Systems. IEEE Access 2019, 7, 110197–110204. [Google Scholar] [CrossRef]
- Szegedy, C.; Liu, W.; Jia, Y.; Sermanet, P.; Reed, S.E.; Anguelov, D.; Erhan, D.; Vanhoucke, V.; Rabinovich, A. Going deeper with convolutions. In Proceedings of the 2015 IEEE Conference on Computer Vision and Pattern Recognition (CVPR), Columbus, OH, USA, 24–27 June 2014; pp. 1–9. [Google Scholar] [CrossRef]
- Liu, M.; Zeng, A.; Chen, M.; Xu, Z.; Lai, Q.; Ma, L.; Xu, Q. Scinet: Time series modeling and forecasting with sample convolution and interaction. In Proceedings of the 36th Conference on Neural Information Processing Systems (NeurIPS 2022), New Orleans, LA, USA, 28 November–9 December 2022; pp. 5816–5828. [Google Scholar] [CrossRef]
- Shao, C.; Giacoumidis, E.; Li, S.; Li, J.; Farber, M.; Kafer, T.; Richter, A. A Novel Machine Learning-based Equalizer for a Downstream 100G PAM-4 PON. In Proceedings of the 2024 Optical Fiber Communication Conference and Exhibition (OFC’24), San Diego, CA, USA, 24–28 March 2024; Available online: https://opg.optica.org/abstract.cfm?uri=ofc-2024-W1H.1&origin=search (accessed on 1 March 2024).
- Zhang, T.; Zhang, Y.; Cao, W.; Bian, J.; Yi, X.; Zheng, S.; Li, J. Less Is More: Fast Multivariate Time Series Forecasting with Light Sampling-oriented MLP Structures. In Proceedings of the Conference on Robot Learning (CoRR 2022), Auckland, New Zealand, 14 December 2022. [Google Scholar] [CrossRef]
- Zeng, A.; Chen, M.; Zhang, L.; Xu, Q. Are Transformers Effective for Time Series Forecasting? In Proceedings of the Conference on Artificial Intelligence (AAAI 2022), Arlington, VA, USA, 17–19 November 2022. [Google Scholar] [CrossRef]
- Kiencke, U.; Eger, R. Messtechnik: Systemtheorie für Elektrotechniker; Springer: Berlin/Heidelberg, Germany, 2008; XII 341; ISBN 978-3-540-78429-6. [Google Scholar]
- Vaswani, A.; Shazeer, N.M.; Parmar, N.; Uszkoreit, J.; Jones, L.; Gomez, A.N.; Kaiser, L.; Polosukhin, I. Attention is All you Need. In Proceedings of the Neural Information Processing Systems (NIPS’17), Long Beach, CA, USA, 4–9 December 2017; pp. 6000–6010. [Google Scholar] [CrossRef]
- Kitaev, N.; Kaiser, L.; Levskaya, A. Reformer: The Efficient Transformer. In Proceedings of the International Conference on Learning Representations (ICLR 2020), Addis Ababa, Ethiopia, 26–30 April 2020. [Google Scholar] [CrossRef]
- Wu, H.; Xu, J.; Wang, J.; Long, M. Autoformer: Decomposition Transformers with Auto-Correlation for Long-Term Series Forecasting. In Proceedings of the Neural Information Processing Systems, (NIPS 2021), Virtual, 6–14 December 2021; Volume 34, pp. 22419–22430. [Google Scholar]
- Li, S.; Jin, X.; Xuan, Y.; Zhou, X.; Chen, W.; Wang, Y.; Yan, X. Enhancing the Locality and Breaking the Memory Bottleneck of Transformer on Time Series Forecasting. In Proceedings of the 33rd Conference on Neural Information Processing Systems (NeurIPS 2019), Vancouver, WA, USA, 8–14 December 2019. [Google Scholar]
- Zhou, H.; Zhang, S.; Peng, J.; Zhang, S.; Li, J.; Xiong, H.; Zhang, W. Informer: Beyond Efficient Transformer for Long Sequence Time-Series Forecasting. In Proceedings of the AAAI conference on artificial intelligence, Vancouver, BC, Canada, 2–9 February 2021; pp. 11106–11115. [Google Scholar] [CrossRef]
- Shabani, A.; Abdi, A.; Meng, L.; Sylvain, T. Scaleformer: Iterative multi-scale refining transformers for time series forecasting. In Proceedings of the International Conference on Learning Representations (2022), Virtual, 25–29 April 2022. [Google Scholar] [CrossRef]
- Chen, W.; Wang, W.; Peng, B.; Wen, Q.; Zhou, T.; Sun, L. Learning to Rotate: Quaternion Transformer for Complicated Periodical Time Series Forecasting. In Proceedings of the 28th ACM SIGKDD Conference on Knowledge Discovery and Data Mining (KDD’22), Association for Computing Machinery, Washington, DC, USA, 14–18 August 2022; pp. 146–156. [Google Scholar] [CrossRef]
- Liu, S.; Yu, H.; Liao, C.; Li, J.; Lin, W.; Liu, A.X.; Dustdar, S. Pyraformer: Low-Complexity Pyramidal Attention for Long-Range Time Series Modeling and Forecasting. In Proceedings of the International Conference on Learning Representations (ICLR 2022), Virtual, 25–29 April 2022. [Google Scholar] [CrossRef]
- Zhou, T.; Ma, Z.; Wen, Q.; Wang, X.; Sun, L.; Jin, R. FEDformer: Frequency Enhanced Decomposed Transformer for Long-term Series Forecasting. In Proceedings of the 39th International Conference on Machine Learning (PMLR 2022), Baltimore, MD, USA, 17–23 July 2022; p. 162. [Google Scholar]
- Zhang, Y.; Yan, J. Crossformer: Transformer Utilizing Cross-Dimension Dependency for Multivariate Time Series Forecasting. In Proceedings of the International Conference on Learning Representations (2023), Kigali, Rwanda, 1–5 May 2023. [Google Scholar]
- Cirstea, R.; Guo, C.; Yang, B.; Kieu, T.; Dong, X.; Pan, S. Triformer: Triangular, Variable-Specific Attentions for Long Sequence Multivariate Time Series Forecasting-Full Version. In Proceedings of the International Joint Conference on Artificial Intelligence (IJCAI 2022), Vienna, Austria, 23–29 July 2022. [Google Scholar] [CrossRef]
- Zerveas, G.; Jayaraman, S.; Patel, D.; Bhamidipaty, A.; Eickhoff, C. A transformer-based framework for multivariate time series representation learning. In Proceedings of the 27th ACM SIGKDD Conference on Knowledge Discovery & Data Mining (KDD 2021), Singapore, 8–14 December 2021; pp. 2114–2124. [Google Scholar] [CrossRef]
- Wu, H.; Hu, T.; Liu, Y.; Zhou, H.; Wang, J.; Long, M. TimesNet: Temporal 2D-Variation Modeling for General Time Series Analysis. In Proceedings of the International Conference on Learning Representations (ICLR 2022), Virtual, 25–29 April 2022. [Google Scholar] [CrossRef]
- Yi, K.; Zhang, Q.; Fan, W.; Wang, S.; Wang, P.; He, H.; An, N.; Lian, D.; Cao, L.; Niu, Z. Frequency-domain MLPs are More Effective Learners in Time Series Forecasting. In Proceedings of the Thirty-Seventh Conference on Neural Information Processing Systems (NIPS 2023), New Orleans, LA, USA, 10–16 December 2023. [Google Scholar] [CrossRef]
- Franceschi, J.; Dieuleveut, A.; Jaggi, M. Unsupervised Scalable Representation Learning for Multivariate Time Series. In Proceedings of the Neural Information Processing Systems (NIPS 2019), Vancouver, WA, USA, 8–14 December 2019. [Google Scholar] [CrossRef]
- Wu, Z.; Pan, S.; Long, G.; Jiang, J.; Zhang, C. Graph WaveNet for Deep Spatial-Temporal Graph Modeling. In Proceedings of the Twenty-Eighth International Joint Conference on Artificial Intelligence (IJCAI-19), Macao, China, 10–16 August 2019. [Google Scholar] [CrossRef]
- Shao, C.; Giacoumidis, E.; Matalla, P.; Li, J.; Li, S.; Randel, S.; Richter, A.; Faerber, M.; Kaefer, T. Advanced Equalization in 112 Gb/s Upstream PON Using a Novel Fourier Convolution-Based Network, Submitted to the European Conference on Optical Communication (ECOC 2024). Available online: https://arxiv.org/pdf/2405.02609 (accessed on 1 March 2024).
- Lew, J.; Shah, D.; Pati, S.; Cattell, S.; Zhang, M.; Sandhupatla, A.; Ng, C.; Goli, N.; Sinclair, M.D.; Rogers, T.G.; et al. Analyzing Machine Learning Workloads Using a Detailed GPU Simulator. In Proceedings of the IEEE International Symposium on Performance Analysis of Systems and Software (ISPASS 2019), Wisconsin, WI, USA, 24–26 March 2019; pp. 151–152. [Google Scholar] [CrossRef]
- Marculescu, D.; Stamoulis, D.; Cai, E. Hardware-Aware Machine Learning: Modeling and Optimization. In Proceedings of the 2018 IEEE/ACM International Conference on Computer-Aided Design (ICCAD), New York, NY, USA, 5–8 November 2018; pp. 1–8. [Google Scholar] [CrossRef]
- Freire, P.J.; Osadchuk, Y.; Spinnler, B.; Napoli, A.; Schairer, W.; Costa, N.; Prilepsky, J.E.; Turitsyn, S.K. Performance Versus Complexity Study of Neural Network Equalizers in Coherent Optical Systems. J. Light. Technol. 2021, 39, 6085–6096. [Google Scholar] [CrossRef]
- Asghar, M.Z.; Abbas, M.; Zeeshan, K.; Kotilainen, P.; Hämäläinen, T. Assessment of Deep Learning Methodology for Self-Organizing 5G Networks. Appl. Sci. 2019, 9, 2975. [Google Scholar] [CrossRef]
- Xu, Z.; Sun, C.; Ji, T.; Manton, J.H.; Shieh, W. Computational complexity comparison of feedforward/radial basis function/recurrent neural network-based equalizer for a 50-Gb/s PAM4 direct-detection optical link. Opt. Express 2019, 27, 36953–36964. [Google Scholar] [CrossRef] [PubMed]
- Bucila, C.; Caruana, R.; Niculescu-Mizil, A. Model compression. In Proceedings of the 12th ACM SIGKDD International Conference on Knowledge Discovery and Data Mining, New York, NY, USA, 20–23 August 2006; pp. 535–541. [Google Scholar] [CrossRef]
- Gou, J.; Yu, B.; Maybank, S.J.; Tao, D. Knowledge Distillation: A Survey. Int. J. Comput. Vis. 2020, 129, 1789–1819. [Google Scholar] [CrossRef]
- Hinton, G.; Vinyals, O.; Dean, J. Distilling the Knowledge in a Neural Network. arXiv 2015, arXiv:1503.02531. [Google Scholar]
- Chang, A.X.; Culurciello, E. Hardware accelerators for recurrent neural networks on FPGA. In Proceedings of the 2017 IEEE International Symposium on Circuits and Systems (ISCAS 2017), Baltimore, MD, USA, 28–31 May 2017; pp. 1–4. [Google Scholar] [CrossRef]
- Srivallapanondh, S.; Freire, P.J.; Spinnler, B.; Costa, N.; Napoli, A.; Turitsyn, S.K.; Prilepsky, J.E. Knowledge Distillation Applied to Optical Channel Equalization: Solving the Parallelization Problem of Recurrent Connection. In Proceedings of the 2023 Optical Fiber Communications Conference and Exhibition (OFC), San Diego, CA, USA, 5–9 March 2023; p. Th1F.7. [Google Scholar] [CrossRef]
- Robert, R.; Yuliana, Z. Parallel and High Performance Computing; Manning Publications: Greenwich, CT, USA, 2021; Volume 704, ISBN 978-161-729-646-8. [Google Scholar]
- Hayashi, S.; Tanimoto, A.; Kashima, H. Long-Term Prediction of Small Time-Series Data Using Generalized Distillation. In Proceedings of the International Joint Conference on Neural Networks (IJCNN 2019), Budapest, Hungary, 14–19 July 2019; pp. 1–8. [Google Scholar] [CrossRef]
- Gray, R.M. Vector quantization. IEEE Assp Mag. 2019, 1, 4–29. [Google Scholar] [CrossRef]
- Pourghasemi, H.R.; Gayen, A.; Lasaponara, R.; Tiefenbacher, J.P. Application of learning vector quantization and different machine learning techniques to assessing forest fire influence factors and spatial modelling. Environ. Res. 2020, 184, 109321. [Google Scholar] [CrossRef] [PubMed]
- Wang, X.; Takaki, S.; Yamagishi, J.; King, S.; Tokuda, K. A Vector Quantized Variational Autoencoder (VQ-VAE) Autoregressive Neural F0 Model for Statistical Parametric Speech Synthesis. IEEE/ACM Trans. Audio Speech Lang. Process. 2019, 28, 157–170. [Google Scholar] [CrossRef]
- Rasul, K.; Park, Y.J.; Ramström, M.N.; Kim, K.M. VQ-AR: Vector Quantized Autoregressive Probabilistic Time Series Forecasting. In Proceedings of the Twelfth International Conference on Learning Representations (ICLR 2024), Vienna, Austria, 7–11 May 2024. [Google Scholar] [CrossRef]
- Ozair, S.; Li, Y.; Razavi, A.; Antonoglou, I.; Van Den Oord, A.; Vinyals, O. Vector quantized models for planning. In Proceedings of the International Conference on Machine Learning (ICML 2021), Virtual, 18–24 July 2021; pp. 8302–8313. [Google Scholar] [CrossRef]
| Models | DFE | FFE | LE | Adaptive Filtering | Viterbi |
|---|---|---|---|---|---|
| Train | |||||
| Inference |
| Models | DNN | GRU | LSTM | RNN | CNN |
|---|---|---|---|---|---|
| Train | |||||
| Inference |
| Models | Efficient Techniques | Literature | |
|---|---|---|---|
| Transformer | Attention | Sparsity inductive bias | Ref. [69] LogTrans leverages convolutional self-attention for improved accuracy with lower memory costs. |
| Low-rank property | Ref. [70] Informer selects dominant queries based on queries and key similarities. | ||
| Learned rotate attention (LRA) | Ref. [72] Quatformer introduces learnable period and phase information to depict intricate periodical patterns. | ||
| Hierarchical pyramidal attention | Ref. [73] Pyraformer proposed one hierarchial attention mechanism with a binary tree following the path with linear time and memory complexity | ||
| Frequency attention | Ref. [74] FEDformer: proposed the attention operation with Fourier transform and wavelet transform. | ||
| Correlation attention | Ref. [68] Autoformer: the Auto-Correlation mechanism to capture sub-series similarity based on auto-correlation and seires decomposition | ||
| Cross-dimension dependency | Ref. [75] Crossformer utilizes multiple attention matrices to capture cross-dimension dependency | ||
| Architecture | triangular patch attention | Ref. [76] Triformer features a triangular, variable-specific patch attention with a lightweight and linear complexity | |
| Multi-scale framework | Ref. [71] Scaleformer iteratively refines a forecasted time series at multiple scales with shared weights | ||
| Positional rncoding | Vallina Position | Ref. [66] cos and sin functions with a sampling rate-relevant period. | |
| Relative positional encoding | Ref. [77] Introduces an embedding layer that learns embedding vectors for each position index. | ||
| Model-based learned | Ref. [69] LogSparse utilize one LSTM to learn relative position between series tokens | ||
| Fourier-NN | Time Domain | Series Decomposition | Ref. [64] DLinear performs one linear series decomposition with multiple layers |
| Frequency Attention | Ref. [78] TimesNet proposes the attention mechanism related to the amplitude of the signal | ||
| Frequency Domain | Frequency MLP | Ref. [79] FreqMLP performs MLP in frequency domain by leveraging the global view and energy compaction characteristic | |
| TConv-NN | Sampling | Continous | Refs. [63,78] both utilize continous sampling to split original signal into windowed subseries similar to short time transformation |
| Interval | Ref. [63] Interval sampling with fixed step to extract periodic feature | ||
| Even-Odd/Multiscale | Ref. [62] proposes one iterative multiscale framework where even and odd series are interacted between layers | ||
| Frequency Continous | Ref. [64] leverages series decomposition module in a iterative manner to decompose signal in frequency domain with function. | ||
| Negative sampling | Ref. [80] custom loss function is employed in an unsupervised manner, wherein distant or non-stationary subseries maximize the loss, while similar subseries minimize the loss. | ||
| Feature module | MLP | Ref. [63] applies an MLP-based structure to both interval sampling and continuous sampling for extracting trend and detail information. | |
| Dilated convolutions | Ref. [81] leverages stacked dilated casual convolutions to handle spatial-temporal graph data with long-range temporal sequences | ||
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Shao, C.; Giacoumidis, E.; Billah, S.M.; Li, S.; Li, J.; Sahu, P.; Richter, A.; Faerber, M.; Kaefer, T. Machine Learning in Short-Reach Optical Systems: A Comprehensive Survey. Photonics 2024, 11, 613. https://doi.org/10.3390/photonics11070613
Shao C, Giacoumidis E, Billah SM, Li S, Li J, Sahu P, Richter A, Faerber M, Kaefer T. Machine Learning in Short-Reach Optical Systems: A Comprehensive Survey. Photonics. 2024; 11(7):613. https://doi.org/10.3390/photonics11070613
Chicago/Turabian StyleShao, Chen, Elias Giacoumidis, Syed Moktacim Billah, Shi Li, Jialei Li, Prashasti Sahu, André Richter, Michael Faerber, and Tobias Kaefer. 2024. "Machine Learning in Short-Reach Optical Systems: A Comprehensive Survey" Photonics 11, no. 7: 613. https://doi.org/10.3390/photonics11070613
APA StyleShao, C., Giacoumidis, E., Billah, S. M., Li, S., Li, J., Sahu, P., Richter, A., Faerber, M., & Kaefer, T. (2024). Machine Learning in Short-Reach Optical Systems: A Comprehensive Survey. Photonics, 11(7), 613. https://doi.org/10.3390/photonics11070613





