Abstract
Lateral inhibition is a prevalent occurrence within the biological neural system, enhancing the human brain’s ability to perceive edge information within a given scene. With the increasing prominence of neural network-based machine vision, there is a significant importance in incorporating this crucial biological mechanism into the field of machine vision. However, current research on lateral inhibition networks is divorced from biological reality, especially in the study of the inhibition coefficient. To address this issue, we proposed a lateral inhibition network based on the cell membrane electrical model and applied it to image enhancement. Firstly, we analyzed the visual formation mechanism and the lateral inhibition principle, laying the theoretical foundation. Secondly, leveraging the cell membrane electrical model, we construct a lateral inhibition network with a negative exponential distribution. Finally, our experiment demonstrates that a lateral inhibition network with a negative exponential distribution has better image enhancement ability than other distributions. Using images processed with lateral inhibition as an input improved the classification accuracy of the GoogLeNet neural network by 3.39%.
1. Introduction
Is the color of the left ring lighter than the right ring in Figure 1b? Is the color inside each block in Figure 1c light on the left and dark on the right? Actually, Figure 1b is the result of splitting Figure 1a down the middle without changing the color of the image. In Figure 1c, each color patch is monochromatic. These captivating visual illusions can be elucidated through the phenomenon of lateral inhibition. Lateral inhibition is a prevalent phenomenon observed in the biological nervous system and holds great importance in the realm of visual perception. Lateral inhibition amplifies the perception of brightness in well-lit regions and intensifies the perception of darkness in poorly lit regions. Lateral inhibition has the potential to augment contrast, accentuate edges, and enhance the overall quality of human visual perception. Figure 1d provides an explanation for the phenomenon depicted in Figure 1c, where the horizontal axis represents spatial position and the vertical axis represents brightness. The objective brightness changes in a stepped pattern across space, and lateral inhibition enhances the brain’s perception of edges, leading to the appearance of two distinct peaks in subjective perception at these edge locations.

Figure 1.
(a) The figure consists of two rectangles and a circular ring, where each color block is monochromatic. (b) The division of (a) in the middle, while ensuring that the colors remain unchanged. (c) Mach band phenomenon. (d) The subjective brightness following lateral inhibition and the objective brightness.
In 1967, Hartline conducted a study on horseshoe crabs and discovered that the compound eyes of horseshoe crabs inhibited each other when exposed to light stimuli, thereby enhancing the visual contrast. Hartline coined the term “lateral inhibition” to describe this phenomenon, which ultimately led to his recognition and receipt of the Nobel Prize in Physiology or Medicine [1]. From a biological perspective, the study of lateral inhibition serves as a crucial avenue for investigating the brain and neurons. Investigating visual effects such as lateral inhibition contributes to the understanding of the visual system, thereby facilitating the development of effective medical interventions for individuals with visual impairments or brain injuries.
Given the characteristics of lateral inhibition, it has proven to be highly valuable in various fields such as image processing, pattern recognition, and imaging guidance. As a result, not only biologists but also engineers and researchers have conducted extensive research on lateral inhibition. In the late 20th century, Hiedebrand, Reichardt, Chen et al. conducted extensive research on lateral inhibition networks [2]. They proved that lateral inhibition networks have the functions of enhancing edges, increasing contrast, and compensating for defects in the visual system. In recent years, many scholars have applied lateral inhibition to image enhancement, particularly in infrared image enhancement [3,4,5,6,7]. In addition, the lateral inhibition has high flexibility in applications, and has been applied in fields such as single-pixel [8] imaging, neural networks [9,10], and circuit design [11]. In conclusion, as a universal phenomenon in the nervous system, lateral inhibition has tremendous application value in engineering.
However, current research on lateral inhibition networks has departed from biological reality, and determining the inhibition coefficient distribution based on biological principles remains a research gap. The inhibition coefficient distribution determines the strength of inhibition for signals inputted at different positions, thereby affecting the effect of lateral inhibition. Commonly used distribution functions include the Gaussian distribution, bimodal Gaussian distribution, negative exponential distribution, etc. In 2003, Chen et al. analyzed the image enhancement effects of different distributions and found that the bimodal Gaussian distribution can better enhance image details [1]. In 2011, Shi et al. improved a lateral inhibition network with Gaussian distribution by adaptively determining the distribution coefficient, effectively improving noise resistance [12]. In 2015, Dai et al. simplified the Gaussian distribution into a negative exponential distribution, reducing computational complexity [4]. Prior methods neglected the biological principles underlying lateral inhibition. While this approach may yield satisfactory outcomes, it can result in inaccurate simulations of lateral inhibition, complicating the identification of the optimal distribution.
This study aimed to establish a reliable model for the inhibition coefficient distribution from a biological perspective, optimize the image enhancement effect of our lateral inhibition network, and promote the application of the lateral inhibition network in areas such as image enhancement and neural networks. We investigated the biological principle of lateral inhibition and the cell membrane electrical model, and thereby established a lateral inhibition network with a negative exponential distribution, providing a biological basis for the inhibition coefficient distribution. The primary contributions of this paper are outlined below.
- We conducted an analysis of the principle of lateral inhibition in human vision and thereby established a lateral inhibition network model;
- Based on the cell membrane electrical model, we developed a lateral inhibition network with a negative exponential distribution;
- The experimental results indicate that compared with the Gaussian distribution and bimodal Gaussian distribution, a lateral inhibition network with a negative exponential distribution can better enhance image details and improve image quality;
- Using images that have been processed with lateral inhibition as an input, we were able to enhance the classification accuracy of the GoogLeNet neural network by 3.39%.
2. Lateral Inhibition Network Model
2.1. The Principle of Lateral Inhibition in Human Vision
To establish our lateral inhibition network model, we first analyzed the process of human visual formation and the principle of lateral inhibition. If we confine our analysis to the fovea, we can assume that the eye is capable of ideal imaging. In this case, key determinants affecting image quality include pupil blur, photoreceptor downsampling, and lateral inhibition.
Light first passes through the pupil, whose size can be modulated according to the intensity of ambient light to control the amount of light entering the eye. Pupil blur refers to the phenomenon where the image is convolved and therefore blurred by the point spread function caused by the finite size of the pupil. Photoreceptors are responsible for converting light signals into neural signals. Due to their finite size, photoreceptors perform a downsampling of the image on the retina. The density of photoreceptors is higher at the fovea, while it is lower in the peripheral regions of the retina. This downsampling is intentional to reduce information overload, allowing the brain to process visual information more effectively. Subsequently, neural signals pass through the retina, undergoing lateral inhibition. Lateral inhibition enhances edges and details, aiding in distinguishing features in the image. Pupil blur, photoreceptor downsampling, and lateral inhibition work together on the human visual system, determining the quality of the image we see by adjusting the intensity of incoming light, signal transmission, and processing.
The prevailing viewpoint posits that lateral inhibition is predominantly attributed to the inhibitory influence exerted by horizontal cells on photoreceptors [13]. The operational mechanism of retinal cells in the human eye is depicted in Figure 2. Photoreceptors generate neural impulses in response to light stimulation, which are subsequently transmitted to bipolar cells. These bipolar cells relay the impulses to ganglion cells. Simultaneously, the activation of photoreceptors also elicits a response in the horizontal cells. Horizontal cells form horizontal connections with multiple photoreceptors and inhibit their excitation. The strength of inhibition decreases as the distance increases. Overall, the activation of photoreceptors by light leads to the excitation of specific ganglion cells, while at the same time inhibiting the activity of neighboring ganglion cells. The strength of lateral inhibition depends on the inhibitory influence exerted by horizontal cells on photoreceptors, and the extent of lateral inhibition is contingent upon the range of photoreceptors linked by horizontal cells, which lays the theoretical groundwork for subsequent mathematical modeling.
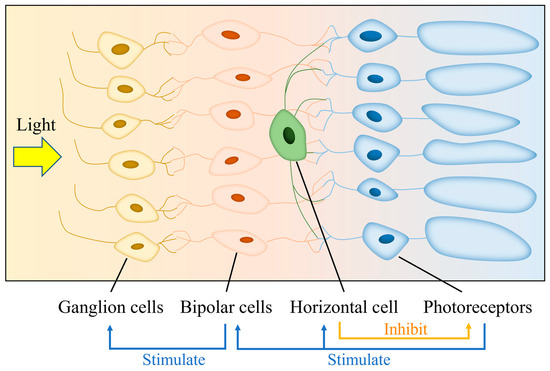
Figure 2.
Retinal structure and lateral inhibition principle. Photoreceptors stimulate bipolar cells and horizontal cells. The bipolar cells, in turn, stimulate ganglion cells. Meanwhile, horizontal cells connect to multiple photoreceptors and inhibit their activity.
Ultimately, the neural signals are transmitted to the brain and form vision. Lateral inhibition can emphasize image edges and increase contrast, assisting in better perception of objects within a scene by humans. We consider an image to have better quality if it can be more easily recognized by the human eye. It is worth mentioning that artificial imaging systems and biological imaging systems share similarities, as the resolution of both is limited by optical blur and downsampling. Therefore, the application of lateral inhibition to artificial imaging systems has the potential to enhance their imaging quality.
2.2. Lateral Inhibition Network and Coefficient Matrix
According to the principle of lateral inhibition, when receptors are stimulated, they will inhibit the activity of neighboring neurons, thereby enhancing the contrast. The one-dimensional lateral inhibition network model is as follows:
The variables in the equation are defined as follows: represents the input stimuli to neurons, represents the output responses, represents the inhibition coefficient between neurons, and determines the size of the lateral inhibition field. In addition to augmenting contrast, lateral inhibition concurrently diminishes the overall output responses of neurons. In biological vision, the brain can adapt to the overall level of neural signals. In the simulation, in order to maintain the overall grayscale of the image, a coefficient is introduced to the positive stimulus. The sum of all coefficients is set to 1, and Equation (2) is as follows:
We have given a detailed explanation of the biological principles of lateral inhibition in Figure 2. To help readers better understand the mathematical model of lateral inhibition, we have presented a simplified diagram of lateral inhibition in Figure 3. As a result, we have omitted the specific cellular structures, using “receptors” and “neurons” instead. We set to 2, to −0.2, to 1.4, and to −0.2. The receptors on the left side receive a stimulus with an intensity of 10, whereas the receptors on the right side receive a stimulus with an intensity of 5. Consequently, the final output is “…10, 10, 11, 4, 5, 5…”, which effectively enhances the contrast.

Figure 3.
A simplified diagram of a lateral inhibition network.
We extend this lateral inhibition network to two dimensions, and its expression is as follows:
where is the input stimuli, is the output responses, determines the size of the lateral inhibition field, and is the two-dimensional inhibition coefficient. We denote the original image as , the enhanced image through lateral inhibition as , and the inhibition coefficient matrix as . Based on the principle of lateral inhibition, this lateral inhibition network model can be expressed as follows:
In the above equation, the ∗ represents a convolution operation. It is worth noting that the inhibition coefficient matrix exhibits the following properties:
- The central neuron undergoes activation while the surrounding neurons experience inhibition. Therefore, the inhibition coefficients within the central region of the matrix exhibit positive values, whereas the remaining coefficients demonstrate negative values;
- The efficacy of lateral inhibition decreases with increasing distance. Consequently, the absolute values of the inhibition coefficients decrease as one moves further away from the center;
- To maintain the overall grayscale of the image, it is necessary for the sum of all inhibition coefficients to be equal to 1.
Figure 4 presents a lateral inhibition coefficient matrix, which corresponds to a specific set of coefficients. With these properties taken into consideration, the determination of all the inhibition coefficients continues to pose a challenge. Below, we will analyze the cell membrane electrical model to determine the distribution of lateral inhibition coefficients.
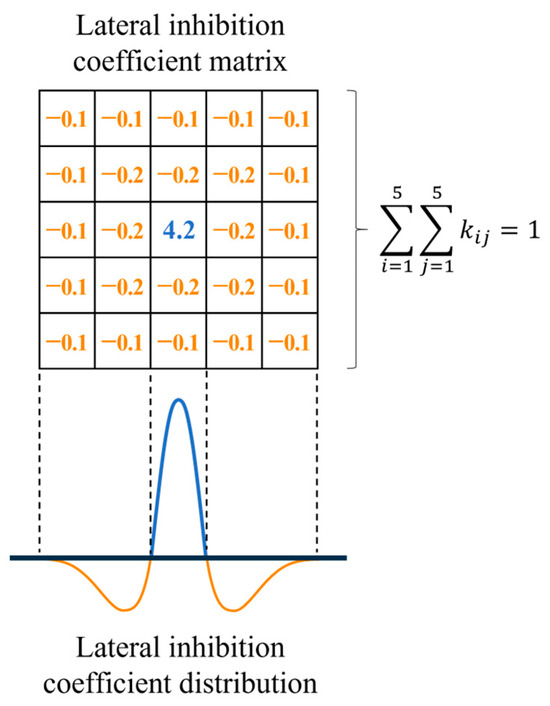
Figure 4.
The lateral inhibition coefficient matrix.
3. Lateral Inhibition Network Based on Cell Membrane Electrical Model
3.1. Cell Membrane Electrical Model
Commonly employed distributions of lateral inhibition coefficients include the Gaussian distribution, hyperbolic distribution, and bimodal Gaussian distribution, among others. According to the analysis presented in Section 2.1, lateral inhibition can be attributed to the inhibitory influence exerted by horizontal cells on photoreceptors. The membrane potential of horizontal cells refers to the voltage difference between the inside and outside of the cell. In the resting state, the membrane potential of horizontal cells is relatively low, with fewer inhibitory neurotransmitters released, resulting in weak inhibition of photoreceptors. Conversely, when horizontal cells are stimulated and excited, the membrane potential increases and more inhibitory neurotransmitters are released, leading to enhanced inhibition of photoreceptors. Therefore, we can assume that the potential level of horizontal cells exhibits a direct proportionality to the degree of inhibition exerted on photoreceptors. By analyzing the pattern of variation in potential levels with distance, it is possible to deduce the inhibition coefficient distribution. To simplify the model, we have not considered factors such as the branch dimensions and positioning of synapses, assuming a radially uniform distribution of potential levels in horizontal cells.
A horizontal cell is a type of local cell that lacks axons and action potentials, exhibiting passive electrophysiological properties, and their depolarization diminishes with increasing distance [13]. The cell membrane is composed of a lipid bilayer, with the interior consisting of an electrolyte, the exterior side consisting of extracellular fluid, and the inner side consisting of intracellular fluid. The electrolyte and intracellular fluid can be regarded as conductive solutions. The lipid bilayer functions as a capacitor in terms of its electrical properties. Furthermore, ion channels are protein complexes on the cell membrane that allow specific ions to pass through the membrane, maintaining the normal electrical potential of the cell. Thus, it can be postulated that the cell membrane can be represented by a parallel combination of a capacitor and a resistor. The electrical model of the cell membrane is illustrated in Figure 5. Below, we will analyze alterations in potential from the standpoint of cellular electrophysiology.

Figure 5.
Cell membrane electrical model.
- 1.
- After horizontal cells are stimulated by photoreceptors, the current is propagated along the cell membrane, leading to a voltage decrease caused by resistance.
- 2.
- During the process of propagation, the transmembrane current exits the cell. The transmembrane current can be divided into two components: the capacitor charging current and leak current . Since we are solely concerned with the spatial variation of potential rather than the temporal variation, is equal to zero. Therefore, we have:
- 3.
- Regarding the leak current for the capacitor, we have:
- 4.
- Based on the equations, we can obtain the following differential equation:
Applying the boundary conditions and , the solution is:
The horizontal cell membrane experiences an exponential decay in potential across space, leading to a corresponding exponential decay in the strength of lateral inhibition. Now, we will establish the lateral inhibition coefficient matrix K using the negative exponential distribution. Assuming has a size of , the distance of each coefficient to the center of the matrix can be determined as follows:
Combined with the conclusions from Section 2.2, each coefficient should satisfy:
Hence, the lateral inhibition network with negative exponential distribution is characterized by four parameters: and . Due to Equation (5), it is only necessary to determine three out of the four parameters. In this study, the values of and were assigned as 1 and 3.5, respectively. Next, we will examine the lateral inhibition field to ascertain the numerical value of .
3.2. Lateral Inhibition Field Selection
The size of the lateral inhibition field governs the scope of its impact. From a biological perspective, the size of the lateral inhibition field is contingent upon the quantity of photoreceptors that are linked to the horizontal cells. In the fovea centralis of the human retina, a solitary horizontal cell forms connections with approximately ten to a hundred photoreceptors [14]. In simulations, each pixel corresponds to a photoreceptor. By manipulating the dimensions of the lateral inhibition coefficient matrix, it is possible to simulate different sizes of lateral inhibition fields. Commonly used sizes include 3 × 3, 5 × 5, and 7 × 7. To evaluate the impact of various lateral inhibition fields on image enhancement, experiments were conducted to compare the information entropy and fuzzy index [15] of the enhanced images. The findings are depicted in Figure 6.

Figure 6.
Comparison of image enhancement effects under different lateral inhibition fields. (a) Original image; (b) 3 × 3 lateral inhibition field; (c) 7 × 7 lateral inhibition field; (d) 13 × 13 lateral inhibition field; (e) variation of information entropy and fuzzy index with lateral inhibition field size.
When the lateral inhibition field is small, the observed effect is not significant. As the lateral inhibition field size increases, the effect of lateral inhibition becomes more pronounced, resulting in enhanced clarity of the image edges. When the lateral inhibition field is excessively large, it results in prominent enhancement of the edges of the image. However, this also leads to amplification of noise and an increase in computational costs. Considering the arrangement of photoreceptors on the human retina, it has been determined that the optimal lateral inhibition field sizes are 5 × 5 and 7 × 7. In this study, a lateral inhibition field of 7 × 7 was used.
4. Results
We conducted an experiment to assess the image enhancement effect of the lateral inhibition network proposed in this paper. Firstly, to verify the superiority of the negative exponential distribution, we compare the image enhancement effects of lateral inhibition networks with different distributions. Secondly, the simulation of human visual perception was conducted by implementing pupil blur and lateral inhibition on the images. Thirdly, the GoogLeNet network was employed to classify images enhanced by lateral inhibition, thereby simulating the cognitive process of image comprehension in the human brain.
4.1. Comparison of Lateral Inhibition Networks with Different Distribution
We compared the image enhancement effects of four different distributions: the negative exponential distribution proposed in this paper, the Gaussian distribution proposed in [6], the bimodal Gaussian distribution proposed in [16], and the specific coefficient distribution commonly used [17,18]. We processed ten images and calculated the information entropy, local contrast, blur index, and natural image quality evaluator (NIQE) [19]. The results are shown in Figure 7, and the data in Table 1 represent the average evaluation measures obtained from multiple images.

Figure 7.
Comparison of different distribution.

Table 1.
Mean evaluation metrics of different distribution.
Based on Figure 7, it can be observed that lateral inhibition enhances the contrast of the image, making it clearer and easier to observe. From Table 1, it can be observed that the information entropy of the images after lateral inhibition has increased, with the negative exponential distribution showing the highest information entropy, indicating a richer distribution of grayscale values in the images. Additionally, the negative exponential distribution has the highest fuzzy index, suggesting that the images contain the most high-frequency information. Concurrently, the negative exponential distribution also exhibits the highest local contrast. Finally, the NIQE values of the images after lateral inhibition have decreased, but the performance of the negative exponential distribution in NIQE is average. Therefore, the lateral inhibition network with negative exponential distribution exhibits the overall best performance.
4.2. Lateral Inhibition in a Simulation of Human Vision
In order to investigate the role of lateral inhibition in human vision, we simulated the process of human visual formation. Based on the analysis in Section 2.1, if we restrict our analysis to imaging solely in the fovea centralis, the key determinants affecting the quality of imaging encompass pupil blur, photoreceptor downsampling, and lateral inhibition.
Firstly, Gaussian blur was employed to simulate pupil blur. According to [20], the pupil diameter is assumed to be , the eye length is considered to be , and the wavelength is set at , which is recognized as the most sensitive wavelength for human eyes. According to the Rayleigh criterion, the diameter of the point spread function can be calculated to be approximately 8 μm. Secondly, the image was downsampled by simulating the photoreceptors, where each pixel represented a photoreceptor with a center spacing of 2.4 μm [21]. Therefore, a 3 × 3 Gaussian filter was employed, with a standard deviation of 0.7, to replicate the point spread function of the pupil. Finally, the images were enhanced utilizing our lateral inhibition network with negative exponential distribution. The experimental procedure is depicted in Figure 8.
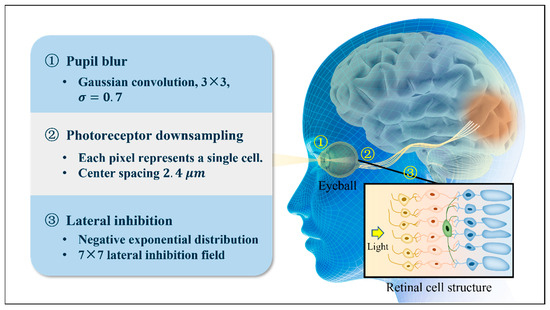
Figure 8.
Experimental procedure.
Each datum in Table 2 represents the average value obtained from ten images. From the analysis of Figure 9 and Table 2, we can draw the following conclusions:

Table 2.
Mean evaluation metrics for ten images.

Figure 9.
Simulating lateral inhibition and human visual perception.
- After pupil blur, the edges underwent blurring, leading to a reduction in information entropy, fuzzy index, and local contrast, and an increase in NIQE;
- After lateral inhibition, the information entropy, blur index, and local contrast of the image increase, and the NIQE decreases. Therefore, the image experienced an enhancement in contrast, leading to more pronounced edges in comparison to the original image.
In conclusion, our study has revealed that the process of visual formation is significantly influenced by lateral inhibition. Lateral inhibition has the potential to enhance the edges, improve contrast, and optimize the image for observation.
4.3. Enhancing Accuracy of Neural Network Image Classification through Lateral Inhibition
In human vision, the goal of lateral inhibition is to enable a clearer perception of images. Therefore, it is not possible to judge the quality of images processed by lateral inhibition solely based on objective evaluation metrics. Additionally, subjective evaluation through visual observation is also not feasible, as there is an occurrence of lateral inhibition in human visual perception apart from that simulated. Moreover, subjective evaluation is highly random and challenging to quantify.
To address this issue, we employ neural networks for image classification to simulate the brain’s processing of information. We trained a neural network using images that had undergone lateral inhibition and images that had not. If the neural network trained on images enhanced by lateral inhibition achieves better image classification, it indicates that the images enhanced by lateral inhibition can be better processed and recognized by the neural network. Thus, lateral inhibition in vision can help the human eye better observe and perceive information.
The GoogLeNet network was selected as the neural network model for the present study. This method was put forth by the Google team in 2014, and since then, it has gained significant popularity for its application in image classification [22]. We utilized the “Flowers Recognition” dataset from the Kaggle website, which contains 4,242 images of various flowers. These images were classified into five distinct categories, namely daisy, dandelion, rose, sunflower, and tulip. The dataset was partitioned into a training set and a testing set, with a ratio of approximately 3:1.
To simulate the realistic conditions of human vision, we initially implemented Gaussian blur on all images in the dataset. Later, we used lateral inhibition networks with different distributions to enhance the images respectively. The standard deviation of the Gaussian filter was set to 0.7. The neural network was separately trained on datasets before and after lateral inhibition. Each training session comprised 30 epochs, and the classification accuracy was computed for each epoch. The experiment was repeated five times. Finally, the data were fitted using the least squares method, and the results are shown in Figure 10.
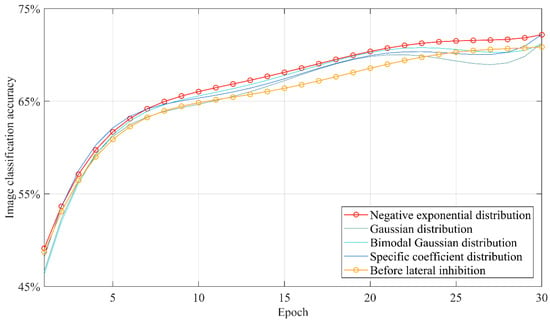
Figure 10.
Trend of image classification accuracy.
It is evident that the dataset, following the implementation of lateral inhibition, demonstrates improved classification accuracy and training efficiency. Comparing with other distributions, our lateral inhibition network with negative exponential distribution demonstrated the best overall performance. Using data from the last 15 epochs, the image classification accuracy increased by 3.39% after processing by our lateral inhibition network with negative exponential distribution, compared to before lateral inhibition. Therefore, lateral inhibition was able to make images more easily recognizable by neural networks, which was beneficial for subsequent computational processes.
5. Discussion
This paper has analyzed the principle of lateral inhibition and the cell membrane electrical model, and thereby proposed a lateral inhibition network with a negative exponential distribution. We utilized lateral inhibition networks with different distributions to enhance images and simulate the process of human visual formation. Additionally, we enhanced the image dataset with lateral inhibition and performed image classification using a neural network. The obtained outcomes are presented below:
- Compared to other distributions, our lateral inhibition network with negative exponential distribution has better image enhancement capabilities;
- In human vision, lateral inhibition can highlight edges and increase contrast, allowing humans to see objects in a scene more clearly;
- The utilization of images that have undergone lateral inhibition processing as an input resulted in an enhancement of 3.39% in the classification accuracy of the GoogLeNet neural network.
Current research has focused on comparing the image enhancement effects of lateral inhibition networks with different inhibition coefficient distributions to find a suitable distribution. This approach overlooks the principle of lateral inhibition and deviates from biological reality. In contrast, our research started from the principle of lateral inhibition, analyzing the variations in potential of horizontal cells to derive the pattern of inhibition strength changing with distance, and subsequently obtaining the inhibition coefficient distribution. Our experiment demonstrates that a lateral inhibition network with a negative exponential distribution outperforms others in both objective evaluation metrics and neural network image classification. This distribution aligns with biological principles, better simulating the inhibitory effect of horizontal cells on photoreceptors and more accurately modeling the visual processing mechanisms in the biological nervous system. Through this approach, we can better understand and simulate biological visual perception, ultimately developing more efficient and accurate algorithms in the fields of image processing and computer vision.
Lateral inhibition amplifies noise while simultaneously enhancing edges. This research endeavored to explore the coefficient distribution of lateral inhibition, with the focus being on the enhancement of image contrast rather than the consideration of noise. To mitigate the impact of noise, numerous researchers have employed various techniques including median filtering, adaptive filtering, and compensation measure factors. Additionally, lateral inhibition can be combined synergistically with other image enhancement methods. Hence, the suppression of noise while emphasizing edges and the design of the algorithm are crucial research concerns. The further development and application of lateral inhibition require the joint efforts of biology and computer science.
By incorporating lateral inhibition as a preprocessing technique, we have effectively enhanced the learning efficiency and robustness of the GoogLeNet neural network. Neural networks are frequently regarded as opaque models, posing challenges in comprehending and interpreting their decision-making mechanisms. Studying biological neural principles, such as lateral inhibition, can help us comprehend the decision-making processes within neural networks and enhance their interpretability.
6. Conclusions
This study has investigated the phenomenon of lateral inhibition in biology and applied it to image enhancement. In response to the problem of the lack of reliable theoretical support for the lateral inhibition network coefficient distribution, a lateral inhibition network with a negative exponential distribution was proposed. Firstly, the mechanisms of lateral inhibition were analyzed, and a model of a lateral inhibition network and coefficient matrix was established. Secondly, based on the cell membrane electrical model, the potential changes in horizontal cell membranes were analyzed, and a lateral inhibition network with a negative exponential distribution was constructed. Finally, the experiment proved that this lateral inhibition network with negative exponential distribution has better image enhancement ability. In human vision, lateral inhibition can increase contrast and help humans better observe the details of objects. Using images processed with lateral inhibition as an input improved the classification accuracy of the GoogLeNet neural network by 3.39%.
In the future, we plan to apply lateral inhibition to infrared image enhancement. With technological advancements, infrared imaging technology is being used in fields such as night operations, firefighting and rescue, medical diagnostics, etc. However, infrared images often have low contrast, making it difficult to discern details. Lateral inhibition can enhance contrast and improve image details, thus offering significant potential for enhancing infrared images. Nevertheless, infrared images tend to have a lot of noise, and while lateral inhibition enhances details, it may also amplify noise. Therefore, improvements need to be made to our lateral inhibition network model to enhance its noise resistance capability.
Author Contributions
Conceptualization, D.-H.Q. and M.-J.S.; Data curation, D.-H.Q. and M.-J.S.; Formal analysis, D.-H.Q. and Q.-Z.C.; Investigation, D.-H.Q.; Methodology, D.-H.Q.; Project administration, M.-J.S.; Software, D.-H.Q. and M.-J.S.; Supervision, Q.-Z.C.; Validation, Q.-Z.C.; Visualization, M.-J.S.; Writing—original draft, D.-H.Q. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
The data presented in this study are available on request from the corresponding author.
Conflicts of Interest
The authors declare no conflicts of interest.
References
- Chen, H.; Ouyang, K. Simulation and Comparison of Lateral Inhibition Network Models for Image Enhancement. J. Syst. Simul. 2003, 1, 100–103. [Google Scholar]
- Chen, L.; Gu, F. Research on the Function of Lateral Inhibition Network in the Compound Eye of Gasterosteus aculeatus. J. Univ. Sci. Technol. China 1978, 1, 138–148. [Google Scholar]
- Dai, S.; Du, Z.; Zhang, Y.; Hu, Y. Edge enhancement using adaptive lateral inhibition. In Proceedings of the 2013 3rd International Conference on Computer Science and Network Technology, Dalian, China, 12–13 October 2013; pp. 1133–1137. [Google Scholar]
- Dai, S.; Liu, Q.; Li, P.; Liu, J.; Xiang, H. Study on infrared image detail enhancement algorithm based on adaptive lateral inhibition network. Infrared Phys. Technol. 2015, 68, 10–14. [Google Scholar] [CrossRef]
- Yun, H.; Wu, Z.; Wang, G.; Tong, G.; Yang, H. Image enhancement algorithm based on improved lateral inhibition network. Infrared Phys. Technol. 2016, 76, 308–314. [Google Scholar] [CrossRef]
- Li, Y.; Song, Y.; Zhao, Y.; Zhao, S.; Li, X.; Li, L.; Tang, S. An infrared target detection algorithm based on lateral inhibition and singular value decomposition. Infrared Phys. Technol. 2017, 85, 238–245. [Google Scholar] [CrossRef]
- Katırcıoğlu, F.; Çay, Y.; Cingiz, Z. Infrared image enhancement model based on gravitational force and lateral inhibition networks. Infrared Phys. Technol. 2019, 100, 15–27. [Google Scholar] [CrossRef]
- Zhang, K.; Cao, J.; Zhang, F.; Jiang, Y.; Cheng, Y.; Wang, D.; Hao, Q. Fourier Single-Pixel Imaging Based on Lateral Inhibition for Low-Contrast Scenes. IEEE Photonics J. 2019, 11, 6901711. [Google Scholar] [CrossRef]
- Marcinek, F. Reproduction of Lateral Inhibition-Inspired Convolutional Neural Network for Visual Attention and Saliency Detection. In Proceedings of the AAAI Conference on Artificial Intelligence, New York, NY, USA, 7–12 February 2020. [Google Scholar]
- Jiang, L.; Liu, Y.; Xiao, S.; Chua, Y. Gradient Mask: Lateral Inhibition Mechanism Improves Performance in Artificial Neural Networks. arXiv 2022, arXiv:2208.06918. [Google Scholar]
- Man, M.; Wei, M.; Zhang, Y.; Ma, G.; Chen, Y. Biomimetic Measurement Method for Surface Electric Potential Imaging Inspired by Visual Lateral Inhibition. IEEE Trans. Ind. Electron. 2023, 71, 9834–9844. [Google Scholar] [CrossRef]
- Shi, M.; Peng, Z.; Zhang, Q.; Li, Q.; Lin, Z. Infrared weak small target detection based on adaptive lateral inhibition network. J. High Power Laser Part. Beams 2011, 23, 5. [Google Scholar]
- Beier, J.B. Biological Psychology; Tsinghua University Press: Beijing, China, 2014. [Google Scholar]
- Zhu, D. Physiology; People’s Medical Publishing House: Beijing, China, 2008. [Google Scholar]
- Huang, W.; Chen, R.; Zhang, J. Improvement and Implementation of Objective Measurement Method for Digital Video Image Quality. J. Beijing Univ. Posts Telecommun. 2005, 4, 87–90. [Google Scholar]
- Zhang, Z.; Chen, Z.; Lv, L.; Wang, X.; Xu, L. Adaptive background suppression method based on visual receptive field. J. Instrum. Meas. 2014, 35, 9. [Google Scholar] [CrossRef]
- Huang, L.; Duan, H.; Wang, Y. Hybrid bio-inspired lateral inhibition and Imperialist Competitive Algorithm for complicated image matching. Opt. Z. Licht- Elektron. J. Light-Electronoptic 2014, 125, 414–418. [Google Scholar] [CrossRef]
- Tian, Q.C.; Cohen, L.D. A variational-based fusion model for non-uniform illumination image enhancement via contrast optimization and color correction. Signal Process. 2018, 153, 210–220. [Google Scholar] [CrossRef]
- Babu, P.; Rajamani, V. Contrast enhancement using real coded genetic algorithm based modified histogram equalization for gray scale images. Int. J. Imaging Syst. Technol. 2015, 25, 24–32. [Google Scholar] [CrossRef]
- Zhang, Y.X. Computational Studies on Human Visual Perception. Opt. Tech. 1988, 5, 6–11. [Google Scholar]
- He, Z.; Ma, S.; Liang, N. Design Principles of Visual Acuity Chart. Chin. J. Opt. Technol. 2004, 3, 77–80. [Google Scholar]
- Szegedy, C.; Liu, W.; Jia, Y.; Sermanet, P.; Reed, S.; Anguelov, D.; Erhan, D.; Vanhoucke, V.; Rabinovich, A. Going Deeper with Convolutions. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition (CVPR), Columbus, OH, USA, 23–28 June 2014; IEEE Computer Society: Washington, DC, USA, 2014. [Google Scholar]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).