Microwave Photonic Frequency Multiplier with Low Phase Noise Based on an Optoelectronic Oscillator
Abstract
1. Introduction
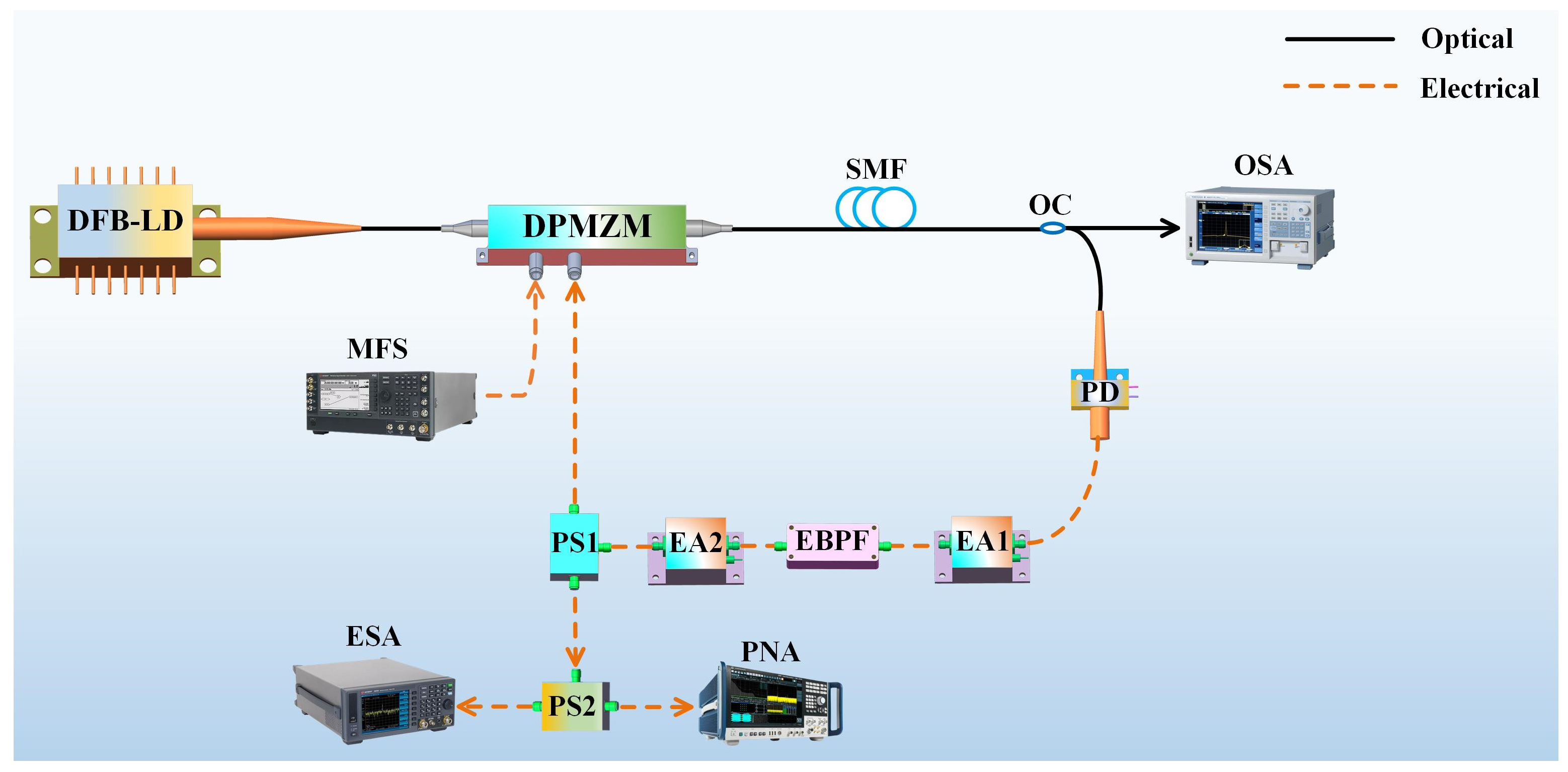
2. Principle
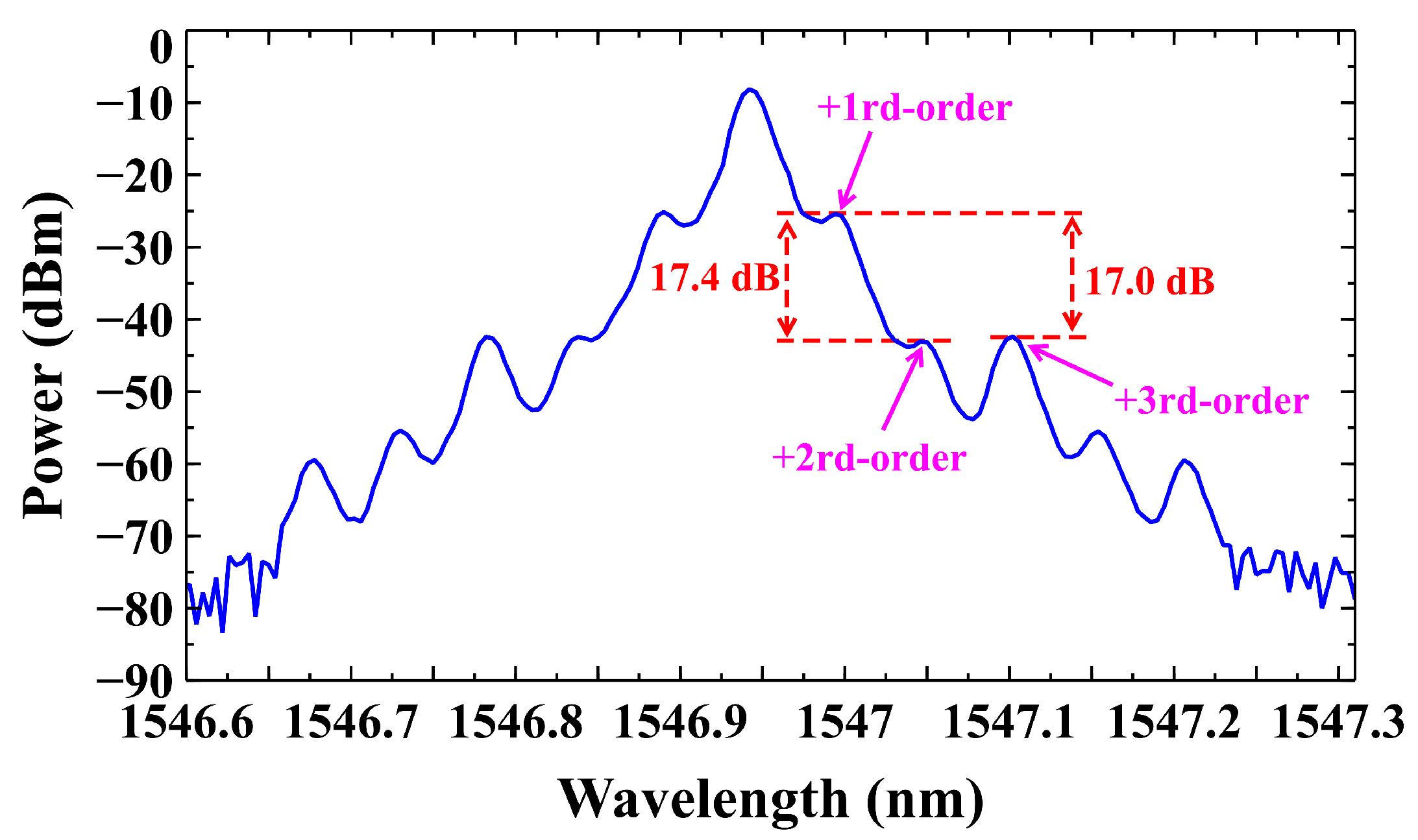
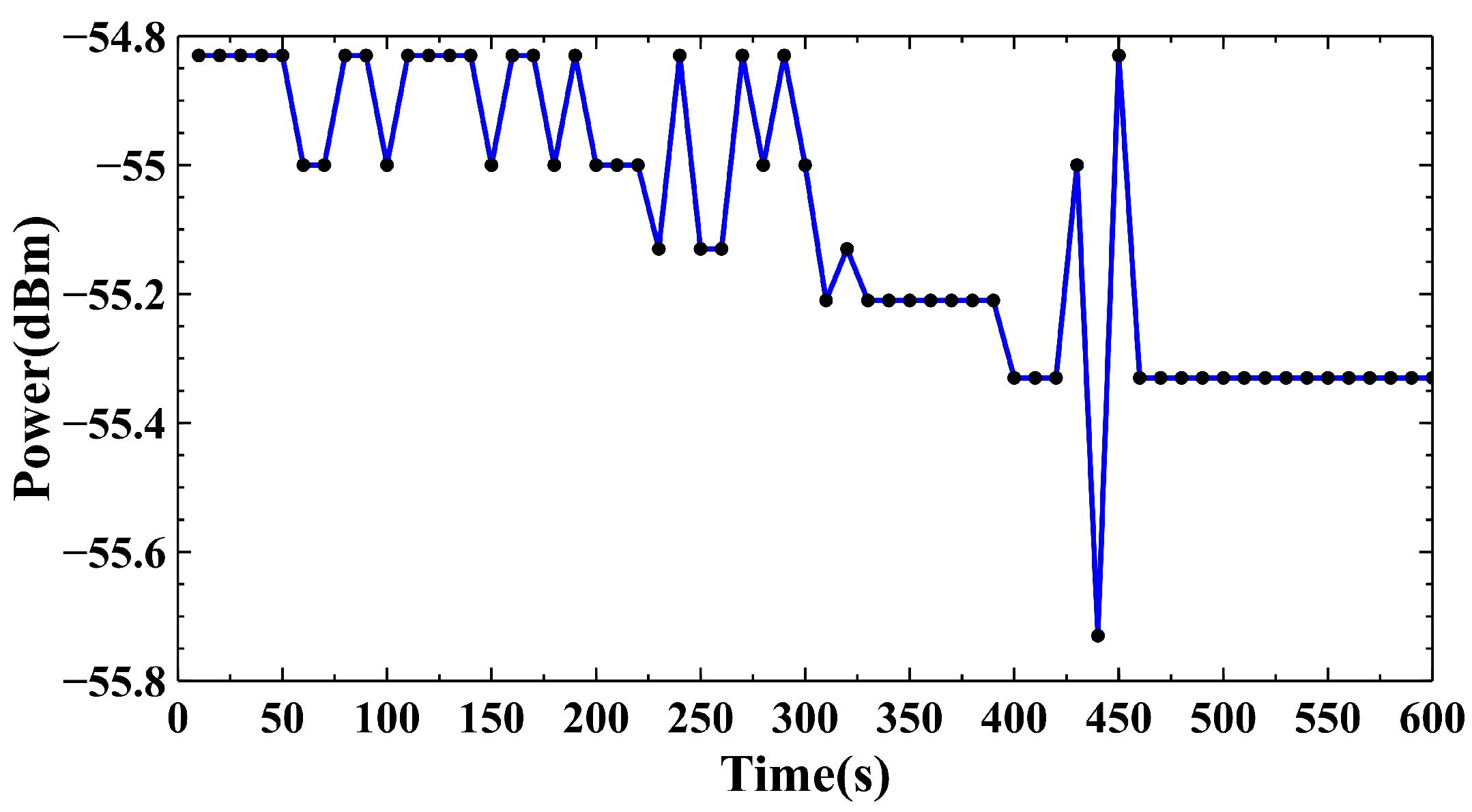
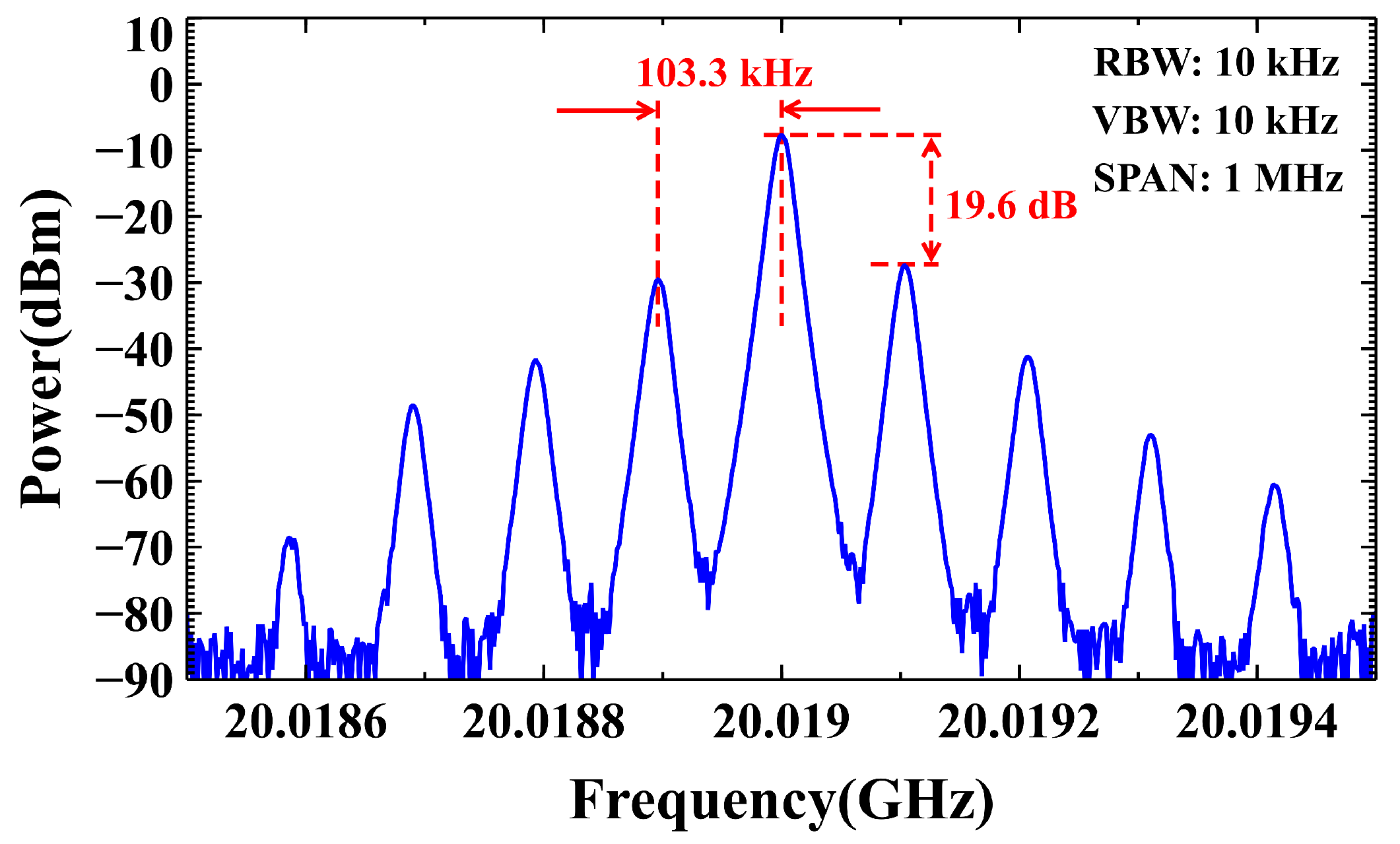
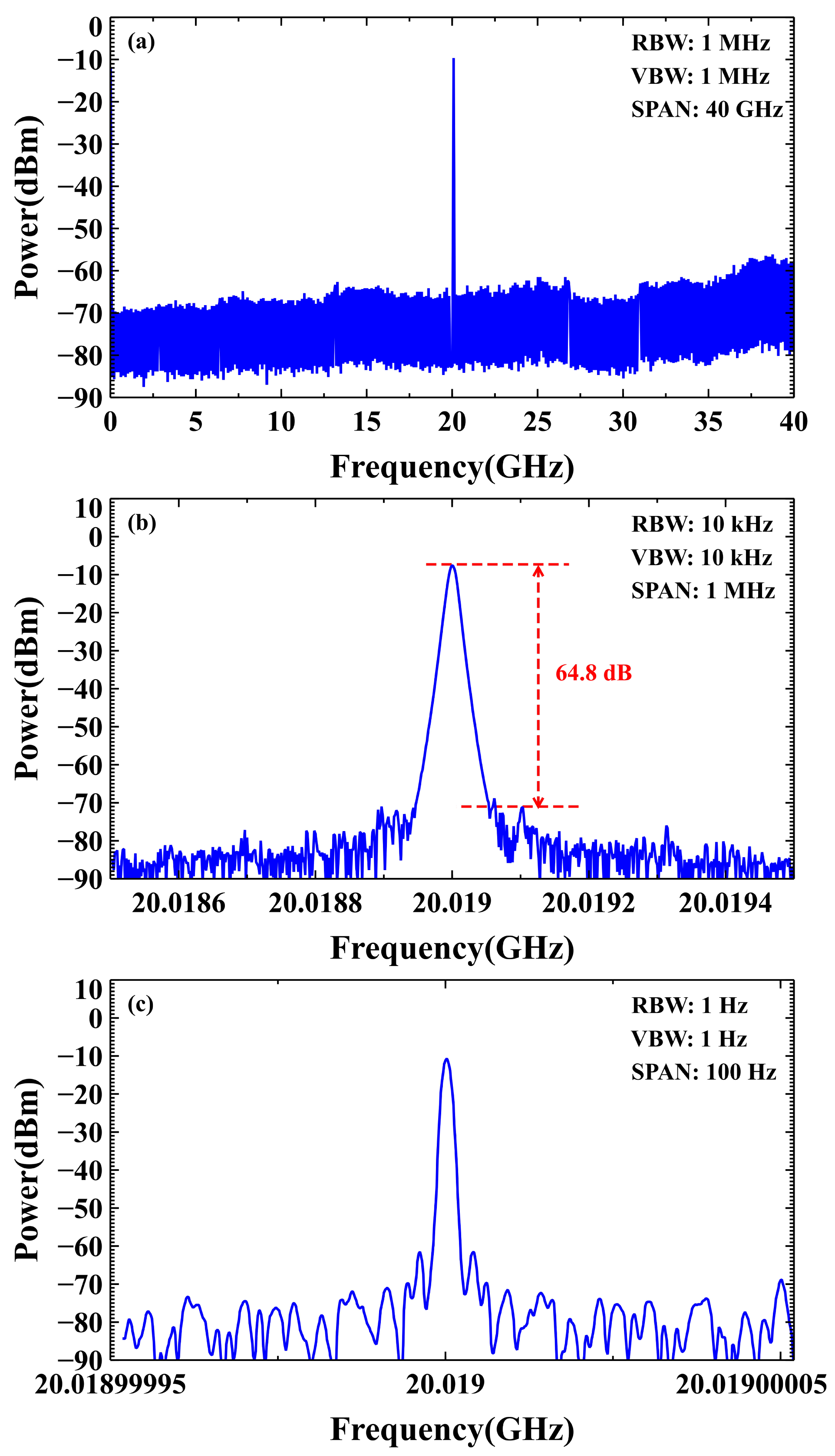
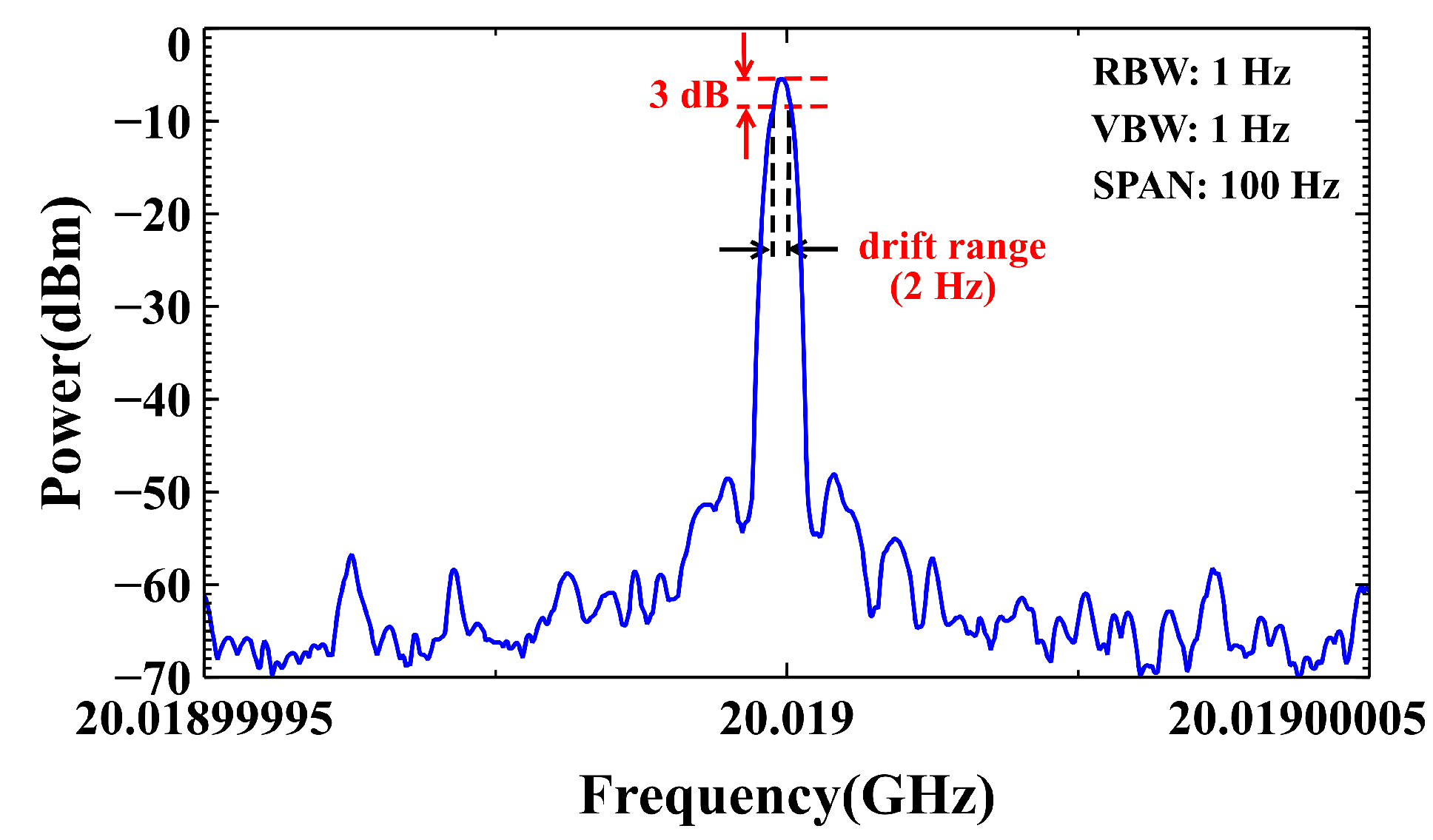
3. Results and Discussion
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Ummethala, S.; Harter, T.; Koehnle, K.; Li, Z.; Muehlbrandt, S.; Kutuvantavida, Y.; Kemal, J.; Mar-in-Palomo, P.; Schaefer, J.; Tessmann, A.; et al. Thz-to-optical conversion in wireless communications using an ultra-broadband plasmonic modulator. Nat. Photonics 2019, 13, 519–524. [Google Scholar] [CrossRef]
- Zhang, Z.; Liu, Y.; Stephens, T.; Eggleton, B.J. Photonic radar for contactless vital sign detection. Nat. Photonics 2023, 17, 791–797. [Google Scholar] [CrossRef]
- Jin, J.; Geng, S.; Shu, L.; Jiang, P.; Shao, X.; Han, C.; Ren, L.; Li, Y.; Yang, L.; Wang, X. High-strength and crack-free welding of 2024 aluminium alloy via zr-core-al-shell wire. Nat. Commun. 2024, 15, 1748. [Google Scholar] [CrossRef] [PubMed]
- Wang, C.-X.; Haider, F.; Gao, X.; You, X.-H.; Yang, Y.; Yuan, D.; Aggoune, H.M.; Haas, H.; Fletcher, S.; Hepsaydir, E. Cellular architecture and key technologies for 5g wireless communication networks. IEEE Commun. Mag. 2014, 52, 122–130. [Google Scholar] [CrossRef]
- Chen, Y. Photonic generation and transmission of triangular and square waveforms with a large repetition rate tunable range. J. Light. Technol. 2018, 36, 3293–3301. [Google Scholar] [CrossRef]
- Xue, C.; Ji, S.; Wang, A.; Jiang, N.; Qiu, K.; Hong, Y. Narrow-linewidth single-frequency photonic microwave generation in optically injected semiconductor lasers with filtered optical feedback. Opt. Lett. 2018, 43, 4184–4187. [Google Scholar] [CrossRef]
- Hao, T.; Tang, J.; Domenech, D.; Li, W.; Zhu, N.; Capmany, J.; Li, M. Toward monolithic integration of oeos: From systems to chips. J. Light. Technol. 2018, 36, 4565–4582. [Google Scholar] [CrossRef]
- Yao, J. Microwave photonics. J. Light. Technol. 2009, 27, 314–335. [Google Scholar] [CrossRef]
- Ding, T.; Tang, Y.; Sun, X.; Huang, Y.; Jiang, B.; Liu, J.; Li, Z.; Zheng, Y.; Chen, X. Experimental demonstration of te/tm polarization-independent frequency upconversion assisted by polarization coupling. Chin. Opt. Lett. 2023, 21, 121901. [Google Scholar] [CrossRef]
- Guo, Q.; Fan, S.; Yin, X.; Jiao, B.; Mu, J.; Ming, N.; Guo, L.; Yuan, J.; Wang, K.; Zhang, X. Highly sensitive frequency upconversion detection from 1 to 3 THz with oh1 crystal. Opt. Express 2023, 31, 38970–38976. [Google Scholar] [CrossRef]
- Zaldívar-Huerta, I.E.; Mbuebue, B.T.; García-Juárez, A.; Kanyinda, E.-Y.T.; Rojas-Laguna, R.; Lee, M.W. An experimental alternative of microwave signal generation through an optical heterodyning technique using a multimode laser diode and a tunable dfb laser. IEEE Lat. Am. 2024, 22, 512–518. [Google Scholar] [CrossRef]
- Liu, G.; Lu, Z.; Liu, J.; Poole, P.J.; Mao, Y.; Xie, X.; Vachon, M.; Song, C.-Y.; Barrios, P. Directly Modulated Quantum-Dash Mode-Locked Lasers for Millimeter-Wave over Fiber Applications. In Terahertz, RF, Millimeter, and Submillimeter-Wave Technology and Applications XVII; SPIE: Bellingham, WA, USA, 2024; Volume 12885, pp. 137–140. [Google Scholar]
- Yuan, J.; Zhang, M.; Mei, Y.; Liu, Q.; Liu, J. Photonic generation of millimeter-wave and multi-waveform signals based on external modulation and polarization control. Appl. Opt. 2022, 61, 8967–8973. [Google Scholar] [CrossRef]
- Dar, A.B.; Ahmad, F.; Jha, R.K. Filterless optical millimeter-wave generation using cascaded-parallel mach–zehnder modulators with tunable frequency multiplication factor. Opt. Quantum Electron. 2021, 53, 1–15. [Google Scholar] [CrossRef]
- Wu, Z.; Cao, C.; Zeng, X.; Feng, Z.; Shen, J.; Yan, X.; Wang, B.; Su, X. Filterless radio-over-fibersystem to generate 40 and 80 ghz millimeter-wave. IEEE Photonics J. 2020, 12, 1–13. [Google Scholar]
- Du, C.; Zhou, W.; Wang, Y.; Wang, M.; Wang, D.; Wang, K.; Dong, W.; Zhang, X. Photonic millimeter-wave ultrawideband signal generation using frequency upconversion based on the stimulated brillouin scattering effect. Opt. Lett. 2018, 43, 4915–4918. [Google Scholar] [CrossRef]
- Zhang, Z.; Xu, Y.; Luo, X.; Chen, M.; Bao, H. Passively stabilized brillouin fiber laser frequency combs for ultralow-noise microwave generation. Appl. Phys. Lett. 2024, 124, 211105. [Google Scholar] [CrossRef]
- Li, X.; Jeon, C.; Pan, S.; Kim, J. Low-noise repetition-rate multiplication by injection locking and gain-saturated amplification. IEEE Photonics Technol. Lett. 2019, 31, 997–1000. [Google Scholar] [CrossRef]
- Jeon, C.J.; Zhang, S.; Shin, J.; Kim, J. Highly tunable repetition-rate multiplication of mode-locked lasers using all-fibre harmonic injection locking. Sci. Rep. 2018, 8, 13875. [Google Scholar] [CrossRef]
- Chen, Y.; Wen, A.; Shang, L. Analysis of an optical mm-wave generation scheme with frequency octupling using two cascaded mach–zehnder modulators. Opt. Commun. 2010, 283, 4933–4941. [Google Scholar] [CrossRef]
- Huang, Z.; Cao, C.; Feng, Z.; Zeng, X.; Wu, J.; Wu, Q.; Wu, Z. Filterless radio-over-fiber system that generates 80 and 160 ghz millimeter waves based on two mzms. Appl. Opt. 2021, 60, 4871–4877. [Google Scholar] [CrossRef] [PubMed]
- Zhou, H.; Fei, C.; Zeng, Y.; Tan, Y.; Chen, M. A rof system based on 18-tuple frequency millimeter wave generation using external modulator and soa. Opt. Fiber Technol. 2021, 61, 102402. [Google Scholar] [CrossRef]
- Awsaj, M.K.; Al-Mashhadani, T.F.; Al-Mashhadani, M.K.S.; Ali, A.Y.; Zan, M.S.D.; Arsad, N. Multiwavelength fiber laser sources with 60 GHz brillouin frequency shift. Opt. Quantum Electron. 2023, 55, 528. [Google Scholar] [CrossRef]
- Xu, L.; Bai, G.-F.; Tang, J.; Tang, Y.-L.; Jiang, Y. All-optical microwave oscillator using cross-gain modulation of semiconductor optical amplifier and cascaded stimulated brillouin scattering effects in optical fiber. Opt. Commun. 2022, 514, 128167. [Google Scholar] [CrossRef]
- Chen, M.; Xu, Y.; Zhang, Z.; Luo, X.; Bao, H. Stabilized brillouin laser with sub-hz fundamental linewidth aided by frequency shifted optical injection locking. APL Photonics 2024, 9, 026103. [Google Scholar] [CrossRef]
- Li, L.; Chen, J.; Zhang, J.; Yao, J. Stepped-frequency microwave waveform generation based on a fourier domain mode-locked optoelectronic oscillator. IEEE Photonics Technol. Lett. 2024, 36, 305–308. [Google Scholar] [CrossRef]
- Ma, Y.; Linghu, S.; Chen, B.; Gu, F. Continuous ultra-wideband signal regeneration in random optoelectronic oscillators through injection locking. Opt. Express 2024, 32, 9847–9856. [Google Scholar] [CrossRef]
- Liu, A.; Dai, J.; Xu, K. Stable and low-spurs optoelectronic oscillators: A review. Appl. Sci. 2018, 8, 2623. [Google Scholar] [CrossRef]
- Fu, J.; Dai, Z.; Han, X.; Yao, J. Wavelength-space parity-time symmetric optoelectronic oscillator using a chirped fiber bragg grating. IEEE Photonics Technol. Lett. 2023, 36, 187–190. [Google Scholar] [CrossRef]
- Li, C.; Mao, J.; Dai, R.; Zhou, X.; Jiang, J. Frequency-sextupling optoelectronic oscillator using a mach–zehnder interferometer and an fbg. IEEE Photonics Technol. Lett. 2016, 28, 1356–1359. [Google Scholar] [CrossRef]
- Wang, H.; Wu, B.; Zhou, H.; Wang, W.; Xu, G. Optical tunable frequency-doubling oeo using a chirped fbg based on orthogonally polarized double sideband modulation. Photonics 2023, 10, 1002. [Google Scholar] [CrossRef]
- Rani, A.; Kedia, D. Mathematical analysis of 24-tupled mm-wave generation using cascaded mzms with polarization multiplexing for rof transmission. Opt. Quantum Electron. 2024, 56, 193. [Google Scholar] [CrossRef]
- Jiang, Y.; Ma, C.; Bai, G.; Qi, X.; Tang, Y.; Jia, Z.; Zi, Y.; Huang, F.; Wu, T. Photonic microwave waveforms generation based on time-domain processing. Opt. Express 2015, 23, 19442–19452. [Google Scholar] [CrossRef]
- Lee, K.-H.; Kim, J.-Y.; Choi, W.-Y. Injection-locked hybrid optoelectronic oscillators for single-mode oscillation. IEEE Photonics Technol. Lett. 2008, 20, 1645–1647. [Google Scholar] [CrossRef]
- Fan, Z.; Su, J.; Lin, Y.; Jiang, D.; Chen, Y.; Li, X.; Qiu, Q. Injection locking and pulling phenomena in an optoelectronic oscillator. Opt. Express 2021, 29, 4681–4699. [Google Scholar] [CrossRef]
- Liu, B.; Diao, S.; Lin, F. An injection-locked frequency doubler with improved odd-order spur suppression. In Proceedings of the 2014 IEEE International Wireless Symposium (IWS 2014), Xi’an, China, 24–26 March 2014; IEEE: Piscataway Township, NJ, USA, 2014; pp. 1–4. [Google Scholar]



Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Luo, H.; Yu, J.; Wang, J.; Ma, C.; Han, X.; Su, X.; Gao, Y.; Jia, S. Microwave Photonic Frequency Multiplier with Low Phase Noise Based on an Optoelectronic Oscillator. Photonics 2024, 11, 588. https://doi.org/10.3390/photonics11070588
Luo H, Yu J, Wang J, Ma C, Han X, Su X, Gao Y, Jia S. Microwave Photonic Frequency Multiplier with Low Phase Noise Based on an Optoelectronic Oscillator. Photonics. 2024; 11(7):588. https://doi.org/10.3390/photonics11070588
Chicago/Turabian StyleLuo, Hao, Jinlong Yu, Ju Wang, Chuang Ma, Xu Han, Xuemin Su, Ye Gao, and Shi Jia. 2024. "Microwave Photonic Frequency Multiplier with Low Phase Noise Based on an Optoelectronic Oscillator" Photonics 11, no. 7: 588. https://doi.org/10.3390/photonics11070588
APA StyleLuo, H., Yu, J., Wang, J., Ma, C., Han, X., Su, X., Gao, Y., & Jia, S. (2024). Microwave Photonic Frequency Multiplier with Low Phase Noise Based on an Optoelectronic Oscillator. Photonics, 11(7), 588. https://doi.org/10.3390/photonics11070588





