Abstract
Using two independent speckle imaging systems based on the recently published LSOCI method operating in contact mode on the skin, we assess the reproducibility of in vivo measurements and conduct an inter-instrument comparison. To this aim, we propose a calibration method to handle each imaging system as a comprehensive unit, which includes the laser source, optics, and camera. Key to our method is the introduction of a new index that quantifies the departure of the temporal contrast observed in vivo from the spatial contrast scattered from a reference static element generating a circular Gaussian speckle field. Using such near-real-time calibration method, we demonstrate that the microcirculation images produced by 2 different instruments exhibit high accuracy and stability, with microcirculation activity values in excellent agreement, thereby paving the way for clinical applications.
1. Introduction
Dynamic speckle imaging represents a highly promising tool for observing microcirculation, which plays a crucial role in delivering nutrients and oxygen to billions of cells with each heartbeat. Alterations in microcirculation are associated with various pathologies, such as cancer [1], diabetes [2,3], hypertension [4], sepsis [5], and viral infections [6]. This field is still very much alive, as witnessed by the new publications on the influence of microcirculation in various pathologies [7], including Covid [8], and the renewed interest in the associated dynamic speckle technology [9,10,11]. Therefore, monitoring the peripheral microcirculation of the body holds significant diagnostic potential.
Since the pioneering work by Briers [12], numerous advancements have been made in both the qualitative and quantitative analysis of blood circulation and microcirculation through dynamic speckle imaging. Recently, our team developed an additional modality to the established laser speckle contrast imaging (LSCI) method, called laser speckle orthogonal contrast imaging (LSOCI) [13]. This technique represents a polarimetric enhancement of traditional laser speckle imaging methodologies, such as laser speckle contrast analysis [12] and laser speckle contrast imaging [14].
LSOCI is based on the polarimetric selection of spatially depolarized scattered fields, primarily driven by the motion of red blood cells. In practice, when the skin is illuminated with a fully polarized laser in the near-infrared spectrum, we observe two principal contributions of backscattered light: one from the skin surface, which can be considered rough at the wavelength scale and that largely conserves the incident polarization, and another emanating from deeper layers that have undergone multiple scattering events, resulting in random polarization [15]. Both scattering sources contribute to the speckle pattern, but the surface-generated contribution can be effectively eliminated using a polarizer aligned orthogonally to the polarimetric state of the illuminating laser. This selective filtering leaves primarily the multi-scattered photons from deeper layers, which are especially sensitive to micro-movements. By employing such a polarimetric filtering system with orthogonal states, we have successfully captured new images of microcirculation at an interesting estimated depth of approximately 3 mm on the face. In fact, purely optical imaging techniques benefit from short wavelengths that favor high spatial resolution but at the expense of short penetration depths, typically in the sub-millimeter range, even for optical coherence tomography. The depth of LSOCI is achieved through the use of both the strongly penetrating near-infrared wavelength and the polarimetric selection of multiple scattering events. Additionally, we operate the device in direct contact with the skin to minimize relative movement between the patient and the instrument during acquisition. Under these conditions, a spatial resolution of 80 m has been achieved [13].
However, overcoming the challenges of adapting this technology for clinical use in pathology detection and diagnostics requires addressing several critical constraints:
- Quantified Indices per Pixel: each pixel in the image should provide a quantified index of microcirculation activity, essential for informing and guiding treatment decisions.
- Stability in Repeated Acquisitions: when imaging the same area with the body at rest, the technology must produce consistently stable images and microcirculation activity values.
- Inter-Instrument Consistency: rResults must be comparable across different imaging systems.
- Dynamic and Accurate Imaging: the imaging system must exhibit sufficient dynamic range, stability, and accuracy to distinguish between different pathological states, despite challenges posed by in vivo conditions such as the cardiac cycle and unavoidable movements.
From a practical standpoint—essential for practitioners—the imaging systems should be compact, lightweight, portable, and quick to deploy. This article aims to address all these points comprehensively.
To this end, we have developed two lightweight and compact imaging systems utilizing the LSOCI method. This paper presents the results regarding the dynamics, stability, and accuracy of measurements from each apparatus, along with a comparative analysis between the two systems. We discuss the conditions necessary for an effective comparison within the framework of a global calibration method specifically elaborated for dynamic speckle imaging.
We first propose comparing both instruments from the perspective of displayed contrast in highly detailed microcirculation structures. To meet this requirement, we performed a minor scratch on the skin, which revealed significant spatial details. Then, to associate each camera pixel with a reliable and comparable microcirculation value between both instruments, we use a global calibration method. This method was developed based on the understanding that the physical signal carrying biophysical information is not the absolute measurement of spatial or temporal speckle contrast but rather a deviation of these contrasts from a reference value, which depends on each imaging system as a whole. Finally, utilizing this calibration procedure, we conduct a quantitative comparison between the two instruments. Despite extensive research into dynamic speckle imaging since the 1980s, to our knowledge, this study presents the first qualitative and quantitative comparisons of two dynamic speckle imaging instruments scanning the same in vivo area.
This article is organized as follows: Section 2 Materials and Methods details the experimental setup and introduces the contrast variation calibration method (CVCM) along with the equation for the normalized Volume Microvascular Activity Index (). Section 3 Results presents the qualitative and quantitative inter-instrument comparison of temporal speckle contrast images, including the assessment of contrast linearity and the analysis of results. Section 4 Discussions distinguishes our approach from state-of-the-art quantified or semi-quantified methods. It clarifies that our philosophy does not seek to align with these approaches but rather to establish a reliable and reproducible signal specifically tailored for practical application in hospital environments. Finally, Section 5, Conclusions and Perspectives, summarizes the main findings and suggests directions for future research, highlighting the potential applications of this technology in medical diagnostics and treatment monitoring.
2. Materials and Methods
2.1. Experimental Setup
Two laser speckle orthogonal contrast imaging instruments, namely LSOCI1 and LSOCI2, use a linearly polarized TEM00 mode laser (Lambdamini from RGB Photonics GmbH, Kelheim, Germany) with a central wavelength around 785 nm. Their laser beam is sent through some diverging optics to illuminate a skin surface of about 12 cm2. Backscattered photons are then filtered by a linear grid polarizer (THO-WP25M-UB from Thorlabs, Newton, NJ, USA) in which the eigenaxis is set orthogonal to the polarization state of the laser illumination before reaching a monochrome CMOS camera of 1.5 million pixels (acA1440-220um from Basler AG, Ahrensburg, Germany), according to our previously published article [13]. LSOCI1 and LSOCI2 emit, due to different diverging optics and laser power, respectively 14 W/m2 and 7.5 W/m2 on the skin surface. Moreover, their cameras are set to have different numerical apertures, which results in a ratio of approximately 2 between their speckle grain size and a similar detected mean intensity. All microcirculation images are calculated from the temporal contrast of 200 raw intensity images with 12 ms integration time each. Both systems are used in contact with the skin in order to minimize movements during acquisitions. They are compact with a size of 210 mm × 185 mm × 55 mm and a weight of 440 g. A handle makes them easy to hold and position on the skin. Their illuminating beam is inclined of 30° with respect to the normal of the skin surface, while the optical axis of their detection arm is aligned with it.
2.2. Contrast Variation Calibration Method (CVCM)
The common calibration procedures used [16,17,18] for absolute flow measurements within the framework of dynamic speckle imaging are primarily based on the experimental determination of the coefficient. This parameter stems from Siegert’s relation [19,20], which links the intensity temporal autocorrelation function to the electric field correlation function. Experimentally, the coefficient is expected to reflect the spectral characteristics of the laser source, polarization effects, and the spatial and temporal averaging of the speckle on the camera. This implicitly includes the coherence effects and the mismatch between the speckle grain size (determined by the intensity autocorrelation function [21]) and the pixel size.
However, these powerful calibration procedures appear more suited to research activities than clinical use due to their complex implementation. Furthermore, temporary perturbations in the imaging instrument, such as those due to temperature variations or optical re-injection affecting the laser source characteristics, could go undetected and potentially yield inconsistent results. Therefore, a near-instantaneous calibration method would be beneficial to verify the consistency and stability of the entire imaging system, even though it may only support semi-quantitative results. We have observed that in several recent articles, was arbitrarily set to 1; however, in our case, such simplification would hinder comparisons between instruments. Thus, we propose a straightforward method called Contrast Variation Calibration Method (CVCM), which allows for near-instantaneous calibration and thereby allows inter-instrument comparison.
Before going deeper into this method, it is important to highlight an intrinsic limitation of our imaging system regarding absolute blood flow measurements: since we rely on multi-scattered photons to generate our signal, we characterize more the activity of microcirculation rather than the absolute linear velocity of blood cells. By activity, we refer to the overall agitation of blood cells in potentially all three spatial dimensions without specifying which direction predominates in general cases. Thus, using the LSOCI method, the introduced in [13] describes how rapidly a global agitation of red blood cells, through multiple scattering, leads to speckle decorrelation. An analogy for the in the context of microcirculation in blood vessels could be the state variable of temperature, which characterizes the agitation and average speed of molecules or atoms in a confined gas. Ultimately, the LSOCI method offers enhanced penetration depth and greater sensitivity to the movement of blood cells due to its reliance on exclusive multiple scattering detection. However, it generally does not allow absolute speed measurements. Therefore, the goal here is to provide guidelines for performing stable, accurate, and comparable semi-quantitative measurements between LSOCI instruments.
2.3. Equation for Normalized VMAI
In previous studies [13,22,23], it was inferred that under both hypotheses of a Lorentzian and Gaussian distribution for the speed of red blood cells, the decorrelation time of the speckle pattern can be expressed as , where T is the integration time of the camera, and denotes the observed contrast in the polarimetric orthogonal configuration between the laser illumination and the polarizer in the detection arm. The Volume Microcirculation Activity Index (VMAI) was defined as the inverse of this decorrelation time, in accordance with the previously defined Blood Flow Index definition [24], resulting in the following equation:
While this equation can be used to assess the general trend of microcirculatory activity, it is not sufficient for performing inter-instrument comparisons. Firstly, we observe that for a spatial contrast of 1, theoretically achievable using a static scatterer generating a circular Gaussian speckle field, such a definition of the introduces an offset value of , which must be removed to meet the correct boundary conditions. Secondly, we suggest that the should tend to infinity as the agitation reaches its maximum and thus decreases the contrast to 0, assuming there is no static scatterer present. Consequently, we propose the following empirical equation for the normalized , denoted as , in Equation (2). This formulation: (1) retains the dependence; (2) normalizes the observed contrast using a reference contrast value ; and (3) eliminates the offset value of when :
with .
represents the maximum speckle contrast achievable on a reference static scatterer using the entire imaging system. This value characterizes the complete imaging setup, encompassing the spectral width of the laser, its polarization properties, and the camera’s numerical aperture and pixel density.
This maximum value is experimentally determined by illuminating a reference scatterer that produces a circular Gaussian speckle field [25,26]. Therefore, the standard deviation of the surface height distribution of this reference scatterer should be at least on the order of the laser wavelength, and the illumination diameter must encompass a sufficient number of roughness correlation cells. Microcirculation activity is then quantified based on deviations of the observed spatial contrast during in vivo measurements from this maximum value. Additionally, under the ergodic hypothesis, is also considered the highest achievable temporal speckle contrast, thus allowing similar treatments as the spatial contrast.
3. Results
3.1. Qualitative Inter-Instrument Comparison for Temporal Speckle Contrast Images
The contact mode used in the LSOCI method effectively minimizes relative movements between the instrument head and the observed area, revealing high spatial details. These details are especially pronounced in images of microcirculation activity within irritated skin areas. Additionally, we noted an important variability in the measurement of microcirculation activity on both the face and hands, influenced by environmental temperature variations. Consequently, we opted to induce a mild irritation on the belly just below a naevus. Both instruments, LSOCI1 and LSOCI2, were used to capture images of the same area before and after the irritation was mechanically induced. To ensure a thorough comparison, both instruments were alternated and repositioned after each acquisition, tracking the entire temporal evolution of the skin’s reaction.
We first illustrate the area that received the scratch in Figure 1. Panel (a) features a red dotted line that precisely indicates the future location of the scratch, and panel (b) highlights the faint red irritated area that was barely visible to the naked eye after the scratch.
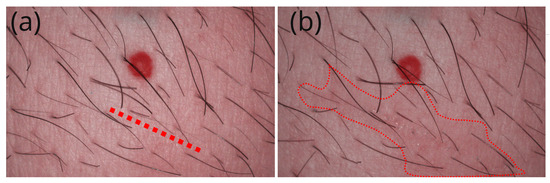
Figure 1.
(a) Image of the studied area with a red dotted line indicating the future location of the scratch, positioned just below a red angioma. (b) Image of the same area taken after the scratch, highlighting a faintly irritated red area that is barely visible to the naked eye, circled in red.
Figure 2 displays 12 sample images out of the 54 acquisitions performed by both instruments. A pronounced skin reaction is clearly observed in the .

Figure 2.
Temporal evolution of a scratch on the belly beneath an angioma, followed by two LSOCI instruments that exhibit very similar microcirculation patterns.
Despite the challenges posed by in vivo conditions, including inevitable movements and the effects of the heartbeat cycle during the acquisition time, both instruments exhibit very similar patterns. It is noted that the heartbeat cycle is only partially averaged, even though the total acquisition time is 200 × 12 ms = 2.4 s. Variations in the onset of acquisition relative to the systolic phase of the heartbeat are non-negligible. In live mode [13], our imaging systems clearly display the heart’s pulsation within the angioma.
The third column of Figure 2 shows a significant reaction in the area surrounding the injury, which markedly increases its blood circulation. This reaction pattern appeared almost immediately after the scratch (<1 s). Generally speaking, both instruments provide very similar pre- and post-injury images throughout the healing process, with the last column relating the microcirculation 4 h and 25 min after the scratch.
As illustrated in Figure 3, common circled details can be observed by both instruments, the smaller one (circled in green) measuring less than 1 mm (4 pixels). Note that the spatial resolution of our imaging systems is determined by the optics and pixel density of the camera; while it can be significantly improved, this enhancement comes at the cost of a smaller field of view. As pointed out earlier, these acquisitions were performed by constantly removing and quickly replacing each instrument on the same area, positioned at roughly a 90° angle relative to the surface of the skin. Therefore, the image stability observed in both instruments represents a very promising result in terms of operator dependency.
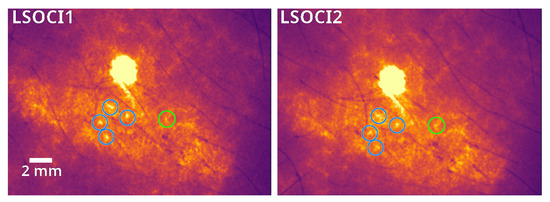
Figure 3.
A zoom into the more intense pattern observed in the previous figure reveals common spatial details, all enclosed in circles. Notably, a submillimeter-sized detail is highlighted in green.
3.2. Quantitative Inter-Instrument Comparison for Temporal Speckle Contrast Images
3.2.1. Contrast Linearity Domain
Before discussing the experimental results of in vivo measurements, it is important to note that a fully or nearly fully developed speckle pattern, composed of very dark and very bright spots, challenges the linearity of the camera due to its highly contrasted structure. Specifically, we aim to characterize the linearity domain of our cameras in terms of the stability of the temporal contrast. This involves determining the range with the corresponding error, within which the temporal or spatial contrast remains primarily stable as the received intensity (or numerical counts, NC) increases.
Figure 4a illustrates the evolution of histograms from left to right when illuminating a white paper sheet (Canson paper, 224 g/m2, previously characterized by polarimetry in [15]) with increasing detection integration times. Between the regimes of too low and too high numerical counts, where respectively dark noise and camera saturation predominate, we can identify an acceptable domain of linearity (highlighted in green in (b)), within which the variation of the contrast is less than 0.01. Therefore, all acquisitions must utilize speckle patterns with histograms falling within this linearity domain for measurements to avoid the need for error compensation.
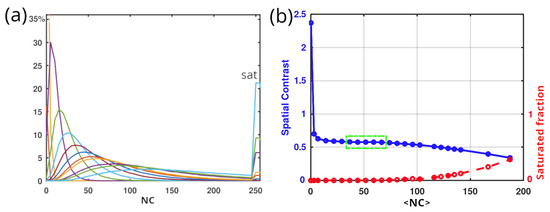
Figure 4.
(a) Experimental circular Gaussian speckle histograms for different integration times. The different colored lines in subfigure (a) represent these varying integration times but do not hold any specific significance. (b) Associated spatial contrasts as a function of the average numerical count (<NC>) of the camera. Three domains are clearly distinguished in (b): on the left, a regime with too low numerical counts corresponds to abnormally high spatial contrast; in the middle, a near-linear regime where the spatial contrast remains relatively stable with increasing <NC>; and on the right, a saturation regime that decreases the spatial contrast as the saturated fraction increases (indicated in red). We choose to operate within the near-linear regime, marked in green, where the contrast variation is less than 0.01.
3.2.2. Measurements and Analysis between Two LSOCI Instruments
As previously mentioned, both imaging systems, LSOCI1 and LSOCI2, do not have the same diverging optics and laser power. Thus, in order to work inside the contrast linearity range of intensity previously described, the optical aperture of the cameras was used to compensate for the difference of energy received. LSOCI1 and LSOCI2, respectively, emitted 14 W/m2 and 7.5 W/m2 onto the skin, but their respective camera apertures were set to achieve both an average numerical count <NC> corresponding to the middle of the contrast linearity range, highlighted in green in Figure 4b. Consequently, this led to a difference in the speckle grain size ratio of approximately 2 between the two imaging systems, with the smaller grain size of LSOCI2 characterized by approximately 2 pixels. This disparity in speckle grain size resulted in different values between the two instruments when illuminating the reference static sample.
For each of the 54 acquisitions performed (27 for each instrument), the values were recorded, resulting in mean values of 0.70 and 0.67 with associated standard deviations of 0.016 and 0.014 for LSOCI1 and LSOCI2, respectively, after camera linearization and shot noise removal. It is noteworthy that the spectral characteristics of lasers used in dynamic speckle imaging have only recently been addressed [27], despite their significant impact on the value through their spectral width. In this experiment, the lasers were not temperature-stabilized, and occasional mode hops could change this reference value, necessitating its update before each acquisition. However, with temperature stabilized single longitudinal mode lasers, a single acquisition value of for each imaging system would likely suffice due to the stability of the longitudinal mode, thus rendering the CVCM calibration procedure particularly simple and nearly instantaneous. Finally, utilizing a different and characteristic for both instruments enables us to replace the calibration procedure while still maintaining the capability to perform semi-quantitative measurements, which are primarily required in clinical applications.
Figure 5 presents quantified observations of the microcirculation skin reaction. Time tracking was performed by both LSOCI1 and LSOCI2 instruments and lasted 4 h and 25 min. Figure 5a,d, Figure 5b,e and Figure 5c,f correspond to selected regions of interest circled in green, respectively located on the angioma, the center of the scratch, and a more peripheral zone farther from the scratch. The objective was to test the CVCM throughout the entire dynamic range of the image. Figure 5d–f are the temporal zooms of Figure 5a–c respectively. LSOCI1 and LSOCI2 are represented by red and blue colors, respectively. Dotted lines indicate the results obtained without calibration, setting to 1 for every acquisition, while solid lines utilize the correction according to the CVCM. In order to partially average the cardiac cycle effect, each point on the curves was obtained by averaging at least three closely timed measurements for each instrument, while adhering to the previously described switch-and-replace procedure between acquisitions. The standard deviation for each group of closely timed acquisitions is represented by vertical bars.
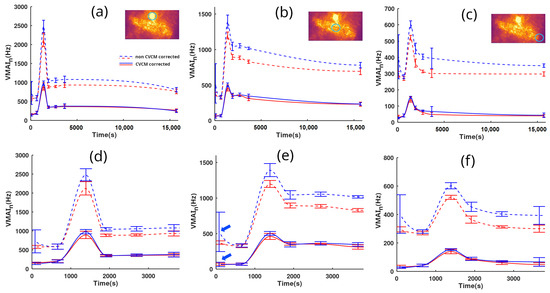
Figure 5.
Measurements of over time by two LSOCI instruments (LSOCI1 in red, LSOCI2 in blue) before and after inducing irritation via a scratch. Each column shows the mean value over a region of interest circled in blue in the thumbnail images above. Panels (d–f) provide temporal zooms of panels (a–c), respectively. Dotted lines represent uncalibrated measurements (), while solid lines show CVCM-corrected measurements with distinct values for each acquisition. Despite partial averaging of the cardiac cycle effect and unavoidable movements, calibrated acquisitions from both instruments yield similar results, unlike the non-calibrated values (dotted lines). Blue arrows in (e) highlight a high mean value and deviation in the non-corrected blue dotted line.
The non-corrected blue dotted curve of the LSOCI2 instrument consistently lies above the red ones. However, this offset is effectively corrected using the CVCM for all values across the full range of acquisitions (between 20 and 1000 Hz). Upon closer examination, as can be observed in panels (d), (e), and (f), the first group of closely timed acquisitions of LSOCI2—indicated by blue arrows only in (e) for clarity—displays a surprisingly high mean value along with an abnormally high deviation in the non-corrected blue dotted line. Both values are noticeably different compared to the simultaneous LSOCI1 measurements and also to subsequent acquisitions performed by both instruments minutes later. Nevertheless, with the CVCM, both the abnormal mean and deviation values are corrected and align well with other measurements, as seen in the corresponding solid lines. This behavior is indicative of a laser mode hop that temporarily altered the value of LSOCI2. However, this variation was successfully detected and corrected using the acquisition on the static scatterer, according to the CVCM. From our experience, such mode hops in the lasers used in this experiment could change the value by up to 25%. Finally, despite the residual effects of the cardiac cycle and potential movements during acquisitions, the CVCM successfully harmonized all the acquisitions performed by both instruments, as demonstrated by the excellent overlay of the full blue and red lines.
4. Discussion
The article [28] categorizes approaches to dynamic speckle imaging into three types: qualitative, semi-quantitative, and quantitative. Qualitative approaches aim to visualize the morphology of blood flow without quantifying a physical parameter. Semi-quantitative methods, such as multiple exposure speckle imaging (MESI) [29,30], attempt to model and distinguish the contributions of static and dynamic layers to speckle contrast. They are generally more complex to implement than simple qualitative methods based on a single exposure time. Our work aligns with semi-quantitative methods in the sense that we do not measure the absolute speed of red blood cells but an activity index linked to their global agitation and circulation speed. Moreover, we use a single exposure time, and our goal differs: we aim to ensure the accuracy and reproducibility of measurements over time and across instruments that eventually have various laser spectral widths, camera apertures, and pixel densities. Therefore, we adopt a pragmatic approach aimed at providing diagnostic activity measurements useful for monitoring the progression of specific pathologies such as scars, tracking the outcomes of skin grafts, or evaluating the efficacy of anti-cancer therapy. For the first time to our knowledge, these measurements are carried out directly on humans in real-time, in vivo, without the need for anesthesia or surgical intervention, and acquisitions along with calibration need only a few seconds. This practical aspect thus facilitates the adoption of these measurements in a hospital setting. Moreover, the reliability of this method has been confirmed in this paper, not only between different instruments but also over extended periods, by observing the evolution of a healing process around a lesion for a wide dynamic range of microcirculation activity values. As described earlier, our method uses a preliminary measurement on a non-biological static reference sample for calibration purposes and leads to the extraction of the value characterizing the whole imaging instrument. However, this measurement can eventually be performed in real time, during in vivo acquisitions, using a small portion of the field of view of the camera dedicated to the static scatterer generating a circulation Gaussian speckle field. This latter static contrast parameter thus becomes the cornerstone of our instrument’s design and lead to a permanent global check of the whole imaging instrument, including tracking mode hops of the laser. We emphasize that we have chosen to estimate contrast in the temporal rather than in the spatial domain to preserve the best spatial resolution. Thus, our criterion compares the deviation of the detected in vivo temporal contrast to the one obtained on a static reference sample generating a circular Gaussian speckle field. That means that our approach is based on the assumption that the measurements are ergodic. Although this has been mainly the case in practice in most of our skin measurements, the effects of ergodicity breaking on CVCM due to the possible presence of static scatterers should be deepened. A noticeable aspect of our method is also based on the use of a linearity domain of the camera in terms of spatial contrast and not, as usual, in terms of the dependence of the numerical counts in function of the intensity received, which appears to be less critical in our case. Furthermore, we observed that even in the absence of a specific microcirculation reaction, the stationary signal is affected by the heart rate, which introduces fluctuations in the measured temporal contrast. To address, at least partially, this issue, each acquisition lasted 2.4 s (without provoking unintentional blurring thanks to the contact mode). However, in spite of the expected presence of several heartbeats inside this acquisition time, variations in the onset of acquisition relative to the systolic phase of the heartbeat were found to be non-negligible. In the future, it can be interesting to focus on the influence of cardiac fluctuations and especially to synchronize the beginning of the acquisition process with the heartbeat cycle in order to improve the accuracy of contrast estimation. This optimization would increase the sensitivity and specificity of the instrument, thereby broadening its clinical application.
5. Conclusions and Perspectives
To enable a quantified comparison between two distinct LSOCI instruments, we have proposed the near-real-time contrast variation calibration method, which characterizes each dynamic speckle imaging system as a comprehensive unit, encompassing the laser source, optics, and camera. This approach utilizes a unique parameter of calibration for each instrument which is the maximum spatial contrast attainable under given acquisition parameters, while imaging a static scatterer producing a circular Gaussian speckle field. The microcirculation activity is then reached through the deviation, whether in temporal or spatial contrast, from this maximum value in response to the agitation and circulation of red blood cells. Using this calibration method, we have followed in time the evolution of a scratch on the belly using 2 similar LSOCI instruments, but with different laser power, optics, and detection apertures. Microcirculation patterns and measures are in excellent agreement between both imaging systems. Thus, despite being limited to semi-quantitative measurements, the LSOCI method with CVCM provides a high dynamic range, accuracy, and stability of the signal, which can moreover be successfully compared between calibrated instruments. We believe that these results are promising for numerous medical applications, such as real-time monitoring of tumor evolution under therapy, accurate characterization of diabetes stage assessment, various surgical applications, and the evaluation of burn evolution. However, the full validity domain of the proposed calibration method should be addressed in function of the laser spectral width, optical aperture, and pixel density of the camera. Moreover, further improvements are expected concerning the choice of the integration time in function of the observed microcirculation activity. In fact, the contact mode reduces the relative movement between the head of the imaging instrument and the observed area during the acquisition. This allows us to use larger integration times than typical values between 5 and 15 ms and thus opens new optimization opportunities, especially for the observation of very slow speeds of circulation.
Author Contributions
Conceptualization, methodology, validation, formal analysis, and investigation, X.O., E.C. and A.P.; supervision, project administration, funding acquisition X.O.; writing—original draft preparation, review and editing, X.O. and E.C. All authors have read and agreed to the published version of the manuscript.
Funding
This work has been led with financial support from the ITMO Cancer AVIESAN (Alliance Nationale pour les Sciences de la Vie et de la Santé, National Alliance for Life Sciences & Health) within the framework of the Cancer Plan (Under Contract No. 18CP112-00).
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Informed consent was obtained from all subjects involved in the study.
Data Availability Statement
The data that support the findings of this study are available from the corresponding author upon reasonable request.
Conflicts of Interest
The authors declare no conflict of interest. The funders had no role in the design of the study; in the collection, analyses, or interpretation of data; in the writing of the manuscript; or in the decision to publish the results.
References
- Stücker, M.; Horstmann, I.; Röchling, A.; Hoffmann, K.; Nüchel, C.; Altmeyer, P. Differential diagnosis of skin tumors using tumor microcirculation. In Skin Cancer and UV Radiation; Springer: Berlin/Heidelberg, Germany, 1997; pp. 999–1006. [Google Scholar]
- Li, J.; Cao, Y.; Liu, W.; Wang, Q.; Qian, Y.; Lu, P. Correlations among diabetic microvascular complications: A systematic review and meta-analysis. Sci. Rep. 2019, 9, 3137. [Google Scholar] [CrossRef]
- Strain, W.D.; Paldánius, P. Diabetes, cardiovascular disease and the microcirculation. Cardiovasc. Diabetol. 2018, 17, 57. [Google Scholar] [CrossRef]
- Lara Rezende, G.; da Silva, M.d.G.; Soares Takano, G.H.; Lopes Sampaio, A.L.; Oliveira Soares, R.; dos Santos Kückelhaus, C.; Souza Kückelhaus, S.A. Hypertension causes structural lesions in the microvasculature of the posterior nasal mucosa. Hypertens. Res. 2021, 44, 591–594. [Google Scholar] [CrossRef]
- De Backer, D.; Creteur, J.; Preiser, J.C.; Dubois, M.J.; Vincent, J.L. Microvascular blood flow is altered in patients with sepsis. Am. J. Respir. Crit. Care Med. 2002, 166, 98–104. [Google Scholar] [CrossRef]
- Damiani, E.; Carsetti, A.; Casarotta, E.; Scorcella, C.; Domizi, R.; Adrario, E.; Donati, A. Microvascular alterations in patients with SARS-CoV-2 severe pneumonia. Ann. Intensive Care 2020, 10, 60. [Google Scholar] [CrossRef]
- Narzulaeva, U. Pathogenetic Mechanisms of Microcirculation disorders. Int. Bull. Med. Sci. Clin. Res. 2023, 3, 60–65. [Google Scholar]
- Zharkikh, E.V.; Loktionova, Y.I.; Fedorovich, A.A.; Gorshkov, A.Y.; Dunaev, A.V. Assessment of blood microcirculation changes after COVID-19 using wearable laser Doppler flowmetry. Diagnostics 2023, 13, 920. [Google Scholar] [CrossRef]
- Sdobnov, A.; Piavchenko, G.; Bykov, A.; Meglinski, I. Advances in dynamic light scattering imaging of blood flow. Laser Photonics Rev. 2024, 18, 2300494. [Google Scholar] [CrossRef]
- Ruan, Z.; Li, R.; Dong, W.; Cui, Z.; Yang, H.; Ren, R. Laser speckle contrast imaging to monitor microcirculation: An effective method to predict outcome in patients with sepsis and septic shock. Front. Bioeng. Biotechnol. 2023, 10, 1067739. [Google Scholar] [CrossRef]
- Golubova, N.; Potapova, E.; Seryogina, E.; Dremin, V. Time–frequency analysis of laser speckle contrast for transcranial assessment of cerebral blood flow. Biomed. Signal Process. Control 2023, 85, 104969. [Google Scholar] [CrossRef]
- Briers, J.D.; Webster, S. Laser speckle contrast analysis (LASCA): A nonscanning, full-field technique for monitoring capillary blood flow. J. Biomed. Opt. 1996, 1, 174–179. [Google Scholar] [CrossRef]
- Colin, E.; Plyer, A.; Golzio, M.; Meyer, N.; Favre, G.; Orlik, X. Imaging of the skin microvascularization using spatially depolarized dynamic speckle. J. Biomed. Opt. 2022, 27, 046003. [Google Scholar] [CrossRef]
- Kirkpatrick, S.J.; Duncan, D.D.; Wells-Gray, E.M. Detrimental effects of speckle-pixel size matching in laser speckle contrast imaging. Opt. Lett. 2008, 33, 2886–2888. [Google Scholar] [CrossRef]
- Dupont, J.; Orlik, X.; Ghabbach, A.; Zerrad, M.; Soriano, G.; Amra, C. Polarization analysis of speckle field below its transverse correlation width: Application to surface and bulk scattering. Opt. Express 2014, 22, 24133–24141. [Google Scholar] [CrossRef]
- Wang, C.; Cao, Z.; Jin, X.; Lin, W.; Zheng, Y.; Zeng, B.; Xu, M. Robust quantitative single-exposure laser speckle imaging with true flow speckle contrast in the temporal and spatial domains. Biomed. Opt. Express 2019, 10, 4097–4114. [Google Scholar] [CrossRef]
- Liu, H.L.; Yuan, Y.; Han, L.; Bi, Y.; Yu, W.Y.; Yu, Y. Wide dynamic range measurement of blood flow in vivo using laser speckle contrast imaging. J. Biomed. Opt. 2024, 29, 016009. [Google Scholar] [CrossRef]
- Postnov, D.D.; Tang, J.; Erdener, S.E.; Kılıç, K.; Boas, D.A. Dynamic light scattering imaging. Sci. Adv. 2020, 6, eabc4628. [Google Scholar] [CrossRef]
- Fercher, A.; Briers, D. Flow visualization by means of single-exposure speckle photography. Opt. Commun. 1981, 37, 326–330. [Google Scholar] [CrossRef]
- Maret, G. Diffusing-wave spectroscopy. Curr. Opin. Colloid Interface Sci. 1997, 2, 251–257. [Google Scholar] [CrossRef]
- Goldfischer, L.I. Autocorrelation function and power spectral density of laser-produced speckle patterns. JOSA 1965, 55, 247–253. [Google Scholar] [CrossRef]
- Duncan, D.D.; Kirkpatrick, S.J. Can laser speckle flowmetry be made a quantitative tool? JOSA A 2008, 25, 2088–2094. [Google Scholar] [CrossRef]
- Ramirez-San-Juan, J.C.; Ramos-Garcia, R.; Guizar-Iturbide, I.; Martinez-Niconoff, G.; Choi, B. Impact of velocity distribution assumption on simplified laser speckle imaging equation. Opt. Express 2008, 16, 3197–3203. [Google Scholar] [CrossRef] [PubMed]
- Sunil, S.; Zilpelwar, S.; Boas, D.A.; Postnov, D.D. Guidelines for obtaining an absolute blood flow index with laser speckle contrast imaging. bioRxiv 2021. [Google Scholar] [CrossRef]
- Goodman, J.W. Statistical Optics; John Wiley & Sons: Hoboken, NJ, USA, 2015. [Google Scholar]
- Bergoënd, I.; Orlik, X.; Lacot, E. Study of a circular Gaussian transition in an optical speckle field. J. Eur. Opt. Soc.-Rapid Publ. 2008, 3. [Google Scholar] [CrossRef]
- Postnov, D.D.; Cheng, X.; Erdener, S.E.; Boas, D.A. Choosing a laser for laser speckle contrast imaging. Sci. Rep. 2019, 9, 2542. [Google Scholar] [CrossRef]
- Qureshi, M.M.; Allam, N.; Im, J.; Kwon, H.S.; Chung, E.; Vitkin, I.A. Advances in laser speckle imaging: From qualitative to quantitative hemodynamic assessment. J. Biophotonics 2024, 17, e202300126. [Google Scholar] [CrossRef]
- Parthasarathy, A.B.; Tom, W.J.; Gopal, A.; Zhang, X.; Dunn, A.K. Robust flow measurement with multi-exposure speckle imaging. Opt. Express 2008, 16, 1975–1989. [Google Scholar] [CrossRef]
- Chammas, M.; Pain, F. Synthetic exposure with a CMOS camera for multiple exposure speckle imaging of blood flow. Sci. Rep. 2022, 12, 4708. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).