Abstract
In this paper, a subset-optimized eight-dimensional trellis-coded quadrature amplitude modulation (SO-8DTCM-16QAM) format for higher-order constellations in high-speed optical communications is proposed. This scheme increases the number of subsets of base 2D constellation divisions. On this basis, it is further optimized by using 2D subsets for Cartesian product combinations to obtain 4D subsets and eliminate the combinations with small Euclidean distances. Finally, the 4D subsets are utilized to construct interrelated 8D subsets for trellis coding modulation and signal transmission. The proposed scheme can effectively reduce the decoding complexity and outperforms the conventional scheme at a high signal-to-noise ratio (SNR). Simulation verification of the proposed scheme is carried out, and the results show that the SO-8DTCM-16QAM achieves signal-to-noise ratio (SNR) gains of 1.60 dB, 1.56 dB, 1.51 dB, and 1.33 dB, respectively, compared with the conventional 8D-16QAM signals when BTB and 5/20/30 km optical signal transmission are performed. The SO-8DTCM-16QAM also achieves an SNR gain of 1.86 dB, 1.75 dB, and 1.22 dB at a net transmission rate of 14/21/28 GBaud. In addition, the SO-8DTCM-16/32/64QAM achieves an SNR gain of 1.27 dB, 0.80 dB, and 1.24 dB, respectively, when compared with the unoptimized 8DTCM-16/32/64QAM. Meanwhile, the proposed eight-subset SO-8DTCM-QAM scheme reduces the complexity of the decoding computation in the subset selection part and the constellation point selection part by 93.75% and 50%, respectively, compared with the unoptimized eight-subset and four-subset 8DTCM-QAM schemes. It can be seen that the proposed scheme simultaneously optimizes the transmission performance and complexity of high-speed optical communication systems and has practical application value.
1. Introduction
With the rapid development of mobile Internet, big data, artificial intelligence, and other information network technologies, the degree of informatization in many industries continues to increase. 4K video, Internet of Things, cloud computing, telecommuting, online education, and many other intelligent industries are becoming more and more popular every day, and along with this, there is the demand for massive data transmission, which makes the importance of high-speed data transmission, especially high-speed optical communication, increasingly prominent. However, in the face of the rapidly growing flood of traffic, the existing optical network standards are becoming increasingly difficult to meet the urgent demand for transmission bandwidth of the fast-growing Internet applications. Therefore, it is urgent to improve the system transmission capacity of existing optical communication networks. Driven by this goal, a large number of researchers have continuously investigated various technical means to achieve the increase in the capacity of optical fiber communication systems, such as wavelength-division multiplexing, the use of higher-order modulation formats, etc., but they all face various technical bottlenecks in the process of development [1,2]. Increasing the number of subchannels within the fiber optic communication window such as WDM can increase the transmission capacity of the system, but in addition to the need for modification of the existing system hardware, it will also lead to a reduction in the channel spacing, causing serious interchannel crosstalk. The use of a higher-order modulation format enables multiple lower-order modulated signals to be combined on a single carrier to achieve higher spectral efficiency (SE) and transmission rate for system gain. However, the higher-order modulation format also brings problems of difficult judgment, increased computational complexity, and reduced interference immunity due to the expanded constellation diagram. Therefore, solving the contradiction between the gain and interference of the high-order modulation format is a key issue in the current development of optical communication to ultralong distances and ultrahigh speeds.
One approach that has been proven to be effective is the trellis-coded modulation (TCM) technique. TCM maximizes the minimum free Euclidean distance between coded signal sequences by extending the signal set to accommodate the information redundancy due to convolutional coding and uses set partitioning to implement the mapping process from bit labels to signals. The coding gain it brings will provide an additional 3–6 dB coding gain after offsetting the gain loss caused by the reduction in the Euclidean distance between the information points due to the expansion of the signal set [3,4], which can effectively improve the transmission performance of the system and reduce the bit error rate (BER) of demodulation. Some conventional communication systems adopt a two-dimensional TCM scheme with a code rate of k/(k + 1), and in higher-order 2D-TCM systems, although the trellis coding still yields a gain from an overall perspective, the signal set expansion results in a loss of coding gain of about 3 dB [5]. In order to reduce this loss, a multidimensional TCM is required that utilizes dimensional apportionment to reduce the impact caused by constellation expansion.
Multidimensional trellis coding uses a multidimensional signal set while using multiple physical dimensions of the carrier to carry the multidimensional signal [6]. It has coding relationships between the multidimensional signals, and the original signals are restored by Viterbi decoding during demodulation. Compared with the traditional multidimensional independent signal, on the basis of meeting the transmission of large-capacity signals, trellis coding can greatly reduce the impact of fiber channel nonlinearities on it and enhance the signal’s anti-interference ability. At the same time, the constellation points in the multidimensional signal set are distributed in a multidimensional space, which has a larger optimization space of geometric and probability distributions compared with the one- or two-dimensional signal set [7] and can achieve the goal of coordinating the spectral efficiency and power efficiency. Therefore, this technique has also received extensive attention from researchers in the industry [8].
In 2019, Stojanovic et al. proposed a four-dimensional trellis-encoded seventh-order pulse amplitude modulation format (4D-TCM-PAM7) that can be applied in data centers, achieving transmission rates of 210/225 Gbit/s in the C band [9]. In the same year, Zhang and Hu proposed a 4D-TCM technique based on ball-filling, which showed some performance improvement in terms of BER and transmission distance compared with the conventional 4D modulation [10]. These studies initially explored the possibility of multidimensional trellis coding in data transmission. However, in the above 4D-TCM scheme, conventional polarization multiplexing is applied to transmit two mutually independent 2DTCM signals [11,12,13]. This scheme does not use TCMs associated with multiple dimensions, does not break the low-dimensional limitations itself, and signal interference between multiple dimensions affects decoding accuracy.
In 2020, Zhang proposed a probabilistic shaping 16QAM modulation scheme based on TCM with nonuniform probabilistic mapping of TCM-16QAM subsets, and successfully demonstrated the scheme in a single-mode fiber optic transmission system at a distance of 25 km, obtaining great optical SNR gain and BER performance [14]. In 2021, Zhang and Liu proposed a high-security multilevel constellation shaping TCM method based on clustered mapping rules, thus obtaining better constellation shaping gain while extending the coding gain of TCM [15]. These studies integrate trellis coding and constellation shaping with each other and provide a new way to improve the performance of TCM. However, the use of constellation shaping reduces the SE of the modulated signal, and these schemes simply combine constellation shaping with trellis coding without more optimization of the trellis coding part.
In 2022, He et al. proposed a four-dimensional trellis-coded modulation quadrature amplitude modulation orthogonal frequency division multiplexing (4D-TCM-QAM-OFDM) combined with a precoding scheme and demonstrated that this scheme has higher SE and receiver sensitivity in W-band fiber optic radio systems [16]. In 2023, Qin et al. proposed a recursive neural network-based joint equalization and decoding method, which can be transmitted over 112.5 Gb/s under a 7% hard-decision forward error correction (7% HD-FEC) threshold, as well as 87.5 Gb/s over 10 km standard single-mode fiber (SSFM) links to achieve higher BER performance compared with the conventional method [17]. These studies integrate trellis coding with precoding, neural networks, and other techniques, further enriching the way trellis coding is applied in optical communications. However, these techniques do not optimize trellis coding at the compiled code level, and the performance improvement is limited by the design of precoding and neural networks.
Therefore, to address the problem that the existing trellis coding dimensions are low and each dimension is independent of the other, which cannot take advantage of the multidimensional trellis demodulation, a higher-order multidimensional trellis coding method suitable for optical transmission is investigated, and an eight-dimensional trellis coding quadrature amplitude modulation scheme based on subset optimization is proposed. In the optical communication system, the scheme applies higher dimensional trellis coding to modulate the signal, while using multiple physical dimensions of the carrier to carry multidimensional signals, and utilizes the dimensions to effectively mitigate the misjudgment caused by the reduced minimum Euclidean distance due to the expansion of the signal set. The scheme takes full advantage of multidimensional trellis coding so that signals in multiple dimensions are correlated with each other in the coding. During decoding, error correction can be performed based on the relationship of multiple transmitted signals. If a sudden error occurs in one channel due to channel problems, the signals in other dimensions can be utilized for correction, and this advantage is especially obvious in channels with high SNR [18]. At the same time, the scheme is further optimized for the low-dimensional subset, which can further increase the minimum Euclidean distance, reduce the impact of various types of noise on the signal in the fiber-optic communication system, and enhance the anti-interference ability of the signal. On this basis, the optimized subset coding can also reduce the complexity of decoding calculation at the demodulation end.
The proposed SO-8DTCM-QAM scheme is simulated and verified under different fiber lengths, net transmission rates, and constellation orders. The results show that when performing BTB, as well as 5/20/30 km optical signal transmission, the proposed SO-8DTCM-16QAM scheme achieves SNR gains of 1.60 dB, 1.56 dB, 1.51 dB, and 1.33 dB, respectively, at 7% HD-FEC threshold compared with the conventional 8D-16QAM scheme. At a net transmission rate of 14/21/28 GBaud, the SO-8DTCM-16QAM scheme achieves SNR gains of 1.86 dB, 1.75 dB, and 1.22 dB, respectively. In addition, for different modulation orders, the SO-8DTCM-16/32/64QAM obtains 1.27 dB, 0.80 dB, and 1.24 dB gains compared with the unoptimized 8DTCM-16/32/64QAM, respectively. Meanwhile, the proposed eight-subset SO-8DTCM-QAM scheme reduces the complexity of decoding computation in the subset selection part and constellation point selection part by 93.75% and 50%, respectively, compared with the unoptimized eight-subset and four-subset 8DTCM-QAM schemes.
2. Principle of the SO-8DTCM-QAM Scheme
The block diagram of signal generation at the transmitter side of the signal is shown in Figure 1. The original random bit signal sequence is input and a serial-parallel transformation is performed on the original sequence according to the required order of the basic 2D constellation. The subsequent coding is divided into three parts: k-bit coded bits, a-bit noncoded bits, and b-bit noncoded bits. The k-bit coded bits are first convolved by a convolutional encoder with a code rate of k/(k + 1), and the 8D subset is selected using the resulting (k + 1) bits. The 4D and 2D subsets are selected using the a-bit noncoding bits. Signal points are selected using b-bit noncoding bits. Constellation mapping of 8D signals is performed based on the selection of subsets and constellation points to obtain the 8DTCM-QAM signal to be transmitted.
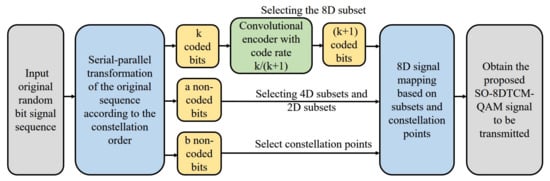
Figure 1.
Block diagram of signal generation at the signal transmitter.
In the trellis coding process, the core operations are the selection of subsets in each dimension from high to low and the selection of constellation points in the lowest dimension signal set. Therefore, the following content first introduces how to optimize the design and construction of 2D/4D/8D subsets and obtain the matching signal set. After that, how to perform specific trellis coding using the original bit sequences to obtain the 8D signals to be transmitted is presented. Finally, the proposed scheme is analyzed for decoding complexity.
2.1. Division and Construction of Optimized Subset
In the construction of 2D/4D/8D subsets, the high-dimensional subsets are combined with the low-dimensional subsets, so in the subset design and partitioning, the subsets of different dimensions are defined sequentially from low to high dimensions, i.e., to obtain the 2D subsets, 4D subsets, and 8D subsets sequentially.
First, in order to obtain the 2D subset, a subset division of the 2D-mQAM base constellation is required, where m is the order of the QAM constellation. The asymptotic coding gain equation of TCM after subset partitioning and noncoding modulation is given by
and denote the average energy of the set of coded and noncoded signals, respectively. and denote the minimum Euclidean distance between signal points in the noncoding constellation diagram and the free distance between coding sequences, respectively. and denote the constellation map energy expansion factor and distance gain factor, respectively. The coding constellations are scaled down to have the same average energy as the noncoding constellations, i.e., . For a TCM system to achieve coding gain, the free distance between coding sequences must be greater than the minimum distance between signal points in the noncoding system:
In order to increase the distance between the coded signals, the traditional TCM scheme divides the 2D-mQAM base constellations into four subsets A–D [19], where each subset contains m/4 constellation points. However, if the higher-order constellations are represented by increasing the number of points in the 2D-mQAM base constellations, it will increase the number of points in each subset, thus raising the probability of misclassification in the constellation point judgment. In this paper, an SO-8DTCM-QAM scheme is proposed to divide the 2D-mQAM base constellation into eight subsets A-H to reduce the number of constellation points contained in each subset in the higher-order constellations, which facilitates the process of optimizing the subset selection in the subsequent subset design, increases the minimum Euclidean distance, and improves the judgment accuracy in the subsequent demodulation. The 2D basic constellation subset division for 16QAM, 32QAM, and 64QAM is shown in Figure 2.
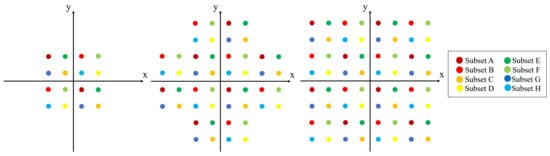
Figure 2.
Two-dimensional base constellation subset segmentation for 16QAM, 32QAM, and 64QAM.
As shown in Figure 3, 16QAM is used as an example to demonstrate the process of dividing 2D constellation subsets. The minimum Euclidean distance of the original constellation points is . After one set division, the minimum Euclidean distance becomes . After second-order set division, the minimum Euclidean distance is . After third-order set division, the minimum Euclidean distance is .
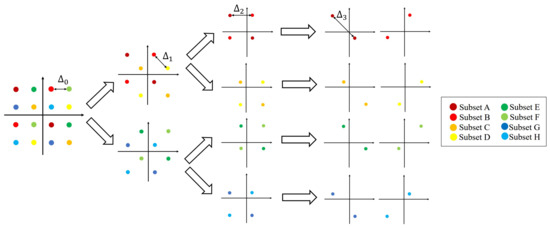
Figure 3.
Segmentation process for 2D subsets of 16QAM.
Second, the 4D subsets are composed using the divided 2D subsets. When composing 4D subsets, 2D subsets of different dimensions are Cartesian multiplied to obtain 2D combinations, and multiple 2D combinations form a 4D subset. Compared with the case of dividing into 4 subsets, if all 2D combinations are represented, the number of combinations increases from 16 to 64, and the number of 2D combinations in each 4D subset increases from 2 to 8. Since metric computation and branch deletion need to be performed on each set of signals based on each 4D subset during decoding, a simple increase in the number of 2D subset divisions will greatly increase the computational complexity and the total computation time. Therefore, this scheme further optimizes the 4D subsets by deleting some of the 2D combinations, thus simplifying the composition of the 4D subsets. After optimization, each 4D subset contains only two 2D combinations, and the minimum Euclidean distance between each 4D subset is guaranteed to be the largest, i.e., the 2D subset with a larger minimum Euclidean distance is preferentially selected to form the 2D combinations, which can effectively reduce the probability of misclassification of the 4D subsets. The selection of 2D combinations in 4D subsets is shown in Table 1.

Table 1.
Selection of 2D combinations in the 4D subset.
Finally, the optimized 4D subsets are used to compose 8D subsets. In composing the 8D subset, the 4D subsets of different dimensions are Cartesian multiplied, and a total of 64 4D combinations are obtained. Every four 4D subset combines a group, i.e., S1–S16 16 8D subsets are obtained to complete the division and construction of optimized subsets. The 2D subsets, 4D subsets, and 8D subsets of SO-8DTCM-QAM are obtained, as shown in Figure 4.
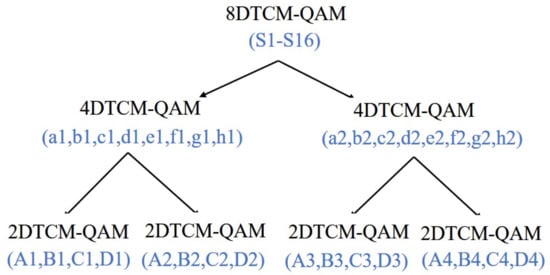
Figure 4.
Two-dimensional/four-dimensional/eight-dimensional subsets of the proposed SO-8DTCM-QAM scheme.
2.2. Trellis-Coded Modulation
After constructing the 2D/4D/8D subsets, the original bit sequence is trellis-coded to obtain the 8D signal to be transmitted. First, the original sequence of random bit signals is input, and a series-parallel transform is performed on the original sequence according to the required order of the basic 2D constellation. Equal probability 01-bit sequences are generated at the input, and after series-parallel transformation, each segment of the bit sequence is of equal length, and each bit segment is trellis-coded to obtain an 8D signal.
In the subsequent coding process, each bit segment needs to be divided into four parts: an 8D subset selection part, a 4D subset selection part, a 2D subset selection part, and a 2D constellation point selection part. In the 8D subset selection part, 3-bit data are needed. The 3-bit data are passed through a convolutional encoder which has a code rate of R = 3/4 and a constraint length of K = 5. One of the sixteen 8D subsets from S1–S16 is selected using the newly generated coded bits b1–b4. The structure of the convolutional encoder and the register state transfer diagram are shown in Figure 5.
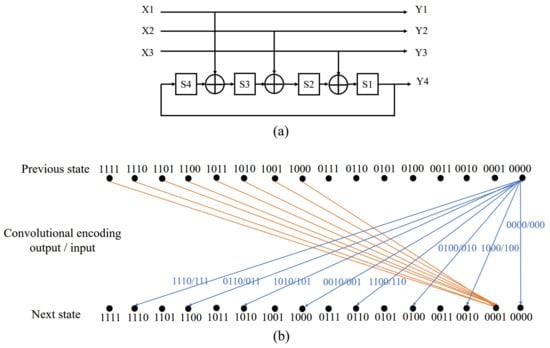
Figure 5.
(a) (4,3,5) convolutional encoder. (b) The state transition diagram of the register.
In the 4D subset selection part, 1 pair of 4D subsets is determined by utilizing 2-bit to select a 4D combination from the selected 8D subset. In the 2D subset selection part, 2-bit is utilized to select a 2D combination from each of the two 4D subsets, and in this way, 2 pairs of 2D subsets are determined, i.e., 4 separate 2D subsets belonging to each of the 4 2D constellations. Finally, in the 2D constellation point selection part, a constellation point is selected from each of the 4 2D subsets using 4 × (logM−3) bits according to the QAM order. For a base 2D constellation of order M, divided into eight 2D subsets, a subset contains M/8 constellation points, which requires (logM−3) bits for representation. The 8D signal requires 4 constellation points to be selected, so the constellation point selection portion requires 4 × (logM−3) bits.
The bit utilization diagram is shown in Figure 6. The total spectral efficiency is 7 + 4 × (logM−3) bit/s/Hz, which consists of (3 + 2 + 2) bit for selecting the 8D, 4D, and 2D subsets, as well as [4 × (logM−3)] bit for selecting the constellation points. The scheme realizes the coding of multidimensional signals in correlation with each other, which makes it possible to utilize multiplexing relations for error correction during decoding.
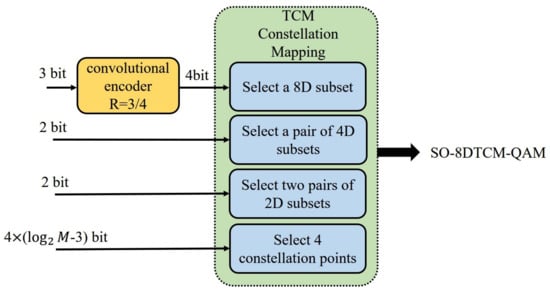
Figure 6.
Bit utilization diagram for the proposed SO-8DTCM-OAM scheme.
2.3. Decoding Complexity Analysis
The computational complexity of decoding for TCM is improved after subset optimization. When decoding an 8D trellis, a large number of operations are required for each update of the branching metrics of all states. The overall operation is divided into two parts: subset selection and constellation point selection. Both parts of the operation are nested sequentially from top to bottom. Thus, if the number of times an operation needs to be performed is doubled, the overall amount of arithmetic is doubled.
The subset selection part of the operation includes register arrival state (8D subset selection), register source state (8D subset selection), 4D combination selection in the 8D subset, 2D combination selection in the first 4D subset, and 2D combination selection in the second 4D subset. The constellation point selection part of the operation includes signal dimension selection and constellation point selection. The following illustrates the functions specifically included in each operation.
- Register arrival states and register source states (8D subset selection): For each decoding, the current number of possible arrival states is 8 and the number of possible source states is also 8. Assume the arrival and source states of the transmitted signal and calculate the distance between the received signal and the assumed signal as a metric. Select the 8D subset with the smallest metric.
- Selection of 4D combinations in the 8D subset: Each 8D subset contains 4 4D combinations. Assume 4D combinations of the transmitted signal and compute 4 metrics. Select the 4D combination with the smallest metric (i.e., a pair of 4D subsets).
- Selection of 2D combinations in the first 4D subset: Each 4D subset has a different number of 2D combinations depending on the scheme. Assume the first 2D combination of the transmitted signal and compute the metrics. Select the 2D combination with the smallest metric (i.e., the first pair of 2D subsets).
- Selection of 2D combinations in the second 4D subset: Assume the second 2D combination of the transmitted signal and compute the metrics. Select the 2D combination with the smallest metric (i.e., the second pair of 2D subsets).
- Signal dimension selection: The 8D signal needs to be calculated separately for each of the four 2D signals it contains.
- Constellation point selection: Each 2D subset has a different number of constellation points depending on the scheme. Assume the constellation points of the transmitted signal and compute the metrics. Select the constellation point with the smallest metric.
As shown in Table 2, two unoptimized 8DTCM-QAM schemes with different numbers of 2D subsets are compared with the SO-8DTCM-QAM scheme proposed in this paper. The table lists the key operations that need to be performed at the demodulation side of the signal for Viterbi decoding, as well as the number of times the metric value computation and comparison need to be performed in the corresponding operations. In each scheme, the computational effort for the same operation is exactly the same, differing only in the number of times the operation is invoked. Therefore, the computational complexity is counted and analyzed with each operation as the smallest unit.

Table 2.
Operations of the three schemes for branching metrics of all states per update.
A comparison is made in terms of BER performance. In both unoptimized schemes, only the number of 2D subset divisions is changed, but the corresponding 4D subset design and optimization are not performed, so the minimum Euclidean distance is the same in both cases, the demodulation BER is the same, and the BER performance is lower than that of the optimized scheme.
A comparison is made in terms of the amount of operations. The unoptimized scheme with 8 subsets has a total multiplier of operations in the subset selection part that is 16 times higher than that of the optimized scheme due to the higher number of 2D combinations. The optimized scheme reduces the computation in this part by 93.75%. The 4-subset unoptimized scheme has the same computation as the optimized solution in the subset selection part, but in the constellation point selection part, the total multiplier of the computation of the 4-subset unoptimized scheme is 2 times more than that of the optimized solution. The optimized scheme reduces the arithmetic in this part by 50%.
3. Simulation Results and Discussion
3.1. Simulation System Setup
In order to evaluate the performance of the SO-8DTCM-QAM scheme, a simulation system, shown in Figure 7, is established. The SO-8D-TCM-QAM signal to be transmitted is first generated at the transmitter side. The random bit sequence is subjected to a serial-parallel transformation according to the modulation format, and the bit data are partitioned into fixed-length data segments. After the TCM and constellation mapping process mentioned above, four 2D signals are obtained.
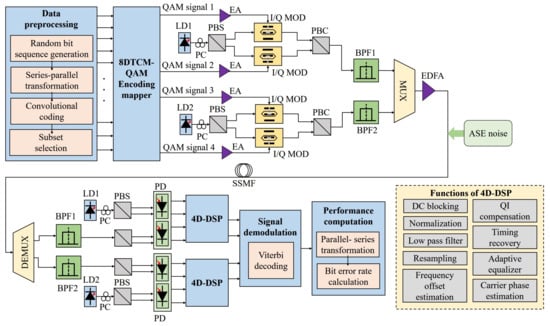
Figure 7.
Simulation system of the proposed SO-8DTCM-OAM scheme.
The light wave emitted by the laser diode is divided into two polarizations, x and y, through a polarization beam splitter for modulating the two 2D signals. The I and Q paths of each 2D signal are modulated using a Mach–Zehnder Modulator (MZM) after passing through the pulse transmitter to obtain the corresponding optical signal, respectively. The two orthogonally polarized optical modulation signals are passed through a polarization combiner to obtain a 4D polarization multiplexed signal. The same is true for the other two 2D signals. In this way, two 4D polarization multiplexed signals are obtained. Afterward, the two 4D signals are passed through bandpass filters and frequency-division multiplexed to both sides of the center frequency. After being amplified by an erbium-doped fiber amplifier (EDFA), they are transmitted in a standard single-mode fiber (SSMF) [20]. The specific parameter settings of the simulation system are shown in Table 3.

Table 3.
Simulation system parameter settings.
At the receiving end, the optical signal is first demultiplexed through a bandpass filter with the same bandwidth as the transmitting end. After that, the optical signal is converted into an electrical signal by coherent reception using a laser with the same frequency as that of the transmitting end. After that, the two 4D polarization-multiplexed signals are compensated separately by a DSP module, whose functions include DC blocking, normalization, low-pass filter, resampling, I/Q compensation, timing recovery, adaptive equalization, frequency offset estimation, and carrier phase estimation to obtain the compensated 8DTCM-QAM signal. Finally, signal demodulation is performed, the compensated 8D signal is decoded by Viterbi decoding, and the bit information is obtained after parallel-serial transformation, which is compared with the original sequence at the transmitter to calculate the BER performance.
3.2. Simulation Results and Performance Analysis
In 2023, Jin et al. performed an experiment to investigate the performance of transmitting 4D/8D-16QAM, as well as 4D/8D-64QAM in standard single-mode fiber using wavelength-division multiplexing (WDM) [21]. In this paper, in order to evaluate the performance of the eight-dimensional trellis-coded quadrature amplitude modulation scheme, the BER performance of the proposed SO-8DTCM-16QAM scheme is first analyzed and compared with that of the conventional 8D-16QAM scheme under different fiber lengths. In a 20 km optical transmission system, the SNR is set to 20 dB, at which time the 2D constellation diagrams of the SO-8DTCM-16QAM signal in four dimensions are shown in Figure 8.
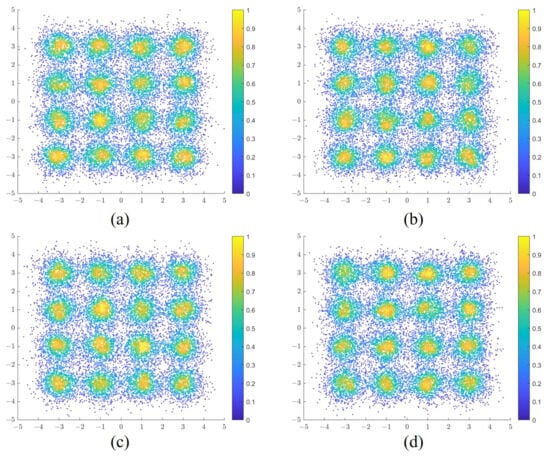
Figure 8.
Two-dimensional constellation diagrams of the proposed SO-8DTCM-16QAM signals in four dimensions: (a) X-polarized signal constellation diagram of subcarrier 1. (b) Y-polarized signal constellation diagram of subcarrier 1. (c) X-polarized signal constellation diagram of subcarrier 2. (d) Y-polarized signal constellation diagram of subcarrier 2.
Simulations are performed at BTB and fiber lengths of 5 km, 20 km, and 30 km, respectively. Due to the information redundancy in both the trellis coding as well as the subset optimization part of the optimization scheme, the SE of the SO-8DTCM-16QAM scheme is 11 bit/s/Hz, while the SE of the conventional 8D-16QAM is 16 bit/s/Hz. Therefore, in order to achieve the same efficiency in transmitting effective information, the SO-8DTCM-16QAM with a transmission bandwidth of 20 GBaud is simulated and compared with conventional 8D-16QAM with a transmission bandwidth of 14 GBaud, at which time the net transmission rate is 14 GBaud. In the range of SNR 13–25 dB, the BER simulation results are obtained as in Figure 9.
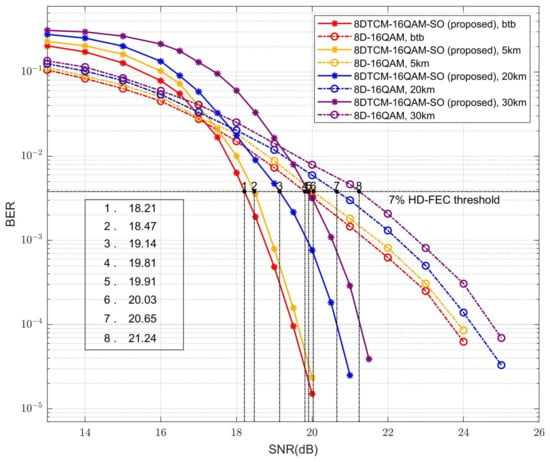
Figure 9.
Performance comparison between proposed SO-8DTCM-16QAM and conventional 8D-16QAM at BTB and 5/20/30 km transmission.
From Figure 9, it can be seen that the shorter the fiber length, the greater the performance gain of the SO-8DTCM-16QAM scheme compared with the conventional 8D-16QAM scheme. When the SNR reaches about 19.50 dB, the performance of the SO-8DTCM-16QAM scheme will be better than that of the conventional 8D-16QAM scheme in all four transmission cases. And in a single transmission case, the SNR gain obtained by the SO-8DTCM-16QAM scheme will increase rapidly when the SNR is further improved. Under the 7% HD-FEC threshold, the SO-8DTCM-16QAM is able to obtain coding gains of 1.60 dB, 1.56 dB, 1.51 dB, and 1.33 dB compared with the 8D-16QAM for the four transmission scenarios, namely BTB, 5 km, 20 km, and 30 km, respectively. This indicates that the proposed subset optimization scheme can meet the transmission requirements well and has more excellent performance at high SNR under different transmission conditions. Meanwhile, the performance of SO-8DTCM-16QAM is slightly lower than that of 8D-16QAM at low SNRs of 13–18 dB, which is due to the fact that the convolutional coding in trellis coding possesses a fixed error-correcting capability, and the output of the decoder will be flooded with errors when the SNR is below a certain threshold. And as the length of the fiber increases, the transmission is affected by the cumulative dispersion in the fiber, which also leads to some degree of performance degradation.
After that, the simulation is performed at a net transmission rate of 28/42/56 GBaud. The center frequency is set to 192.6 THz, the fiber length is 20 km, and the parameter settings of the transmission system for both SO-8DTCM-16QAM and 8D-16QAM schemes are shown in Table 4. In the range of 14–25 dB SNR, the BER simulation results are obtained as in Figure 10.

Table 4.
Parameter settings for SO-8DTCM-16QAM and 8D-16QAM schemes.
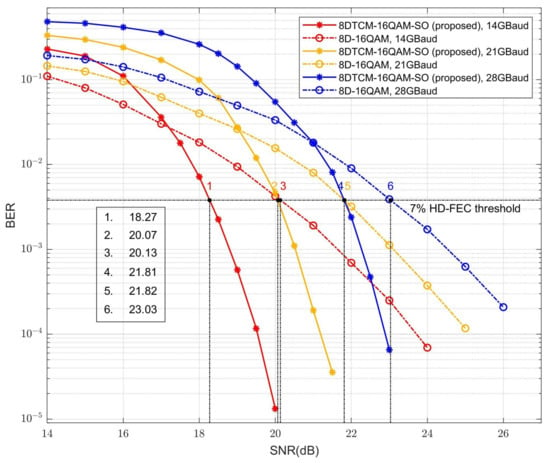
Figure 10.
Performance comparison between proposed SO-8DTCM-16QAM and conventional 8D-16QAM at net transfer rates of 14/21/28 GBaud.
From Figure 10, it can be seen that the smaller the net transmission rate, the larger the performance gain of the SO-8DTCM-16QAM scheme compared with the conventional 8D-16QAM scheme. When the SNR reaches about 21 dB, the performance of the SO-8DTCM-16QAM scheme at all three net transmission rates will be better than that of the conventional 8D-16QAM scheme. And at a single net transmission rate, the SNR gain obtained by the SO-8DTCM-16QAM scheme will increase rapidly when the SNR is further increased. Under the 7% HD-FEC threshold, the SO-8DTCM-16QAM signals obtain SNR gains of 1.86 dB, 1.75 dB, and 1.22 dB compared with the 8D-16QAM signals at net transmission rates of 14 GBaud, 21 GBaud, and 28 GBaud, respectively. This indicates that the proposed subset optimization scheme can meet the transmission requirements well and has more excellent performance at high SNR for different net transmission rates. Similar to the simulation results at different fiber lengths, as the net transmission rate increases, the cumulative dispersion in the fiber increases, which has a greater impact on the accuracy of the Euclidean distance judgment of the convolutional decoding at the demodulation end, and the gain obtained by the optimization scheme will be reduced by a small amount.
The subset optimization method is used to construct higher-order 8D trellis-coded quadrature amplitude modulation signals, which can achieve better system transmission performance compared with the conventional 8D format. The BER performance of the conventional 8D-16/32/64QAM, the unoptimized 8DTCM-16/32/64QAM, and the proposed SO-8DTCM-16/32/64QAM are analyzed and compared under a fiber length of 20 km. The 2D constellation diagram of SO-8DTCM-16/32/64QAM in one of the 2D dimensions at an SNR of 20 dB is shown in Figure 11. The BER simulation results for nine signals in the range of SNR of 14–40 dB are shown in Figure 12.
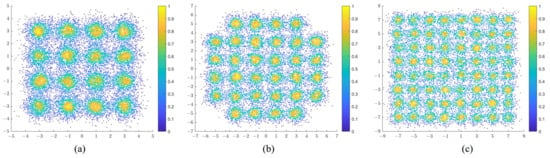
Figure 11.
Two-dimensional constellation diagram for SO-8DTCM-QAM in one of the 2D dimensions: (a) Two-dimensional constellation diagram for SO-8DTCM-16QAM in one of the 2D dimensions. (b) Two-dimensional constellation diagram for SO-8DTCM-32QAM in one of the 2D dimensions. (c) Two-dimensional constellation diagram for SO-8DTCM-64QAM in one of the 2D dimensions.
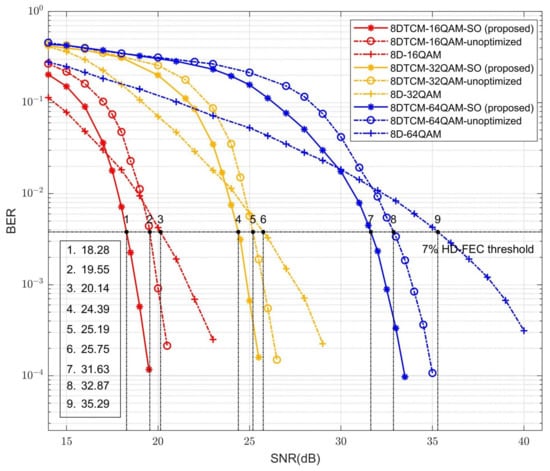
Figure 12.
BER performance of conventional 8D-16/32/64QAM, unoptimized 8DTCM-16/32/64QAM, and proposed SO-8DTCM-16/32/64QAM.
From Figure 12, it can be seen that the performance of conventional 8D-QAM, unoptimized 8DTCM-QAM, and SO-8DTCM-QAM are all better when the order is smaller and the constellation points are fewer. The slightly better BER performance of 8D-QAM than unoptimized 8DTCM-QAM and SO-8DTCM-QAM at a single order when the SNR is low is due to the fact that the information redundancy of the convolutional coding in the trellis coding causes it to be swamped by the noise at lower SNR, and it is not able to decode well. When the SNR is increased, the SNR gain obtained by the SO-8DTCM-16QAM scheme and the unoptimized 8DTCM-QAM scheme will increase rapidly, and their BER performance will exceed that of the conventional 8D-QAM scheme.
At a 7% HD-FEC threshold, the SO-8DTCM-16/32/64QAM scheme achieves 1.27 dB, 0.80 dB, and 1.24 dB SNR gains over the unoptimized 8DTCM-16/32/64QAM scheme, respectively. The SO-8DTCM-16/32/64QAM scheme achieves 1.86 dB, 1.36 dB, and 3.66 dB SNR gains over the conventional 8D-16/32/64QAM scheme, respectively. The gain of SO-8DTCM-QAM over the unoptimized 8DTCM-QAM signal comes from the increased Euclidean distance of the low-dimensional constellation points due to subset optimization, and the elimination of neighboring 4D combinations effectively reduces the probability of misclassification as a neighboring 2D subset. The lower gain obtained by trellis coding at 32QAM is due to the fact that the points at the edges of the constellation are not well reproduced when the not completely square constellations are optimized in the DSP module. The 8D-32QAM also suffers from this effect, making its performance lower than that of the 8D-64QAM with square constellations at a low SNR of 14–18 dB.
At 64QAM, compared with the conventional 8D-QAM signal, the most significant gain of the SO-8DTCM-QAM compared with conventional 8D-QAM signals is due to the fact that conventional 8D-QAM signals are encoded with each path independent of each other and hard judgments are used for decoding, whereas trellis coding encodes the constellations in different dimensions in correlation with each other, and soft demodulation based on the Euclidean distance is used for decoding. Especially at higher-order constellations, the likelihood of misclassification to other constellation points increases in conventional coding. In trellis coding, however, the subset division increases the Euclidean distance between constellation points, and at the same time, the use of Viterbi soft decoding with multiple dimensional interconnections can greatly reduce this misclassification probability due to the increase in constellation points. Overall, the proposed subset optimization scheme can meet the transmission requirements well and has optimal performance at high SNRs of different orders.
4. Conclusions
In this paper, the proposed subset-optimized eight-dimensional trellis-coded quadrature amplitude modulation format for higher-order constellations is verified to have excellent performance in terms of BER performance and decoding complexity through theoretical analysis and numerical simulation. The simulation results show that the SO-8DTCM-16QAM achieves SNR gains of 1.60 dB, 1.56 dB, 1.51 dB, and 1.33 dB at a 7% HD-FEC threshold, respectively, compared with the conventional 8D-16QAM signals when performing BTB, as well as 5/20/30 km optical signal transmission. The SNR gains are 1.86 dB, 1.75 dB, and 1.22 dB at 14/21/28 GBaud net transmission rates, respectively. In addition, for different modulation orders, SO-8DTCM-16/32/64QAM obtains 1.27 dB, 0.80 dB, and 1.24 dB gains compared with unoptimized 8DTCM-16/32/64QAM, respectively. The optimized eight-subset 8DTCM-QAM scheme reduces the complexity of decoding computation in the subset selection part by 93.75% compared with the unoptimized eight-subset 8DTCM-QAM scheme and reduces the complexity of decoding computation in the constellation point selection part by 50% compared with the unoptimized four-subset 8DTCM-QAM scheme. It can be seen that the proposed scheme optimizes the transmission performance of the high-speed optical communication system with a higher tolerance to noise, which leads to the improvement of the BER performance of its receive demodulation under different transmission conditions. At the same time, it reduces the complexity of decoding and facilitates integration, which has considerable practical application value. The proposed SO-8DTCM-16QAM scheme shows some limitations in the lower SNR region due to the fact that the convolutional coding in trellis coding has a fixed error correction capability. In real-world ultra-long-distance and ultra-high-speed optical communication systems, adaptive modulation and coding (AMC) can be used in order to solve this problem. By adjusting the modulation and coding rate of channel transmission, the quality of information transmission is ensured while maximizing the transmission rate. When the channel quality is poor, i.e., the SNR is low, the conventional 8D modulation scheme with a small order is selected. When the channel quality is good, i.e., the SNR is high, the SO-8DTCM-QAM scheme with a large order is selected.
Author Contributions
Conceptualization, J.C. and Q.Z. (Qi Zhang); methodology, J.C.; software, J.C. and Q.Z. (Qihan Zhao); validation, J.C. and Q.Z. (Qihan Zhao); formal analysis, J.C.; investigation, J.C.; resources, Q.Z. (Qi Zhang), F.T., Y.W., Q.T. and L.Y.; data curation, J.C.; writing—original draft preparation, J.C.; writing—review and editing, Q.Z. (Qi Zhang) and Q.Z. (Qihan Zhao); visualization, J.C.; supervision, Q.Z. (Qi Zhang), L.R., F.W. and S.Z.; project administration, Q.Z. (Qi Zhang), X.X., R.G. and H.Y.; funding acquisition, Q.Z. (Qi Zhang). All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded in part by the National Natural Science Foundation of China (NSFC) under Grant 61935005, 61835002, in part by the Funds for Creative Research Groups of China under Grant 62021005, and in part by Jiangsu Province’s IndustryOutlook and Key CoreTechnologies–Key Projects (BE2022055-4).
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
The data presented in this study are available on request from the corresponding author.
Conflicts of Interest
The authors declare no conflicts of interest.
Abbreviations
The following abbreviations are used in this manuscript:
| BER | bit error rate |
| SO-8DTCM-QAM | subset-optimized 8-dimensional trellis-coded quadrature amplitude modulation |
| SNR | signal-to-noise ratio |
| TCM | trellis-coded modulation |
| SE | spectral efficiency |
| HD-FEC | hard decision forward error correction |
| SSFM | standard single-mode fiber |
| MZM | Mach–Zehnder Modulator |
| EDFA | erbium-doped fiber amplifier |
References
- Kim, J.; Mainali, M. Analysis of High Rate Punctured Trellis Coded M-APSK for Multimedia Data Transmissions. In Proceedings of the 2022 IEEE International Symposium on Broadband Multimedia Systems and Broadcasting (BMSB), Bilbao, Spain, 15–17 June 2022; pp. 1–4. [Google Scholar]
- Li, Y.; Zhang, Q.; Yao, H.; Gao, R.; Xin, X.; Tian, F.; Tian, Q.; Feng, W.; Chen, D. Swarm-Intelligence-Based Routing and Wavelength Assignment in Optical Satellite Networks. IEEE Trans. Netw. Sci. Eng. 2024, 11, 1303–1319. [Google Scholar] [CrossRef]
- Mano, T.; Ahn, C.J. Joint Polar Code and Trellis Coded Modulation with Known Bits Puncturing. In Proceedings of the 2021 International Symposium on Intelligent Signal Processing and Communication Systems (ISPACS), Hualien City, Taiwan, 16–19 November 2021; pp. 1–2. [Google Scholar]
- Sharma, J.; Lalitha, V. Learning to Decode Trellis Coded Modulation. In Proceedings of the 2021 National Conference on Communications (NCC), Kanpur, India, 27–30 July 2021; pp. 1–6. [Google Scholar]
- Wang, J.; Ha, Y.; Chen, R.; Zou, P.; Chi, N. Comparation of Nonlinear Trellis-Coded-Modulation, Duobinary and QAM Modulation Formats in Visible Light Communication System. In Proceedings of the 2021 IEEE 9th International Conference on Information, Communication and Networks (ICICN), Xi’an, China, 25–28 November 2021; pp. 205–209. [Google Scholar]
- Chen, Y.; Yi, X. Application of Trellis-Coded Modulation in Long-Haul Optical Fiber Transmissions. In Proceedings of the 2023 21st International Conference on Optical Communications and Networks (ICOCN), Qufu, China, 31 July–3 August 2023; pp. 1–3. [Google Scholar]
- Cui, H.; Sun, Z.; Huang, X.; Tang, D.; Xie, F.; Qiao, Y. Trellis-Coded Modulation-Enabled Probabilistic Shaping with Simplified Viterbi Decoder for Bandwidth-Limited IMDD Systems. IEEE Photonics J. 2023, 15, 1–10. [Google Scholar] [CrossRef]
- Tuncer, M.M.; Angjo, J.; Yıldız, S. Frank-Zadoff Precoded Space-Time Trellis Coded MIMO-OFDM System Design. In Proceedings of the 2023 31st Signal Processing and Communications Applications Conference (SIU), Istanbul, Turkiye, 5–8 July 2023; pp. 1–4. [Google Scholar]
- Stojanović, N.; Prodaniuc, C.; Liang, Z.; Wei, J.; Calabró, S.; Rahman, T.; Xie, C. 4D PAM-7 Trellis Coded Modulation for Data Centers. IEEE Photonics Technol. Lett. 2019, 31, 369–372. [Google Scholar] [CrossRef]
- Zhang, Y.; Hu, G.; Yang, X.; Sun, Y. Four-dimensional trellis-coded modulation using sphere packing non-cubic constellations. Optik 2019, 186, 84–92. [Google Scholar] [CrossRef]
- Kojima, K.; Yoshida, T.; Koike-Akino, T.; Millar, D.S.; Parsons, K.; Pajovic, M.; Arlunno, V. Nonlinearity-Tolerant Four-Dimensional 2A8PSK Family for 5–7 Bits/Symbol Spectral Efficiency. J. Light. Technol. 2017, 35, 1383–1391. [Google Scholar] [CrossRef]
- Chen, B.; Alvarado, A.; van der Heide, S.; van den Hout, M.; Hafermann, H.; Okonkwo, C. Analysis and Experimental Demonstration of Orthant-Symmetric Four-Dimensional 7 bit/4D-Sym Modulation for Optical Fiber Communication. J. Light. Technol. 2021, 39, 2737–2753. [Google Scholar] [CrossRef]
- Xiang, M.; Xing, Z.; Li, X.; El-Fiky, E.; Morsy-Osman, M.; Zhuge, Q.; Plant, D.V. Experimental study of performance enhanced IM/DD transmissions combining 4D Trellis coded modulation with precoding. Opt. Express 2018, 26, 32522–32531. [Google Scholar] [CrossRef] [PubMed]
- Zhang, Z.; Zhang, Q.; Wang, X.; Xin, X.; Gao, R.; Zhang, H.; Ren, J.; Wu, X.; Xu, X.; Tian, Q.; et al. Probabilistic shaping 16 quadrature amplitude modulation scheme based on trellis-coded modulation for short-reach optical communication. Opt. Eng. 2020, 59, 076109. [Google Scholar] [CrossRef]
- Zhang, J.; Liu, B.; Ren, J.; Mao, Y.; Chen, S.; Tang, R.; Song, X.; Bai, Y.; Wu, X.; Wang, F.; et al. High-security multi-level constellation shaping trellis-coded modulation method based on clustering mapping rules. Opt. Express 2022, 30, 15401–15415. [Google Scholar] [CrossRef] [PubMed]
- He, J.; Xu, L.; Zhou, Z. Performance Enhancement of W-Band RoF System Using 4D Trellis Coded Modulation OFDM with Precoding. J. Light. Technol. 2022, 40, 6151–6157. [Google Scholar] [CrossRef]
- Qin, X.; Yang, C.; Guo, H.; Gao, Y.; Zhou, Q.; Wang, X.; Wang, Z. Recurrent Neural Network Based Joint Equalization and Decoding Method for Trellis Coded Modulated Optical Communication System. J. Light. Technol. 2023, 41, 1734–1741. [Google Scholar] [CrossRef]
- Che, M.; Kuboki, T.; Kato, K. Trellis Coded Three Dimensional Carrierless Amplitude and Phase Modulation. In Proceedings of the 2019 24th OptoElectronics and Communications Conference (OECC) and 2019 International Conference on Photonics in Switching and Computing (PSC), Fukuoka, Japan, 7–11 July 2019; pp. 1–3. [Google Scholar]
- Bai, Y.; Liu, B.; Wu, X.; Ullah, R.; Ren, J.; Mao, Y.; Chen, S.; Zhang, J.; Song, X.; Wu, Y.; et al. Performance-Enhanced Three-Dimensional Trellis Coded Modulation Based on Four-Winged Fractional-Order Chaotic Encryption for Physical Layer Security. J. Light. Technol. 2022, 40, 7701–7710. [Google Scholar] [CrossRef]
- Xie, T.; Xin, X.; Fang, L.; Yan, H.; Pan, X.; Li, X. SC and OFDM hybrid coherent optical transmission scheme based on 1-bit bandpass delta-sigma modulation. Opt. Express 2024, 32, 11337–11345. [Google Scholar] [CrossRef] [PubMed]
- Jin, T.; Yi, X.; Lin, H.; Zhang, J.; Huang, X.; Bai, L.; Zhang, Q.; Qiu, K. Phase rearrangement shell mapping in single-span nonlinear optical fiber communication system. Opt. Commun. 2023, 530, 129107. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).