A Study on the Irradiance Scintillation Characteristics of Monochromatic LED-Based Visible Light Communication Systems in Weak-to-Strong Turbulence
Abstract
1. Introduction
2. Propagation of Monochromatic LED Beams with Spatially Incoherent Property in Weak-to-Strong Turbulence
2.1. Irradiance Scintillation Index in Weak Turbulence
2.2. Irradiance Scintillation Index in Weak-to-Strong Turbulence
2.3. Fading Probability
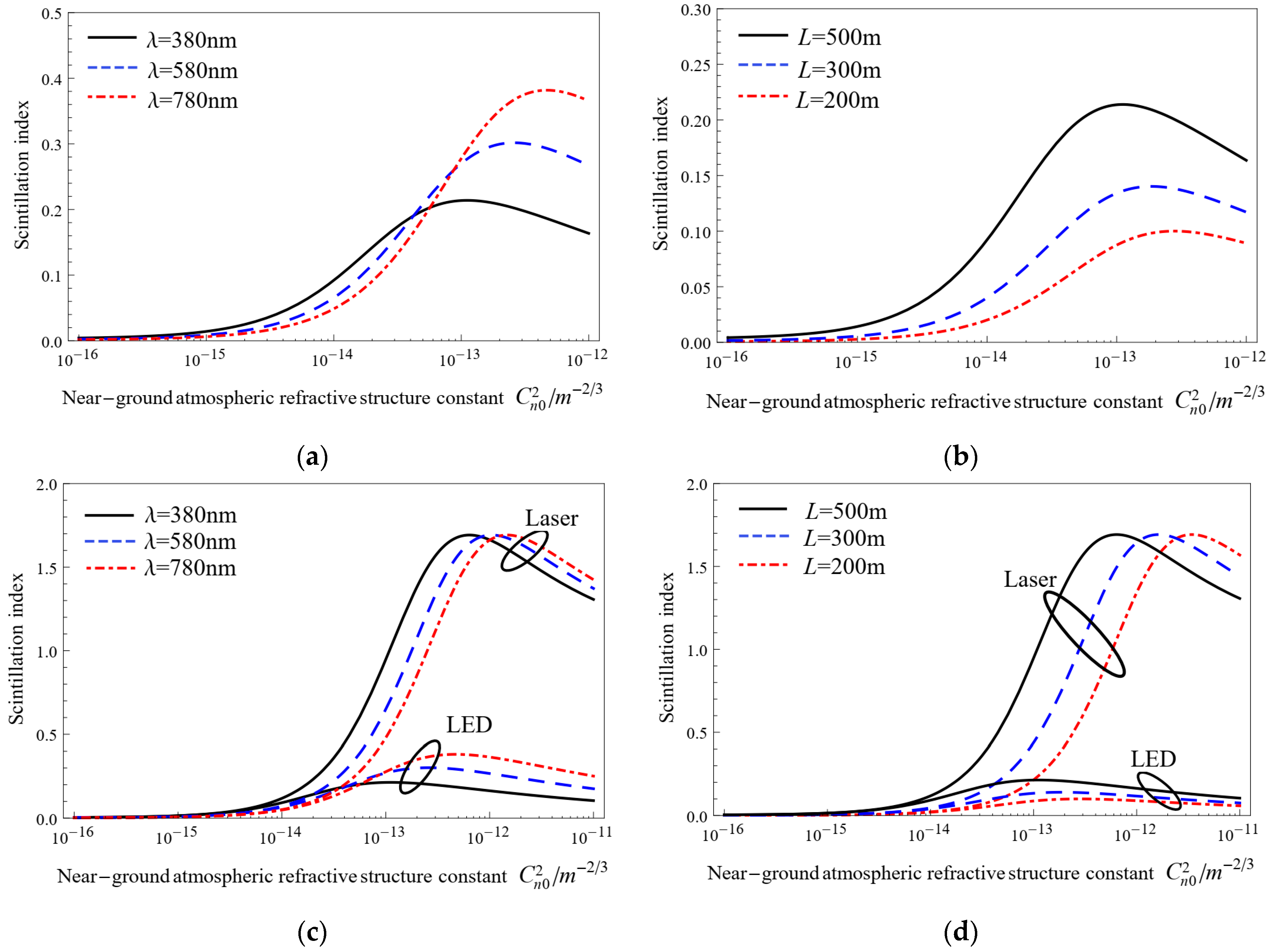
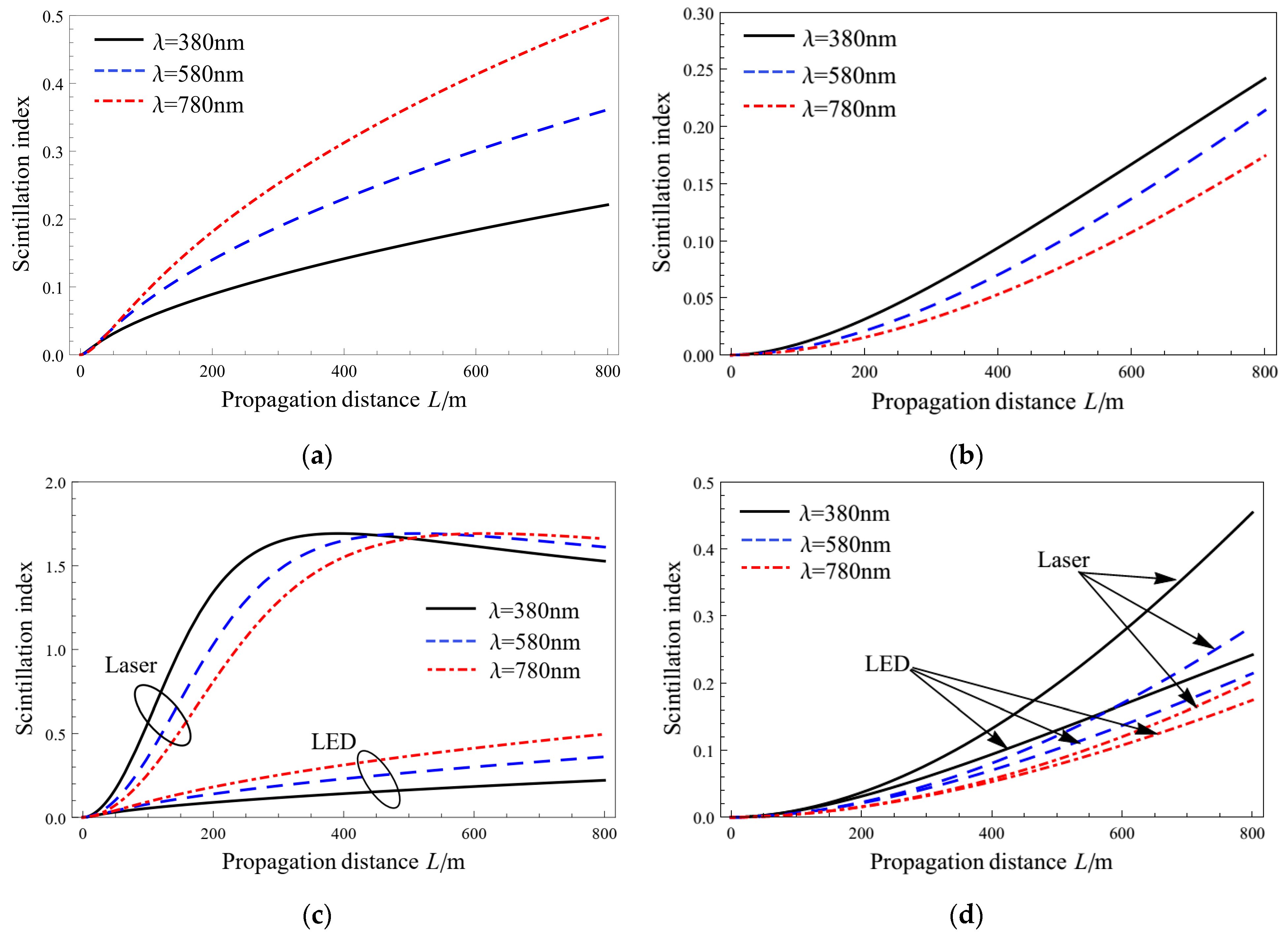
3. Numerical Results and Discussions
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Tanaka, Y.; Komine, T.; Haruyama, S.; Nakagawa, M. Indoor visible light data transmission system utilizing white LED lights. IEICE Trans. Commun. 2003, 86, 2440–2454. [Google Scholar]
- Chi, N. LED-Based Visible Light Communications; Springer: Berlin, Germany, 2018. [Google Scholar]
- Shen, C.; Ma, C.; Li, D.; Hu, J.; Li, G.; Zou, P.; Chi, N. High-speed visible laser light communication: Devices, systems and applications. In Broadband Access Communication Technologies XV; SPIE: San Diego, CA, USA, 2021; Volume 11711, pp. 18–27. [Google Scholar]
- Andrews, L.C.; Phillips, R.L. Laser Beam Propagation through Random Media; SPIE Press: Bellingham, WA, USA, 2005. [Google Scholar]
- Komine, T.; Nakagawa, M. Fundamental analysis for visible-light communication system using LED lights. IEEE Trans. Consum. Electron. 2004, 50, 100–107. [Google Scholar] [CrossRef]
- Yamazato, T.; Takai, I.; Okada, H.; Fujii, T.; Yendo, T.; Arai, S.; Kawahito, S. Image-sensor-based visible light communication for automotive applications. IEEE Commun. Mag. 2014, 52, 88–97. [Google Scholar] [CrossRef]
- Shi, M.; Wang, C.; Li, G.; Liu, Y.; Wang, K.; Chi, N. A 5Gb/s 2*2 MIMO Real-Time Visible Light Communication System Based on Silicon Substrate LEDs. In Proceedings of the 2019 Global LIFI Congress (GLC), Paris, France, 12–13 June 2019; pp. 1–5. [Google Scholar]
- Wu, T.; Ma, J.; Yuan, R.; Su, P.; Cheng, J. Single-scatter model for short-range ultraviolet communication in a narrow beam case. IEEE Photonics Technol. Lett. 2019, 31, 265–268. [Google Scholar] [CrossRef]
- Eso, E.; Ghassemlooy, Z.; Zvanovec, S.; Sathian, J.; Abadi, M.M.; Younus, O.I. Performance of vehicular visible light communications under the effects of atmospheric turbulence with aperture averaging. Sensors 2021, 21, 2751. [Google Scholar] [CrossRef] [PubMed]
- Nguyen, Q.D.; Nguyen, N.H. Mobile Application for Visible Light Communication Systems: An Approach for Indoor Positioning. Photonics 2024, 11, 293. [Google Scholar] [CrossRef]
- Shen, T.; Guo, J.; Liang, H.; Li, Y.; Li, K.; Dai, Y.; Ai, Y. Research on a Blue–Green LED Communication System Based on an Underwater Mobile Robot. Photonics 2023, 10, 1238. [Google Scholar] [CrossRef]
- Apolo, J.A.; Ortega, B.; Almenar, V. Hybrid POF/VLC Links Based on a Single LED for Indoor Communications. Photonics 2021, 8, 254. [Google Scholar] [CrossRef]
- Geng, Z.; Khan, F.N.; Guan, X.; Dong, Y. Advances in Visible Light Communication Technologies and Applications. Photonics 2022, 9, 893. [Google Scholar] [CrossRef]
- Yahia, S.; Meraihi, Y.; Ramdane-Cherif, A.; Gabis, A.B.; Acheli, D.; Guan, H. A survey of channel modeling techniques for visible light communications. J. Netw. Comput. Appl. 2021, 194, 103206. [Google Scholar] [CrossRef]
- Álvarez-Roa, C.; Álvarez-Roa, M.; Raddo, T.R.; Jurado-Navas, A.; Castillo-Vázquez, M. Cooperative Terrestrial–Underwater FSO System: Design and Performance Analysis. Photonics 2024, 11, 58. [Google Scholar] [CrossRef]
- Korotkova, O.; Toselli, I. Non-classic atmospheric optical turbulence. Appl. Sci. 2021, 11, 8487. [Google Scholar] [CrossRef]
- Manzoor, H.U.; Manzoor, S.; Manzoor, T.; Khan, T.; Hussain, A. Improved transmission length in the presences of ambient noise and scintillation effect using duobinary modulation in 40 Gbps free space optical channel. Microw. Opt. Technol. Lett. 2020, 62, 3163–3169. [Google Scholar] [CrossRef]
- Ding, H.; Chen, G.; Majumdar, A.K.; Sadler, B.M.; Xu, Z. Turbulence modeling for non-line-of-sight ultraviolet scattering channels. In Atmospheric Propagation VIII; SPIE: Orlando, FL, USA, 2011; Volume 8038. [Google Scholar]
- Jurado-Navas, A.; Raddo, T.R.; Garrido-Balsells, J.M.; Borges, B.H.V.; Olmos, J.J.V.; Monroy, I.T. Hybrid optical CDMA-FSO communications network under spatially correlated gamma-gamma scintillation. Opt. Express 2024, 15, 16799–16814. [Google Scholar] [CrossRef] [PubMed]
- Liao, L.; Li, Z.; Lang, T.; Chen, G. UV LED array based NLOS UV turbulence channel modeling and experimental verification. Opt. Express 2023, 17, 21825–21835. [Google Scholar] [CrossRef] [PubMed]
- Ishimaru, A. Wave Propagation and Scattering in Random Media; Academic Press: New York, NY, USA, 1978. [Google Scholar]
- Fante, R.L. Intensity fluctuations of an optical wave in a turbulent medium effect of source coherence. Opt. Acta Int. J. Opt. 1981, 28, 1203–1207. [Google Scholar] [CrossRef]
- Wu, S.; Hu, X.; Han, Y.; Wu, X.; Su, C.; Luo, T.; Li, X. Measurement and analysis of atmospheric optical turbulence in Lhasa based on thermosonde. J. Atmos. Sol.-Terr. Phys. 2020, 201, 105241. [Google Scholar] [CrossRef]
- Tyson, R.K. Adaptive optics and ground-to-space laser communications. Appl. Opt. 1996, 35, 3640–3646. [Google Scholar] [CrossRef]
- Dirkx, D.; Noomen, R.; Prochazka, I.; Bauer, S.; Vermeersen, L.L.A. Influence of atmospheric turbulence on planetary transceiver laser ranging. Adv. Space Res. 2014, 54, 2349–2370. [Google Scholar] [CrossRef]
- Jakeman, E.; Pusey, P.N. Significance of K distributions in scattering experiments. Phys. Rev. Lett. 1978, 40, 546. [Google Scholar] [CrossRef]
- Yi, X.; Liu, Z.; Yue, P. Optical scintillations and fade statistics for FSO communications through moderate-to-strong non-Kolmogorov turbulence. Opt. Laser Technol. 2013, 47, 199–207. [Google Scholar] [CrossRef]
- Al-Habashm, A.; Andrewsl, C.; Phillipsr, L. Mathematical model for the irradiance probability density function of a laser beam propagating through turbulent media. Opt. Eng. 2001, 40, 1554–1562. [Google Scholar] [CrossRef]



| Parameter | Value |
|---|---|
| Height | 1 m |
| Beam radius of the Gaussian source | 1 cm |
| Wind speed | 21 m/s |
| Working light wavelength | 380/580/780 nm |
| Near-earth atmosphere refractive index structural parameters | // |
| Signal propagation distances | 200/300/500 m |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ji, Y.; Chen, W.; Wang, D.; Cheng, C. A Study on the Irradiance Scintillation Characteristics of Monochromatic LED-Based Visible Light Communication Systems in Weak-to-Strong Turbulence. Photonics 2024, 11, 567. https://doi.org/10.3390/photonics11060567
Ji Y, Chen W, Wang D, Cheng C. A Study on the Irradiance Scintillation Characteristics of Monochromatic LED-Based Visible Light Communication Systems in Weak-to-Strong Turbulence. Photonics. 2024; 11(6):567. https://doi.org/10.3390/photonics11060567
Chicago/Turabian StyleJi, Yao, Wensheng Chen, Danning Wang, and Chen Cheng. 2024. "A Study on the Irradiance Scintillation Characteristics of Monochromatic LED-Based Visible Light Communication Systems in Weak-to-Strong Turbulence" Photonics 11, no. 6: 567. https://doi.org/10.3390/photonics11060567
APA StyleJi, Y., Chen, W., Wang, D., & Cheng, C. (2024). A Study on the Irradiance Scintillation Characteristics of Monochromatic LED-Based Visible Light Communication Systems in Weak-to-Strong Turbulence. Photonics, 11(6), 567. https://doi.org/10.3390/photonics11060567




