Abstract
The theoretical and experimental characteristics of all-solid-state self-mode-locked burst pulse lasers are investigated in this study. The time–frequency and spectrum analyses of the lasers incorporating Fabry–Pérot (F-P) structures are presented, along with the development of the corresponding theoretical model. Self-mode-locked burst pulse lasers are experimentally constructed to reduce intracavity losses using the front and rear end surfaces of the gain media to form F-P structures. When the laser cavity length is 600 mm and the gain media lengths are 5, 6, and 10 mm, each burst pulse produced contains 56, 47, and 28 subpulses, respectively, with the same burst pulse width of 2 ns. The burst pulse train with beam quality M2 = 1.37 and an average output power of 0.23 W is obtained when the gain medium length is 5 mm and the pump power is 4.5 W. The corresponding burst pulse repetition frequency is 0.25 GHz and the subpulse repetition frequency is 13.66 GHz. The time–frequency spectral analyses of the laser signals provide a good representation of laser spectral information that even the currently available highest-resolution spectrometers cannot resolve.
1. Introduction
Burst pulse lasers emit a sequence of subpulses within each laser pulse burst, offering flexibility in adjusting laser outputs by controlling the number, duration, and separation of subpulses []. Compared to high-repetition-rate mode-locked pulse lasers, burst pulse lasers effectively reduce the adverse effects of severe heat accumulation and mitigate damage caused by large pulse energy. Their ability to simultaneously deliver controllable high repetition rates and high pulse energy within a short duration makes burst pulse lasers valuable in optical imaging, photoablation, photomedicine, and other fields [,,,].
Recently, studies on the mechanism of burst pulse generation have received significant attention. For example, Y. F. Ma et al. [] demonstrated in 2014 a miniaturized pulse-pumped Cr4+:YAG and passively Q-switched Nd:YAG pulse burst laser. In both plane–plane and plane–convex cavities, burst pulses with a repetition frequency higher than 20 kHz and a pulse energy higher than 10 mJ were obtained. They then demonstrated a four-beam, pulse-burst, passively Q-switched laser in 2015. The pulse burst contained a maximum of five, three, two, and three pulses for corresponding repetition rates of 10.8, 7.2, 6.8, and 5.2 kHz, respectively []. According to Pan. H et al. [], an 878.6 nm pulsed LD end-pumped intracavity acousto-optical Q-switched composite Nd:YVO4 laser achieved burst pulses at a repetition rate of 10–100 kHz in a 1 ms burst duration. X. D. Li et al. [] demonstrated a pulsed LD-pumped burst-mode YVO4/Nd:YVO4 laser with acousto-optically Q-switched technology. The duration of the Q-switching burst pulses was 1 ms, and the energy of a single burst-mode pulse was 45 mJ. A burst-mode pulse consisted of approximately 10–500 subpulses with an active Q-switching frequency ranging from 10 to 500 kHz. Both passive and active Q switching technologies flexibly regulate the burst pulse parameters under the Q switching mechanism; however, the repetition frequencies of the burst pulse and subpulse are relatively low. Chao. He et al. [] present a composite cavity comprising a main cavity and an auxiliary cavity within a Nd:YVO4 laser for the generation of picosecond burst-pulse with a pulse duration of 20.6 ps and a repetition rate of 76 MHz. The number of pulses within the burst train can be regulated by rotating the half-wave plate (HWP) inserted into the main cavity. The time interval between two adjacent pulses within the burst envelope can be adjusted by varying the length mismatch between the two cavities.
In 2017, S. M. Wang et al. [] generated burst pulses ranging from picoseconds to sub-picoseconds, achieving a subpulse repetition frequency of 400 GHz. This accomplishment was realized by integrating a birefringence filter with a free spectral range (FSR) of 100 GHz into a hybrid phase-modulated mode-locked Erbium-doped fiber laser. However, the laser structure is complex, making it difficult to fine-tune the repetition frequency of the subpulses. In 2020, S. C. Li et al. [] investigated the burst pulse operation mechanism within a multi-pass passively mode-locked solid-state laser employing an intracavity Fabry–Pérot (F-P) element. Within the laser cavity, a flat mirror acted as the F-P element. By varying the optical thickness of the F-P elements, burst pulse trains with subpulse repetition frequencies spanning from 11.13 to 33.12 GHz were generated. In 2024, Q. Ruan et al. [] demonstrated stable burst-mode pulse in passively mode-locked all-fiber lasers at wavelengths of 543.3 nm and 602.5 nm. The burst-mode pulses exhibit fundamental repetition rates of 3.779 MHz and 5.662 MHz, generating long bursts comprising ultrashort pulses with intra-burst repetition rates of 0.85 GHz and 0.76 GHz, respectively. The generation of ultrashort intra-burst pulses is attributed to the dissipative four-wave mixing effect within the highly nonlinear fiber loop mirror, coupled with intracavity F-P filtering. Though these studies provide a method for flexible regulation of high-frequency burst pulse and subpulse parameters, the introduction of additional elements causes additional losses in the laser resonators.
According to the studies, the implementation of burst pulses in solid-state lasers involves two methods. One method utilizes pulse-pumped passively or actively Q-switched lasers, yielding burst pulses with a pulse width on the order of microseconds to milliseconds. Another method involves the incorporation of a comb-like filter, such as an F-P filter, within the cavity of a passively or actively mode-locked laser. However, the inclusion of F-P elements introduces additional intracavity losses, lowering the average output power. Based on the above situations, an all-solid-state self-mode-locked burst pulse laser, with no additional intracavity loss but only using the front and rear ends of the gain medium to form an intracavity F-P structure, is presented. The laser’s time–frequency and spectrum analyses are presented, which further provides a good representation of the very fine laser spectral information. The second section explains the simulation model; the third section describes the experimental setup; the fourth section includes the analysis of experimental results; the fifth part is a discussion of all experimental results; and the conclusion is provided in the fifth section.
2. Theoretical Model
A standing-wave resonator based on a homogeneous broadening gain medium typically exhibits the output characteristics of multiple longitudinal modes in the absence of any longitudinal mode selection elements in the solid-state laser cavity. Because of the Kerr effect of the gain medium, the interaction between the longitudinal modes forms the self-mode-locked pulse trains [,,]. When multimode oscillation occurs, the F-P effect, or spatial hole burning (SHB) effect in a standing-wave resonator leading to longitudinal modes grouping, changes the self-mode-locked pulse waveforms to the burst pulse waveforms [,,,,]. In the experiment, by adjusting the optical length of the gain medium and laser cavity, output burst pulse trains with different characteristics were achieved. The following is a theoretical model of the burst pulses generation mechanism. When 2M+1 longitudinal modes oscillate in the laser resonator, the laser’s electric field is expressed as follows:
where represents the repetition frequency of the burst pulses. The gain distribution of the longitudinal modes follows a Gaussian distribution. Provided that the gain medium’s rear and front end surfaces form a F-P cavity, the normalized transmission coefficient Am for an electromagnetic wave with finite round trips in the resonator can be expressed as follows [,]:
where R1 and R2 represent the reflectivities of the gain medium’s rear and front end surfaces, respectively, and n represents the refractive index. represents the total optical length of the laser cavity, represents the length of the gain medium, and b represents the effective number of round trips for electromagnetic waves.
Define K as the number of subpulses within a single burst pulse, as follows:
where represents the repetition frequency of the subpulses. Equation (3) shows that the number of subpulses K in a burst pulse equals the optical length ratio of the laser cavity to the gain medium. The greater the ratio K, the more subpulses can be achieved in a single burst pulse. When the laser cavity length is set to 600 mm and the gain media (Nd:YVO4 crystal) lengths are 3, 5, 6, and 10 mm, the characteristics of the burst pulses are simulated using the above theoretical model. Figure 1 shows the number of subpulses in a burst pulse, time waveform of the subpulses, and longitudinal mode spectral distributions.
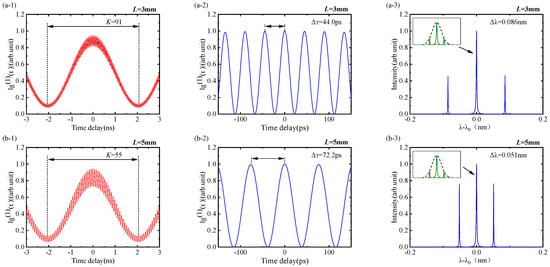
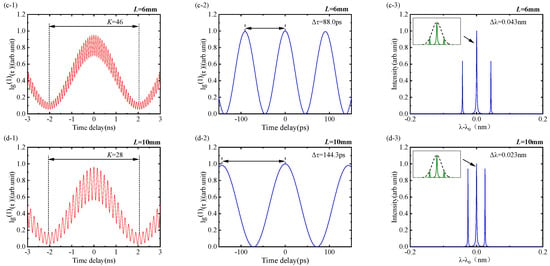
Figure 1.
The simulation of the output characteristics of burst pulses with gain media lengths of 3, 5, 6, and 10 mm: (a1–d1) single burst pulse waveform (left); (a2–d2) sub-pulse waveform (middle); (a3–d3) longitudinal mode spectral distribution (right).
The simulated results in Figure 1 show that the generated burst pulses have different characteristics when the laser cavity is 600 mm and the Nd:YVO4 crystal lengths are 3, 5, 6, and 10 mm. The pulse width (full width at half height) of the burst pulses is determined by the laser cavity optical length and calculated by , where c represents the speed of light, resulting in a pulse width of 2 ns. The number of subpulses within a burst pulse equals the ratio of the laser cavity optical length to the Nd:YVO4 crystal. As shown in Figure 1(a-1,b-1,c-1,d-1), the number of subpulses is 91, 55, 46, and 28, respectively, corresponding to the crystal lengths of 3, 5, 6, and 10 mm. Figure 1 shows the subpulse waveforms (a-2), (b-2), (c-2), and (d-2). The subpulse repetition intervals are 44.0, 72.2, 88.0, and 144.3 ps, and the calculated repetition frequencies of the subpulses are 22.73, 13.64, 11.36, and 6.82 GHz, respectively. Figure 1(a-3,b-3,c-3,d-3) show the longitudinal mode distribution of the burst pulses. The longitudinal mode intervals are determined by the Nd:YVO4 crystal-formed F-P cavity FSR as 0.086, 0.051, 0.043, and 0.023 nm, which is consistent with the subpulses repetition frequency of Figure 1(a-2,b-2,c-2,d-2). The laser cavity fundamental longitudinal mode (sub-longitudinal mode) spectra are plotted in the inset of Figure 1(a-3,b-3,c-3,d-3), and the laser cavity FSR determines the sub-longitudinal mode spacing.
Figure 2 shows the detailed diagram of the theoretical simulation laser spectra. The sub-longitudinal mode spacing is 0.93 pm, which corresponds to the FSR of 600 mm length laser cavity. The longitudinal mode spacing is 0.086 nm, 0.051 nm, 0.043 nm, and 0.023 nm, corresponding to the crystal lengths of 3 mm, 5 mm, 6 mm, and 10 mm.
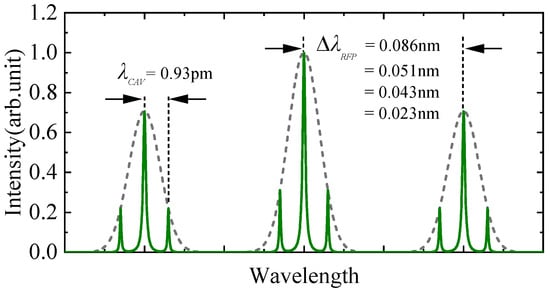
Figure 2.
Simulation of theoretical laser spectra of different gain medium lengths.
3. Experimental Setup
As shown in Figure 3, the pumping source is an 808 nm fiber-coupled laser diode with a fiber core diameter of 400 μm and a numerical aperture of 0.22. The gain media are 1 at.% doped a-cut Nd:YVO4 crystals with 3 × 3 mm cross sections and lengths of = 3, 5, 6, and 10 mm. All the rear surfaces of the Nd:YVO4 crystals are coated for high reflection at 1064 nm (HR, R = 99.8%) and high transmission at 808 nm (HT, T = 99.8%), while their front surfaces are coated for high transmission at 808 and 1064 nm (HT, T = 99.8%). The Nd:YVO4 crystals are wrapped in indium foil and mounted in a water-cooled aluminum sink to maintain the temperature at 20 °C, and thus reduce the thermal effect. To increase the cavity length to 600 mm, the laser resonator uses the design of a folding cavity, in which the mirror M1 is coated for high reflection at 1064 nm (HR, R = 99.8%), and the output mirror M2 is coated for high reflection at 1064 nm (R = 95%). The overall laser cavity length is kept at 600 mm, with L1 = 400 mm and L2 = 200 mm cavity arms.
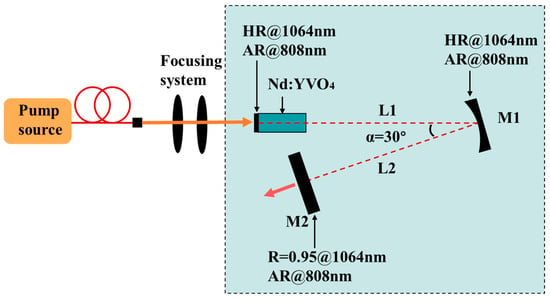
Figure 3.
The experimental setup generates burst pulses.
A digital oscilloscope (Agilent, Santa Clara, CA, USA, DSO81204) with a 40 GS/s sampling rate and 12 GHz bandwidth is used to record the time waveform of the burst pulse trains, and the bandwidth of the optical detector (Lightsensing, Beijing, China, LSHIPD-A18G) is 18 GHz. The output power is detected using a power meter (Thorlabs, Newton, MA, USA, PM100A) with a range of 100 pW–200 W. The laser spectra are measured using an optical spectral analyzer (OSA, Advantest, Tokyo, Japan, Q8384) with a resolution of 0.01 nm. The laser output beam profile is measured using a CCD camera (Thorlabs, BC106N-VIS) with an adjustable attenuator.
4. Experimental Results
4.1. Influence on the Characteristics of Output Burst Pulses
The length of laser cavity is 600 mm. The Nd:YVO4 crystal lengths are 3, 5, 6, and 10 mm. In the experiment, we observed burst pulses generated at pump power ranging from 0.3W to 4.5 W. As the power increased, the stability of the burst pulses improved. When the pump power is 4.5 W, the output characteristics of four groups of burst pulses were experimentally compared. The experimentally obtained burst pulse time and spectral characteristics are shown in Figure 4.
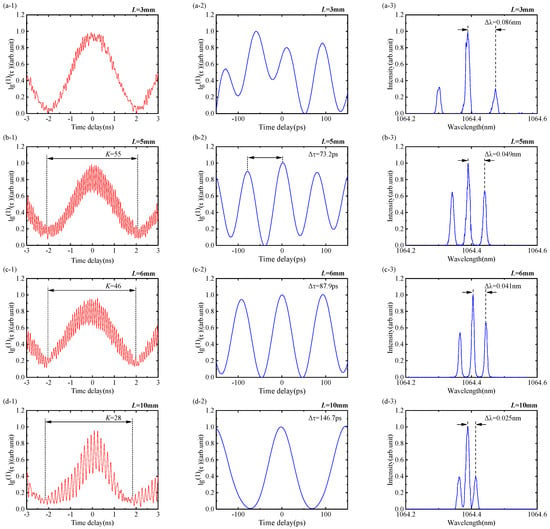
Figure 4.
Experimental characteristics of burst pulses with Nd:YVO4 crystal lengths of 3, 5, 6, and 10 mm: (a1–d1) single burst pulse waveform (left); (a2–d2) sub-pulse waveform (middle); (a3–d3) longitudinal mode spectra (right).
Figure 4(a-1) shows the laser pulses recorded by the oscilloscope with the Nd:YVO4 crystal length of 3 mm. The laser pulse exhibits a burst mode, and the time waveform of the burst pulse is shown in Figure 4(a-2). From the laser spectrum shown in Figure 4(a-3), the longitudinal mode interval corresponding to the subpulses is 0.086 nm, and thus the repetition frequency of the subpulses, is calculated as 22.73 GHz. The time waveform of the subpulses observed on the oscilloscope is a little chaotic because the repetition frequency of the subpulses exceeds the bandwidth of the oscilloscope, and the number of subpulses within a single burst pulse is also difficult to distinguish.
As shown in Figure 4(b-1,c-1,d-1), when the Nd:YVO4 crystal lengths are 5, 6, and 10 mm, respectively, the laser’s burst pulses and subpulses are clearly distinguishable, and the number of subpulses is 55, 46, and 28, as shown in Figure 4(b-2,c-2,d-2), respectively. The time intervals of the subpulses are approximately 73.2, 87.9, and 146.6 ps, and the corresponding repetition frequencies are 13.66, 11.37, and 6.82 GHz, respectively, which are in good agreement with the simulated results.
The experiment results show that, as the length of the Nd:YVO4 crystal increased from 5 to 10 mm, the number of subpulses decreased from 55 to 28, the time interval between subpulses increased from 73.3 to 146.6 ps, and the repetition frequency decreased from 13.66 to 6.82 GHz. It is also observed that the number of subpulses within a single burst pulse is approximately the ratio of the optical length of the laser cavity to the Nd:YVO4 crystal, which is consistent with theoretical analyses. As shown in Figure 4(b-3,c-3,d-3), an OSA was used to observe the longitudinal mode spectra of the burst pulses with crystal lengths of 5, 6, and 10 mm. Because the OSA resolution is 0.01 nm, the sub-longitudinal mode intervals corresponding to the laser resonator’s fundamental longitudinal mode are indistinguishable. Only the longitudinal mode envelopes corresponding to the F-P cavity FSR formed by the Nd:YVO4 crystal are observed.
The longitudinal modes intervals corresponding to the FSR of the laser crystals are 0.049, 0.041, and 0.026 nm. The longitudinal mode intervals in Figure 4(b-3,c-3,d-3) correspond to the repetition frequencies of the subpulses in Figure 4(b-2,c-2,d-2), which are 13.66, 11.37, and 6.82 GHz, respectively. They are also in good agreement with the simulation results. In addition, as shown in Figure 4(a-3,b-3,c-3,d-3), it can be observed that the different Nd:YVO4 lengths have little influence on the center wavelengths of the burst pulses. All laser signals have the highest gains near 1064.4 nm, and the mode intensity distributions show Gaussian types.
Because the laser cavity length is 600 mm and the calculated fundamental longitudinal mode (sub-longitudinal mode) spacing is 0.93 pm, the resolution of the currently available spectrometer is insufficient to distinguish the sub-longitudinal modes. In this study, we innovatively analyze sub-longitudinal mode distribution using the time–frequency spectra of the burst pulses. The time–frequency spectra are obtained through the fast Fourier transform (FFT) of the burst pulse time domain signals. Considering laser crystal lengths of 6 and 10 mm as examples, the following explores how to estimate the sub-longitudinal mode distributions using the time–frequency spectra of burst pulses.
Figure 5a,b show the time–frequency spectra of the burst pulses for laser crystal lengths of 6 and 10 mm. The sub-longitudinal mode distribution estimated by the time spectrum of the burst pulse is shown as the solid line in Figure 5c,d, while the dashed line represents the spectral envelope measured in the experiment, which corresponds to Figure 4(c-3,d-3).The frequency component of 0.25 GHz is observed in the low-frequency range when the Nd:YVO4 crystal is 6 mm as shown in Figure 5a. The two frequency components of 11.40 and 11.65 GHz are observed in the high-frequency range. According to Figure 4(c-3), because the FSR of a 6 mm laser crystal is 11.35 GHz, the output laser spectra are optical spectral envelopes with an interval of 11.40 GHz, and each envelope contains 1 to 2 fundamental sub-longitudinal modes. From the option of 1:2:1 or 2:1:2 types, considering the Gaussian distribution of the laser spectra, the specific distribution form of sub-longitudinal mode spectrum is shown in Figure 5c as 1:2:1 type. In addition, when the Nd:YVO4 crystal is 10 mm, as shown in Figure 5b, the frequency component of 0.25 GHz and the harmonic frequency component of 0.5 GHz are observed in the low-frequency range. In the high frequency range, four frequency components of 6.31, 6.56, 6.81, and 7.06 GHz are observed, with a frequency difference of 0.25 GHz. Considering the FSR of a 10 mm laser crystal is 6.81 GHz, the output laser spectra are optical spectral envelopes with an interval of 6.81 GHz, and each envelope contains two to three sub-longitudinal modes, as shown in Figure 4(d-3). Considering the Gaussian distribution of the laser spectrum, the specific distribution form of sub-longitudinal mode spectra is shown in Figure 5d as 2:3:2 type.
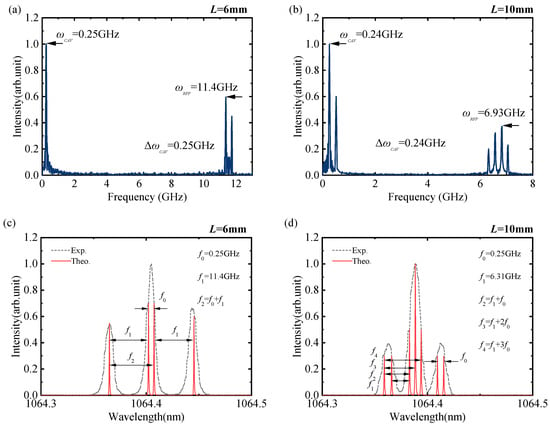
Figure 5.
Time–frequency spectra (a,b) and laser spectra (c,d) of burst pulse lasers. (a,c) Nd:YVO4 crystal = 6 mm and (b,d) Nd:YVO4 crystal = 109 mm.
Even more interestingly, analyzing finer sub-longitudinal modes requires the use of a lower bandwidth oscilloscope. To the best of our knowledge, this is the first time that the fine mode distribution within the self-mode-locking laser cavity has been depicted using such a common oscilloscope.
4.2. Study on Beam Quality and Output Power of the Burst Pulses
Figure 6a,b show the output powers and beam qualities of the burst pulses at laser crystal lengths of 3, 5, 6, and 10 mm. Figure 6a shows that all the laser threshold powers are approximately 0.21 W. When the Nd:YVO4 lengths are 3, 5, 6, and 10 mm, the slope efficiencies are 5.17, 12.09, 14.90, and 18.55%, respectively, and the corresponding optical conversion efficiencies are 5.14, 11.63, 14.33, and 17.84%. The maximum output powers of the burst pulses are 165, 230, 241, and 402 mW, respectively. The results show that increasing the lengths of the Nd:YVO4 crystals increases the laser efficiencies, but the increase trends gradually slow down because of the thermal effects.
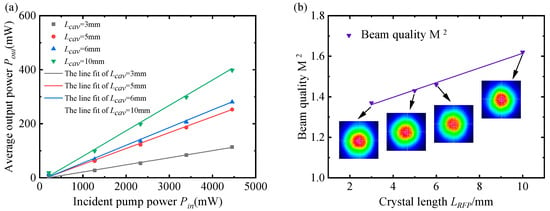
Figure 6.
With Nd:YVO4 crystal, = 3, 5, 6, and 10 mm for the output powers and beam qualities of the burst pulses. (a) The relationship of average output power and pumping power ; (b) the beam qualities.
Finally, the beam qualities of burst pulses with different Nd:YVO4 crystal lengths are observed when the pump power is set to 4.5 W and the Nd:YVO4 crystal sink temperature is set to 20 °C. As shown in Figure 6b, the beam quality M2 is 1.37 when the length of the Nd:YVO4 crystal is 3 mm. The beam qualities M2 degenerate to 1.43, 1.46, and 1.62 as the lengths of the Nd:YVO4 crystals increase to 5 mm, 6 mm, and10 mm. The experimental results show that when the gain medium is shorter, the output beam quality is better. With the lengthening of the gain medium, strong thermal effects will cause the distortion of the beam, resulting in poor beam quality.
5. Discussion
In this paper, the burst pulses laser is directly obtained by the self-mode-locking phenomenon of Nd:YVO4 laser crystal. By maintaining a cavity length of 600 mm and varying the crystal length to 5 mm, 6 mm, and 10 mm, burst pulses capable of producing 56, 47, and 28 subpulses are obtained, respectively. The time intervals of the subpulses are approximately 73.2, 87.9, and 146.6 ps, respectively. Correspondingly, the repetition frequencies of the subpulses are 13.66 GHz, 11.37 GHz, and 6.82 GHz, respectively. The flexibility of this method lies in its ability to adjust the repetition frequency of subpulses by modifying the crystal length, while the number of subpulses can be controlled by adjusting the length difference between the cavity and the crystal. Compared to existing techniques, this approach boasts a simple structure, with no additional components required inside the cavity aside from the gain medium. Furthermore, it allows for precise and flexible adjustments of subpulse repetition frequency and pulse number. Moreover, through spectrum and spectral analysis of the burst pulses, this study anticipates the presence of a fine mode distribution within the laser cavity. Lastly, the study reveals an interesting trend where the optical conversion efficiency of the burst pulses increases with crystal length. Remarkably, when the crystal length reaches 10 mm, the optical conversion efficiency peaks at 17.84%. The beam quality of sudden pulses deteriorates with crystal length. When the crystal length is 10mm, the beam quality of M2 is 1.62. This study provides a useful method for generating mode-locked burst-mode pulses with a controllable pulse number and pulse repetition frequency.
6. Conclusions
The burst pulses are directly obtained by self-mode-locked Nd:YVO4 lasers, without any additional intracavity F-P elements. When the laser cavity length is 600 mm, varying the crystal lengths from 5 to 10 mm yields burst pulses with 56, 47, and 28 subpulses, respectively. In comparison with existing methods for generating burst pulses, the time repetition frequency and the pulse number of sub-pulses can be adjusted flexibly by changing the crystal length. We innovatively anticipate the fine mode distribution of the self-mode-locked burst pulse laser using time–frequency and spectrum analyses of the burst pulses. It is of great significance for the in-depth understanding of the formation mechanism of burst pulses and the realization of all-solid-state self-mode-locked lasers for stable and adjustable burst pulses.
Author Contributions
Conceptualization, M.X.; methodology, M.X. and M.H.; software, Z.L., M.X. and J.F.; validation, Z.L., M.H., S.W. and Y.J.; formal analysis, M.X. and Z.L.; investigation, M.X.; resources, M.H., M.B., X.Z., and H.L.; data curation, M.X.; writing—original draft preparation, Z.L., J.W. and J.F.; writing—review and editing, M.X. and M.H.; visualization, M.H. and Z.L.; supervision, S.P. and C.L.; project administration, M.H. and M.X.; funding acquisition, M.H. and M.X. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by Primary Research and Development Plan of Zhejiang Province (2023C03014); Key Research and Development Program of Zhejiang Province (2022C03037);the Fundamental Research Funds for the Provincial Universities of Zhejiang (GK20990729901-018).
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
Data underlying the results presented in this paper are not publicly available at this time but may be obtained from the authors upon reasonable request.
Acknowledgments
The authors would like to thank Zhejiang Institute of Metrology, Key Laboratory of Energy and Environmental Protection Measurement of Zhejiang Province for their helpful discussion.
Conflicts of Interest
The authors declare no conflicts of interest. The funders had no role in the design of the study; in the collection, analyses, or interpretation of data; in the writing of the manuscript; or in the decision to publish the results.
References
- Slipchenko, M.N.; Miller, J.D.; Roy, S.; Meyer, T.R.; Mance, J.G.; Gord, J.R. 100 kHz, 100 ms, 400 J burst-mode laser with dual-wavelength diode-pumped amplifiers. Opt. Lett. 2014, 39, 4735–4738. [Google Scholar] [CrossRef] [PubMed]
- Slipchenko, M.N.; Miller, J.D.; Roy, S.; Gord, J.R.; Danczyk, S.A.; Meyer, T.R. Quasi-continuous burst-mode laser for high-speed planar imaging. J. Opt. Lett. 2012, 37, 1346–1348. [Google Scholar] [CrossRef] [PubMed]
- Gattass, R.R.; Cerami, L.R.; Mazur, E. Micromachining of bulk glass with bursts of femtosecond laser pulses at variable repetition rates. J. Opt. Express 2006, 14, 5279–5284. [Google Scholar] [CrossRef] [PubMed]
- Dowling, K.; Dayel, M.J.; Lever, M.J.; French, P.M.W.; Hares, J.D.; Dymoke-Bradshaw, A.K.L. Fluorescence lifetime imaging with picosecond resolution for biomedical applications. J. Opt. Lett. 1998, 23, 810–812. [Google Scholar] [CrossRef] [PubMed]
- Halls, B.R.; Jiang, N.; Meyer, T.R.; Roy, S.; Slipchenko, M.N.; Gord, J.R. 4D spatiotemporal evolution of combustion intermediates in turbulent flames using burst-mode volumetric laser-induced fluorescence. J. Opt. Lett. 2017, 42, 2830–2833. [Google Scholar] [CrossRef] [PubMed]
- Ma, Y.; Li, X.; Yu, X.; Fan, R.; Yan, R.; Peng, J.; Xu, X.; Sun, R.; Chen, D. A novel miniaturized passively Q-switched pulse-burst laser for engine ignition. J. Opt. Express 2014, 22, 24655–24665. [Google Scholar] [CrossRef] [PubMed]
- Ma, Y.; He, Y.; Yu, X.; Li, X.; Li, J.; Yan, R.; Peng, J.; Zhang, X.; Sun, R.; Pan, Y.; et al. Multiple-beam, pulse-burst, passively Q-switched ceramic Nd:YAG laser under micro-lens array pumping. Opt. Express 2015, 23, 24955–24961. [Google Scholar] [CrossRef]
- Pan, H.; Yan, R.; Fa, X.; Yu, X.; Ma, Y.; Fan, R.; Li, X.; Chen, D.; Zhou, Z. High-peak-power, high-repetition-rate LD end-pumped Nd:YVO4 burst mode laser. J. Opt. Rev. 2016, 23, 386–390. [Google Scholar] [CrossRef]
- Li, X.; Xu, H.; Yan, R.; Jiang, Y.; Fan, R.; Dong, Z.; Chen, D. Burst-mode YVO4/Nd:YVO4 laser oscillator with pulse repetition rate up to 500 kHz. J. Optik 2021, 228, 165789. [Google Scholar] [CrossRef]
- He, C.; Yu, H.; Zhang, J.; Zou, S.; Zhao, P.; Lin, X. Flexible picosecond burst generation in a mode-locked Nd:YVO4 laser with a compound cavity. J. Appl. Phys. B 2019, 125, 147. [Google Scholar] [CrossRef]
- Wang, S.-M.; Lai, Y. Up to 400 GHz burst-mode pulse generation from a hybrid harmonic mode-locked Er-doped fibre laser. J. Laser Phys. Lett. 2017, 14, 025102. [Google Scholar] [CrossRef]
- Li, S.C.; Huang, T.L.; Hsieh, Y.H.; Liang, H.C.; Huang, K.F.; Chen, Y.F. Generation and characterization of burst modes in passively mode-locked lasers with internal Fabry–P Erot cavities. J. Opt. Lett. 2020, 45, 61–64. [Google Scholar] [CrossRef]
- Ruan, Q.; Zou, J.; Feng, C.; Chen, T.; Wang, H.; Dong, Z.; Luo, Z. Burst-mode pulse generation in passively mode-locked all-fiber green/orange lasers at 543 nm and 602 nm. J. Photonics Res. 2024, 12, 1231–1238. [Google Scholar] [CrossRef]
- Zhou, B.K. The Principles of Laser; National Defense Industry Press: Beijing, China, 2014; pp. 143–144. [Google Scholar]
- Sung, C.L.; Lee, C.Y.; Cho, H.H.; Huang, Y.J.; Chen, Y.F.; Pan, Z.B.; Yu, H.H.; Zhang, H.J.; Wang, J.Y. Theoretical and experimental studies for high-repetition-rate disordered crystal lasers with harmonic self-mode locking. J. Opt. Express 2016, 24, 3832–3838. [Google Scholar] [CrossRef] [PubMed]
- Lin, S.T.; Huang, C.H. Effects of nonlinear phase in cascaded mode-locked Nd:YVO4 laser. J. Opt. Express 2019, 27, 504–511. [Google Scholar] [CrossRef] [PubMed]
- Lührmann, M.; Theobald, C.; Wallenstein, R.; L’huillier, J.A. Efficient generation of mode-locked pulses in Nd:YVO4 With a pulse duration adjustable between 34 ps and 1 ns. J. Opt. Express 2009, 17, 6177–6186. [Google Scholar] [CrossRef] [PubMed]
- Tuan, P.H.; Chang, C.C.; Lee, C.Y.; Cho, C.Y.; Liang, H.C.; Chen, Y.F. Exploiting concave-convex linear resonators to design end-pumped solid-state lasers with flexible cavity lengths: Application for exploring the self-mode-locked operation. J. Opt. Express 2016, 24, 26024. [Google Scholar] [CrossRef] [PubMed]
- Jin, Y.; Hu, M.; Xu, M.; Yan, H.; Liu, C.; Chen, L.; Li, H.; Bi, M.; Zhou, X. Exploiting the etalon effect to manipulate the pulse characteristics of a self-mode-locked Nd:YVO4 laser with a flexible cavity length. J. Opt. Commun. 2022, 517, 128331. [Google Scholar] [CrossRef]
- Jin, Y.; Xv, M.; Hu, M.; Zhang, Y.; Zhang, P.; Zhang, Z.; Zhang, H.; Liang, Q. High-repetition pulsed Nd:YVO4 laser based on the multi-longitudinal-mode beat note. J. Opt. Eng. 2021, 60, 066106. [Google Scholar] [CrossRef]
- Chen, Y.F.; Chang, M.T.; Huang, T.L.; Tung, J.C.; Huang, K.F.; Liang, H.C. Orthogonally Polarized Self-Mode-Locked Lasers With Repetition Rate Multiplication up to Hundreds of Gigahertz: Observation Of Temporal Carpet. J. IEEE J. Sel. Top. Quant. 2018, 24, 1101806. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).