A Terahertz Programmable Digital Metasurface Based on Vanadium Dioxide
Abstract
1. Introduction
2. Design of -Based Unit Cell
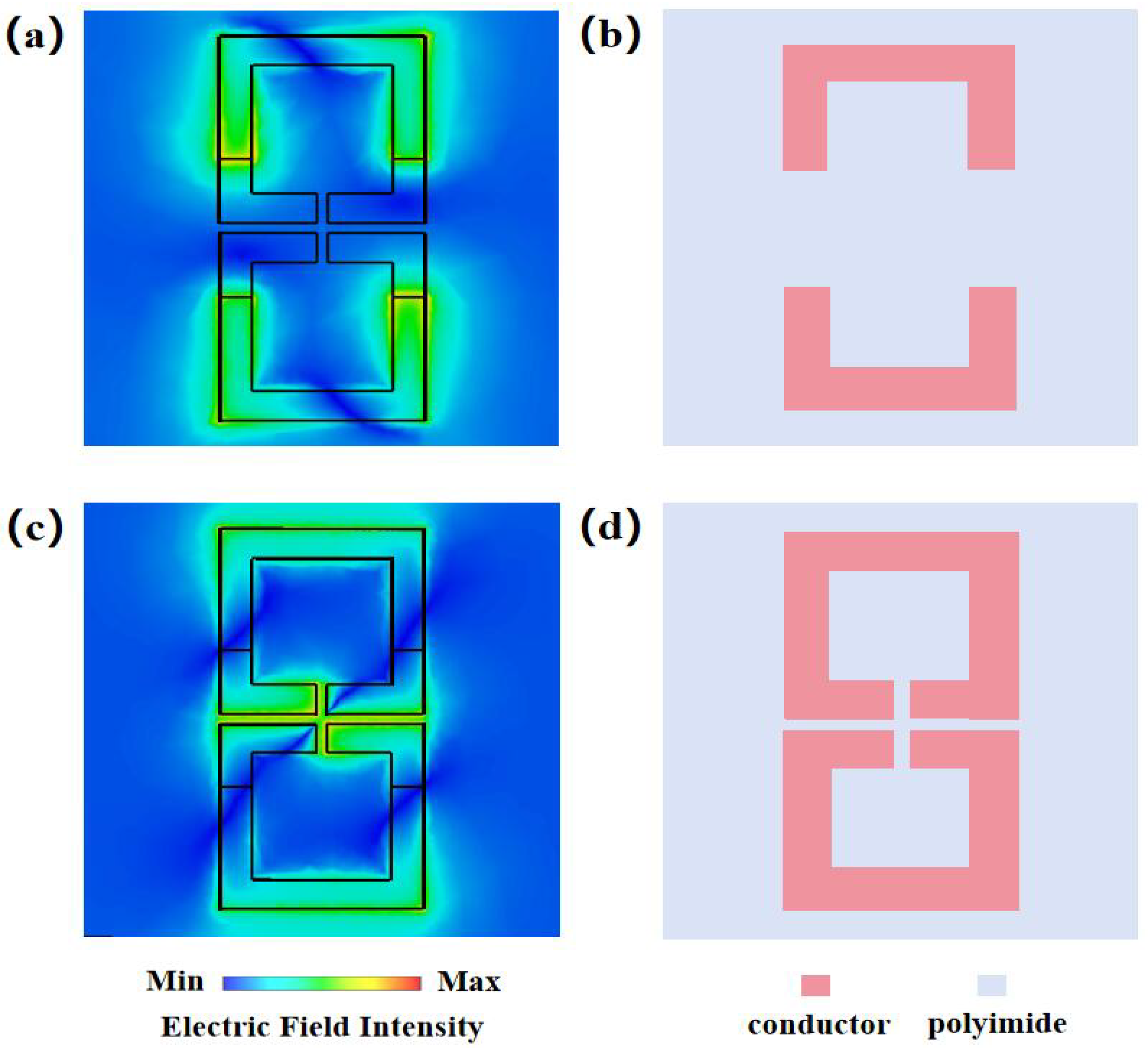
2.1. Structure of the Designed Unit Cell
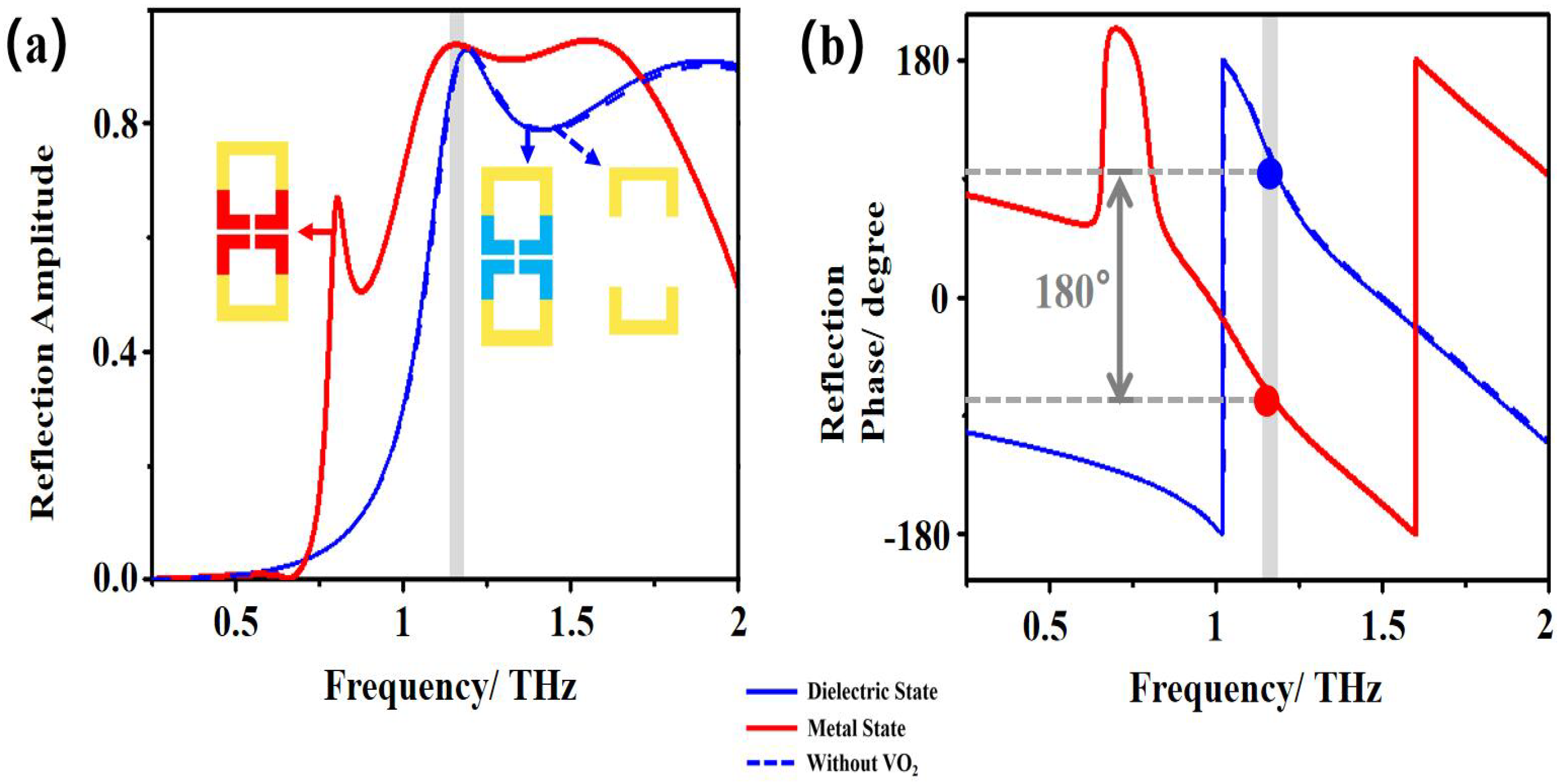
2.2. Analyses of Reflection Electromagnetic Response for Unit Cells
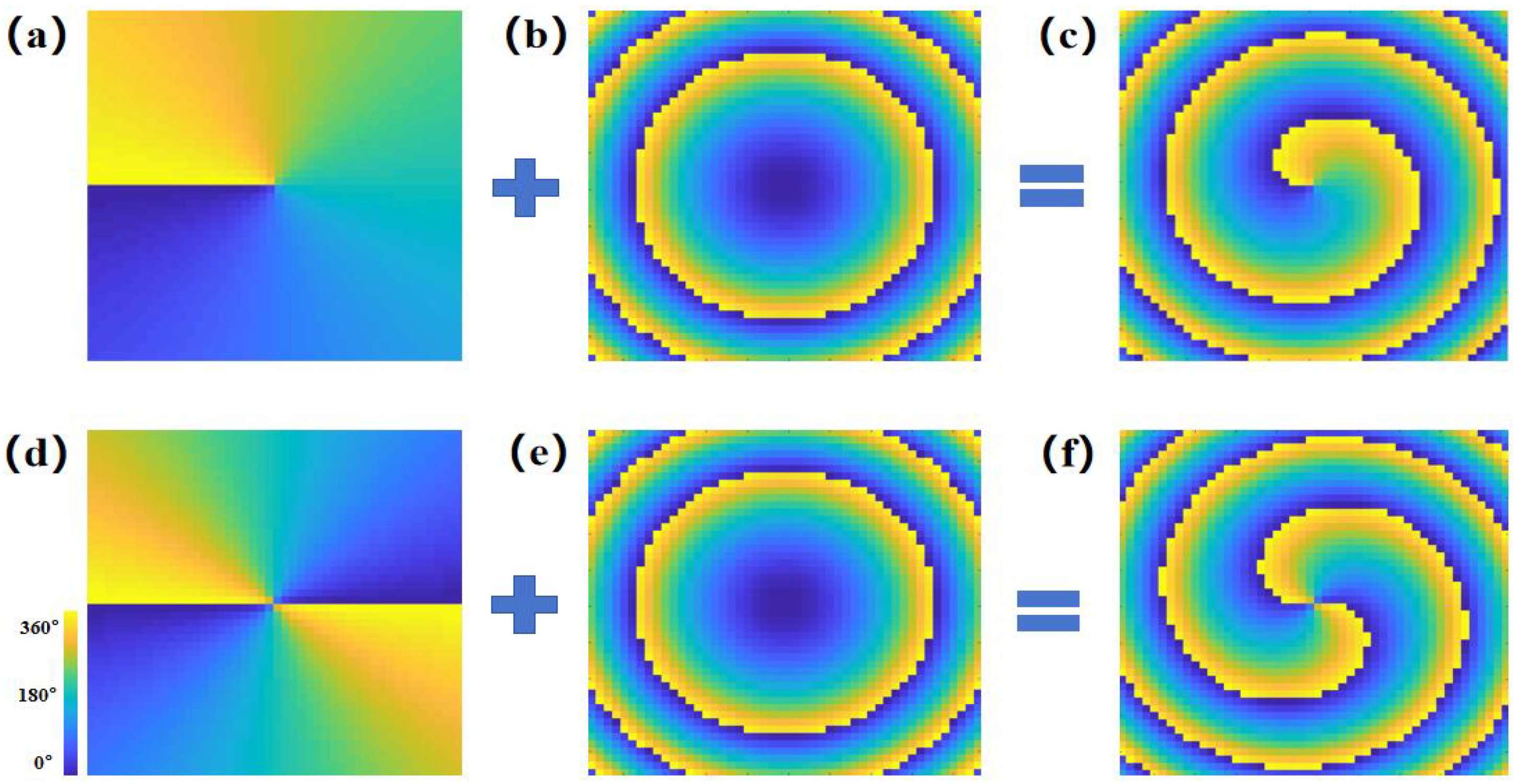
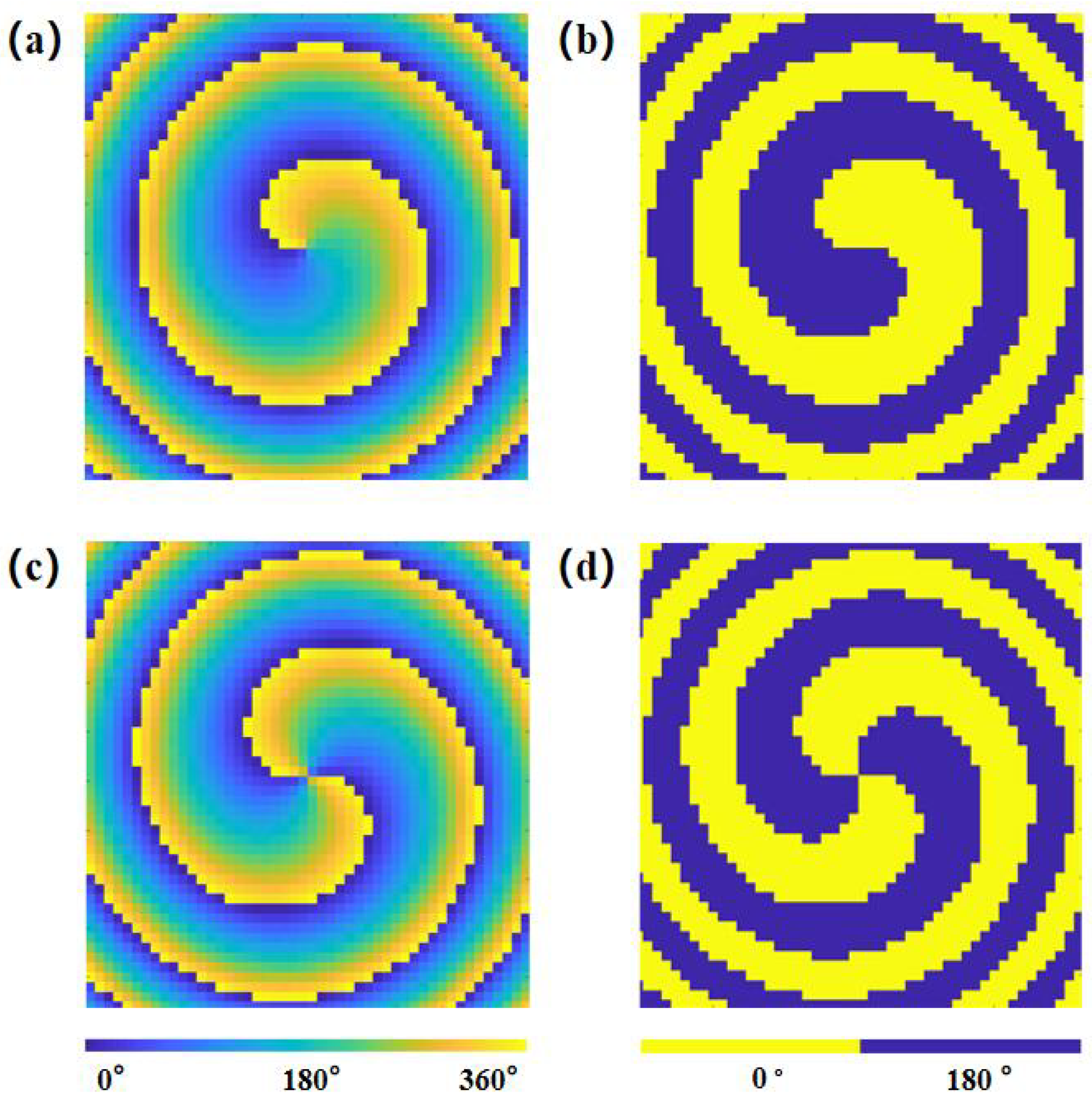
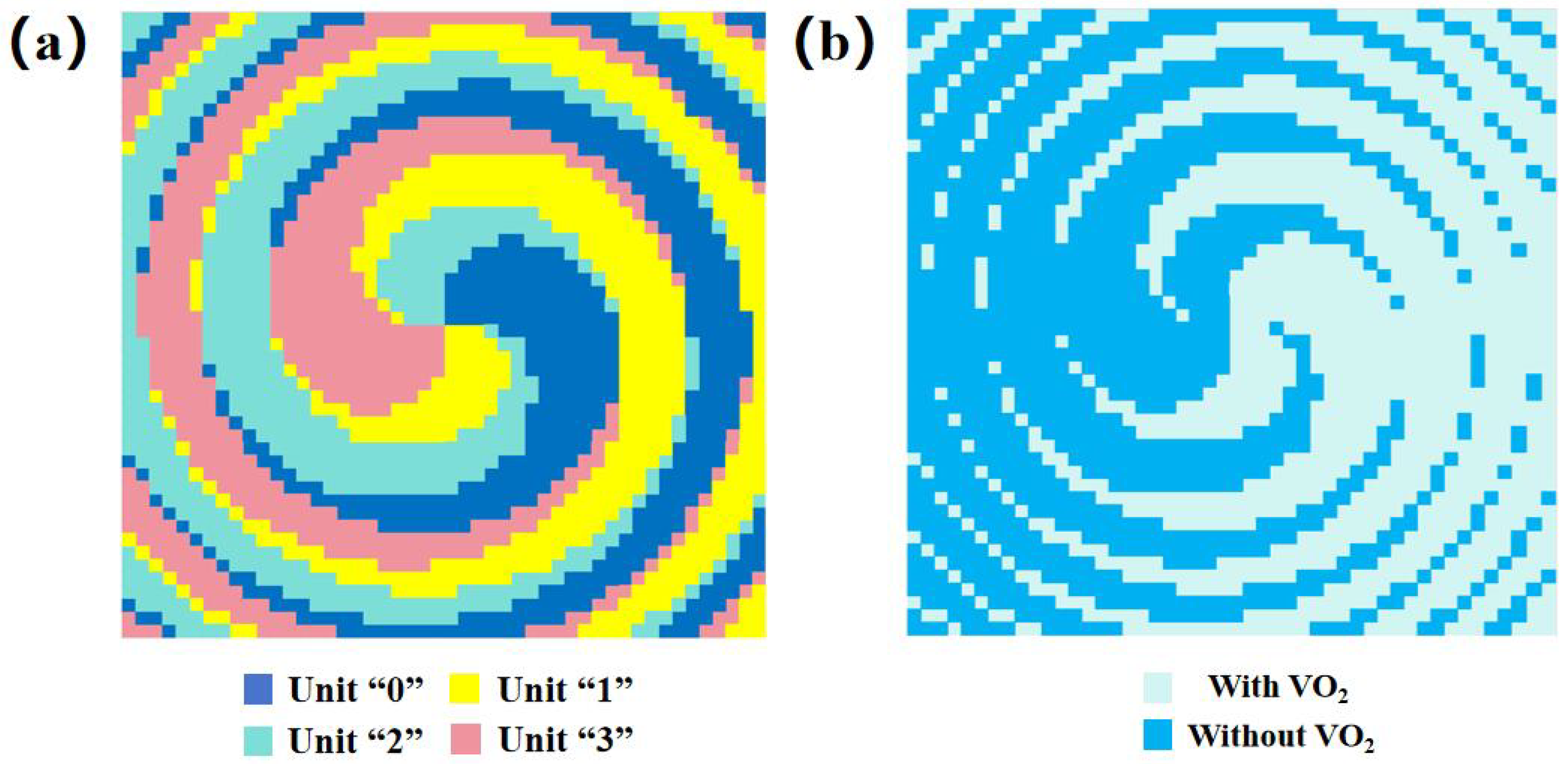
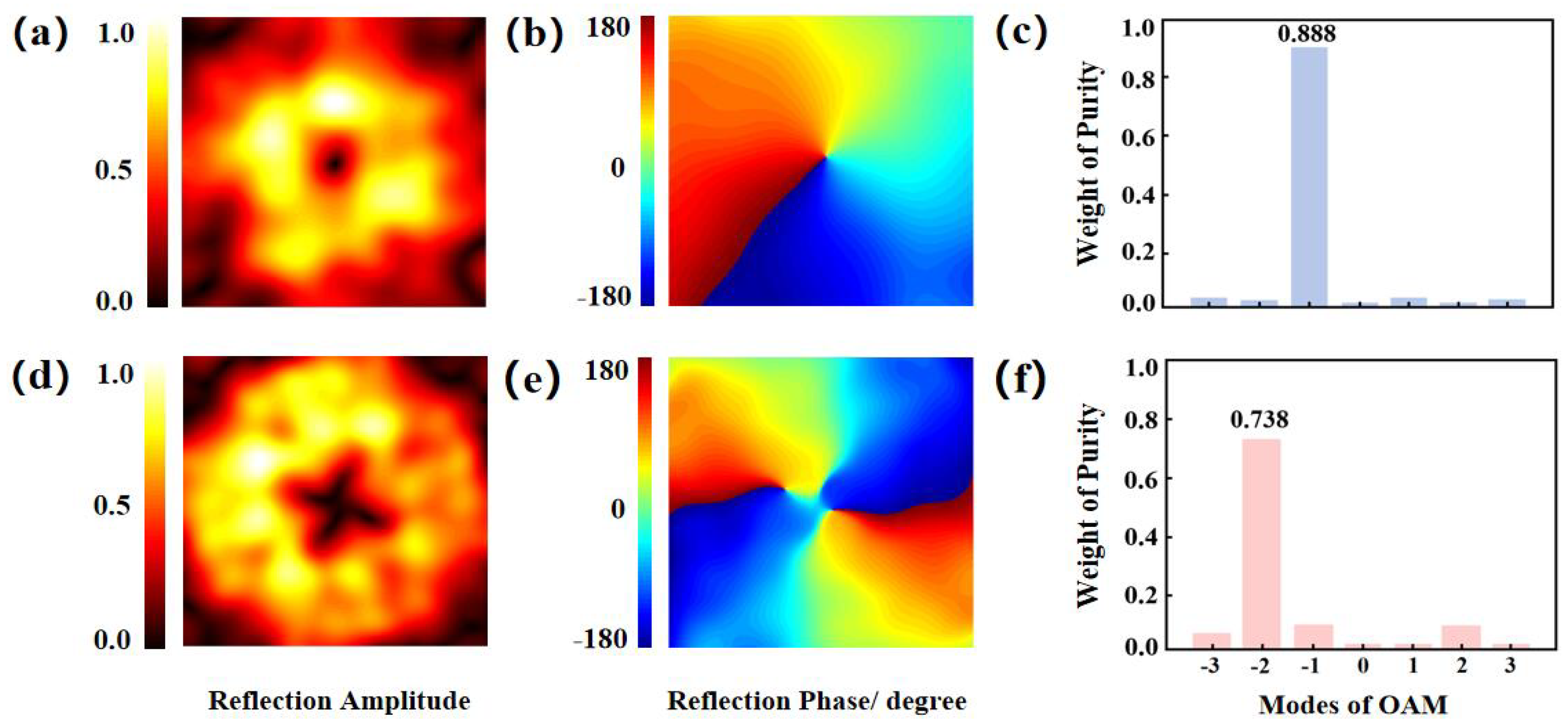
3. Design and Analyses of the OAM Manipulation Metasurface
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Abbreviations
| vanadium dioxide | |
| EMT | effective media theory |
| P-B phase | Pancharatnam-Berry phase |
| SSRR | split square resonant ring |
| FDTD | Finite-Difference Time Domain |
| RCP | right-handed circularly polarized |
| OAM | orbital angular momentum |
References
- Shin, J.-H.; Park, K.-H.; Ryu, H.-C. A Band-Switchable and Tunable THz Metamaterial Based on an Etched Vanadium Dioxide Thin Film. Photonics 2022, 9, 89. [Google Scholar] [CrossRef]
- Jiang, Z.-X.; Leng, J.; Li, J.; Li, J.-F.; Li, B.-Y.; Yang, M.; Wang, X.-L.; Shi, Q.-W. Flexible Terahertz Metamaterials Absorber based on VO2. Photonics 2023, 10, 621. [Google Scholar] [CrossRef]
- Shabanpour, J.; Beyraghi, S.; Cheldavi, A. Ultrafast reprogrammable multifunctional vanadium- dioxide- assisted metasurface for dynamic THz wavefront engineering. Sci. Rep. 2020, 10, 8950. [Google Scholar] [CrossRef]
- Liang, S.; Xu, F.; Li, W.; Yang, W.; Cheng, S.; Yang, H.; Chen, J.; Yi, Z.; Jiang, P. Tunable smart mid infrared thermal control emitter based on phase change material VO2 thin film. Appl. Therm. Eng 2023, 232, 121074. [Google Scholar] [CrossRef]
- Li, W.; Cheng, S.; Zhang, H.; Yi, Z.; Tang, B.; Ma, C.; Wu, P.; Zeng, Q.; Raza, R. Multi-functional metasurface: Ultra-wideband/multi-band absorption switching by adjusting guided mode resonance and local surface plasmon resonance effects. Commun. Theor. Phys. 2024, 76, 065701. [Google Scholar] [CrossRef]
- Bang, S.; Kim, J.; Yoon, G.; Tanaka, T.; Rho, J. Recent Advances in Tunable and Reconfigurable Metamaterials. Micromachines 2018, 9, 560. [Google Scholar] [CrossRef]
- Luo, J. Manipulations of Electromagnetic Waves by Coding Metamaterials and Their Applications. Master’s Thesis, Southeast University, Nanjing, China, 2019. [Google Scholar]
- Shangguan, Q.; Zhao, Y.; Song, Z.; Wang, J.; Yang, H.; Chen, J.; Liu, C.; Cheng, S.; Yang, W.; Yi, Z. High sensitivity active adjustable graphene absorber for refractive index sensing applications. Diam. Relat. Mater. 2022, 128, 109273. [Google Scholar] [CrossRef]
- Rouhi, K.; Rajabalipanah, H.; Abdolali, A. Multi-bit graphene-based bias-encoded metasurfaces for real-time terahertz wavefront shaping: From controllable orbital angular momentum generation toward arbitrary beam tailoring. Carbon 2019, 149, 125–138. [Google Scholar] [CrossRef]
- Wang, J.-L.; Dong, X.-C.; Yin, L.; Yang, Z.-X.; Wan, H.-D.; Chen, H.-M.; Zhong, K. Vanadium dioxide based terahertz dual-frequency multi-function coding metasurface. Acta Phys. Sin. 2023, 72, 098101. [Google Scholar] [CrossRef]
- Cui, T.-J.; Qi, M.-Q.; Wan, X.; Zhao, J.; Cheng, Q. Coding metamaterials, digital metamaterials and programmable metamaterials. Light Sci. Appl. 2014, 3, e218. [Google Scholar] [CrossRef]
- Jiang, W.-X.; Tian, H.-W.; Song, C.; Zhang, X.-G. Digital Coding Metasurfaces: Toward Programmable and Smart Manipulations of Electromagnetic Functions. J. Radars. 2022, 11, 1003–1022. [Google Scholar]
- Wang, L.; Yang, Y.; Gao, F.; Teng, S.-H.; Tan, Z.-G.; Zhang, X.; Lou, J.; Deng, L. Terahertz reconfigurable dielectric metasurface hybridized with vanadium dioxide for two-dimensional multichannel multiplexing. Front. Phys. 2022, 10, 992037. [Google Scholar] [CrossRef]
- Pan, Y.-B. Research on the Terahertz Vortex Beam Based on Coding Metasurface. Master’s Thesis, University of Electronic Science and Technology of China, Chengdu, China, 2022. [Google Scholar]
- Wang, L.; Yang, Y.; Deng, L.; Hong, W.-J.; Zhang, C.; Li, S.-F. Vanadium dioxide embedded frequency reconfigurable metasurface for multi-dimensional multiplexing of terahertz communication. J. Phys. D Appl. Phys. 2021, 54, 255003. [Google Scholar] [CrossRef]
- Chen, B.-W.; Wang, X.-R.; Li, W.-L.; Li, C.; Wang, Z.-S.; Guo, H.-B.; Wu, J.-B.; Fan, K.-B.; Zhang, C.-H.; He, Y.-B.; et al. Electrically addressable integrated intelligent terahertz metasurface. Sci. Adv. 2022, 8, eadd1296. [Google Scholar] [CrossRef]
- Li, J.-H.; Zhang, Y.-T.; Li, J.-N.; Li, J.; Li, J.-T.; Zheng, C.-L.; Yang, Y.; Huang, J.; Ma, Z.-Z.; Ma, C.-Q.; et al. Terahertz coding metasurface based vanadium dioxide. Acta Phys. Sin. 2020, 69, 228101. [Google Scholar] [CrossRef]
- Chen, B.-W.; Yang, S.-X.; Chen, J.; Wu, J.-B.; Chen, K.; Li, W.-L.; Tan, Y.-H.; Wang, Z.-S.; Qiu, H.-S.; Fan, K.-B.; et al. Directional terahertz holography with thermally active Janus metasurface. Light Sci. Appl. 2023, 12, 136. [Google Scholar] [CrossRef]
- Dong, J.-Q.; Cheng, Y.-Q.; Lin, S.-Y.; Zhou, Y.; Chen, Q. Reconfigurable Mode Vortex Beam Generation Based on Metasurface Using VO2 at Different Metal-Insulator Transition Temperatures. In Proceedings of the 2023 IEEE 11th Asia-Pacific Conference on Antennas and Propagation (APCAP), Guangzhou, China, 22 November 2024. [Google Scholar]
- Guan, S.-N.; Cheng, J.-R.; Chang, S.-J. Recent progress of terahertz spatial light modulators. Adv. Photonics Nexus. 2022, 13, 1637. [Google Scholar]
- Sırmacı, Y.D.; Barreda Gomez, A.; Pertsch, T.; Schmid, J.H.; Cheben, P.; Staude, I. All Dielectric Huygens’ Meta-Waveguides for Resonant Integrated Photonics. Laser Photonics Rev. 2023, 17, 2200860. [Google Scholar] [CrossRef]
- Bakker, R.M.; Yu, Y.F.; Paniagua-Domínguez, R.; Luk’yanchuk, B.; Kuznetsov, A.I. Resonant Light Guiding Along a Chain of Silicon Nanoparticles. Nano Lett. 2017, 17, 3458–3464. [Google Scholar] [CrossRef]
- Qiu, R.; Zhang, G.-M.; Zhang, Q.; Zhu, J.-C.; Feng, Y.-H.; Du, S.-K.; Liu, J.; Bi, K.-Y. Vanadium dioxide-based broadband spin-decoupled metasurface for wavefront control and modulation. Opt. Commun. 2023, 545, 129399. [Google Scholar] [CrossRef]
- Yang, J.-K.; Jeong, H.-S. Switchable Metasurface with VO2 Thin Film at Visible Light by Changing Temperature. Photonics 2021, 8, 57. [Google Scholar] [CrossRef]
- Drude, P. Zur Elektronentheorie der Metalle. Ann. Phys. 1900, 306, 566–613. [Google Scholar] [CrossRef]
- Verleur, H.W.; Barker, A.S., Jr.; Berglund, C.N. Optical Properties of VO2 between 0.25 and 5 eV. Phys. Rev. 1968, 172, 788–798. [Google Scholar] [CrossRef]
- Zhang, C.-H.; Zhou, G.-C.; Wu, J.-B.; Tang, Y.-H.; Wen, Q.-Y.; Li, S.-X.; Han, J.-G.; Jin, B.-B.; Chen, J.; Wu, P.-H. Active Control of Terahertz Waves Using Vanadium-Dioxide-Embedded Metamaterials. Phys. Rev. Appl. 2019, 11, 054016. [Google Scholar] [CrossRef]
- Spanos, I.; Stevens, C.J.; Solymar, L.; Shamonina, E. Tailoring the dispersion characteristics in planar arrays of discrete and coalesced split ring resonators. Sci. Rep. 2023, 13, 19981. [Google Scholar] [CrossRef]
- Lv, X.; Li, C.; Que, Y.; Li, G.; Hou, X.; Li, Y.; Li, L.; Sun, Y.; Guo, Y. Experimental demonstration of broadband impedance matching using coupled electromagnetic resonators. Sci. Rep. 2020, 10, 7437. [Google Scholar] [CrossRef]
- Liao, H.; Li, J.-S.; Guo, Y.-S. Theoretical and experimental study of the electric resonant coupling between two metamaterial resonators. Acta Phys. Sin. 2015, 64, 144101. [Google Scholar]
- Li, J.; Yang, Y.; Li, J.-N.; Zhang, Y.-T.; Zhang, Z.; Zhao, H.-L.; Li, F.-Y.; Tang, T.-T.; Dai, H.-T.; Yao, J.-Q. All-optical Switchable Vanadium Dioxide Integrated Coding Metasurfaces for Wavefront and Polarization Manipulation of Terahertz Beams. Adv. Theory Simul. 2019, 3, 1900183. [Google Scholar] [CrossRef]
- Liu, J.-Q.; Cheng, Y.-Z.; Chen, F.; Luo, H.; Li, X.-C. High- Efficiency wavefront manipulation based on geometric phase metasurface for circularly polarized terahertz wave at two frequencies dependently. Infrared Laser Eng. 2023, 52, 20220377. [Google Scholar]
- Li, J.; Li, J.-T.; Zhang, Y.-T.; Li, J.-N.; Yang, Y.; Zhao, H.-L.; Zheng, C.-L.; Li, J.-H.; Huang, J.; Li, F.-Y.; et al. All-optical switchable terahertz spin-photonic devices based on vanadium dioxide integrated metasurfaces. Opt. Commun. 2020, 460, 124986. [Google Scholar] [CrossRef]
- Yang, D.-Q.; Wang, W.-G.; Lv, E.; Wang, H.-M.; Liu, B.-C.; Hou, Y.-Z.; Chen, J.-H. Programmable VO2 metasurface for terahertz wave beam steering. iScience 2022, 25, 104824. [Google Scholar] [CrossRef]
- Liu, C.-X.; Yang, F.; Fu, X.-J.; Wu, J.-W.; Zhang, L.; Yang, J.; Cui, T.-J. Programmable Manipulations of Terahertz Beams by Transmissive Digital Coding Metasurfaces Based on Liquid Crystals. Adv. Optical Mater. 2021, 9, 2100932. [Google Scholar] [CrossRef]
- Li, X.-N.; Zhou, L.; Zhao, G.-Z. Terahertz vortex beam generation based on reflective metasurface. Acta Phys. Sin. 2019, 68, 238101. [Google Scholar] [CrossRef]
- Han, X.-B.; Chen, J.-X.; Wang, Y.; Zhou, Y.-G. Terahertz orbital angular momentum generation based on ultra-wideband reflective metasurface. J. Appl. Opt. 2024, 45, 282–291. [Google Scholar]



Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Pan, T.; Liu, C.; Peng, S.; Lu, H.; Zhang, H.; Xu, X.; Yang, F. A Terahertz Programmable Digital Metasurface Based on Vanadium Dioxide. Photonics 2024, 11, 527. https://doi.org/10.3390/photonics11060527
Pan T, Liu C, Peng S, Lu H, Zhang H, Xu X, Yang F. A Terahertz Programmable Digital Metasurface Based on Vanadium Dioxide. Photonics. 2024; 11(6):527. https://doi.org/10.3390/photonics11060527
Chicago/Turabian StylePan, Tianrui, Chenxi Liu, Shuang Peng, Haiying Lu, Han Zhang, Xiaoming Xu, and Fei Yang. 2024. "A Terahertz Programmable Digital Metasurface Based on Vanadium Dioxide" Photonics 11, no. 6: 527. https://doi.org/10.3390/photonics11060527
APA StylePan, T., Liu, C., Peng, S., Lu, H., Zhang, H., Xu, X., & Yang, F. (2024). A Terahertz Programmable Digital Metasurface Based on Vanadium Dioxide. Photonics, 11(6), 527. https://doi.org/10.3390/photonics11060527




