Optimized Wide-Angle Metamaterial Edge Filters: Enhanced Performance with Multi-Layer Designs and Anti-Reflection Coatings
Abstract
1. Introduction
2. Design Methods and Models
2.1. Design Methods
- CST Simulation of Optical MFL: We began with CST simulations to accurately characterize the spectral profiles of the SiNP-based MFL. This involved parameter sweeps in the unit cell models, altering periodicity, nanoparticle size, and the properties of the host medium.
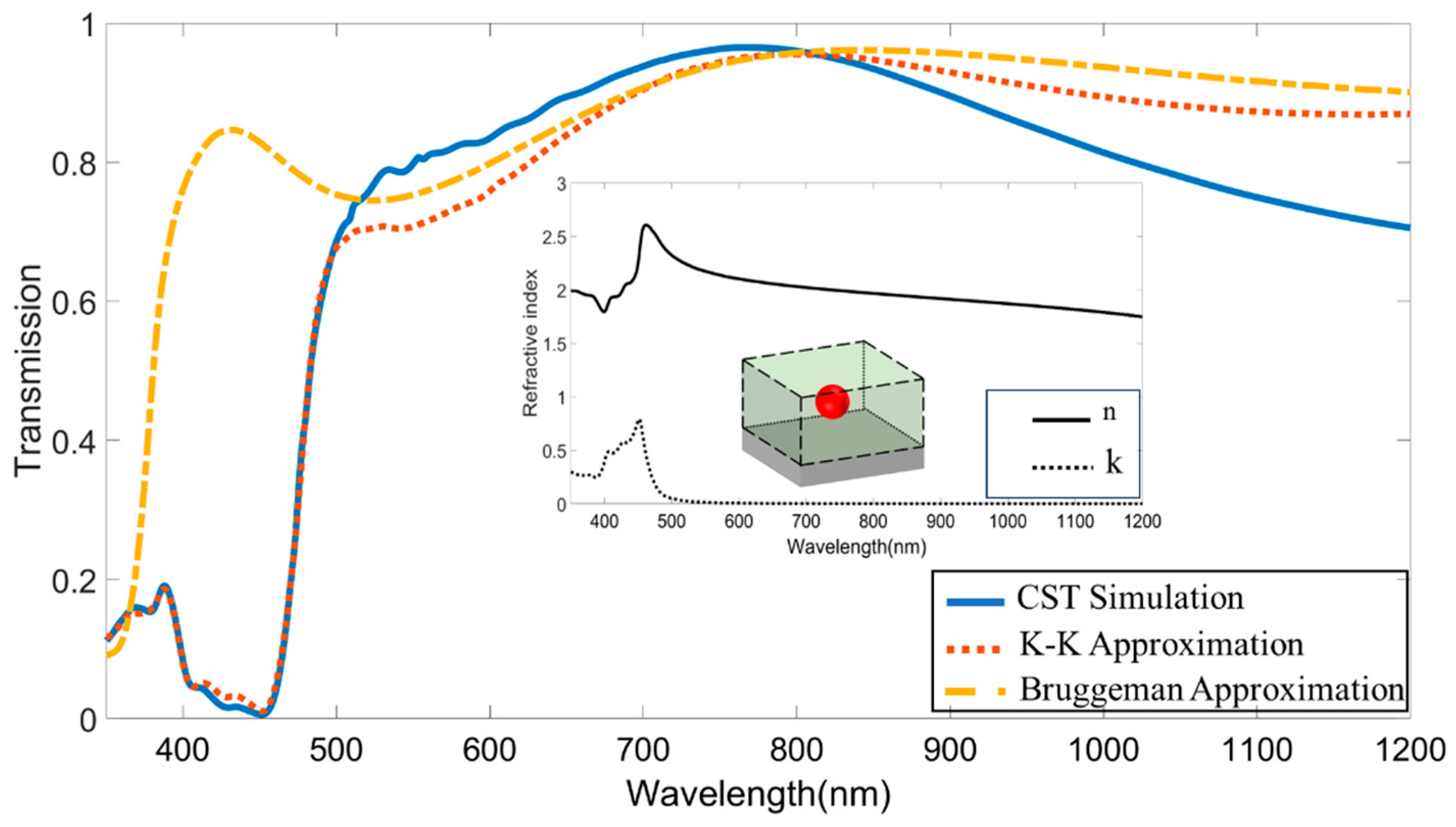
- Effective Refractive Index Calculation: We then extracted the effective refractive index from the CST simulation outcomes, a critical factor for adapting the CST model to an ESM-compatible format.
- Multi-Layer and ARC Design Optimization in ESM: Using the effective refractive index, we converted the CST models into the ESM platform and employed the needle synthesis function for the efficient optimization of multi-layer designs ( and in this case), including the introduction of the ARC. During synthesis, we locked the refractive index and thickness of all of the MFLs. A target reflection from 425 nm to 1200 nm, with a step width of 25 nm, was set to attain 0 at , , and AOI in transverse electric (TE) polarization. No need was found to set transverse magnetic (TM) polarization, as the transmission of the filter in this model is naturally considerable in all AOIs.
- CST Verification and Fine-Tuning: Subsequently, we refined the designs derived from the ESM using CST simulations to finalize an enhanced design, ensuring superior performance metrics.
2.2. Models for Effective Refractive Index
2.3. Designs
3. Results and Discussion
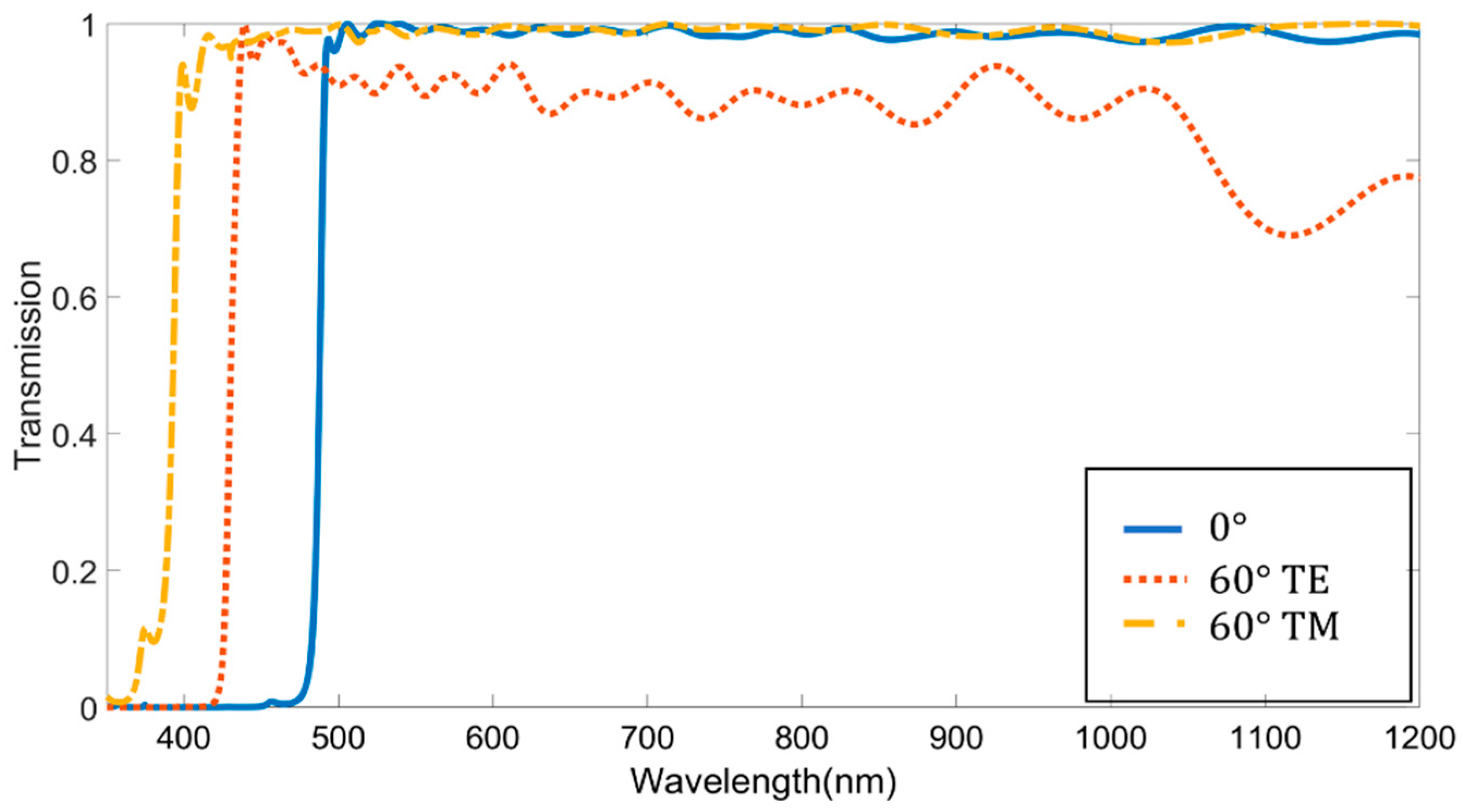
3.1. Traditional Thin-Film Filters
3.2. K–K Model and Bruggeman Model
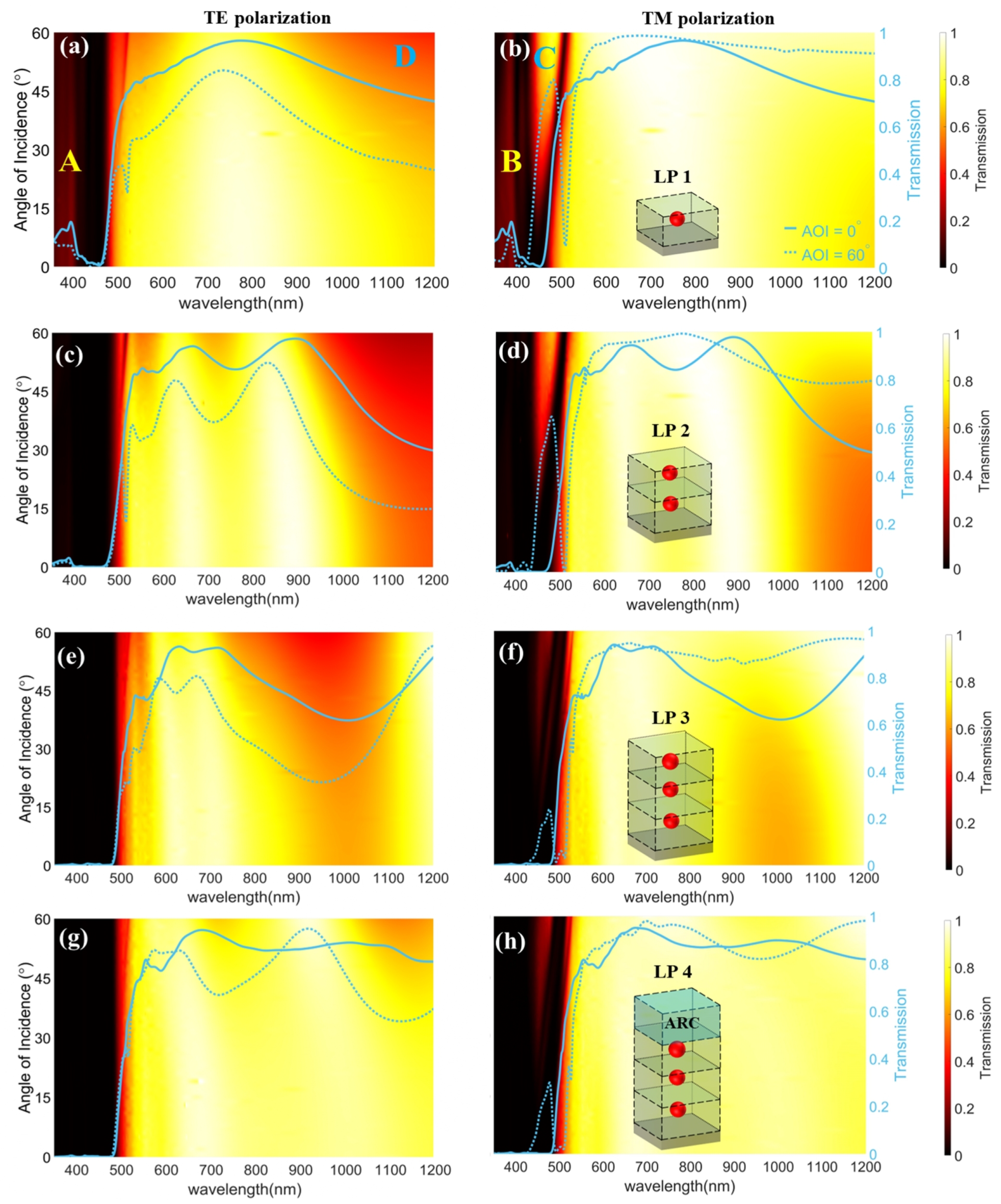
3.3. Metamaterial Edge Filters
3.4. Comparison of Designed Filters
3.5. Tunability of Edge Wavelength
3.6. Limitation and Future Work
4. Conclusions
Supplementary Materials
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Pan, H.; Chen, X.; Xia, X. A review on the evolvement of optical-frequency filtering in photonic devices in 2016–2021. Renew. Sustain. Energy Rev. 2022, 161, 112361. [Google Scholar] [CrossRef]
- Silva, M.F.; Granado, T.C.; Gonnella, R.H.; Costa, J.P.C.; Assagra, Y.A.O.; Correia, J.H.; Carmo, J.P. Optical filters for narrow-band imaging on medical devices. In Proceedings of the 2017 SBMO/IEEE MTT-S International Microwave and Optoelectronics Conference (IMOC), Aguas de Lindoia, Brazil, 27–30 August 2017. [Google Scholar]
- Kallos, E.; Palikaras, G. Volume manufacturing and industrial applications of metamaterials: Rolling lithography, holography, laser filtering and photovoltaics. In Proceedings of the 2017 11th International Congress on Engineered Materials Platforms for Novel Wave Phenomena (Metamaterials), Marseille, France, 27 August–2 September 2017. [Google Scholar]
- Chang, P.; Shi, H.; Wang, Z.; Miao, J.; Shi, T.; Guo, H.; Chen, J. Cesium Faraday Optical Filter for Wireless Optical Communication System. In Proceedings of the 2021 13th International Conference on Wireless Communications and Signal Processing (WCSP), Changsha, China, 20–22 October 2021. [Google Scholar]
- Frey, L.; Masarotto, L.; Armand, M.; Charles, M.L.; Lartigue, O. Multispectral interference filter arrays with compensation of angular dependence or extended spectral range. Optics Express 2015, 9, 11799–11812. [Google Scholar] [CrossRef] [PubMed]
- Elbashar, Y.H.; Rashad, M.M.; Rayan, D.A. Protection glass eyewear against a YAG laser based on a bandpass absorption filter. Silicon 2016, 9, 111–116. [Google Scholar] [CrossRef]
- Ji, C.; Yang, C.; Shen, W.; Lee, K.; Zhang, Y.; Liu, X.; Guo, L.J. Decorative near-infrared transmission filters featuring high-efficiency and angular-insensitivity employing 1D photonic crystals. Nano Res. 2019, 12, 543–548. [Google Scholar] [CrossRef]
- Baqir, M.A.; Choudhury, P.K. Hyperbolic metamaterial-based UV absorber. IEEE Photonics Technol. Lett. 2017, 29, 1548–1551. [Google Scholar] [CrossRef]
- Chowdhury, M.Z.B.; Islam, M.T.; Hoque, A.; Alshammari, A.S.; Alzamil, A.; Alsaif, H.; Alshammari, B.M.; Hossain, I.; Samsuzzaman, M. Design and Parametric Analysis of a Wide-Angle and Polarization Insensitive Ultra-Broadband Metamaterial Absorber for Visible Optical Wavelength Applications. Nanomaterials 2022, 12, 4253. [Google Scholar] [CrossRef] [PubMed]
- Zhu, P.; Guo, L.J. High performance broadband absorber in the visible band by engineered dispersion and geometry of a metal-dielectric-metal stack. Appl. Phys. Lett. 2012, 101, 241116. [Google Scholar] [CrossRef]
- Soni, A.; Purohit, S.; Hegde, R.S. Multilayered aluminum plasmonic metasurfaces for ultraviolet bandpass filtering. IEEE Photonics Technol. Lett. 2017, 29, 110–113. [Google Scholar] [CrossRef]
- Park, J.; Hong, S.K.; Chuang, H. Numerical demonstration of angle-independent electromagnetic transparency in short-wavelength infrared regime. IEEE Access 2022, 10, 40402–40409. [Google Scholar]
- Wells, B.; Lotti, F.; Nasir, M.E.; Zayats, A.V.; Podolskiy, V.A. Angle-insensitive plasmonic nanorod metamaterial-based band-pass optical filters. Optics Express 2021, 29, 11562–11569. [Google Scholar] [CrossRef]
- Monks, J.N.; Yue, L.; Yan, B.; Aldred, B.; Hurst, A.; Wang, Z. A wide-angle shift-free metamaterial filter design for anti-laser striking application. Opt. Commun. 2018, 429, 53–59. [Google Scholar] [CrossRef]
- Lotti, F.; Mirzaei, A.; Wang, P.; Miroshnichenko, A.E.; Zayats, A.V. Nanoparticle-based metasurfaces for angular-independent spectral filtering applications. J. Appl. Phys. 2019, 126, 213101. [Google Scholar] [CrossRef]
- Estrada-Wiese, D.; Del Río, J.A. Refractive index evaluation of porous silicon using Bragg reflectors. Rev. Mex. Física 2018, 64, 72–81. [Google Scholar] [CrossRef]
- Hong, W.Q. Extraction of extinction coefficient of weak absorbing thin s from special absorption. J. Phys D Appl. Phys. 1989, 22, 384–1385. [Google Scholar] [CrossRef]
- Bertie, J.E.; Zhang, S.L. Infrared intensities of liquids. ix. the Kramers–Kronig transform, and its approximation by the finite Hilbert transform via Fast Fourier transforms. Can. J. Chem. 1992, 70, 520–531. [Google Scholar]
- Silva, M.F.; Pimenta, S.; Rodrigues, J.A.; Freitas, J.R.; Ghaderi, M.; Goncalves, L.M.; de Graaf, G.; Wolffenbuttel, R.F.; Correia, J.H. Magnesium fluoride as low-refractive index material for near-ultraviolet filters applied to optical sensors. Vacuum 2020, 181, 109673. [Google Scholar] [CrossRef]
- Luke, K.; Okawachi, Y.; Lamont, M.R.; Gaeta, A.L.; Lipson, M. Broadband mid-infrared frequency comb generation in a Si3N4 microresonator. Opt. Lett. 2015, 20, 4823–4826. [Google Scholar] [CrossRef] [PubMed]
- Dodge, M.J. Refractive properties of magnesium fluoride. Appl. Opt. 1984, 23, 1980–1985. [Google Scholar] [CrossRef] [PubMed]
- Schinke, C.; Christian Peest, P.; Schmidt, J.; Brendel, R.; Bothe, K.; Vogt, M.R.; Kröger, I.; Winter, S.; Schirmacher, A.; Lim, S.; et al. Uncertainty analysis for the coefficient of band-to-band absorption of crystalline silicon. AIP Adv. 2015, 5, 067168. [Google Scholar] [CrossRef]
- Vogt, M.R.; Hahn, H.; Holst, H.; Winter, M.; Schinke, C.; Köntges, M.; Brendel, R.; Altermatt, P.P. Measurement of the optical constants of soda-lime glasses in dependence of iron content, and modeling of iron-related power losses in crystalline Si solar cell modules. IEEE J. Photovolt. 2016, 6, 111–118. [Google Scholar] [CrossRef]
- Monks, J.N.; Williams, J.; Hurst, A.; Wang, Z. Shift-free fixed-line laser protection filter technology. In Proceedings of the SPIE 11539, Technologies for Optical Countermeasures XVII; and High-Power Lasers: Technology and Systems, Platforms, Effects IV, Online, 20 September 2020; Volume 1153908. [Google Scholar]
- Shilkin, D.A.; Lyubin, E.V.; Shcherbakov, M.R.; Lapine, M.; Fedyanin, A.A. Directional optical sorting of silicon nanoparticles. ACS Photonics 2017, 4, 2312–2319. [Google Scholar] [CrossRef]
- Li, W.; Liu, M.; Cheng, S.; Zhang, H.; Yang, W.; Yi, Z.; Zeng, Q.; Tang, B.; Ahmad, S.; Sun, T. Polarization independent tunable bandwidth absorber based on single-layer graphene. Diam. Relat. Mater. 2024, 142, 110793. [Google Scholar] [CrossRef]
- Luk ‘yanchuk, B.S.; Tribelsky, M.I.; Wang, Z.B.; Zhou, Y.; Hong, M.H.; Shi, L.P.; Chong, T.C. Extraordinary scattering diagram for nanoparticles near plasmon resonance frequencies. Appl. Phys. A 2007, 89, 259–264. [Google Scholar] [CrossRef]
- Chen, W.; Luo, Q.; Zhang, C.; Shi, J.; Deng, X.; Yue, L.; Wang, Z.; Chen, X.; Huang, S. Effects of down-conversion CeO2:Eu3+ nanophosphors in perovskite solar cells. J. Mater. Sci. Mater. Electron. 2017, 28, 11346–11357. [Google Scholar] [CrossRef]
- Lupi, F.F.; Giammaria, T.; Volpe, F.; Lotto, F.; Seguini, G.; Pivac, B.; Laus, M.; Perego, M. High Aspect Ratio PS-b-PMMA Block Copolymer Mask for Lithographic Applications. ACS Appl. Mater. Interfaces 2014, 6, 21389–21396. [Google Scholar] [CrossRef]
- Monks, J.N. Shift-free Wide-angle Metamaterial Narrowband Filters for Anti-laser Striking Applications. Ph.D. Thesis, Doctor of Philosophy, Bangor University, Bangor, UK, 2019. [Google Scholar]
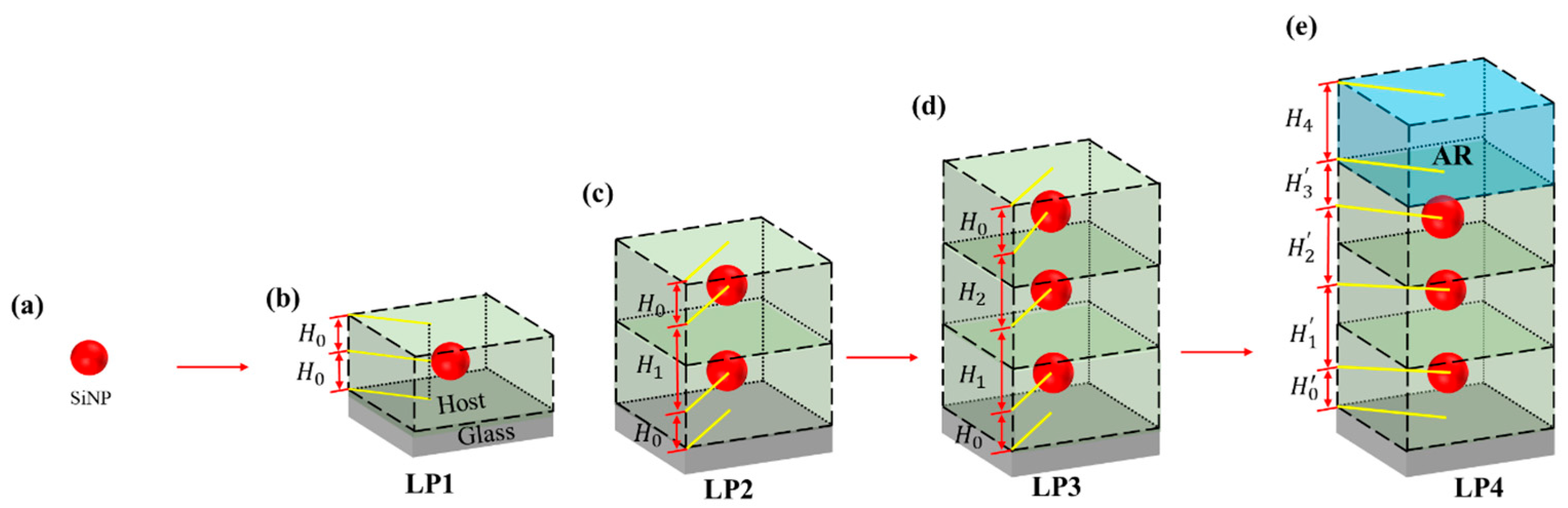
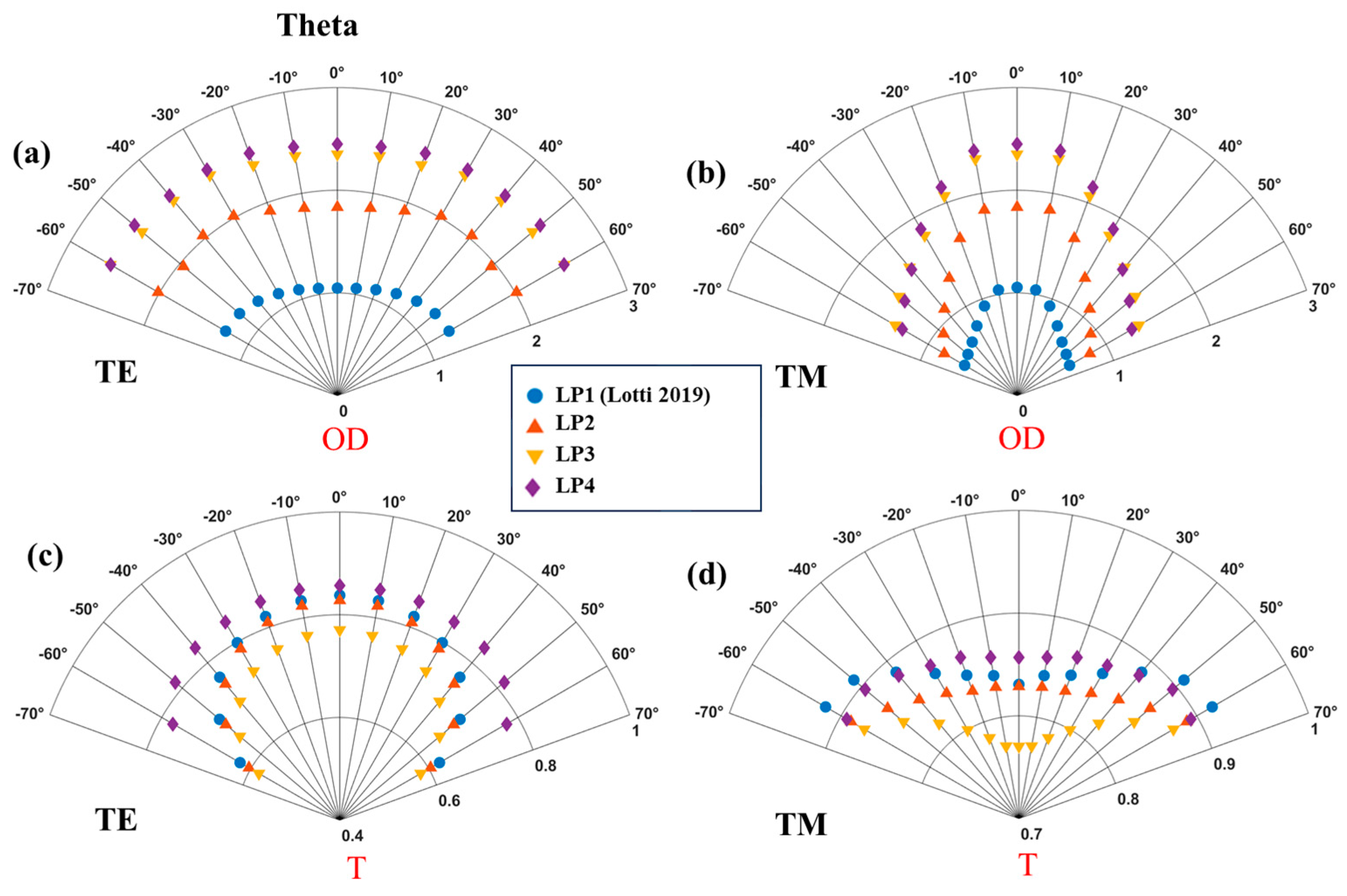


| Design ID | Long-Pass (LP) Edge Filter (H: High-index material layer with quarter-wavelength thickness, L: Low-index material layer with quarter-wavelength thickness, and the reference wavelength is 445 nm) used as anti-reflection coating) |
|---|---|
| LP0 | |
| LP1 | (Figure 1b) |
| LP2 | (Figure 1c) |
| LP3 | (Figure 1d) |
| LP4 | (Figure 1e) |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wu, B.; Monks, J.N.; Yue, L.; Hurst, A.; Wang, Z. Optimized Wide-Angle Metamaterial Edge Filters: Enhanced Performance with Multi-Layer Designs and Anti-Reflection Coatings. Photonics 2024, 11, 446. https://doi.org/10.3390/photonics11050446
Wu B, Monks JN, Yue L, Hurst A, Wang Z. Optimized Wide-Angle Metamaterial Edge Filters: Enhanced Performance with Multi-Layer Designs and Anti-Reflection Coatings. Photonics. 2024; 11(5):446. https://doi.org/10.3390/photonics11050446
Chicago/Turabian StyleWu, Baidong, James N. Monks, Liyang Yue, Andrew Hurst, and Zengbo Wang. 2024. "Optimized Wide-Angle Metamaterial Edge Filters: Enhanced Performance with Multi-Layer Designs and Anti-Reflection Coatings" Photonics 11, no. 5: 446. https://doi.org/10.3390/photonics11050446
APA StyleWu, B., Monks, J. N., Yue, L., Hurst, A., & Wang, Z. (2024). Optimized Wide-Angle Metamaterial Edge Filters: Enhanced Performance with Multi-Layer Designs and Anti-Reflection Coatings. Photonics, 11(5), 446. https://doi.org/10.3390/photonics11050446







