Abstract
Refractive index measurements have been an important task for a long time because that index plays an essential role in describing the optical properties of a material. Many methods have been developed to perform that task. Some of them use interferometry to achieve high precision. However, these configurations are complicated. Some measure the critical angle using simple structures, but their accuracy is unsatisfactory because it is difficult to judge the exact critical angle with intensity variations. Here, we propose several new schemes based on measuring the polarization change in the total internal reflection. The proposed method has the merits of simple structure and easy incident angle determination that gives the maximum phase change. Additionally, it is possible to find the material dispersion by measuring the wavelength dependence of the polarization ellipticity. Some useful formulas relating the refractive index to the maximum phase change are obtained. This work can provide valuable alternatives for refractive index measurement.
1. Introduction
Refractive indexing is one of the most important characteristic parameters of optical materials, especially transparent ones. It is defined as the ratio of the velocity of light in a vacuum and in the material. Many methods based on various principles [1] have been proposed to measure the refractive index of a material or liquid, such as prism coupling [2], interferometry [3], ellipsometry [4], Brewster angle [5], photoacoustic microscopy [6,7], and holography [8]. One method uses the total internal reflection (TIR) to achieve that measurement goal. It is noted that image reconstruction can be achieved by detecting the optical evanescent wave of TIR [7]. Usually, there are two categories utilizing TIR. The first measures the critical angle of a material by detecting the reflection or refraction intensity variation across the critical angle [9,10,11]. The refractive index can then be calculated via the relationship between the critical angle and the refractive index. Some useful refractometers, such as the Pulfich type, utilize this principle [12]. The advantages of the measurement method are the following: simple structure, low cost, and easy handling. However, its disadvantages lie mainly in its time consumption and lower precision because it takes time to scan the incident angle. The reflected light intensity variation across the critical angles is difficult to judge precisely [10]. The second method measures the phase shift carried by the reflected beam after TIR, and for that purpose, a phase meter [13] or an interferometer [14] is needed. Contrary to the -measurement method, the advantages of the -measurement method are high-precision and time-saving because angle scanning is not needed. Usually, these configurations are more complicated or require sophisticated skills to perform the task. Of course, the cost is generally higher.
In this work, we propose several different approaches to measure the refractive index based on measuring the TIR polarization changes. The first method derives the analytical equation between the refractive index and the incident angle to give the maximum phase change. Once that angle is measured by varying the incident angle experimentally, the refractive index can be calculated. The second method measures the polarization ellipticity for any incident angle. The refractive index can then be obtained using the relationship derived between them. Finally, a new way to measure material dispersion is also suggested. The details and merits of these schemes will be given in the next section.
The structure of the work is as follows: Section 1 is the introduction. Section 2 includes four subsections. The first reviews a conventional scheme that is a good contrast to the second method provided by us. The third and fourth subsections suggest two other configurations with different merits. The conclusions and discussion are presented in Section 3.
2. Theory and Numerical Results
As mentioned in the introduction, there are many different ways to determine the refraction index of a transparent material. Here, we review a famous historical method [15] because it is a good contrast with our method.
2.1. Method of Measuring Minimum Angular Deviation of a Prism
Figure 1a shows a typical dispersing prism with an apex angle and refractive index n1 (at a specified wavelength of the incident light). A parallel light beam is incident from the left with an incident angle at the first interface of the prism. It leaves the second interface with an angle , which is deviated from its original incident direction with an angular deviation . The symbols and indicate the refraction angle and the incident angle for the first and second refraction of the two interfaces, respectively. From the geometry of the prism triangle, we have
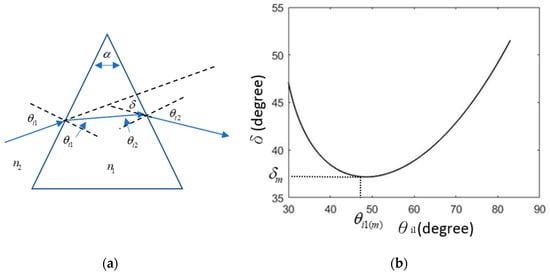
Figure 1.
(a) Schematic and notations for a prism scheme. (b) Angular deviation versus the incident angle for the case of = 600 and n1 = 1.5.
Using some algebra and manipulation, we find that the angular deviation can be written as a function of and only. When reaches its minimum , the ray traverses the prism symmetrically, that is, parallel to its base (). Under that situation, we have
where m in the subscript indicates the minimum value for minimum , as shown in Figure 1b.
Applying Snell’s law to the first refraction and assuming the medium around the prism is air or vacuum with a refractive index = 1.0, the prism’s refractive index is
Thus, by varying to find and knowing , the refractive index of the prism can be determined. Figure 1b shows the angular deviation versus the incident for the case of = 600 and n = 1.5; the minimum is 37.20 at the incident angle = 48.60.
2.2. Method Measuring the Maximum Phase Change in TIR
Now, we consider another scheme proposed by us to measure the refractive index. Figure 2 illustrates a situation in which a light beam is incident into a transparent semi-circle cylinder (or a semi-sphere) with refractive index n1, and that of the surrounding medium is with . It is well known that when the incident angle is larger than the critical angle , the total internal reflection (TIR) occurs. As TIR exists, the light beam reflects into the same material without refracting into the medium. Here, the semi-circle shape is chosen for convenience of discussion. The TIR is on the top interface without considering the refraction at the boundaries of the material (i.e., when the light wave enters and leaves the material). It is further assumed that some anti-reflection coating is applied to the boundaries (except the top surface); thus, all of the incident power aimed at the center of the semi-circle with angle is reflected and leaves the material at the same angle without taking the Fresnel loss at the boundaries into account. We also know that under TIR, the reflected light wave will gain different phase changes for different polarizations as follows [12]:
where and are the phase changes for p and s polarizations, respectively, and is the refractive index ratio of and , which is less than 1. Figure 2b shows (blue line) and (red line) versus for the case of and (n = 2/3) with the critical angle . The phase changes start from zero at and increase monotonically to 1800 when reaches 900, and is larger than in the whole interval. Because the phase differences exist for the two polarizations, there is a polarization change if the incident wave polarization is not parallel with one of the polarizations. For example, as shown in Figure 3a, if an incident wave is linearly polarized 450 with respect to the x axis, its polarization state will be an elliptical polarization after the TIR. The ellipticity depends on the incident angle and refractive index ratio . This feature is used as a quarter wave plate that transforms a linear polarization into a circular polarization, called a Fresnel rhomb [12]. Its advantage over the traditional birefringent wave plate is that it is much less wavelength-sensitive. The phase difference is defined as , and it can be written as
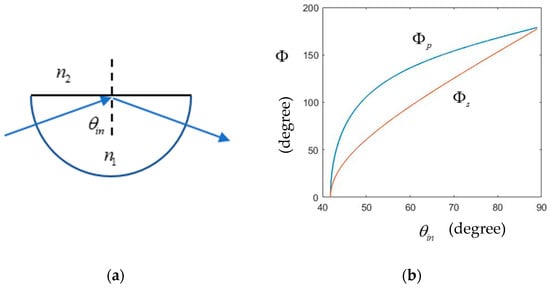
Figure 2.
(a) Schematic and notations for a transparent semi-circle cylinder with TIR. (b) Plot for phase vs. incident angle for the two polarizations under TIR.
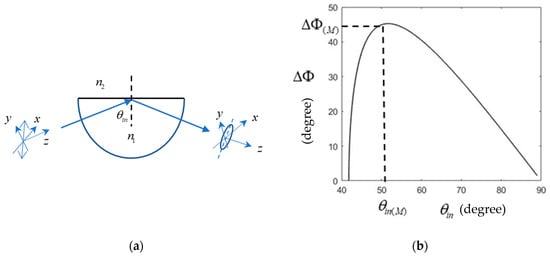
Figure 3.
(a) Schematic for the polarization state change, from a linear one to an elliptical one, after TIR. (b) Plot for phase difference vs. incident angle under TIR. The wave is propagating along the z direction, and y and x are the parallel (p-polarization) and vertical (s-polarization) directions, respectively.
Figure 3b shows for the case of n = 2/3 ( and ). Note that at the two incident angles, 50.230 or 53.260, reaches 450; thus, after two TAR reflections, the total phase change accumulated is 900 (i.e., quarter wave), which is the Fresnel rhomb principle. It is also interesting to find that there is a maximum for the ; in this case, it is for , where the (M) in the subscript indicates the maximum. By differentiating the right side of Equation (5) with respect to and setting it to zero to find , we can have
Equation (6) is of value because it gives analytical results for and . It is interesting to compare Figure 3b with Figure 1b, where both have extreme incident angle values for giving minimum deviation angle or maximum phase change. It is natural to expect this property can be used to measure a unknown refractive index as in the prism case. Since the phase change leads to polarization state change, we need to modify the configuration properly to detect it. Considering Figure 4, without plotting the hemi-circle boundary, there are two polarizers added outside the material, and the Jones matrices [16] are employed to analyze the polarization change. As shown in the figure, the light wave is incident along the z direction. There are two polarizers, P1 and P2, which make the angle and respect their local x coordinate, respectively. The Jones matrices indicated at the bottom of the figure for P1, TIR, and P2 are , , and , respectively. Since we need to polarize the light beam at to gain , we can assume, without losing generality, that the Jones vector of the incident light field is , a unit vector also polarized at and the T in the superscript is a transport operation. Using the cascade matrices manipulation, the output field is
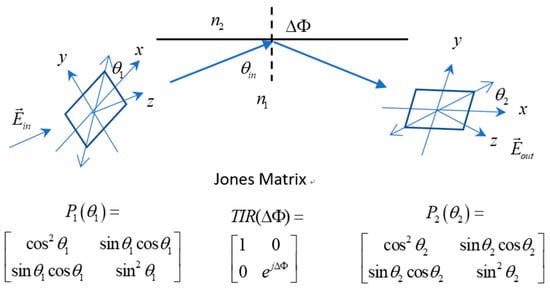
Figure 4.
Configuration, coordinates, and Jones matrices of each element.
Finally, we can obtain the output intensity as follows:
It is noted that when of P2 is at the angle of 450 or 1350, the output intensities are denoted as or , respectively.
Taking measurement as an example, if we keep increasing the incident angle from and detect the intensity , it reaches its maximum when , as can be seen from Figure 3b and Equation (9). This behavior is shown in Figure 5.
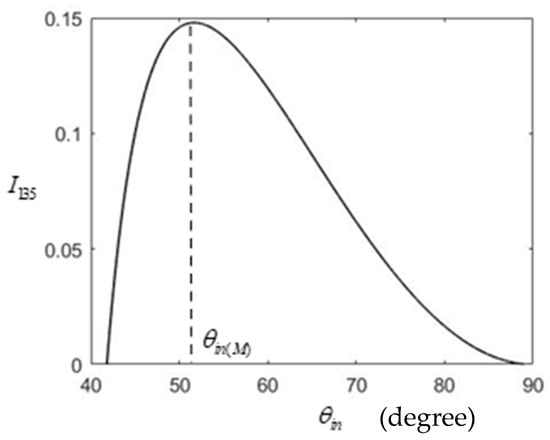
Figure 5.
Plot of output intensity versus for the case of n = 2/3.
Consequently, by varying the incident angle, the maximum of can be reached to determine , and the right half of Equation (6) can be used to calculate n as
Since is the refractive index ratio, we need to know the of the surrounding medium. If we take for air, the material’s refractive index is . This is compared with the scheme that determines the refractive index by finding the critical angle, which is not easy to exactly determine. This method works well by finding , which should be easier to determine more precisely because this angle is usually not close to the critical angle. It is noted that a previous work [17] calculated the refractive index by measuring the maximum phase change. They used a polarization camera to detect it. In our scheme, the refractive index is calculated from the incident angle that gives maximum phase change. Their method utilized a more complicated setup, but it can reach high accuracy. Our measurement configuration is simpler, and the precision depends on the resolution of the rotation stage and the intensity detector.
2.3. Method for Measuring Ellipticity of TIR (without Scanning the Incident Angle)
In the last section, we successfully find the refractive index by looking for the incident angle that gives maximum phase change in TIR. This is similar to the method in Section 2.1, which looks for the incident angle that gives the minimum deviation angle. In this section we would like to introduce another possibility in which no incident angle scanning is necessary. This method may be considered an advanced or improved version. This scheme can be seen by examining Equation (5), giving that phase change only depends on the incident angle and the index ratio . Thus, it is possible to find if can be found for a given without using a phase meter or an interferometer. Let us show how it proceeds.
As shown in Figure 4 and Equation (9), this configuration can be used to measure and by simply rotating the of P2 to 45 and 135 degrees, respectively. Note that by taking the square root of the ratio / and using Equation (5), we have
where is the ellipticity of the polarization ellipse shown in Figure 3a. The ellipticity is defined as the ratio of the short axis to the long axis of the polarization ellipse of the field, which is the ratio of field amplitude taken at 1350 and 450, respectively. After finding at any selected incident angle , the refractive index ratio, from Equation (11), is obtained as
Thus, the material refractive index can be determined. The advantage of this method is that we do not need to vary the incident angle to find n. However, it is suggested to select the incident angle carefully to have a larger value (i.e., bigger ), in order to increase the signal intensity or S/N ratio.
2.4. Dispersion Measurement with Polychromatic Light
In the last section, we present a scheme for obtaining the refractive index by finding the ellipticity of the polarization. Here, we would like to show how to use this feature to obtain the dispersion of the material by employing a polychromatic source [18]. It is known that material dispersion is a property such that the refractive index depends on the wavelength of the incident light wave, i.e., the refractive index is actually a function of wavelength , written as from now on. Considering that we can prepare an incident flat-top spectrum in the dispersion interval of interest from to , as shown in Figure 6. As illustrated in Figure 7, it is incident into a material with and with ; thus, the index ratio is . Initially, this spectrum is polarized at 450 as in the last section; however, because of the material dispersion, each wavelength component experiences a different amount of the polarization change . Consequently, the output spectrum has different ellipticity of polarization ellipse for different wavelengths, as shown in the right of the figure. Similarly, as conducted in the last section, this time, a spectrometer is utilized to detect by setting the polarization angle of P2 to 45 and 135 degrees, and they are denoted as and , respectively. The ellipticity dependence of , as seen in Equation (11), is the square root of the ratio of , that is
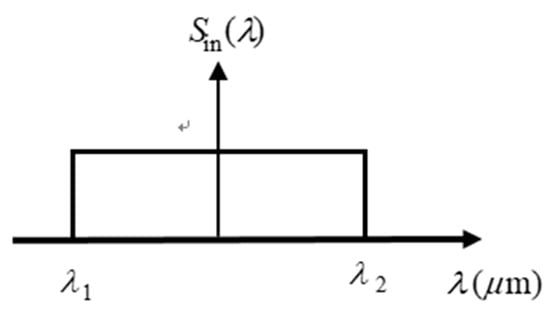
Figure 6.
An incident spectrum with a flat-top distribution.
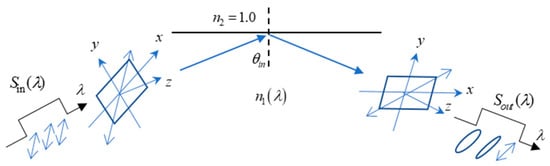
Figure 7.
Schematic for the illustration of polarization ellipse change for different spectrum wavelength components.
Consequently, as in Equation (12), the dispersion of the material is
3. Conclusions and Discussion
Several original schemes were proposed to measure the refractive index n of a material based on the TIR. After reviewing the traditional prism method by looking for the minimum deviation incident angle, our first scheme illustrated how n could be determined by measuring the maximum phase change angle. This can be achieved because a valuable relationship between the incident angle and n is established when the maximum phase change occurs. Compared to the prism method, the advantage of the proposed method is that the apex angle is not needed. The second method we suggested determines the refractive index by measuring the TIR polarization ellipticity at an arbitrary incident angle. The merit of this method is that it can save time because the incident angle does not need to be scanned. Another advantage is that the ellipticity comes from the intensity ratio at two different output polarization angles. We do not need to worry about the absolute value of the intensity, which may be affected by some factors such as the partial reflection at the material boundaries or the absorption of the polarizers. The third method determines the material dispersion with a polychromatic light by measuring the polarization ellipticity wavelength dependence. This is a simple way to obtain material dispersion information. Although incident angle scanning is not required, it is still suggested to select it close to the in order to have a larger ellipticity value. It is noted that the above schemes can work only if the output intensities can be detected well (i.e., signal-to-noise ratio is high enough). Since there is no loss in the TIR and the Fresnel losses at the boundaries are ignored, material absorption is the only factor that affects the output intensities. Thus, a highly transparent material with lower absorption and smaller thickness is more favorable to utilizing these methods.
Finally, we may say something about the accuracy or the precision of above-mentioned schemes. Our methods depend on how accurately or precisely the angle or a specified angle can be measured; thus, the uncertainty comes mainly from the precision of the rotation stage varying or selecting the incident angle. It is helpful to estimate this effect based on some available information from existing products or from published works. First, we need to know how the uncertainty of the angle measurement propagates and affects that of the refractive index calculation. From Equation (11), we have
where is assumed in deriving Equation (15). Now, considering the usual transparent glass with a refractive index in the range of 1.4–1.7, the falls within the interval of 45–55 degrees, which makes the term in front of in Equation (15) have a value of about 1.6–2.4. This means that the uncertainty in the refractive index of the glass is in about the same order as the uncertainty in the incident angle measurement (in radians). If we take a rotation stage (BOCIC MRS-101, used in reference [5]) with precision about degree ( radian) as an example, the refractive index uncertainty is also about , which is comparable to the result in ref citation [5]. Of course, for real experiments, the uncertainty in the polarizer angle and repeatability should also be considered.
The second uncertainty may come from the precision of the detector, or the sensor used that judges if the maximum of is reached in the first method. In the second method, it is the accuracy of the polarization ellipticity (i.e., the intensity values of and ) affecting that of the index measurement. In the third scheme, a spectrometer is utilized to measure the spectrum to infer the dispersion message; thus, the accuracy of the spectrometer should be taken into account. To sum up, this work introduced some advantageous schemes to measure the refractive index or material dispersion, which should be of interest to the related fields.
Author Contributions
Conceptualization, J.-P.C. and P.H.; methodology, C.-M.T.; validation, J.-H.W.; data curation, C.-M.T.; writing—original draft preparation, J.-P.C.; writing—review and editing, P.H.; and funding acquisition P.H. All authors have read and agreed to the published version of the manuscript.
Funding
This work was supported by the Ministry of Science and Technology (MOST) of Taiwan under contract numbers MOST 111-2221-E-005-033-MY2 and 112-2221-E-005-086-MY2.
Data Availability Statement
Data are contained within the article.
Acknowledgments
The authors are grateful for all the support and discussion from Donati Silvano and Sabina Merlo in University of Pavia. Also, we would like to express our thanks for the support from National Chung Hsing University.
Conflicts of Interest
The authors declare no conflicts of interest.
References
- Singh, S. Refractive index measurement and its applications. Phys. Scr. 2002, 65, 167–180. [Google Scholar] [CrossRef]
- Cardin, J.; Leduc, D. Determination of refractive index, thickness, and the optical losses of thin films from prism-film coupling measurements. Appl. Opt. 2008, 47, 894–900. [Google Scholar] [CrossRef] [PubMed]
- Choi, H.J.; Lim, H.H.; Moon, H.S.; Eom, T.B.; Ju, J.J.; Cha, M. Measurement of refractive index and thickness of transparent plate by dual-wavelength interference. Opt. Express 2010, 18, 9429–9434. [Google Scholar] [CrossRef] [PubMed]
- Pedinoff, M.E.; Braunstein, M.; Stafsudd, O.M. Refractive indices of ir materials: 10.6-μm ellipsometer measurements. Appl. Opt. 1977, 16, 2849–2856. [Google Scholar] [CrossRef] [PubMed]
- Hu, Y.; Lv, J.; Hao, Q. Refractive Index Measurement of Glass with Arbitrary Shape Based on Brewster’s Law and a Focusing Probe Beam. Sensors 2021, 21, 2421. [Google Scholar] [CrossRef] [PubMed]
- Song, W.; Yang, F.; Min, C.; Zhu, S.; Yuan, X. Toward Ultrasensitive, Broadband, Reflection-Mode In Vivo Photoacoustic Microscopy Using a Bare Glass. Laser Photonics Rev. 2022, 17, 2200030. [Google Scholar] [CrossRef]
- Yuan, H.; Yang, F.; Song, W.; Yuan, X. Optical Microscopic Evanescent Sensing of Ultrasound with Ultrabroad Bandwidth. IEEE Sens. J. 2024, 24, 7663–7670. [Google Scholar] [CrossRef]
- Ash, W.M.; Kim, M.K. Digital holography of total internal reflection. Opt. Express 2008, 16, 9811–9820. [Google Scholar] [CrossRef] [PubMed]
- Keuren, E.R.V. Refractive index measurement using total internal reflection. Am. J. Phys. 2005, 73, 611–614. [Google Scholar] [CrossRef]
- Calhoun, W.R.; Maeta, H.; Roy, S.; Bali, L.M.; Bali, S. Sensitive real-time measurement of the refractive index and attenuation coefficient of milk and milk-cream mixtures. J. Dairy Sci. 2010, 93, 3497–3504. [Google Scholar] [CrossRef] [PubMed]
- Li, H.; Xie, S. Measurement method of the refractive index of biotissue by total internal reflection. Appl. Opt. 1996, 35, 1793–1795. [Google Scholar] [CrossRef] [PubMed]
- Iizuka, K. Elements of Photonics; Wiley: Hoboken, NJ, USA, 2002; Volume 1, pp. 164, 137, 138. [Google Scholar]
- Chiu, M.H.; Lee, J.Y.; Su, D.C. Refractive-index measurement based on the effects of total internal reflection and the uses of heterodyne interferometry. Appl. Opt. 1997, 36, 2936–2939. [Google Scholar] [CrossRef] [PubMed]
- Zhou, Y.; Zou, H.; Zhong, L.; Li, J.; Li, B.; Tian, J.; Lu, X. Dynamic refractive index distribution measurement of dynamic process by combining dual-channel simultaneous phaseshifting interferometry and total internal reflection. Sci. Rep. 2018, 8, 15231. [Google Scholar] [CrossRef] [PubMed]
- Hecht, E. Optics, 4th ed.; Addison Wesley: Boston, MA, USA, 2002; p. 188. [Google Scholar]
- Teich, M.; Saleh, B. Fundamentals of Photonics, 2nd ed.; Wiley: Hoboken, NJ, USA, 2007; p. 203. [Google Scholar]
- Lee, J.Y.; Chiang, C.Y.; Sung, W.Y.; Weng, T.Y.; Chen, J.H.; Hsu, C.C. Measurement of the refractive index of lenses from the maximum phase difference of the total internal reflection with a polarization camera. Appl. Opt. 2021, 60, B106–B112. [Google Scholar] [CrossRef] [PubMed]
- Han, P. Spatial–Spectral Correspondence Relationship for Mono—Poly chromatic Light Diffraction. In Progress in Optics; Visser, T.D., Ed.; Elsevier: Amsterdam, The Netherlands, 2018; Volume 63, pp. 33–87. [Google Scholar]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).