Simulation Study of Localized, Multi-Directional Continuous Dynamic Tailoring for Optical Skyrmions

Abstract

The topological properties of optical skyrmions have enormous application value in fields such as optical communication and polarization sensing. At present, research on optical skyrmions focuses primarily on the topological principles of skyrmions and their applications. Nonetheless, extant research devoted to skyrmion-array manipulation remains meager. The sole manipulation scheme has a limited effect on the movement direction of the whole skyrmion array. Based on the interference principle of the surface plasmon polariton (SPP) wave, we propose an upgraded scheme for the tailoring of electric-field optical skyrmions. A distributed Gaussian-focused spots array is deployed. Unlike the existing manipulation, we customize the phase of the light source to be more flexible, and we have discovered optical-skyrmion tailoring channels and shaping channels. Specifically, we move the skyrmions within the channel in both directions and manipulate the shape of the topological domain walls to achieve customized transformation. This work will evolve towards a more flexible regulatory plan for tailoring optical-skyrmion arrays, and this is of great significance for research in fields such as optical storage and super-resolution microimaging.

1. Introduction

Magnetic skyrmions have topologically stable spin structures; these can be characterized by skyrmion number and they are classical solutions of the Sigma model [1]. As early as 1962, the British scientist Tony Skyrme predicted their existence and they have subsequently been discovered in fields such as quantum Hall ferromagnets [2], single-layer ferromagnets [3], Bose–Einstein condensate [4], etc. This has demonstrated an active relationship between condensed matter systems and magnetic skyrmions. The photoinduced nucleation of magnetic skyrmion can be localized about their lateral position in a thin magnetic film [5]. Their unique dynamic response in the external field affords possibilities for application in spintronic devices [6]. Magnetic skyrmions evince valuable characteristics such as high speed [7], high density [8], stable topological structure and low current drive [9].

In recent years, with the rapid development of topological photonics, condensed-matter physical phenomena, such as the quantum spin Hall effect [10], have been discovered in the field of optics [11]. In turn, this demonstrates that, in comparison with electronic systems, photon systems have higher design and control flexibility [12]. In particular, proposals and research regarding optical skyrmions are of great significance and they have become an important branch of structured light-field [13] control.

Initially, researchers at the Israel Institute of Technology utilized the interference of SPP waves to achieve an optical skyrmion lattice with an electric-field vector, and this conformed to the standard, Néel–type skyrmion characteristics [14]. The research group led by Yuan Xiaocong at Shenzhen University, meanwhile, has successfully used optical skyrmions to characterize the transverse spin vector in near-field vortex evanescent waves [15]. Since then, research on optical skyrmions has rapidly developed. Bai et al., for instance, used finite–difference time–domain (FDTD) simulation to investigate the deformation and movement of SPP optical skyrmions under hexagonal grating phase distribution [16]. Lin et al., moreover, utilized the phase diagram of a spatial light modulator (SLM) to achieve high-precision translation of near-field spin–vector optical skyrmions, while maintaining the same skyrmion type [17] and while utilizing a dielectric particle metal-film structure to achieve transverse and longitudinal spin imaging. In addition, a method for mapping the Stokes vector, describing the polarization state of light to the Poincaré sphere, can also be used to construct optical skyrmions [18]. Regarding the dynamic characteristics of optical skyrmions on the time scale, the dynamic characteristics of electric-field spin textures were demonstrated via PEEM technology [19]. The 2PPE–PEEM technology was used to perform high spatiotemporal resolution ultra-fast vector imaging of electric-field optical skyrmion arrays [20].

Nonetheless, the existing manipulation for tailoring skyrmions has limitations. Aside from evincing fewer directions of movement, optical skyrmions manipulated in local fields are all whole bodies. Moreover, they cannot move relative to each other and cannot be independently manipulated. This presents limitations for the application of topology control diversity. Therefore, this study proposes an upgrade scheme, given that the vector light field of multiple 4F systems can customize the excitation–focused spots [21]. We have completed distributed multi–pair of focused spot excitation, where every pair of spots is arranged on hexagonal slits symmetrically and can be used to control the shape and motion of optical skyrmions independently. We use Finite–Difference–Time–Domain (FDTD) software (FDTD Solutions 2016a) to simulate and verify the flexible manipulation. Our research can further improve the control of electric–field optical skyrmions, providing ideas for high–density information storage [22] and polarization sensing [23].

2. Structure Design and Principle Analysis

In this article, the electric-field skyrmion lattice, as the solution to Maxwell’s equations, can be seen as a result of the superposition of SPP wave interference. Generally, we assume that a Gaussian beam is vertically focused along the Z–axis, on a hexagonal slit in the transverse plane, and the intensity of the electric-field component of Z–axial decays. The wave number in this propagation direction is k_z, the transverse-plane wave number is k_|| and the free–space wave number is k₀. The relationship satisfies the following equation: k_z² + k_||² = k₀². Our simulation meets the following two assumptions: the magnitude of the electric field is far larger than the imaginary part with relatively small losses in most systems; in addition, the area in which we examine the field should be far smaller than the propagation length of the SPP waves and that the real part of the transverse–plane wave dominates. Therefore, within the frequency domain range, the total electric field of finite N pairs of interference wave can be expressed as Equation (1) [14]:

$${\overrightarrow{E}}^{\left(\omega \right)}=\left[\begin{array}{c}{E}_x^{\left(\omega \right)}\\ E_y^{\left(\omega \right)}\\ E_z^{\left(\omega \right)}\end{array}\right]=E_o{e}^{-ikz}{\displaystyle \sum _{n=1}^N\left[\begin{array}{c}i\frac{k_z\cos \left({\theta }_n\right)}{k_{\left|\right|}}\sin \left(k_{\left|\right|}\right)\left[x\cos \theta +y\sin \theta \right]\\ i\frac{k_z\sin \left({\theta }_n\right)}{k_{\left|\right|}}\sin \left(k_{\left|\right|}\right)\left[x\cos \theta +y\sin \theta \right]\\ \cos \left(k_{\left|\right|}\right)\left[x\cos \theta +y\sin \theta \right]\end{array}\right]}$$

(1)

The x, y and z cited above are three Cartesian coordinates. Meanwhile, θ signifies the angular coordinates of the column coordinate system and ${\theta }_m$ represents the angular coordinates of different pairs of SPP waves (m = 1, 2, 3, …). Considering the phase ${\varphi }_n$ of each excited focused spot reaching the position of six slits, the polarization direction of each pair of focused spots introduces a phase difference of $-\pi$. The charge distribution has an additional phase π on both sides of the centrally symmetrical slits. The total field, above, takes the SPP phase into account and Equation (1) becomes ${{\overrightarrow{E}}_{x,y}}^{\left(\omega \right)}{e}^{i{\psi }_{{spp}_n}}$. As regards the Z-axial, there is no phase of SPP waves. Due to the fact that N (N = 2 m) is an even number and the value of N is important in this paper, it cannot solely determine the flexibility of optical skyrmion modulation; it also cannot violate the actual size of the focused spot. According to the above definition, Equation (1) can be further expressed as Equation (2):

$${\overrightarrow{E}}^{\left(\omega \right)}=\left[\begin{array}{c}{E}_x^{\left(\omega \right)}\\ E_y^{\left(\omega \right)}\\ E_z^{\left(\omega \right)}\end{array}\right]=E_o{e}^{-ikz}{\displaystyle \sum _{n=1}^N\left[\begin{array}{c}i\beta \frac{k_z\cos \left({\theta }_n\right)}{k_{\left|\right|}}\sin \left(k_{\left|\right|}\right)\left[x\cos \theta +y\sin \theta \right]e^{i{\psi }_{sp{p}_n}}\\ i\beta \frac{k_z\sin \left({\theta }_n\right)}{k_{\left|\right|}}\sin \left(k_{\left|\right|}\right)\left[x\cos \theta +y\sin \theta \right]e^{i{\psi }_{sp{p}_n}}\\ \cos \left(k_{\left|\right|}\right)\left[x\cos \theta +y\sin \theta \right]\end{array}\right]}$$

(2)

where $\beta$ is a constant in Equation (2), while the components of the X-axis and components of the Y-axis of the electric field in Equation (2) are further simplified into Equation (3), based on the Euler formula and trigonometric function.

$${\overrightarrow{E}}^{\left(\omega \right)}=E_o{e}^{-ikz}{\displaystyle \sum _{n=1}^{2m}\left[\begin{array}{c}i\beta \frac{k_z\cos \left({\theta }_n\right)}{k_{\left|\right|}}\sin \left(k_{\left|\right|}\right)\left[x\cos \theta +y\sin \theta \right]\cos \left(\frac{{\psi }_{sp{p}_{m,1}}-{\psi }_{sp{p}_{m,2}}}{2}\right)\exp i\left(\frac{{\psi }_{sp{p}_{m,1}}+{\psi }_{sp{p}_{m,2}}}{2}\right)\\ i\beta \frac{k_z\sin \left({\theta }_n\right)}{k_{\left|\right|}}\sin \left(k_{\left|\right|}\right)\left[x\cos \theta +y\sin \theta \right]\cos \left(\frac{{\psi }_{sp{p}_{m,1}}-{\psi }_{sp{p}_{m,2}}}{2}\right)\exp i\left(\frac{{\psi }_{sp{p}_{m,1}}+{\psi }_{sp{p}_{m,2}}}{2}\right)\\ \cos \left(k_{\left|\right|}\right)\left[x\cos \theta +y\sin \theta \right]\end{array}\right]}$$

(3)

From the derivation results in the equation above, one finds that the electric-field vector intensity of the SPP interference field is affected by the phase of each distributed focused spot [24]. By controlling the phase of the N (N = 2 m) distributed focused spots, one may also control the state of the skyrmion lattice at the center of the transverse plane, and this effect is independent. Meanwhile, ${spp}_{m,1}$ represents one of the two interference waves in one group of two distributed focused spots, and ${spp}_{m,2}$ correspondingly represents the other.

In theory and brief, one may state that only the phase difference of one pair of focused spots needs to change among all the pairs, while the other phases remain initialized to the value of 0. The optical–skyrmion electric field is still modulated, and clearly, this result varies with the different phase-distribution designs of the laser-focused spots at the excitation points. In Section 3, this paper provides detailed information on different allocation schemes. The movement of optical skyrmions is regular, with both commonality and difference, and this is significantly different from the reported control of electric-field optical-skyrmion arrays. Our distributed phase-modulation scheme has the advantage that when a single spot size is perfectly coupled with the slit, or when an infinite number of pairs of focused spots are densely arranged in the slit, the convergence result is essentially the overall modulation of the local optical skyrmion field. Nonetheless, the general form of the latter is our modulation scheme and, evidently, our scheme can customize more modulation directions and topological domain walls. The optical skyrmions have a stable spin structure and their topological essence derives from the size of the skyrmion number, which is a real number.

A is the integral region of a two–dimensional plane, while the electric field in Equation (4) can be expressed as Equation (5). We simplify Equation (5) by substituting it into Equation (4), resulting in Equation (6). We map the distribution of the defined electric-field vector [25] onto a unit sphere, the skyrmion-number integral formula can be simplified as the product of the polarity P and vorticity M of two physical quantities [26]. With consideration of generality, the result of normalization of the real part of the electric-field vector is defined in Equation (5):

$$S=\frac{1}{4\pi }{\displaystyle \underset{A}{\int }\left[\overrightarrow{\mathrm{e}}\cdot \left(\frac{\partial \overrightarrow{\mathrm{e}}}{\partial x}\times \frac{\partial \overrightarrow{\mathrm{e}}}{\partial y}\right)\right]}dA$$

(4)

$$\overrightarrow{\mathrm{e}}=\frac{\mathrm{Re}\left[E_x^{\left(\omega \right)},E_y^{\left(\omega \right)},E_z^{\left(\omega \right)}\right]}{\sqrt{{E_x^{\left(\omega \right)}}^2+{E_y^{\left(\omega \right)}}^2+{E_z^{\left(\omega \right)}}^2}}=(\cos \alpha (\varphi )\sin \beta (r),\sin \alpha (\varphi )\sin \beta (r),\cos \beta (r))$$

(5)

$$\begin{array}{l}S=\frac{1}{4\pi }{\displaystyle \iint \frac{d\beta (r)}{dr}}\frac{d\alpha (\varphi )}{d\varphi }\sin \beta (r)drd\varphi \\ =\frac{1}{4\pi }{\displaystyle \underset{0}{\overset{r_o}{\int }}drd\varphi }{\displaystyle \underset{0}{\overset{2\pi }{\int }}\frac{d\beta (r)}{dr}\frac{d\alpha (\varphi )}{d\varphi }\sin \beta (r)}\\ =\frac{1}{4\pi }{\left[\cos \beta (r)\right]}_{r=0}^{r=r_o}{\left[\alpha (\varphi )\right]}_{\varphi =0}^{\varphi =2\pi }\\ \underset{\frac{1}{2\pi }{\left[\alpha (\varphi )\right]}_{\varphi =0}^{\varphi =2\pi }=M}{\overset{\frac{1}{2}{\left[\cos \beta (r)\right]}_{r=0}^{r=r_o}=P}{\to }}\\ =P\cdot M\end{array}$$

(6)

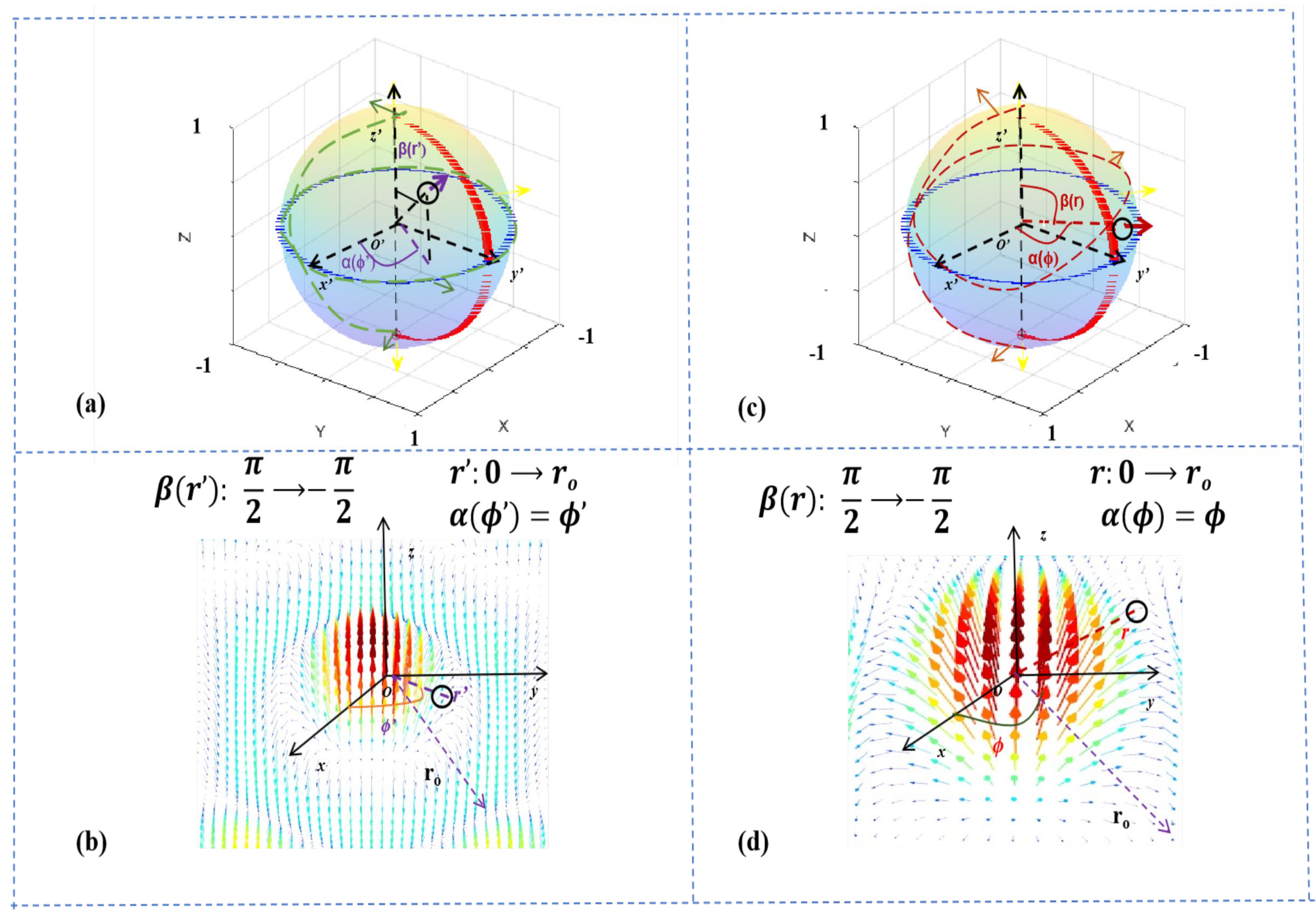
More specifically, the skyrmions vector is three–dimensional; we define the projection of the three–dimensional skyrmions vector on the XY transverse plane in Figure 1b,d: $\varphi$ is the angular coordinate of the electric field vector projection, and r is the radial coordinate of the electric field vector projection. The r_o is the distance from the center of the skyrmions to the edge. The vector mapped onto the unit sphere is closely related to the electric field vector. Firstly, the vector on the unit sphere is also three-dimensional and the angular coordinates $\mathsf{\alpha }$ of the unit sphere vector projected onto the X’Y’ plane depend on $\varphi$. Especially for the optical skyrmions in our simulation, the relationship is clear: $\alpha \left(\varphi \right)=\varphi$. However, for different radial coordinates r away from the center of the skyrmion, there is a significant change in the angle between the skyrmion vector and the positive Z–axis. In addition, it can be determined that the angle $\beta \left(r\right)$, which is the angle between the mapped unit sphere vector and the positive Z’–axis is equal to the angle between the skyrmion vector and the positive Z–axis.

For the simulated skyrmion array, different topological domain walls were generated during the manipulation, such as the hexagonal Néel–type optical skyrmion in Figure 1b and the deformed Néel–type optical skyrmion in Figure 1d. According to Equation (4), we cannot find the exact and convergent integration region very well. Therefore, we attempt to use the method of mapping the skyrmion vectors and approximate the skyrmion number. Strictly, each skyrmion vector in Figure 1b,d corresponds to the unit sphere vector in Figure 1a,c. The angle between the unit sphere vector and the positive Z’–axis flips from $0.5\mathsf{\pi }$ to $-0.5\mathsf{\pi }$, and the angular direction of the unit sphere vector surrounds a circumference. The green dashed line in Figure 1a and the red dashed line in Figure 1c indicates that this mapping relationship allows the unit sphere vector to travel along the surface of the unit sphere accompanied by an uncertain path determined by the shape of topological domain walls, which can be approximated as having a skyrmion number of 1. With the skyrmion–number calculation above, although the optical-skyrmion edge does not evince a standard circle, the generated Néel–type optical skyrmions have topological stability.

3. Simulation and Discussions

3.1. Simulation Set Up

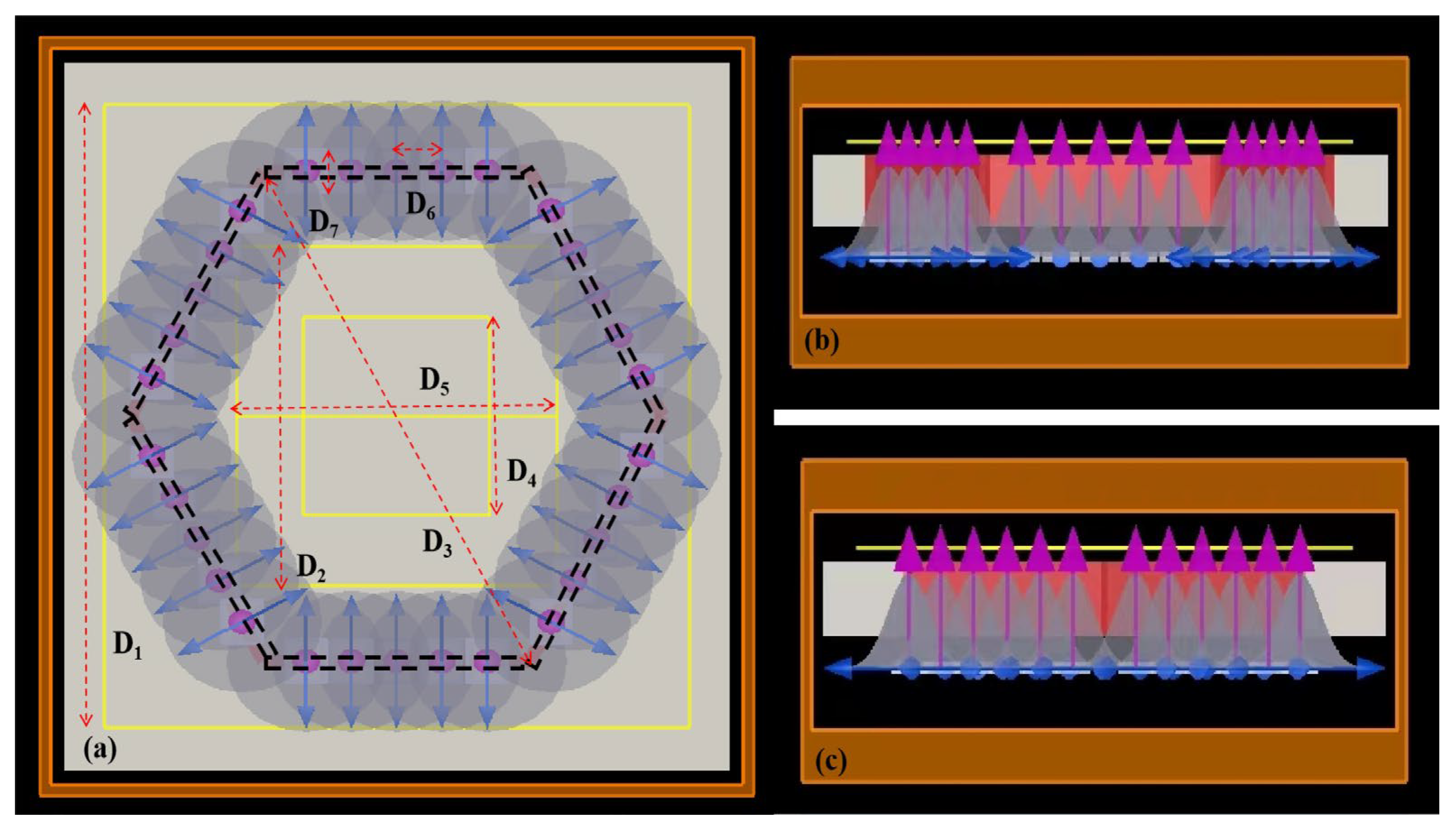
We established the excitation model for SPP optical skyrmions by FDTD software (FDTD Solutions 2016a). Figure 2 depicts the basic mode. The important parameters are as follows: we assume that the diameter of focused spots D₇ is 300 nm and the width of the hexagonal slit to 100 nm, hollowed out on the silver surface with a thickness of 120 nm. The length 0.5D₃ of the slit is defined as $2 \mathsf{\mu }\mathrm{m}$. The slit is surrounded by distributed focused spots, the phases of which are independently controlled. The size of adjacent focused spots (D₆–D₇) is separated by 40 nm at the edge and the incident light wavelength is 632.8 nm; all of this is Gaussian linearly polarized light, with a polarization direction perpendicular to the hexagon slit. The height of 30 focused spots are set at the Z-coordinate $-0.05 \mathsf{\mu }\mathrm{m}$. Boundary conditions are PML. D₁, D₂ and D₄ represent the widths of frequency-domain field and power monitors with side lengths of $2.2 \mathsf{\mu }\mathrm{m}$,$1.2 \mathsf{\mu }\mathrm{m}$ and 0.7 $\mathsf{\mu }\mathrm{m}$, respectively. As well as an X–direction line, frequency-domain field and power monitor with a length D₅ of 1.2 $\mathsf{\mu }\mathrm{m}$ were also installed at 20 nm above the silver plate. The planar monitor was used to present the full view of the electric field vector and the energy flux density. The line monitor was used to record the electric field in the front view of an optical-skyrmion lattice in the transverse plane.

Relying on proven theories, we can control multiple parameters of the focused spots, including phase. Therefore, when changing the phase difference of any pair of the 15 pairs of excitation light sources, the phase difference of the corresponding SPP waves can be adjusted.

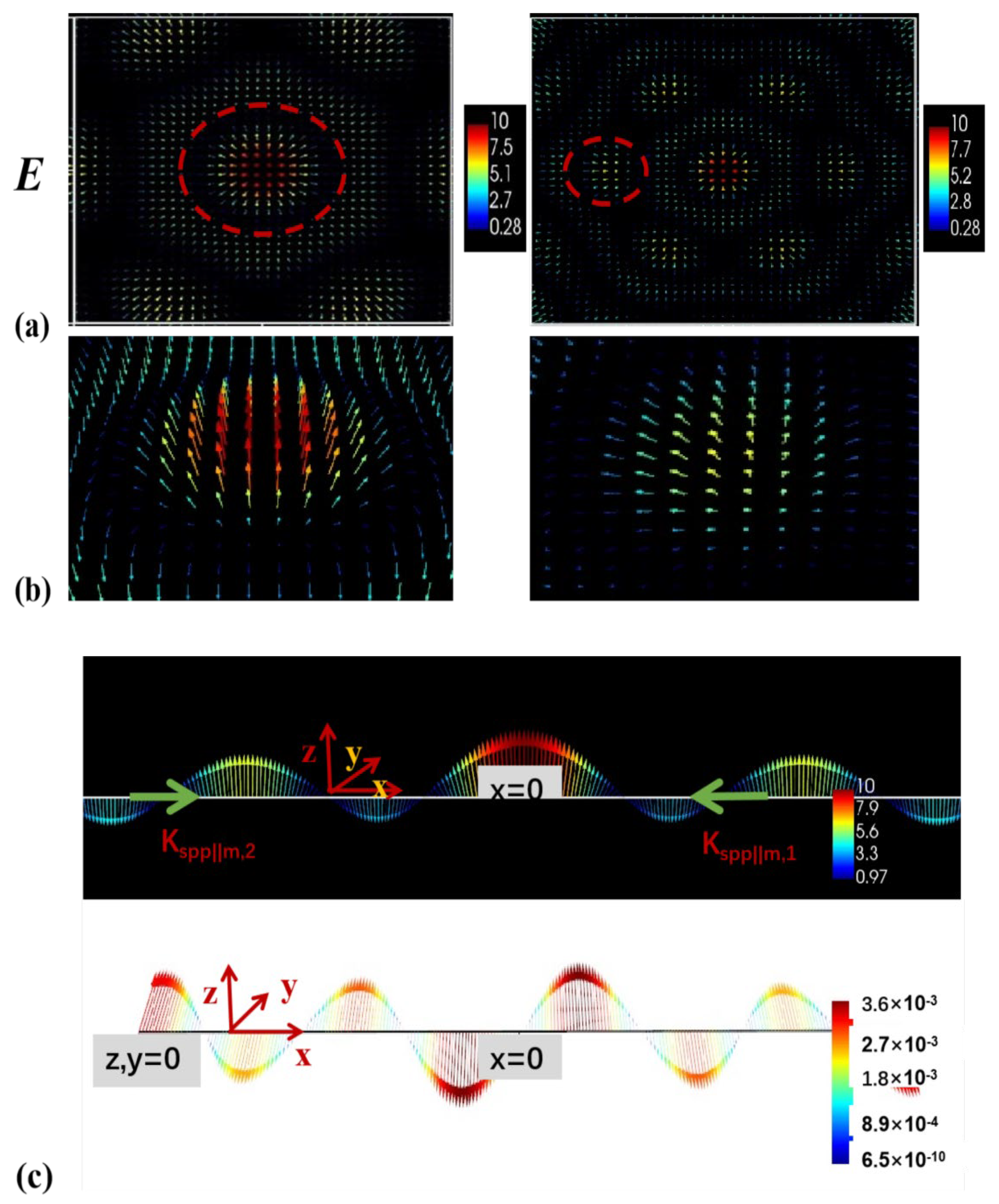
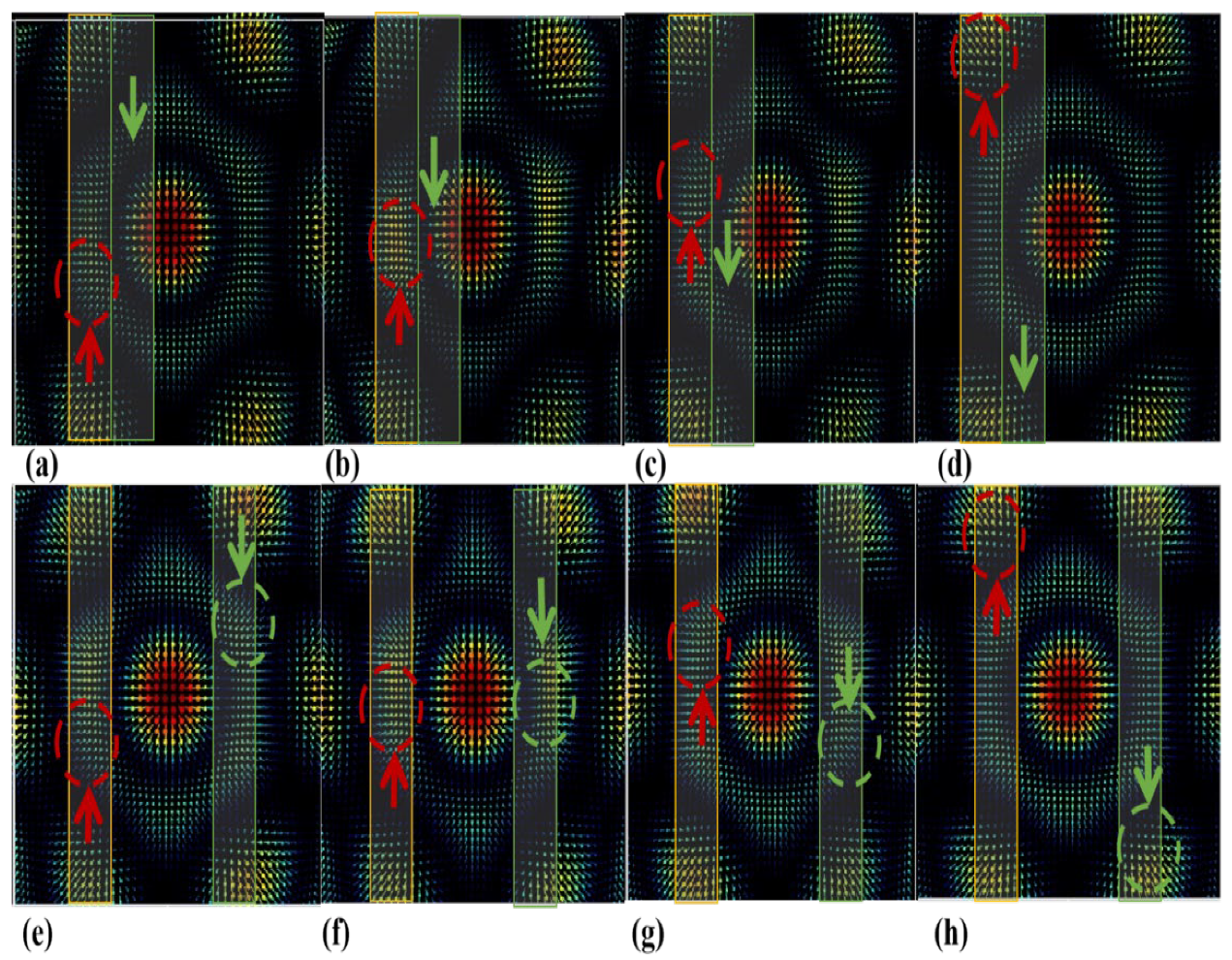
As shown in Figure 3a, a complete optical-skyrmion hexagonal lattice appears at the center of the interference field and each optical skyrmion is well embedded in one unit. In addition, the enlarged image of the optical–skyrmion vector, as circled in Figure 3a, is shown in Figure 3b. The darker the red depth of these vector fields, the greater the electric field strength; conversely, the darker the blue depth, the smaller the electric field strength. The common feature of the vector–field distribution is the flow from inside out and from bottom to top.

In order better to demonstrate the symmetry-reversal characteristics of skyrmion vectors, we observed them using the line monitor, as shown in Figure 3c. It is useful to note that Figure 3c reflects the electric-field distribution in the XZ plane for multiple pairs of SPP standing waves, where any group of standing waves interferes. Nonetheless, due to the transverse wave characteristics of electromagnetic waves, the magnetic field is distributed in the XY plane. Given the skyrmion integral formula cited above, it is evident that the calculated skyrmion vector for the magnetic field is 0. Therefore, the simulated Néel-type optical-skyrmion vector is characterized by an electric-field vector. In addition, we also note that our distributed focused spots can excite SPP optical skyrmions on the surfaces of metals and media: this topology is rigorous in a square area, with a side length of $1.2 \mathsf{\mu }\mathrm{m}$. This vector reversal is strikingly clear in the line-monitor results.

3.2. Parallel Dual-Channel Dynamic Tailoring of Optical Skyrmions

We chose two slits parallel to the X-axis, located above the latter, as the control position. Ten excitation light sources simultaneously excite the two slits. Based on the previous derivation, we designed phase differences for these five groups of distributed multi-light source-focused spots and the tailoring results of two kinds of parallel channels under different phase differences are described in Figure 4.

We unify the definition of the distribution positions of all slits and excitation distributed multi-light source focused spots. Firstly, we designate the first group of slits in the XY plane in a clockwise direction, parallel to the X-axis direction, with a positive Y-coordinate value. Six slits are arranged in a clockwise formation, with each focused spot numbered n. Meanwhile, n is numbered in a clockwise direction, as −2, −1, 0, 1, 2. The middle light source is numbered 0 and other light sources are symmetrically distributed along the middle. The phase of each light source is recorded separately and we have customized the phase-distribution scheme to achieve localized, linear optical-skyrmion tailoring.

Due to the limited number of excitation positions and interference sources, the generated optical-skyrmion lattice can be said to be a sub-array of closely packed lattices. We can understand the linearity as the longitudinal direction of the channel, although it does not affect the topological characteristics and position of the skyrmions. For the purpose of multi-directional regulation, it is necessary to study the relationship of two types of skyrmion channels.

More specifically, without considering the collision of skyrmions in the sub-array during the process of tailoring, the linear direction without skyrmions and the linear direction with skyrmions are related (in their respective ways) to the excitation phase difference.

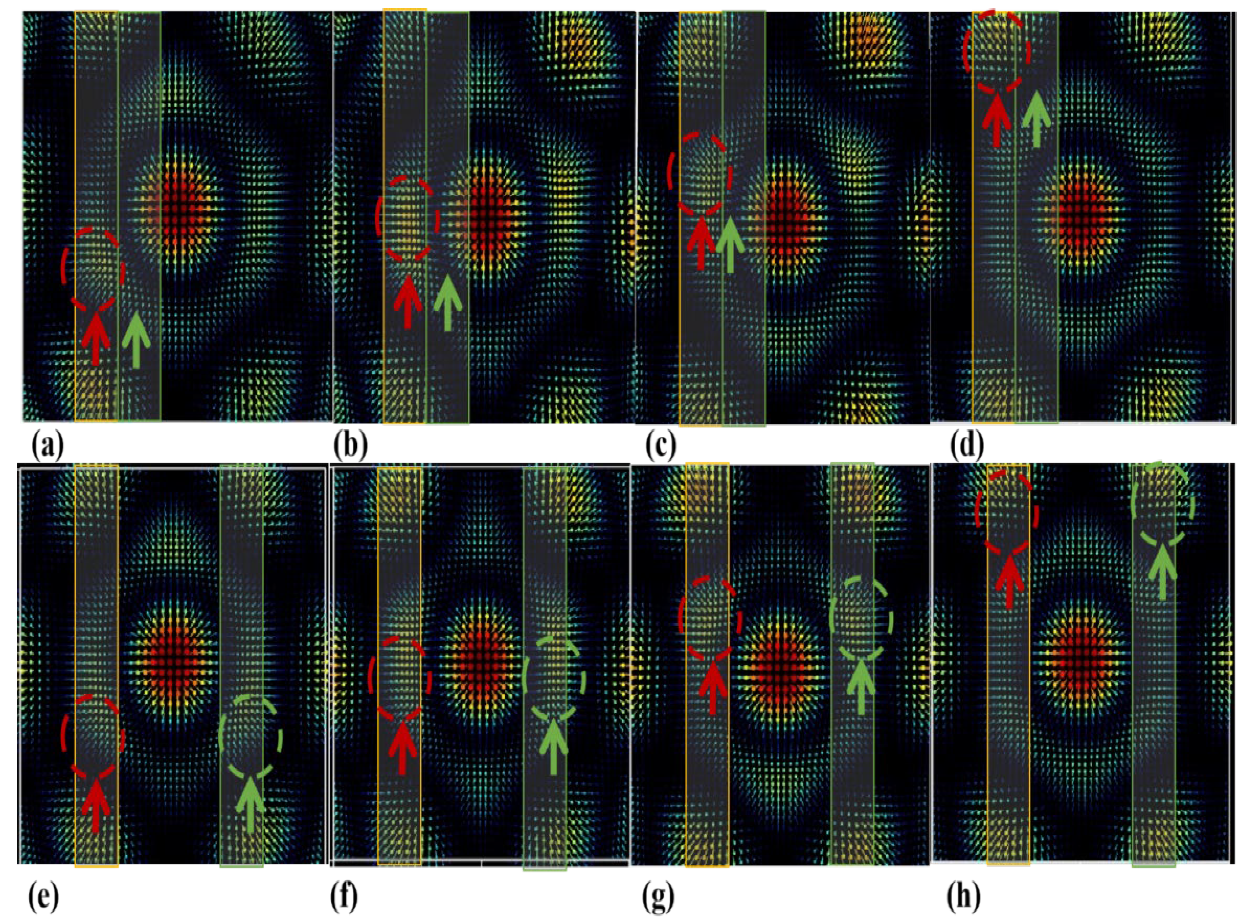
The optical skyrmions in Figure 4 move in a single direction within a width range of about 120 nm. We circle the center of skyrmion motion and when the phase difference acts in the linear direction of the skyrmion distribution, the optical skyrmions move. When the linear direction of the phase difference does not have an optical skyrmion distribution, the phase difference shapes the topological domain walls of optical skyrmions. We use green arrows to indicate the direction of phase difference in this shaped track.

Phases in Figure 4a–d are set as follows: ${\varphi }_{\mathrm{1,0}}-{\varphi }_{\mathrm{4,0}}={\varphi }_{1,-1}-{\varphi }_{4,-1}=0.5\pi$, ${\varphi }_{\mathrm{1,0}}-{\varphi }_{\mathrm{4,0}}={\varphi }_{1,-1}-{\varphi }_{4,-1}=\pi$, ${\varphi }_{\mathrm{1,0}}-{\varphi }_{\mathrm{4,0}}={\varphi }_{1,-1}-{\varphi }_{4,-1}=1.5\pi$, ${\varphi }_{\mathrm{1,0}}-{\varphi }_{\mathrm{4,0}}={\varphi }_{1,-1}-{\varphi }_{4,-1}=2\pi$. The period of motion in the yellow channel is ${\lambda }_{SPP}$, corresponding to the optical skyrmion moving ${0.125\lambda }_{SPP}$, ${0.25\lambda }_{SPP}$, ${0.375\lambda }_{SPP}$, and ${0.5\lambda }_{SPP}$ along the positive Y axis. The length of space in the green channel and the topological domain walls of the middle skyrmion are shaped under the effect of phase difference, followed by downward water droplets, ellipses, upward water droplets and circles. Nonetheless, this shape is not symmetrically positioned around the origin, because it lacks the phase-difference effect of symmetric interference. The lower-left corner of the downward water droplet deforms inwards, while the elliptical, upward water droplets, together with the circular shapes, undergo the same shaping. Phases in Figure 4e–h are set as follows: ${\varphi }_{\mathrm{1,1}}-{\varphi }_{\mathrm{4,1}}={\varphi }_{1,-1}-{\varphi }_{4,-1}=0.5\pi$, ${\varphi }_{\mathrm{1,1}}-{\varphi }_{\mathrm{4,1}}={\varphi }_{1,-1}-{\varphi }_{4,-1}=\pi$, ${\varphi }_{\mathrm{1,1}}-{\varphi }_{\mathrm{4,1}}={\varphi }_{1,-1}-{\varphi }_{4,-1}=1.5\pi$, ${\varphi }_{1,1}-{\varphi }_{4,1}={\varphi }_{1,-1}-{\varphi }_{4,-1}=2\pi$.

The period of motion in the yellow channel is ${\mathsf{\lambda }}_{\mathrm{S}\mathrm{P}\mathrm{P}}$, corresponding to the set of optical skyrmions moving along the positive Y axis of the two channels, with lengths of ${0.125\mathsf{\lambda }}_{\mathrm{S}\mathrm{P}\mathrm{P}}$, ${0.25\mathsf{\lambda }}_{\mathrm{S}\mathrm{P}\mathrm{P}}$, ${0.375\mathsf{\lambda }}_{\mathrm{S}\mathrm{P}\mathrm{P}}$, and ${0.5\mathsf{\lambda }}_{\mathrm{S}\mathrm{P}\mathrm{P}}$. There are optical skyrmions in the linear direction along the Y-axis in the green and yellow channels. Under the action of motion, the topological domain walls of the middle skyrmion are shaped. This is followed by a downward water-droplet shape, an elliptical shape, an upward water-droplet shape and a circular shape, and all shapes are symmetrical around the origin. Therefore, and essentially, the following can be obtained: it is possible to achieve single linear-direction optical-skyrmion tailoring through phase difference customization, and at the same time, the phase difference affects the shape of the topological domain walls within the undistributed skyrmion local range.

In order to render the regulation more general, Figure 5a–d are set as follows: ${\varphi }_{\mathrm{1,0}}-{\varphi }_{\mathrm{4,0}}=0.5\pi ,{\varphi }_{1,-1}-{\varphi }_{4,-1}=-0.5\pi$, ${\varphi }_{\mathrm{1,0}}-{\varphi }_{\mathrm{4,0}}=\pi ,{\varphi }_{1,-1}-{\varphi }_{4,-1}=-\pi$, ${\varphi }_{\mathrm{1,0}}-{\varphi }_{\mathrm{4,0}}=1.5\pi ,{\varphi }_{1,-1}-{\varphi }_{4,-1}=-1.5\pi$, ${\varphi }_{\mathrm{1,0}}-{\varphi }_{\mathrm{4,0}}=2\pi ,{\varphi }_{1,-1}-{\varphi }_{4,-1}=-2\pi$.

The period of motion in the yellow channel is ${\lambda }_{SPP}$, corresponding to the optical skyrmion moving along the positive Y axis, with space lengths of ${0.125\lambda }_{SPP}$, ${0.25\lambda }_{SPP}$, ${0.375\lambda }_{SPP}$, and 0.5${\lambda }_{SPP}$. In the green channel, under the effect of phase difference, the topological domain walls of the middle skyrmion are shaped, in the order of near circular, elliptical, near circular, and circular. The difference from the result in Figure 4a–d lies in the coupling influence of the double-track reverse effect. In line with the aforementioned principle, the phase difference lies in the even-function area, so the positive or negative of the phase difference does not affect the motion result. Firstly, based on the optical-skyrmion motion in the channel, the red circle represents the center position of the optical skyrmion. Secondly, based on the shape of the topological domain walls of the intermediate optical skyrmion, the direction affected by the shaping channel is inferred, as represented by the direction of the green arrow and via the use of the same method. Figure 5e–h are set as follows: ${\varphi }_{\mathrm{1,1}}-{\varphi }_{\mathrm{4,1}}=0.5\pi , {\varphi }_{1,-1}-{\varphi }_{4,-1}=-0.5\pi , {\varphi }_{\mathrm{1,1}}-{\varphi }_{\mathrm{4,1}}=\pi , {\varphi }_{1,-1}-{\varphi }_{4,-1}=-\pi , {\varphi }_{\mathrm{1,1}}-{\varphi }_{\mathrm{4,1}}=1.5\pi , {\varphi }_{1,-1}-{\varphi }_{4,-1}=-1.5\pi , {\varphi }_{\mathrm{1,1}}-{\varphi }_{\mathrm{4,1}}=2\pi , {\varphi }_{1,-1}-{\varphi }_{4,-1}=-2\pi .$

Corresponding to these settings, the optical skyrmions move along the Y-axis of two channels in two directions, with a spatial length of ${0.125\lambda }_{SPP}$, ${0.25\lambda }_{SPP}$, ${0.375\lambda }_{SPP}$ and 0.5${\lambda }_{SPP}$. The linear direction of motion along the Y axis in the green and yellow channels is mutually opposite and the shapes are symmetrical around the origin.

3.3. Multi-Channel Comprehensive Tailoring of Optical Skyrmions

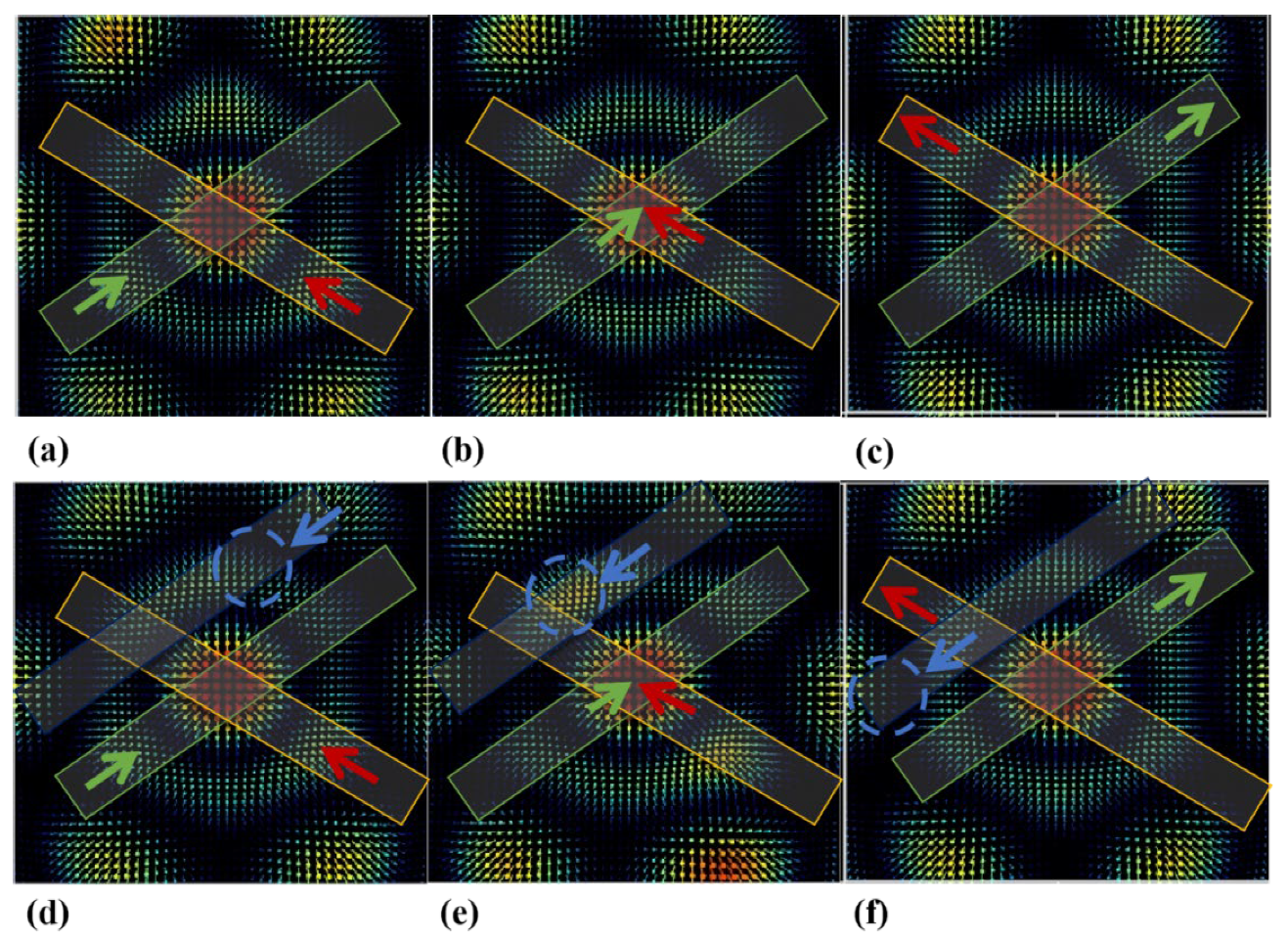
To achieve multi-directional movement of electric-field skyrmions within a local range and a customized design for the shapes of the topological domain walls, we must verify that the above rules remain suitable for both the optical-skyrmion motion channels and the shaping channels, as the direction of movement is concatenated. Figure 6a–c are set as follows: ${\varphi }_{\mathrm{2,0}}-{\varphi }_{\mathrm{5,0}}=0.5\pi , {\varphi }_{\mathrm{3,0}}-{\varphi }_{\mathrm{6,0}}=0.5\pi ; {\varphi }_{\mathrm{2,0}}-{\varphi }_{\mathrm{5,0}}=\pi , {\varphi }_{\mathrm{3,0}}-{\varphi }_{\mathrm{6,0}}=\pi ; {\varphi }_{\mathrm{2,0}}-{\varphi }_{\mathrm{5,0}}=2\pi , {\varphi }_{\mathrm{3,0}}-{\varphi }_{\mathrm{6,0}}=2\pi$.

From the results, one may see that there is no optical-skyrmion motion in either channel range (i.e., as about the skyrmion-shaping channel). In addition, when compared with Figure 4a and Figure 5a, it is found that the topological domain walls of the intermediate optical skyrmion near the channel have undergone significant shaping, changing from the original non-Y-axis symmetry to a flatter shape and moved downward. Figure 6b,c shows the same trend of change. Figure 6d–f is set as follows: ${\varphi }_{\mathrm{2,0}}-{\varphi }_{\mathrm{5,0}}=0.5\pi , {\varphi }_{\mathrm{3,0}}-{\varphi }_{\mathrm{6,0}}=0.5\pi , {\varphi }_{2,-1}-{\varphi }_{5,-1}=-0.5\pi ; {\varphi }_{\mathrm{2,0}}-{\varphi }_{\mathrm{5,0}}=\pi , {\varphi }_{\mathrm{3,0}}-{\varphi }_{\mathrm{6,0}}=\pi , {{\varphi }_{2,-1}-{\varphi }_{5,-1}=-\pi ; \varphi }_{\mathrm{2,0}}-{\varphi }_{\mathrm{5,0}}=2\pi , {\varphi }_{\mathrm{3,0}}-{\varphi }_{\mathrm{6,0}}=2\pi , {\varphi }_{2,-1}-{\varphi }_{5,-1}=-2\pi$.

It can be seen from the results that there is an additional set of skyrmion-motion channels. The center position of the optical skyrmion is circled in blue and the direction of motion is indicated by a blue arrow. It is demonstrated by Figure 6d–f, which shows that when the corresponding excitation-phase difference of the channels is the same, the control direction remains in the same direction; this is the case, even under the combined action of the two types of channel within the cross-channel. The blue channel moves in the opposite direction to the green channel and this conforms to the regulation rule.

4. Conclusions

To conclude, the research team generated SPP electric-field skyrmions by exciting hexagonal slits through a tightly distributed focused-spot array and found that localized linear directions can generate skyrmion tailoring channels. Furthermore, we found that the phase difference not only moves optical skyrmions but also continuously tunes the topological domain walls of optical skyrmions under topological protection conditions in the sub-array. This special channel is referred to as a shaping channel and the direction of action and the independence of operation of these two types of channels are summarized.

As optical skyrmions comprise a new direction [27] for the study of topological quantum states [28], their topological transformations have attracted much attention in the fields of vector holography [29], quantum communication [30], information processing and even in nonquantum systems. Our discovery allows for more precise tailoring of the skyrmion lattice. This may entail the use of position information, as controlled by the optical-skyrmion two-dimensional plane, as complex plane coordinates; encoding of the skyrmion topological domain-wall information in the adjacent shaping channels of the motion channel into multiple discrete values (thereby achieving storage of two-dimensional plane data) or precise labeling of three-dimensional spatial discrete points. Such research has exciting prospects.