Polarimeter Optical Spectrum Analyzer
Abstract
1. Introduction
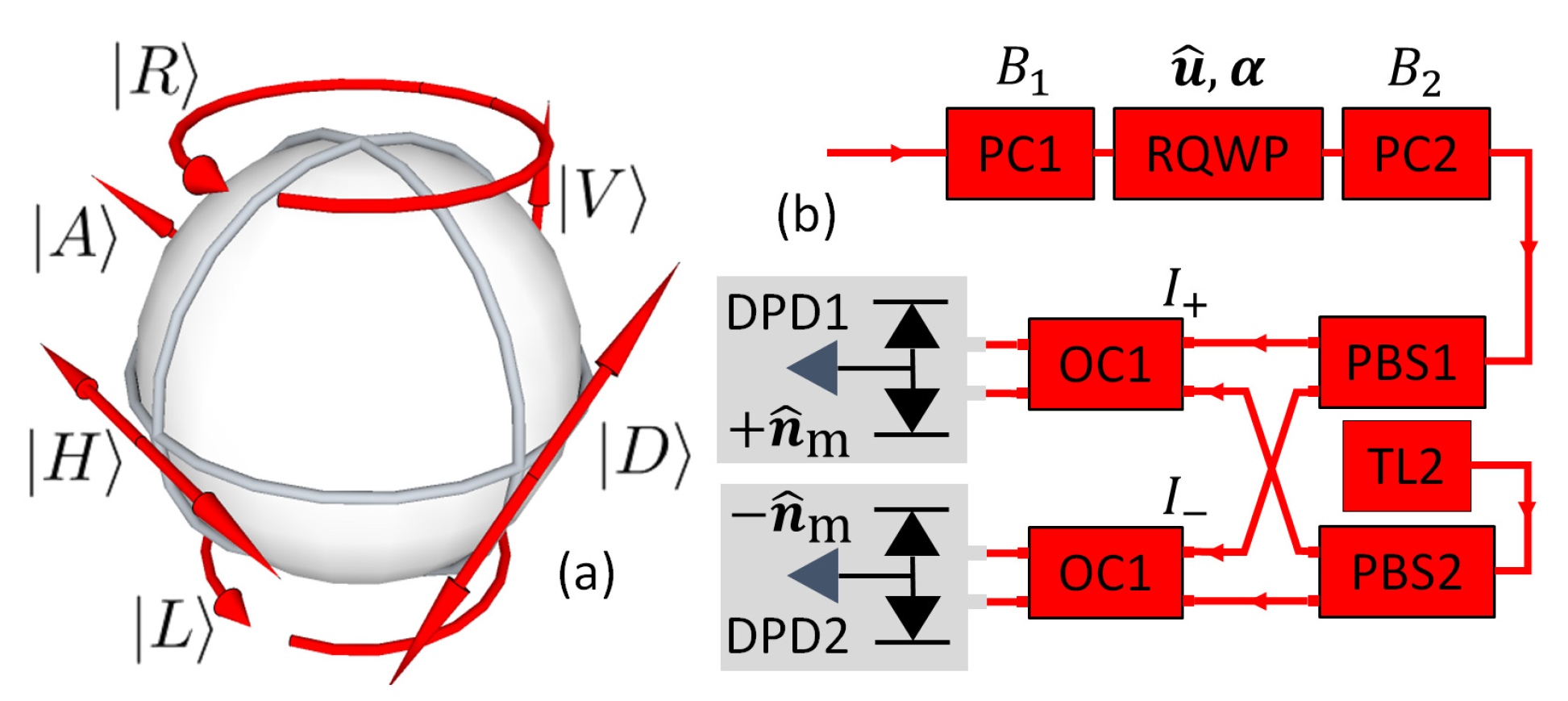
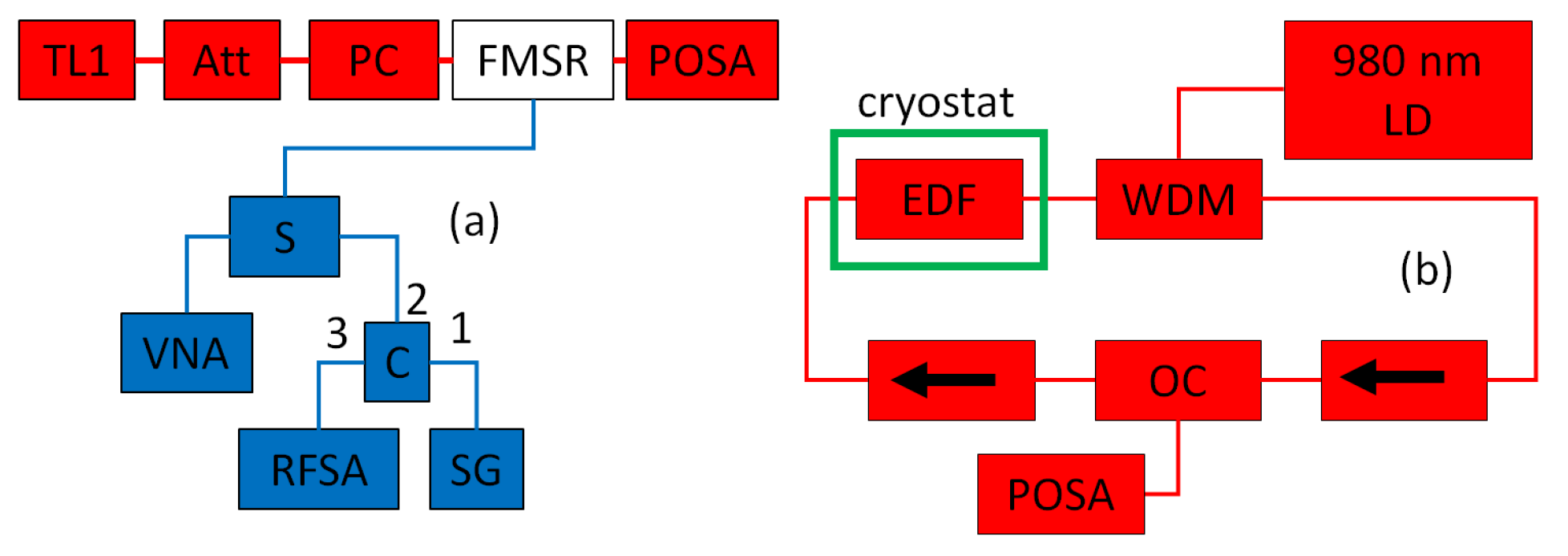
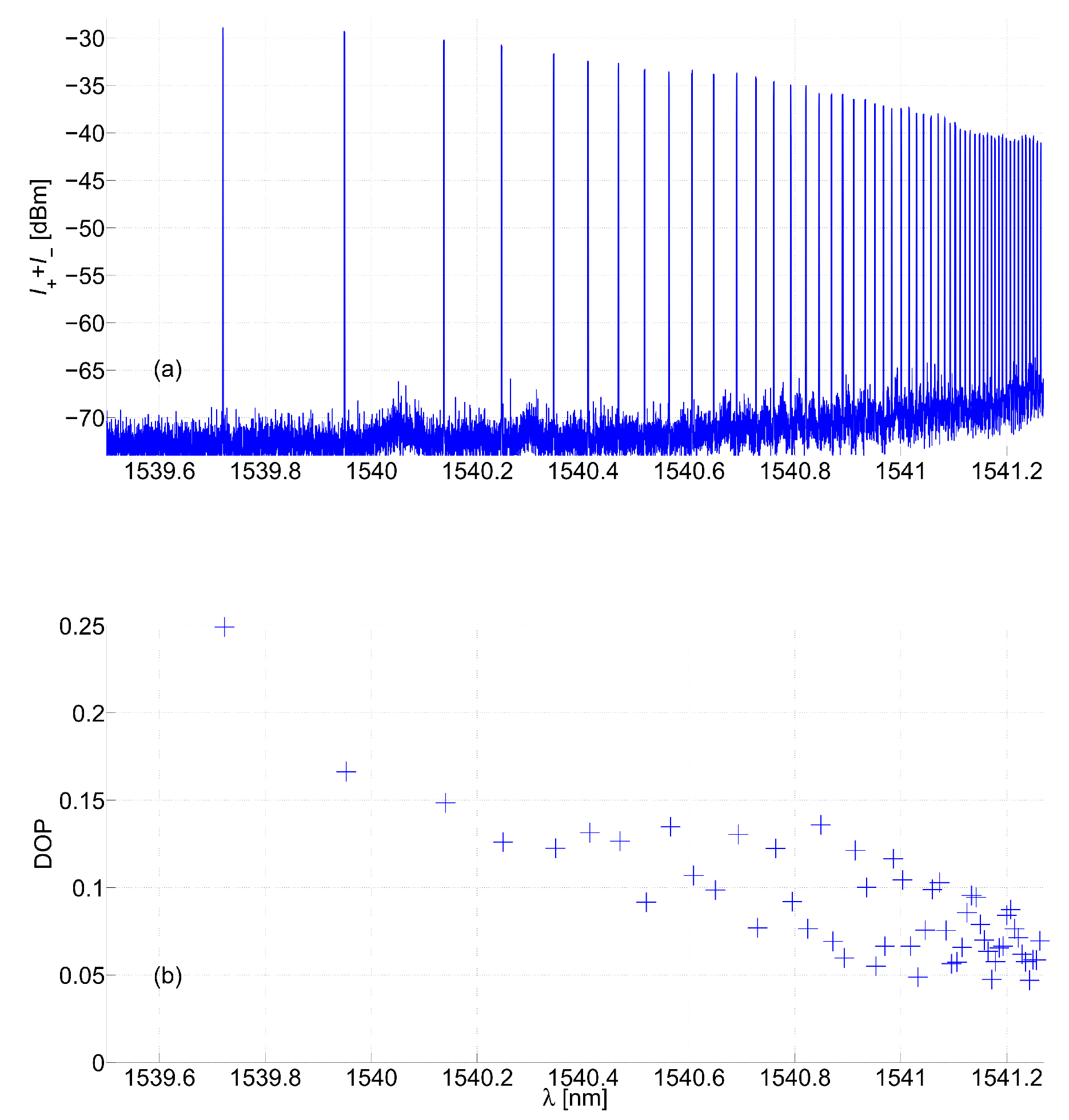
2. POSA
3. FMSR Modulator
4. FMSR Transverse Dielectric Tensor
5. USOC
6. Discussion and Summary
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Goldstein, D.H. Polarized Light; CRC Press: Boca Raton, FL, USA, 2017. [Google Scholar]
- Yao, X.S.; Zhang, B.; Chen, X.; Willner, A.E. Real-time optical spectrum analysis of a light source using a polarimeter. Opt. Express 2008, 16, 17854–17863. [Google Scholar] [CrossRef]
- Kim, E.; Dave, D.; Milner, T.E. Fiber-optic spectral polarimeter using a broadband swept laser source. Opt. Commun. 2005, 249, 351–356. [Google Scholar] [CrossRef]
- Kim, H.K.; Kim, S.K.; Park, H.G.; Kim, B.Y. Polarimetric fiber laser sensors. Opt. Lett. 1993, 18, 317–319. [Google Scholar] [CrossRef] [PubMed]
- Baney, D.M.; Szafraniec, B.; Motamedi, A. Coherent optical spectrum analyzer. IEEE Photonics Technol. Lett. 2002, 14, 355–357. [Google Scholar] [CrossRef]
- Feng, K.; Cui, J.; Dang, H.; Wu, W.; Sun, X.; Jiang, X.; Tan, J. An optoelectronic equivalent narrowband filter for high resolution optical spectrum analysis. Sensors 2017, 17, 348. [Google Scholar] [CrossRef] [PubMed]
- Dang, H.; Liu, H.; Cheng, L.; Tian, Y.; Chen, J.; Feng, K.; Cui, J.; Shum, P.P. Deconvolutional suppression of resolution degradation in coherent optical spectrum analyzer. J. Light. Technol. 2023, 13, 4430. [Google Scholar] [CrossRef]
- Haigh, J.A.; Nunnenkamp, A.; Ramsay, A.J.; Ferguson, A.J. Triple-resonant brillouin light scattering in magneto-optical cavities. Phys. Rev. Lett. 2016, 117, 133602. [Google Scholar] [CrossRef] [PubMed]
- Chai, C.Z.; Shen, Z.; Zhang, Y.L.; Zhao, H.Q.; Guo, G.C.; Zou, C.L.; Dong, C.H. Single-sideband microwave-to-optical conversion in high-q ferrimagnetic microspheres. Photonics Res. 2022, 10, 820–827. [Google Scholar] [CrossRef]
- Buks, E. Low temperature spectrum of a fiber loop laser. Phys. Lett. A 2023, 458, 128591. [Google Scholar] [CrossRef]
- Potton, R.J. Reciprocity in optics. Rep. Prog. Phys. 2004, 67, 717. [Google Scholar] [CrossRef]
- Rameshti, B.Z.; Kusminskiy, S.V.; Haigh, J.A.; Usami, K.; Lachance-Quirion, D.; Nakamura, Y.; Hu, C.; Tang, H.X.; Bauer, G.E.W.; Blanter, Y.M. Cavity magnonics. Phys. Rep. 2022, 979, 1–61. [Google Scholar] [CrossRef]
- Kusminskiy, S.V. Cavity optomagnonics. In Optomagnonic Structures: Novel Architectures for Simultaneous Control of Light and Spin Waves; World Scientific: Singapore, 2021; pp. 299–353. [Google Scholar]
- Zhu, N.; Zhang, X.; Han, X.; Zou, C.; Tang, H.X. Inverse faraday effect in an optomagnonic waveguide. arXiv 2020, arXiv:2012.11119. [Google Scholar] [CrossRef]
- Juraschek, D.M.; Wang, D.S.; Narang, P. Sum-frequency excitation of coherent magnons. Phys. Rev. B 2021, 103, 094407. [Google Scholar] [CrossRef]
- Bittencourt, V.A.S.V.; Liberal, I.; Kusminskiy, S.V. Light propagation and magnon-photon coupling in optically dispersive magnetic media. Phys. Rev. B 2022, 105, 014409. [Google Scholar] [CrossRef]
- Zhang, X.; Zhu, N.; Zou, C.; Tang, H.X. Optomagnonic whispering gallery microresonators. Phys. Rev. Lett. 2016, 117, 123605. [Google Scholar] [CrossRef] [PubMed]
- der Ziel, J.P.V.; Pershan, P.S.; Malmstrom, L.D. Optically-induced magnetization resulting from the inverse faraday effect. Phys. Rev. Lett. 1965, 15, 190. [Google Scholar] [CrossRef]
- Zheng, S.; Wang, Z.; Wang, Y.; Sun, F.; He, Q.; Yan, P.; Yuan, H.Y. Tutorial: Nonlinear magnonics. arXiv 2023, arXiv:2303.16313. [Google Scholar] [CrossRef]
- Stancil, D.D.; Prabhakar, A. Spin Waves; Springer: Berlin/Heidelberg, Germany, 2009. [Google Scholar]
- Oraevsky, A.N. Whispering-gallery waves. Quantum Electron. 2002, 32, 377. [Google Scholar] [CrossRef]
- Schunk, G.; Fürst, J.U.; Förtsch, M.; Strekalov, D.V.; Vogl, U.; Sedlmeir, F.; Schwefel, H.G.L.; Leuchs, G.; Marquardt, C. Identifying modes of large whispering-gallery mode resonators from the spectrum and emission pattern. Opt. Express 2014, 22, 30795–30806. [Google Scholar] [CrossRef]
- Gorodetsky, M.L.; Fomin, A.E. Geometrical theory of whispering-gallery modes. IEEE J. Sel. Top. Quantum Electron. 2006, 12, 33–39. [Google Scholar] [CrossRef]
- Walker, L.R. Magnetostatic modes in ferromagnetic resonance. Phys. Rev. 1957, 105, 390. [Google Scholar] [CrossRef]
- Osada, A.; Gloppe, A.; Nakamura, Y.; Usami, K. Orbital angular momentum conservation in brillouin light scattering within a ferromagnetic sphere. New J. Phys. 2018, 20, 103018. [Google Scholar] [CrossRef]
- Osada, A.; Hisatomi, R.; Noguchi, A.; Tabuchi, Y.; Yamazaki, R.; Usami, K.; Sadgrove, M.; Yalla, R.; Nomura, M.; Nakamura, Y. Cavity optomagnonics with spin-orbit coupled photons. Phys. Rev. Lett. 2016, 116, 223601. [Google Scholar] [CrossRef] [PubMed]
- Sharma, S.; Blanter, Y.M.; Bauer, G.E.W. Light scattering by magnons in whispering gallery mode cavities. Phys. Rev. B 2017, 96, 094412. [Google Scholar] [CrossRef]
- Sharma, S.; Blanter, Y.M.; Bauer, G.E.W. Optical cooling of magnons. Phys. Rev. Lett. 2018, 121, 087205. [Google Scholar] [CrossRef] [PubMed]
- Almpanis, E. Dielectric magnetic microparticles as photomagnonic cavities: Enhancing the modulation of near-infrared light by spin waves. Phys. Rev. B 2018, 97, 184406. [Google Scholar] [CrossRef]
- Zivieri, R.; Vavassori, P.; Giovannini, L.; Nizzoli, F.; Fullerton, E.E.; Grimsditch, M.; Metlushko, V. Stokes–anti-stokes brillouin intensity asymmetry of spin-wave modes in ferromagnetic films and multilayers. Phys. Rev. B 2002, 65, 165406. [Google Scholar] [CrossRef]
- Desormiere, B.; Gall, H.L. Interaction studies of a laser light with spin waves and magnetoelastic waves propagating in a yig bar. IEEE Trans. Magn. 1972, 8, 379–381. [Google Scholar] [CrossRef]
- Liu, Z.; Wang, B.; Xiong, H.; Wu, Y. Magnon-induced high-order sideband generation. Opt. Lett. 2018, 43, 3698–3701. [Google Scholar] [CrossRef] [PubMed]
- Zhu, N.; Zhang, X.; Han, X.; Zou, C.; Zhong, C.; Wang, C.; Jiang, L.; Tang, H.X. Waveguide cavity optomagnonics for microwave-to-optics conversion. Optica 2020, 7, 1291–1297. [Google Scholar] [CrossRef]
- Li, J.; Wang, Y.; Wu, W.; Zhu, S.; You, J.Q. Quantum network with magnonic and mechanical nodes. PRX Quantum 2021, 2, 040344. [Google Scholar] [CrossRef]
- Nayak, B.K.; Buks, E. Polarization-selective magneto-optical modulation. J. Appl. Phys. 2022, 132, 193905. [Google Scholar] [CrossRef]
- Liu, Z.X.; Xiong, H. Magnon laser based on brillouin light scattering. Opt. Lett. 2020, 45, 5452–5455. [Google Scholar] [CrossRef] [PubMed]
- Sandercock, J.R.; Wettling, W. Light scattering from thermal acoustic magnons in yttrium iron garnet. Solid State Commun. 1973, 13, 1729–1732. [Google Scholar] [CrossRef]
- Hu, H.L.; Morgenthaler, F.R. Strong infrared-light scattering from coherent spin waves in yttrium iron garnet. Appl. Phys. Lett. 1971, 18, 307–310. [Google Scholar] [CrossRef]
- Ghasemian, E. Dissipative dynamics of optomagnonic nonclassical features via anti-stokes optical pulses: Squeezing, blockade, anti-correlation, and entanglement. Sci. Rep. 2023, 13, 12757. [Google Scholar] [CrossRef] [PubMed]
- Kusminskiy, S.V.; Tang, H.X.; Marquardt, F. Coupled spin-light dynamics in cavity optomagnonics. Phys. Rev. A 2016, 94, 033821. [Google Scholar] [CrossRef]
- Wettling, W.; Cottam, M.G.; Sandercock, J.R. The relation between one-magnon light scattering and the complex magneto-optic effects in yig. J. Phys. Solid State Phys. 1975, 8, 211. [Google Scholar] [CrossRef]
- Cottam, M.G.; Lockwood, D.J. Light Scattering in Magnetic Solids; Wiley: New York, NY, USA, 1986. [Google Scholar]
- Liu, T.; Zhang, X.; Tang, H.X.; Flatté, M.E. Optomagnonics in magnetic solids. Phys. Rev. B 2016, 94, 060405. [Google Scholar] [CrossRef]
- Haigh, J.A.; Nunnenkamp, A.; Ramsay, A.J. Polarization dependent scattering in cavity optomagnonics. Phys. Rev. Lett. 2021, 127, 143601. [Google Scholar] [CrossRef]
- Hisatomi, R.; Noguchi, A.; Yamazaki, R.; Nakata, Y.; Gloppe, A.; Nakamura, Y.; Usami, K. Helicity-changing brillouin light scattering by magnons in a ferromagnetic crystal. Phys. Rev. Lett. 2019, 123, 207401. [Google Scholar] [CrossRef] [PubMed]
- Hisatomi, R.; Osada, A.; Tabuchi, Y.; Ishikawa, T.; Noguchi, A.; Yamazaki, R.; Usami, K.; Nakamura, Y. Bidirectional conversion between microwave and light via ferromagnetic magnons. Phys. Rev. B 2016, 93, 174427. [Google Scholar] [CrossRef]
- Wu, W.J.; Wang, Y.P.; Wu, J.Z.; Li, J.; You, J.Q. Remote magnon entanglement between two massive ferrimagnetic spheres via cavity optomagnonics. Phys. Rev. A 2021, 104, 023711. [Google Scholar] [CrossRef]
- Lazzarini, V.; Timoney, J.; Lysaght, T. Asymmetric-spectra methods for adaptive fm synthesis. In Proceedings of the DAFX-08 the 11th Int. Conference on Digital Audio Effects, Espoo, Helsinki, Finland, 1–4 September 2008. [Google Scholar]
- Li, W.; Wang, W.T.; Wang, L.X.; Zhu, N.H. Optical vector network analyzer based on single-sideband modulation and segmental measurement. IEEE Photonics J. 2014, 6, 1–8. [Google Scholar] [CrossRef]
- Shimotsu, S.; Oikawa, S.; Saitou, T.; Mitsugi, N.; Kubodera, K.; Kawanishi, T.; Izutsu, M. Single side-band modulation performance of a linbo 3 integrated modulator consisting of four-phase modulator waveguides. IEEE Photonics Technol. Lett. 2001, 13, 364–366. [Google Scholar] [CrossRef] [PubMed]
- Onbasli, M.C.; Beran, L.; Zahradník, M.; Kučera, M.; Antoš, R.; Mistrík, J.; Dionne, G.F.; Veis, M.; Ross, C.A. Optical and magneto-optical behavior of cerium yttrium iron garnet thin films at wavelengths of 200–1770 nm. Sci. Rep. 2016, 6, 23640. [Google Scholar] [CrossRef] [PubMed]
- Buks, E. Intermode coupling in a fiber loop laser at low temperatures. J. Light. Technol. 2024, 42, 2951. [Google Scholar] [CrossRef]
- Fletcher, P.C.; Bell, R.O. Ferrimagnetic resonance modes in spheres. J. Appl. Phys. 1959, 30, 687–698. [Google Scholar] [CrossRef]
- Sharma, S. Cavity Optomagnonics: Manipulating Magnetism by Light. Ph.D. Thesis, Delft University of Technology, Delft, The Netherlands, 2019. [Google Scholar]
- Jin, T.L. Design of a Yig-Tuned Oscillator. Master’s Thesis, New Jersey Institute of Technology, Newark, NJ, USA, 1974. [Google Scholar]
- Freiser, M. A survey of magnetooptic effects. IEEE Trans. Magn. 1968, 4, 152–161. [Google Scholar] [CrossRef]
- Boardman, A.D.; Xie, M. Magneto-optics: A critical review. Introd. Complex Mediu. Opt. Electromagn. 2003, 123, 197. [Google Scholar]
- Boardman, A.D.; Velasco, L. Gyroelectric cubic-quintic dissipative solitons. IEEE J. Sel. Top. Quantum Electron. 2006, 12, 388–397. [Google Scholar] [CrossRef]
- Wood, D.L.; Remeika, J.P. Effect of impurities on the optical properties of yttrium iron garnet. J. Appl. Phys. 1967, 38, 1038–1045. [Google Scholar] [CrossRef]
- Prokhorov, A.M.; Smolenskiĭ, G.A.; Ageev, A.N. Optical phenomena in thin-film magnetic waveguides and their technical application. Sov. Phys. Uspekhi 1984, 27, 339. [Google Scholar] [CrossRef]
- Prabhakar, A.; Stancil, D.D. Spin Waves: Theory and Applications; Springer: Berlin/Heidelberg, Germany, 2009; Volume 5. [Google Scholar]
- Buks, E. Quantum Mechanics–Lecture Notes. 2024. Available online: http://buks.net.technion.ac.il/teaching/ (accessed on 10 May 2024).
- Buks, E. Tunable multimode lasing in a fiber ring. Phys. Rev. Appl. 2023, 19, L051001. [Google Scholar] [CrossRef]
- Yamashita, S.; Hotate, K. Multiwavelength erbium-doped fibre laser using intracavity etalon and cooled by liquid nitrogen. Electron. Lett. 1996, 32, 1298–1299. [Google Scholar] [CrossRef]
- Liu, H.; He, W.; Liu, Y.; Dong, Y.; Zhu, L. Erbium-doped fiber laser based on femtosecond laser inscribed fbg through fiber coating for strain sensing in liquid nitrogen environment. Opt. Fiber Technol. 2022, 72, 102988. [Google Scholar] [CrossRef]
- Lopez, J.; Kerbertt, H.; Plata, M.; Hernandez, E.; Stepanov, S. Two-wave mixing in erbium-doped-fibers with spectral-hole burning at 77k. J. Opt. 2020, 22, 085401. [Google Scholar] [CrossRef]
- Gouët, J.L.; Oudin, J.; Perrault, P.; Abbes, A.; Odier, A.; Dubois, A. On the effect of low temperatures on the maximum output power of a coherent erbium-doped fiber amplifier. J. Light. Technol. 2019, 37, 3611–3619. [Google Scholar] [CrossRef]
- Wei, S.; Jing, B.; Zhang, X.; Liao, J.; Li, H.; You, L.; Wang, Z.; Wang, Y.; Guang-Wei, D.; Song, H.; et al. Storage of 1650 modes of single photons at telecom wavelength. arXiv 2022, arXiv:2209.00802. [Google Scholar]
- Ortu, A.; Rakonjac, J.V.; Holzäpfel, A.; Seri, A.; Grandi, S.; Mazzera, M.; de Riedmatten, H.; Afzelius, M. Multimode capacity of atomic-frequency comb quantum memories. Quantum Sci. Technol. 2022, 7, 035024. [Google Scholar] [CrossRef]
- Liu, D.C.; Li, P.Y.; Zhu, T.X.; Zheng, L.; Huang, J.Y.; Zhou, Z.Q.; Li, C.F.; Guo, G.C. On-demand storage of photonic qubits at telecom wavelengths. arXiv 2022, arXiv:2201.03692. [Google Scholar] [CrossRef] [PubMed]
- Veissier, L.; Falamarzi, M.; Lutz, T.; Saglamyurek, E.; Thiel, C.W.; Cone, R.L.; Tittel, W. Optical decoherence and spectral diffusion in an erbium-doped silica glass fiber featuring long-lived spin sublevels. Phys. Rev. B 2016, 94, 195138. [Google Scholar] [CrossRef]
- Shafiei, S.; Saglamyurek, E.; Oblak, D. Hour-long decay-time of erbium spins in an optical fiber at milli-kelvin temperatures. In Proceedings of the Quantum Information and Measurement 2021, Washington, DC, USA, 1–5 November 2021; p. F2A–4. [Google Scholar]
- Liem, A.; Limpert, J.; Schreiber, T.; Reich, M.; Zellmer, H.; Tunnermann, A.; Carter, A.; Tankala, K. High power linearly polarized fiber laser. In Proceedings of the Conference on Lasers and Electro-Optics, San Francisco, CA, USA, 16–21 May 2004; p. CMS4. [Google Scholar]
- Trujillo-Bueno, J.; Moreno-Insertis, F.; Sánchez, F. Astrophysical Spectropolarimetry; Cambridge University Press: Cambridge, UK, 2002. [Google Scholar]
- Belyaev, D.A.; Yushkov, K.B.; Anikin, S.P.; Dobrolenskiy, Y.S.; Laskin, A.; Mantsevich, S.N.; Molchanov, V.Y.; Potanin, S.A.; Korablev, O.I. Compact acousto-optic imaging spectro-polarimeter for mineralogical investigations in the near infrared. Opt. Express 2017, 25, 25980–25991. [Google Scholar] [CrossRef] [PubMed]

Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Buks, E. Polarimeter Optical Spectrum Analyzer. Photonics 2024, 11, 486. https://doi.org/10.3390/photonics11060486
Buks E. Polarimeter Optical Spectrum Analyzer. Photonics. 2024; 11(6):486. https://doi.org/10.3390/photonics11060486
Chicago/Turabian StyleBuks, Eyal. 2024. "Polarimeter Optical Spectrum Analyzer" Photonics 11, no. 6: 486. https://doi.org/10.3390/photonics11060486
APA StyleBuks, E. (2024). Polarimeter Optical Spectrum Analyzer. Photonics, 11(6), 486. https://doi.org/10.3390/photonics11060486




