Polarization-Dependent Fiber Metasurface with Beam Collimating and Deflecting
Abstract
1. Introduction
2. Design of the Polarization-Dependent Metasurface
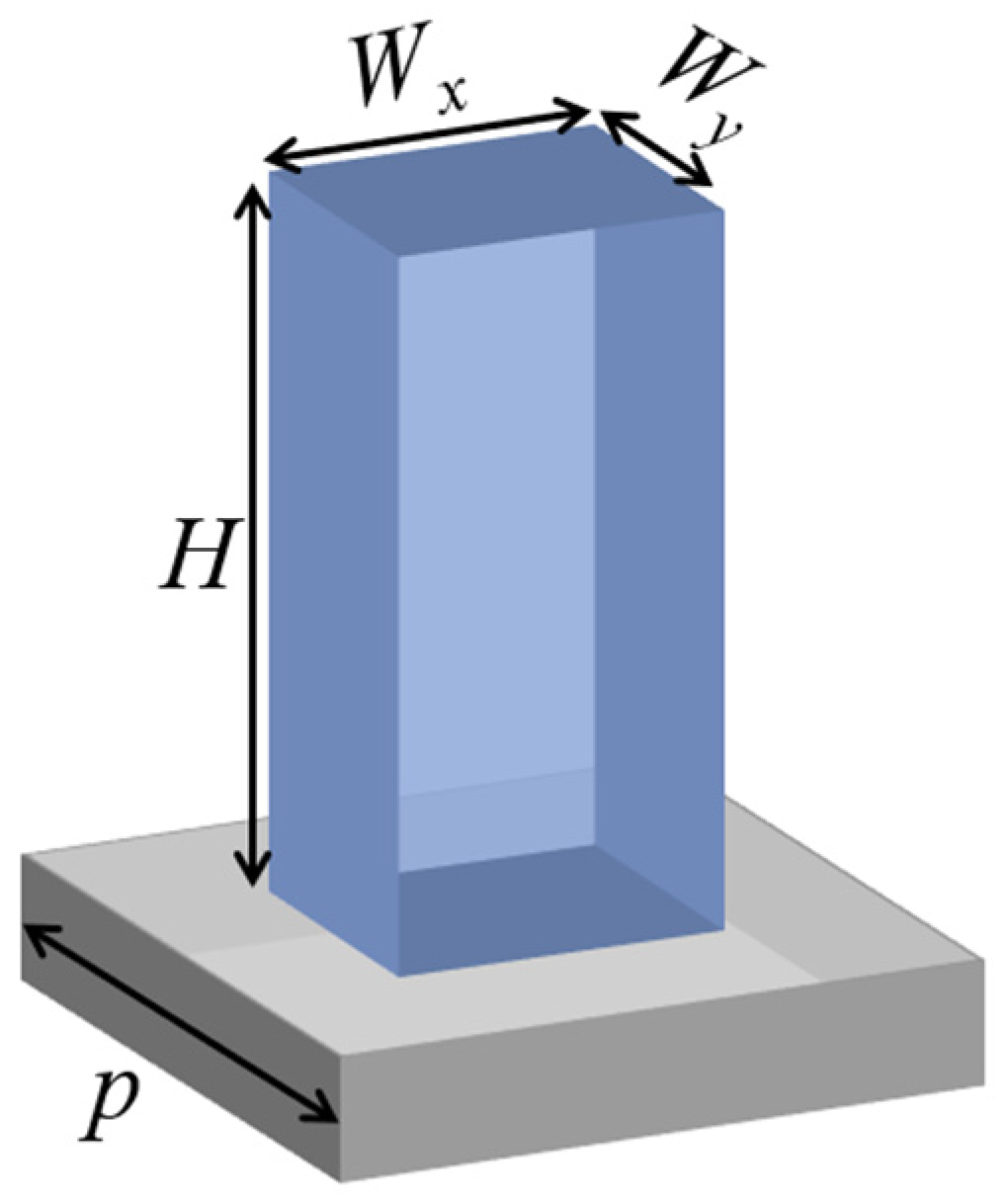
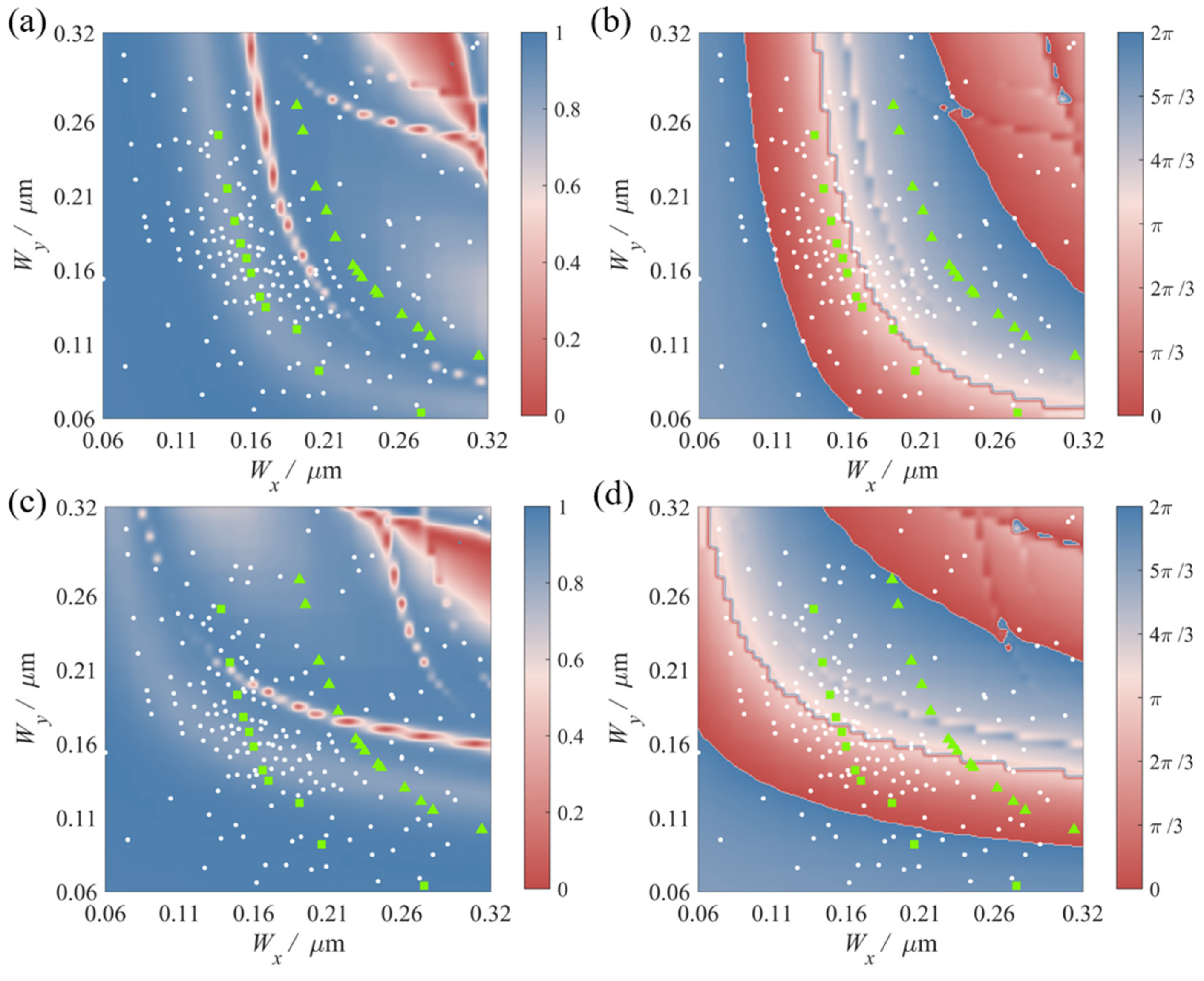
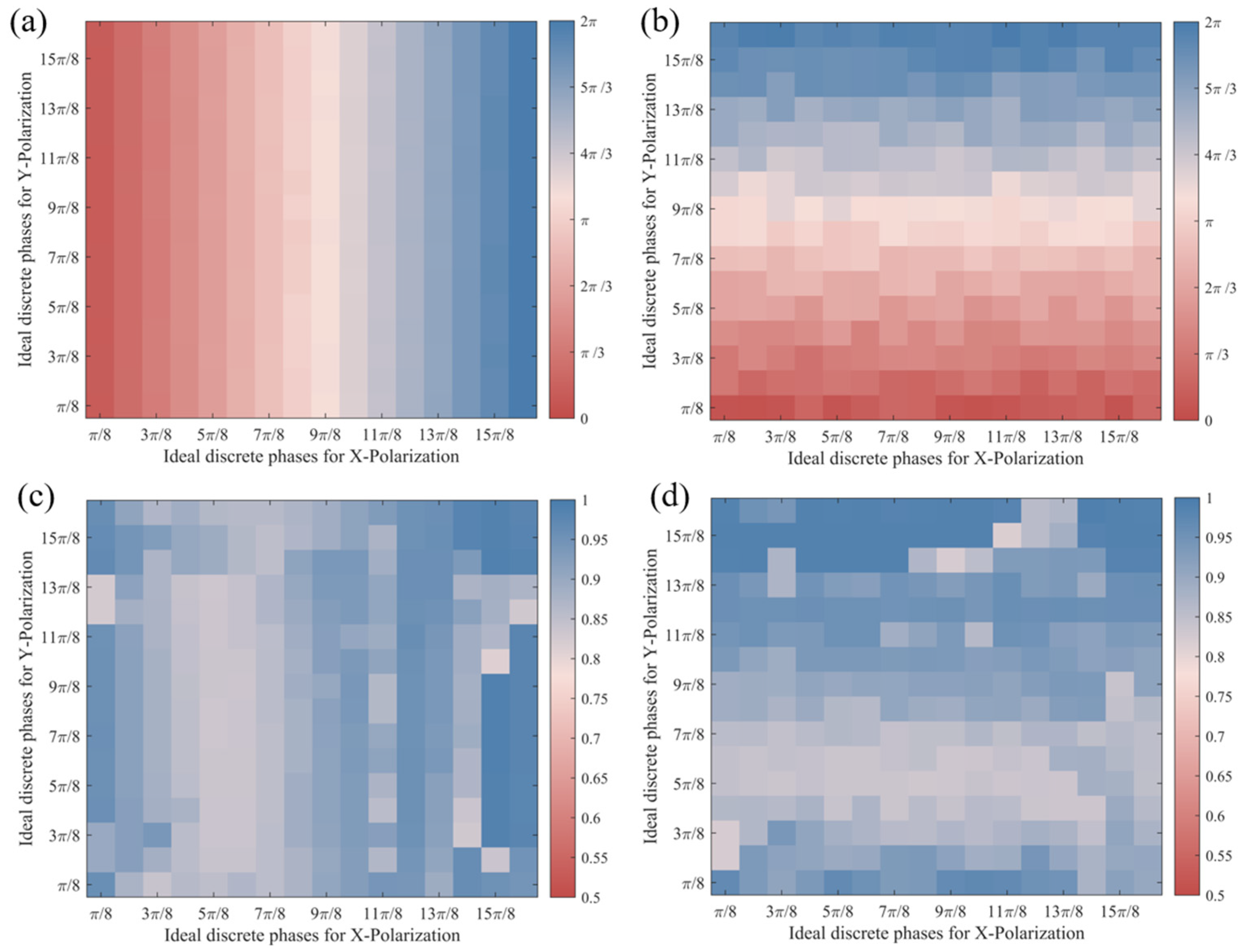
2.1. Design of Birefringent Meta-Atoms
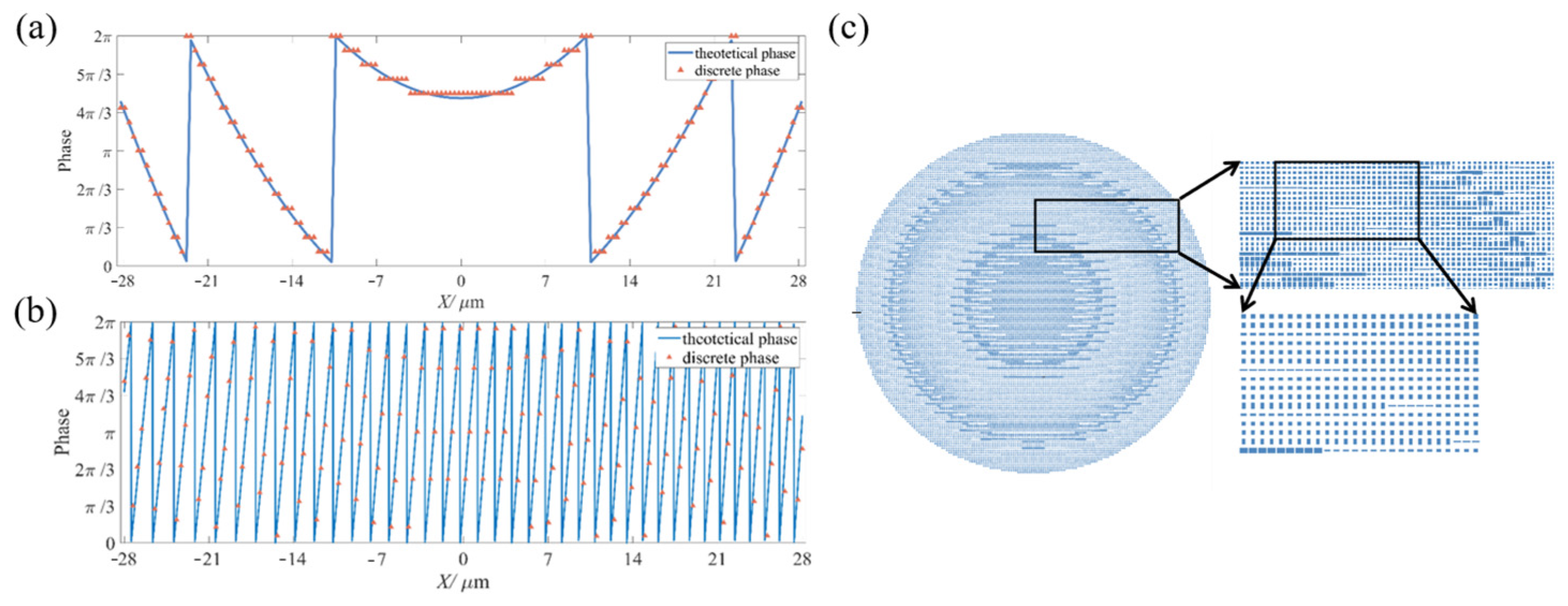
2.2. Design of Metasurface
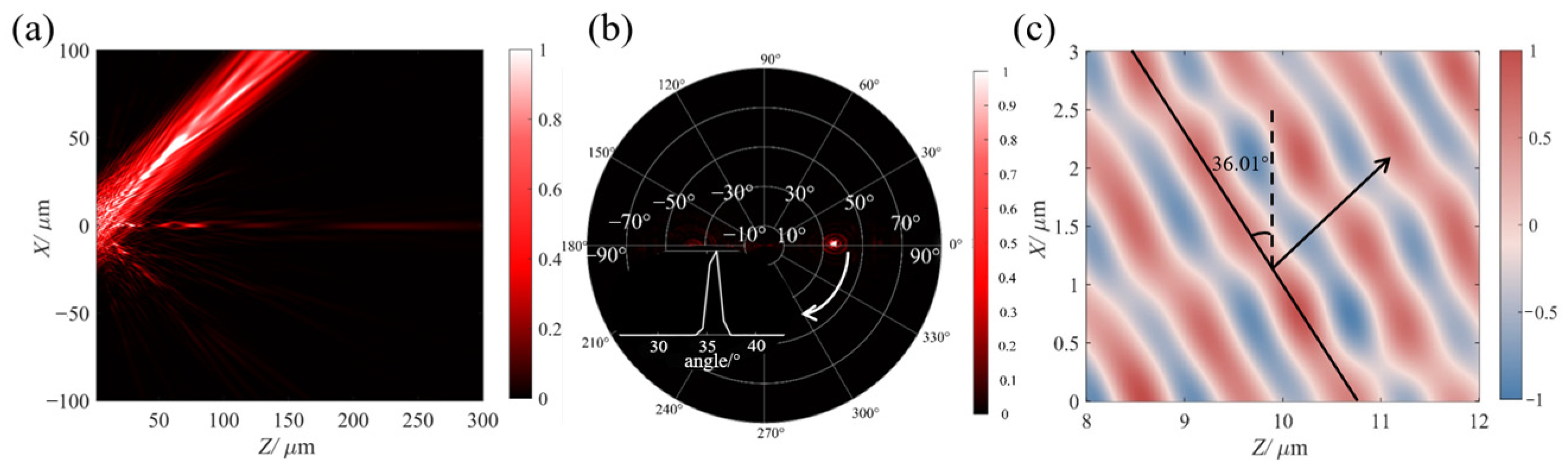
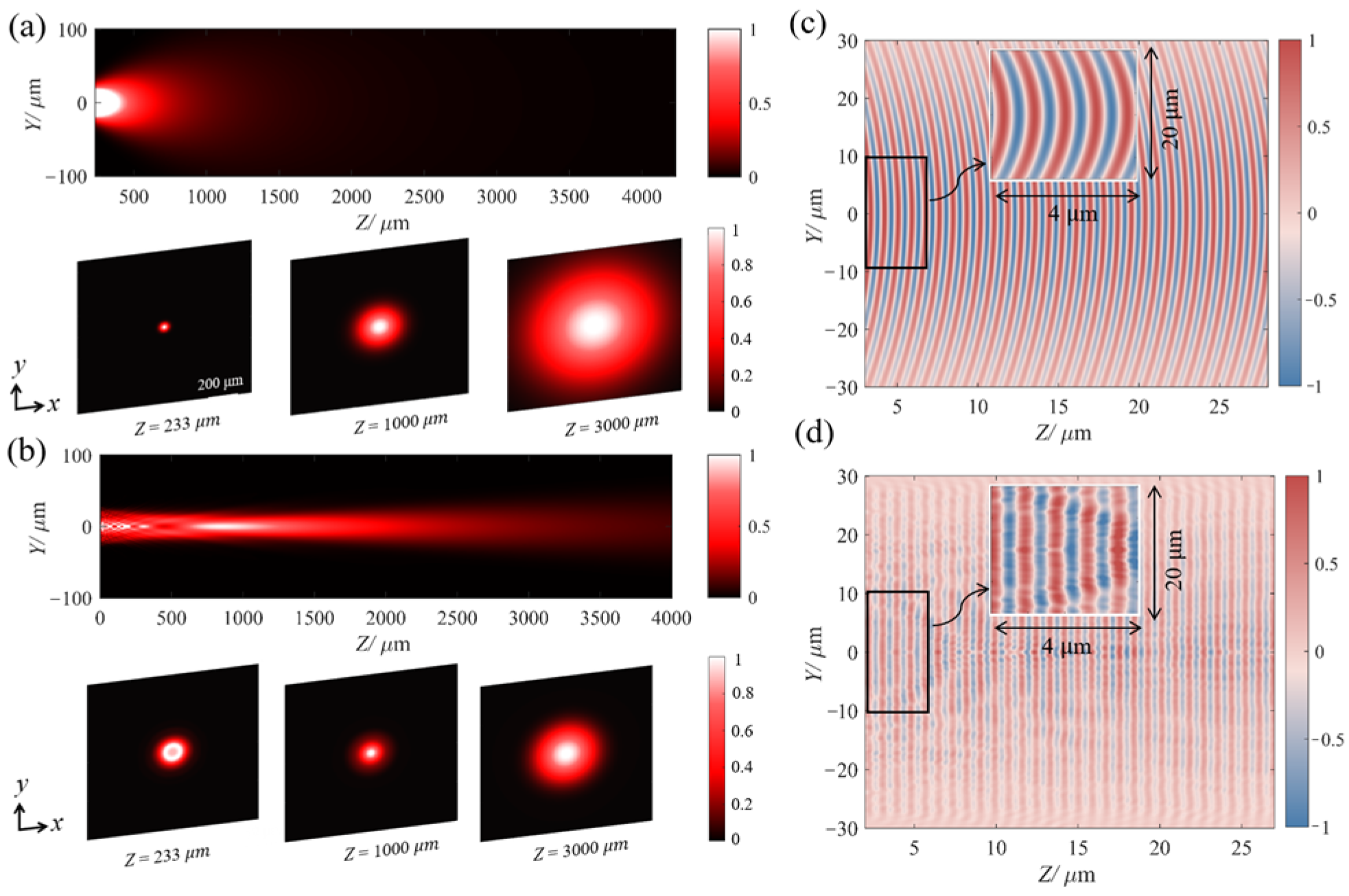
3. Results
4. Discussion
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Principe, M.; Consales, M.; Castaldi, G.; Galdi, V.; Cusano, A. Evaluation of fiber-optic phase-gradient meta-tips for sensing applications. Nanomater. Nanotechnol. 2019, 9, 184798041983272. [Google Scholar] [CrossRef]
- Yang, Y.B.; Wang, D.N.; Xu, B.; Wang, Z.K. Optical fiber tip interferometer gas pressure sensor based on anti-resonant reflecting guidance mechanism. Opt. Fiber Technol. 2018, 42, 11–17. [Google Scholar] [CrossRef]
- Pahlevaninezhad, H.; Khorasaninejad, M.; Huang, Y.-W.; Shi, Z.; Hariri, L.P.; Adams, D.C.; Ding, V.; Zhu, A.; Qiu, C.-W.; Capasso, F.; et al. Nano-optic endoscope for high-resolution optical coherence tomography in vivo. Nat. Photonics 2018, 12, 540–547. [Google Scholar] [CrossRef]
- Mao, R.Q.; Lin, Y.; Yang, K.; An, Q.; Fu, Y.Q. A High-Efficiency Fiber-Coupled Rydberg-Atom Integrated Probe and Its Imaging Applications. IEEE Antennas Wirel. Propag. Lett. 2023, 22, 352–356. [Google Scholar] [CrossRef]
- Kasztelanic, R.; Filipkowski, A.; Anuszkiewicz, A.; Stafiej, P.; Stepniewski, G.; Pysz, D.; Krzyzak, K.; Stepien, R.; Klimczak, M.; Buczynski, R. Integrating Free-Form Nanostructured GRIN Microlenses with Single-Mode Fibers for Optofluidic Systems. Sci. Rep. 2018, 8, 5072. [Google Scholar] [CrossRef] [PubMed]
- Guggenheim, J.A.; Li, J.; Allen, T.J.; Colchester, R.J.; Noimark, S.; Ogunlade, O.; Parkin, I.P.; Papakonstantinou, I.; Desjardins, A.E.; Zhang, E.Z.; et al. Ultrasensitive plano-concave optical microresonators for ultrasound sensing. Nat. Photonics 2017, 11, 714–719. [Google Scholar] [CrossRef]
- Zhao, M.T.; Huang, Y.; Kang, J.U. Sapphire ball lens-based fiber probe for common-path optical coherence tomography and its applications in corneal and retinal imaging. Opt. Lett. 2012, 37, 4835–4837. [Google Scholar] [CrossRef] [PubMed]
- Mo, J.H.; Zheng, W.; Huang, Z.W. Fiber-optic Raman probe couples ball lens for depth-selected Raman measurements of epithelial tissue. Biomed. Opt. Express 2010, 1, 17–30. [Google Scholar] [CrossRef] [PubMed]
- Soukoulis, C.M.; Wegener, M. Past achievements and future challenges in the development of three-dimensional photonic metamaterials. Nat. Photonics 2011, 5, 523–530. [Google Scholar] [CrossRef]
- Sang, D.; Xu, M.F.; Pu, M.B.; Zhang, F.; Guo, Y.H.; Li, X.; Ma, X.L.; Fu, Y.Q.; Luo, X.G. Toward High-Efficiency Ultrahigh Numerical Aperture Freeform Metalens: From Vector Diffraction Theory to Topology Optimization. Laser Photonics Rev. 2022, 16, 2200265. [Google Scholar] [CrossRef]
- Zang, X.F.; Xu, W.W.; Gu, M.; Yao, B.S.; Chen, L.; Peng, Y.; Xie, J.Y.; Balakin, A.V.; Shkurinov, A.P.; Zhu, Y.M.; et al. Polarization-Insensitive Metalens with Extended Focal Depth and Longitudinal High-Tolerance Imaging. Adv. Opt. Mater. 2020, 8, 1901342. [Google Scholar] [CrossRef]
- Ahmed, H.; Kim, H.; Zhang, Y.B.; Intaravanne, Y.; Jang, J.; Rho, J.; Chen, S.Q.; Chen, X.Z. Optical metasurfaces for generating and manipulating optical vortex beams. Nanophotonics 2022, 11, 941–956. [Google Scholar] [CrossRef]
- Liu, B.Y.; Sain, B.; Reineke, B.; Zhao, R.Z.; Meier, C.; Huang, L.L.; Jiang, Y.Y.; Zentgraf, T. Nonlinear Wavefront Control by Geometric-Phase Dielectric Metasurfaces: Influence of Mode Field and Rotational Symmetry. Adv. Opt. Mater. 2020, 8, 1902050. [Google Scholar] [CrossRef]
- Zhao, Q.; Yuan, W.; Qu, J.; Cheng, Z.; Peng, G.-D.; Yu, C. Optical Fiber-Integrated Metasurfaces: An Emerging Platform for Multiple Optical Applications. Nanomaterials 2022, 12, 793. [Google Scholar] [CrossRef] [PubMed]
- Ding, F.; Chang, B.; Wei, Q.; Huang, L.; Guan, X.; Bozhevolnyi, S.I. Versatile Polarization Generation and Manipulation Using Dielectric Metasurfaces. Laser Photonics Rev. 2020, 14, 2000116. [Google Scholar] [CrossRef]
- Overvig, A.C.; Shrestha, S.; Malek, S.C.; Lu, M.; Stein, A.; Zheng, C.X.; Yu, N.F. Dielectric metasurfaces for complete and independent control of the optical amplitude and phase. Light-Sci. Appl. 2019, 8, 92. [Google Scholar] [CrossRef] [PubMed]
- Lee, G.Y.; Yoon, G.; Lee, S.Y.; Yun, H.; Cho, J.; Lee, K.; Kim, H.; Rho, J.; Lee, B. Complete amplitude and phase control of light using broadband holographic metasurfaces. Nanoscale 2018, 10, 4237–4245. [Google Scholar] [CrossRef] [PubMed]
- Ren, H.; Jang, J.; Li, C.; Aigner, A.; Plidschun, M.; Kim, J.; Rho, J.; Schmidt, M.A.; Maier, S.A. An achromatic metafiber for focusing and imaging across the entire telecommunication range. Nat. Commun. 2022, 13, 4183. [Google Scholar] [CrossRef] [PubMed]
- Shalaev, M.I.; Sun, J.B.; Tsukernik, A.; Pandey, A.; Nikolskiy, K.; Litchinitser, N.M. High-Efficiency All-Dielectric Metasurfaces for Ultracompact Beam Manipulation in Transmission Mode. Nano Lett. 2015, 15, 6261–6266. [Google Scholar] [CrossRef]
- Liu, M.Z.; Zhu, W.Q.; Huo, P.C.; Feng, L.; Song, M.W.; Zhang, C.; Chen, L.; Lezec, H.J.; Lu, Y.Q.; Agrawal, A.; et al. Multifunctional metasurfaces enabled by simultaneous and independent control of phase and amplitude for orthogonal polarization states. Light-Sci. Appl. 2021, 10, 107. [Google Scholar] [CrossRef]
- Rahman, B.M.A.; Viphavakit, C.; Chitaree, R.; Ghosh, S.; Pathak, A.K.; Verma, S.; Sakda, N. Optical Fiber, Nanomaterial, and THz-Metasurface-Mediated Nano-Biosensors: A Review. Biosensors 2022, 12, 42. [Google Scholar] [CrossRef] [PubMed]
- Saleh, A.A.E.; Sheikhoelislami, S.; Gastelum, S.; Dionne, J.A. Grating-flanked plasmonic coaxial apertures for efficient fiber optical tweezers. Opt. Express 2016, 24, 20593–20603. [Google Scholar] [CrossRef] [PubMed]
- Liberale, C.; Minzioni, P.; Bragheri, F.; De Angelis, F.; Di Fabrizio, E.; Cristiani, I. Miniaturized all-fibre probe for three-dimensional optical trapping and manipulation. Nat. Photonics 2007, 1, 723–727. [Google Scholar] [CrossRef]
- Sun, Y.; Wang, C.; Zheng, S.; Tao, X.; Liu, X.; Li, Y.; Wu, F.; Zheng, Z. Double-layer polarization-independent achromatic metasurface array for optical fiber bundle coupling in microendoscope. Sci. Rep. 2022, 12, 20476. [Google Scholar] [CrossRef] [PubMed]
- Xie, N.; Carson, M.D.; Froch, J.E.; Majumdar, A.; Seibel, E.J.; Bohringer, K.F. Large field-of-view short-wave infrared metalens for scanning fiber endoscopy. J. Biomed. Opt. 2023, 28, 094802. [Google Scholar] [CrossRef] [PubMed]
- Ghimire, I.; Yang, J.; Gurung, S.; Mishra, S.K.; Lee, H.W.H. Polarization-dependent photonic crystal fiber optical filters enabled by asymmetric metasurfaces. Nanophotonics 2022, 11, 2711–2717. [Google Scholar] [CrossRef]
- Li, J.; Li, R.; Xue, X.; Jiang, X.; Chen, X.; Chui, H.-C. Achromatic Flat Metasurface Fiber Couplers within Telecom Bands. Photonics 2022, 10, 28. [Google Scholar] [CrossRef]
- Mao, R.Q.; Lin, Y.; Fu, Y.Q.; Ma, Y.M.; Yang, K. Digital Beamforming and Receiving Array Research Based on Rydberg Field Probes. IEEE Trans. Antennas Propag. 2024, 72, 2025–2029. [Google Scholar] [CrossRef]
- Prajapati, N.; Rotunno, A.P.; Berweger, S.; Simons, M.T.; Artusio-Glimpse, A.B.; Voran, S.D.; Holloway, C.L. TV and video game streaming with a quantum receiver: A study on a Rydberg atom-based receiver’s bandwidth and reception clarity. AVS Quantum Sci. 2022, 4, 035001. [Google Scholar] [CrossRef]
- Lin, Y.; Wu, F.-C.; Mao, R.-Q.; Yao, J.-W.; Liu, Y.; An, Q.; Fu, Y.-Q. Development of three-port fiber-coupled vapor cell probe and its application in microwave digital communication. Acta Phys. Sin. 2022, 71, 170702. [Google Scholar] [CrossRef]
- Saleh, B.E.; Teich, M.C. Fundamentals of Photonics, 2nd ed.; John Wiley & Sons: Hoboken, NJ, USA, 2007. [Google Scholar]
- Fan, Z.B.; Shao, Z.K.; Xie, M.Y.; Pang, X.N.; Ruan, W.S.; Zhao, F.L.; Chen, Y.J.; Yu, S.Y.; Dong, J.W. Silicon Nitride Metalenses for Close-to-One Numerical Aperture and Wide-Angle Visible Imaging. Phys. Rev. Appl. 2018, 10, 014005. [Google Scholar] [CrossRef]
- Grann, E.B.; Moharam, M.G.; Pommet, D.A. Optimal design for antireflective tapered two-dimensional subwavelength grating structures. J. Opt. Soc. Am. A 1995, 12, 333–339. [Google Scholar] [CrossRef]
- Yoda, H.; Polynkin, P.; Mansuripur, M. Beam quality factor of higher order modes in a step-index fiber. J. Light. Technol. 2006, 24, 1350–1355. [Google Scholar] [CrossRef]
- Ye, H.; Sun, Q.; Guo, Z.; Hou, Y.; Wen, F.; Yuan, D.; Qin, F.; Zhou, G. Theoretical realization of single-mode fiber integrated metalens for beam collimating. Opt. Express 2021, 29, 27521–27529. [Google Scholar] [CrossRef]
- Marcuse, D. Gaussian approximation of the fundamental modes of graded-index fibers. J. Opt. Soc. Am. 1978, 68, 103–109. [Google Scholar] [CrossRef]
- Yu, N.; Genevet, P.; Kats, M.A.; Aieta, F.; Tetienne, J.P.; Capasso, F.; Gaburro, Z. Light propagation with phase discontinuities: Generalized laws of reflection and refraction. Science 2011, 334, 333–337. [Google Scholar] [CrossRef]
- Egorov, V.; Eitan, M.; Scheuer, J. Genetically optimized all-dielectric metasurfaces. Opt. Express 2017, 25, 2583–2593. [Google Scholar] [CrossRef]


Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ma, Y.; Sang, D.; Lin, Y.; An, Q.; Sun, Z.; Fu, Y. Polarization-Dependent Fiber Metasurface with Beam Collimating and Deflecting. Photonics 2024, 11, 474. https://doi.org/10.3390/photonics11050474
Ma Y, Sang D, Lin Y, An Q, Sun Z, Fu Y. Polarization-Dependent Fiber Metasurface with Beam Collimating and Deflecting. Photonics. 2024; 11(5):474. https://doi.org/10.3390/photonics11050474
Chicago/Turabian StyleMa, Yuemin, Di Sang, Yi Lin, Qiang An, Zhanshan Sun, and Yunqi Fu. 2024. "Polarization-Dependent Fiber Metasurface with Beam Collimating and Deflecting" Photonics 11, no. 5: 474. https://doi.org/10.3390/photonics11050474
APA StyleMa, Y., Sang, D., Lin, Y., An, Q., Sun, Z., & Fu, Y. (2024). Polarization-Dependent Fiber Metasurface with Beam Collimating and Deflecting. Photonics, 11(5), 474. https://doi.org/10.3390/photonics11050474



