Moving Bragg Solitons in a Dual-Core System Composed of a Linear Bragg Grating with Dispersive Reflectivity and a Uniform Nonlinear Core
Abstract
1. Introduction
2. The Model
3. Discussion of Results
3.1. Analysis of the Linear Spectrum
3.2. BG Soliton Solutions
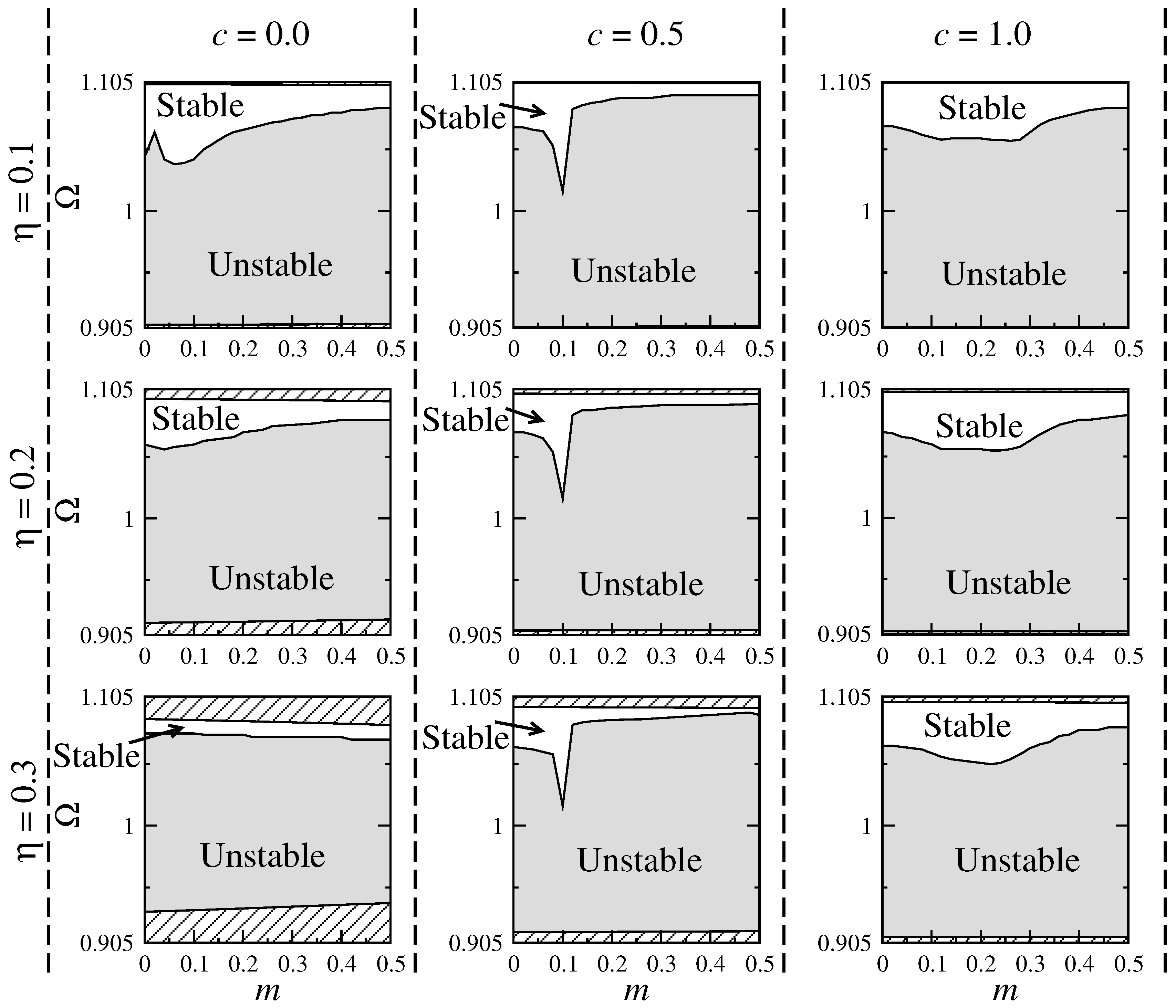
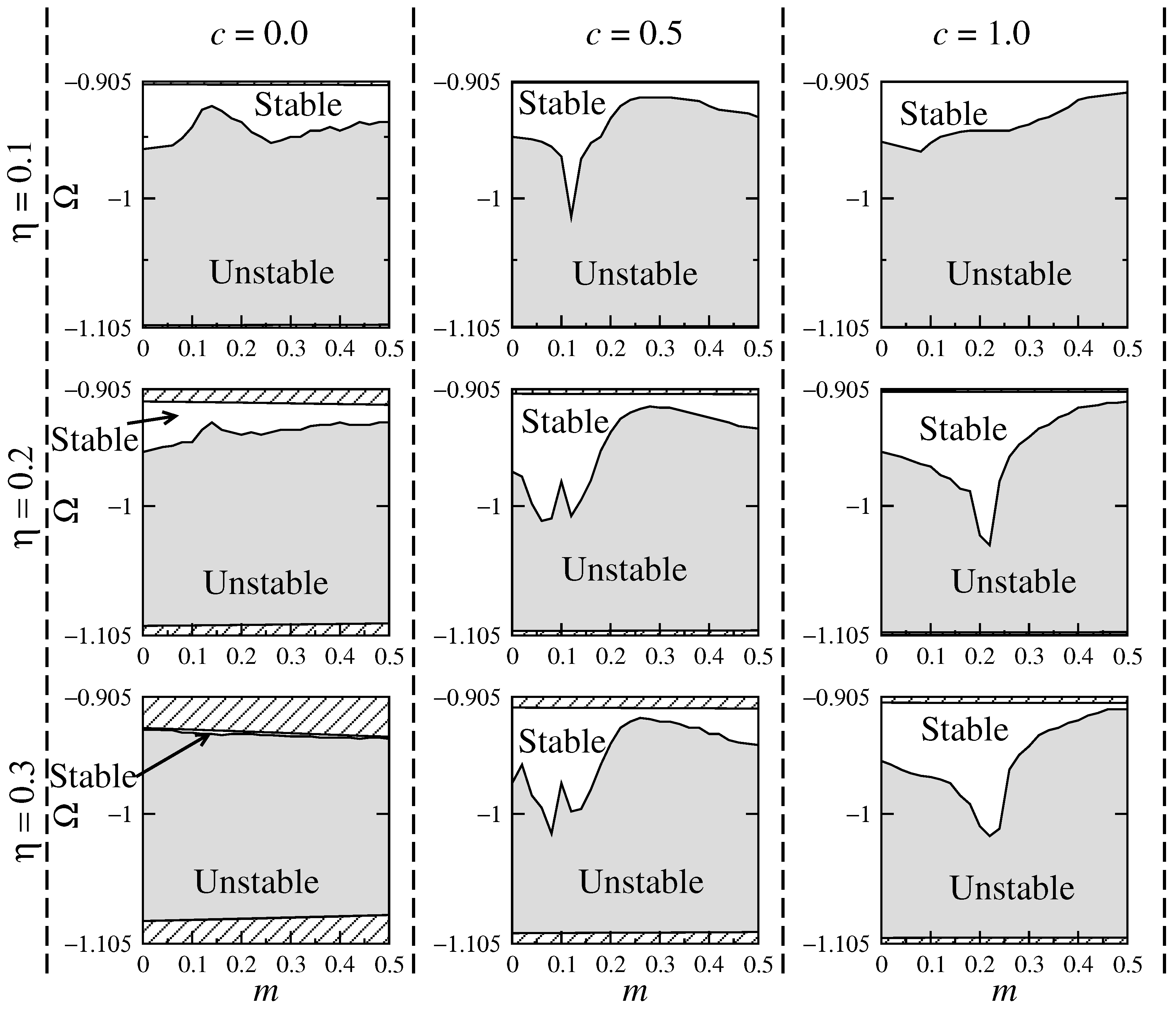
3.3. Stability Analysis
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Kashyap, R. Fiber Bragg Gratings; Academic Press: San Diego, CA, USA; London, UK, 1999. [Google Scholar]
- Krug, P.A.; Stephens, T.; Yoffe, G.; Ouellette, F.; Hill, P.; Dhosi, G. Dispersion compensation over 270 km at 10 Gbit/s using an offset-core chirped fibre Bragg grating. Electron. Lett. 1995, 31, 1091. [Google Scholar] [CrossRef]
- Loh, W.H.; Laming, R.I.; Robinson, N.; Cavaciuti, A.; Vaninetti, F.; Anderson, C.J.; Zervas, M.N.; Cole, M.J. Dispersion compensation over distances in excess of 500 km for 10-Gb/s systems using chirped fiber gratings. IEEE Photon. Technol. Lett. 1996, 24, 944–946. [Google Scholar] [CrossRef]
- Radic, S.; George, N.; Agrawal, G.P. Theory of low-threshold optical switching in nonlinear phase-shifted periodic structures. J. Opt. Soc. Am. B 1995, 12, 671–680. [Google Scholar] [CrossRef]
- De Sterke, C.M.; Eggleton, B.J.; Krug, P.A. High-intensity pulse propagation in uniform gratings and grating superstructures. J. Light. Technol. 1997, 15, 1494–1502. [Google Scholar] [CrossRef]
- Winful, H.G.; Marburger, J.H.; Garmire, E. Theory of bistability in nonlinear distributed feedback structures. Appl. Phys. Lett. 1979, 75, 379–381. [Google Scholar] [CrossRef]
- Cao, H.; Atai, J.; Shu, X.; Chen, G. Direct design of high channel-count fiber Bragg grating filters with low index modulation. Opt. Express 2012, 20, 12095–12110. [Google Scholar] [CrossRef] [PubMed]
- Cao, H.; Shu, X.; Atai, J.; Gbadebo, A.; Xiong, B.; Fan, T.; Tang, H.; Yang, W.; Yu, Y. Optimally-designed single fiber Bragg grating filter scheme for RZ-OOK/DPSK/DQPSK to NRZ-OOK/DPSK/DQPSK format conversion. Opt. Express 2014, 22, 30442–30460. [Google Scholar] [CrossRef] [PubMed]
- Eggleton, B.J.; de Sterke, C.M.; Slusher, R.E. Nonlinear pulse propagation in Bragg gratings. J. Opt. Soc. America. B Opt. Phys. 1997, 14, 2980–2993. [Google Scholar] [CrossRef]
- De Sterke, C.M.; Sipe, J.E. Gap solitons. Prog. Opt. 1994, 33, 203–260. [Google Scholar]
- Marangos, J. Slow light in cool atoms. Nature 1999, 397, 559–560. [Google Scholar] [CrossRef]
- McDonald, K.T. Slow light. Am. J. Phys. 2000, 68, 293–294. [Google Scholar] [CrossRef]
- Krauss, T.F. Why do we need slow light? Nat. Photon. 2008, 2, 448–450. [Google Scholar] [CrossRef]
- Chiao, R.Y.; Garmire, E.; Townes, C.H. Self-Trapping of Optical Beams. Phys. Rev. Lett. 1964, 13, 479–482. [Google Scholar] [CrossRef]
- Hasegawa, A.; Tappert, F. Transmission of stationary nonlinear optical pulses in dispersive dielectric fibers. I. Anomalous dispersion. Appl. Phys. Lett. 1973, 23, 142–144. [Google Scholar] [CrossRef]
- Hayata, K.; Koshiba, M. Multidimensional solitons in quadratic nonlinear media. Phys. Rev. Lett. 1993, 71, 3275–3278. [Google Scholar] [CrossRef] [PubMed]
- Torner, L.; Mazilu, D.; Mihalache, D. Walking Solitons in Quadratic Nonlinear Media. Phys. Rev. Lett. 1996, 77, 2455–2458. [Google Scholar] [CrossRef] [PubMed]
- Kivshar, Y.S.; Agrawal, G.P. Optical Solitons: From Fibers to Photonic Crystals; Academic Press: San Diego, CA, USA, 2003; p. xvi. 540p. [Google Scholar]
- AlQahtani, S.A.; Shohib, R.M.A.; Alngar, M.E.M.; Alawwad, A.M. High-stochastic solitons for the eighth-order NLSE through Itô calculus and STD with higher polynomial nonlinearity and multiplicative white noise. Opt. Quantum Electron. 2023, 55, 1227. [Google Scholar] [CrossRef]
- AlQahtani, S.A.; Al-Rakhami, M.S.; Shohib, R.M.A.; Alngar, M.E.M.; Pathak, P. Dispersive optical solitons with Schrödinger–Hirota equation using the P6-model expansion approach. Opt. Quantum Electron. 2023, 55, 701. [Google Scholar] [CrossRef]
- Christodoulides, D.N.; Joseph, R.I. Slow Bragg solitons in nonlinear periodic structures. Phys. Rev. Lett. 1989, 62, 1746–1749. [Google Scholar] [CrossRef]
- Aceves, A.B.; Wabnitz, S. Self-induced transparency solitons in nonlinear refractive periodic media. Phys. Lett. A 1989, 141, 37–42. [Google Scholar] [CrossRef]
- Malomed, B.A.; Tasgal, R.S. Vibration modes of a gap soliton in a nonlinear optical medium. Phys. Rev. E 1994, 49, 5787–5796. [Google Scholar] [CrossRef]
- De Rossi, A.; Conti, C.; Trillo, S. Stability, Multistability, and Wobbling of Optical Gap Solitons. Phys. Rev. Lett. 1998, 81, 85–88. [Google Scholar] [CrossRef]
- Barashenkov, I.V.; Pelinovsky, D.E.; Zemlyanaya, E.V. Vibrations and Oscillatory Instabilities of Gap Solitons. Phys. Rev. Lett. 1998, 80, 5117–5120. [Google Scholar] [CrossRef]
- Littler, I.C.M.; Mok, J.T.; Eggleton, B.J.; de Sterke, C.M. Dispersionless slow light using gap solitons. Nat. Phys. 2006, 2, 775–780. [Google Scholar]
- Skryabin, D. Coupled core-surface solitons in photonic crystal fibers. Opt. Express 2004, 12, 4841–4846. [Google Scholar] [CrossRef]
- Monat, C.; de Sterke, M.; Eggleton, B.J. Slow light enhanced nonlinear optics in periodic structures. J. Opt. 2010, 12, 104003. [Google Scholar] [CrossRef]
- Atai, J.; Malomed, B.A.; Merhasin, I.M. Stability and collisions of gap solitons in a model of a hollow optical fiber. Opt. Commun. 2006, 265, 342–348. [Google Scholar] [CrossRef]
- Atai, J.; Malomed, B.A. Bragg-grating solitons in a semilinear dual-core system. Phys. Rev. E 2000, 62, 8713–8718. [Google Scholar] [CrossRef] [PubMed]
- Atai, J.; Malomed, B.A. Solitary waves in systems with separated Bragg grating and nonlinearity. Phys. Rev. E 2001, 64, 066617. [Google Scholar] [CrossRef]
- Mak, W.C.K.; Chu, P.L.; Malomed, B.A. Solitary waves in coupled nonlinear waveguides with Bragg gratings. J. Opt. Soc. Am. B 1998, 15, 1685–1692. [Google Scholar] [CrossRef]
- Tsofe, Y.J.; Malomed, B.A. Quasisymmetric and asymmetric gap solitons in linearly coupled Bragg gratings with a phase shift. Phy. Rev. E 2007, 75, 056603. [Google Scholar] [CrossRef]
- Mandelik, D.; Morandotti, R.; Aitchison, J.S.; Silberberg, Y. Gap solitons in waveguide arrays. Phys. Rev. Lett. 2004, 92, 093904. [Google Scholar] [CrossRef] [PubMed]
- Dong, R.; Rüter, C.E.; Kip, D.; Cuevas, J.; Kevrekidis, P.G.; Song, D.; Xu, J. Dark-bright gap solitons in coupled-mode one-dimensional saturable waveguide arrays. Phys. Rev. A 2011, 83, 063816. [Google Scholar] [CrossRef]
- Tan, Y.; Chen, F.; Beličev, P.P.; Stepić, M.; Maluckov, A.; Rüter, C.E.; Kip, D. Gap solitons in defocusing lithium niobate binary waveguide arrays fabricated by proton implantation and selective light illumination. Appl. Phys. B 2009, 95, 531–535. [Google Scholar] [CrossRef]
- Gorbach, A.; Malomed, B.; Skryabin, D. Gap polariton solitons. Phys. Lett. A 2009, 373, 3024–3027. [Google Scholar] [CrossRef]
- Conti, C.; Trillo, S.; Assanto, G. Doubly resonant Bragg simultons via second-harmonic generation. Phys. Rev. Lett. 1997, 78, 2341–2344. [Google Scholar] [CrossRef]
- He, H.; Drummond, P.D. Ideal soliton environment using parametric band gaps. Phys. Rev. Lett. 1997, 78, 4311–4315. [Google Scholar] [CrossRef]
- Mak, W.C.K.; Malomed, B.A.; Chu, P.L. Three-wave gap solitons in waveguides with quadratic nonlinearity. Phys. Rev. E 1998, 58, 6708–6722. [Google Scholar] [CrossRef]
- Atai, J.; Malomed, B.A. Spatial solitons in a medium composed of self-focusing and self-defocusing layers. Phys. Lett. A 2002, 298, 140–148. [Google Scholar] [CrossRef]
- Atai, J.; Malomed, B.A. Families of Bragg-grating solitons in a cubic-quintic medium. Phys. Lett. A 2001, 284, 247–252. [Google Scholar] [CrossRef]
- Atai, J. Interaction of Bragg grating solitons in a cubic-quintic medium. J. Opt. B Quantum Semiclass. 2004, 6, S177–S181. [Google Scholar] [CrossRef]
- Dasanayaka, S.; Atai, J. Moving Bragg grating solitons in a cubic-quintic nonlinear medium with dispersive reflectivity. Phys. Rev. E 2013, 88, 022921. [Google Scholar] [CrossRef] [PubMed]
- Dasanayaka, S.; Atai, J. Stability and collisions of moving Bragg grating solitons in a cubic-quintic nonlinear medium. J. Opt. Soc. Am. B 2013, 30, 396–404. [Google Scholar] [CrossRef]
- Jensen, S.M. The Nonlinear Coherent Coupler. IEEE Trans. Microw. Theory Tech. 1982, 30, 1568–1571. [Google Scholar] [CrossRef]
- Maier, A.A. Optical transistors and bistable devices utilizing non- linear transmission of light in systems with undirectional coupled waves. Sov. J. Quantum Electron. 1982, 12, 11490–11494. [Google Scholar] [CrossRef]
- Maier, A.A. Possible practical use of self-switching of radiation in coupled waveguides for amplification of the useful modulation of a signal. Sov. J. Quantum Electron. 1987, 17, 1013–1017. [Google Scholar] [CrossRef]
- Yang, C.C. All-optical ultrafast logic gates that use asymmetric nonlinear directional couplers. Opt. Lett. 1991, 16, 1641–1643. [Google Scholar] [CrossRef] [PubMed]
- Chen, Y.; Atai, J. Parametric spatial solitary waves. Opt. Lett. 1994, 19, 1287–1289. [Google Scholar] [CrossRef] [PubMed]
- Chen, Y.; Atai, J. Stability of fundamental solitons of coupled nonlinear Schrödinger equations. Opt. Commun. 1998, 150, 381–389. [Google Scholar] [CrossRef]
- Nistazakis, H.E.; Frantzeskakis, D.J.; Atai, J.; Malomed, B.A.; Efremidis, N.; Hizanidis, K. Multichannel pulse dynamics in a stabilized Ginzburg-Landau system. Phys. Review. E Stat. Nonlinear Soft Matter Phys. 2002, 65, 036605. [Google Scholar] [CrossRef]
- Atai, J.; Chen, Y. Nonlinear couplers composed of different nonlinear cores. J. Appl. Phys. 1992, 72, 24–27. [Google Scholar] [CrossRef]
- Atai, J.; Chen, Y. Nonlinear mismatches between two cores of saturable nonlinear couplers. IEEE J. Quant. Electron. 1993, 29, 242–249. [Google Scholar] [CrossRef]
- Archambault, J.L.; Russell, P.S.J.; Barcelos, S.; Hua, P.; Reekie, L. Grating-frustrated coupler: A novel channel-dropping filter in single-mode optical fiber. Opt. Lett. 1994, 19, 180–182. [Google Scholar] [CrossRef] [PubMed]
- Erdogan, T. Optical add–drop multiplexer based on an asymmetric Bragg coupler. Opt. Commun. 1998, 157, 249–264. [Google Scholar] [CrossRef]
- Aslund, M.; Poladian, L.; Canning, J.; de Sterke, C. Add-drop multiplexing by dispersion inverted interference coupling. J. Light. Technol. 2002, 20, 1585–1589. [Google Scholar] [CrossRef]
- An, H.; Ashton, B.; Fleming, S. Long-period-grating-assisted optical add–drop filter based on mismatched twin-core photosensitive-cladding fiber. Opt. Lett. 2004, 29, 343–345. [Google Scholar] [CrossRef] [PubMed]
- Shnaiderman, R.; Tasgal, R.S.; Band, Y.B. Creating very slow optical gap solitons with a grating-assisted coupler. Opt. Lett. 2011, 36, 2438–2440. [Google Scholar] [CrossRef] [PubMed]
- Li, H.; Deng, Z.; Huang, J.; Fu, S.; Li, Y. Slow-light all-optical soliton diode based on tailored Bragg-grating structure. Opt. Lett. 2015, 40, 2572–2575. [Google Scholar] [CrossRef]
- Shapira, Y.P.; Horowitz, M. Optical AND gate based on soliton interaction in a fiber Bragg grating. Opt. Lett. 2007, 32, 1211–1213. [Google Scholar] [CrossRef] [PubMed]
- Raphael Broderick, N.G.; de Sterke, C.M. Theory of grating superstructures. Phys. Rev. E 1997, 55, 3634–3646. [Google Scholar] [CrossRef]
- Khurgin, J.B. Light slowing down in Moiré fiber gratings and its implications for nonlinear optics. Phys. Review. A At. Mol. Opt. Phys. 2000, 62, 013821. [Google Scholar] [CrossRef]
- Janner, D.; Galzerano, G.; Valle, G.D.; Laporta, P.; Longhi, S.; Belmonte, M. Slow light in periodic superstructure Bragg gratings. Phys. Review. E Stat. Nonlinear Soft Matter Phys. 2005, 72, 056605. [Google Scholar] [CrossRef] [PubMed]
- Gnan, M.; Bellanca, G.; Chong, H.M.H.; Bassi, P.; De La Rue, R.M. Modelling of Photonic Wire Bragg Gratings. Opt. Quantum Electron. 2006, 38, 133–148. [Google Scholar] [CrossRef]
- Atai, J.; Malomed, B.A. Gap solitons in Bragg gratings with dispersive reflectivity. Phys. Lett. A 2005, 342, 404–412. [Google Scholar] [CrossRef]
- Royston Neill, D.; Atai, J.; Malomed, B.A. Dynamics and collisions of moving solitons in Bragg gratings with dispersive reflectivity. J. Opt. A Pure Appl. Opt. 2008, 10, 085105. [Google Scholar] [CrossRef]
- Ahmed, T.; Atai, J. Bragg solitons in systems with separated nonuniform Bragg grating and nonlinearity. Phys. Rev. E 2017, 96, 032222. [Google Scholar] [CrossRef] [PubMed]
- Chowdhury, S.A.M.S.; Atai, J. Moving Bragg grating solitons in a semilinear dual-core system with dispersive reflectivity. Sci. Rep. 2017, 7, 4021. [Google Scholar] [CrossRef]
- Ahmed, T.; Atai, J. Effect of Dispersive Reflectivity on the Stability of Gap Solitons in Systems with Separated Bragg Grating and Nonlinearity. In Proceedings of the 4th International Conference on Photonics, Optics and Laser Technology, Rome, Italy, 27–29 February 2016; pp. 231–235. [Google Scholar]
- Conti, C.; Trillo, S. Bifurcation of gap solitons through catastrophe theory. Phys. Rev. E 2001, 64, 036617. [Google Scholar] [CrossRef]

Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ahmed, T.; Atai, J. Moving Bragg Solitons in a Dual-Core System Composed of a Linear Bragg Grating with Dispersive Reflectivity and a Uniform Nonlinear Core. Photonics 2024, 11, 324. https://doi.org/10.3390/photonics11040324
Ahmed T, Atai J. Moving Bragg Solitons in a Dual-Core System Composed of a Linear Bragg Grating with Dispersive Reflectivity and a Uniform Nonlinear Core. Photonics. 2024; 11(4):324. https://doi.org/10.3390/photonics11040324
Chicago/Turabian StyleAhmed, Tanvir, and Javid Atai. 2024. "Moving Bragg Solitons in a Dual-Core System Composed of a Linear Bragg Grating with Dispersive Reflectivity and a Uniform Nonlinear Core" Photonics 11, no. 4: 324. https://doi.org/10.3390/photonics11040324
APA StyleAhmed, T., & Atai, J. (2024). Moving Bragg Solitons in a Dual-Core System Composed of a Linear Bragg Grating with Dispersive Reflectivity and a Uniform Nonlinear Core. Photonics, 11(4), 324. https://doi.org/10.3390/photonics11040324




