Compressed Sensing Image Reconstruction with Fast Convolution Filtering
Abstract
1. Introduction
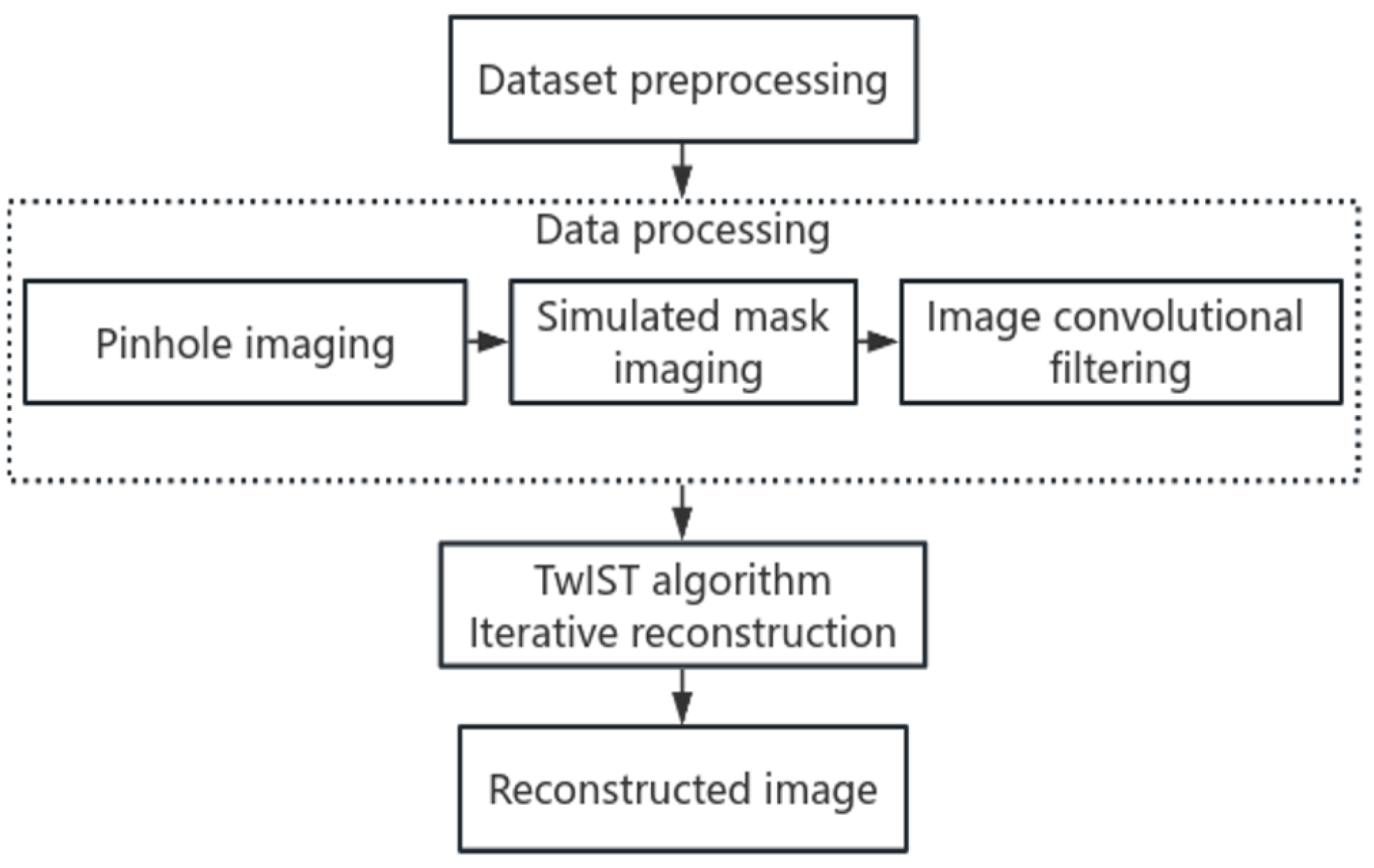
2. Principle and Optimization
2.1. Principle of Compressed Sensing Reconstruction
2.2. Optimization of Compressed Sensing Reconstruction
3. Experimental Results and Discussion
3.1. Design of Evaluation Criteria
3.2. Performance of Compressed Sensing Reconstruction with Fast Convolution Filtering
3.3. Comparison of Objective Indicators between Different Reconstruction Methods
3.4. Comparison of Subjective Indicators between Different Reconstruction Methods
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Miao, J.; Charalambous, P.; Kirz, J.; Sayre, D. Extending the methodology of X-ray crystallography to allow imaging of micrometre-sized non-crystalline specimens. Nature 1999, 400, 342–344. [Google Scholar] [CrossRef]
- Marchesini, S.; He, H.; Chapman, H.N.; Hau-Riege, S.P.; Noy, A.; Howells, M.R.; Weierstall, U.; Spence, J.C. X-ray image reconstruction from a diffraction pattern alone. Phys. Rev. B 2003, 68, 140101. [Google Scholar] [CrossRef]
- Rodenburg, J.M. Ptychography and related diffractive imaging methods. Adv. Imaging Electron Phys. 2008, 150, 87–184. [Google Scholar]
- Zheng, G.; Horstmeyer, R.; Yang, C. Wide-field, high-resolution Fourier ptychographic microscopy. Nat. Photonics 2013, 7, 739–745. [Google Scholar] [CrossRef] [PubMed]
- Gao, Z.; Radner, H.; Büttner, L.; Ye, H.; Li, X.; Czarske, J. Distortion correction for particle image velocimetry using multiple-input deep convolutional neural network and Hartmann-Shack sensing. Opt. Express 2021, 29, 18669–18687. [Google Scholar] [CrossRef] [PubMed]
- Zhang, H.; Kuschmierz, R.; Czarske, J.; Fischer, A. Camera-based speckle noise reduction for 3-D absolute shape measurements. Opt. Express 2016, 24, 12130–12141. [Google Scholar] [CrossRef] [PubMed]
- Zhang, H.; Kuschmierz, R.; Czarske, J. Miniaturized interferometric 3-D shape sensor using coherent fiber bundles. Opt. Lasers Eng. 2018, 107, 364–369. [Google Scholar] [CrossRef]
- Kuschmierz, R.; Scharf, E.; Ortegón-González, D.F.; Glosemeyer, T.; Czarske, J.W. Ultra-thin 3D lensless fiber endoscopy using diffractive optical elements and deep neural networks. Light Adv. Manuf. 2021, 2, 415–424. [Google Scholar] [CrossRef]
- Zhang, H. Laser interference 3-D sensor with line-shaped beam based multipoint measurements using cylindrical lens. Opt. Lasers Eng. 2022, 159, 107218. [Google Scholar] [CrossRef]
- Candès, E.J.; Romberg, J.; Tao, T. Robust uncertainty principles: Exact signal reconstruction from highly incomplete frequency information. IEEE Trans. Inf. Theory 2006, 52, 489–509. [Google Scholar] [CrossRef]
- Pilastri, A.L.; Tavares, J.M.R. Reconstruction algorithms in compressive sensing: An overview. In Proceedings of the 11th Edition of the Doctoral Symposium in Informatics Engineering (DSIE-16), Porto, Portugal, 3 February 2016. [Google Scholar]
- Donoho, D.L. Compressed sensing. IEEE Trans. Inf. Theory 2006, 52, 1289–1306. [Google Scholar] [CrossRef]
- Needell, D.; Ward, R. Stable image reconstruction using total variation minimization. SIAM J. Imaging Sci. 2013, 6, 1035–1058. [Google Scholar] [CrossRef]
- Zhu, T. New over-relaxed monotone fast iterative shrinkage-thresholding algorithm for linear inverse problems. IET Image Process. 2019, 13, 2888–2896. [Google Scholar] [CrossRef]
- Pati, Y.C.; Rezaiifar, R.; Krishnaprasad, P.S. Orthogonal matching pursuit: Recursive function approximation with applications to wavelet decomposition. In Proceedings of the 27th Asilomar Conference on Signals, Systems and Computers, Pacific Grove, CA, USA, 1–3 November 1993; pp. 40–44. [Google Scholar]
- Kulkarni, K.; Lohit, S.; Turaga, P.; Kerviche, R.; Ashok, A. Reconnet: Non-iterative reconstruction of images from compressively sensed measurements. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Las Vegas, NV, USA, 27–30 June 2016; pp. 449–458. [Google Scholar]
- Yao, H.; Dai, F.; Zhang, S.; Zhang, Y.; Tian, Q.; Xu, C. Dr2-net: Deep residual reconstruction network for image compressive sensing. Neurocomputing 2019, 359, 483–493. [Google Scholar] [CrossRef]
- Du, J.; Xie, X.; Wang, C.; Shi, G.; Xu, X.; Wang, Y. Fully convolutional measurement network for compressive sensing image reconstruction. Neurocomputing 2019, 328, 105–112. [Google Scholar] [CrossRef]
- Sun, Y.; Chen, J.; Liu, Q.; Liu, B.; Guo, G. Dual-path attention network for compressed sensing image reconstruction. IEEE Trans. Image Process. 2020, 29, 9482–9495. [Google Scholar] [CrossRef]
- Lesnikov, V.; Naumovich, T.; Chastikov, A. Analysis of Periodically Non-Uniform Sampled Signals. In Proceedings of the 2022 24th International Conference on Digital Signal Processing and its Applications (DSPA), Moscow, Russian, 30 March–1 April 2022; pp. 1–4. [Google Scholar]
- Li, C. An Efficient Algorithm for Total Variation Regularization with Applications to the Single Pixel Camera and Compressive Sensing. Master’s Thesis, Rice University, Houston, TX, USA, 2010. [Google Scholar]
- Bioucas-Dias, J.M.; Figueiredo, M.A. A new TwIST: Two-step iterative shrinkage/thresholding algorithms for image restoration. IEEE Trans. Image Process. 2007, 16, 2992–3004. [Google Scholar] [CrossRef]
- Devaney, A.J. A filtered backpropagation algorithm for diffraction tomography. Ultrason. Imaging 1982, 4, 336–350. [Google Scholar] [CrossRef] [PubMed]
- Park, S.C.; Park, M.K.; Kang, M.G. Super-resolution image reconstruction: A technical overview. IEEE Signal Process. Mag. 2003, 20, 21–36. [Google Scholar] [CrossRef]
- Kumar, B.; Singh, S.P.; Mohan, A.; Anand, A. Performance of quality metrics for compressed medical images through mean opinion score prediction. J. Med. Imaging Health Inform. 2012, 2, 188–194. [Google Scholar] [CrossRef]


| Iterations | 10 | 50 | 100 | 200 | 300 | 500 |
|---|---|---|---|---|---|---|
| 932.75 | 675.22 | 659.60 | 613.53 | 555.17 | 456.28 | |
| (dB) | 18.43 | 19.84 | 19.94 | 20.25 | 20.69 | 21.54 |
| 0.79 | 0.82 | 0.82 | 0.82 | 0.83 | 0.84 |
| CS | Sample Size | Resolution | (dB) | Time (s) | ||
| 1 | 3517.651 | 12.668 | 0.562 | 35.407 | ||
| 20 | 3545.595 | 12.921 | 0.523 | 689.741 | ||
| 50 | 3221.781 | 13.445 | 0.530 | 1797.955 | ||
| F-CS | Sample Size | Resolution | (dB) | Time (s) | ||
| 1 | 3541.930 | 12.638 | 0.573 | 4.831 | ||
| 20 | 3524.768 | 12.952 | 0.533 | 89.822 | ||
| 50 | 3186.801 | 13.495 | 0.541 | 229.565 |
| F-CS | Sample Size | Resolution | (dB) | Time (s) | CPU Usage Rate | RAM Usage Rate | GPU Usage Rate | ||
| 1 | 2845.28 | 13.56 | 0.74 | 5.15 | |||||
| 20 | 1868.85 | 18.57 | 0.83 | 101.16 | 15.1% | 12.9% | 0% | ||
| 50 | 1381.65 | 18.11 | 0.83 | 254.15 | |||||
| BP | Sample Size | Resolution | (dB) | Time (s) | |||||
| 1 | 6114.53 | 10.27 | 0.37 | 0.06 | |||||
| 20 | 4889.76 | 12.27 | 0.48 | 1.53 | 7.0% | 11.0% | 0% | ||
| 50 | 4480.22 | 12.29 | 0.51 | 3.48 | |||||
| SR | Sample Size | Resolution | (dB) | Time (s) | |||||
| 1 | 166.61 | 25.91 | 0.78 | 2.82 | |||||
| 20 | 272.85 | 25.86 | 0.89 | 43.80 | 17.4% | 67.2% | 15% | ||
| 50 | 509.01 | 22.89 | 0.75 | 122.36 |
| Reconstruction Image | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | 16 | 17 | 18 | 19 | 20 |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| F-CS | 3.3 | 3.7 | 3.7 | 3.55 | 3.55 | 3.45 | 3.65 | 4.75 | 3.5 | 3.65 | 3.3 | 3.35 | 3.4 | 3.55 | 3.55 | 3.35 | 3.4 | 3.45 | 3.45 | 4.35 |
| BP | 1.6 | 3.55 | 3.7 | 1.5 | 3.55 | 3.6 | 3.3 | 1.7 | 1.4 | 1.35 | 1.5 | 3.55 | 1.65 | 1.4 | 3.6 | 1.5 | 3.55 | 1.45 | 1.45 | 3.45 |
| SR | 4.6 | 4.4 | 3.45 | 3.45 | 3.45 | 3.4 | 4.65 | 3.45 | 3.55 | 3.45 | 3.5 | 3.55 | 3.3 | 3.75 | 4.5 | 3.55 | 3.35 | 3.55 | 3.4 | 3.35 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Guo, R.; Zhang, H. Compressed Sensing Image Reconstruction with Fast Convolution Filtering. Photonics 2024, 11, 323. https://doi.org/10.3390/photonics11040323
Guo R, Zhang H. Compressed Sensing Image Reconstruction with Fast Convolution Filtering. Photonics. 2024; 11(4):323. https://doi.org/10.3390/photonics11040323
Chicago/Turabian StyleGuo, Runbo, and Hao Zhang. 2024. "Compressed Sensing Image Reconstruction with Fast Convolution Filtering" Photonics 11, no. 4: 323. https://doi.org/10.3390/photonics11040323
APA StyleGuo, R., & Zhang, H. (2024). Compressed Sensing Image Reconstruction with Fast Convolution Filtering. Photonics, 11(4), 323. https://doi.org/10.3390/photonics11040323





