Wavelet Decomposition Layer Selection for the φ-OTDR Signal
Abstract
1. Introduction
2. Principle
2.1. Wavelet Denoising
- Decompose the noisy signal using a designated wavelet basis and Decomposition Level (DL).
- Eliminate the noise component from the wavelet coefficients of each DL using a specified threshold and threshold function.
- Reconstruct the wavelet coefficients subjected to threshold shrinkage through wavelet inversion, resulting in the denoised signal.
2.2. Method Noise
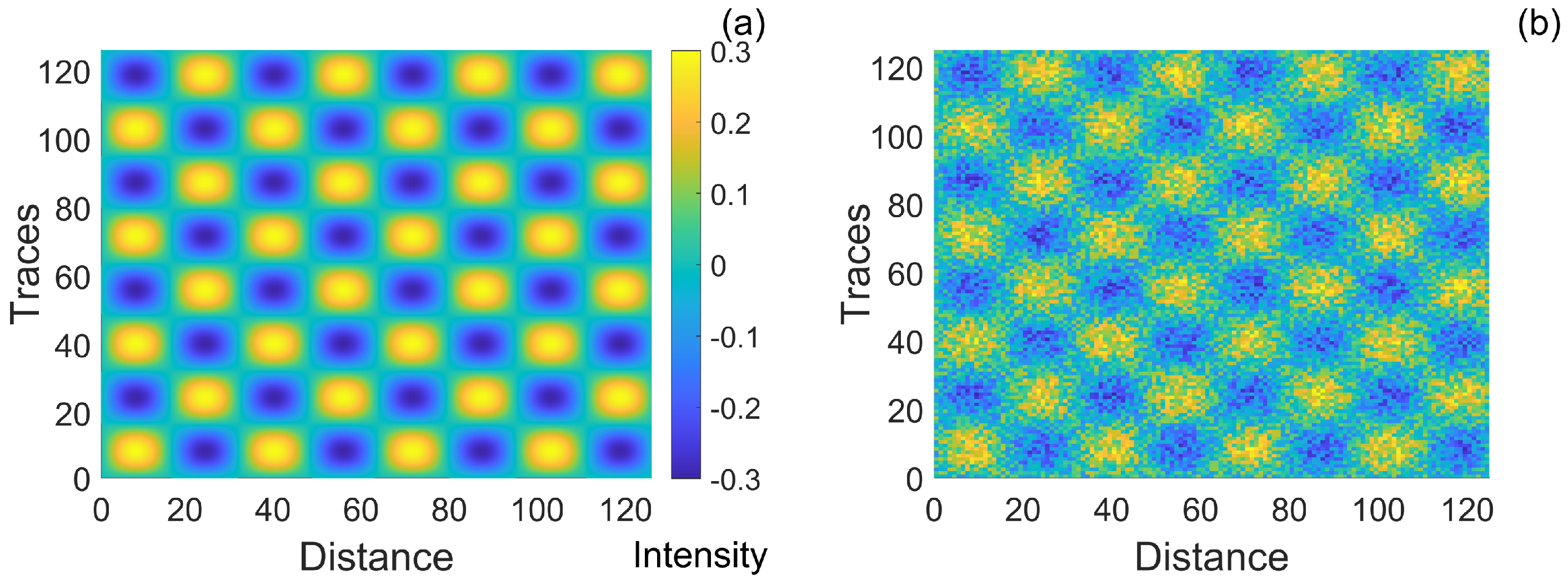
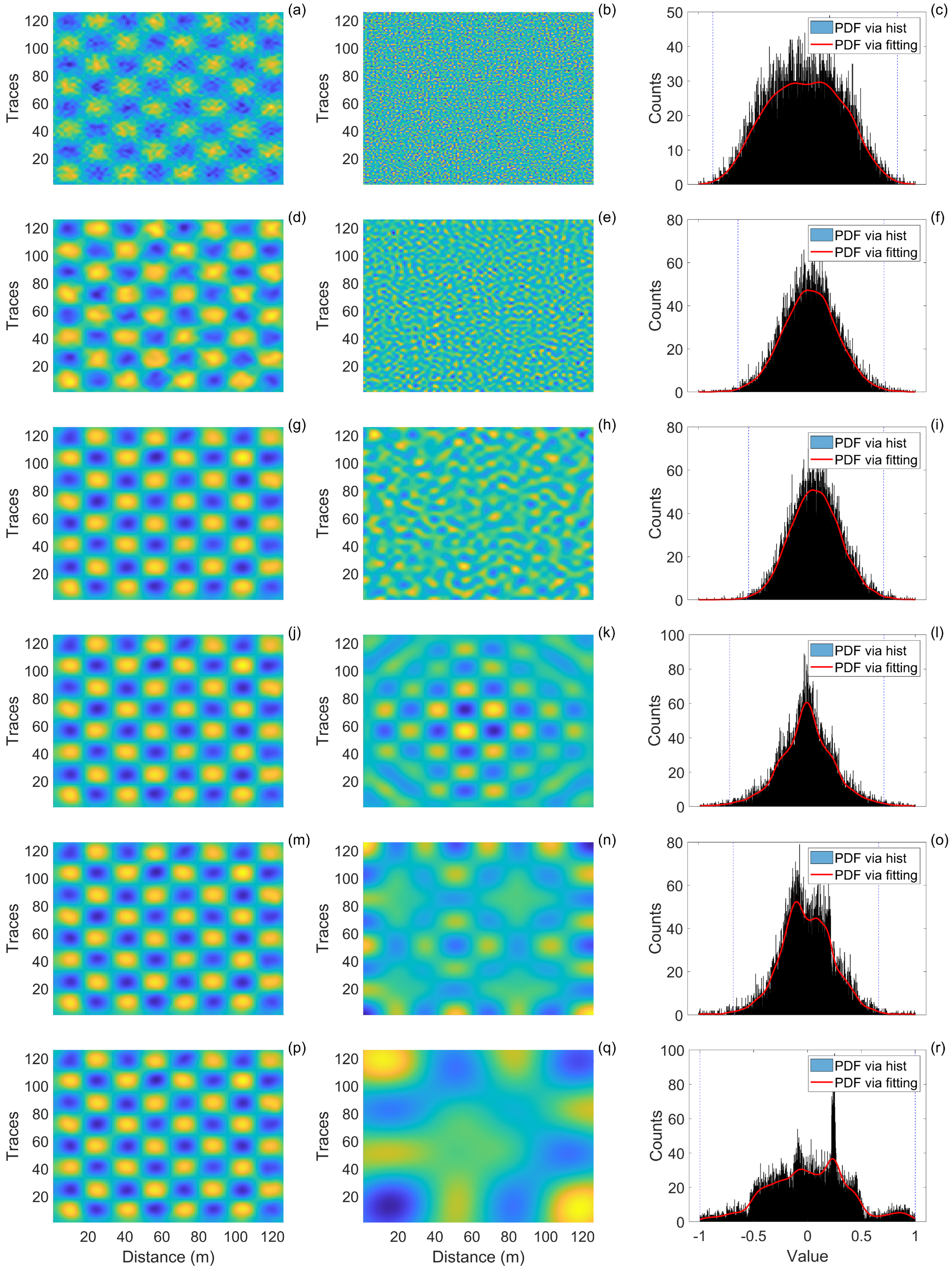
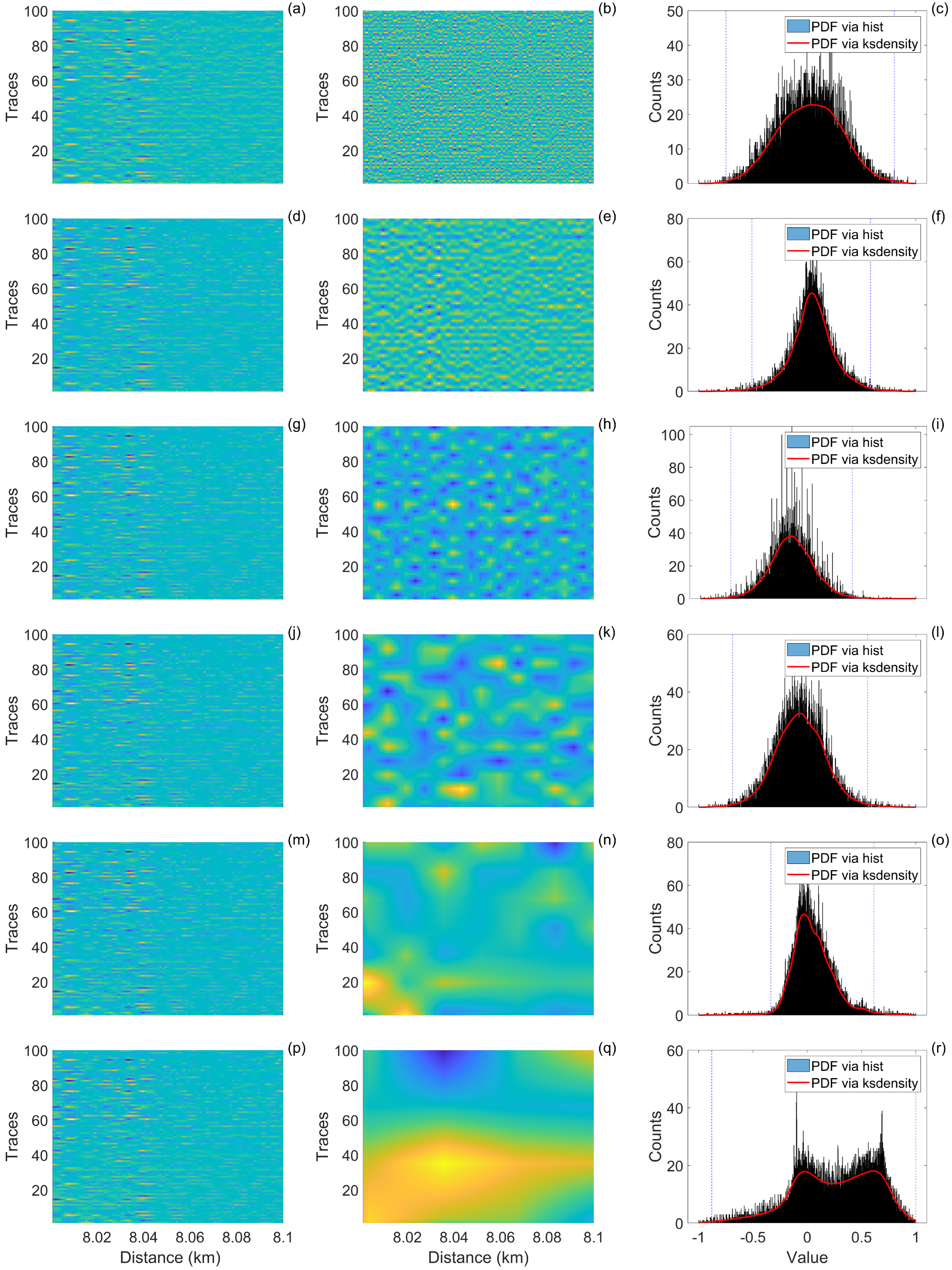
- Obtain the MN and its PDF distribution by subtracting the wavelet denoised signal obtained using the first DL from the noisy signal.
- Similarly, obtain the corresponding MN and PDF distributions for various DLs by subtracting denoised signals obtained from different DLs from the noisy signal.
- Calculate the similarity between the PDF distributions of different DLs and the PDF distribution of the first DL.
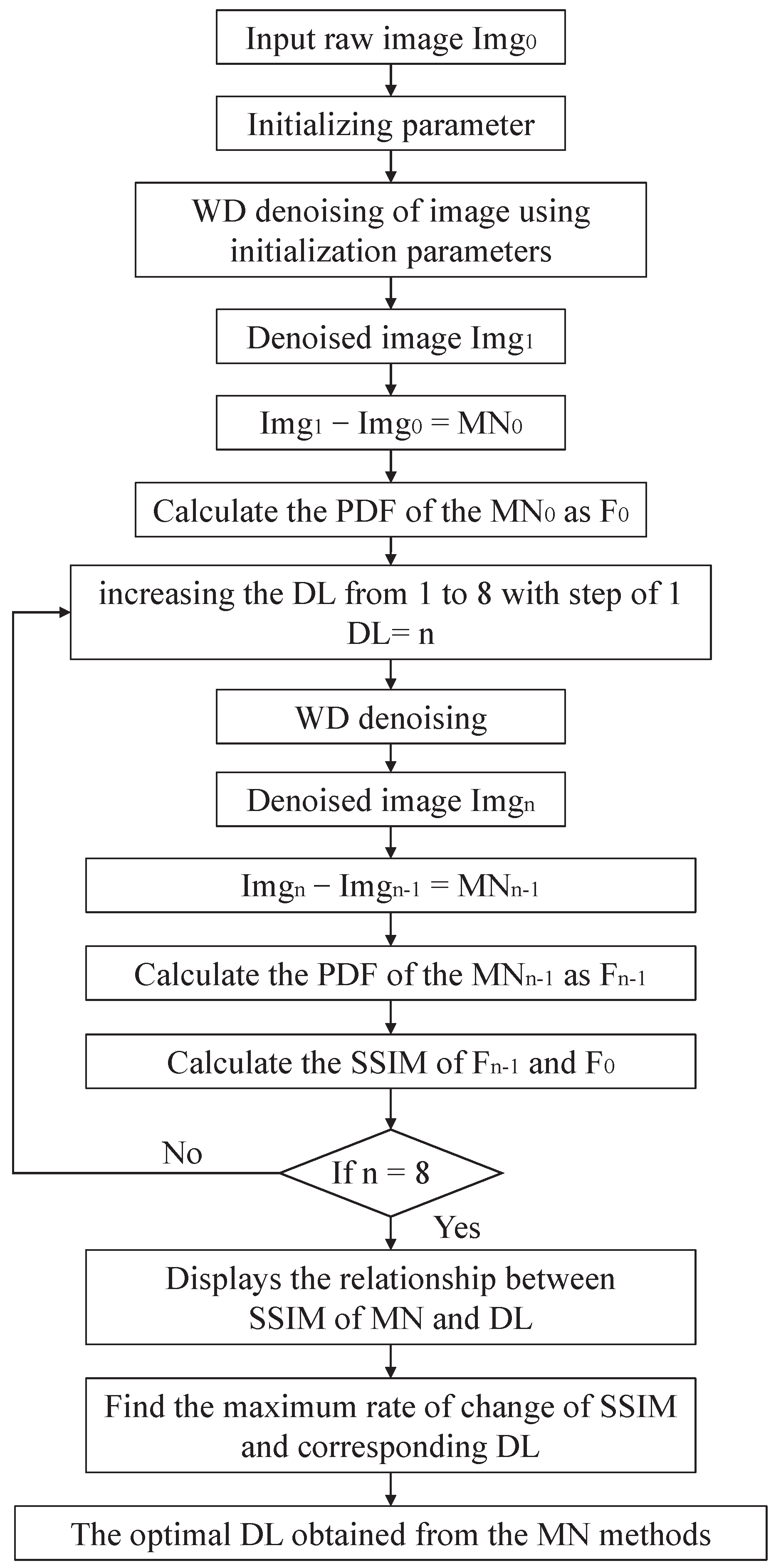
- Initialize the parameter of WD as “Dmey” wavelet base, soft threshold function, DL = 1. Then, the wavelet coefficient of each DL are obtained using Matlab command “wavedec2”, and the threshold of each DL is optimized by FCL-ACF based thresholding method [33].
- Denoise the noisy image by WD with the initial parameters.
- Calculate the MN0 of raw image and denoised image .
- Calculate the PDF of MN0 that is used as the reference.
- Increase the DL from 1 to 8 with step of 1.
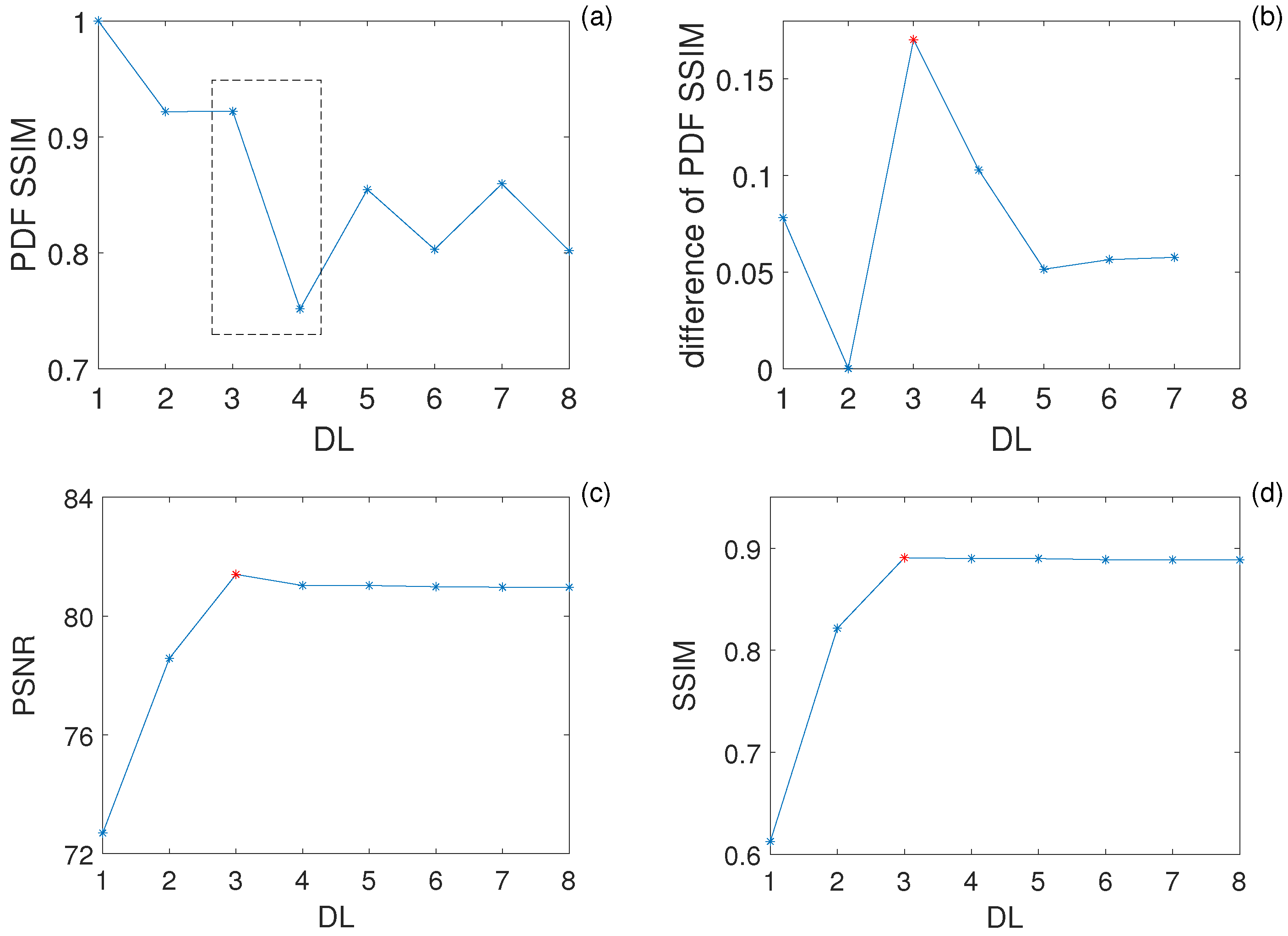
- Repeat the above steps to obtain the SSIM of MN of each DL until DL reaches 8.
- Identify the DL that has the largest rate of change in SSIM of the PDF of MN, i.e., the best layer.
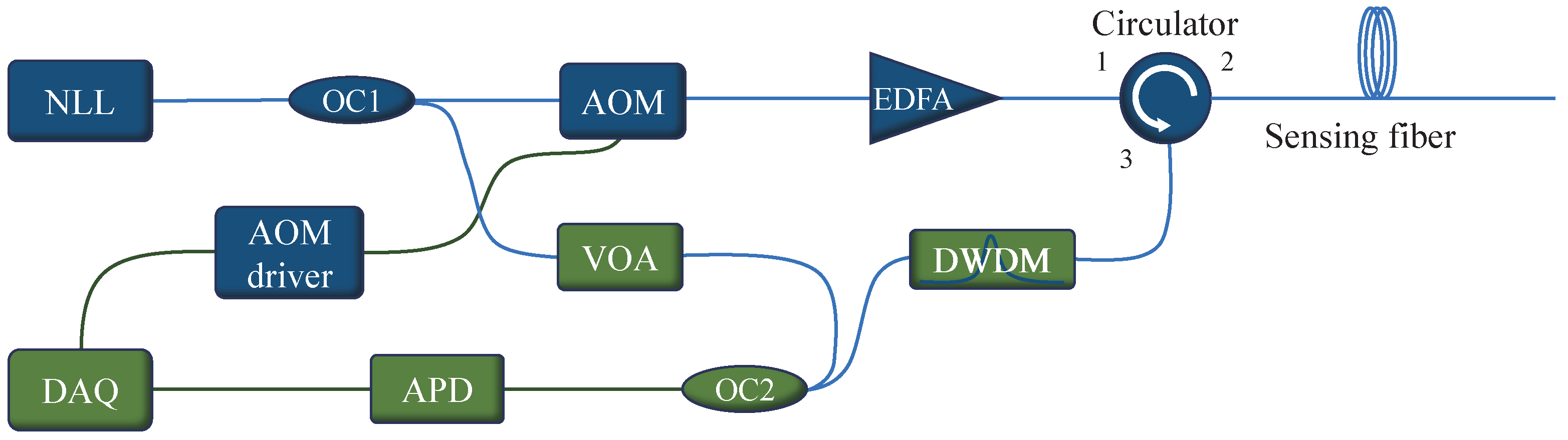
2.3. -OTDR
3. Decomposition Layer Optimization Based on Method Noise
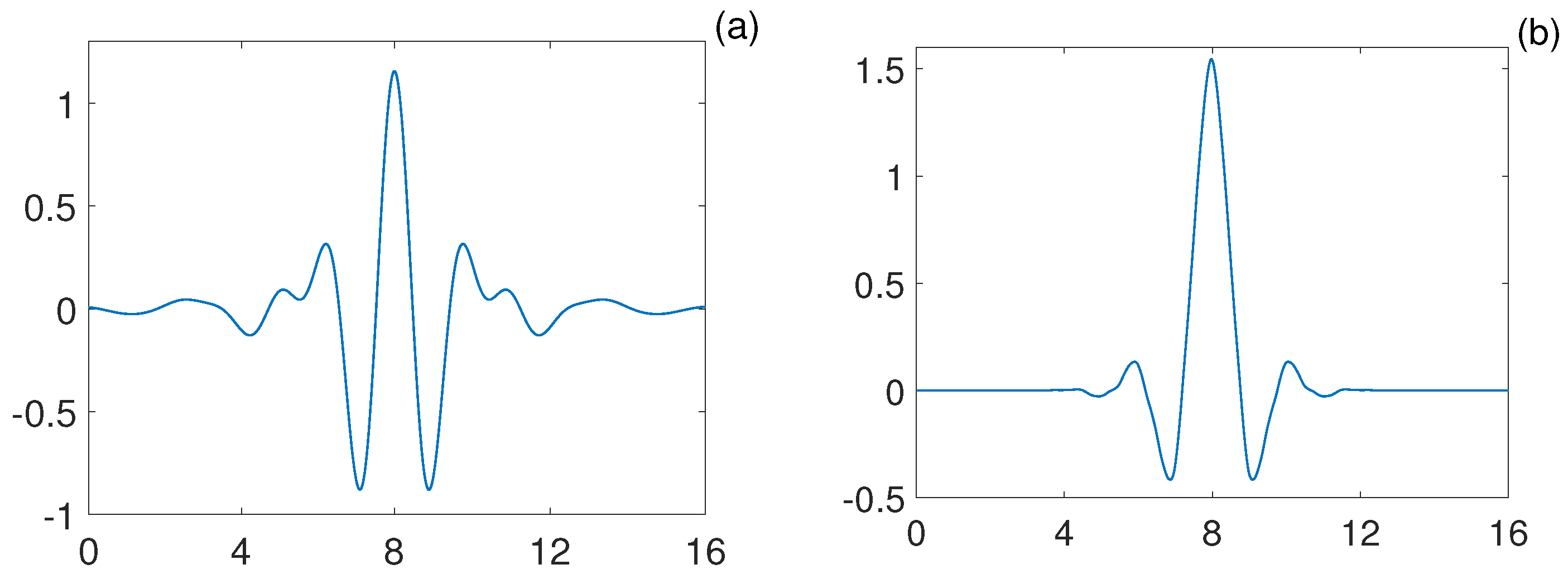
3.1. Hypothetical Signal
3.2. Measured -OTDR Signal
4. Discussion
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Zhao, H.D.; Wu, D.F.; Zeng, M.Y.; Ling, J.M. Support conditions assessment of concrete pavement slab using distributed optical fiber sensor. Transp. A-Transp. Sci. 2019, 15, 71–90. [Google Scholar] [CrossRef]
- Dang, Y.L.; Zhao, Z.Y.; Wang, X.F.; Liao, R.L.; Lu, C. Simultaneous distributed vibration and temperature sensing using multicore fiber. IEEE Access 2019, 7, 151818–151826. [Google Scholar] [CrossRef]
- Li, P.F.; Fu, C.L.; Du, B.; He, J.; Zhong, H.J.; Du, C.; Wang, L.; Wang, Y.P. High-spatial-resolution strain sensor based on distance compensation and image wavelet denoising method in OFDR. J. Light. Technol. 2021, 39, 6334–6339. [Google Scholar] [CrossRef]
- Wang, Y.J.; Yao, H.P.; Wang, J.J.; Xin, X.J. Distributed optical fiber sensing system for large infrastructure temperature monitoring. IEEE Internet Things J. 2022, 9, 3333–3345. [Google Scholar] [CrossRef]
- Zeng, M.Y.; Zhao, H.D.; Gao, D.C.; Bian, Z.Y.; Wu, D.F. Reconstruction of vehicle-induced vibration on concrete pavement using distributed fiber optic. IEEE Trans. Intell. Transp. Syst. 2022, 23, 24305–24317. [Google Scholar] [CrossRef]
- Chen, B.; Su, L.H.; Zhang, Z.Y.; Liu, X.Z.; Dai, T.G.; Song, M.P.; Yu, H.; Wang, Y.H.; Yang, J.Y. Wavelet convolutional neural network for robust and fast temperature measurements in Brillouin optical time domain reflectometry. Opt. Express 2022, 30, 13942–13958. [Google Scholar] [CrossRef]
- Fu, H.W.; Zhang, Z.; Yan, X.Y.; Wang, X.L.; Zhao, Z.L. Improved wavelet modulus maximum method for distributed optical fiber temperature sensing. Opt. Eng. 2022, 61, 116109. [Google Scholar] [CrossRef]
- Fu, C.L.; Li, P.F.; Sui, R.L.; Peng, Z.W.; Zhong, H.J.; Yin, X.Y.; Wang, Y.P. High-spatial-resolution OFDR distributed temperature sensor based on step-by-step and image wavelet denoising methods. Sensors 2022, 22, 9972. [Google Scholar] [CrossRef]
- Ershov, I.A.; Stukach, O.V. Choice of wavelet for filtering of signal from fiber-optic temperature sensor. In Proceedings of the 2022 Moscow Workshop on Electronic and Networking Technologies (MWENT), Moscow, Russia, 9–11 June 2022; pp. 1–4. [Google Scholar]
- Lyu, C.G.; Niu, Z.H.; Tian, J.C.; Jin, J.; Yang, J.C.; Ge, C.F. Identification of intrusion events based on distributed optical fiber sensing in complex environment. IEEE Internet Things J. 2022, 9, 24212–24220. [Google Scholar] [CrossRef]
- Yu, Z.; Liu, Z.; Zhan, G.; Cheng, P.; Wang, B.; Fei, W. DAS noise attenuation using wavelet stack. In Proceedings of the Second International Meeting for Applied Geoscience & Energy, Houston, TX, USA, 28 August–2 September 2022; pp. 592–596. [Google Scholar]
- Fan, L.; Wang, Y.J.; Zhang, H.X.; Li, C.; Huang, X.Y.; Zhang, Q.; Xin, X.J. Quaternion wavelet transform and a feedforward neural network-aided intelligent distributed optical fiber sensing system. Sensors 2023, 23, 3637. [Google Scholar] [CrossRef] [PubMed]
- An, Y.H.; Ma, J.H.; Xu, T.W.; Cai, Y.P.; Liu, H.Y.; Sun, Y.T.; Yan, W.F. Traffic vibration signal analysis of DAS fiber optic cables with different coupling based on an improved wavelet thresholding method. Sensors 2023, 23, 5727. [Google Scholar] [CrossRef] [PubMed]
- Wu, H.; Zhang, Y.; Chen, H.; Xiao, W.; Huang, L.; Xiao, Y.; Duan, J.; He, X.; Zeng, J.; Chao, Y. The improved wavelet denoising scheme based on robust principal component analysis for distributed fiber acoustic sensor. IEEE Sens. J. 2023, 23, 22944–22951. [Google Scholar] [CrossRef]
- Song, Q.S.; Yan, G.P.; Tang, G.W.; Ansari, F. Robust principal component analysis and support vector machine for detection of microcracks with distributed optical fiber sensors. Mech. Syst. Signal Process. 2021, 146, 107019. [Google Scholar] [CrossRef]
- Li, J.; Lu, B.; Wang, Y.; Liu, X.; Bai, Q.; Jin, B. Distributed optical fiber vibration sensor for the identification of pipeline leakage using relevant vector machine. In Proceedings of the Optics Frontiers Online 2020: Distributed Optical Fiber Sensing Technology and Applications, SPIE, Online, 24–25 July 2020; Volume 11607, pp. 108–111. [Google Scholar]
- Wijaya, H.; Rajeev, P.; Gad, E.; Vivekanamtham, R. Distributed optical fibre sensor for condition monitoring of mining conveyor using wavelet transform and artificial neural network. Struct. Control Health Monit. 2021, 28, e2827. [Google Scholar] [CrossRef]
- Li, J.C.; Wang, Y.; Wang, P.F.; Bai, Q.; Gao, Y.; Zhang, H.J.; Jin, B.Q. Pattern recognition for distributed optical fiber vibration sensing: A review. IEEE Sens. J. 2021, 21, 11983–11998. [Google Scholar] [CrossRef]
- Pan, Y.N.; Wen, T.K.; Ye, W. Time attention analysis method for vibration pattern recognition of distributed optic fiber sensor. Optik 2022, 251, 168127. [Google Scholar] [CrossRef]
- He, T.; Sun, Q.Z.; Zhang, S.X.; Li, H.; Yan, B.Q.; Fan, C.Z.; Yan, Z.J.; Liu, D.M. A dual-stage-recognition network for distributed optical fiber sensing perimeter security system. J. Light. Technol. 2023, 41, 4331–4340. [Google Scholar] [CrossRef]
- Zhu, C.Y.; Yang, K.X.; Yang, Q.M.; Pu, Y.Y.; Chen, C.L.P. A comprehensive bibliometric analysis of signal processing and pattern recognition based on distributed optical fiber. Measurement 2023, 206, 112340. [Google Scholar] [CrossRef]
- Huang, Z.H.; Mao, C.G.; Guan, S.Y.; Tang, H.; Chen, G.H.; Liu, Z.H. Security threshold setting algorithm of distributed optical fiber monitoring and sensing system based on big data in smart city. Soft Comput. 2023, 27, 5147–5157. [Google Scholar] [CrossRef]
- Turov, A.T.; Barkov, F.L.; Konstantinov, Y.A.; Korobko, D.A.; Lopez-Mercado, C.A.; Fotiadi, A.A. Activation function dynamic averaging as a technique for nonlinear 2D data denoising in distributed acoustic sensors. Algorithms 2023, 16, 440. [Google Scholar] [CrossRef]
- Lv, Y.; Wang, P.; Wang, Y.; Liu, X.; Bai, Q.; Li, P.; Zhang, H.; Gao, Y.; Jin, B. Eliminating phase drift for distributed optical fiber acoustic sensing system with empirical mode decomposition. Sensors 2019, 19, 5392. [Google Scholar] [CrossRef]
- Zhu, X.; Zhao, S.; Li, X.; Zhang, R.; Kong, M. Optimization of the moving averaging–moving differential algorithm for Φ-OTDR. Appl. Opt. 2022, 61, 5633–5639. [Google Scholar] [CrossRef]
- Soto, M.A.; Ramirez, J.A.; Thevenaz, L. Intensifying the response of distributed optical fibre sensors using 2D and 3D image restoration. Nat. Commun. 2016, 7, 10870. [Google Scholar] [CrossRef]
- Soto, M.A.; Yang, Z.S.; Ramirez, J.A.; Zaslawski, S.; Thevenaz, L. Evaluating measurement uncertainty in Brillouin distributed optical fibre sensors using image denoising. Nat. Commun. 2021, 12, 4901. [Google Scholar] [CrossRef] [PubMed]
- Wu, M.F.; Chen, Y.F.; Zhu, P.B.; Chen, W. NLM parameter optimization for phi-OTDR signal. J. Light. Technol. 2022, 40, 6045–6051. [Google Scholar] [CrossRef]
- Wu, H.; Wang, L.; Zhao, Z.Y.; Guo, N.; Shu, C.; Lu, C. Brillouin optical time domain analyzer sensors assisted by advanced image denoising techniques. Opt. Express 2018, 26, 5126–5139. [Google Scholar] [CrossRef] [PubMed]
- Wang, B.W.; Wang, L.; Yu, C.Y.; Lu, C. Long-distance BOTDA sensing systems using video-BM3D denoising for both static and slow varying environment. Opt. Express 2019, 27, 36100–36113. [Google Scholar] [CrossRef] [PubMed]
- Ge, Z.; Shen, L.; Zhao, C.; Wu, H.; Zhao, Z.Y.; Tang, M. Enabling variable high spatial resolution retrieval from a long pulse BOTDA sensor. IEEE Internet Things J. 2023, 10, 1813–1821. [Google Scholar] [CrossRef]
- Datta, A.; Raj, V.; Sankar, V.; Kalyani, S.; Srinivasan, B. Measurement accuracy enhancement with multi-event detection using the deep learning approach in Raman distributed temperature sensors. Opt. Express 2021, 29, 26745–26764. [Google Scholar] [CrossRef] [PubMed]
- Chen, Y.F.; Zhu, P.B.; Yin, Y.; Wu, M.F.; Yu, K.M.; Feng, L.; Chen, W. Objective assessment of IPM denoising quality of phi-OTDR signal. Measurement 2023, 214, 112775. [Google Scholar] [CrossRef]
- Guo, T.T.; Zhang, T.P.; Lim, E.; Lopez-Benitez, M.; Ma, F.; Yu, L.M. A review of wavelet analysis and its applications: Challenges and opportunities. IEEE Access 2022, 10, 58869–58903. [Google Scholar] [CrossRef]
- Wu, Y.N.; Liang, S.; Lou, S.Q.; Sheng, X.Z. An interrogation method to enhance SNR for far-end disturbances in fiber-optic distributed disturbance sensor based on phi-OTDR. IEEE Sens. J. 2019, 19, 1064–1072. [Google Scholar] [CrossRef]
- Sun, Z.S.; Liu, K.; Jiang, J.F.; Xu, T.H.; Wang, S.; Guo, H.R.; Liu, T.G. High accuracy and real-time positioning using MODWT for long range asymmetric interferometer vibration sensors. J. Light. Technol. 2021, 39, 2205–2214. [Google Scholar] [CrossRef]
- Feng, L.; Chen, Y.F.; Yu, K.M.; Zhu, P.P.; Chen, W. Improved wavelet thresholding function for multi-mode fiber microvibration signal processing. Opt. Fiber Gyro 2023, 12968, 489–494. [Google Scholar]
- Yu, K.; Feng, L.; Chen, Y.; Wu, M.; Zhang, Y.; Zhu, P.; Chen, W.; Wu, Q.; Hao, J. Accurate wavelet thresholding method for ECG signals. Comput. Biol. Med. 2024, 169, 107835. [Google Scholar] [CrossRef]
- Pradhan, P.S.; King, R.L.; Younan, N.H.; Holcomb, D.W. Estimation of the number of decomposition levels for a wavelet-based multi-resolution multisensor image fusion. IEEE Trans. Geosci. Remote Sens. 2006, 44, 3674–3686. [Google Scholar] [CrossRef]
- Han, Y.; Shi, P. An adaptive level-selecting wavelet transform for texture defect detection. Image Vis. Comput. 2007, 25, 1239–1248. [Google Scholar] [CrossRef]
- Sang, Y.F.; Wang, D.; Wu, J.C. Entropy-based method of choosing the decomposition level in wavelet threshold de-noising. Entropy 2010, 12, 1499–1513. [Google Scholar] [CrossRef]
- Kaplun, D.; Voznesenskiy, A.; Romanov, S.; Nepomuceno, E.; Butusov, D. Optimal estimation of wavelet decomposition level for a matching pursuit algorithm. Entropy 2019, 21, 843. [Google Scholar] [CrossRef]
- Yang, M.Y.; Sang, Y.F.; Liu, C.M.; Wang, Z.G. Discussion on the choice of decomposition level for wavelet based hydrological time series modeling. Water 2016, 8, 197. [Google Scholar] [CrossRef]
- Buades, A.; Coll, B.; Morel, J.M. A review of image denoising algorithms, with a new one. Multiscale Model. Simul. 2005, 4, 490–530. [Google Scholar] [CrossRef]
- Zhang, X.B. Image denoising using local Wiener filter and its method noise. Optik 2016, 127, 6821–6828. [Google Scholar] [CrossRef]
- Zhong, H.; Yang, C.; Zhang, X.H. A new weight for nonlocal means denoising using method noise. IEEE Signal Process. Lett. 2012, 19, 535–538. [Google Scholar] [CrossRef]
- Qian, X.Y.; Jia, X.H.; Wang, Z.N.; Zhang, B.; Xue, N.T.; Sun, W.; He, Q.H.; Wu, H. Noise level estimation of BOTDA for optimal non-local means denoising. Appl. Opt. 2017, 56, 4727–4734. [Google Scholar] [CrossRef]
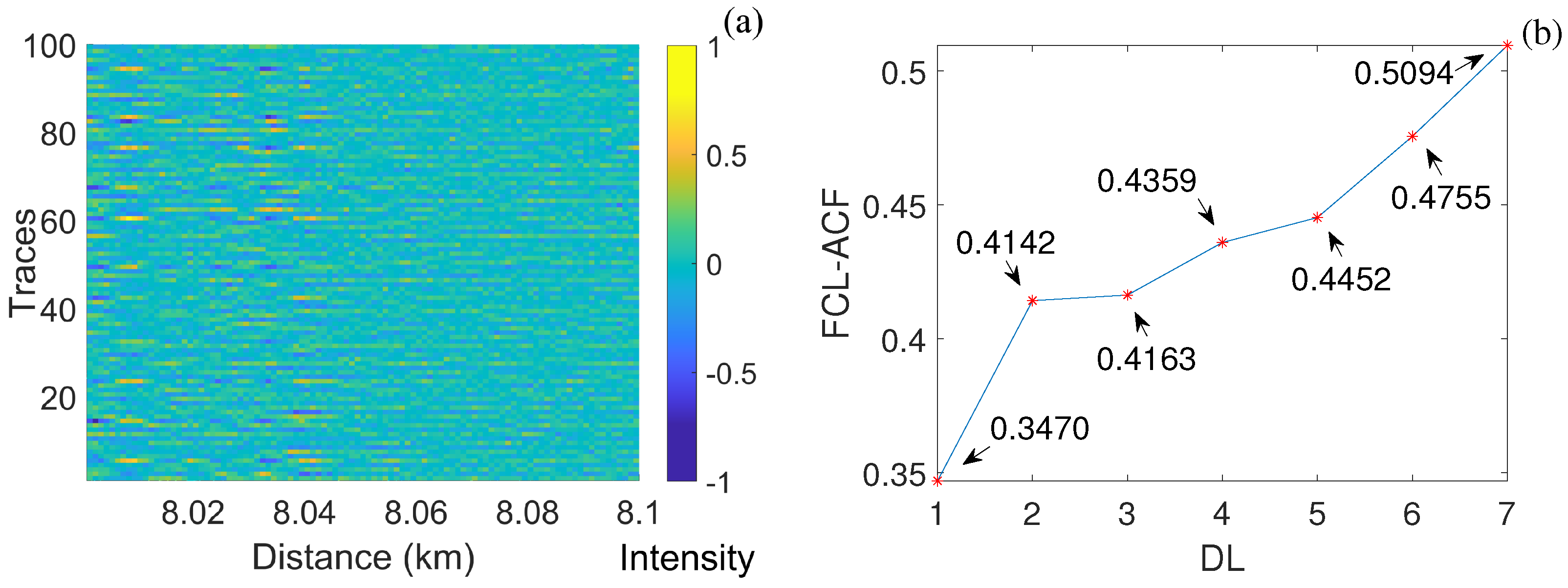
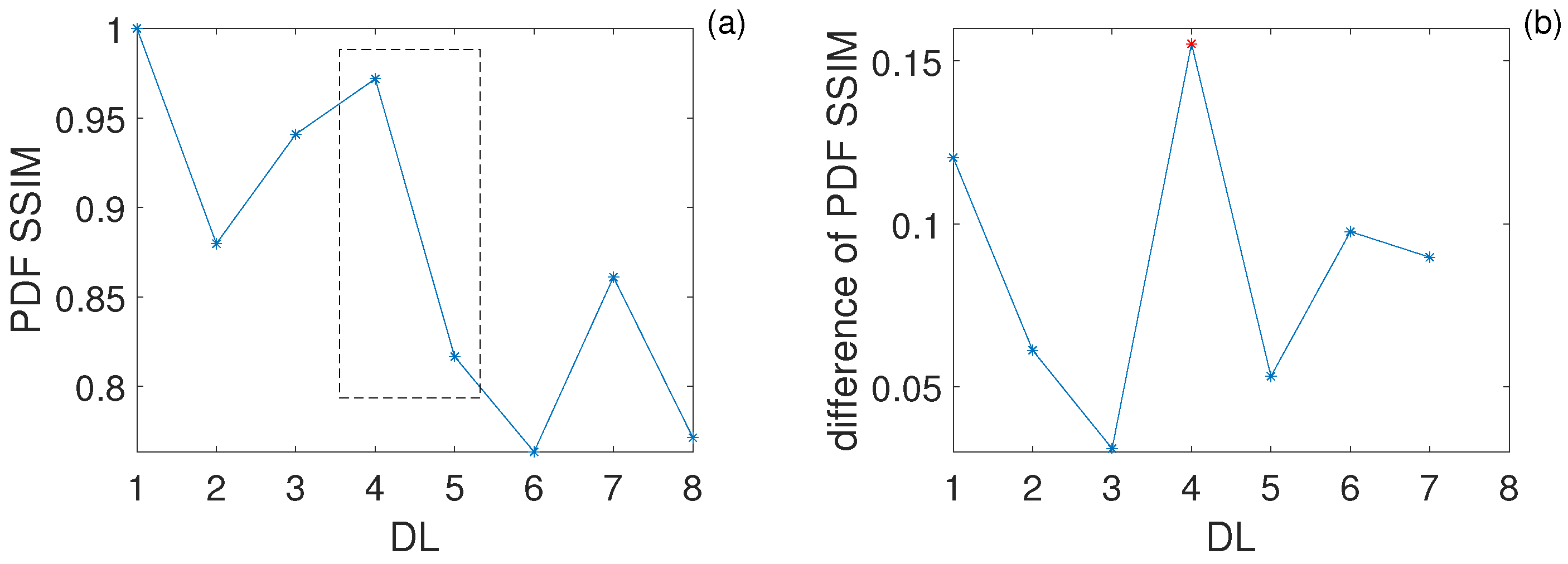
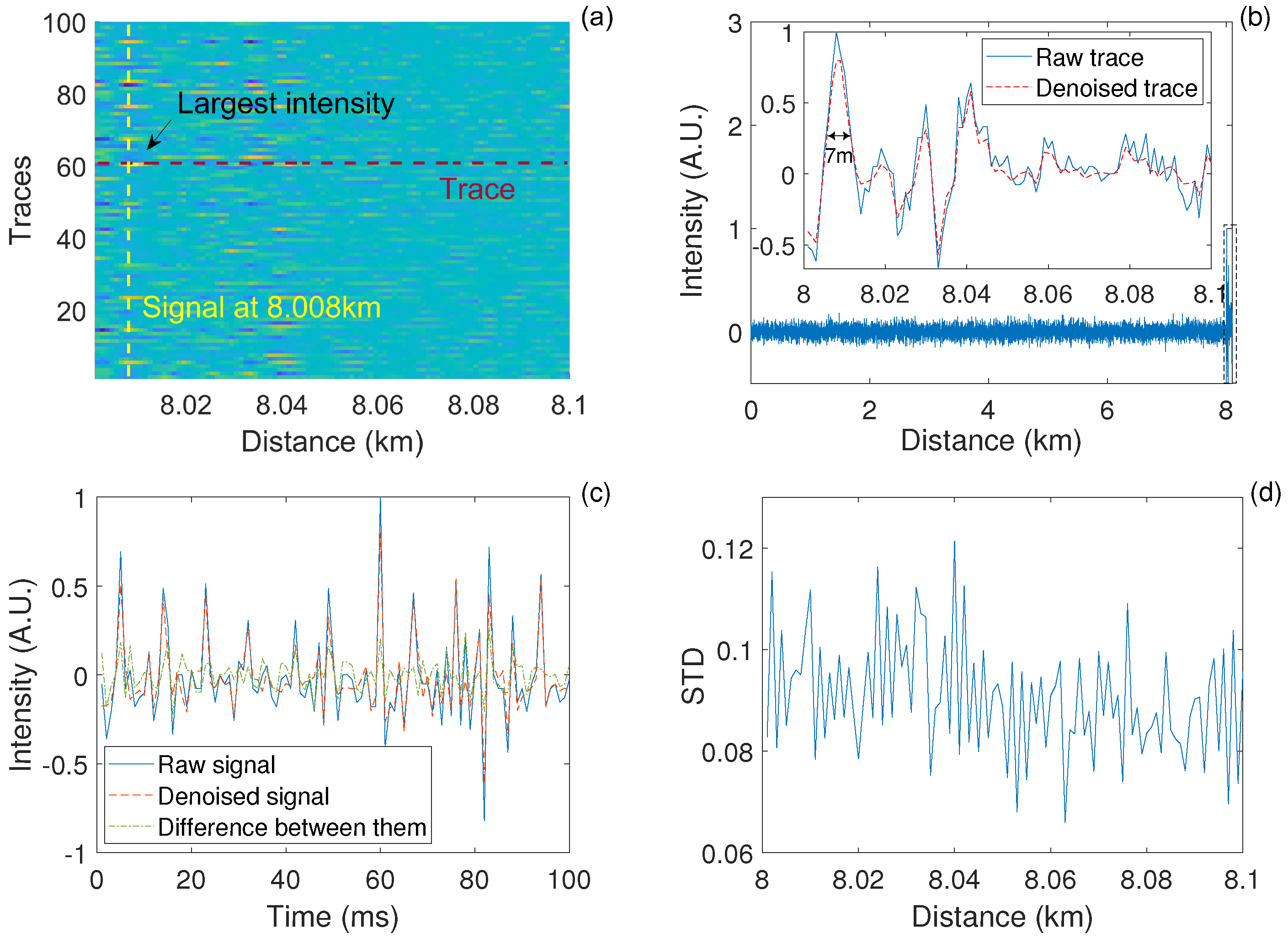
| DL | 1 | 2 | 3 | 4 | 5 | 6 | 7 |
|---|---|---|---|---|---|---|---|
| FCL-ACF | 0.3470 | 0.4142 | 0.4163 | 0.4359 | 0.4452 | 0.4755 | 0.5094 |
| Time (s) | 1.0824 | 2.2738 | 3.6594 | 5.0467 | 6.3418 | 7.8427 | 9.3678 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Chen, Y.; Yu, K.; Wu, M.; Feng, L.; Zhang, Y.; Zhu, P.; Chen, W.; Hao, J. Wavelet Decomposition Layer Selection for the φ-OTDR Signal. Photonics 2024, 11, 137. https://doi.org/10.3390/photonics11020137
Chen Y, Yu K, Wu M, Feng L, Zhang Y, Zhu P, Chen W, Hao J. Wavelet Decomposition Layer Selection for the φ-OTDR Signal. Photonics. 2024; 11(2):137. https://doi.org/10.3390/photonics11020137
Chicago/Turabian StyleChen, Yunfei, Kaimin Yu, Minfeng Wu, Lei Feng, Yuanfang Zhang, Peibin Zhu, Wen Chen, and Jianzhong Hao. 2024. "Wavelet Decomposition Layer Selection for the φ-OTDR Signal" Photonics 11, no. 2: 137. https://doi.org/10.3390/photonics11020137
APA StyleChen, Y., Yu, K., Wu, M., Feng, L., Zhang, Y., Zhu, P., Chen, W., & Hao, J. (2024). Wavelet Decomposition Layer Selection for the φ-OTDR Signal. Photonics, 11(2), 137. https://doi.org/10.3390/photonics11020137






