Exploration of Four-Channel Coherent Optical Chaotic Secure Communication with the Rate of 400 Gb/s Using Photonic Reservoir Computing Based on Quantum Dot Spin-VCSELs

Abstract

In this work, we present a novel four-channel coherent optical chaotic secure communication (COCSC) system, incorporating four simultaneous photonic reservoir computers in tandem with four coherent demodulation units. We employ a quartet of photonic reservoirs that capture the chaotic dynamics of four polarization components (PCs) emitted by a driving QD spin-VCSEL. These reservoirs are realized utilizing four PCs of a corresponding reservoir QD spin-VCSEL. Through these four concurrent photonic reservoir structures, we facilitate high-quality wideband-chaos synchronization across four pairs of PCs. Leveraging wideband chaos synchronization, our COCSC system boasts a substantial 4 × 100 GHz capacity. High-quality synchronization is pivotal for the precise demasking or decoding of four distinct signal types, QPSK, 4QAM, 8QAM and 16QAM, which are concealed within disparate chaotic PCs. After initial demodulation via correlation techniques and subsequent refinement through a variety of digital signal processing methods, we successfully reconstruct four unique baseband signals that conform to the QPSK, 4QAM, 8QAM and 16QAM specifications. Careful examination of the eye diagrams, bit error rates, and temporal trajectories of the coherently demodulated baseband signals indicates that each set of baseband signals is flawlessly retrieved. This is underscored by the pronounced eye openings in the eye diagrams and a negligible bit error rate for each channel of baseband signals. Our results suggest that delay-based optical reservoir computing employing a QD spin-VCSEL is a potent approach for achieving multi-channel coherent optical secure communication with optimal performance and enhanced security.

1. Introduction

As is well known, there are several methods for optical communication multiplexing, including wavelength division multiplexing (WDM), optical time division multiplexing (OTDM), and polarization multiplexing (PM). Coherent optical communication based on polarization-multiplexing was extensively studied in the 1980s due to the high sensitivity of coherent receivers, which could enhance unrepeated transmission distance [1]. However, related research and development were interrupted in the 1990s due to the rapid advances in high-capacity WDM systems. In 2005, the demonstration of digital carrier-phase estimation in coherent receivers sparked renewed interest in coherent optical communications [2,3]. This was because the digital coherent receiver allowed for a variety of spectrally efficient modulation formats, such as M-ary phase-shift keying and quadrature-amplitude modulation (QAM), which rely upon stable carrier-phase estimation in the digital domain. Additionally, linear transmission impairments, such as group-velocity dispersion (GVD) and polarization-mode dispersion (PMD) of transmission fibers, can be addressed via digital signal processing (DSP). These advantages of the born-again coherent receiver afford considerable potential for innovating existing optical communication systems. Recently, 100-Gb/s transmission systems, which employ QPSK modulation, polarization-division multiplexing, and phase diversity homodyne detection assisted with high-speed DSP at a symbol rate of 25 GBd, have been developed and introduced into commercial networks [4]. Worldwide efforts are now underway to develop coherent receivers that can handle a bit rate of over 400 Gb/s per WDM channel.

In recent decades, there has been a growing focus on enhancing the security of fiber-optic communication through the use of optical chaotic secure communications that employ various devices [5]. As these methods have become increasingly capable of high-speed and high-capacity data transmission, most of the current studies are focused on multi-channel optical chaotic secure communications, including WDM, OTDM and PM chaotic secure communications. Efforts in this area aim to develop secure communication systems that can operate over multiple channels simultaneously, with the goal of improving both the speed and security of fiber-optic communication. Several researchers have already demonstrated successful implementations of WDM and OTDM chaotic secure communications. Furthermore, as digital signal processing (DSP) becomes increasingly integrated with coherent optical communication, high-speed coherent optical transmission systems are poised to play a more significant role in the global optical network infrastructure. The ongoing evolution of fiber-optic communication promises significant enhancements in both capacity and security. As a result, coherent optical chaotic secure communication (COCSC) has generated considerable interest from researchers and industry experts who are working to explore and develop this promising technology. However, it is worth noting that to date, COCSC has not been widely reported and there are several new challenges in key areas of the technology that will need to be addressed moving forward. These new challenges include the following: first, knowing how to realize multi-channel COCSCs with high-speed and high-capacity, and second, knowing how to achieve high-quality chaotic synchronization and coherent demodulation.

It is anticipated that quantum dot spin vertical-cavity surface-emitting lasers (QD-Spin-VCSELs) can be employed to implement high-speed and high-capacity multi-channel coherent optical chaotic secure communications (COCSCs). QD-Spin-VCSELs possess femtosecond dynamic characteristics [6], temperature stability [7], lower lasing current [8], ultra-large bandwidth [9], and independent control of output polarization [10,11,12], making them well-suited for the realization of multi-channel COCSCs with high-speed and high-capacity. Furthermore, these lasers can achieve ultrafast operation from both their ground and excited states, presenting promising opportunities for ultrafast dual-wavelength laser modules that emit ultrafast dynamics. Each beam of light emitted from the ground state (GS) and excited state (ES) includes components with right circular polarization (RCP) and left circular polarization (LCP). The utilization of ultrafast chaotic RCPs and LCPs from the ground and excited states holds significant potential for realizing a four-channel COCSC system with high speed and high capacity. However, one of the challenges in such a COCSC system pertains to achieving high-quality chaotic synchronization and coherent demodulation. Traditional chaotic synchronization methods, such as leading synchronization and lagging synchronization, are limited by the symmetry between the driving laser and the response laser, as well as the need for a perfect match of their parameters. However, recently developed photon reservoir computing (RC) systems have demonstrated promising performances in chaotic synchronization prediction and chaotic signal separation. These RC systems are expected to alleviate the challenges faced in high-speed COCSC. In particular, a QD spin-VCSEL can generate four polarization components (PCs) from the GS and ES emissions. Four parallel RCs system are constructed by using the four PCs from its GS and ES emissions, where the spacing between two nonlinear nodes is very short. These four parallel RCs are potentially applied to address the challenge of high-quality chaos synchronizations.

Photon reservoir computing systems utilize the nonlinear dynamics of chaotic lasers to process and predict information [13,14]. They consist of a chaotic laser, which acts as a “reservoir” of nonlinear dynamics, and a readout layer that learns to map the reservoir dynamics to the desired output. This enables the system to capture and utilize the complex dynamics of chaotic signals for various applications [15,16,17], including chaos synchronization and prediction. The advantage of photon RC systems lies in their ability to effectively handle the mismatch between the driving laser and the response laser, as well as the variability in their parameters. By utilizing the reservoir dynamics, these systems can adapt and learn from the input chaotic signals, allowing for robust synchronization and separation even in the presence of imperfections and parameter mismatches. In the context of high-speed COCSC, photon RC systems hold great potential for enhancing the synchronization performance and enabling coherent demodulation in multi-channel communication systems. By leveraging the capabilities of photon RC systems, it is expected that the challenges associated with achieving high-quality chaotic synchronization and coherent demodulation can be effectively addressed.

Recently, there have been several works proposing a delay-based photon RC system based on electronically pumped spin-VCSELs [15,18]. This RC system utilizes the nonlinear dynamical x polarization component (X-PC) and Y-PC from the VCSEL output to perform two parallel reservoir computers, which are capable of predicting two independent optical chaotic time-series simultaneously and their synchronizations. The output X-PC and Y-PC from the electronically pumped spin-VCSEL can be interchanged continuously under external perturbations and optical feedback, which can affect the predictive performance of the two parallel RCs. Compared to an electrically-pumped VCSEL, a QD spin-VCSEL offers flexible spin control of the lasing output and provides more control parameters [19,20]. This enables better controllability for polarization switching and weakly correlated GS and ES dynamics [21,22]. These advantages allow for the realization of four parallel RCs using the four PCs from the GS and ES emissions of the QD-spin-VCSEL. Additionally, a QD-spin-VCSEL can generate ultrafast chaotic dynamics when subjected to short feedback delays, resulting in very short spacing between two virtual nodes with sufficient nodes. Therefore, four RCs using the four PCs from the ground state and excited state emissions can effectively handle four high-speed chaotic time-series in parallel and their synchronizations.

In this study, we introduce a unique four-channel COCSC system that uses four concurrent photonic reservoir computers coupled with a coherent demodulation device. Within this system, a QD-spin-VCSEL is employed as the driving laser, and a separate QD-spin-VCSEL serves as the reservoir laser. We individually modulate four distinct encoded messages (QPSK, 4QAM, 8QAM and 16QAM) to four PCs, originating from the GS and ES emissions in the drive laser QD-spin-VCSEL. Additionally, we build four parallel photonic reservoirs using four PCs, sourced from the GS and ES of the reservoir QD-spin-VCSEL, maintaining a minimal distance between two non-linear nodes. By leveraging a concurrent simulation of Matlab and VPI [23], these four photonic RCs help us overcome the obstacle of chaos synchronization for four pairs of PCs generated by the drive and reservoir QD-spin-VCSELs. We exhibit a four-channel COCSC with a 4 × 100 GHz capacity using chaos synchronizations founded on these quartet parallel photonic reservoirs. Once the output weights are trained within the nonlinear node states, the four parallel reservoirs can be employed for synchronization and decryption. Further, we coherently demodulate four channels of baseband signals (or bit sequence signals) hidden in modulation messages through a polarization diversity digital coherent receiver (PDDCR) and a variety of DSP methods. We examine the impact of the sampling period and the interval of the virtual nodes on training errors. We approximate the effects of the injection and feedback strengths on chaotic synchronizations. Conclusively, we evaluate the transmission performances of the four-channel baseband signals within this COCSC system, analyzing elements such as bit error rates and eye diagrams.

2. Theoretical Framework and Simulation Experiment Setup

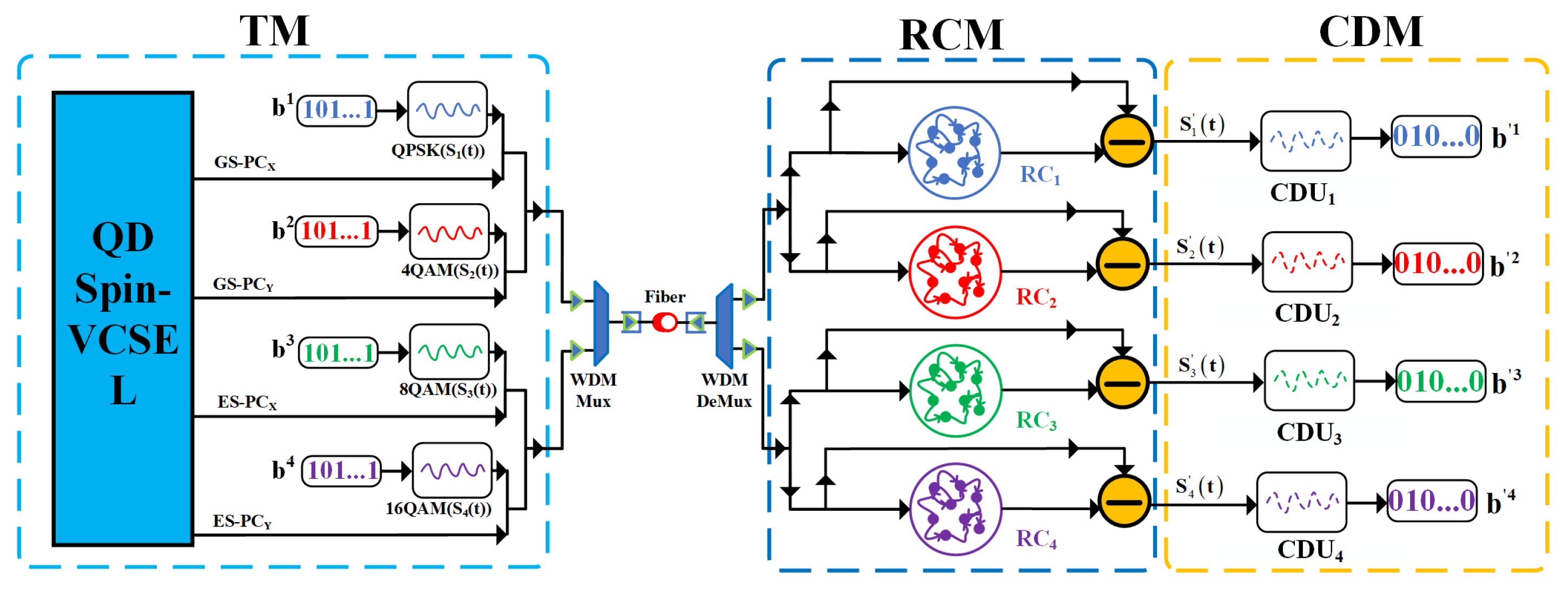
Figure 1 displays the fundamental block diagram of a quad-channel COCSC system, built on four concurrent photonic reservoir computers. This intricate system is composed of the transmitter module (TM), the reservoir computing module (RCM), and the coherent demodulation module (CDM). Within the TM, the ground state of the QD-spin-VSEL generates the chaotic X-PC and Y-PC, marked as GS-PC_x and GS-PC_y, respectively. Interestingly, its excited state yields two additional photonic currents recognizable as ES-PC_x and ES-PC_y. Each of the QPSK, 4QAM, 8QAM and 16QAM is IQ modulated with a group of bit sequences (baseband signal). In this scheme, there are four distinct groups of bit sequence signals, as depicted as $b^1$–$b^4$, individually. For the convenience of discussion, the temporal dynamics of the QPSK, 4QAM, 8QAM and 16QAM are described by $S_1$(t), $S_2$(t), $S_3$(t) and $S_4$(t), respectively. The QPSK, 4QAM, 8QAM and 16QAM are masked within the chaotic GS-PC_x, GS-PC_y, ES-PC_x and ES-PC_y, respectively. These four channels of chaotic masked signals are integrated into a single optical fiber utilizing a wavelength division multiplexer (WDM Mux). In the RCM, after fiber transmission, the combined signals are partitioned into four-channel chaotic masked signals via a wavelength division demultiplexer (WDM DeMux). Each channel of chaotic masked signal is subsequently bisected into dual beams. A singular beam of chaotic masked signal is introduced to a photonic RC. Here, the predicted outputs from the RC₁–RC₄ are denoted as the GS-${\mathrm{PC}}_x^{\prime }$, GS-${\mathrm{PC}}_y^{\prime }$, ES-${\mathrm{PC}}_x^{\prime }$ and ES-${\mathrm{PC}}_y^{\prime }$, respectively. Once output weights are precisely trained within the non-linear node states of each photonic RC, the GS-PC_x, GS-PC_y, ES-PC_x and ES-PC_y can be perfectly synchronized with GS-${\mathrm{PC}}_x^{\prime }$, GS-${\mathrm{PC}}_y^{\prime }$, ES-${\mathrm{PC}}_x^{\prime }$ and ES-${\mathrm{PC}}_y^{\prime }$ correspondingly. In this scenario, signal types QPSK, 4QAM, 8QAM and 16QAM can be demodulated by applying synchronous subtraction between the chaotic masked signal and each RC’s predicted output. These demodulated messages, noted as $S_1^{\prime }$(t), $S_2^{\prime }$(t), $S_3^{\prime }$(t) and $S_4^{\prime }$(t), are then channeled into their respective coherent demodulation units (CDUs with the subscripts of 1–4). Post coherent demodulation and DSP, four sets of bit sequence signals are further decoded. These reinstated signal bits are referred to as $b^{\prime 1}$–$b^{\prime 4}$, respectively.

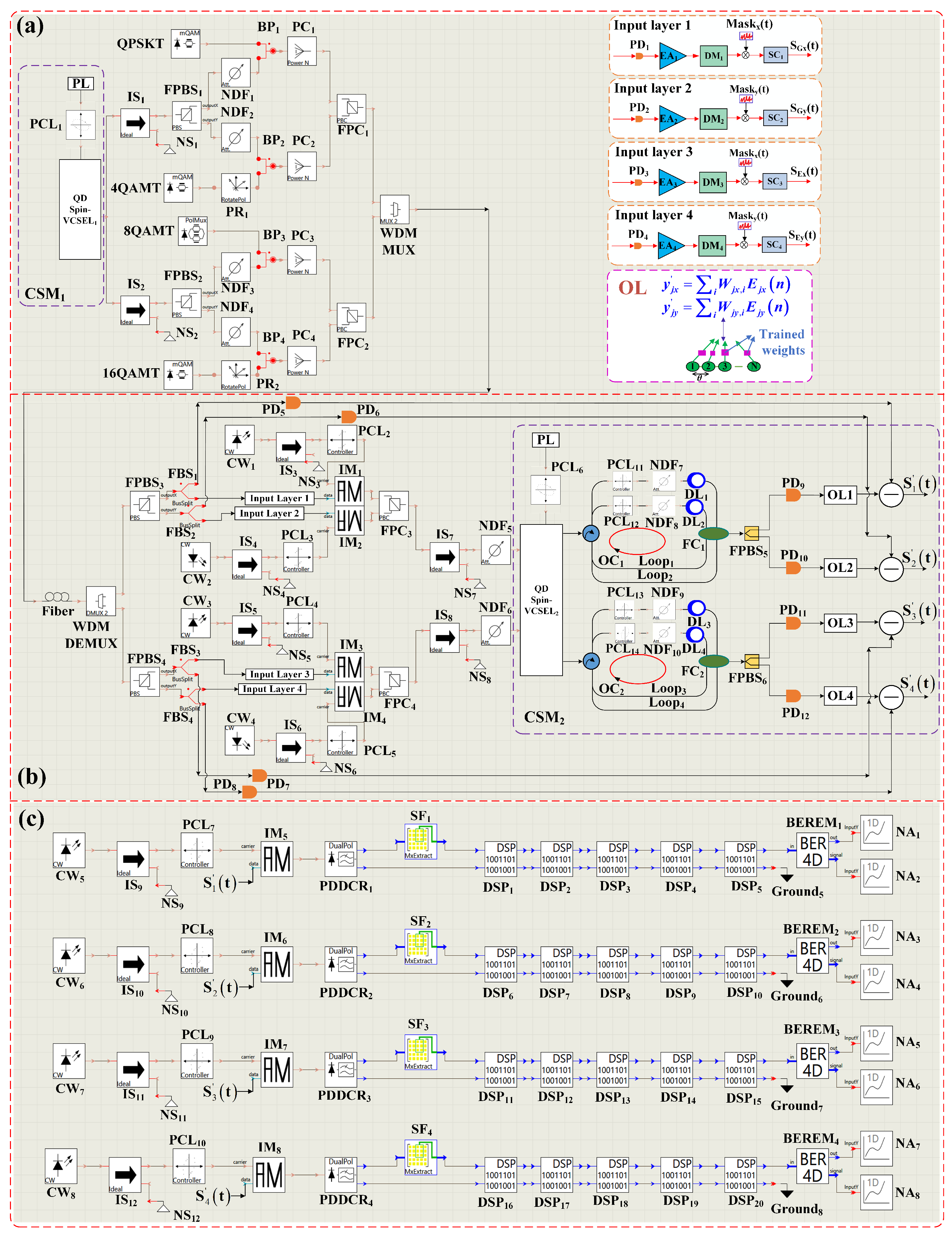
Following the principal block diagram displayed in Figure 1, Figure 2a,b illustrate the simulation experiment setup for a four-channel COCSC system. In this configuration, the QD spin-VCSEL marked with subscript 1 functions as the driving laser, while the QD spin-VCSEL designated by subscript 2 serves as the reserve laser. The CWs, labelled from 1–8, represent the continuous wave lasers. Optical Isolators (ISs, with subscripts from 1–12) are put into service to prevent optical feedback. The neutral density filters (NDFs, labelled from 1–10) are employed to regulate light intensity. The QPSK transmitter (QPSKT), 4QAM transmitter (4QAMT), 8QAM transmitter (8QAMT) and 16QAM transmitter (16QAMT) generate QPSK, 4QAM, 8QAM and 16QAM signals, respectively. The fiber polarization beam splitters (FPBS), carrying subscripts 1–6, are used to partition the light into two distinct polarization components. Bidirectional ports (BPs, labelled 1–4) combine two bidirectional ports into a singular bidirectional multiport of width 2. Lastly, photodiodes (PDs), labeled from 1–12, are designated to convert light waves into corresponding current signals.

In Figure 2a,b, in the QPSKT, the QPSK modulation scheme utilizes a baseband signal $b^1$ for its in-phase (I) and quadrature (Q) components. Similarly, in the 4QAMT, for 4QAM modulation, the I and Q components are modulated using the odd and even parts of the signal $b^2$. In the 8QAMT, for 8QAM modulation, the odd and even parts of the signal $b^3$ are used as the respective signals for the I and Q components. Lastly, for 16QAM modulation, the I and Q components are modulated using the odd and even parts of the signal $b^4$. In these four modules (QPSKT, 4QAMT, 8QAMT and 16QAMT), QPSK, 4QAM, 8QAM and 16QAM signals are optically modulated using continuous wave lasers and then converted into optical signals at the output ports of these modules. In the QD spin-VCSEL labeled with subscript 1, the light emitted from its ground state (GS) is divided into two chaotic polarization components (GS-PC_x and GS-PC_y) using the FPBS₁, with their amplitudes represented as $E_{Gx}$(t) and $E_{Gy}$(t), respectively. Likewise, the light emitted from its excited state (ES) is separated into two chaotic polarization components (ES-PC_x and ES-PC_y) using the FPBS₂, and their amplitudes are indicated by $E_{Ex}$(t) and $E_{Ey}$(t), respectively. The QPSK and 4QAM signals are concealed within the chaotic GS-PC_x and GS-PC_y using the power combiners 1 and 2 (PC₁ and PC₂), respectively. These two chaotic hidden signals can be described as ($E_{Gx}$(t) + $S_1$(t)) and ($E_{Gy}$(t) + $S_2$(t)), respectively, and are combined into a single beam through the fiber polarization coupler 1 (FPC₁). The 8QAM and 16QAM signals are masked within the ES-PC_x and ES-PC_y using the PC₃ and PC₄, respectively. These two chaotic masked signals are represented as ($E_{Ex}$(t) + $S_3$(t)) and ($E_{Ey}$(t) + $S_4$(t)), respectively, and merged into a single beam via FPC₂. The mixed light-waves from FPC₁ and FPC₂ are coupled into an optical fiber through the WDM Mux. After fiber transmission, the multiplexed light-waves are split into two beams with different wavelengths via the WDM DeMux. One beam of light from the WDM DeMux is divided into GS-PC_x and GS-PC_y, which contain hidden messages, via the FPBS₃. The GS-PC_x, carrying the QPSK signal, is further split into two parts using the fiber beam splitter 1 (FBS₁). One part is injected into input layer 1, and the other is converted into a current signal by the PD₅. The GS-PC_y with 4QAM, ES-PC_x with 8QAM and ES-PC_y with 16QAM are processed similarly.

The input layers provide the connections to the reservoirs. Initially, in input layers 1 and 2, the GS-PC_x, including QPSK and the GS-PC_y with 4QAM, are transformed into two distinct current signals via the PD₁ and PD₂, amplified using electric amplifiers EA₁ and EA₂, and eventually sampled as separate input data series through the discrete modules DM₁ and DM₂, respectively. These data series are designated as $u_{Gx}$(n−$L_{Gx}$) and $u_{Gy}$(n−$L_{Gy}$). Moreover, the sampled time series of the QPSK, 4QAM, 8QAM and 16QAM are respectively described as $I_1$(n), $I_2$(n), $I_3$(n) and $I_4$(n), where $I_1$(n) = $|S_1{(n)|}^2$, $I_2$(n) = $|S_2{(n)|}^2$, $I_3$(n) = $|S_3{(n)|}^2$ and $I_4$(n) = $|S_4{(n)|}^2$. As a result, $u_{Gx}$(n−$L_{Gx}$) = ($C_{Gx}$(n−$L_{Gx}$) + $I_1$(n−$L_{Gx}$)), $u_{Gy}$(n−$L_{Gy}$) = ($C_{Gy}$(n−$L_{Gy}$) + $I_2$(n−$L_{Gy}$)), where $C_{Gx}$(n−$L_{Gx}$) = $|E_{Gx}(n-L_{Gx}){|}^2$ and $C_{Gy}$(n−$L_{Gy}$) = $|E_{Gy}(n-L_{Gy}){|}^2$. The term n denotes the discrete time index, while $L_{Gx}$ and $L_{Gy}$ signify the discrete channel delay lengths for GS-PC_x and GS-PC_y, respectively. Input layers 3 and 4 process ES-PC_x containing 8QAM and ES-PC_y carrying 16QAM in a similar manner, yielding respective input data as $u_{Ex}$(n−$L_{Ex}$) and $u_{Ey}$(n−$L_{Ey}$). Here, $u_{Ex}$(n−$L_{Ex}$) equals ($C_{Ex}$(n−$L_{Ex}$) + $I_3$(n−$L_{Ex}$)) and $u_{Ey}$(n−$L_{Ey}$) corresponds to ($C_{Ey}$(n−$L_{Ey}$) + $I_4$(n−$L_{Ey}$)), where $C_{Ex}$(n−$L_{Ex}$) = $|E_{Ex}(n-L_{Ex}){|}^2$ and $C_{Ey}$(n−$L_{Ey}$) = $|E_{Ey}(n-L_{Ey}){|}^2$. $L_{Ex}$ represents the discrete channel delay length for the ES-PC_x and $L_{Ey}$ illustrates that of the ES-PC_y. Importantly, $C_{Gx}$(n−$L_{Gx}$), $C_{Gy}$(n−$L_{Gy}$), $C_{Ex}$(n−$L_{Ex}$) and $C_{Ey}$(n−$L_{Ey}$) are considered four distinct prediction targets. The sampled data, $u_{Gx}$(n−$L_{Gx}$) and $u_{Ex}$(n−$L_{Ex}$), are multiplied by the mask signal, Mask_x, while $u_{Gy}$(n−$L_{Gy}$) and $u_{Ey}$(n−$L_{Ey}$) are multiplied by Mask_y. Both Mask_x and Mask_y are chaotic signals, as illustrated in [24]. Post scaling with a scaling factor $\gamma$ through the scaling operation circuits (SC₁–SC₄), the four input layers yield output signals denoted as $S_{Gx}$(n), $S_{Gy}$(n), $S_{Ex}$(n) and $S_{Ey}$(n), respectively. These are respectively modulated with the optical-field phases of CW₁–CW₄. The FPC₃ first couples the modulated $S_{Gx}$(n) and $S_{Gy}$(n) into a single beam, which is then injected into the ground state of the reservoir QD spin-VCSEL. Similarly, the FPC₄ couples the modulated $S_{Ex}$(n) and $S_{Ey}$(n) into a single beam, which is subsequently injected into the excited state of the reservoir QD spin-VCSEL.

Within the reservoir, the GS and ES of the QD spin-VCSEL are both influenced by dual feedback mechanisms. The feedback loops for the GS are denoted by subscripts 1 and 2, while those for the ES are indicated by subscripts 3 and 4. Each loop employs a NDF and a PCL to adjust the feedback intensity and polarization direction of the feedback beam, respectively. The delay time established by the delay lines (DL₁–DL₄) is defined as $\tau$. In the output layers (OLs), the GS-${\mathrm{PC}}_x^{\prime }$ and GS-${\mathrm{PC}}_y^{\prime }$ emissions from the QD spin-VCSEL are bifurcated using FPBS₅. Similarly, the ES-${\mathrm{PC}}_x^{\prime }$ and ES-${\mathrm{PC}}_y^{\prime }$ emissions are split through FPBS₆. The intensity values of GS-${\mathrm{PC}}_x^{\prime }$, GS-${\mathrm{PC}}_y^{\prime }$, ES-${\mathrm{PC}}_x^{\prime }$ and ES-${\mathrm{PC}}_y^{\prime }$ are sampled at intervals of $\theta$ and are considered as virtual nodes. Accordingly, the total number N of virtual nodes along each delay line is determined by the ratio N = $\tau$/$\theta$. The states of the N virtual nodes along the DL₁–DL₄ are weighted and linearly summed up. The combined weighted states from the DL₁ and DL₂ are represented as ${\mathrm{y}}_{\mathit{Gx}}^{\prime }$(n) and ${\mathrm{y}}_{\mathit{Gy}}^{\prime }$(n), respectively, while those from the DL₃ and DL₄ are signified as ${\mathrm{y}}_{\mathit{Ex}}^{\prime }$(n) and ${\mathrm{y}}_{\mathit{Ey}}^{\prime }$(n). In this setup, by calibrating the output weights, ${\mathrm{y}}_{\mathit{Gx}}^{\prime }$(n) and ${\mathrm{y}}_{\mathit{Gy}}^{\prime }$(n) can achieve synchronization with $C_{Gx}$(n−$L_{Gx}$) and $C_{Gy}$(n−$L_{Gy}$), respectively. Likewise, ${\mathrm{y}}_{\mathit{Ex}}^{\prime }$(n) and ${\mathrm{y}}_{\mathit{Ey}}^{\prime }$(n) can be attuned to synchronize with $C_{Ex}$(n−$L_{Ex}$) and $C_{Ey}$(n−$L_{Ey}$). Under these synchronization conditions, the concealed messages QPSK and 4QAM are decoded by the synchronous subtraction of ${\mathrm{y}}_{\mathit{Gx}}^{\prime }$(n) from $C_{Gx}$(n−$L_{Gx}$) and ${\mathrm{y}}_{\mathit{Gy}}^{\prime }$(n) from $C_{Gy}$(n−$L_{Gy}$), with the retrieved messages designated as $S_1^{\prime }$(t) and $S_2^{\prime }$(t), respectively. In a similar fashion, the messages 8QAM and 16QAM are decoded by the synchronous subtraction of ${\mathrm{y}}_{\mathit{Ex}}^{\prime }$(n) from $C_{Ex}$(n−$L_{Ex}$) and ${\mathrm{y}}_{\mathit{Ex}}^{\prime }$(n) from $C_{Ey}$(n−$L_{Ey}$), with their decoded equivalents presented as $S_3^{\prime }$(t) and $S_4^{\prime }$(t), correspondingly.

As illustrated in Figure 2c, the decoded messages, $S_1^{\prime }$(t), $S_2^{\prime }$(t), $S_3^{\prime }$(n) and $S_4^{\prime }$(n), are initially modulated with the optical field phases of the CW₅–CW₈ using intensity modulators (IM₁–IM₄) and then each injected into its corresponding coherent demodulation unit (CDU). Each CDU comprises a polarization-diversity digital coherent receiver (PDDCR), a submatrix finder (SF), a set of five digital signal processors (DSPs), and a bit error rate estimation module (BEREM). The PDDCR, depicted in VPI [23], models an optical coherent quadrature receiver that encompasses a local oscillator, optical hybrids, post-detection electrical filters, and analog-to-digital converters. The SF is used to extract specified elements of the input matrix. The DSPs with subscripts 1, 6, 11 and 16 address the compensation of group velocity dispersion and nonlinear effects within the optical fiber, whereas the DSPs labeled with subscripts 2, 7, 12 and 17 are designated to down-sample the in-phase and quadrature signals to match the baud rate. The DSPs marked with subscripts 3, 8, 13 and 18 are dedicated to estimating and correcting frequency discrepancies between the received optical signal and the local oscillator. The DSPs inscribed with subscripts 4, 9, 14 and 19 adjust and align the clock phase of both transmitter and receiver. The DSPs tagged with the subscripts 5, 10, 15 and 20 are dedicated to estimating and correcting phase discrepancies between the received optical signal and the local oscillator. The BEREMs labeled with subscripts 1-4, as four-dimensional bit error rate modules, are capable of generating $BER$s for the baseband signals and facilitating their demodulation. After processing through the four CDUs, four sets of baseband signals (or bit streams) encapsulated within the decoded modulation messages, $S_1^{\prime }$(t), $S_2^{\prime }$(t), $S_3^{\prime }$(t) and $S_4^{\prime }$(t) are effectively reconstructed. These recovered bit streams are denoted as $b^{\prime 1}$-$b^{\prime 4}$, respectively.

Drawing on the spin-flip model (SFM) of vertical-cavity surface-emitting lasers (VCSELs) put forth by Miguel et al. [25], the interconnected rate equations characterizing the QD spin-VCSEL₁ (which serves as the driving QD spin-VCSEL) are delineated as follows [19,26]:

$$\begin{array}{cc}\hfill \frac{d{n}_{D,WL}^{\pm }}{dt}=& \frac{h_{D,2}}{e{N}_{QD}}\left[{\eta }^{\pm }(I_{E,th}-I_{G,th})+I_{G,th}\right]-{\gamma }_{D,0}{n}_{D,WL}^{\pm }(\frac{h_{D,2}-n_{D,ES}^{\pm }}{2h_{D,2}})\hfill \\ \hfill & -{\gamma }_{D,n}{n}_{D,WL}^{\pm }\mp {\gamma }_{D,s}(n_{D,WL}^{+}-n_{D,WL}^{-}),\hfill \end{array}$$

(1)

$$\begin{array}{cc}\hfill \frac{d{n}_{D,ES}^{\pm }}{dt}=& \frac{1}{4}{\gamma }_{D,0}{n}_{D,WL}^{\pm }(\frac{h_{D,2}-n_{D,ES}^{\pm }}{h_{D,2}})-{\gamma }_{D,n}(h_{D,2}+n_{D,ES}^{\pm })-2{\gamma }_{D,n}{n}_{D,ES}^{\pm }|E_{D,ES}^{\pm }{|}^2\hfill \\ \hfill & -{{\gamma }_{D,}}_{21}(h_{D,2}+n_{D,ES}^{\pm })(\frac{h_{D,1}-n_{D,GS}^{\pm }}{2h_{D,1}})\mp {\gamma }_{D,s}(n_{D,ES}^{+}-n_{D,ES}^{-}),\hfill \end{array}$$

(2)

$$\begin{array}{cc}\hfill \frac{d{n}_{D,GS}^{\pm }}{dt}=& {\gamma }_{D,21}(\frac{h_{D,2}+n_{D,ES}^{\pm }}{h_{D,2}})(h_{D,1}-n_{D,GS}^{\pm })-{\gamma }_{D,n}(h_{D,1}+n_{D,GS}^{\pm })\hfill \\ \hfill & -2{\gamma }_{D,n}{n}_{D,GS}^{\pm }|E_{D,GS}^{\pm }{|}^2\mp {\gamma }_{D,s}(n_{D,GS}^{+}-n_{D,GS}^{-}),\hfill \end{array}$$

(3)

$$\begin{array}{cc}\hfill \frac{d{E}_{D,GS}^{\pm }}{dt}=& k_D(n_{D,GS}^{\pm }-1)(1+i{\alpha }_D)E_{D,GS}^{\pm }-({\gamma }_{D,a}+i{\gamma }_{D,p})E_{D,GS}^{\mp }+\sqrt{{\beta }_{sp}}{\xi }_{D,GS}^{\pm },\hfill \end{array}$$

(4)

$$\begin{array}{cc}\hfill \frac{d{E}_{D,ES}^{\pm }}{dt}=& k_D(n_{D,ES}^{\pm }-1)(1+i{\alpha }_{\mathrm{D}})E_{D,ES}^{\pm }-({\gamma }_{D,a}+i{\gamma }_{D,p})E_{D,ES}^{\mp }+\sqrt{{\beta }_{sp}}{\xi }_{D,ES}^{\pm }.\hfill \end{array}$$

(5)

The interrelated rate equations governing the QD spin-VCSEL₂ (the reservoir QD spin-VCSEL) under the influence of optical feedback and optical injection are revised as follows [19,26]:

$$\begin{array}{cc}\hfill \frac{d{n}_{WL}^{\pm }}{dt}=& \frac{h_2}{e{N}_{QD}}\left[{\eta }^{\pm }(I_{E,th}-I_{G,th})+I_{G,th}\right]-{\gamma }_0{n}_{WL}^{\pm }(\frac{h_2-n_{ES}^{\pm }}{2h_2})-{\gamma }_n{n}_{WL}^{\pm }\mp {\gamma }_s(n_{WL}^{+}-n_{WL}^{-}),\hfill \end{array}$$

(6)

$$\begin{array}{cc}\hfill \frac{d{n}_{ES}^{\pm }}{dt}=& \frac{1}{4}{\gamma }_0{n}_{WL}^{\pm }(\frac{h_2-n_{ES}^{\pm }}{h_2})-{\gamma }_n(h_2+n_{ES}^{\pm })-{\gamma }_{21}(h_2+n_{ES}^{\pm })(\frac{h_1-n_{GS}^{\pm }}{2h_1})\hfill \\ \hfill & -2{\gamma }_n{n}_{ES}^{\pm }|E_{ES}^{\pm }{|}^2\mp {\gamma }_s(n_{ES}^{+}-n_{ES}^{-}),\hfill \end{array}$$

(7)

$$\begin{array}{cc}\hfill \frac{d{n}_{GS}^{\pm }}{dt}=& {\gamma }_{21}(\frac{h_2+n_{ES}^{\pm }}{h_2})(h_1-n_{GS}^{\pm })-{\gamma }_n(h_1+n_{GS}^{\pm })-2{\gamma }_n{n}_{GS}^{\pm }|E_{GS}^{\pm }{|}^2\mp {\gamma }_s(n_{GS}^{+}-n_{GS}^{-}),\hfill \end{array}$$

(8)

$$\begin{array}{cc}\hfill \frac{d{E}_{GS}^{\pm }}{dt}=& k(n_{GS}^{\pm }-1)(1+i\alpha )E_{GS}^{\pm }-({\gamma }_a+i{\gamma }_p)E_{GS}^{\mp }\hfill \\ \hfill & -i\Delta {\omega }_G{E}_{GS}^{\pm }+k_{inj}{E}_{inj}^{1,2}+k_f{E}_{GS}^{\pm }(t-\tau )e^{-i{\omega }_G\tau }+\sqrt{{\beta }_{sp}}{\xi }_{GS}^{\pm },\hfill \end{array}$$

(9)

$$\begin{array}{cc}\hfill \frac{d{E}_{ES}^{\pm }}{dt}=& k(n_{ES}^{\pm }-1)(1+i\alpha )E_{ES}^{\pm }-({\gamma }_a+i{\gamma }_p)E_{ES}^{\mp }\hfill \\ \hfill & -i\Delta {\omega }_E{E}_{ES}^{\pm }+k_{inj}{E}_{inj}^{3,4}+k_f{E}_{ES}^{\pm }(t-\tau )e^{-i{\omega }_E\tau }+\sqrt{{\beta }_{sp}}{\xi }_{ES}^{\pm }.\hfill \end{array}$$

(10)

In Equations (1)–(10), the subscript D designates the driving QD spin-VCSEL. The symbols + and − represent the right circular polarization (RCP) and left circular polarization (LCP) of the emitted light, respectively. The dynamic variables, indicated by $n_{WL}$ and $n_{GS}$($n_{ES}$), signify the normalized carrier concentrations in the Wetting Layer (WL) and at the ground (excited) state energy levels. Lasing is facilitated via the transitions from the excited state or the ground state to the valence band (VB), generating right ($E_{ES}^{+}$, $E_{GS}^{+}$) and left ($E_{ES}^{-}$, $E_{GS}^{-}$ ) circularly polarized light at two distinct wavelengths. The carrier injection thresholds for the excited and ground states are symbolized by $I_{E,th}$ and $I_{G,th}$, respectively. The remaining parameters for the aforementioned QD Spin-VCSELs are as follows: k and $k_D$ are the photon decay rates; $\alpha$ and ${\alpha }_D$ represent the linewidth enhancement factors; $h_1$ and $h_{D,1}$ are the normalized differential gain coefficients for the ground state transitions; and $h_2$ and $h_{D,2}$ are those for the excited state transitions. ${\gamma }_{D,n}$ and ${\gamma }_n$ represent the carrier recombination rates; ${\gamma }_{D,21}$ and ${\gamma }_{21}$ denote the intradot relaxation rates at which spin-polarized carriers relax from the excited state to the spin-up (down) ground state; ${\gamma }_{D,0}$ and ${\gamma }_0$ are the rates of carrier capture from the WL into the excited state; ${\gamma }_{D,s}$ and ${\gamma }_s$ correspond to the spin relaxation rates; ${\gamma }_{D,p}$ and ${\gamma }_p$ represent the birefringence rates; and ${\gamma }_{D,\gamma }$ and ${\gamma }_{\gamma }$ are related to the dichroism rates. $\tau$ indicates the feedback time along any of the delay lines (DL₁–DL₄) shown in Figure 2; ${\omega }_G$ is the resonant frequency of the light emitted from the ground state; and ${\omega }_E$ is the resonant frequency of light emitted from the excited state. $\Delta {\omega }_G$ represents the frequency detuning between CW₁ (CW₂) and the ground state emission of the reservoir QD Spin-VCSEL; $\Delta {\omega }_E$ denotes the frequency detuning between CW₃ (CW₄) and the excited state emission of the reservoir QD Spin-VCSEL. ${\beta }_{sp}$ is the rate of spontaneous emission, also viewed as an indicator of noise strength. The terms ${\xi }_{D,GS}^{\pm }$, ${\xi }_{D,ES}^{\pm }$, ${\xi }_{DS}^{\pm }$ and ${\xi }_{ES}^{\pm }$ embody independent Gaussian white noise sources with zero mean and unit variance. $k_f$ is the feedback coupling strength; $k_{inj}$ stands for the strength of optical injection. $E_{inj}^1$ and $E_{inj}^2$ are the slowly varying complex amplitudes of the CW₁ and CW₂, which are converted to RCP and LCP by the PCL₂ and PCL₃; $E_{inj}^3$ and $E_{inj}^4$ are the injected optical fields for the CW₃ and CW₄, likewise converted by the PCL₄ and PCL₅. $E_{inj}^1$ and $E_{inj}^2$ account for the light fields $E_{GS}^{+}$ and $E_{GS}^{-}$, respectively, while $E_{inj}^3$ and $E_{inj}^4$ are charged with generating the optical fields $E_{ES}^{+}$ and $E_{GS}^{-}$. The total pump strengths $\eta$ = ${\eta }^{+}$ + ${\eta }^{-}$, ${\eta }^{+}$ and ${\eta }^{-}$ are the pump intensities for the RCP and LCP components, respectively.

The left and right circular polarization components of the GS and ES emissions of the driving QD Spin-VCSEL are replaced with the orthogonal linear components as follows:

$$\begin{array}{cc}\hfill & E_{D,Gx}=\frac{E_{D,GS}^{+}+E_{D,GS}^{-}}{\sqrt{2}},E_{D,Gy}=-i\frac{E_{D,GS}^{+}-E_{D,GS}^{-}}{\sqrt{2}},\hfill \\ \hfill & E_{D,Ex}=\frac{E_{D,ES}^{+}+E_{D,ES}^{-}}{\sqrt{2}},E_{D,Ey}=-i\frac{E_{D,ES}^{+}-E_{D,ES}^{-}}{\sqrt{2}}.\hfill \end{array}$$

(11)

The left and right circular polarization components of the GS and ES emissions of the reservoir QD Spin-VCSEL are rewritten in terms of the orthogonal linear components as follows:

$$\begin{array}{cc}\hfill & E_{Gx}=\frac{E_{GS}^{+}+E_{GS}^{-}}{\sqrt{2}},E_{Gy}=-i\frac{E_{GS}^{+}-E_{GS}^{-}}{\sqrt{2}},\hfill \\ \hfill & E_{Ex}=\frac{E_{ES}^{+}+E_{ES}^{-}}{\sqrt{2}},E_{Ey}=-i\frac{E_{ES}^{+}-E_{ES}^{-}}{\sqrt{2}}.\hfill \end{array}$$

(12)

In the QPSKT and m-QAMT (m equals 4, 8, 16) presented in Figure 2a, the QPSK and m-QAM signals can be generated through the process of IQ modulation, where baseband signals ($b^1$–$b^4$) modulate a continuous light source. Subsequently, these modulated signals are combined via polarization beam combining techniques. The resulting QPSK and m-QAM signals are characterized by

$$S_j\left(t\right)=\frac{1}{2}{E}_{in,j}\left(t\right)\left[\sum _{k=1}^{L_k}cos({\phi }_{1k}^j)+i\sum _{k=1}^{L_k}cos({\varphi }_{2k}^j)\right],$$

(13)

where the subscript j = 1 denotes QPSK. The subscripts j = 2, 3, 4 represent 4-QAM, 8-QAM, and 16-QAM, respectively. When j = 1 and 2, $L_k$ = 4. If j = 3, $L_k$ = 8, while j = 4, $L_k$ = 16. The subscript k indicates the kth group of bits in the time sequence. In Equation (13), the phases ${\phi }_{1k}^j$ and ${\varphi }_{2k}^j$ are respectively written as follows:

$${\phi }_{1k}^j=arcsin\left[\mathrm{Re}(I{Q}_k^j)\right],{\varphi }_{2k}^j=arcsin\left[\mathrm{Im}(I{Q}_k^j)\right],$$

(14)

where the terms $I{Q}_k^1$–$I{Q}_k^4$ are respectively described as

$$I{Q}_{,k}^1=cos\left(\frac{2\pi ·n_k^1}{2^m}\right)+i·sin\left(\frac{2\pi ·n_k^1}{2^m}\right),$$

(15)

$$I{Q}_{x,k}^{j_n}=\frac{{\displaystyle \sum _{l=1}^{m/2}}{2}^{m/2-l}\left(2·I_{\left(k-1\right)·m/2+l}^{j_n}-1\right)+i·{\displaystyle \sum _{l=1}^{m/2}}{2}^{m/2-l}\left(2·Q_{\left(k-1\right)·m/2+l}^{j_n}-1\right)}{2^{m/2-1}},$$

(16)

where the superscript $j_n$ = 2, 3, 4. The variables $n_k^1$, I and Q can be expressed as follows: $n_k^1$ = ${\sum }_m^{l=1}{b}_{(k-l)·m+l}^1·2^{l-1}$, $I_{\ell }^{j_n}$ = $b_{2\ell -1}^{j_n}$ and $Q_{\ell }^{j_n}$ = $b_{2\ell }^{j_n}$, where ℓ = 1, 2, ⋯, N.

In Equations (9) and (10), the slowly varying amplitudes $E_{inj}^1$–$E_{inj}^4$ of the complex electric field can be described as [15]

$$\begin{array}{cc}\hfill & E_{inj}^1(t)=\sqrt{S_{Gx}(t)·I_{d1}},E_{inj}^2(t)=\sqrt{S_{Gy}(t)·I_{d2}},\hfill \\ \hfill & E_{inj}^3(t)=\sqrt{S_{Ex}(t)·I_{d3}},E_{inj}^4(t)=\sqrt{S_{Ey}(t)·I_{d4}},\hfill \end{array}$$

(17)

where the light intensities $I_{d1}$ = $|E_{inj,0}^1{|}^2$, $I_{d2}$ = $|E_{inj,0}^2{|}^2$, $I_{d3}$ = $|E_{inj,0}^3{|}^2$ and $I_{d4}$ = $|E_{inj,0}^4{|}^2$. The terms $E_{inj,0}^1$, $E_{inj,0}^2$, $E_{inj,0}^3$ and $E_{inj,0}^4$ are the amplitudes of the continuous-wave lasers CW₁–CW₄, respectively. The masked input signals $S_{Gx}(t)$, $S_{Gy}(t)$, $S_{Ex}(t)$ and $S_{Ey}(t)$ can be expressed as

$$\begin{array}{cc}\hfill & S_{Gx}(t)={\mathrm{Mask}}_x(t)\times C_{Gx}(n-L_{Gx})\times \gamma ,S_{Gy}(t)={\mathrm{Mask}}_y(t)\times C_{Gy}(n-L_{Gy})\times \gamma ,\hfill \\ \hfill & S_{Ex}(t)={\mathrm{Mask}}_x(t)\times C_{Ex}(n-L_{Ex})\times \gamma ,S_{Ey}(t)={\mathrm{Mask}}_y(t)\times C_{Ey}(n-L_{Ey})\times \gamma ,\hfill \end{array}$$

(18)

where the masked signals ${\mathrm{Mask}}_x(t)$ and ${\mathrm{Mask}}_y(t)$ are chaotic signals, as presented in [24]. $\gamma$ is a scaling factor. The discrete channel delay lengths $L_{Gx}$, $L_{Ex}$ = ${\tau }_x$/h, and $L_{Gy}$, $L_{Ey}$ = ${\tau }_y$/h, where h is the step size, ${\tau }_x$ is the channel delay of the GS-PC_x or ES-PC_x, and ${\tau }_y$ is the channel delay of the GS-PC_y or ES-PC_y.

In such a system presented in Figure 2, chaos synchronization between each pair of PCs (i.e., GS-PC_x and GS-${\mathrm{PC}}_x^{\prime }$, GS-PC_y and GS-${\mathrm{PC}}_y^{\prime }$, ES-PC_x and ES-${\mathrm{PC}}_x^{\prime }$, and ES-PC_y and ES-${\mathrm{PC}}_y^{\prime }$) plays a key role in in security and encrypted message recovery. In the following, we use four parallel RCs to address chaos synchronization between each pair of PCs. According to lag chaotic synchronization theory, the lag synchronization solution is obtained as follows.

$$\begin{array}{cc}\hfill & y_{Gx}^{\prime }(n)=C_{Gx}(n-L_{Gx}),y_{\mathit{Gy}}^{\prime }(n)=C_{Gy}(n-L_{Gy}),\hfill \\ \hfill & y_{\mathit{Ex}}^{\prime }(n)=C_{Ex}(n-L_{Ex}),y_{\mathit{Ey}}^{\prime }(n)=C_{Ey}(n-L_{Ey}),\hfill \end{array}$$

(19)

where the time-dependent outputs $y_{\mathit{Gx}}^{\prime }$, $y_{\mathit{Gy}}^{\prime }$, $y_{\mathit{Ex}}^{\prime }$ and $y_{\mathit{Ey}}^{\prime }$ are respectively regarded as linear functions of the GS-PC_x, GS-PC_y, ES-PC_x and ES-PC_y such that

$$\begin{array}{ccc}\hfill & y_{Gx}^{\prime }(n)=\hfill & \hfill W_{Gx,1}{b}_{out}+W_{Gx,2}{C}_{Gx}(n-L_{Gx})+\sum _{i=1}^N{W}_{Gx,i+2}{I}_{Gx,i}(n),\\ \hfill & y_{Gy}^{\prime }(n)=\hfill & \hfill W_{Gy,1}{b}_{out}+W_{Gy,2}{C}_{Gy}(n-L_{Gy})+\sum _{i=1}^N{W}_{Gy,i+2}{I}_{Gy,i}(n),\\ \hfill & y_{Ex}^{\prime }(n)=\hfill & \hfill W_{Ex,1}{b}_{out}+W_{Ex,2}{C}_{Ex}(n-L_{Ex})+\sum _{i=1}^N{W}_{Ex,i+2}{I}_{Ex,i}(n),\\ \hfill & y_{Ey}^{\prime }(n)=\hfill & \hfill W_{Ey,1}{b}_{out}+W_{Ey,2}{C}_{Ey}(n-L_{Ey})+\sum _{i=1}^N{W}_{Ey,i+2}{I}_{Ey,i}(n),\end{array}$$

(20)

where ${\mathbf{W}}_{Gx}$, ${\mathbf{W}}_{Gy}$, ${\mathbf{W}}_{Ex}$ and ${\mathbf{W}}_{Ey}$ represent the output weight matrix; $W_{Gx,i}$, $W_{Gy,i}$, $W_{Ex,i}$ and $W_{Ey,i}$ respectively represent the ith-element of ${\mathbf{W}}_{Gx}$, ${\mathbf{W}}_{Gy}$, ${\mathbf{W}}_{Ex}$ and ${\mathbf{W}}_{Ey}$; $I_{Gx,i}(n)$, $I_{Gy,i}(n)$, $I_{Ex,i}(n)$ and $I_{Ey,i}(n)$ respectively represent the ith output state of the GS-${\mathrm{PC}}_x^{\prime }$, GS-${\mathrm{PC}}_y^{\prime }$, ES-${\mathrm{PC}}_x^{\prime }$ and ES-${\mathrm{PC}}_y^{\prime }$. Here, $I_{Gx,i}(n)$ = $|E_{Gx}{(i)|}^2$, $I_{Gy,i}(n)$ = $|E_{Gy}{(i)|}^2$, $I_{Ex,i}(n)$ = $|E_{Ex}{(i)|}^2$ and $I_{Ey,i}(n)$ = $|E_{Ey}{(i)|}^2$. $b_{out}$ is a constant and equal to 1. Previous studies have shown that these output weight matrices can be analytically given by [27]

$$\begin{array}{cc}\hfill & {\mathbf{W}}_{Gx}={\mathbf{Y}}_{Gx}{\mathbf{X}}^{\mathrm{Tr}}{\left({\mathbf{X}}_{Gx}{\mathbf{X}}_{Gx}^{\mathrm{Tr}}+\mu \mathbf{\Pi }\right)}^{-1},{\mathbf{W}}_{Gy}={\mathbf{Y}}_{Gy}{\mathbf{X}}^{\mathrm{Tr}}{\left({\mathbf{X}}_{Gy}{\mathbf{X}}_{Gy}^{\mathrm{Tr}}+\mu \mathbf{\Pi }\right)}^{-1},\hfill \\ \hfill & {\mathbf{W}}_{Ex}={\mathbf{Y}}_{Ex}{\mathbf{X}}^{\mathrm{Tr}}{\left({\mathbf{X}}_{Ex}{\mathbf{X}}_{Ex}^{\mathrm{Tr}}+\mu \mathbf{\Pi }\right)}^{-1},{\mathbf{W}}_{Ey}={\mathbf{Y}}_{Ey}{\mathbf{X}}^{\mathrm{Tr}}{\left({\mathbf{X}}_{Ey}{\mathbf{X}}_{Ey}^{\mathrm{Tr}}+\mu \mathbf{\Pi }\right)}^{-1},\hfill \end{array}$$

(21)

where the superscript $T_r$ represents the transpose of the matrix; $\mathbf{\Pi }$ is an identity matrix; $\mu$ is utilized to avoid overfitting the ridge regression parameter, which is set to ${10}^{-6}$; ${\mathbf{X}}_{Gx}$, ${\mathbf{X}}_{Gy}$, ${\mathbf{X}}_{Ex}$ and ${\mathbf{X}}_{Ey}$ all are matrices and their lth columns are [$b_{out}$; $C_{Gx}(l-L_{Gx})$; $I_{Gx,i}(l)$], [$b_{out}$; $C_{Gy}(l-L_{Gy})$; $I_{Gy,i}(l)$], [$b_{out}$; $C_{Ex}(l-L_{Ex})$; $I_{Ex,i}(l)$] and [$b_{out}$; $C_{Ey}(l-L_{Ey})$; $I_{Ey,i}(l)$], respectively; ${\mathbf{Y}}_{Gx}$ and ${\mathbf{Y}}_{Ex}$ both are matrices, and their lth columns are [$C_{Gx}(l-L_{Gx}+1)$] and [$C_{Ex}(l-L_{Ex}+1)$], respectively; and ${\mathbf{Y}}_{Gy}$ and ${\mathbf{Y}}_{Ey}$ both are matrices, and their lth columns are [$C_{Gy}(l-L_{Gy}+1)$] and [$C_{Ey}(l-L_{Ey}+1)$], respectively. According to the complete lag synchronization theory (see Equations (19)), we obtain

$$\begin{array}{cc}\hfill & S_1^{\prime }(n)\approx S_1(n-L_{Gx}),S_2^{\prime }(n)\approx S_2(n-L_{Gy}),\hfill \\ \hfill & S_3^{\prime }(n)\approx S_1(n-L_{Ex}),S_4^{\prime }(n)\approx S_2(n-L_{Ey}).\hfill \end{array}$$

(22)

3. Results and Discussions

The parameter values for the driving quantum dot (QD) spin-vertical cavity surface-emitting laser (VCSEL) are detailed in

Table 1. Parameter values of the driving QD Spin-VCSEL.

The Parameter and Symbol	Value	The Parameter and Symbol	Value
The photon decay rate ${\kappa }_D$	250 ${\mathrm{ns}}^{-1}$	The capture rate ${\gamma }_{D,0}$	400 ${\mathrm{ns}}^{-1}$
Linewidth enhancement factor ${\alpha }_D$	3	Intradot relaxation rate ${\gamma }_{D,21}$	50 ${\mathrm{ns}}^{-1}$
Total pump intensity $\eta$	4	Spin relaxation rate ${\gamma }_{D,s}$	10 ${\mathrm{ns}}^{-1}$
Dichroism ${\gamma }_{D,a}$	0 ${\mathrm{ns}}^{-1}$	Carrier recombination rate ${\gamma }_{D,n}$	1 ${\mathrm{ns}}^{-1}$
Birefringence ${\gamma }_{D,p}$	30 ${\mathrm{ns}}^{-1}$	Electron charge e	1.6 $\times {10}^{-19}$ C
Quantum dot density $N_{QD}$	1.5 $\times {10}^{17}$ ${\mathrm{m}}^{-2}$	The gain coefficient $h_{D,1}$	1.1995

, while those for the reservoir QD spin-VCSEL are outlined in

Table 2. Parameter values of the reservoir QD Spin-VCSEL.

The Parameter and Symbol	Value	The Parameter and Symbol	Value
The field decay rate $\kappa$	300 ${\mathrm{ns}}^{-1}$	Central frequency detuning $\Delta {\omega }_E$	−20 $\times {10}^9\mathrm{rad}/\mathrm{s}$
Line-width enhancement factor $\alpha$	3	The capture rate ${\gamma }_0$	600 ${\mathrm{ns}}^{-1}$
Total pump intensity $\eta$	4	Intradot relaxation rate ${\gamma }_{21}$	40 ${\mathrm{ns}}^{-1}$
Dichroism ${\gamma }_a$	0.1 ${\mathrm{ns}}^{-1}$	Spin relaxation rate ${\gamma }_s$	20 ${\mathrm{ns}}^{-1}$
Birefringence ${\gamma }_p$	20 ${\mathrm{ns}}^{-1}$	Carrier recombination rate ${\gamma }_n$	1 ${\mathrm{ns}}^{-1}$
Center frequency ${\omega }_G$	2 $\times {10}^{14}\mathrm{rad}/\mathrm{s}$	Injection strength $k_{inj}$	35 ${\mathrm{ns}}^{-1}$
Center frequency ${\omega }_E$	${10}^{14}\mathrm{rad}/\mathrm{s}$	Feedback strength $k_f$	30 ${\mathrm{ns}}^{-1}$
Central frequency detuning $\Delta {\omega }_G$	0 $\mathrm{rad}/\mathrm{s}$	The gain coefficient $h_1$	1.1665

. Our initial step is to model the power spectral density (PSD) profiles and temporal samples stemming from the driving QD spin-VCSEL, employing concurrent simulations within Matlab (version R2021a) and VPI (version 11.1) software environments. Within Matlab, Equations (1)–(5) are executed via the fourth-order Runge–Kutta numerical approach, adopting a time step (h) of 0.78 ps. The sampling periods for the four distinct input data streams ($u_{Gx}$(n−$L_{Gx}$), $u_{Gy}$(n−$L_{Gy}$), $u_{Ex}$(n−$L_{Ex}$), $u_{Ey}$(n−$L_{Ey}$)) are denoted by T and are uniformly set at 10 ps. The constants $L_{Gx}$, $L_{Gy}$, $L_{Ex}$ and $L_{Ey}$ are all given the value of 2.0513 $\times {10}^4$, which is based on ${\tau }_x$, ${\tau }_y$ being 16 ns and h amounting to 0.78 ps. Concurrently, the dynamical output from the four parallel reservoirs, utilizing the reservoir QD spin-VCSEL, is also modeled with the integration of Matlab and VPI, where Equations (6)–(10) are solved through the fourth-order Runge–Kutta method with a finer time step of 0.048 ps. Within the present framework, both the encoding rate of the messages and the data processing speed of the reservoirs are influenced by the effective bandwidths of the driving and reservoir VCSELs. 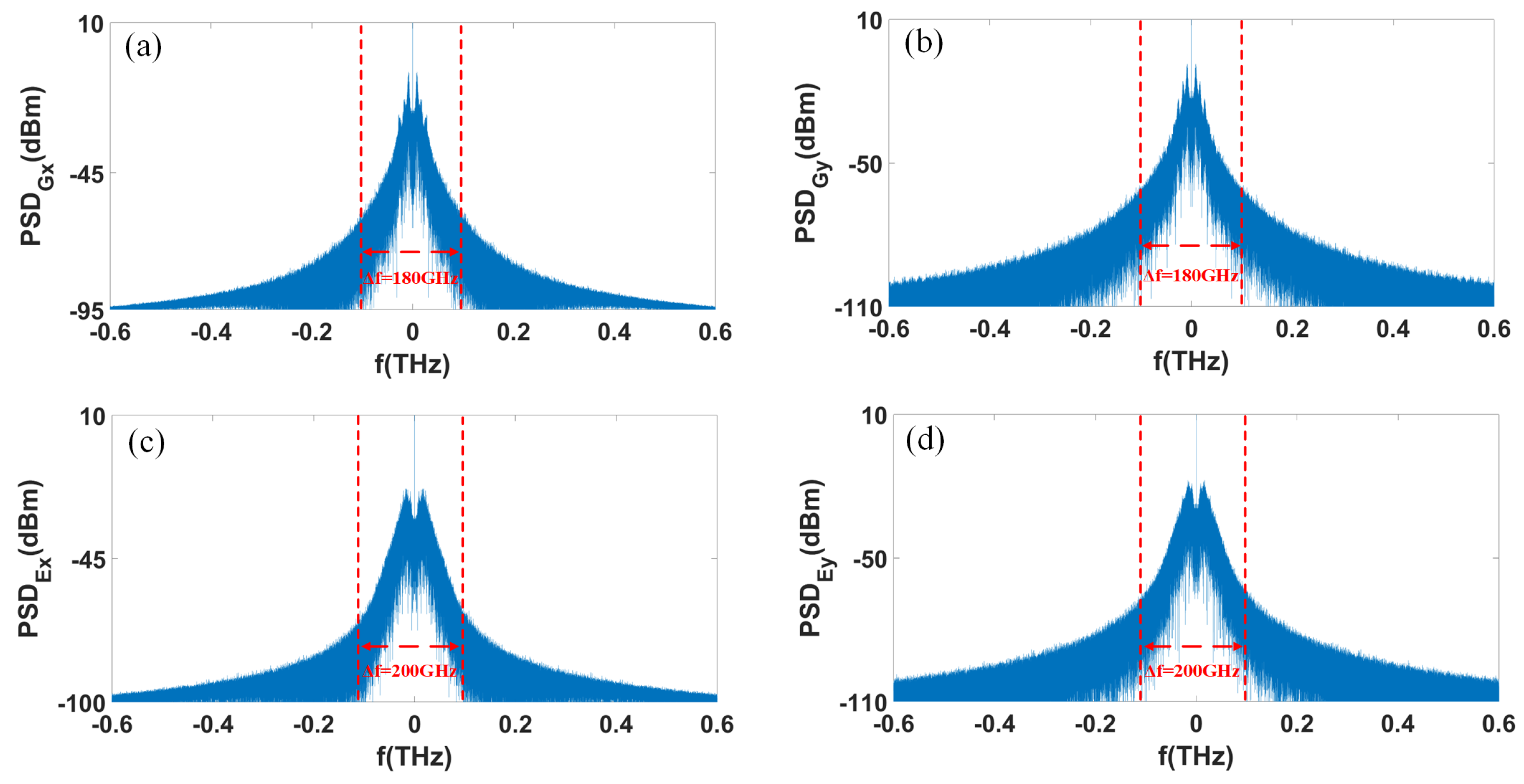Figure 3a–d depict the PSD distributions of the GS-PC_x and GS-PC_y, as well as the ES-PC_x and ES-PC_y emitted by the driving QD spin-VCSEL. According to the representations in Figure 3, the PSD distributions for these PCs consistently demonstrate chaotic behavior. The effective 3 dB bandwidths for both the GS-PC_x and GS-PC_y are calculated to be 180 GHz, whereas the ES-PC_x and ES-PC_y are slightly higher at 200 GHz. Correspondingly, the effective 3 dB bandwidths for the GS-${\mathrm{PC}}_x^{\prime }$, GS-${\mathrm{PC}}_y^{\prime }$, ES-${\mathrm{PC}}_x^{\prime }$ and ES-${\mathrm{PC}}_y^{\prime }$ of the reservoir system exhibit similar characteristics to those of their driving system counterparts (GS-PC_x, GS-PC_y, ES-PC_x and ES-PC_y, respectively). These outcomes suggest that our system is capable of achieving high-speed, four-channel coherent optical chaotic secure communications.

The chaotic GS-${\mathrm{PC}}_x^{\prime }$, GS-${\mathrm{PC}}_y^{\prime }$, ES-${\mathrm{PC}}_x^{\prime }$ and ES-${\mathrm{PC}}_y^{\prime }$ produced by the reservoir QD spin- VCSEL, as four parallel reservoirs, are utilized to perform the predictions of the delayed outputs GS-PC_x, GS-PC_y, ES-PC_x and ES-PC_y, respectively. We collect 5096 samples of these delayed outputs at a sampling interval of 10 ps. After discarding the initial 1000 samples to remove transients, we allocate 2048 samples for training each of the four reservoirs, and an equivalent number of subsequent points for testing the corresponding reservoir. Moreover, the prediction performance is bolstered by implementing chaotic mask signals derived from two coupled semiconductor lasers, detailed in [24]. These mask signals are normalized with standard deviations set to 1 and mean values calibrated to 0. Each reservoir’s virtual node interval, denoted by $\theta$, is fixed at 40 fs. Here, all rates for the QPSK, 4QAM, 8QAM and 16QAM are 100 Gb/s. The input data sampling period T is maintained at 10 ps, resulting in a data processing rate of 100 Gb/s. We establish the number of virtual nodes, N, at 250, where N = $\tau$/$\theta$ and $\tau$ = T. We maintain the scale factor $\gamma$, at a value of 1. To assess the predictions for the GS-PC_x, GS-PC_y, ES-PC_x and ES-PC_y made by these four parallel reservoirs using the reservoir QD spin-VCSEL, we introduce the normalized mean square error ($NMSE$) as a metric to compare the delayed predictive targets against their associated reservoir outputs, which is given as follows:

$$\begin{array}{cc}\hfill & NMS{E}_{jx}=\frac{1}{L}\frac{{\displaystyle \sum _{n=1}^L}{(y_{jx}^{\prime }(n)-C_{jx}(n-L_{jx}))}^2}{\mathrm{var}(y_{jx}^{\prime }(n))},(j=G,E)\hfill \\ \hfill & NMS{E}_{jy}=\frac{1}{L}\frac{{\displaystyle \sum _{n=1}^L}{(y_{jy}^{\prime }(n)-C_{jy}(n-L_{jy}))}^2}{\mathrm{var}(y_{jy}^{\prime }(n))},(j=G,E)\hfill \end{array}$$

(23)

where the subscripts $Gx$, $Ex$, $Gy$ and $Ey$ represent GS-PC_x, ES-PC_x, GS-PC_y and ES-PC_y, respectively. $L_{Gx}$, $L_{Gy}$, $L_{Ex}$ and $L_{Ey}$ are the defined lengths of the testing data set for each variable. L represents the total number of data points in the testing data set. The term “var” denotes the variance of the data. When $NMS{E}_{jx}$ and $NMS{E}_{jy}$ are both 0, it means that the outputs of the reservoirs (GS-PC_x, GS-PC_y, ES-PC_x and ES-PC_y) perfectly match with their corresponding predicted targets ($C_{Gx}$(n−$L_{Gx}$), $C_{Gy}$(n−$L_{Gy}$), $C_{Ex}$(n−$L_{Ex}$) and $C_{Ey}$(n−$L_{Ey}$), respectively). On the other hand, if $NMS{E}_{jx}$ and $NMS{E}_{jy}$ both are 1, it means that the reservoir outputs are completely different from the predicted targets. When $NMS{E}_{jx}$ and $NMS{E}_{jy}$ are both less than 0.1, it indicates that each reservoir is able to accurately infer the chaotic dynamics of its corresponding predicted target, which is the PC of the driving QD Spin-VCSEL output.

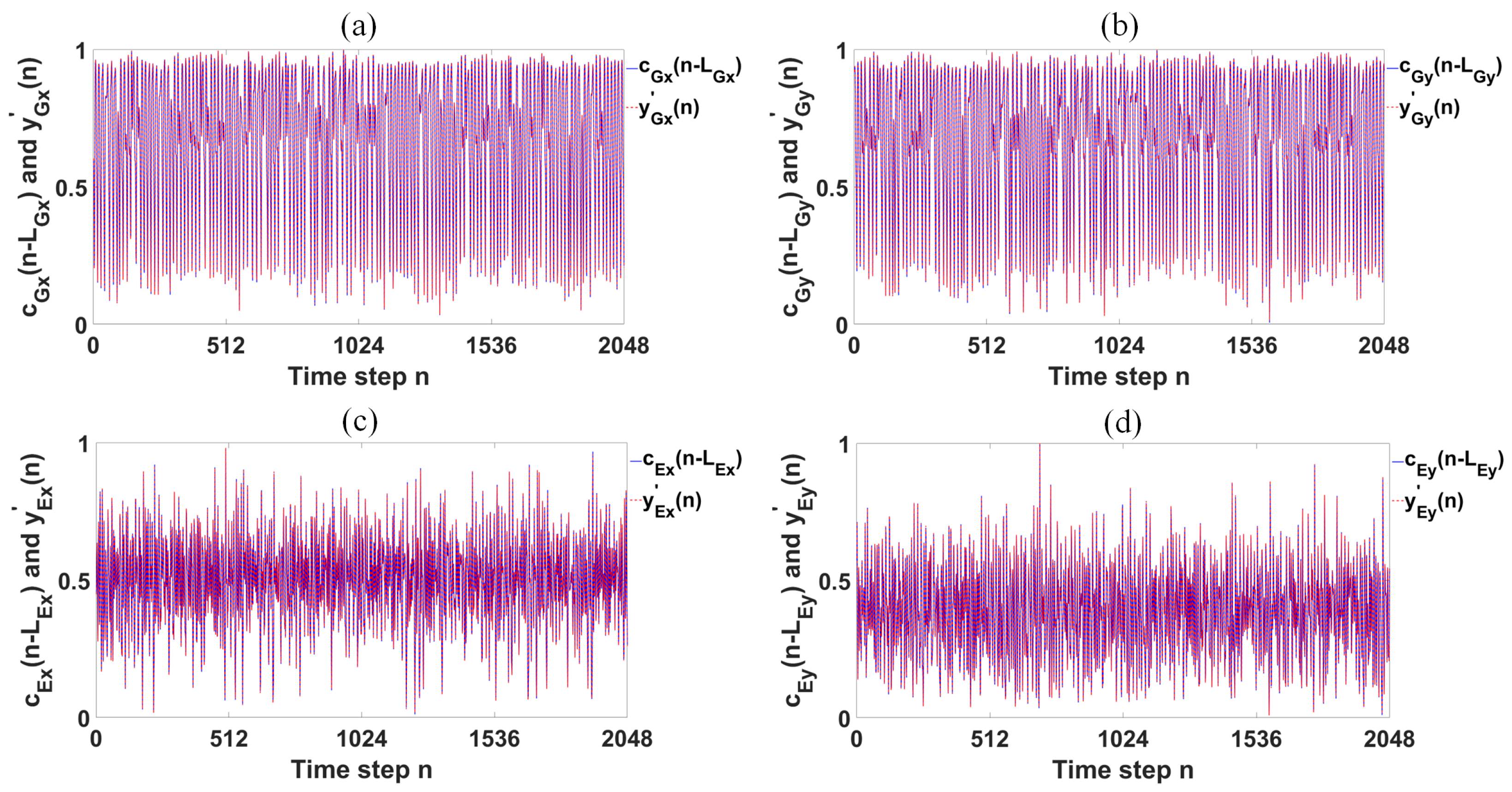
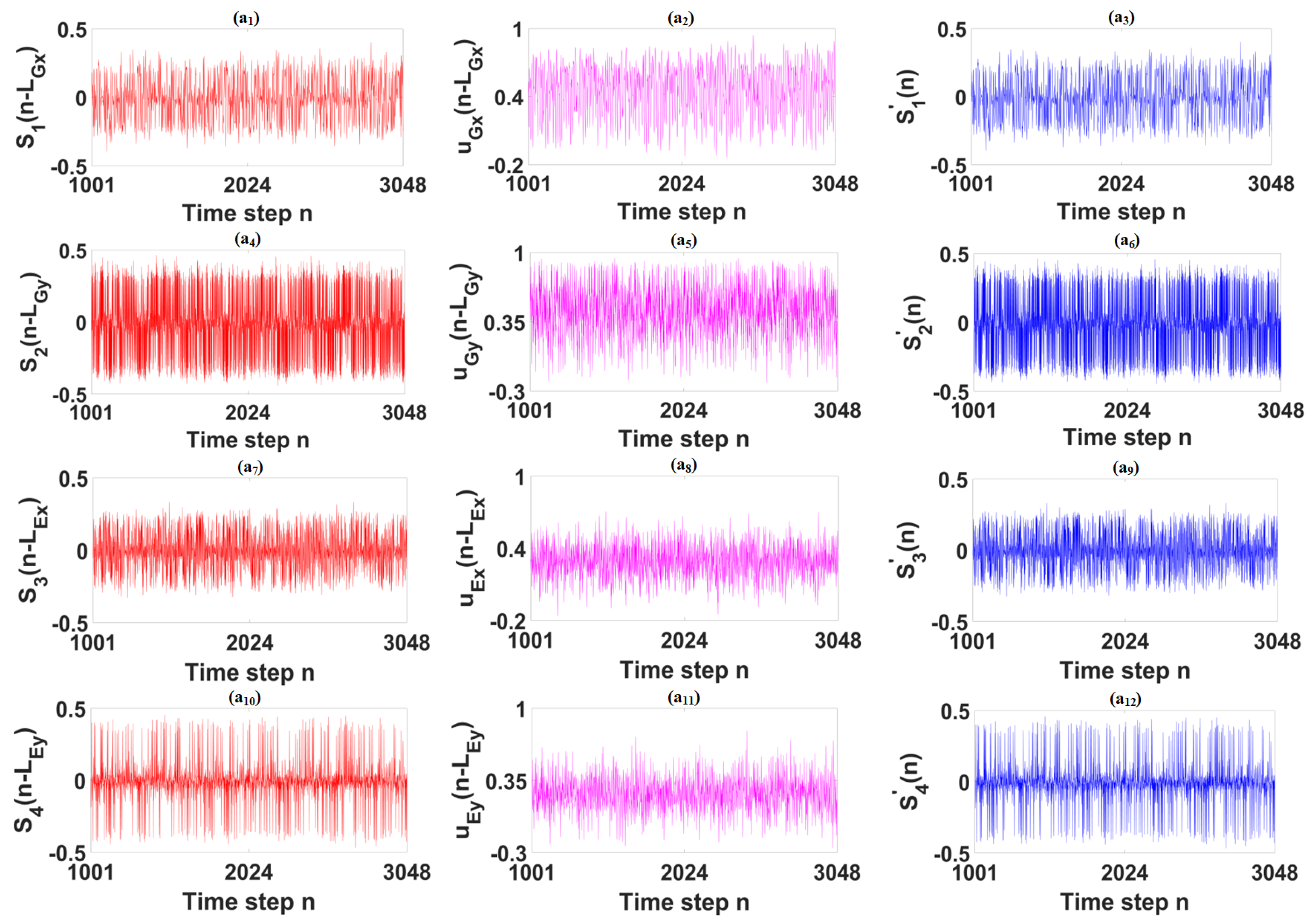
To intuitively observe the ability to predict the chaotic dynamics of the GS-PC_x, ES-PC_x, GS-PC_y and ES-PC_y in our system, Figure 4 presents their predictive results. In this figure, T = 10 ps, $\theta$ = 40 fs, and N = 250. The samples of the delayed GS-PC_x, GS-PC_y, ES-PC_x and ES-PC_y from the driving QD Spin-VCSEL output are denoted as $C_{Gx}$(n−$L_{Gx}$), $C_{Gy}$(n−$L_{Gy}$), $C_{Ex}$(n−$L_{Ex}$) and $C_{Ey}$(n−$L_{Ey}$), respectively. The samples of the trained GS-${\mathrm{PC}}_x^{\prime }$, GS-${\mathrm{PC}}_y^{\prime }$, ES-${\mathrm{PC}}_x^{\prime }$ and ES-${\mathrm{PC}}_y^{\prime }$ from the reservoir QD spin-VCSEL output are denoted as $y_{Gx}^{\prime }(n)$, $y_{Gy}^{\prime }(n)$, $y_{\mathit{Ex}}^{\prime }(n)$ and $y_{\mathit{Ey}}^{\prime }(n)$, respectively. As observed from Figure 4, the chaotic trajectories of the $C_{Gx}$(n−$L_{Gx}$), $C_{Gy}$(n−$L_{Gy}$), $C_{Ex}$(n−$L_{Ex}$) and $C_{Ey}$(n−$L_{Ey}$) are almost identical to those of the $y_{\mathit{Gx}}^{\prime }(n)$, $y_{\mathit{Gy}}^{\prime }(n)$, $y_{\mathit{Ex}}^{\prime }(n)$ and $y_{\mathit{Ey}}^{\prime }(n)$, respectively. In Figure 5a, when T = 10 ps, $\theta$ = 40 fs, and N = 250, the prediction errors ($NMS{E}_{Gx}$ and $NMS{E}_{Gy}$) of the GS-PC_x and GS-PC_y are 0.0359 and 0.0375, respectively. The $NMS{E}_{Ex}$ and $NMS{E}_{Ey}$ for the ES-PC_x and ES-PC_y are 0.0995 and 0.0865, respectively. These indicate that the four parallel reservoirs based on the reservoir QD spin-VCSEL can accurately predict the chaotic dynamics of the GS-PC_x, GS-PC_y, ES-PC_x and ES-PC_y, respectively.

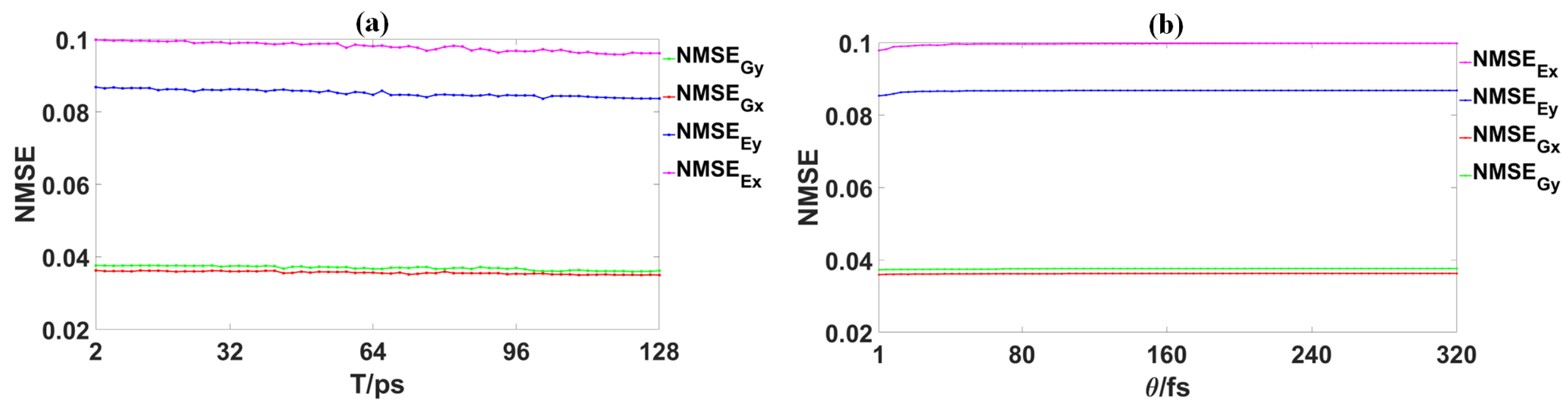
To comprehensively observe the prediction abilities of the four parallel reservoirs on the chaotic dynamics of the delayed GS-PC_x, GS-PC_y, ES-PC_x and ES-PC_y, Figure 5a illustrates the relationship between the prediction errors ($NMS{E}_{Gx}$, $NMS{E}_{Gy}$, $NMS{E}_{Ex}$ and $NMS{E}_{Ey}$) and the sampling period T when $\theta$ is 40 fs. As shown in Figure 5a, $NMS{E}_{Gx}$ and $NMS{E}_{Gy}$ exhibit an almost linear decrease from 0.0362 to 0.0350 and from 0.0376 to 0.0366, respectively, as T increases from 2 ps to 128 ps. Similarly, the $NMS{E}_{Ex}$ and $NMS{E}_{Ey}$ also reveal a linear decrease from 0.0998 to 0.0961 and from 0.0867 to 0.0836, respectively. The reason why a longer sampling period T leads to reduced training error might be explained as follows. In this work, $\theta$ = T/N is fixed at 40 fs, and a smaller N is associated with a smaller T, resulting in a lower-dimensional state space. This situation can make the training of the four parallel reservoirs based on the reservoir QD spin-VCSEL become unstable and more difficult, consequently leading to a larger $NMSE$. Additionally, when T is fixed at a certain value, the $NMS{E}_{Ex}$ and $NMS{E}_{Ey}$ are significantly larger than $NMS{E}_{Gx}$ and $NMS{E}_{Gy}$. This may be explained by the fact that ES-PC_x and ES-PC_y have more complex chaotic dynamics than GS-PC_x and GS-PC_y, respectively, making the predictions of ES-PC_x and ES-PC_y more challenging compared to those of GS-PC_x and GS-PC_y. Figure 5b shows the relationship between the prediction errors ($NMS{E}_{Gx}$, $NMS{E}_{Gy}$, $NMS{E}_{Ex}$ and $NMS{E}_{Ey}$) and the virtual node interval $\theta$ when T is fixed at 10 ps. From the observations in Figure 5, it can be seen that as $\theta$ increases from 1 fs to 320 fs, the $NMS{E}_{Ex}$ and $NMS{E}_{Ey}$ slowly increase from 0.0979 to 0.0998 and from 0.0853 to 0.0868, respectively. Then, they gradually stabilize at 0.0998 and 0.0865. On the other hand, the $NMS{E}_{Gx}$ and $NMS{E}_{Gy}$ remain nearly constant at 0.0363 and 0.0376, respectively. The results indicate that when T = 10 ps, the choice of the virtual node interval $\theta$ has a slight impact on the prediction accuracy for the GS-PC_x and GS-PC_y. However, for the ES-PC_x and ES-PC_y, the prediction errors slightly increase with an increase in $\theta$, suggesting a potential sensitivity to the chosen $\theta$.

The results obtained from Figure 4 and Figure 5 demonstrate that the four parallel reservoirs, based on the reservoir QD spin-VCSEL, are capable of reproducing the chaotic dynamics of the GS-PC_x, GS-PC_y, ES-PC_x and ES-PC_y emitted by the driving QD spin-VCSEL. This indicates that the delayed GS-PC_x, GS-PC_y, ES-PC_x and ES-PC_y can successfully synchronize with the GS-${\mathrm{PC}}_x^{\prime }$, GS-${\mathrm{PC}}_y^{\prime }$, ES-${\mathrm{PC}}_x^{\prime }$ and ES-${\mathrm{PC}}_y^{\prime }$ outputs by the reservoir QD spin-VCSEL, respectively. To further analyze the qualities of their chaos synchronizations, the correlation coefficients are introduced and defined as follows.

$$\begin{array}{cc}\hfill & {\rho }_{jx}=\frac{〈\left[C_{jx}(n-L_{jx})-〈C_{jx}(n-L_{jx})〉\right]\left[y_{jx}^{\prime }(n)-〈y_{jx}^{\prime }(n)〉\right]〉}{{〈{\left[C_{jx}(n-L_{jx})-〈C_{jx}(n-L_{jx})〉\right]}^2〉}^{1/2}{〈{\left[y_{jx}^{\prime }(n)-〈y_{jx}^{\prime }(n)〉\right]}^2〉}^{1/2}},\hfill \\ \hfill & {\rho }_{jy}=\frac{〈\left[C_{jy}(n-L_{jy})-〈C_{jy}(n-L_{jy})〉\right]\left[y_{jy}^{\prime }(n)-〈y_{jy}^{\prime }(n)〉\right]〉}{{〈{\left[C_{jy}(n-L_{jy})-〈C_{jy}(n-L_{jy})〉\right]}^2〉}^{1/2}{〈{\left[y_{jy}^{\prime }(n)-〈y_{jy}^{\prime }(n)〉\right]}^2〉}^{1/2}},\hfill \end{array}$$

(24)

where j = G,E (the same below). The symbol 〈 〉 represents the time average. $\rho$ ranges from −1 to 1. With the bigger absolute value of $\rho$, the higher quality of synchronization can be obtained. When $\rho$ equals to ±1, the in-phase and anti-phase synchronous solutions in this system exist.

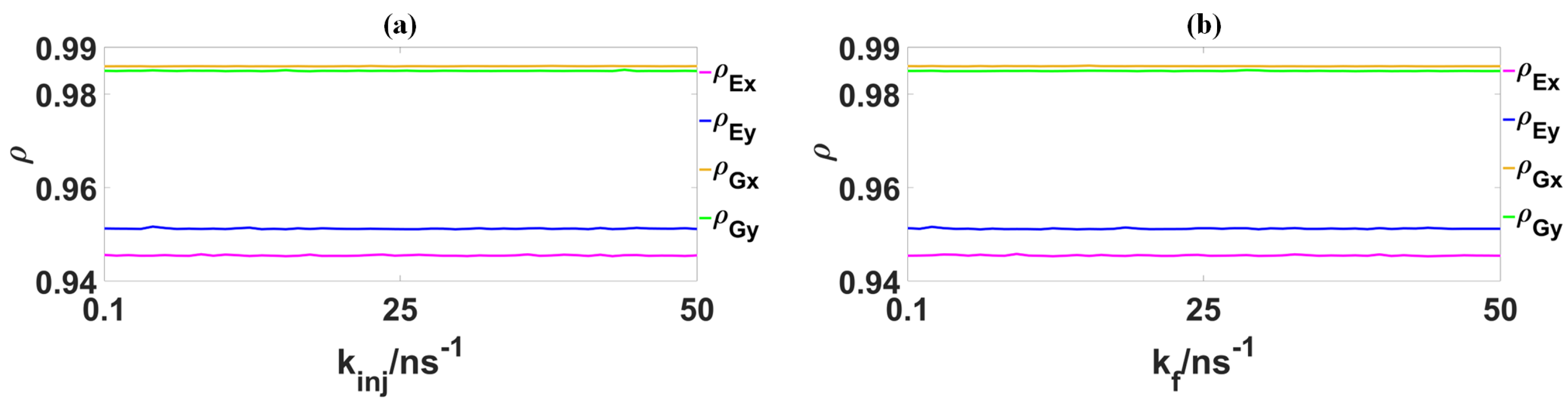
In Figure 6, the correlations ${\rho }_{Gx}$, ${\rho }_{Gy}$, ${\rho }_{Ex}$ and ${\rho }_{Ey}$ are shown as a function of $k_{inj}$ and $k_f$. It can be observed that ${\rho }_{Gx}$, ${\rho }_{Gy}$, ${\rho }_{Ex}$ and ${\rho }_{Ey}$ exhibit minimal changes as $k_{inj}$ and $k_f$ increase in the range of 0.1 ${\mathrm{ns}}^{-1}$ to 50 ${\mathrm{ns}}^{-1}$. Within these two parameter spaces, ${\rho }_{Gx}$ and ${\rho }_{Gy}$ both range between 0.9849 and 0.9857, while ${\rho }_{Ex}$ and ${\rho }_{Ey}$ fluctuate between 0.949 and 0.96. This indicates that ${\rho }_{Gx}$, ${\rho }_{Gy}$, ${\rho }_{Ex}$ and ${\rho }_{Ey}$ possess strong robustness to variations in $k_{inj}$ and $k_f$, which are key parameters of the reservoir QD spin-VCSEL. Furthermore, as all ${\rho }_{Gx}$, ${\rho }_{Gy}$, ${\rho }_{Ex}$ and ${\rho }_{Ey}$ are greater than 0.949, it can be concluded that the GS-${\mathrm{PC}}_x^{\prime }$, GS-${\mathrm{PC}}_y^{\prime }$, ES-${\mathrm{PC}}_x^{\prime }$ and ES-${\mathrm{PC}}_y^{\prime }$ can effectively synchronize with the delayed GS-PC_x, GS-PC_y, ES-PC_x and ES-PC_y, respectively. Notably, ${\rho }_{Gx}$ and ${\rho }_{Gy}$ are higher than ${\rho }_{Ex}$ and ${\rho }_{Ey}$, respectively. This is attributed to the fact that the $NMS{E}_{Gx}$ and $NMS{E}_{Gy}$ for the GS-PC_x and GS-PC_y are lower compared to the $NMS{E}_{Gx}$ and $NMS{E}_{Gy}$ for the ES-PC_x and ES-PC_y, respectively.

Here, by optimizing some key parameter values of the reservoir QD spin-VCSEL, ${\rho }_{Gx}$, ${\rho }_{Gy}$, ${\rho }_{Ex}$ and ${\rho }_{Ey}$ are taken as 0.9856, 0.9851, 0.9495 and 0.9581, respectively. The optimized parameters are as follows: T = 10 ps; $\theta$ = 40 fs; $\eta$ = 4; $k_f$ = 30 ${\mathrm{ns}}^{-1}$; and $k_{inj}$ = 30 ${\mathrm{ns}}^{-1}$. By performing high-quality chaos synchronization between each pair of PCs (i.e., GS-PC_x and GS-${\mathrm{PC}}_x^{\prime }$, GS-PC_y and GS-${\mathrm{PC}}_x^{\prime }$, ES-PC_x and ES-${\mathrm{PC}}_x^{\prime }$, and ES-PC_y and ES-${\mathrm{PC}}_y^{\prime }$) using the reservoir QD spin-VCSEL, one of the messages QPSK, 4QAM, 8QAM and 16QAM can be decoded by synchronously dividing a reservoir-generated chaos and a delayed chaos masked message. The temporal traces of the delayed encoding message ($S_1$(n−$L_{Gx}$), or QPSK), the delayed chaos masked message ($U_{Gx}$(n−$L_{Gx}$)), and the decoding message ($S_1^{\prime }$(n)) are displayed in Figure 7(a₁–a₃). As observed from Figure 7(a₁–a₃), the temporal trajectory of $S_1$(n−$L_{Gx}$) is very similar to that of ($S_1^{\prime }$(n)). Furthermore, $U_{Gx}$(n−$L_{Gx}$) exhibits a chaotic state. Figure 7(a₄–a₆) present the temporal trajectories of $S_2$(n−$L_{Gy}$) (4QAM), $U_{Gy}$(n−$L_{Gy}$) and ($S_2^{\prime }$(n)). As seen from these figures, the temporal trajectory of $S_2$(n−$L_{Gy}$) is basically identical to that of ($S_2^{\prime }$(n)), while $U_{Gy}$(n−$L_{Gy}$) shows a chaotic state. Moreover, as displayed in Figure 7(a₇–a₁₂), the temporal trajectories of $S_3$(n−$L_{Ex}$) (8QAM) and $S_4$(n−$L_{Ey}$) (16QAM) are almost the same as those of ($S_3^{\prime }$(n)) and ($S_4^{\prime }$(n)), respectively. $U_{Ex}$(n−$L_{Ex}$) and $U_{Ey}$(n−$L_{Ey}$) both exhibit a chaotic state. 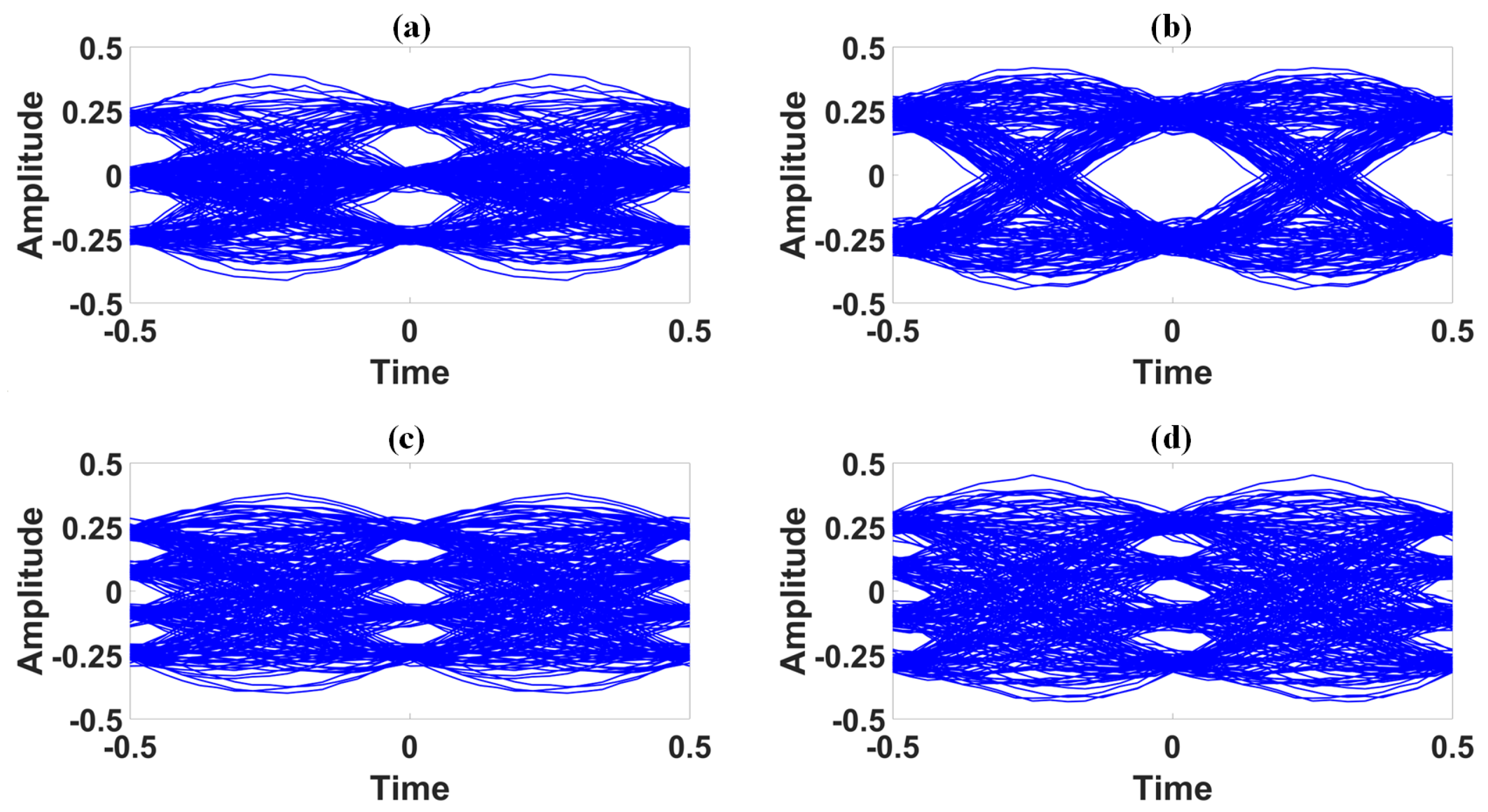Moreover, as in Figure 8, we present the eye-diagrams for these four decoded messages ($S_1^{\prime }$(n), $S_2^{\prime }$(n), $S_3^{\prime }$(n) and $S_4^{\prime }$(n)). One sees from this figure that the “eyes” sizes of the eye-diagrams of these decoded messages are enough large, indicating that the decoded messages of the system have a relatively large tolerance error for noise and jitter and have good quality. However, the superposition of multiple decoded messages causes the signal line of each eye-diagram to become thicker and appear fuzzy. The reason is that very small synchronization errors may be converted into noise and superimposed on the signal line of the eye-diagram. These results indicate that the encoding messages QPSK, 4QAM, 8QAM and 16QAM can be effectively masked in a chaotic carrier and successfully recovered using reservoir computing.

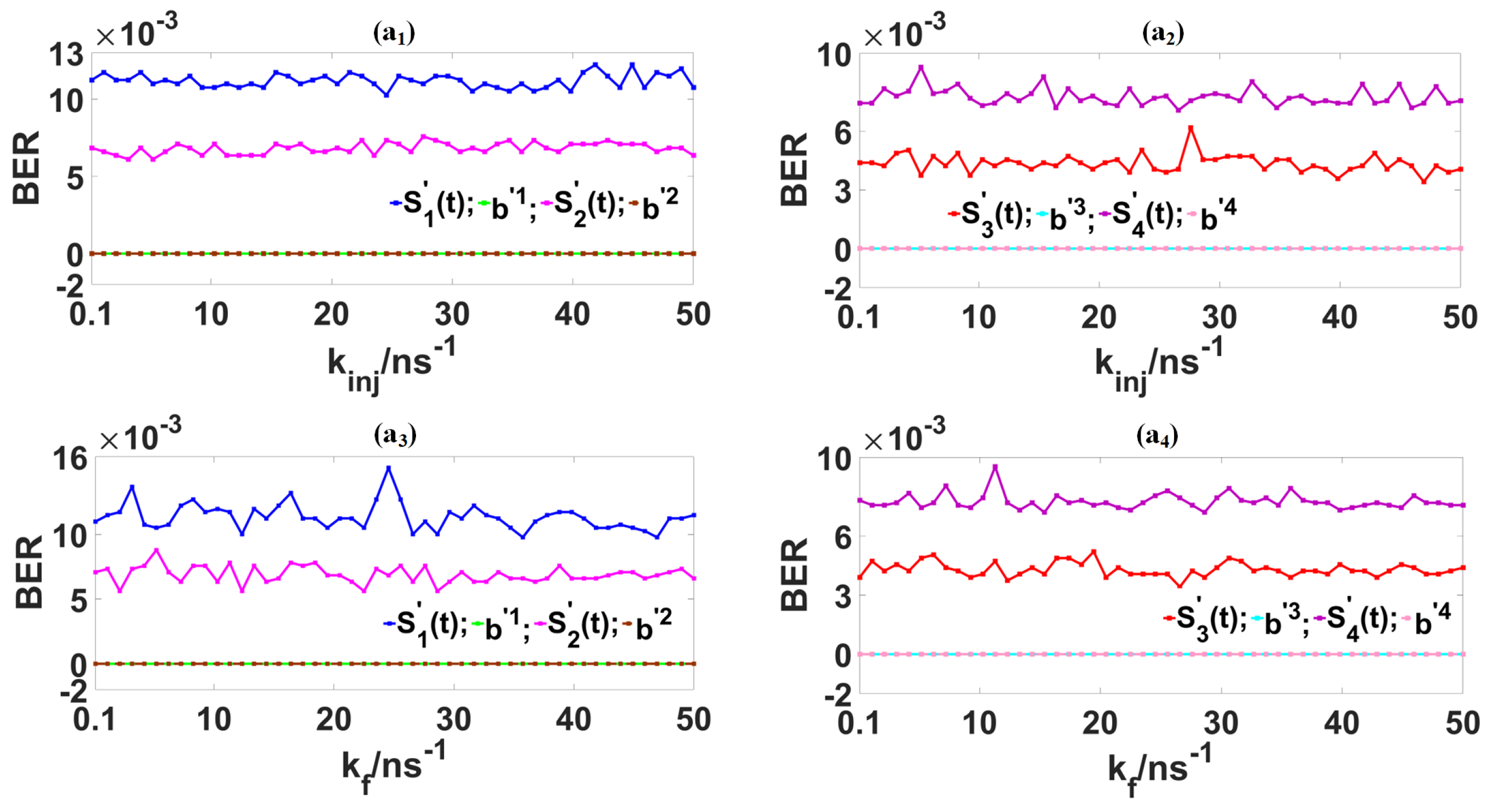
The bit error rate ($BER$) is a commonly utilized metric to gauge the quality of data transmission in optical chaos-based secure communication systems [15]. The $BER$ is defined as the ratio of the number of errored bits to the overall number of bits transmitted. Figure 9 showcases the dependences of the $BER$s for the decoded messages ($S_1^{\prime }$(t), $S_2^{\prime }$(t), $S_3^{\prime }$(t) and $S_4^{\prime }$(t)) and their associated baseband signals ($b_1^{\prime }$, $b_2^{\prime }$, $b_3^{\prime }$ and $b_4^{\prime }$) on two key parameters ($k_{inj}$ and $k_f$). As evidenced by Figure 9(a₁,a₂), the $BER$s for $S_1^{\prime }$(t), $S_2^{\prime }$(t), $S_3^{\prime }$(t) and $S_4^{\prime }$(t) exhibit oscillatory behavior as $k_{inj}$ is adjusted within the range of 0.1 ${\mathrm{ns}}^{-1}$ to 50 ${\mathrm{ns}}^{-1}$. Their $BER$ values, respectively, fluctuate within the following ranges: from 1.02 $\times {10}^{-2}$ to 1.22 $\times {10}^{-2}$ for $S_1^{\prime }$(t), from 6.1 $\times {10}^{-3}$ to 7.5 $\times {10}^{-3}$ for $S_2^{\prime }$(t), from 3.4 $\times {10}^{-3}$ to 6.1 $\times {10}^{-3}$ for $S_3^{\prime }$(t), and from 7.1 $\times {10}^{-3}$ to 9.2 $\times {10}^{-3}$ for $S_4^{\prime }$(t). Within this $k_{inj}$ range, all four decoded messages demonstrate minor oscillatory fluctuations in their $BER$s. The $BER$s cap at 1.5 $\times {10}^{-2}$ for $S_1^{\prime }$(t) and at 8.7 $\times {10}^{-3}$ for $S_2^{\prime }$(t), while those for $S_3^{\prime }$(t) and $S_4^{\prime }$(t) do not surpass 3.4 $\times {10}^{-2}$ and 9.5 $\times {10}^{-3}$, respectively. Based on findings from earlier studies [28,29,30], a $BER$ that closes at or below 0.01 is indicative of potentially high-quality data transmission within an optical chaos communication framework. As depicted in Figure 2c, when demodulated through correlation and refined by various digital signal processing methods, four distinct baseband signal sets (or bitstreams) encapsulated within the decoded messages $S_1^{\prime }$(t), $S_2^{\prime }$(t), $S_3^{\prime }$(t) and $S_4^{\prime }$(t) are successfully reconstructed. Consequently, the $BER$ ranges for these retrieved baseband signals ($b_1^{\prime }$, $b_2^{\prime }$, $b_3^{\prime }$ and $b_4^{\prime }$) remain constant and effectively zero, irrespective of $k_{inj}$ and $k_f$ variations. 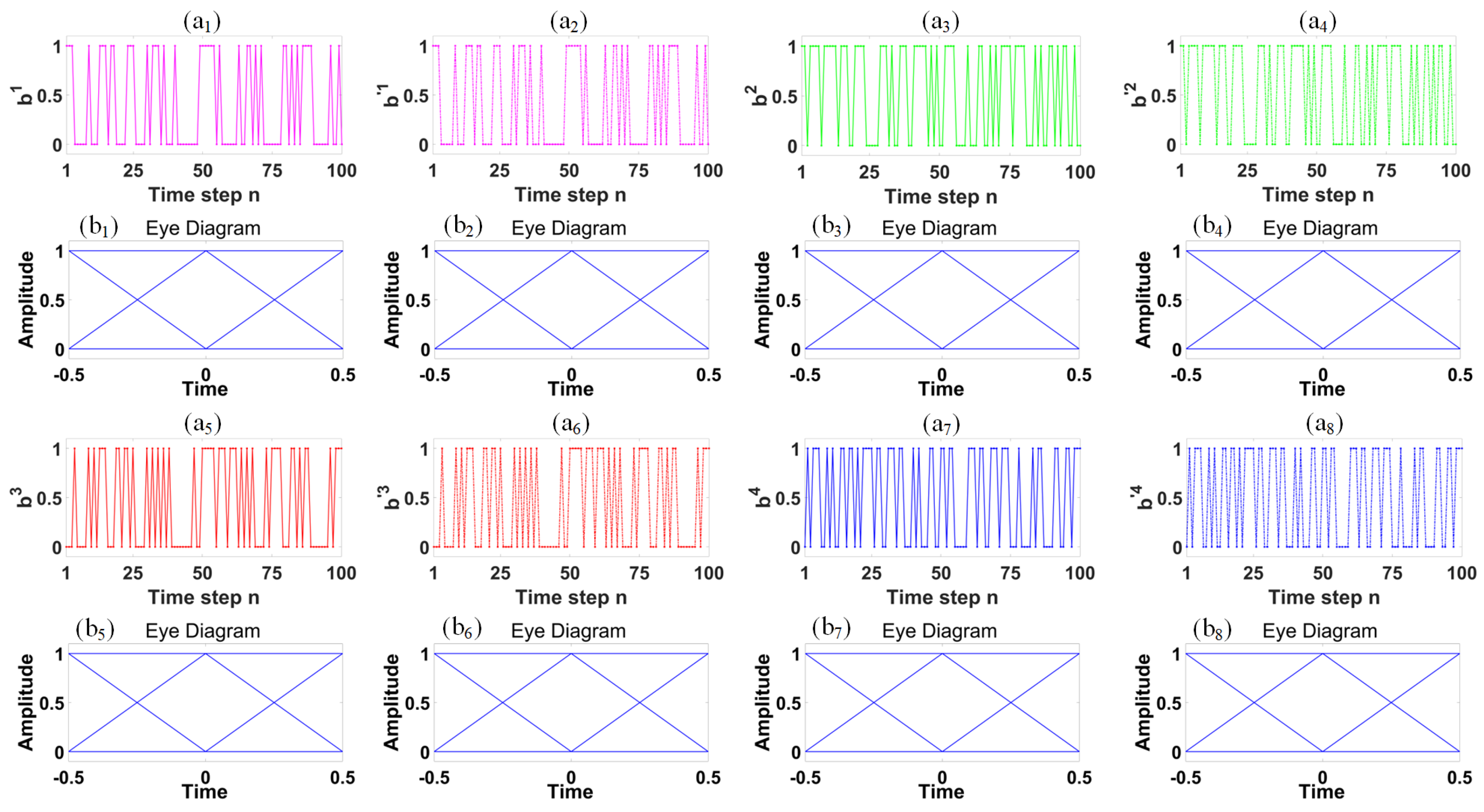Figure 10 delves into the performance of the four retrieved baseband signals by presenting their temporal trajectories and eye-diagrams alongside those of the original baseband signals $b_1$–$b_4$. An inspection of Figure 10 reveals a striking similarity between the temporal profiles of the original signals $b_1$, $b_2$, $b_3$ and $b_4$ and their retrieved counterparts $b_1^{\prime }$, $b_2^{\prime }$, $b_3^{\prime }$ and $b_4^{\prime }$, respectively. The eye-diagrams corresponding to the original and retrieved baseband signals also correspond closely, with $b_1$, $b_2$, $b_3$ and $b_4$, showing a remarkable resemblance to $b_1^{\prime }$, $b_2^{\prime }$, $b_3^{\prime }$ and $b_4^{\prime }$. Notably, the eye openings in the eye-diagrams for $b_1^{\prime }$, $b_2^{\prime }$, $b_3^{\prime }$ and $b_4^{\prime }$ are sufficiently large, which is an important indicator of signal integrity. The insights gathered from Figure 9 and Figure 10 strongly support the effectiveness of our proposed coherent optical chaotic communication system in delivering secure and high-quality data transmission.

4. Conclusions

In conclusion, we introduce a novel four-channel coherent optical chaotic secure communication (COCSC) system that integrates four simultaneous photonic reservoir computers with a coherent demodulation apparatus. This system utilizes a QD-spin-VCSEL as the driving laser, while an autonomous QD-spin-VCSEL acts as the reservoir laser. Individually, the four encoded messages, QPSK, 4QAM, 8QAM and 16QAM are modulated onto four distinct polarization components derived from the ground state (GS) and excited state (ES) emissions in the drive QD-spin-VCSEL. Moreover, we construct four concurrent photonic reservoirs using the polarization components originating from the GS and ES of the reservoir QD-spin-VCSEL. Our system achieves a four-channel COCSC system with a capacity of 4 × 100 GHz through chaos synchronization founded on these four parallel photonic reservoirs. Within this arrangement, we ensure robust wideband chaos synchronization between corresponding polarization components of the driving and reservoir lasers. This precise synchronization allows for the accurate decoding of the four distinct messages (QPSK, 4QAM, 8QAM and 16QAM), each masked within different chaotic polarization components. The decoded messages are then demodulated via correlation techniques and further processed using various digital signal processing methodologies, successfully reconstructing the four separate baseband signals encapsulated within the QPSK, 4QAM, 8QAM and 16QAM formats. Through detailed analysis with eye diagrams, bit error rates, and temporal trajectories of the coherently demodulated baseband signals, we observe that each baseband-signal set is impeccably recovered, evidenced by large eye openings in the eye diagrams and a bit error rate that approaches zero for each baseband-signal set. This innovative approach, which harnesses the power of reservoir computing based on a QD spin-VCSEL, paves the way towards advancing multi-channel coherent optical chaotic communications with enhanced security features.