Performance Enhancement in a Few-Mode Rayleigh-Brillouin Optical Time Domain Analysis System Using Pulse Coding and LMD Algorithm
Abstract
1. Introduction
2. Principles and Method
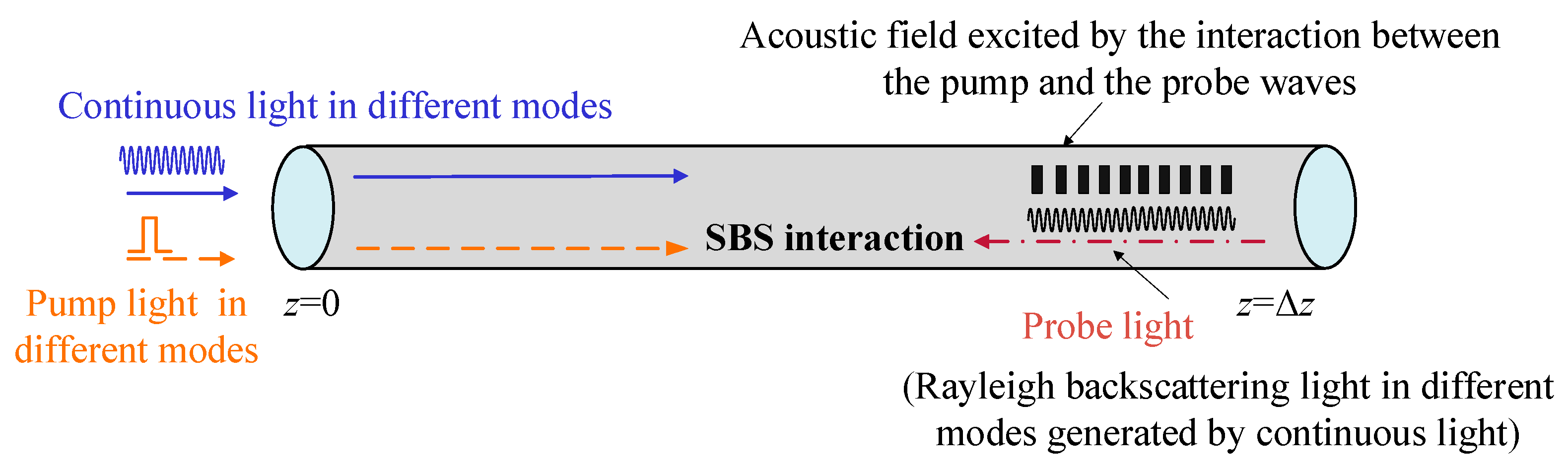
2.1. Rayleigh BOTDA with FMF
2.2. Golay Codes Principle
2.3. LMD Method
3. Experimental Setup
3.1. Experimental Setup
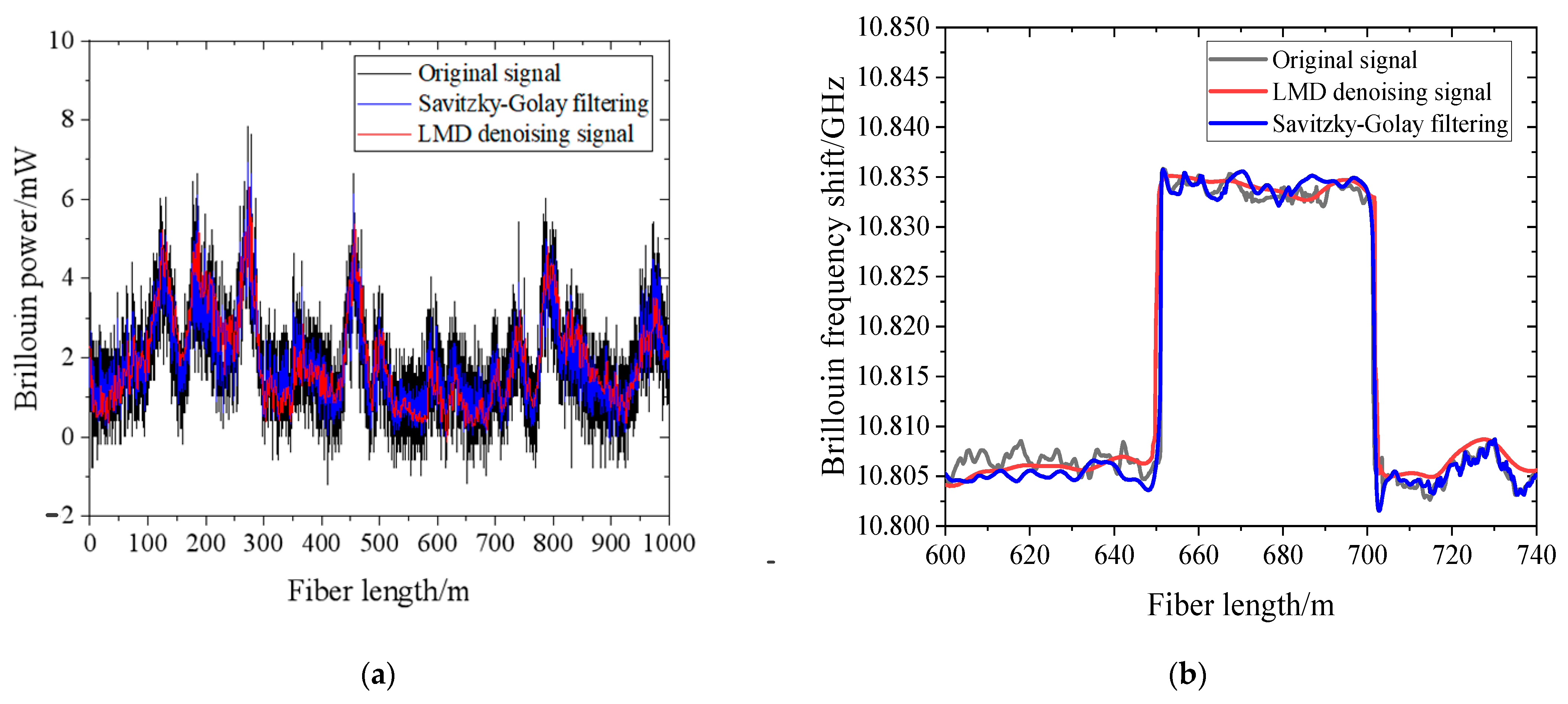
3.2. Results and Discussion
3.2.1. Single Pulse
3.2.2. Coded Pulse
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Zhang, X.; Yang, J.; Qian, Y.; Zhang, Z.; Wang, X.; Xue, Y.; Yuan, Y.; Wang, Y.; Qin, Y. High Spatial Resolution Internal Stress Testing and Analysis of Fiber Optic Winding Structure Using BOTDA. J. Light. Technol. 2023, 41, 5138–5145. [Google Scholar] [CrossRef]
- Gao, S.; Wen, Z.; Wang, H.; Baker, C.; Chen, L.; Cai, Y.; Bao, X. Stimulated Brillouin Scattering and Longitudinal Strain Performance of BOTDA-Based Nonuniform As2Se3-PMMA Tapered Fibers. J. Light. Technol. 2023, 41, 4359–4365. [Google Scholar] [CrossRef]
- Dong, Y. High-Performance Distributed Brillouin Optical Fiber Sensing. Photonic Sens. 2021, 11, 69–90. [Google Scholar] [CrossRef]
- Luo, K.; Wang, B.; Guo, N.; Yu, K.; Yu, C.; Lu, C. Enhancing SNR by Anisotropic Diffusion for Brillouin Distributed Optical Fiber Sensors. J. Light. Technol. 2020, 38, 5844–5852. [Google Scholar] [CrossRef]
- Qi, D.; Guan, X.; Cheng, Y.; Chan, C. Peak-Tracking BOTDA with Dynamic Ternary Search. Opt. Express 2023, 31, 31946–31954. [Google Scholar] [CrossRef] [PubMed]
- Wu, W.; Xing, G.; Feng, X. Research on Structure State Identification Method of Segmented Pipeline Based on Distributed Optical Fiber Sensing. J. Civ. Struct. Health Monit. 2023, 14, 255–268. [Google Scholar] [CrossRef]
- Wang, Y.; Chen, L.; Bao, X. Single-Shot Chirped Pulse BOTDA for Static and Dynamic Strain Sensing. Opt. Lett. 2021, 46, 5774. [Google Scholar] [CrossRef] [PubMed]
- Hoshino, K.; Saito, D.; Endo, Y.; Hasegawa, T.; Tanaka, Y. Brillouin Gain Spectrum Manipulation Using Multifrequency Pump and Probe for Slope-Assisted BOTDA with Wider Dynamic Range. Appl. Phys. Express 2022, 15, 022009. [Google Scholar] [CrossRef]
- Minardo, A.; Coscetta, A.; Bernini, R.; Zeni, L. Heterodyne Slope-Assisted Brillouin Optical Time-Domain Analysis for Dynamic Strain Measurements. J. Opt. 2016, 18, 025606. [Google Scholar] [CrossRef]
- Huang, L.; Fan, X.; He, Z. Scanning-Free Hybrid Rayleigh–Brillouin Distributed Fiber-Optic Sensing System. Opt. Lett. 2023, 48, 4629. [Google Scholar] [CrossRef]
- Cui, Q.; Pamukcu, S.; Lin, A.; Xiao, W.; Herr, D.; Toulouse, J.; Pervizpour, M. Distributed Temperature Sensing System Based on Rayleigh Scattering BOTDA. IEEE Sens. J. 2011, 11, 399–403. [Google Scholar] [CrossRef]
- Cui, Q.; Pamukcu, S.; Pervizpour, M. Impact Wave Monitoring in Soil Using a Dynamic Fiber Sensor Based on Stimulated Brillouin Scattering. Sensors 2015, 15, 8163–8172. [Google Scholar] [CrossRef] [PubMed]
- Chen, W.; Hu, G.; Liu, F.; Wang, F.; Song, C.; Li, X.; Yu, Y. Threshold for Stimulated Brillouin Scattering in Few-Mode Fibers. Appl. Opt. 2019, 58, 4105–4110. [Google Scholar] [CrossRef] [PubMed]
- Song, K.Y.; Kim, Y.H. Characterization of Stimulated Brillouin Scattering in a Few-Mode Fiber. Opt. Lett. 2013, 38, 4841–4844. [Google Scholar] [CrossRef] [PubMed]
- Wu, H.; Tang, M.; Wang, M.; Zhao, C.; Zhao, Z.; Wang, R.; Liao, R.; Fu, S.; Yang, C.; Tong, W.; et al. Few-Mode Optical Fiber Based Simultaneously Distributed Curvature and Temperature Sensing. Opt. Express 2017, 25, 12722. [Google Scholar] [CrossRef] [PubMed]
- Li, A.; Wang, Y.; Fang, J.; Li, M.; Kim, B.Y.; Shieh, W. Few-Mode Fiber Multi-Parameter Sensor with Distributed Temperature and Strain Discrimination. Opt. Lett. 2015, 40, 1488. [Google Scholar] [CrossRef]
- Sui, Q.; Zhang, H.; Downie, J.D.; Wood, W.A.; Hurley, J.; Mishra, S.; Lau, A.P.T.; Lu, C.; Tam, H.-Y.; Wai, P.K.A. Long-Haul Quasi-Single-Mode Transmissions Using Few-Mode Fiber in Presence of Multi-Path Interference. Opt. Express 2015, 23, 3156. [Google Scholar] [CrossRef]
- Sheng, D.; Han, Z.; Qiao, Z.; Dong, T.; Wang, C.; Tian, H. Distributed Multi-Parameter Sensor Based on Brillouin Scattering in an Etched Few-Mode Multi-Core Fiber. Opt. Commun. 2024, 552, 130085. [Google Scholar] [CrossRef]
- Kim, Y.H.; Song, K.Y. Characterization of Distributed Brillouin Sensors Based on Elliptical-Core Two-Mode Fiber. IEEE Sens. J. 2019, 19, 2155–2161. [Google Scholar] [CrossRef]
- Kim, Y.H.; Song, K.Y. Recent Progress in Distributed Brillouin Sensors Based on Few-Mode Optical Fibers. Sensors 2021, 21, 2168. [Google Scholar] [CrossRef]
- Li, L.; Jiang, C.; Hu, C.; Gao, J.; Deng, L.; Cao, T.; Li, H. Highly Sensitive Strain Sensor Based on Tapered Few-Mode Fiber. Rev. Sci. Instrum. 2023, 94, 075006. [Google Scholar] [CrossRef] [PubMed]
- Horiguchi, T.; Shimizu, K.; Kurashima, T.; Tateda, M.; Koyamada, Y. Development of a Distributed Sensing Technique Using Brillouin Scattering. J. Light. Technol. 1995, 13, 1296–1302. [Google Scholar] [CrossRef]
- Feng, L.; Liu, Y.; He, W.; You, Y.; Wang, L.; Xu, X.; Chou, X. Intramode Brillouin Scattering Properties of Single-Crystal Lithium Niobate Optical Fiber. Appl. Sci. 2022, 12, 6476. [Google Scholar] [CrossRef]
- Zhang, Y.; Gao, H.; Fu, X.; Tian, Y. Characterization of Brillouin scattering in a few-mode fiber. Acta Phys. Sin. 2017, 66, 024207. [Google Scholar] [CrossRef]
- Li, A.; Hu, Q.; Shieh, W. Characterization of Stimulated Brillouin Scattering in a Circular-Core Two-Mode Fiber Using Optical Time-Domain Analysis. Opt. Express 2013, 21, 31894–31906. [Google Scholar] [CrossRef]
- Li, Z.; Zhou, Y.; Hua, Z.; Yan, L. Balanced Detection for Performance Enhancement in a Pulse-Coded Brillouin Optical Time Domain Analyzer. IEEE Sens. J. 2023, 23, 1166–1171. [Google Scholar] [CrossRef]
- Zan, M.S.D.B.; Horiguchi, T. A Dual Golay Complementary Pair of Sequences for Improving the Performance of Phase-Shift Pulse BOTDA Fiber Sensor. J. Light. Technol. 2012, 30, 3338–3356. [Google Scholar] [CrossRef]
- Soto, M.A.; Floch, S.L.; Thévenaz, L. Bipolar Optical Pulse Coding for Performance Enhancement in BOTDA Sensors. Opt. Express 2013, 21, 16390–16397. [Google Scholar] [CrossRef] [PubMed]
- Bao, Y.; Huang, Q.; Sun, J. Theoretical Research on the Characteristics of BOTDR with Raman Amplification. Opt. Commun. 2021, 487, 126775. [Google Scholar] [CrossRef]
- Esmaeelpour, M.; Ryf, R.; Fontaine, N.K.; Chen, H.; Gnauck, A.H.; Essiambre, R.J.; Toulouse, J.; Sun, Y.; Lingle, R. Transmission Over 1050-Km Few-Mode Fiber Based on Bidirectional Distributed Raman Amplification. J. Light. Technol. 2016, 34, 1864–1871. [Google Scholar] [CrossRef]
- Soto, M.A.; Bolognini, G.; Pasquale, F.D. Optimization of Long-Range BOTDA Sensors with High Resolution Using First-Order Bi-Directional Raman Amplification. Opt. Express 2011, 19, 4444–4457. [Google Scholar] [CrossRef] [PubMed]
- Zhao, J.; Wang, T.; Zhang, Q.; Zhang, M.; Zhang, J.; Qiao, L.; Gao, S.; Liu, J.; Li, J. Signal-to-Noise Ratio Improvement of Brillouin Optical Time Domain Analysis System Based on Empirical Mode Decomposition and Finite Impulse Response. Appl. Opt. 2020, 59, 4220. [Google Scholar] [CrossRef] [PubMed]
- Soto, M.A.; Ramírez, J.A.; Thévenaz, L. Intensifying the Response of Distributed Optical Fibre Sensors Using 2D and 3D Image Restoration. Nat. Commun. 2016, 7, 10870. [Google Scholar] [CrossRef] [PubMed]
- Farahani, M.A.; Castillo-Guerra, E.; Colpitts, B.G. Acceleration of Measurements in BOTDA Sensors Using Adaptive Linear Prediction. IEEE Sens. J. 2013, 13, 263–272. [Google Scholar] [CrossRef]
- Qian, X.; Jia, X.; Wang, Z.; Zhang, B.; Xue, N.; Sun, W.; He, Q.; Wu, H. Noise Level Estimation of BOTDA for Optimal Non-Local Means Denoising. Appl. Opt. 2017, 56, 4727. [Google Scholar] [CrossRef]
- Li, B.; Jiang, N.; Han, X. Denoising of BOTDR Dynamic Strain Measurement Using Convolutional Neural Networks. Sensors 2023, 23, 1764. [Google Scholar] [CrossRef] [PubMed]
- Li, B.; Jiang, N.; Han, X. Denoising of Brillouin Gain Spectrum Images for Improved Dynamic Measurements of BOTDR. IEEE Photonics J. 2023, 15, 1–8. [Google Scholar] [CrossRef]
- Zhang, Y.; Lu, Y.; Chen, L.; Wu, T.; He, C. Segmented Noise Reduction Based on Brillouin-Spectrum-Partition in Brillouin Optical Time Domain Sensors. IEEE Sens. J. 2021, 21, 22792–22802. [Google Scholar] [CrossRef]
- Zha, J.; Meng, Y.; Li, D.; Yin, H.; Wang, D.; Yu, W. Determination of Average Times for Brillouin Optical Time Domain Analysis Sensor Denoising by Non-Local Means Filtering. Opt. Commun. 2018, 426, 648–653. [Google Scholar] [CrossRef]
- Yang, Z.; Li, Z.; Zaslawski, S.; Thévenaz, L.; Soto, M.A. Design Rules for Optimizing Unipolar Coded Brillouin Optical Time-Domain Analyzers. Opt. Express 2018, 26, 16505–16523. [Google Scholar] [CrossRef]
- Sun, Q.; Tu, X.; Sun, S.; Meng, Z. Long-Range BOTDA Sensor over 50 Km Distance Employing Pre-Pumped Simplex Coding. J. Opt. 2016, 18, 055501. [Google Scholar] [CrossRef]
- Wang, Q.; Bai, Q.; Liang, C.; Wang, Y.; Liu, Y.; Jin, B. Random Coding Method for SNR Enhancement of BOTDR. Opt. Express 2022, 30, 11604–11618. [Google Scholar] [CrossRef] [PubMed]
- Zhou, Y.; Yan, L.; Li, Z.; He, H.; Ye, J.; Pan, W.; Luo, B. Long-Range High-Spatial-Resolution Distributed Brillouin Sensing Enabled by Correlation-Domain Encoding. Opt. Lett. 2023, 48, 3143–3146. [Google Scholar] [CrossRef] [PubMed]
- Zheng, H.; Yan, Y.; Wang, Y.; Shen, X.; Lu, C. Deep Learning Enhanced Long-Range Fast BOTDA for Vibration Measurement. J. Light. Technol. 2022, 40, 262–268. [Google Scholar] [CrossRef]
- Nordin, N.D.; Zan, M.S.D.; Abdullah, F. Comparative Analysis on the Deployment of Machine Learning Algorithms in the Distributed Brillouin Optical Time Domain Analysis (BOTDA) Fiber Sensor. Photonics 2020, 7, 79. [Google Scholar] [CrossRef]
- Wu, H.; Wang, L.; Guo, N.; Shu, C.; Lu, C. Brillouin Optical Time-Domain Analyzer Assisted by Support Vector Machine for Ultrafast Temperature Extraction. J. Light. Technol. 2017, 35, 4159–4167. [Google Scholar] [CrossRef]
- Azad, A.K.; Wang, L.; Guo, N.; Lu, C.; Tam, H.Y. Temperature Sensing in BOTDA System by Using Artificial Neural Network. Electron. Lett. 2015, 51, 1578–1580. [Google Scholar] [CrossRef]
- Lv, T.; Ye, X.; Huang, K.; Zheng, Y.; Ge, Z.; Xu, Z.; Sun, X. Cascaded Feedforward Neural Network Based Simultaneously Fast and Precise Multi-Characteristics Extraction and BFS Error Estimation. J. Light. Technol. 2022, 40, 7937–7945. [Google Scholar] [CrossRef]
- Krivosheev, A.I.; Barkov, F.L.; Konstantinov, Y.A.; Belokrylov, M.E. State-of-the-Art Methods for Determining the Frequency Shift of Brillouin Scattering in Fiber-Optic Metrology and Sensing (Review). Instrum. Exp. Tech. 2022, 65, 687–710. [Google Scholar] [CrossRef]
- Zhang, Y.; Lu, Y.; Zhang, Z.; Wang, J.; He, C.; Wu, T. Noise Reduction by Brillouin Spectrum Reassembly in Brillouin Optical Time Domain Sensors. Opt. Lasers Eng. 2020, 125, 105865. [Google Scholar] [CrossRef]
- Wu, H.; Wan, Y.; Tang, M.; Chen, Y.; Zhao, C.; Liao, R.; Chang, Y.; Fu, S.; Shum, P.P.; Liu, D. Real-Time Denoising of Brillouin Optical Time Domain Analyzer With High Data Fidelity Using Convolutional Neural Networks. J. Light. Technol. 2019, 37, 2648–2653. [Google Scholar] [CrossRef]
- Li, S.; Sun, S.; Shu, Q.; Chen, M.; Zhang, D.; Zhou, D. Partial Discharge Signal Denoising Method Based on Frequency Spectrum Clustering and Local Mean Decomposition. IET Sci. Meas. Amp Technol. 2021, 14, 853–861. [Google Scholar] [CrossRef]
- Hsueh, H.-C.; Chien, S.-Y. On-Line Local Mean Decomposition and Its Application to ECG Signal Denoising. In Proceedings of the 2014 IEEE Biomedical Circuits and Systems Conference (BioCAS) Proceedings, Lausanne, Switzerland, 22–24 October 2014; pp. 17–20. [Google Scholar]
- Smith, J.S. The Local Mean Decomposition and Its Application to EEG Perception Data. J. R. Soc. Interface 2005, 2, 443–454. [Google Scholar] [CrossRef] [PubMed]
- Kovalev, V.I.; Harrison, R.G. Observation of Inhomogeneous Spectral Broadening of Stimulated Brillouin Scattering in an Optical Fiber. Phys. Rev. Lett. 2000, 85, 1879–1882. [Google Scholar] [CrossRef] [PubMed]
- Kovalev, V.I.; Harrison, R.G. Waveguide-Induced Inhomogeneous Spectral Broadening of Stimulated Brillouin Scattering in Optical Fiber. Opt. Lett. 2002, 27, 2022. [Google Scholar] [CrossRef] [PubMed]
- Jedwab, J.; Parker, M.G. Golay Complementary Array Pairs. Des. Codes Cryptogr. 2007, 44, 209–216. [Google Scholar] [CrossRef]
- Zhang, Q.; Wang, T.; Zhao, J.; Liu, J.; Wang, Y.; Zhang, J.; Qiao, L.; Zhang, M. Denoising Algorithm for Brillouin Optical Time-Domain Analysis Sensing Systems Based on Local Mean Decomposition. Acta Opt. Sin. 2021, 41, 1306009. [Google Scholar] [CrossRef]








Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhang, L.; Li, X.; Wang, J.; Zhang, L.; Li, Y. Performance Enhancement in a Few-Mode Rayleigh-Brillouin Optical Time Domain Analysis System Using Pulse Coding and LMD Algorithm. Photonics 2024, 11, 308. https://doi.org/10.3390/photonics11040308
Zhang L, Li X, Wang J, Zhang L, Li Y. Performance Enhancement in a Few-Mode Rayleigh-Brillouin Optical Time Domain Analysis System Using Pulse Coding and LMD Algorithm. Photonics. 2024; 11(4):308. https://doi.org/10.3390/photonics11040308
Chicago/Turabian StyleZhang, Lixin, Xuan Li, Jianjian Wang, Lei Zhang, and Yongqian Li. 2024. "Performance Enhancement in a Few-Mode Rayleigh-Brillouin Optical Time Domain Analysis System Using Pulse Coding and LMD Algorithm" Photonics 11, no. 4: 308. https://doi.org/10.3390/photonics11040308
APA StyleZhang, L., Li, X., Wang, J., Zhang, L., & Li, Y. (2024). Performance Enhancement in a Few-Mode Rayleigh-Brillouin Optical Time Domain Analysis System Using Pulse Coding and LMD Algorithm. Photonics, 11(4), 308. https://doi.org/10.3390/photonics11040308




