Photoreflectance Analysis of InAsPSb/InGaAs Multi-Quantum Well LED Structures with Different Well/Barrier Numbers
Abstract
1. Introduction
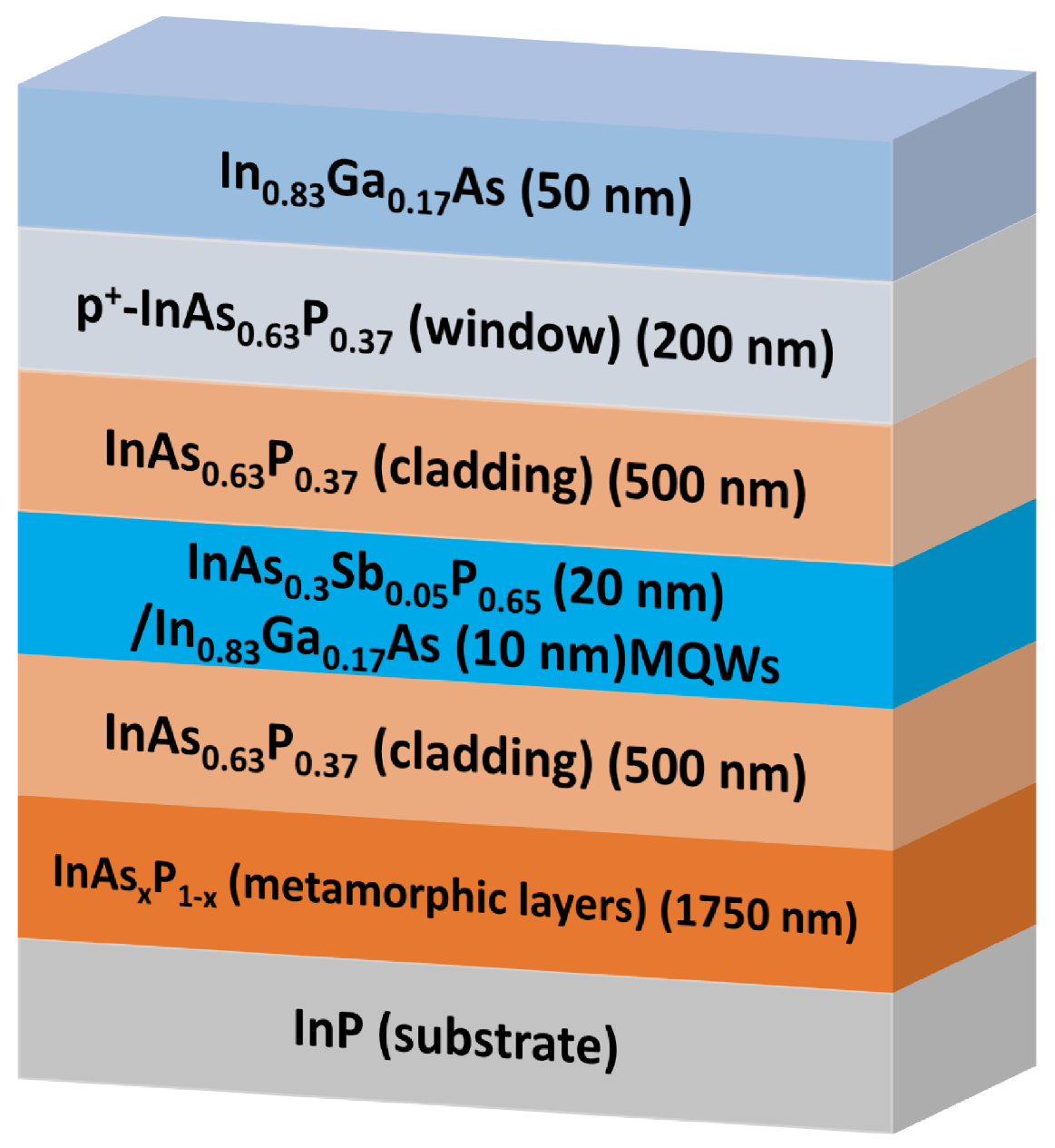
2. Experimental Method
3. Results and Discussion
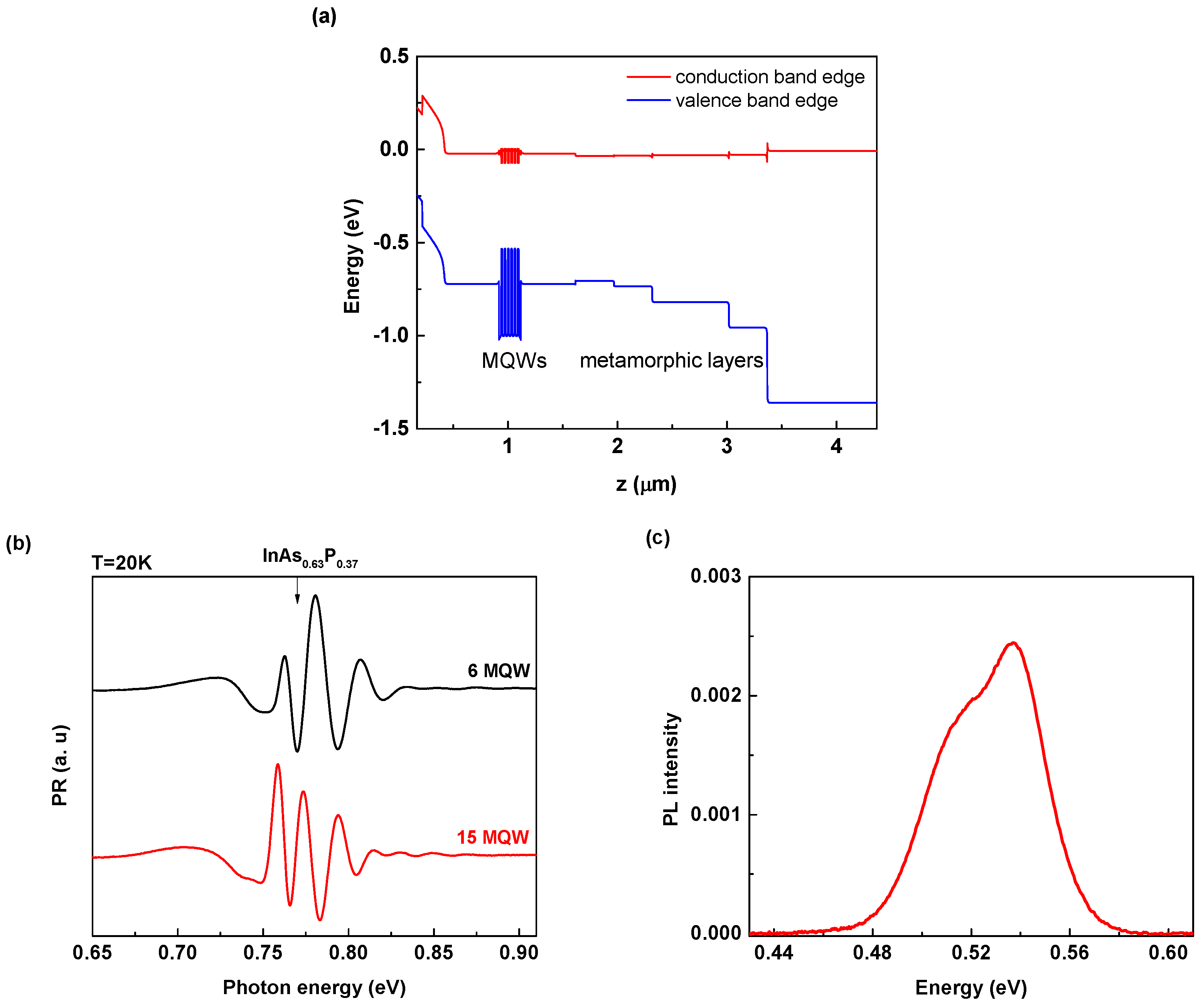
3.1. Band Diagram and PR Spectra
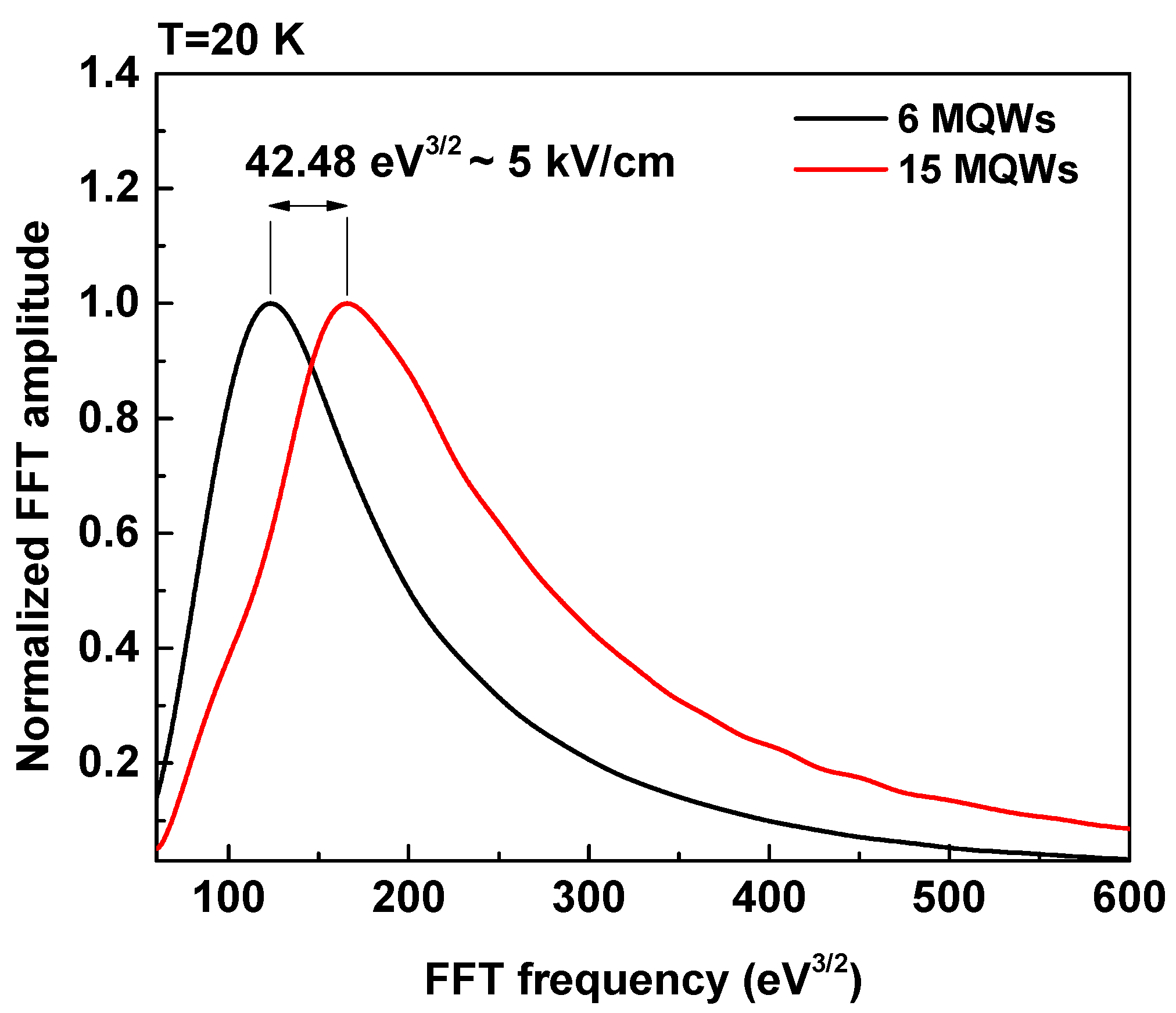
3.2. Fast Fourier Transform (FFT) of the PR Spectra
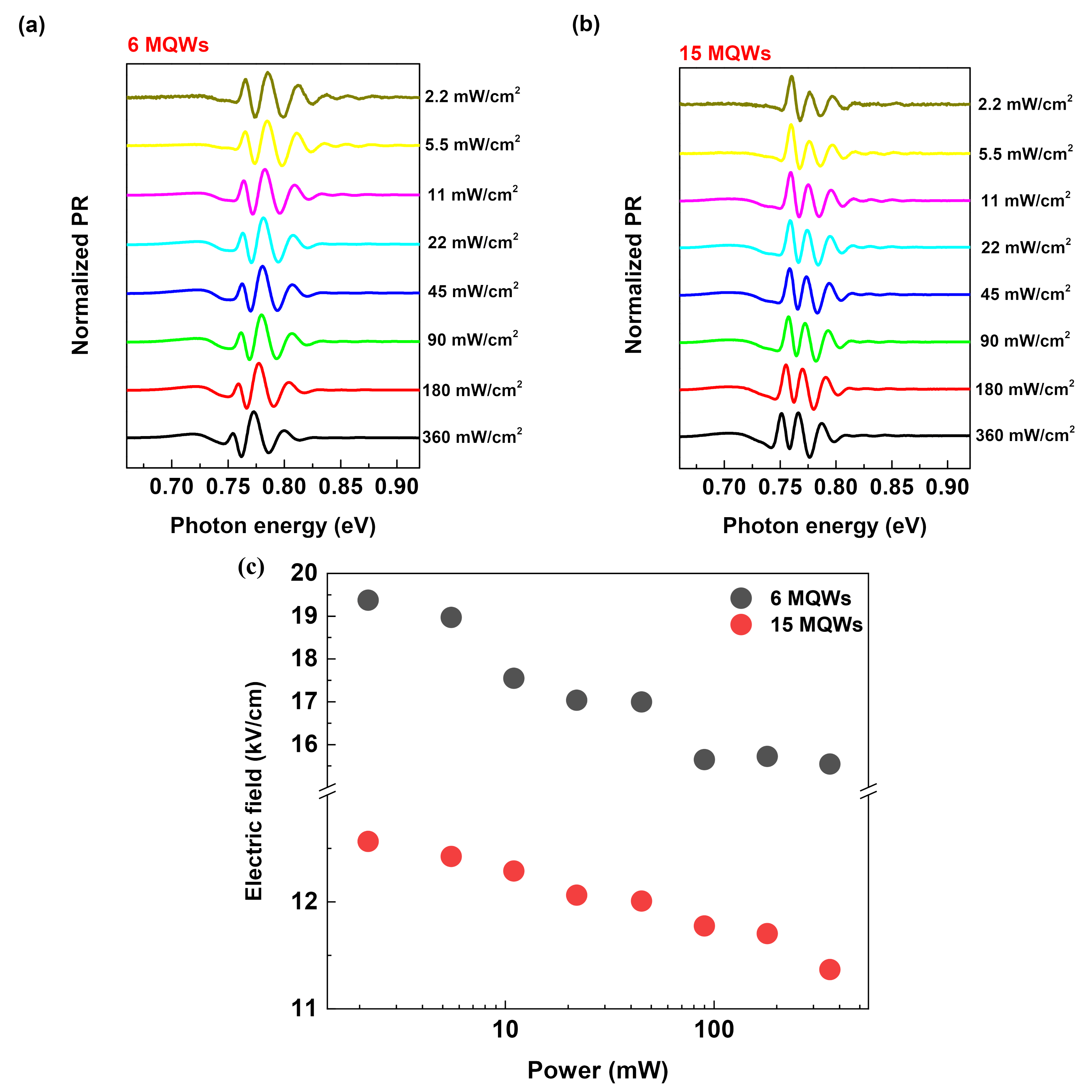
3.3. Power Dependence PR Spectra
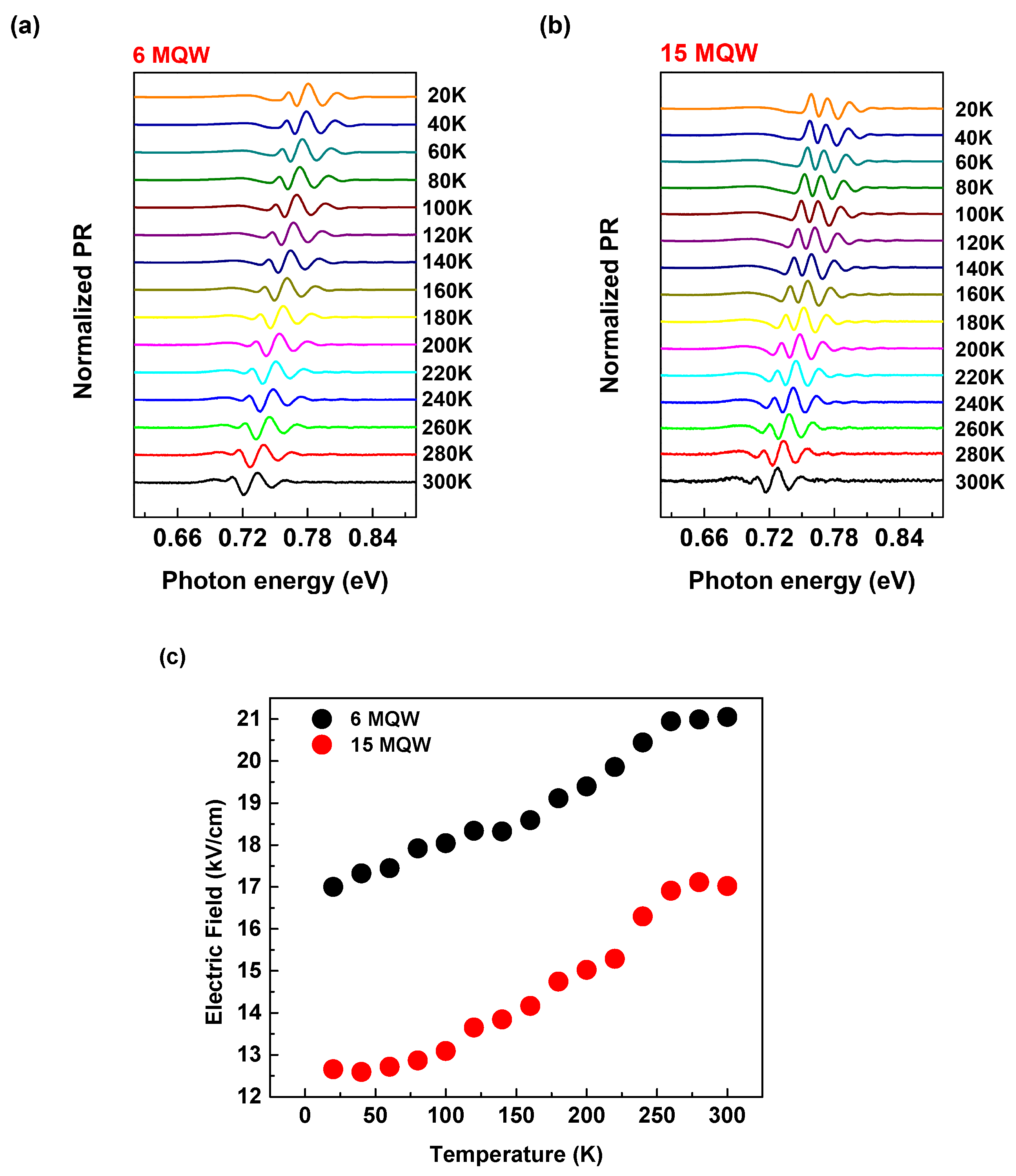
3.4. Temperature Dependence PR Spectra
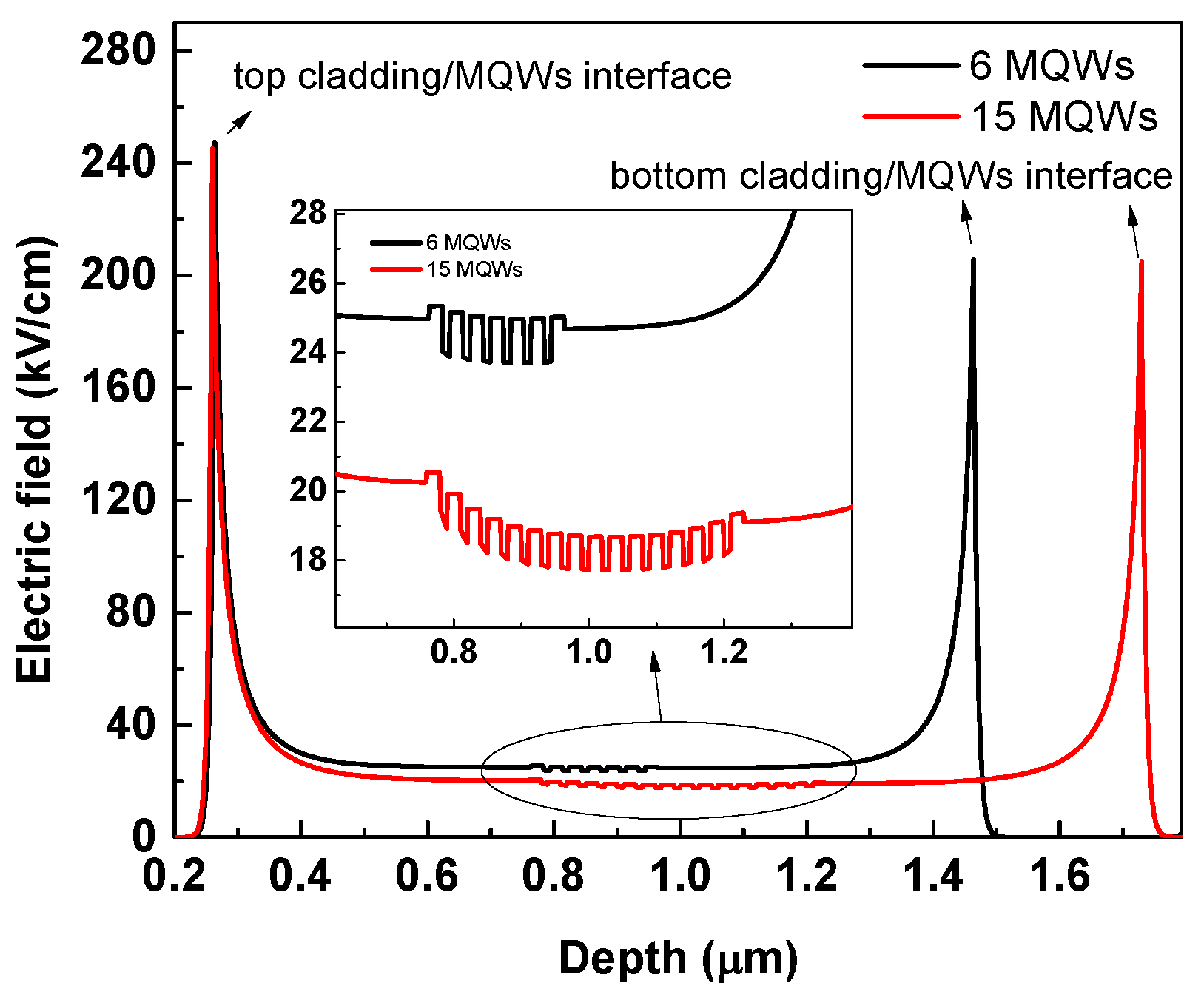
3.5. Electric Field Simulations
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Repiso, E.; Broderick, C.A.; de la Mata, M.; Arkani, R.; Lu, Q.; Marshall, A.R.J.; Molina, S.I.; O’Reilly, E.P.; Carrington, P.J.; Krier, A. Optical properties of metamorphic typeI InAs1−xSbx/AlyIn1−yAs quantum wells grown on GaAs for the mid-infrared spectral range. J. Phys. D Appl. Phys. 2019, 52, 465102. [Google Scholar] [CrossRef]
- Mikhailov, N.N.; Dvoretsky, S.A.; Remesnik, V.G.; Uzhakov, I.N.; Shvets, V.A.; Aleshkin, V.Y. Interband Electron Transitions Energy in Multiple HgCdTe Quantum Wells at Room Temperature. Photonics 2023, 10, 430. [Google Scholar] [CrossRef]
- Chen, B.; Chen, Y.; Deng, Z. Recent advances in high speed photodetectors for eSWIR/MWIR/LWIR applications. Photonics 2021, 8, 14. [Google Scholar] [CrossRef]
- Popov, A.A.; Sherstnev, V.V.; Yakovlev, Y.P.; Baranov, A.N.; Alibert, C. Powerful mid-infrared light emitting diodes for pollution monitoring. Electron. Lett. 1997, 33, 86–88. [Google Scholar] [CrossRef]
- Stephan, S.; Frederic, D.; Markus Christian, A. Novel Inp and GaSb based light sources for the near to far infrared. Semicond. Sci. Technol. 2016, 31, 113005. [Google Scholar] [CrossRef]
- Koike, M.; Shibata, N.; Kato, H.; Takahashi, Y. Development of high efficiency GaN-based multiquantum-well light-emitting diodes and their applications. IEEE J. Sel. Top. Quantum Electron. 2002, 8, 271–277. [Google Scholar] [CrossRef]
- Wu, S.; Zhang, L.; Wan, R.; Zhou, H.; Lee, K.H.; Chen, Q.; Huang, Y.C.; Gong, X.; Tan, C.S. Ge0.92Sn0.08/Ge multi-quantum-well LEDs operated at 2 μm-wavelength on a 12 inch Si substrate. Photonics Res. 2023, 11, 1606–1612. [Google Scholar] [CrossRef]
- Peng, L.; Li, X.; Zheng, J.; Liu, X.; Li, M.; Liu, Z.; Xue, C.; Zuo, Y.; Cheng, B. Room-temperature direct-bandgap electroluminescence from type-I GeSn/SiGeSn multiple quantum wells for 2 μm LEDs. J. Lumin. 2020, 228, 117539. [Google Scholar] [CrossRef]
- Hlavatsch, M.; Mizaikoff, B. Advanced mid-infrared lightsources above and beyond lasers and their analytical utility. Anal. Sci. 2022, 38, 1125–1139. [Google Scholar] [CrossRef]
- Mensz, P.M.; Dror, B.; Ajay, A.; Bougerol, C.; Monroy, E.; Orenstein, M.; Bahir, G. Design and implementation of bound-to-quasibound GaN/AlGaN photovoltaic quantum well infrared photodetectors operating in the short wavelength infrared range at room temperature. J. Appl. Phys. 2019, 125, 174505. [Google Scholar] [CrossRef]
- Seyedein Ardebili, S.B.; Kim, J.S.; Ha, J.; Kang, T.I.; Zeinalvand Farzin, B.; Kim, Y.; Lee, S.J. Band-to-Band Transitions in InAs/GaSb Multi-Quantum-Well Structures Using kp Theory: Effects of Well/Barrier Width and Temperature. Energies 2023, 16, 1162. [Google Scholar] [CrossRef]
- Altayar, A.R.; Al-Saymari, F.A.; Repiso, E.; Hanks, L.; Craig, A.P.; Bentley, M.; Delli, E.; Carrington, P.J.; Krier, A.; Marshall, A.R.J. Electroluminescence characterization of mid-infrared InAsSb/AlInAs multi-quantum well light emitting diodes heteroepitaxially integrated on GaAs and silicon wafers. J. Cryst. Growth 2022, 586, 126627. [Google Scholar] [CrossRef]
- Krier, A.; Huang, X.L.; Sherstnev, V.V. Mid-infrared electroluminescence in LEDs based on InAs and related alloys. In Mid-Infrared Semiconductor Optoelectronics; Springer: Berlin/Heidelberg, Germany, 2006; pp. 359–394. [Google Scholar]
- Delli, E.; Hodgson, P.D.; Bentley, M.; Repiso, E.; Craig, A.P.; Lu, Q.; Beanland, R.; Marshall, A.R.J.; Krier, A.; Carrington, P.J. Mid-infrared type-II InAs/InAsSb quantum wells integrated on silicon. Appl. Phys. Lett. 2020, 117, 131103. [Google Scholar] [CrossRef]
- Cheetham, K.J.; Krier, A.; Patel, I.I.; Martin, F.L.; Tzeng, J.S.; Wu, C.J.; Lin, H.H. Raman scattering in InAsxSbyP1−x−y alloys grown by gas source MBE. J. Phys. D Appl. Phys. 2011, 44, 085405. [Google Scholar] [CrossRef]
- Keen, J.A.; Lane, D.; Kesaria, M.; Marshall, A.R.J.; Krier, A. InAs/InAsSb type-II strained-layer superlattices for mid-infrared LEDs. J. Phys. D Appl. Phys. 2018, 51, 075103. [Google Scholar] [CrossRef]
- Vurgaftman, I.; áR Meyer, J.; Ram-Mohan, L.R. Band parameters for III–V compound semiconductors and their alloys. J. Appl. Phys. 2001, 89, 5815–5875. [Google Scholar] [CrossRef]
- Park, S.; Nguyen, P.D.; Kim, M.; Jeon, J.; Kim, Y.; Lee, S.J. Monolithic In0.83Ga0.17As multiple quantum well light-emitting diodes using InAsPSb wide bandgap barrier. In Advanced Solid State Lasers; Greater Tacoma Convention Center Tacoma: Washington, DA, USA, 2022; p. JTu6A-1. [Google Scholar]
- Park, S.; Jeon, J.; More, V.M.; Lee, R.S.; Seo, Y.; Kim, M.; Nguyen, P.D.; Kim, M.; Kim, J.S.; Kim, Y.; et al. Monolithic two-color short-wavelength InGaAs infrared photodetectors using InAsP metamorphic buffers. Appl. Surf. Sci. 2022, 581, 152421. [Google Scholar] [CrossRef]
- Misiewicz, J.; Sitarek, P.; Sek, G.; Kudrawiec, R. Semiconductor heterostructures and device structures investigated by photoreflectance spectroscopy. Mater. Sci. 2003, 21, 263–318. [Google Scholar]
- Zhang, B.; Qiu, W.Y.; Chen, P.P.; Wang, X.J. Photoreflectance and photoreflectance excitation study of optical transitions in GaAsBi/GaAs heterostructure. J. Appl. Phys. 2018, 123, 035702. [Google Scholar] [CrossRef]
- Vashisht, G.; Porwal, S.; Haldar, S.; Dixit, V.K. Influence of interface states on built-in electric field and diamagnetic-Landau energy shifts in asymmetric modulation-doped InGaAs/GaAs QWs. J. Phys. D Appl. Phys. 2022, 55, 385101. [Google Scholar] [CrossRef]
- Zeinalvand Farzin, B.; Lee, D.; Kang, T.I.; Kim, J.S.; Kim, G.H.; Lee, S.J.; Kim, Y. Phase-sensitive analysis of a two-color infrared photodetector using photoreflectance spectroscopy. J. Appl. Phys. 2023, 134, 135305. [Google Scholar] [CrossRef]
- Saladukha, D.; Clavel, M.B.; Murphy-Armando, F.; Greene-Diniz, G.; Grüning, M.; Hudait, M.K.; Ochalski, T.J. Direct and indirect band gaps in Ge under biaxial tensile strain investigated by photoluminescence and photoreflectance studies. Phys. Rev. B 2018, 97, 195304. [Google Scholar] [CrossRef]
- Zeinalvand Farzin, B.; Lee, D.; Kim, G.H.; Ha, J.; Kim, J.S.; Kim, Y.; Lee, S.J. Correlation between the time constant of a photoreflectance signal and the quantum efficiency of a pn junction. J. Korean Phys. Soc. 2023, 82, 692–698. [Google Scholar] [CrossRef]
- Jani, H.; Chen, L.; Duan, L. Pre-emission study of photoelectron dynamics in a GaAs/AlGaAs photocathode. IEEE J. Quantum Electron. 2019, 56, 1–8. [Google Scholar] [CrossRef]
- Zhou, R.; Jani, H.; Zhang, Y.; Qian, Y.; Duan, L. Photoelectron transportation dynamics in GaAs photocathodes. J. Appl. Phys. 2021, 130, 113101. [Google Scholar] [CrossRef]
- Zhou, R.; Jani, H.; Zhang, Y.; Qian, Y.; Duan, L. Dynamic photoelectron transport in stepwise-doped GaAs photocathodes. Sci. Rep. 2022, 12, 12936. [Google Scholar] [CrossRef] [PubMed]
- Komkov, O.S.; Khakhulin, S.A.; Firsov, D.D.; Avdienko, P.S.; Sedova, I.V.; Sorokin, S.V.E. Investigation of built-in electric fields at the GaSe/GaAs interface by photoreflectance spectroscopy. Semiconductors 2020, 54, 1198–1204. [Google Scholar] [CrossRef]
- Jin, J.; Tian, D.; Shi, J.; Li, T. Study on the effects of well number on temperature characteristics in 1.3 μm InGaAsP/InP quantum-well lasers. Infrared Phys. Technol. 2004, 45, 209–215. [Google Scholar] [CrossRef]
- Goharrizi, A.Z.; Alahyarizadeh, G.; Hassan, Z.; Hassan, H.A. Study on effect of quantum well number on performance characteristics of GaN-based vertical cavity surface emitting laser. Phys. E Low Dimens. Syst. Nanostruct. 2013, 50, 61–66. [Google Scholar] [CrossRef]
- Choi, H.S.; Zheng, D.G.; Kim, H.; Shim, J.I.; Shin, D.S. Effects of the number of quantum wells on the performance of near-ultraviolet light-emitting diodes. J. Korean Phys. Soc. 2015, 66, 1554–1558. [Google Scholar] [CrossRef]
- Bushnell, D.B.; Tibbits, T.N.D.; Barnham, K.W.J.; Connolly, J.P.; Mazzer, M.; Ekins-Daukes, N.J.; Roberts, J.S.; Hill, G.; Airey, R. Effect of well number on the performance of quantum-well solar cells. J. Appl. Phys. 2005, 97, 124908. [Google Scholar] [CrossRef]
- Ganesh, K.S.; Fan, L.; Wang, B.; Jeevan Kumar, P.; Zhu, B. Built-in electric field for efficient charge separation and ionic transport in LiCoO2/SnO2 semiconductor junction fuel cells. ACS Appl. Energy Mater. 2022, 5, 12513–12522. [Google Scholar] [CrossRef]
- Su, L.; Yang, W.; Cai, J.; Chen, H.; Fang, X. Self-powered ultraviolet photodetectors driven by built-in electric field. Small 2017, 13, 1701687. [Google Scholar] [CrossRef]
- Xu, H.; Li, J.; Chu, X. Interfacial built-in electric-field for boosting energy conversion electrocatalysis. Nanoscale Horiz. 2023, 8, 441–452. [Google Scholar] [CrossRef]
- Gladysiewicz, M.; Janicki, L.; Misiewicz, J.; Sobanska, M.; Klosek, K.; Zytkiewicz, Z.R.; Kudrawiec, R. Engineering of electric field distribution in GaN(cap)/AlGaN/GaN heterostructures: Theoretical and experimental studies. J. Phys. D Appl. Phys. 2016, 49, 345106. [Google Scholar] [CrossRef]
- Dyakonova, N.; Karandashev, S.A.; Levinshtein, M.E.; Matveev, B.A.; Remennyi, M.A.; Usikova, A.A. Low frequency noise in p-InAsSbP/n-InAs infrared light emitting diode-photodiode pairs. Infrared Phys. Technol. 2021, 117, 103867. [Google Scholar] [CrossRef]
- Dyakonova, N.; Karandashev, S.A.; Levinshtein, M.E.; Matveev, B.A.; Remennyi, M.A. Low frequency noise in p-InAsSbP/n-InAs/n-InAsSbP and p-InAsSbP/n-InAsSbP mid-IR light emitting diodes. Infrared Phys. Technol. 2022, 125, 104301. [Google Scholar] [CrossRef]
- Harutyunyan, V.G.; Gambaryan, K.M.; Aroutiounian, V.M.; Harutyunyan, I.G. InAsSbP quantum dot mid-IR photodetectors operating at room temperature. Infrared Phys. Technol. 2015, 70, 12–14. [Google Scholar] [CrossRef]
- Chakrabarti, P. Numerical modeling of an InAsSb/InAsSbP double heterojunction light emitting diode for mid-infrared (2–5 μm) applications. Infrared Phys. Technol. 2014, 67, 382–386. [Google Scholar]
- Brunkov, P.N.; Il’inskaya, N.D.; Karandashev, S.A.; Karpukhina, N.G.; Lavrov, A.A.; Matveev, B.A.; Remennyi, M.A.; Usikova, A.A. Low dark current p-InAsSbP/n-InAs/n-InAsSbP/n+-InAs double heterostructure back-side illuminated photodiodes. Infrared Phys. Technol. 2016, 76, 542–545. [Google Scholar] [CrossRef]
- Sukach, G.A.; Bogoslovskaya, A.B.; Oleksenko, P.F. Effect of Auger recombination on thermal processes in InGaAs and InAsSbP IR-emitting diodes. Infrared Phys. Technol. 2000, 41, 299–306. [Google Scholar] [CrossRef]
- Krier, A.; Mao, Y. High performance uncooled InAsSbP/InGaAs photodiodes for the 1.8–3.4 μm wavelength range. Infrared Phys. Technol. 1997, 38, 397–403. [Google Scholar] [CrossRef]
- Gong, X.Y.; Kan, H.; Makino, T.; Watanabe, K.; Iida, T.; Suzuki, H.; Aoyama, M.; Yamaguchi, T. Light Emitting Diodes Fabricated from Liquid Phase Epitaxial InAs/InAsxP1−x−ySby/InAsx′P1−x′−y′Sby′ and InAs/InAs1−xSbx Multi-Layers. Cryst. Res. Technol. 2000, 35, 549–555. [Google Scholar] [CrossRef]
- Klem, J.F.; Olesberg, J.T.; Hawkins, S.D.; Weiner, P.H.; Deitz, J.; Kadlec, C.N.; Shaner, E.A.; Coon, W.T. Extended-short-wavelength infrared AlInAsSb and InPAsSb detectors on InAs. Infrared Technol. Appl. XLVII 2021, 11741, 19–27. [Google Scholar]
- Shen, H.; Dutta, M. Sweeping photoreflectance spectroscopy of semiconductors. Appl. Phys. Lett. 1990, 57, 587–589. [Google Scholar] [CrossRef]
- Majaron, B.; Verkruysse, W.; Tanenbaum, B.S.; Milner, T.E.; Nelson, J.S. Spectral variation of the infrared absorption coefficient in pulsed photothermal profiling of biological samples. Phys. Med. Biol. 2002, 47, 1929. [Google Scholar] [CrossRef] [PubMed]
- Wada, M.; Araki, S.; Kudou, T.; Umezawa, T.; Nakajima, S.; Ueda, T. Temperature dependence of the band gap in InAsyP1−y. Appl. Phys. Lett. 2000, 76, 2722–2724. [Google Scholar] [CrossRef]
- Yoon, S.; Lee, S.H.; Shin, J.C.; Kim, J.S.; Lee, S.J.; Leem, J.Y.; Krishna, S. Photoreflectance study on the photovoltaic effect in InAs/GaAs quantum dot solar cell. Curr. Appl. Phys. 2018, 18, 667–672. [Google Scholar] [CrossRef]
- Neamen, D. Semiconductor Physics and Devices; McGraw-Hill, Inc.: New York, NY, USA, 2002. [Google Scholar]
- Tanaka, K.; Fujiwara, M.; Happo, N.; Takahashi, S. Minibands of eigen-state energies of In0.53Ga0.47As multi-quantum wells lattice-matched to InP. Opt. Quantum Electron. 2018, 50, 301. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zeinalvand Farzin, B.; Seyedein Ardebili, S.B.; Kang, T.I.; Kim, J.S.; Nguyen, P.D.; Lee, S.J. Photoreflectance Analysis of InAsPSb/InGaAs Multi-Quantum Well LED Structures with Different Well/Barrier Numbers. Photonics 2024, 11, 277. https://doi.org/10.3390/photonics11030277
Zeinalvand Farzin B, Seyedein Ardebili SB, Kang TI, Kim JS, Nguyen PD, Lee SJ. Photoreflectance Analysis of InAsPSb/InGaAs Multi-Quantum Well LED Structures with Different Well/Barrier Numbers. Photonics. 2024; 11(3):277. https://doi.org/10.3390/photonics11030277
Chicago/Turabian StyleZeinalvand Farzin, Behnam, S. Bahareh Seyedein Ardebili, Tae In Kang, Jong Su Kim, Phuc Dinh Nguyen, and Sang Jun Lee. 2024. "Photoreflectance Analysis of InAsPSb/InGaAs Multi-Quantum Well LED Structures with Different Well/Barrier Numbers" Photonics 11, no. 3: 277. https://doi.org/10.3390/photonics11030277
APA StyleZeinalvand Farzin, B., Seyedein Ardebili, S. B., Kang, T. I., Kim, J. S., Nguyen, P. D., & Lee, S. J. (2024). Photoreflectance Analysis of InAsPSb/InGaAs Multi-Quantum Well LED Structures with Different Well/Barrier Numbers. Photonics, 11(3), 277. https://doi.org/10.3390/photonics11030277




