Analysis of Plasma Dynamics in He-Ne Lasers with Different Gas Ratios
Abstract
1. Introduction
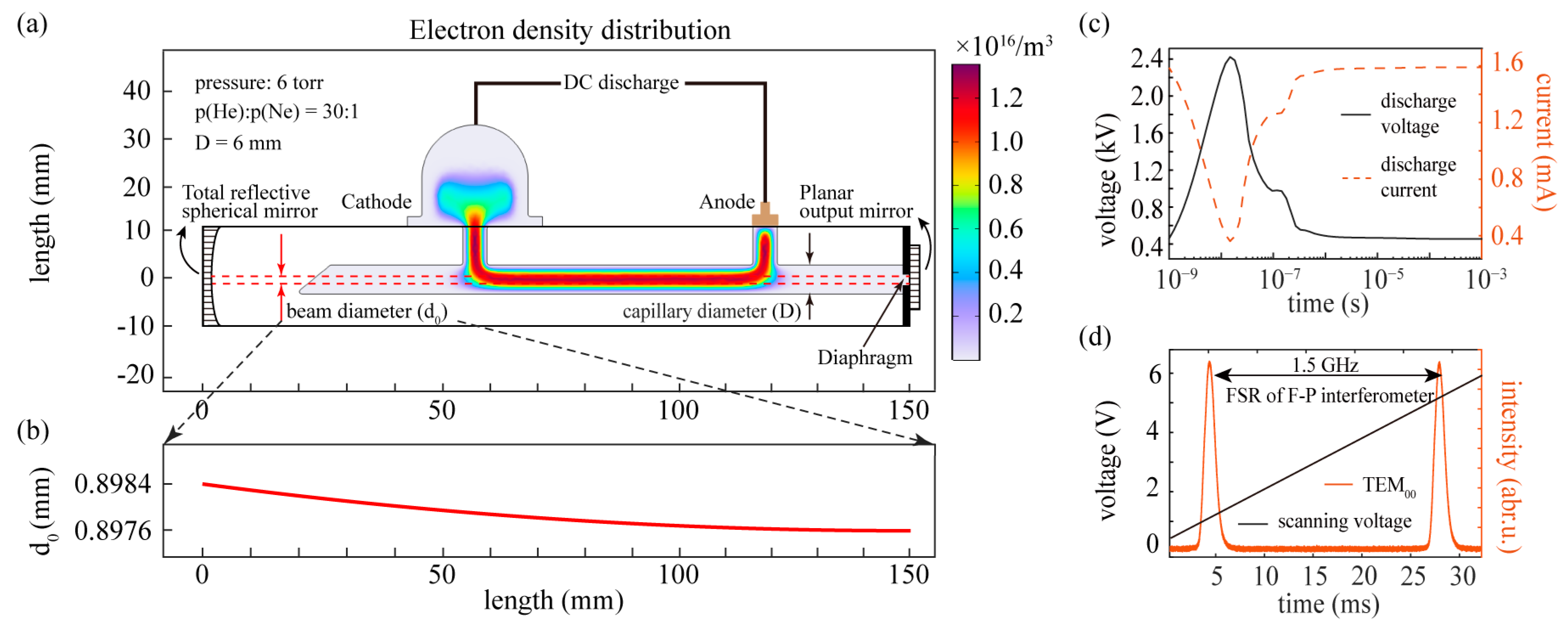
2. Plasma Simulation of DC Discharge in He-Ne Lasers
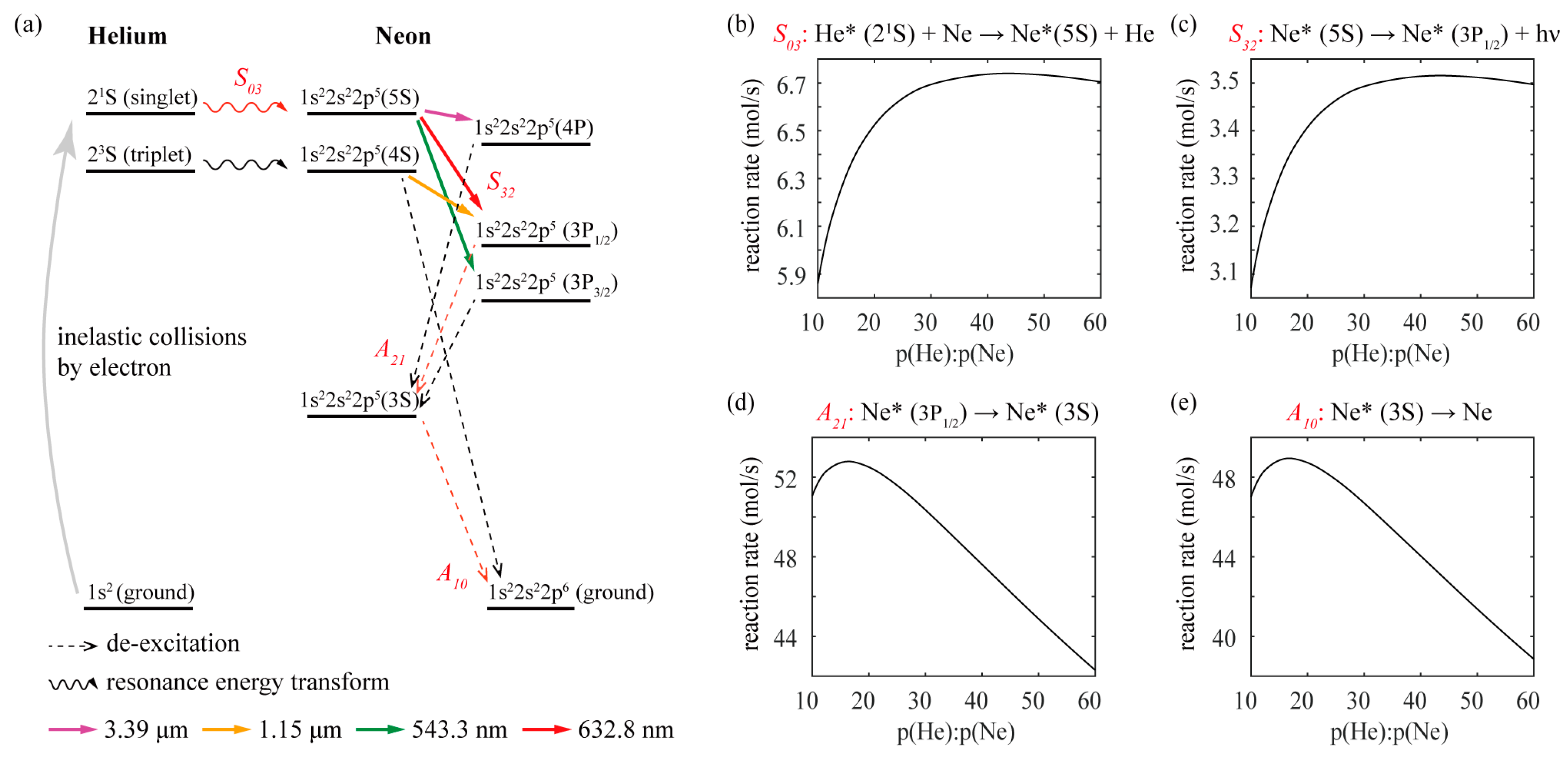
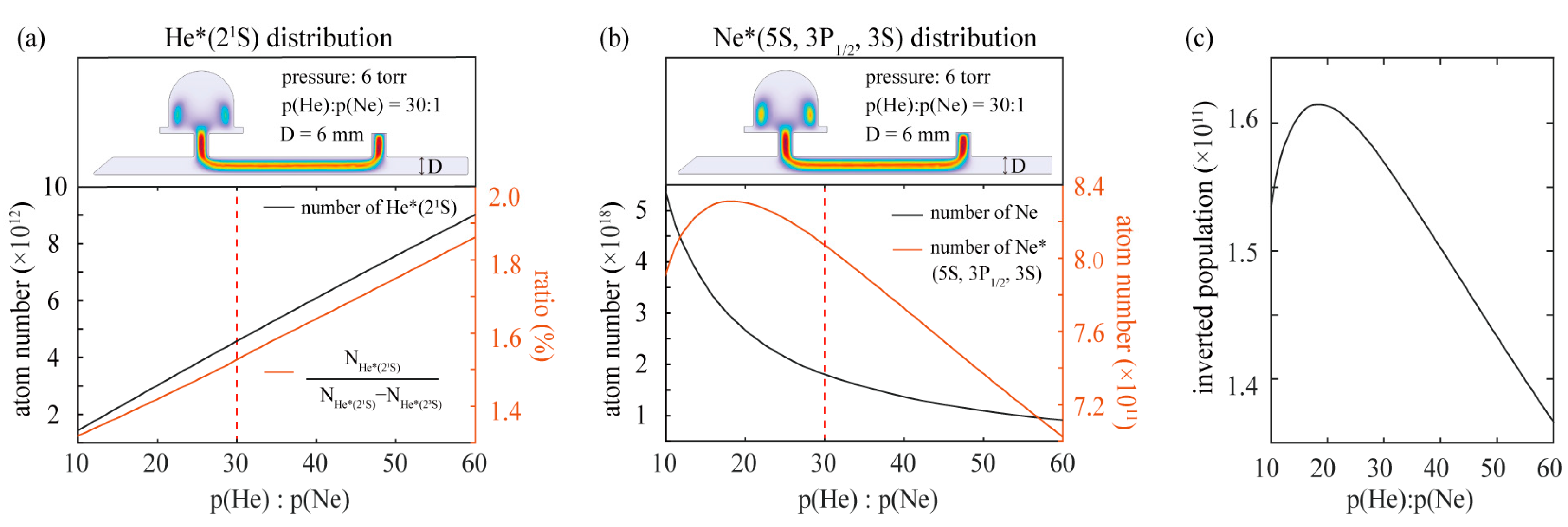
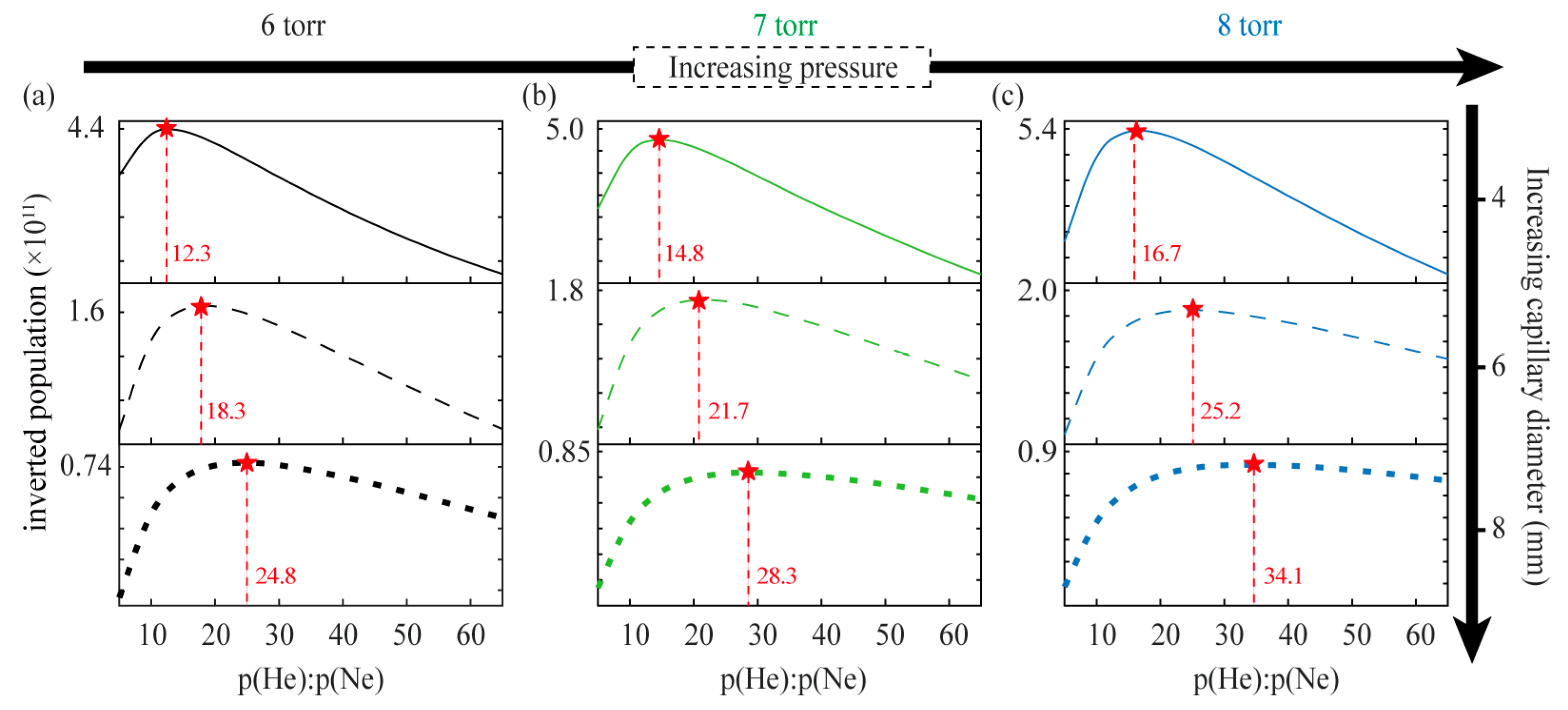
3. Optimal He/Ne Gas Ratio
4. Discussion and Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
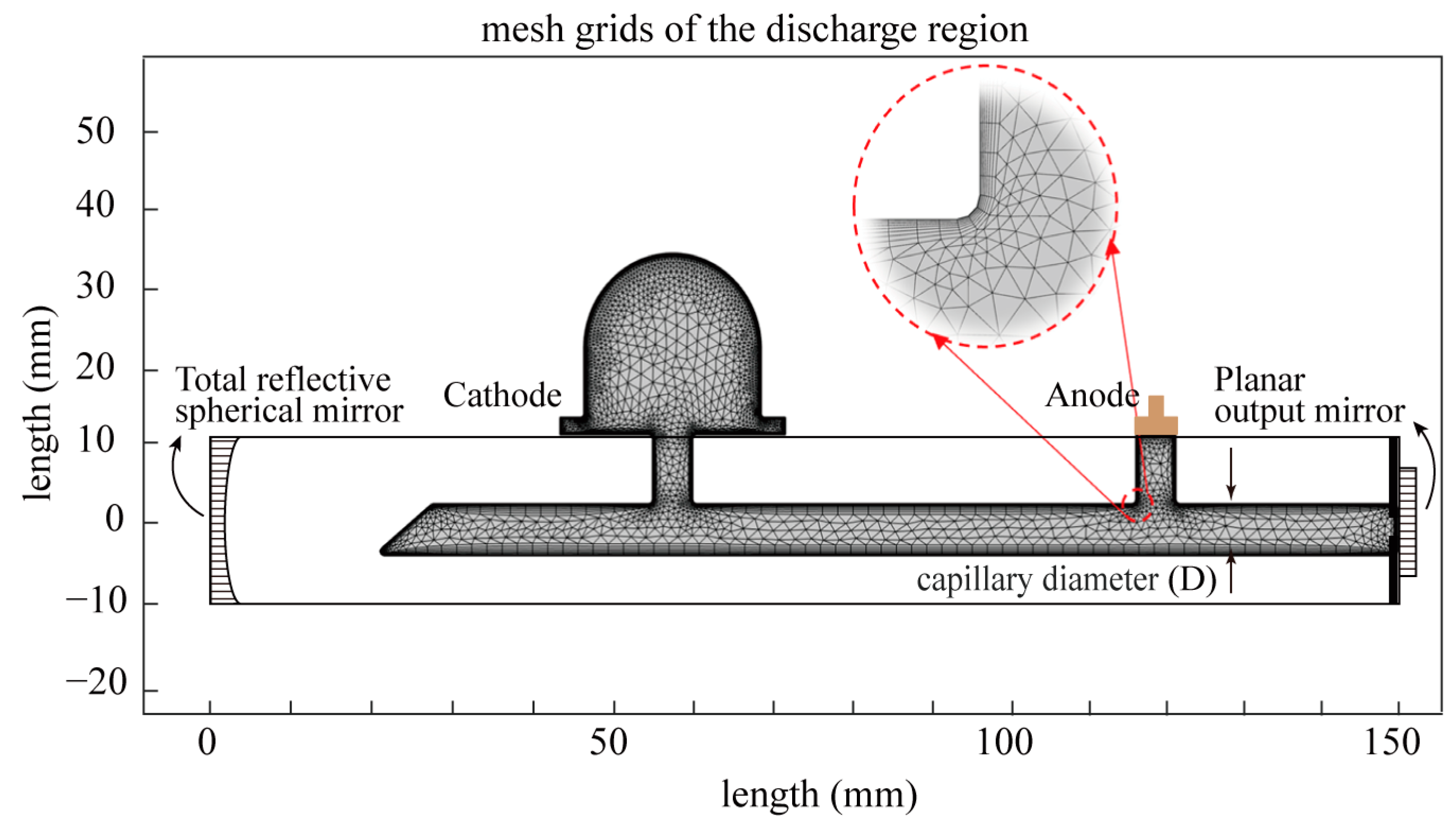
Appendix A. Methods of He-Ne Plasma DC-Discharged Modelling
| Parameters | Value | Description |
|---|---|---|
| 0.03 | secondary electron emission coefficient | |
| 5 (eV) | wall work function | |
| 0.004 (kg/mol) | molar mass of He | |
| 2.58 () | potential characteristic length of He | |
| 0.02 (kg/mol) | molar mass of Ne | |
| 2.82 () | potential characteristic length of Ne | |
| 1014 (1/m3) | initial electron density | |
| 300 (K) | gas temperature |
References
- Weber, A.; Porto, S.P.S. He–Ne Laser as a Light Source for High-Resolution Raman Spectroscopy. J. Opt. Soc. Am. 1965, 55, 1033–1034. [Google Scholar] [CrossRef]
- Hall, J.L. Stabilized Lasers and Precision Measurements. Science 1978, 202, 147–156. [Google Scholar] [CrossRef]
- Udem, T.; Holzwarth, R.; Hänsch, T.W. Optical Frequency Metrology. Nature 2002, 416, 233–237. [Google Scholar] [CrossRef] [PubMed]
- Smith, R.P.; Roos, P.A.; Wahlstrand, J.K.; Pipis, J.A.; Rivas, M.B.; Cundiff, S.T. Optical Frequency Metrology of an Iodine-Stabilized He-Ne Laser Using the Frequency Comb of a Quantum-Interference-Stabilized Mode-Locked Laser. J. Res. Natl. Inst. Stand. Technol. 2007, 112, 289–296. [Google Scholar] [CrossRef] [PubMed]
- Schreiber, K.U.; Klügel, T.; Wells, J.-P.R.; Hurst, R.B.; Gebauer, A. How to Detect the Chandler and the Annual Wobble of the Earth with a Large Ring Laser Gyroscope. Phys. Rev. Lett. 2011, 107, 173904. [Google Scholar] [CrossRef]
- Tartaglia, A.; Di Virgilio, A.; Belfi, J.; Beverini, N.; Ruggiero, M.L. Testing General Relativity by Means of Ring Lasers. Eur. Phys. J. Plus 2017, 132, 73. [Google Scholar] [CrossRef]
- Schreiber, K.U.; Kodet, J.; Hugentobler, U.; Klügel, T.; Wells, J.R. Variations in the Earth’s Rotation Rate Measured with a Ring Laser Interferometer. Nat. Photonics 2023, 17, 1054–1058. [Google Scholar] [CrossRef]
- Diao, X.; Tan, J.; Hu, P.; Yang, H.; Wang, P. Frequency Stabilization of an Internal Mirror He-Ne Laser with a High Frequency Reproducibility. Appl. Opt. 2013, 52, 456–460. [Google Scholar] [CrossRef] [PubMed]
- Liu, M.; Gong, B. A Three-Dimensional Laser Interferometer Gravitational-Wave Detector. Sci. Rep. 2020, 10, 16285. [Google Scholar] [CrossRef] [PubMed]
- Igel, H.; Schreiber, K.U.; Gebauer, A.; Bernauer, F.; Egdorf, S.; Simonelli, A.; Lin, C.; Wassermann, J.; Donner, S.; Hadziioannou, C.; et al. ROMY: A Multicomponent Ring Laser for Geodesy and Geophysics. Geophys. J. Int. 2021, 225, 684–698. [Google Scholar] [CrossRef]
- Endo, M.; Walter, R.F. Gas Lasers; CRC Press: Boca Raton, FL, USA, 2018; ISBN 9781315221304. [Google Scholar]
- Spiller, E. Experimental Investigations on Gain and Maximum Output of the He-Ne Laser. Z. Phys. 1965, 182, 487–498. [Google Scholar] [CrossRef]
- Burlamacchi, P.; Pratesi, R. Study of Power Enhancements during the Initial and Afterglow Transients of Pulsed He-Ne Gas Lasers. IEEE J. Quantum Electron. 1966, 2, 121. [Google Scholar] [CrossRef]
- Petrů, F.; Veselá, Z. The Output Power of 633nm He-Ne Lasers. Opto-Electronics 1972, 4, 1–20. [Google Scholar] [CrossRef]
- Schreiber, U.; Schneider, M.; Rowe, C.H.; Stedman, G.E.; Cooper, S.J.; Schlüter, W.; Seeger, H. The C-II Ring Laser Project. Phys. Chem. Earth Part A Solid Earth Geod. 2000, 25, 805–807. [Google Scholar] [CrossRef]
- Schreiber, U.; Igel, H.; Cochard, A.; Velikoseltsev, A.; Flaws, A.; Schuberth, B.; Drewitz, W.; Müller, F. The GEOsensor Project: Rotations—A New Observable for Seismology. In Observation of the Earth System from Space; Springer: Berlin/Heidelberg, Germany, 2006; pp. 427–443. ISBN 3540295208. [Google Scholar]
- Hurst, R.B.; Stedman, G.E.; Schreiber, K.U.; Thirkettle, R.J.; Graham, R.D.; Rabeendran, N.; Wells, J.-P.R. Experiments with an 834 M2 Ring Laser Interferometer. J. Appl. Phys. 2009, 105, 113115. [Google Scholar] [CrossRef]
- Di Virgilio, A.D.V. Sagnac Gyroscopes and the GINGER Project. Front. Astron. Space Sci. 2020, 7, 49. [Google Scholar] [CrossRef]
- Tian, S.; Li, Y.; Zhong, J.; Li, L.; Wang, S. Study on Li Ion Migration of Glass-Ceramic in Discharge Area of Space Triaxial Laser Gyroscope. Infrared Laser Eng. 2023, 52, 20220819. [Google Scholar] [CrossRef]
- Zheng, X.; Li, Y. Loss Variation of Space Triaxial Laser Gyro Mirrors Exposed to Discharge Plasma. Chin. J. Lasers 2023, 50, 2301005. [Google Scholar]
- Macé, J.S.; Maynard, G.; Virdis, A. Influence of Diffusion and Non-Local Radiation Transport on the Laser Amplification of a He–Ne Ring Laser Gyro. Plasma Sources Sci. Technol. 2014, 23, 045013. [Google Scholar] [CrossRef]
- Coffey, D.; Lorents, D.C.; Smith, F.T. Collision Spectroscopy. II. Inelastic Scattering of He+ by Ne. Phys. Rev. A 1970, 2, 549. [Google Scholar] [CrossRef]
- Olson, R.E.; Smith, F.T. Collision Spectroscopy. IV. Semiclassical Theory of Inelastic Scattering with Application to He+ + Ne. Phys. Rev. A 1972, 6, 526. [Google Scholar] [CrossRef]
- Nayfeh, M.H.; Chen, C.H.; Payne, M.G. Kinetic Study of Energy Transfer from He(N = 2,3) to Ne, Ar, Kr, and Xe. Phys. Rev. A 1976, 14, 1739–1744. [Google Scholar] [CrossRef]
- Manique, J.; Nielsen, S.E.; Dahler, J.S. Excitation Cross Sections and Polarization of Impact Radiation in Li/Na-He/Ne High-Energy Collisions: A Comparison of Model Potential Calculations. J. Phys. B At. Mol. Phys. 1977, 10, 1703–1722. [Google Scholar] [CrossRef]
- Hitachi, A.; Davies, C.; King, T.A.; Kubota, S.; Doke, T. Deexcitation of Rydberg States of He by He, Ne, Ar, Kr, and Xe. Phys. Rev. A 1980, 22, 856–862. [Google Scholar] [CrossRef]
- Krenos, J. Electronic Energy Transfer in He*(21S) + Ne Collisions: Propensity for Odd-J Levels of Ne*(5s, 5s′, 4d). Phys. Rev. A 1984, 29, 1844–1849. [Google Scholar] [CrossRef]
- Phelps, A.V.; Greene, C.H.; Burke, J.P.; Phelps, A. V Collision Cross Sections for Argon Atoms with Argon Atoms for Energies from 0.01 EV to 10 KeV. J. Phys. B At. Mol. Opt. Phys. 2000, 33, 2965–2981. [Google Scholar] [CrossRef]
- Ariyasinghe, W.M.; Goains, C.; Powers, D.; Wijeratne, T.; Palihawadana, P. Total Electron Scattering Cross Sections of He, Ne and Ar at Intermediate Electron Energies. Nucl. Instrum. Methods Phys. Res. Sect. B Beam Interact. Mater. Atoms 2004, 225, 191–197. [Google Scholar] [CrossRef]
- Ivanov, V.A.; Petrovskaya, A.S.; Skoblo, Y.E. Population of 2p 55s Levels of Neon in He-Ne Plasma: I. The Evolution of Mechanisms in the Discharge and the Afterglow. Opt. Spectrosc. 2013, 114, 688–695. [Google Scholar] [CrossRef]
- NIST Handbook of Basic Atomic Spectroscopic Data. Available online: https://www.nist.gov/pml/handbook-basic-atomic-spectroscopic-data (accessed on 1 December 2023).
- An, K. Fundamentals of Laser Physics; World Scientific: Singapore, 2023; ISBN 978-981-12-6527-3. [Google Scholar]
- Boersch, H.; Herziger, G.; Weber, H. Strahlungsintensität Des He/Ne-Laser Als Funktion von Druck und Mischungsverhältnis Der Gase. Phys. Lett. 1963, 4, 191–194. [Google Scholar] [CrossRef]
- Belousova, I.M.; Danilov, O.B.; El’kina, I.A. Optimum Operating Mode of an Optical Quantum Generator Using a Neon-Helium Mixture. J. Exp. Theor. Phys. 1963, 17, 748–749. [Google Scholar]
- Field, R.L. Operating Parameters of Dc-Excited He-Ne Gas Lasers. Rev. Sci. Instrum. 1967, 38, 1720–1722. [Google Scholar] [CrossRef]
- Stedman, G.E. Ring-Laser Tests of Fundamental Physics and Geophysics. Rep. Prog. Phys. 1997, 60, 615–688. [Google Scholar] [CrossRef]
- Hurst, R.B.; Rabeendran, N.; Schreiber, K.U.; Wells, J.-P.R. Correction of Backscatter-Induced Systematic Errors in Ring Laser Gyroscopes. Appl. Opt. 2014, 53, 7610–7618. [Google Scholar] [CrossRef] [PubMed]

| Reactions Types | Reactions Equations | Reactions Coefficients |
|---|---|---|
| Electron-He collisions | Collision section data from NIST | |
| (Tg/Te)−2 × 10−20 (mm3/s) | ||
| 8.7 × 10−7(Tg/0.025)1/2 (mm3/s) | ||
| Electron-Ne collisions | Collision section data from NIST | |
| He-Ne collisions | 4 × 10−8 (mm3/s) | |
| 4 × 10−9 (mm3/s) | ||
| Ne radiations | 2.92 × 106 (s−1) | |
| 3.39 × 106 (s−1) | ||
| 2.83 × 105 (s−1) | ||
| 1.07 × 107 (s−1) | ||
| 8.70 × 105 (s−1) | ||
| 1.81 × 107 (s−1) | ||
| 1.01 × 107 (s−1) | ||
| 4.40 × 107 (s−1) | ||
| De-excitations by wall collisions | Sticking coefficient is 1 Secondary electron emission coefficient is 0.03 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Mao, Y.; Hu, J.; Ji, H.; Guan, S.; Chen, D.; Gong, Q.; Liu, W.; Long, X.; Tan, Z. Analysis of Plasma Dynamics in He-Ne Lasers with Different Gas Ratios. Photonics 2024, 11, 276. https://doi.org/10.3390/photonics11030276
Mao Y, Hu J, Ji H, Guan S, Chen D, Gong Q, Liu W, Long X, Tan Z. Analysis of Plasma Dynamics in He-Ne Lasers with Different Gas Ratios. Photonics. 2024; 11(3):276. https://doi.org/10.3390/photonics11030276
Chicago/Turabian StyleMao, Yuanhao, Jing Hu, Hongteng Ji, Shiyu Guan, Dingbo Chen, Qiucheng Gong, Wei Liu, Xingwu Long, and Zhongqi Tan. 2024. "Analysis of Plasma Dynamics in He-Ne Lasers with Different Gas Ratios" Photonics 11, no. 3: 276. https://doi.org/10.3390/photonics11030276
APA StyleMao, Y., Hu, J., Ji, H., Guan, S., Chen, D., Gong, Q., Liu, W., Long, X., & Tan, Z. (2024). Analysis of Plasma Dynamics in He-Ne Lasers with Different Gas Ratios. Photonics, 11(3), 276. https://doi.org/10.3390/photonics11030276





