Small Footprint and High Extinction Ratio Cladding-Modulated Bragg Grating Structure as a Wideband Bandstop Filter
Abstract
1. Introduction
2. Working Principles of BG Structure and Numerical Model
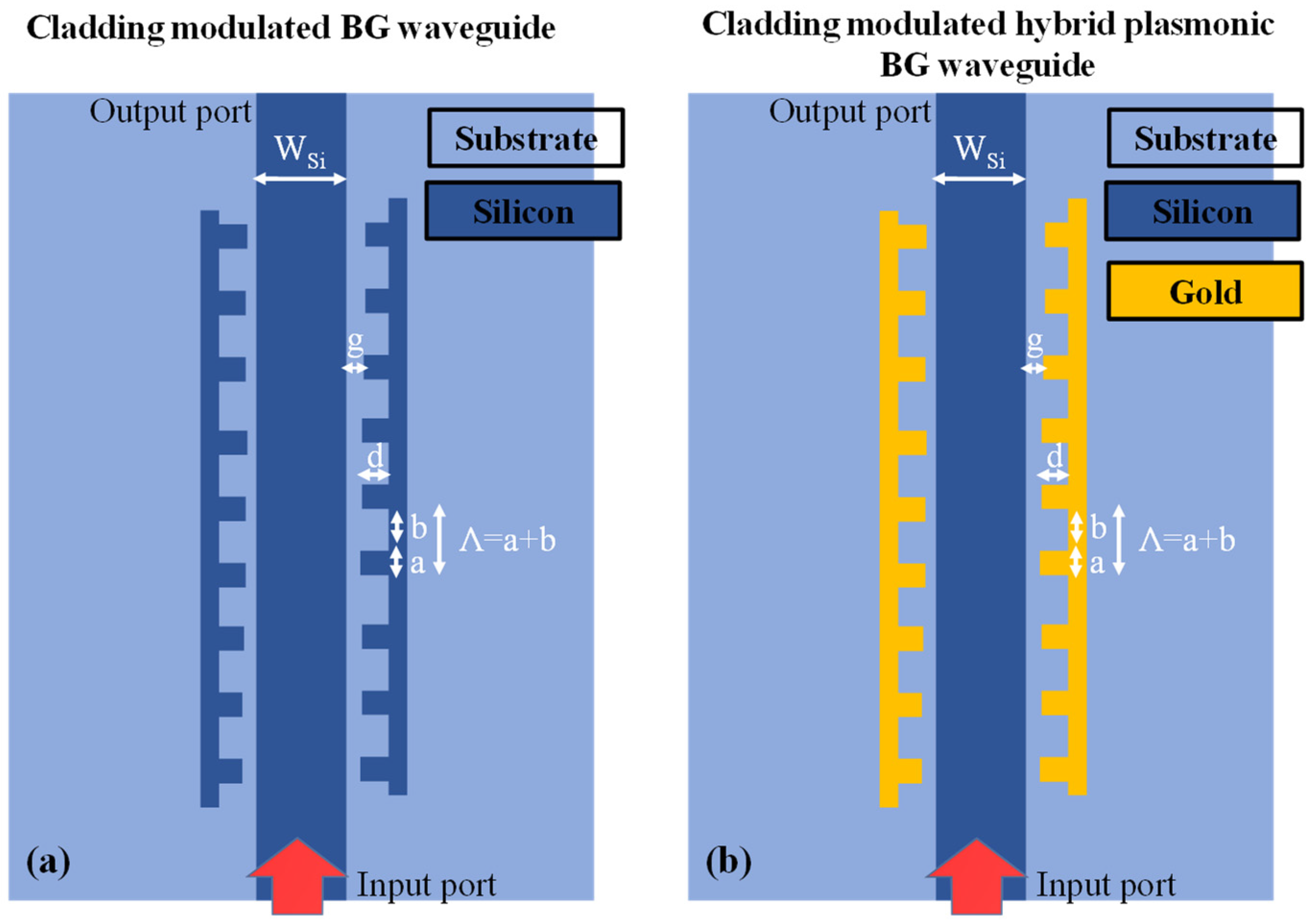
3. Cladding-Modulated BG Waveguide Designs and Optimization Process
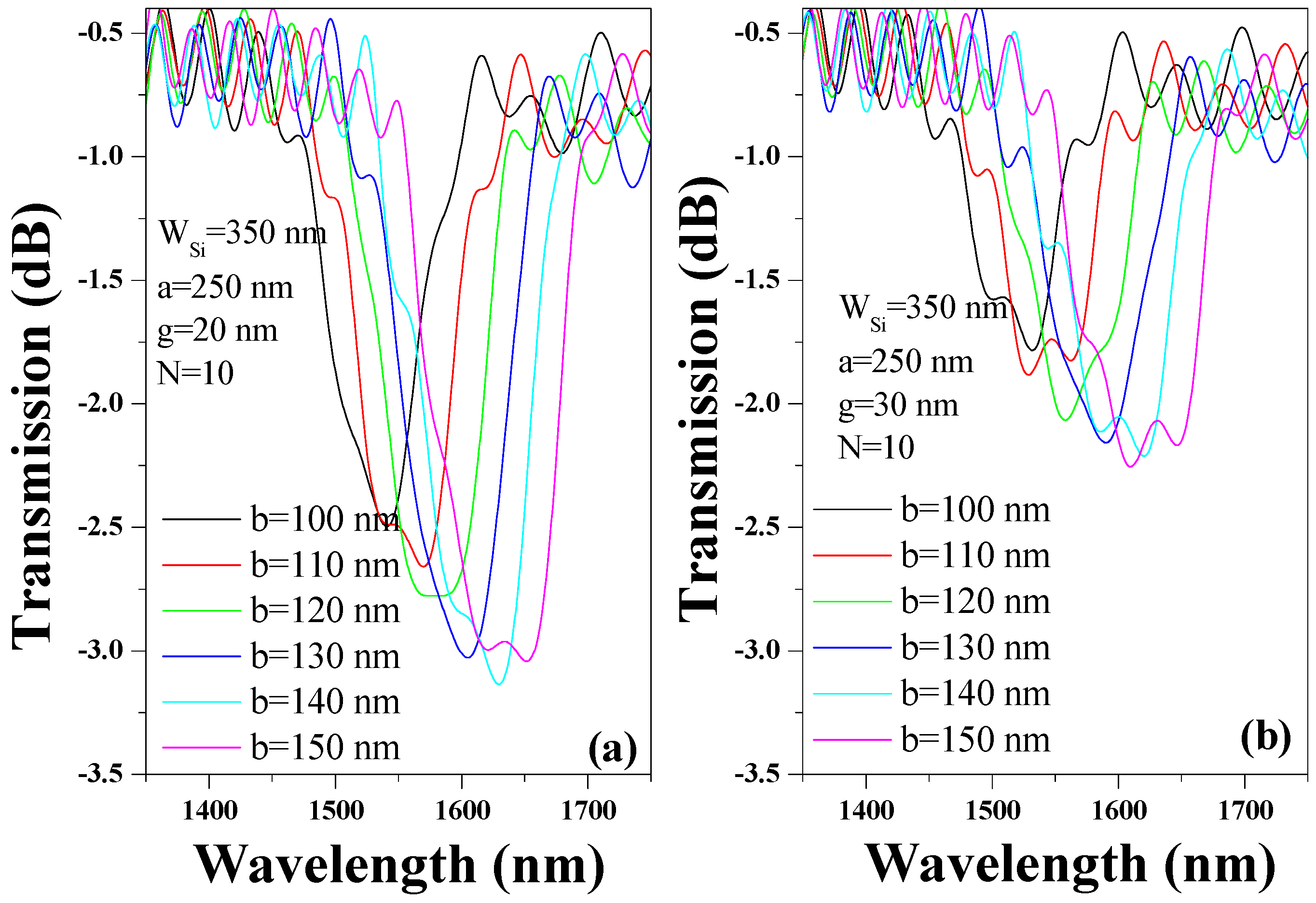
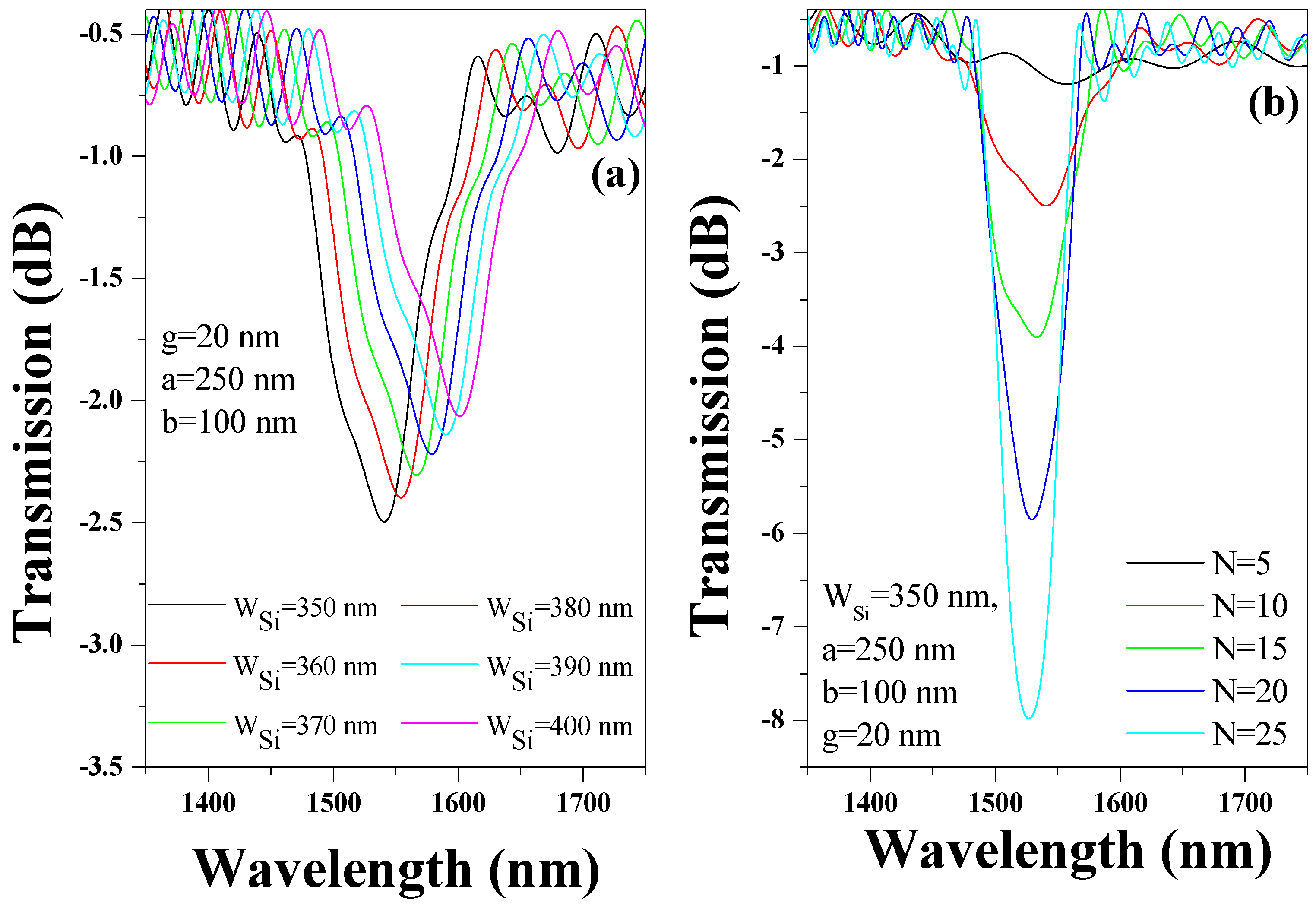
3.1. Silicon Corrugated Cladding BG Waveguide Structure
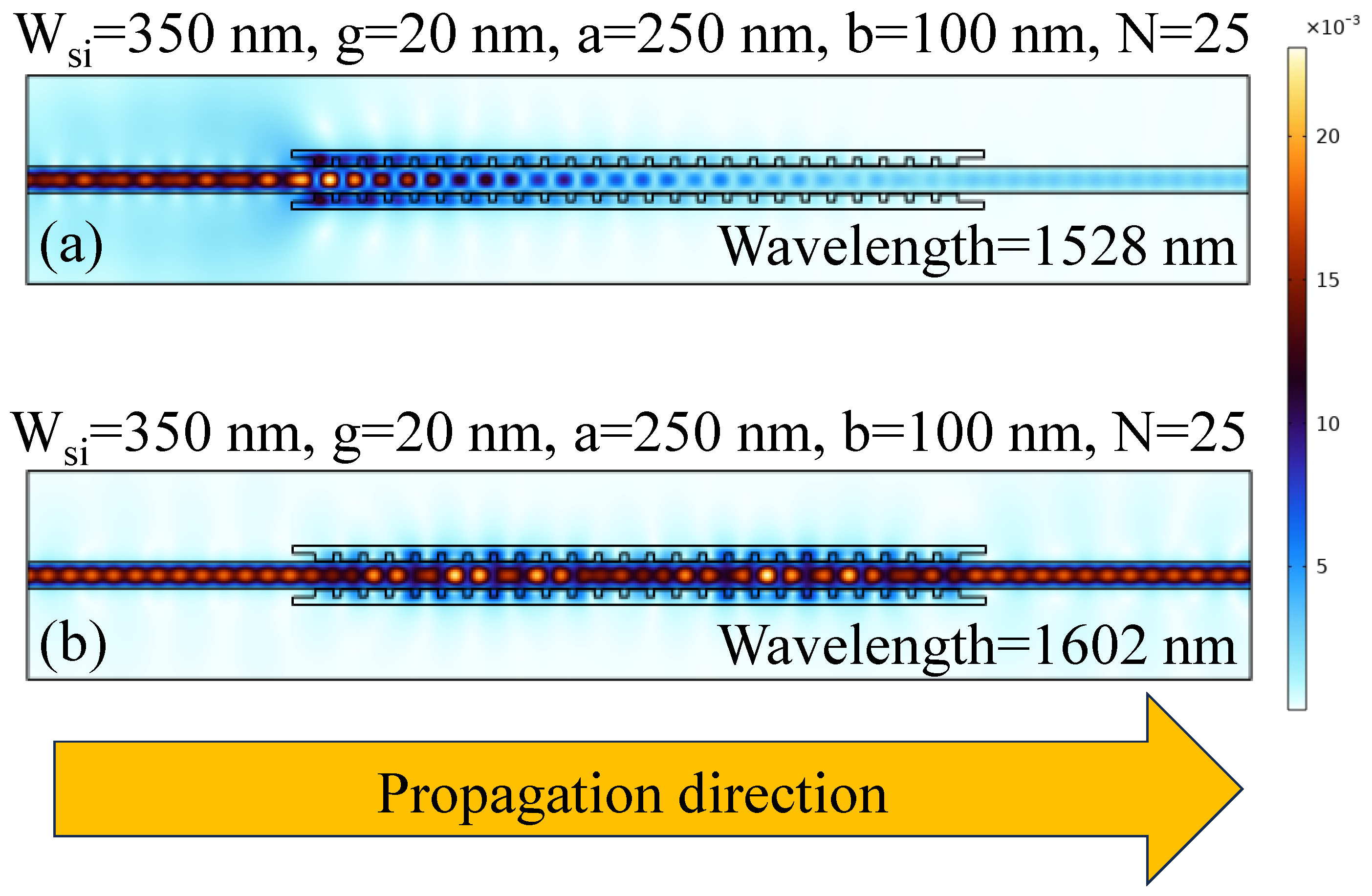
3.2. Au Corrugated Cladding BG Waveguide Structure
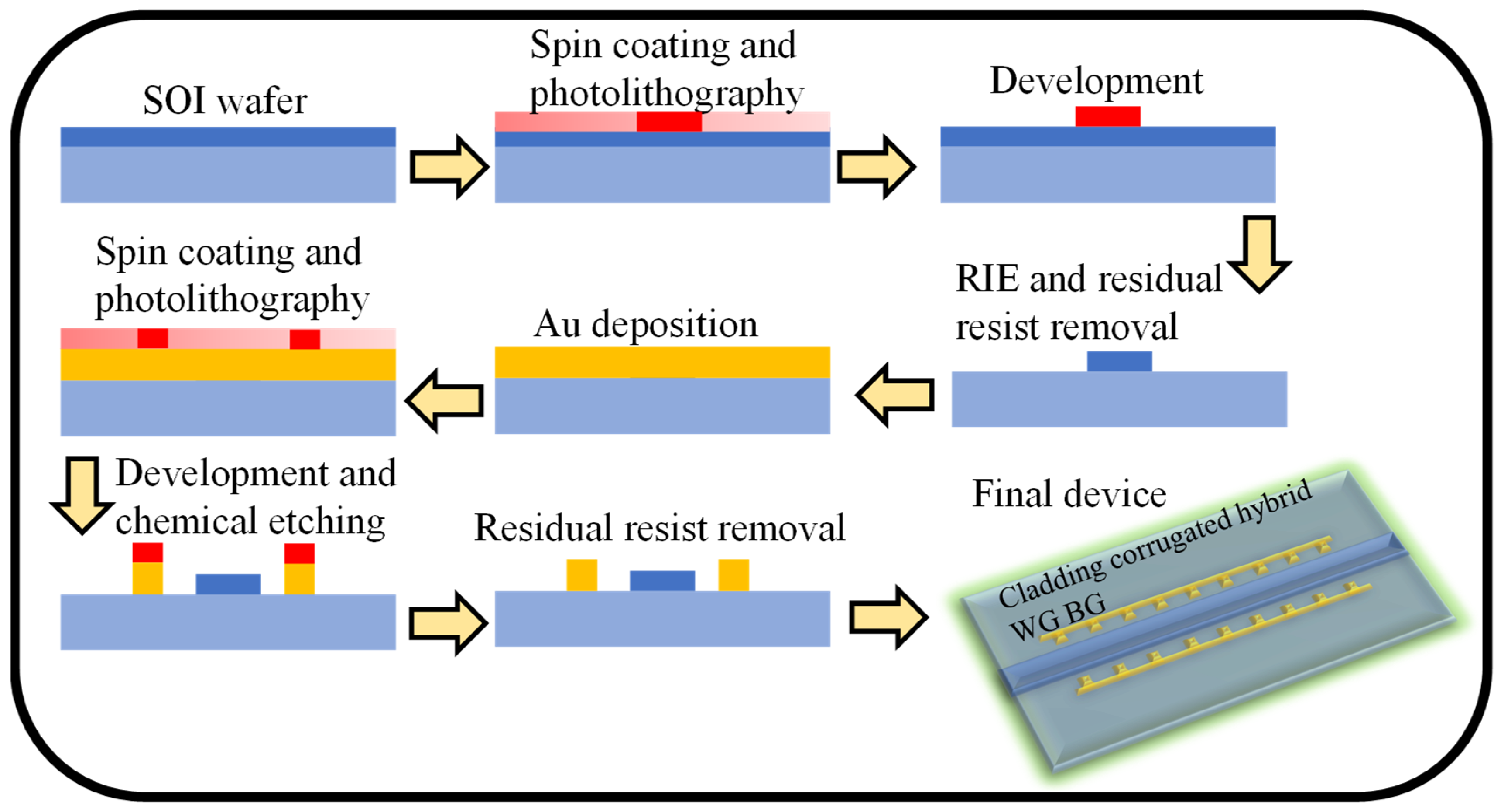
4. Proposed Fabrication Procedure
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Kaushal, S.; Cheng, R.; Ma, M.; Mistry, A.; Burla, M.; Chrostowski, L.; Azaña, J. Optical signal processing based on silicon photonics waveguide Bragg gratings: Review. Front. Optoelectron. 2018, 11, 163–188. [Google Scholar] [CrossRef]
- Burla, M.; Cortés, L.R.; Li, M.; Wang, X.; Chrostowski, L.; Azaña, J. Integrated waveguide Bragg gratings for microwave photonics signal processing. Opt. Express 2013, 21, 25120–25147. [Google Scholar] [CrossRef] [PubMed]
- Ams, M.; Dekker, P.; Gross, S.; Withford, M.J. Fabricating waveguide Bragg gratings (WBGs) in bulk materials using ultrashort laser pulses. Nanophotonics 2017, 6, 743–763. [Google Scholar] [CrossRef]
- Dual Phase-Shift Bragg Grating Silicon Photonic Modulator Operating up to 60 Gb/s. Available online: https://opg.optica.org/oe/fulltext.cfm?uri=oe-24-3-2413&id=335910 (accessed on 23 November 2023).
- Shi, W.; Veerasubramanian, V.; Plant, D.V.; Jaeger, N.A.F.; Chrostowski, L. Silicon photonic Bragg-grating couplers for optical communications. In Next-Generation Optical Networks for Data Centers and Short-Reach Links; SPIE: Washington, DC, USA, 2014; pp. 63–74. [Google Scholar] [CrossRef]
- Zhang, W.; Yao, J. A fully reconfigurable waveguide Bragg grating for programmable photonic signal processing. Nat. Commun. 2018, 9, 1. [Google Scholar] [CrossRef] [PubMed]
- Khonina, S.N.; Kazanskiy, N.L.; Butt, M.A.; Karpeev, S.V. Optical Multiplexing Techniques and Their Marriage for on-Chip and Optical Fiber Communication: A Review. Opto-Electron. Adv. 2022, 5, 210127. [Google Scholar] [CrossRef]
- Butt, M.A.; Kazanskiy, N.L.; Khonina, S.N. Advances in Waveguide Bragg Grating Structures, Platforms, and Applications: An Up-to-Date Appraisal. Biosensors 2022, 12, 497. [Google Scholar] [CrossRef] [PubMed]
- Klimov, N.N.; Mittal, S.; Berger, M.; Ahmed, Z. On-chip silicon waveguide Bragg grating photonic temperature sensor. Opt. Lett. 2015, 40, 3934–3936. [Google Scholar] [CrossRef] [PubMed]
- Missinne, J.; Teigell Benéitez, N.; Mattelin, M.-A.; Lamberti, A.; Luyckx, G.; Van Paepegem, W.; Van Steenberge, G. Bragg-Grating-Based Photonic Strain and Temperature Sensor Foils Realized Using Imprinting and Operating at Very Near Infrared Wavelengths. Sensors 2018, 18, 2717. [Google Scholar] [CrossRef]
- Sherman, S.; Zappe, H. Printable Bragg Gratings for Polymer-based Temperature Sensors. Procedia Technol. 2014, 15, 702–709. [Google Scholar] [CrossRef]
- Yao, J.; Zhang, W. Fully Reconfigurable Waveguide Bragg Gratings for Programmable Photonic Signal Processing. J. Light. Technol. 2020, 38, 202–214. [Google Scholar] [CrossRef]
- Butt, M.; Khonina, S.; Kazanskiy, N. A compact design of a modified Bragg grating filter based on a metal-insulator-metal waveguide for filtering and temperature sensing applications. Optik 2022, 251, 168466. [Google Scholar] [CrossRef]
- Li, H.; Zhu, Z.; Meng, W.; Cao, L.; Wang, Y.; Lin, Z.; Li, E.; Prades, J.D. Silicon-photonics-based waveguide Bragg grating sensor for blood glucose monitoring. Opt. Express 2022, 30, 41554–41566. [Google Scholar] [CrossRef]
- Missinne, J.; Vasiliev, A.; Elmogi, A.; Beneitez, N.T.; Bosman, E.; Van Hoe, B.; Van Steenberge, G. Bragg Grating Sensors in Laser-written Single Mode Polymer Waveguides. Procedia Eng. 2015, 120, 878–881. [Google Scholar] [CrossRef]
- Tan, D.T.H.; Ikeda, K.; Fainman, Y. Cladding-modulated bragg gratings in silicon waveguides. In Proceedings of the 2009 Conference on Lasers and Electro-Optics and 2009 Conference on Quantum Electronics and Laser Science Conference, Baltimore, MD, USA, 2–4 June 2009; pp. 1–2. [Google Scholar] [CrossRef]
- Yoon, J.; Kim, J.-Y.; Kim, J.; Hong, S.; Neseli, B.; Park, J.; Park, H.-H.; Kurt, H. Cladding modulated silicon waveguide Bragg grating with TM-polarized light for optical true time delay line. Appl. Phys. Lett. 2023, 123, 191106. [Google Scholar] [CrossRef]
- Pereira-Martín, D.; Luque-González, J.M.; Wangüemert-Pérez, J.G.; Hadij-ElHouati, A.; Molina-Fernández, Í.; Cheben, P.; Schmid, J.H.; Wang, S.; Ye, W.N.; Čtyroký, J.; et al. Complex spectral filters in silicon waveguides based on cladding-modulated Bragg gratings. Opt. Express 2021, 29, 15867–15881. [Google Scholar] [CrossRef]
- Tan, D.T.H.; Ikeda, K.; Fainman, Y. Cladding-modulated Bragg gratings in silicon waveguides. Opt. Lett. 2009, 34, 1357–1359. [Google Scholar] [CrossRef] [PubMed]
- Sahu, S.; Ali, J.; Yupapin, P.P.; Singh, G. Optical biosensor based on a cladding modulated grating waveguide. Optik 2018, 166, 103–109. [Google Scholar] [CrossRef]
- Zhang, M.; Liu, J.; Cheng, W.; Cheng, J.; Zheng, Z. A Tunable Optical Bragg Grating Filter Based on the Droplet Sagging Effect on a Superhydrophobic Nanopillar Array. Sensors 2019, 19, 3324. [Google Scholar] [CrossRef] [PubMed]
- COMSOL. COMSOL: Multiphysics Software for Optimizing Designs. Available online: https://www.comsol.com/ (accessed on 26 September 2023).
- Dhavamani, V.; Chakraborty, S.; Ramya, S.; Nand, S. Design and Simulation of Waveguide Bragg Grating based Temperature Sensor in COMSOL. J. Phys. Conf. Ser. 2022, 2161, 012047. [Google Scholar] [CrossRef]
- Butt, M.; Kazanskiy, N.; Khonina, S. Tapered waveguide mode converters for metal-insulator-metal waveguide plasmonic sensors. Measurement 2023, 211, 112601. [Google Scholar] [CrossRef]
- Okamoto, H.; Kamada, S.; Haraguchi, M.; Okamoto, T. Design of a hybrid plasmonic waveguide device using a trench structure. J. Phys. Commun. 2020, 4, 095022. [Google Scholar] [CrossRef]
- Butt, M.A.; Piramidowicz, R. Standard slot waveguide and double hybrid plasmonic waveguide configurations for enhanced evanescent field absorption methane gas sensing. Photonics Lett. Pol. 2022, 14, 1. [Google Scholar] [CrossRef]
- Klitis, C.; Cantarella, G.; Strain, M.J.; Sorel, M. High-extinction-ratio TE/TM selective Bragg grating filters on silicon-on-insulator. Opt. Lett. 2017, 42, 3040–3043. [Google Scholar] [CrossRef] [PubMed]
- Butt, M.A. Numerical investigation of a small footprint plasmonic Bragg grating structure with a high extinction ratio. Photonics Lett. Pol. 2020, 12, 3. [Google Scholar] [CrossRef]
- Butt, M.A. Integrated Optics: Platforms and Fabrication Methods. Encyclopedia 2023, 3, 824–838. [Google Scholar] [CrossRef]
- Zheng, Y.; Gao, P.; Jiang, L.; Kai, X.; Duan, J. Surface Morphology of Silicon Waveguide after Reactive Ion Etching (RIE). Coatings 2019, 9, 478. [Google Scholar] [CrossRef]



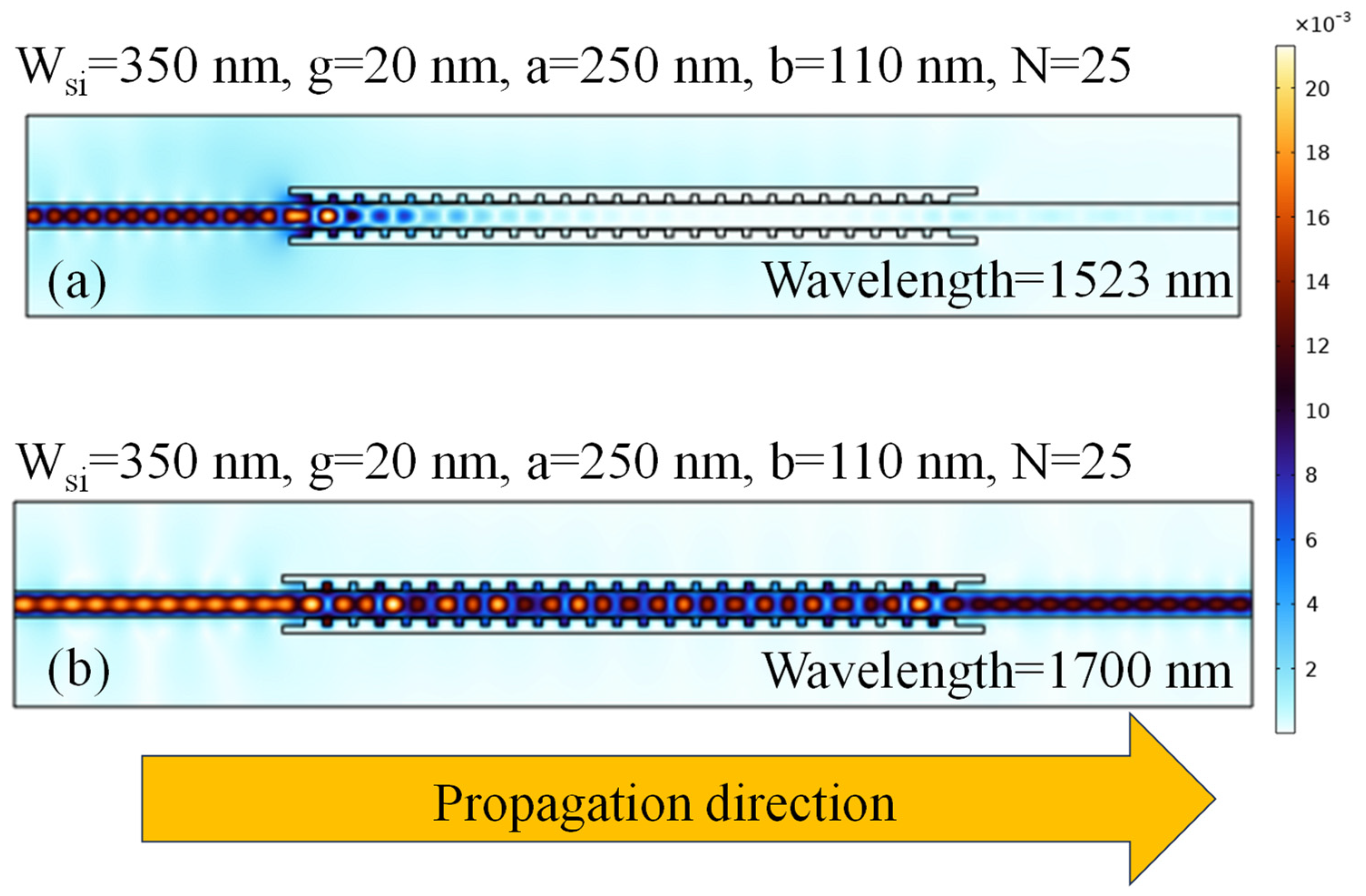
| Variable | Value | Expression |
|---|---|---|
| WSi | from 350 nm to 400 nm | Width of a silicon waveguide |
| a | 250 nm | Length of the unetched segment |
| b | from 100 nm to 150 nm | Length of the etched segment |
| d | 100 nm | Depth of corrugation |
| N | 5, 10, 15, 20, and 25 | Number of periods |
| g | 10, 20,30, and 40 nm | Gap between silicon waveguide and corrugated cladding |
| g = 20 nm | g = 30 nm | g = 40 nm | g = 50 nm | |
|---|---|---|---|---|
| ∆neff in Silicon corrugated cladding | 0.2295 | 0.1722 | 0.1335 | 0.1058 |
| ∆neff in Au corrugated cladding | 0.3617 | 0.2636 | 0.2011 | 0.1582 |
| Silicon Corrugated Cladding | Au Corrugated Cladding | |||||
|---|---|---|---|---|---|---|
| N | Footprint (µm)2 | Maximum ER (dB) | Bandstop Bandwidth (nm) | Footprint (µm)2 | Maximum ER (dB) | Bandstop Bandwidth (nm) |
| 5 | 3.6 × 3 | 1.11 | - | 3.7 × 3 | 5.1 | ~207 |
| 10 | 6.8 × 3 | 2.49 | ~111 | 6.9 × 3 | 14.27 | ~148 |
| 15 | 10 × 3 | 3.89 | ~81 | 10.3 × 3 | 14.54 | ~147 |
| 20 | 13.2 × 3 | 5.85 | ~64 | 13.6 × 3 | 18.66 | ~144 |
| 25 | 16.4 × 3 | 7.98 | ~50 | 16.9 × 3 | 19.96 | ~143 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Butt, M.A.; Piramidowicz, R. Small Footprint and High Extinction Ratio Cladding-Modulated Bragg Grating Structure as a Wideband Bandstop Filter. Photonics 2024, 11, 158. https://doi.org/10.3390/photonics11020158
Butt MA, Piramidowicz R. Small Footprint and High Extinction Ratio Cladding-Modulated Bragg Grating Structure as a Wideband Bandstop Filter. Photonics. 2024; 11(2):158. https://doi.org/10.3390/photonics11020158
Chicago/Turabian StyleButt, Muhammad A., and Ryszard Piramidowicz. 2024. "Small Footprint and High Extinction Ratio Cladding-Modulated Bragg Grating Structure as a Wideband Bandstop Filter" Photonics 11, no. 2: 158. https://doi.org/10.3390/photonics11020158
APA StyleButt, M. A., & Piramidowicz, R. (2024). Small Footprint and High Extinction Ratio Cladding-Modulated Bragg Grating Structure as a Wideband Bandstop Filter. Photonics, 11(2), 158. https://doi.org/10.3390/photonics11020158






