Wide and Deep Learning-Aided Nonlinear Equalizer for Coherent Optical Communication Systems

Abstract

In this study, we developed a wide and deep network-based nonlinear equalizer to compensate for nonlinear impairment in coherent optical communication systems. In our proposed equalizer, the power feature factor and inter-symbol feature sequence in the received signal are analyzed by two combined networks, wide and deep, respectively, so that the information contained in the signal can be fully utilized. We designed an experiment using a 120 Gbit/s 64-quadrature amplitude modulation (64-QAM) coherent optical communication system over a 375 km standard single-mode fiber (SSMF) to verify the performance of the proposed wide and deep network-based nonlinear equalizer. The experimental results showed that the proposed wide and deep network-based nonlinear equalizer achieved better performance at lower complexity compared with the traditional neural network-based nonlinear equalizer. The proposed equalizer significantly improved the equalization effect at a cost of a 0.3% increase in parameters, which indicates the potential of the proposed method for application in coherent optical communication systems.

1. Introduction

With the development of technology, modern society has become increasingly dependent on the Internet. Advances in digitization have led to an increasing demand for the capacity and quality of data transfer. Ensuring the capacity of fiber optic communication technology, a pillar of data transmission, is one of the greatest challenges [1,2,3,4,5]. The coherent optical communication technology transmission system is widely used in long-distance transmission because of its higher multiplexing efficiency compared with the intensity modulation–direct detection (IM-DD) system [6,7]. However, nonlinear effects limit the performance of high-speed coherent optical communication systems [8]. Nonlinear phase noise, expressed as the nonlinear Schrödinger equation, is proportional to signal power [9].

High-power optical signals are inhibited by the interference of nonlinear effects [10]. The high-order modulation technique is an effective method for improving the transmission capacity of transmission systems since the fiber nonlinearity problem in the optical network has a considerably greater impact on system transmission compared with the general modulation method. In such ways, solving nonlinear disturbances in transmission systems is of great significance for improving the performance of fiber optic communication systems [11]. Otherwise, signal constellation points show serious overlapping and nonlinear deflection, especially peripheral constellation points, which are more sensitive to nonlinear effects and prone to more serious nonlinear distortions than central points [12,13]. In Ref. [14], the authors studied constellation points that could not be correctly classified using the machine learning-based nonlinear equalization algorithm. The authors proposed an equalization strategy based on constellation diagram segmentation to improve the accuracy of the machine learning-based nonlinear equalization algorithm. In Ref. [15], the authors proposed a recurrent neural network-based equalization technique that analyzes interdimensional interference to improve optical transmission performance. The results indicated the potential of a neural network-based equalizer to provide a new means of solving interference issues in multimode transmission systems. The experimental results showed that current symbol I-channel data and Q-channel data have the greatest influence on the current symbol classification. In [16], the authors utilized the attention mechanism to study and understand the contribution of each input symbol in the input feature sequence and its corresponding data to the predicted symbols in a nonlinear equalizer based on a bidirectional recurrent neural network (Bi-RNN). The experimental results showed that the current symbol I-way data and Q-way data, as well as the nearest-neighbor symbol I-way data and Q-way data, received great attention and had the greatest impact on the results of the equalizer. The results of the above two studies demonstrated that the power of the current symbol has a significant influence on the results of machine learning techniques used for nonlinear equalization of signals. Therefore, when using machine learning techniques (especially neural networks) for the nonlinear equalization of signals, the power of the signals should be included as a unique feature factor that has a significant impact on the results.

Among the current neural network-based nonlinear equalization schemes, the target symbol is usually combined with its preceding k and following k symbols to form an input feature sequence of the current symbol, which contains the power of the symbols together with the nonlinear interference relationship between the symbols [17]. Using neural networks to process the sequence of signal features is equivalent to gradually fusing and extracting the relationships between the features, in which the depth of the latter is well condensed. However, the breadth of the features (e.g., the power of the current signal) may be weakened during gradual feature fusion and extraction, which then impacts the nonlinear equalization results [18,19,20]. It has been shown that inter-channel crosstalk in wavelength division multiplexing WDM systems significantly affects transmission capacity and transmission distance. Compensating for the nonlinear impairments generated between channels is helpful in improving system’s performance [21].

The low latency requirements of fiber optic communication systems for the transceiver side somewhat limit the complexity of digital signal processing on the receiver side. Equalizers with low complexity and high performance are in line with the needs of high-speed mode division multiplexing systems. In Ref. [22], the authors proposed a probability distribution equalizer based on neural networks, which effectively compensates for random impairments in the OAM system and improved the performance of the system with lower complexity. The results demonstrated the demand for nonlinear compensation in OAM systems and provided a research direction for the design of low-complexity, high-performance equalizers.

This paper proposes a nonlinear equalization method based on the wide and deep architecture, which uses both wide and deep networks to process the power feature factor of the current symbol and the feature sequences containing the nonlinear interference relationship between symbols in parallel. The wide network focuses on the power of the current symbol, which is a unique feature factor that is important for determining the results. Deep networks, meanwhile, process feature sequences that include nonlinear interference relationships between symbols. The results of the two networks are combined to provide the final nonlinear equalization results. By using the wide and deep architecture, both the depth and breadth information of the signal’s features can be fully utilized. In this study, we analyzed the effects of the proposed method on system performance by comparing the Q-factors of various equalizers. The complexity of the proposed equalizer was analyzed by comparing the number of parameters calculated and the number of multipliers to verify the performance and efficiency of the equalizer.

2. Principles

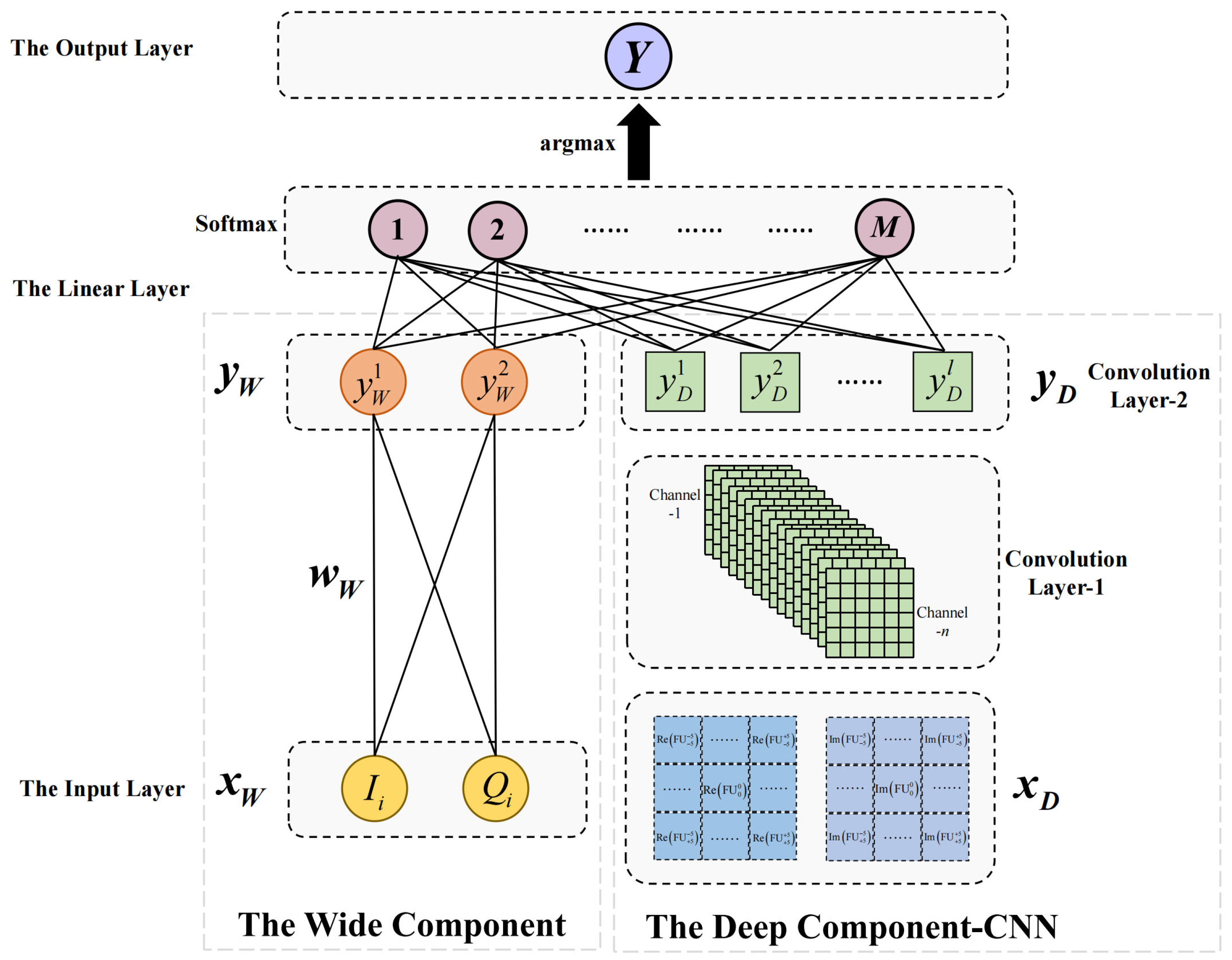
Figure 1 and Figure 2 present the architectures of the wide and deep learning-enhanced nonlinear equalizer for coherent optical communication systems. Figure 1 illustrates the design of the wide and deep CNN-based nonlinear equalizer, while Figure 2 demonstrates the structure of the wide and deep BiGRU-based nonlinear equalizer. In this section, we describe the details of these two contributing equalizers and evaluate the computational complexity of the proposed overall wide and deep learning-aided nonlinear equalizer.

2.1. Wide and Deep CNN-Based Nonlinear Equalizer

As shown in Figure 1, the structure of the wide and deep CNN-based nonlinear equalizer consists of the wide component, the deep component-CNN, a linear layer, and an output layer.

The wide component is a generalized linear model of the form ${\mathit{y}}_{\mathit{W}}={\mathit{w}}_{\mathit{W}}{\mathit{x}}_{\mathit{W}}+{\mathit{b}}_{\mathit{W}}$, as shown in the bottom left corner of Figure 1, where ${\mathit{x}}_{\mathit{W}}$ is the input of the wide component, ${\mathit{x}}_{\mathit{W}}=\left[I_i,Q_i\right]$, ${\mathit{x}}_{\mathit{W}}$ contains two values (data of in-phase (I) and quadrature (Q) components of the i-th M-QAM signal for the received M-QAM signal sequence), ${\mathit{w}}_{\mathit{W}}$ is the weight matrix of the input ${\mathit{x}}_{\mathit{W}}$, ${\mathit{b}}_{\mathit{W}}$ is the bias matrix, and ${\mathit{y}}_{\mathit{W}}$ is the output of the wide component, which consists of xw and variable parameters in the network and memorizes the power information of the M-QAM signal.

The deep component is a convolutional neural network (CNN), as shown in the bottom right corner of Figure 1. Our previous work [23] described the structure of the CNN in detail. The dimensions of ${\mathit{x}}_{\mathit{D}}$ are mainly related to the receiving sequence. We use the sliding window length of S to intercept the receiving sequence and then calculate the position relationship between each value in the intercepting sequence. Because of the real part and the imaginary part, the third term was 2. Thus, the dimensions of ${\mathit{x}}_{\mathit{D}}$ were S × S × 2. Choosing a large S allowed for including more values in the calculation, which benefited the equalization performance. However, a large S can also introduce issues of complexity. Considering the trade-off between performance and complexity, we set S at 11 to achieve better performance with acceptable complexity. After determining the value of S, the dimensions of ${\mathit{x}}_{\mathit{D}}$ were $11\times 11\times 2$.The $11\times 11\times 2$ input feature map ${\mathit{x}}_{\mathit{D}}$ was composed of intra-channel cross-phase modulation (IXPM) and intra-channel four-wave mixing (IFWM) triplets in the M-QAM signal. Then, the $11\times 11\times 2$ input feature map ${\mathit{x}}_{\mathit{D}}$ contained the information on the inter-symbol interferences of the current polarization and the other polarization of the M-QAM signal. Two convolutional layers were used to extract information on the input feature map layer by layer. Our previous work [24] demonstrated the performance of the convolution part of the neural network. The main point of setting the parameters of the convolutional layers is the trade-off between performance and complexity. The kernel size and number of layers are related to the complexity of equalization, which will be discussed in detail in Section 2.3. The input feature map was $11\times 11\times 2$, while the output feature map of the convolution part was $1\times 1\times \mathit{C}$, where $\mathit{C}$ is a variable parameter of the convolutional layer. Thus, we followed the previous convolutional layer structure. In the first convolutional layer, the kernel size was $6\times 6$, and the number of channels was 16; thus, the size of the output feature map was $6\times 6\times 16$. In the second convolutional layer, the kernel size was $6\times 6$, and the number of channels was 128; thus, the size of the output feature map was $1\times 1\times 128$.

The outputs of the wide component ${\mathit{y}}_{\mathit{W}}$ and the deep component-CNN ${\mathit{y}}_{\mathit{D}}$ are fully connected to the linear layer. The number of nodes in the linear layer is the same as the number of classes of the M-QAM signals. Then, the linear layer outputs the probabilities that the current signal maps to each class. Finally, the output layer outputs the corresponding predicted class $\mathit{Y}$ of the current signal with the maximum probability.

Building on our previous work [23], the operation of the wide component and the full connection of the deep component-CNN output to the linear layer are added.

2.2. Wide and Deep BiGRU-Based Nonlinear Equalizer

As shown in Figure 2, the structure of the wide and deep BiGRU-based nonlinear equalizer consists of the wide component, the deep component-BiGRU, a linear layer, and an output layer.

The wide component is a generalized linear model represented by the formula ${\mathit{y}}_{\mathit{W}}={\mathit{w}}_{\mathit{W}}{\mathit{x}}_{\mathit{W}}+{\mathit{b}}_{\mathit{W}}$, as shown in the bottom left corner of Figure 2. This model plays a crucial role in capturing and preserving the power information of the M-QAM signal. The input to the wide component, ${\mathit{x}}_{\mathit{W}}=\left[I_i,Q_i\right]$, ${\mathit{x}}_{\mathit{W}}$ contains two distinct values: data on the in-phase (I) and the quadrature (Q) components of the i-th M-QAM signal within the received M-QAM signal sequence. The weight matrix of the input ${\mathit{x}}_{\mathit{W}}$ ${\mathit{w}}_{\mathit{W}}$, and the bias matrix ${\mathit{b}}_{\mathit{W}}$ are parameters that are fine-tuned during the training process.

The deep component is a bidirectional gated recurrent unit (BiGRU) neural network, as shown in the bottom right corner of Figure 2. Our previous work [23] described the structure of the BiGRU neural network in detail. The $2k+1$ input feature sequence ${\mathit{x}}_{\mathit{D}}$ is composed of the data on the I and Q components of the current M-QAM signal and its k preceding and k succeeding symbols. Then, the $2k+1$ input feature sequence ${\mathit{x}}_{\mathit{D}}$ contains the information on the inter-symbol interferences in the M-QAM signal. The BiGRU layer consists of two GRU units that operate in opposite directions, making it bidirectional. This allows information from both the future and the past to influence the current states. The recurrent time step of the BiGRU model was set to $2k+1$. As a result, the output of the BiGRU layer ${\mathit{y}}_{\mathit{D}}$ contained the flow of symbol information across the recurrent time steps.

The wide component’s output ${\mathit{y}}_{\mathit{W}}$ and the deep component-BiGRU’s output ${\mathit{y}}_{\mathit{D}}$ are both fully connected to the linear layer. The number of nodes in the linear layer is set to match the number of classes in the M-QAM signals. The linear layer then computes the probabilities that the current signal belongs to each class. Finally, the output layer determines the predicted class $\mathit{Y}$ of the current signal based on the maximum probability.

Building on our previous work [23], the operation of the wide component and the full connection of the deep component-BiGRU output to the linear layer are added.

2.3. Complexity Analysis

In this section, we describe in detail our proposed wide and deep learning-aided nonlinear equalizer by examining its computational complexity. Our analysis centers on two primary factors: the number of parameters in the neural networks utilized in the equalization process, and the number of multiplications required for the nonlinear equalizer during the equalization of each M-QAM symbol.

In the wide and deep CNN-based nonlinear equalizer, the parameters of the nonlinear equalizer consist of three main parts: the parameters of the wide component, the kernel size and layers of the deep component-CNN, and the length of the linear layer. The number of parameters of the wide component was set at 6. Based on the kernel size and the number of layers in the deep component-CNN layer, the number of parameters in the second part is given by ${\displaystyle {\sum }_{l=1}^D\left(K_l\cdot C_{in,l}\cdot C_{out,l}\right)}$. Here, D and l represent the count and sequential order of the convolutional layers, respectively. K denotes the convolution kernel size, while C_in and C_out represent the number of input and output channels for each convolutional layer. The number of parameters in the linear layer was calculated as $2\times M+C_{out,D}\times M$, where M represents the length of the linear layer, and C_out,D is the output of the convolutional layer. Thus, the number of parameters in the wide and deep CNN-based nonlinear equalizer was $6+{\displaystyle {\sum }_{l=1}^D\left(K_l\cdot C_{in,l}\cdot C_{out,l}\right)}+2\times M+C_{out,D}\times M$. When compared with our previous work [23], only $6+2\times M$ parameters were added.

The computational demands of the wide and deep CNN-based nonlinear equalizer, in terms of the number of multiplications required for each M-QAM symbol, encompass three primary components: the multiplications in the wide component, those in the deep component-CNN, and the multiplications in the linear layer. There were four multiplications in the wide component because there were only four weights among the six parameters that required multiplications for their implementation. The multiplications in the deep component-CNN were calculated as ${\displaystyle {\sum }_{l=1}^D\left(O_l\cdot K_l\cdot C_{in,l}\cdot C_{out,l}\right)}$, where D and l represent the number and numerical order of convolutional layers, O denotes the size of the feature vector output from each convolution kernel, K represents the kernel size for convolution, and C_in and C_out denote the input channels and output channels for each convolutional layer. Multiplications of the linear layer were performed using $2\times M+C_{out,D}\times M$. Therefore, the cumulative number of multiplications required for the wide and deep CNN-based nonlinear equalizer was $4+{\displaystyle {\sum }_{l=1}^D\left(O_l\cdot K_l\cdot C_{in,l}\cdot C_{out,l}\right)}+2\times M+C_{out,D}\times M$. Compared with our previous work [23], only $4+2\times M$ multiplications were added, which was due to the wide component and the output neural layer in its output feature map. In terms of analyzing the interactions between symbols, the input feature map of the deep component is usually a multiple of the feature map input to the wide component, which signifies that the convolutional layer will require more multiplications to analyze the input feature map.

In the wide and deep BiGRU-based nonlinear equalizer, the number of parameters in the nonlinear equalizer encompasses the parameters of the wide component, those of the deep component-BiGRU, and the length of the linear layer. It is worth noting that the wide component in the wide and deep BiGRU architecture was identical to that of the wide and deep-CNN. We used the same wide component parameter settings, so the number of parameters of the wide component was set at 6.

The wide and deep BiGRU-based nonlinear equalizer required a specific number of multiplications for each M-QAM symbol to achieve equalization. These multiplications are primarily attributed to the wide component, the deep component-BiGRU, and the linear layer. Here, the wide component required a multiplication count of 4.

The number of multiplications of the deep component-LSTM was $2\times 4\times \left(FH+H^2+2H\right)$, where F denotes the size of the input feature and H denotes the state of hidden layer $h_t$ at moment t. The number of multiplications of the linear layer was $2\times M+2HM+M$. Consequently, the number of parameters required for the wide and deep BiGRU-based nonlinear equalizer was $6+2\times 4\times \left(FH+H^2+2H\right)+2\times M+2HM+M$.

For the multiplications, the wide and deep BiGRU-based nonlinear equalizer requires three main components to equalize each M-QAM symbol: the number of multiplications in the wide component, the multiplications required in the deep component-LSTM, and the number of multiplications in the linear layer. The number of multiplications of the wide component was 4 since two bias parameters only needed adders. The number of multiplications of the deep component-LSTM was $2\times \left[4\times \left(FH+H^2\right)+3H\right]\times L$, where L denotes the number of convolutional layers. The number of multiplications of the linear layer was $2\times M+2HM$. Thus, the number of multiplications required for the wide and deep BiGRU-based nonlinear equalizer was $4+2\times \left[4\times \left(FH+H^2\right)+3H\right]\times L+2\times M+2HM$. It was found that there was only an additional $4+2\times M$ increase in the complexity. The increases in complexity were the same in the wide and deep BiGRU and the wide and deep CNN. However, the deep component required more multiplications in the BiGRU network than in the CNN network for general purposes. These results indicate that wide components are more efficient in the BiGRU network, meaning it has greater significance than the CNN network for equalization.

3. Experimental Setup

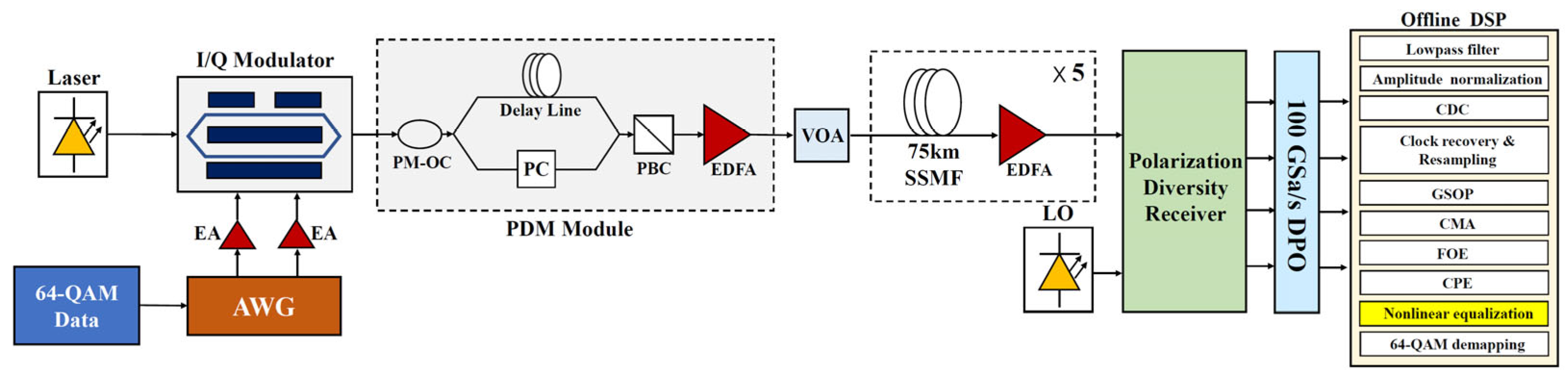
Figure 3 illustrates the experimental setup for a 120 Gb/s 64-QAM coherent optical communication system that transmits over a distance of 375 km.

The transmitting end consists of several components, including an external cavity laser with a nominal linewidth of 100 kHz, an in-phase/quadrature (I/Q) modulator, an arbitrary waveform generator (AWG) with a sampling rate of 25 GSa/s, two electric amplifiers (EAs), a polarization-division-multiplexing (PDM) module, and a variable optical attenuator (VOA). The 64-QAM symbol data are generated using a MATLAB program and then uploaded to an arbitrary waveform generator (AWG) to obtain an analog signal. The output of the two analog signals outputted from the AWG are amplified by the two EAs, and they will then be sent into the I/Q modulator. The light source generated by the ECL is fed to the I/Q modulator. After receiving the light source, the I/Q modulator will produce a modulated 64-QAM optical signal that is then fed into the PDM module for polarization multiplexing. The PDM module comprises five essential components: a polarization-maintaining optical coupler (PM-OC), an optical delay line, a polarization controller (PC), a polarization beam combiner (PBC), and an Erbium-doped fiber amplifier (EDFA). Each component plays a crucial role in the polarization multiplexing process. EDFA is used to amplify the 64-QAM optical signal. The VOA is used to adjust the power of the 64-QAM optical signal.

The transmission link consists of five spans of standard single-mode fiber (SSMF) with a total length of 75 km. To compensate for fiber loss at the end of each span, five separate and independent Erbium-doped fiber amplifiers (EDFAs) are utilized.

At the receiving end, in order to achieve coherent detection, the local oscillator (LO) is provided by an ECL with a 100 kHz linewidth. The 64-QAM optical signal is detected by optical polarization and a phase-diversity coherent receiver. A 4-channel digital phosphor oscilloscope (DPO) with a sampling rate of 100 GSa/s is used to digitize the 64-QAM signal. The offline digital signal processing (DSP) algorithms encompass a range of operations, including lowpass filtering, amplitude normalization, chromatic dispersion compensation (CDC), clock recovery, resampling, the Gram–Schmidt orthogonalizing process (GSOP), constant modulus algorithm (CMA) equalization, frequency offset estimation (FOE), carrier phase estimation (CPE) based on blind phase search, nonlinear equalization, and 64-QAM demapping.

In this experiment, the measured launched optical power range was set from −4 dBm to 5 dBm. Each dataset of launched optical power contained approximately 2²⁰ symbols. The entire dataset was divided into training and testing data in an 8:2 ratio. The building, training, and evaluating of the nonlinear equalization models were performed in PyTorch 1.6.0.

4. Results and Discussion

In this experiment, for each 64-QAM signal, the I-channel data and Q-channel data of the current 64-QAM signal were set as the first features of the 64-QAM signal data to construct the first feature sequence corresponding to each 64-QAM signal. The second feature data, which were used to construct the second feature map of each 64-QAM signal, were generated by the triple-product term of the current 64-QAM signal. The value of hyperparameter L denoted the topological charge number of the orbital angular momentum. During the experiment, the data in mode l = 5 were representative. Thus, in the following equation, the value of L is set at 5. The second feature unit corresponding to each 64-QAM signal was as follows: $U_{\mathrm{Re}}^{(i)}=\left[\begin{array}{ccc}\mathrm{Re}{\left(F^{(i)}\right)}_{-5}^{-5}& \cdots \cdots & \mathrm{Re}{\left(F^{(i)}\right)}_{-5}^{+5}\\ \cdots \cdots & \mathrm{Re}{\left(F^{(i)}\right)}_0^0& \cdots \cdots \\ \mathrm{Re}{\left(F^{(i)}\right)}_{+5}^{-5}& \cdots \cdots & \mathrm{Re}{\left(F^{(i)}\right)}_{+5}^{+5}\end{array}\right]$ and $U_{\mathrm{Im}}^{(i)}=\left[\begin{array}{ccc}\mathrm{Im}{\left(F^{(i)}\right)}_{-5}^{-5}& \cdots \cdots & \mathrm{Im}{\left(F^{(i)}\right)}_{-5}^{+5}\\ \cdots \cdots & \mathrm{Im}{\left(F^{(i)}\right)}_0^0& \cdots \cdots \\ \mathrm{Im}{\left(F^{(i)}\right)}_{+5}^{-5}& \cdots \cdots & \mathrm{Im}{\left(F^{(i)}\right)}_{+5}^{+5}\end{array}\right]$, respectively. The second feature map of each corresponding 64-QAM signal was $x_D^{(i)}=\left[U_{\mathrm{Re}}^{(i)};U_{\mathrm{Im}}^{(i)}\right]$ of size $11\times 11\times 2$.

The deep component CNN model consisted of two convolutional layers. The size of the convolution kernel of the first layer was $6\times 6$ with 16 channels. Thus, the output feature map was of size $6\times 6\times 16$. The size of the kernel in the second layer was $6\times 6$ with 128 channels. Thus, the output feature map was of size $1\times 1\times 128$.

Figure 4 displays the relationship of Q-factor and the launched optical power. The CNN-based nonlinear equalizer (CNN NLE) model with the same structure is used as a comparison in the figure.

In the

Table 1. Comparison of the complexity of linear equalizer models.

Nonlinear Equalizer Model	Parameters	Multiplications
CNN NLE	83,072	123,392
Wide and deep CNN NLE	83,206	123,524

, we list the number of parameters and multiplications used in the equalizer when processing the 64-QAM signal with the CNN NLE and wide and deep CNN NLE.

Compared with the CNN NLE, the proposed wide and deep CNN nonlinear equalizer model achieves better results with only 134 additional parameters and 132 additional multiplications per symbol. In the model with this parameter setting, complexity increases by only 0.1%. When the number of parameters in the deep module increases, the complexity increase ratio is even lower, which demonstrates the lightness of the wide net structure.

In this experiment, the number of adjacent symbols before and after l was set to 11, so the length of the input feature sequence was 23.

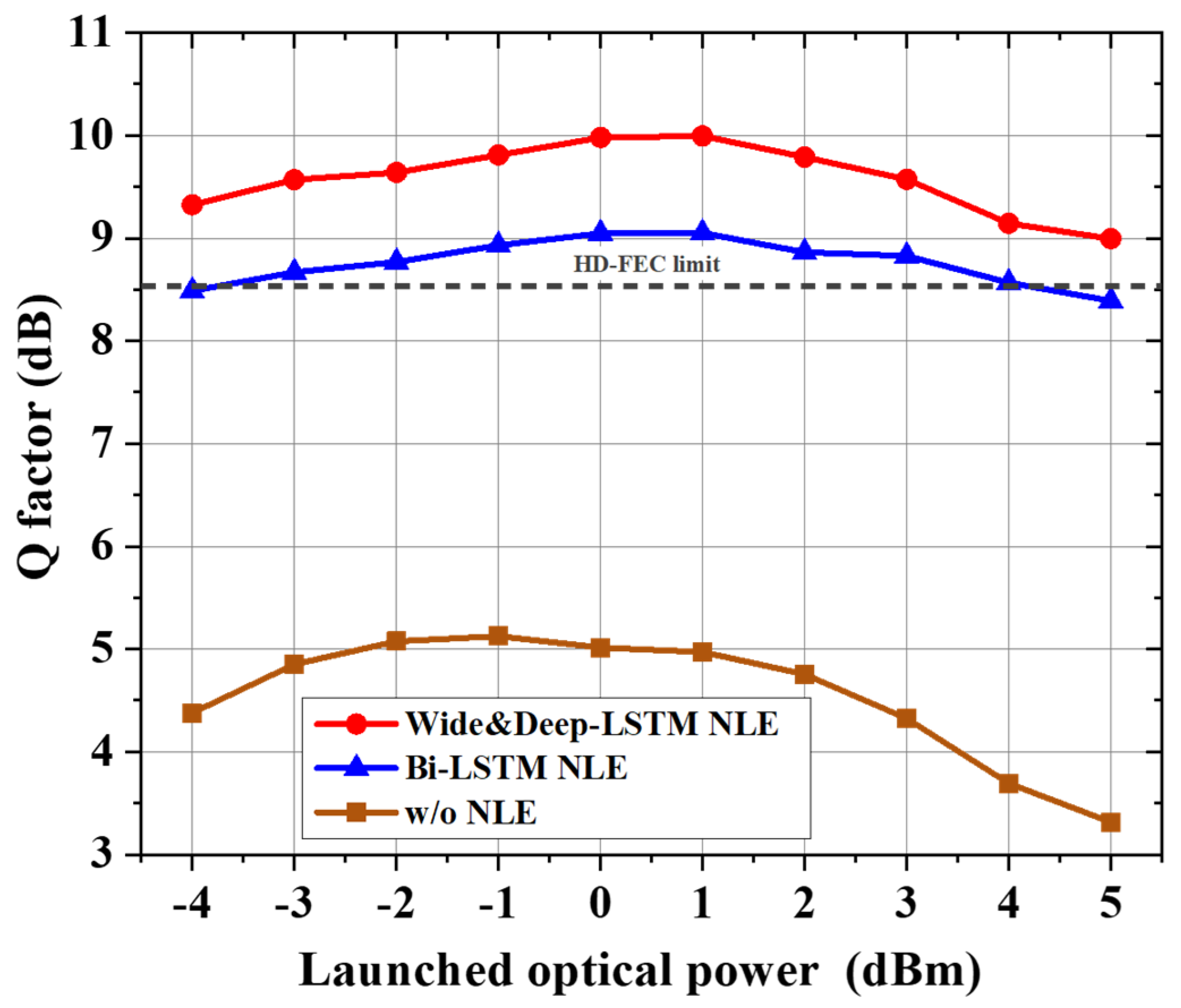
Figure 5 shows the relationship of the Q-factor and the launched optical power. The Bi-LSTM-based nonlinear equalizer (Bi-LSTM NLE) model with the same structure is used as a comparison in the figure.

In the

Table 2. Comparison of the complexity of linear equalizer models.

Nonlinear Equalizer Model	Parameters	Multiplications
Bi-LSTM NLE	43,072	794,240
Wide and deep LSTM NLE	43,206	794,372

, we list the number of parameters and multiplications used in the equalizer when processing the 64-QAM signal with Bi-LSTM NLE and wide and deep LSTM NLE.

Compared with Bi-LSTM, the proposed wide and deep LSTM nonlinear equalizer model achieves better results with only 134 additional parameters and 132 additional multiplications per symbol. System performance is improved by 1 dB at a cost of 0.016% in complexity.

5. Conclusions

In this paper, we have proposed a wide and deep network-based nonlinear equalizer. A wide network can better capture the power feature factor of a single symbol, while the deep network processes the feature sequences that contain nonlinear interference relationships between symbols. To demonstrate the performance of the proposed wide and deep network-based nonlinear equalizer, an experimental 120 Gb/s 64-QAM coherent optical communication system with a transmission distance of 375 km was established. In this experiment, we compared the proposed equalizer with the corresponding network-based equalizer. The results indicate that the wide and deep network can significantly improve system performance by approximately 1 dB at a cost of less than 0.1% in complexity. Because the structure of the Bi-LSTM network is complex, the combination of two networks in the proposed wide and deep network-based nonlinear equalizer increased the efficiency of the system. The results show that wide and deep structures have better results on high-complexity networks, although they are otherwise only equally as effective as other neural network-based equalizers.