Femtosecond Laser Fabrication of Gradient Index Micro-Optics in Chalcogenide Glass
Abstract
1. Introduction
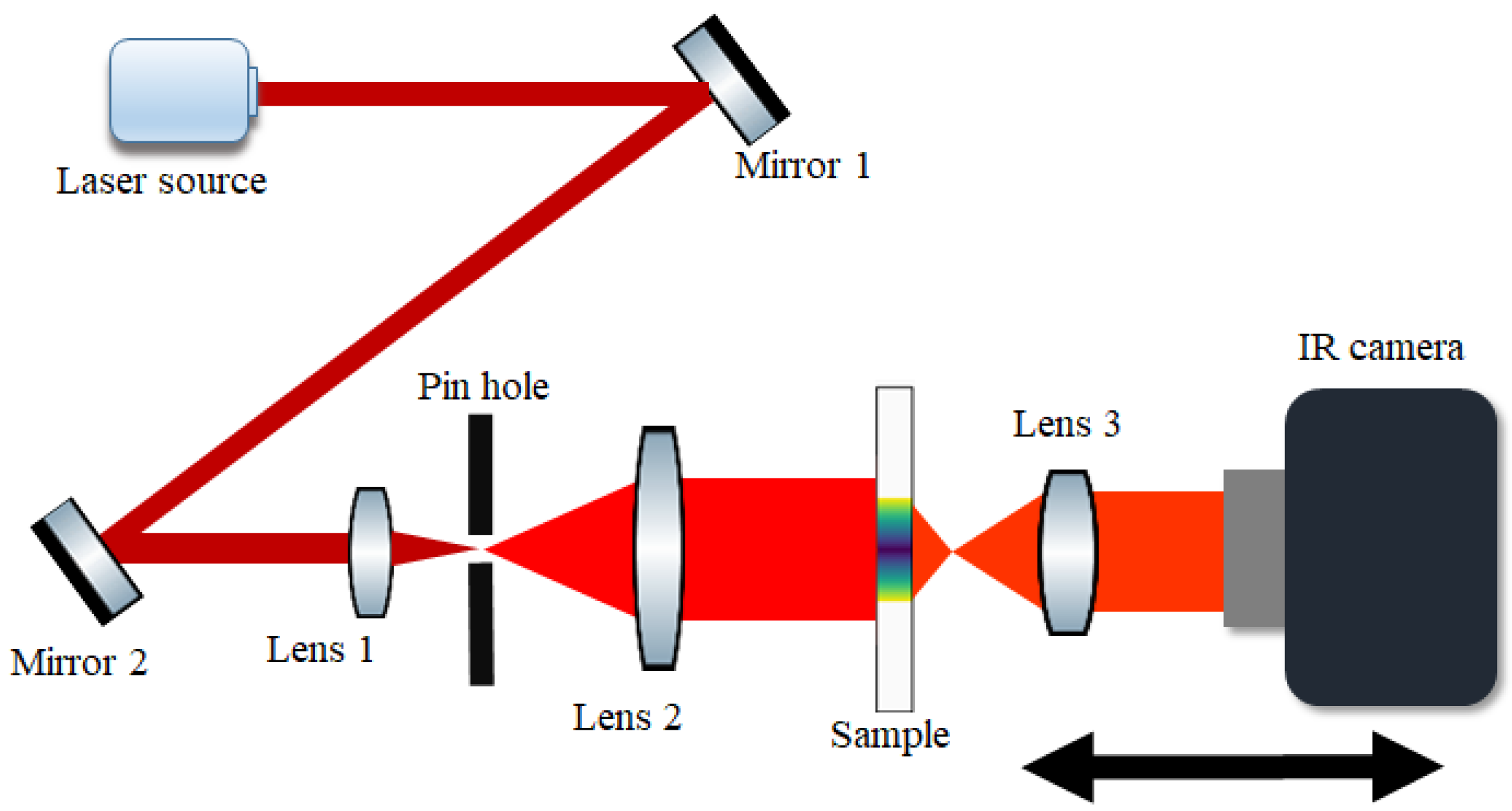
2. Materials and Methods
3. Results
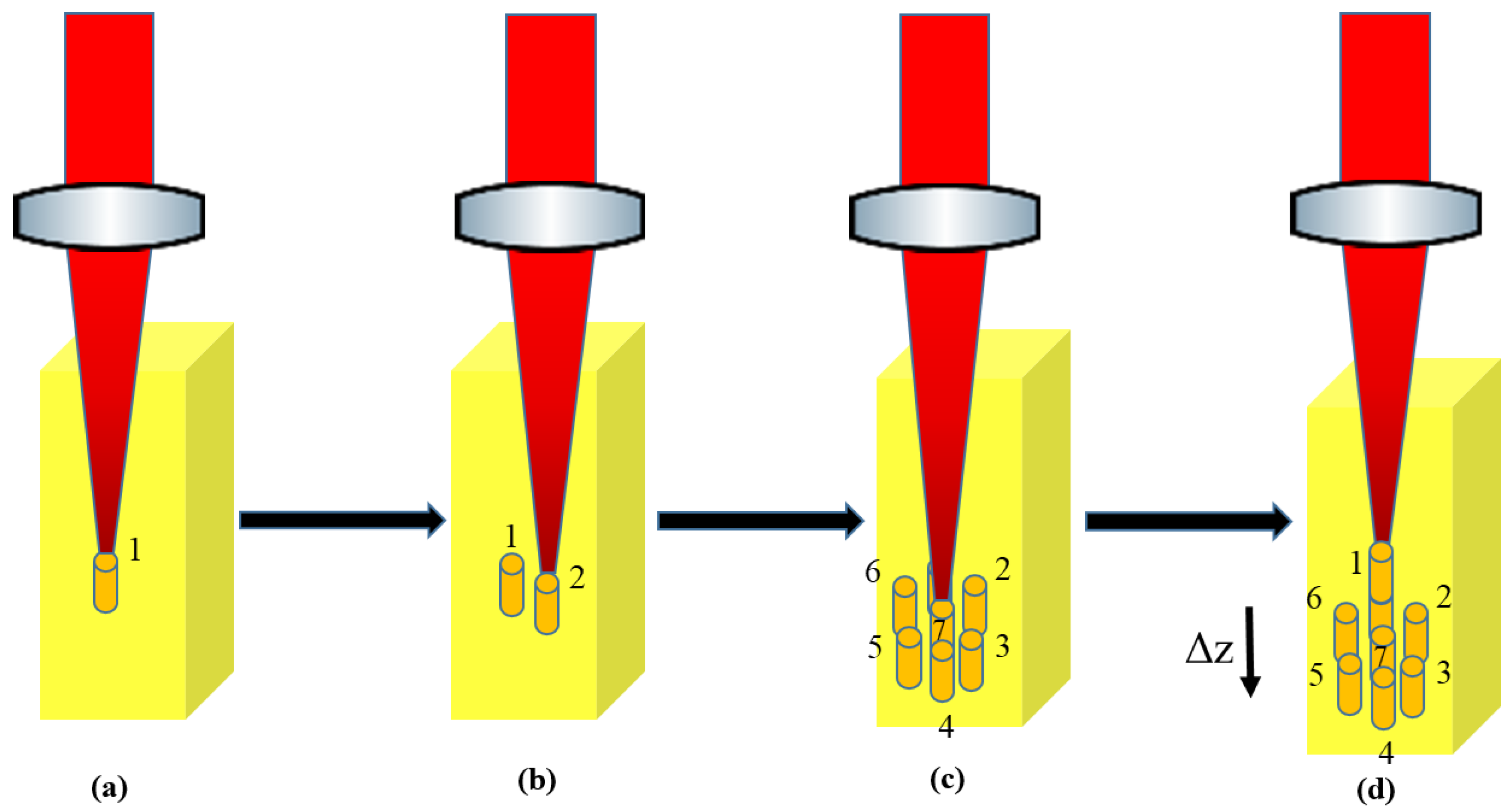
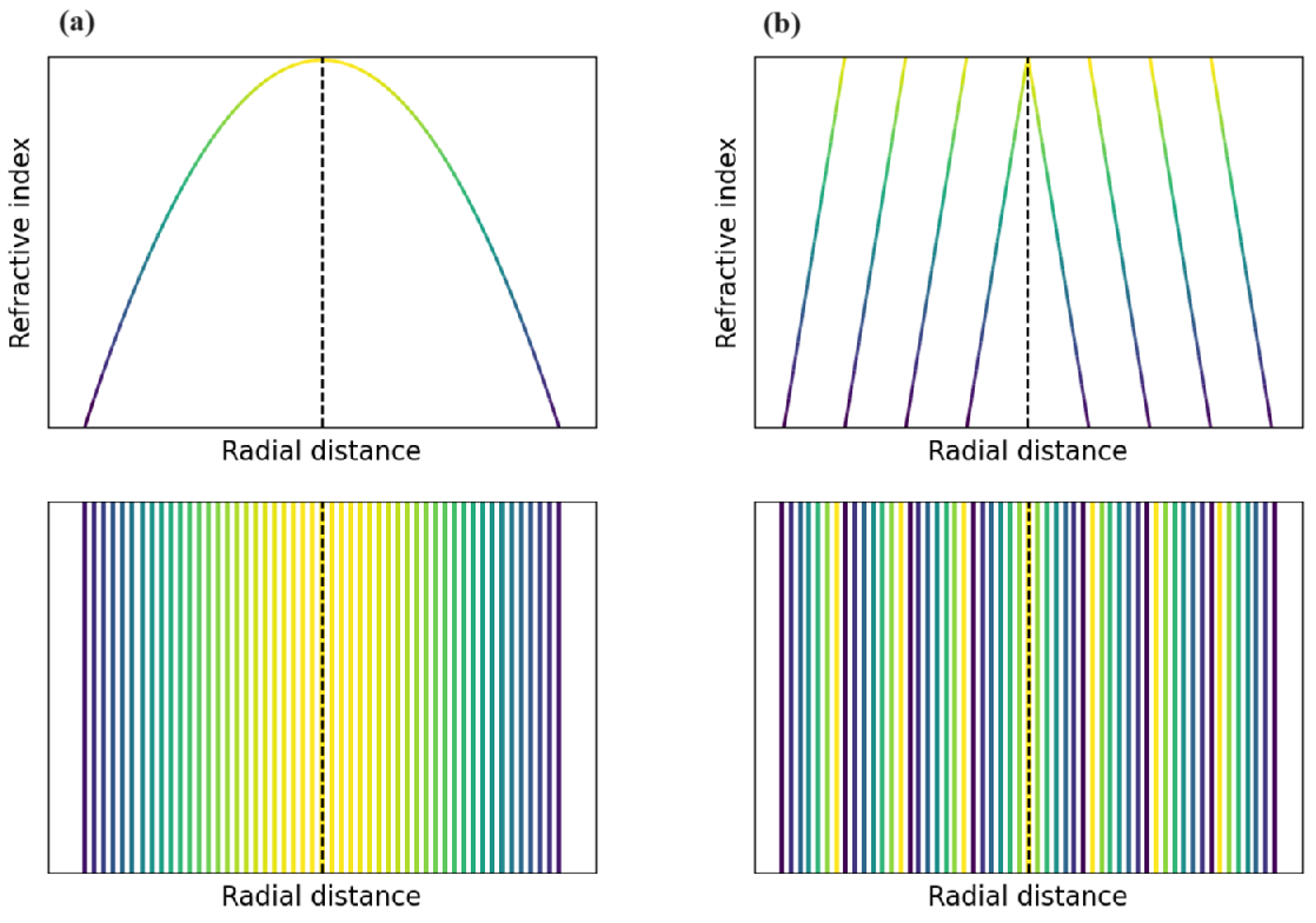
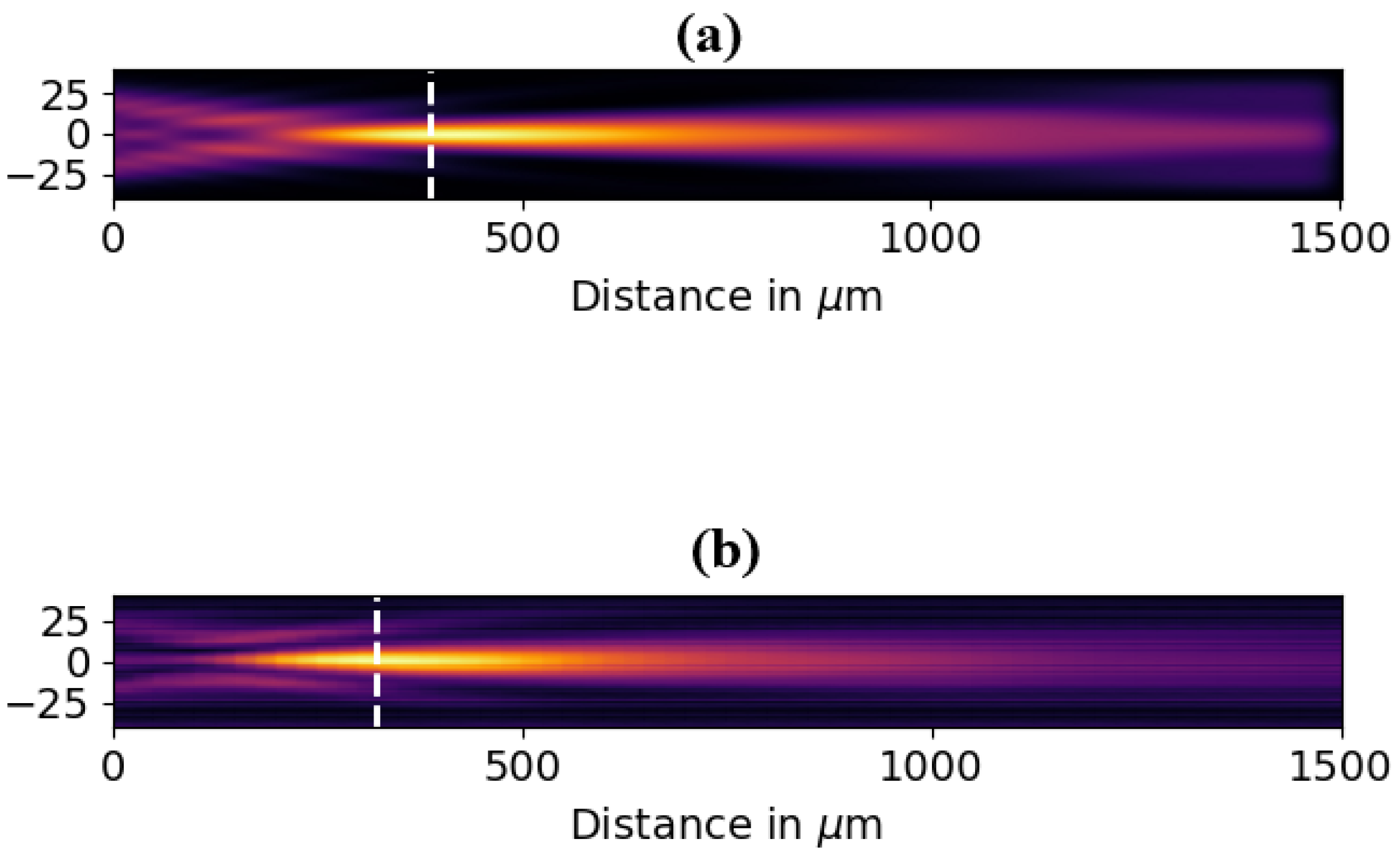
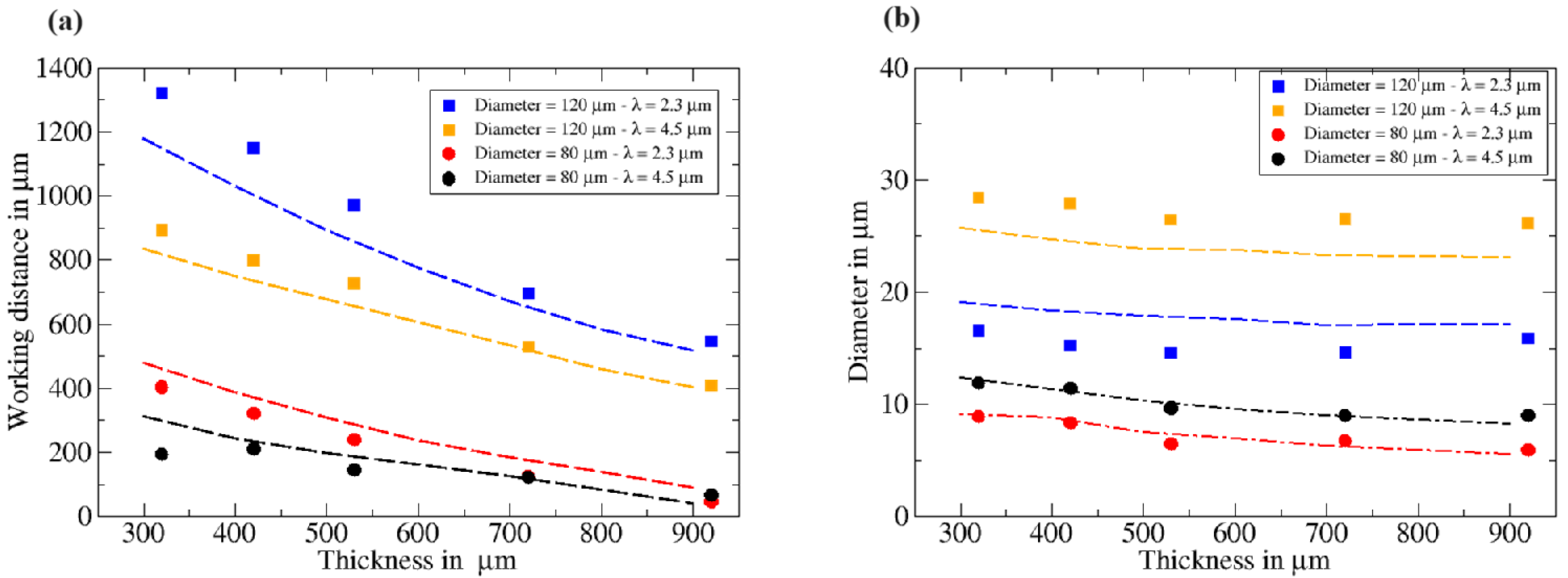
3.1. Micro-Lenses
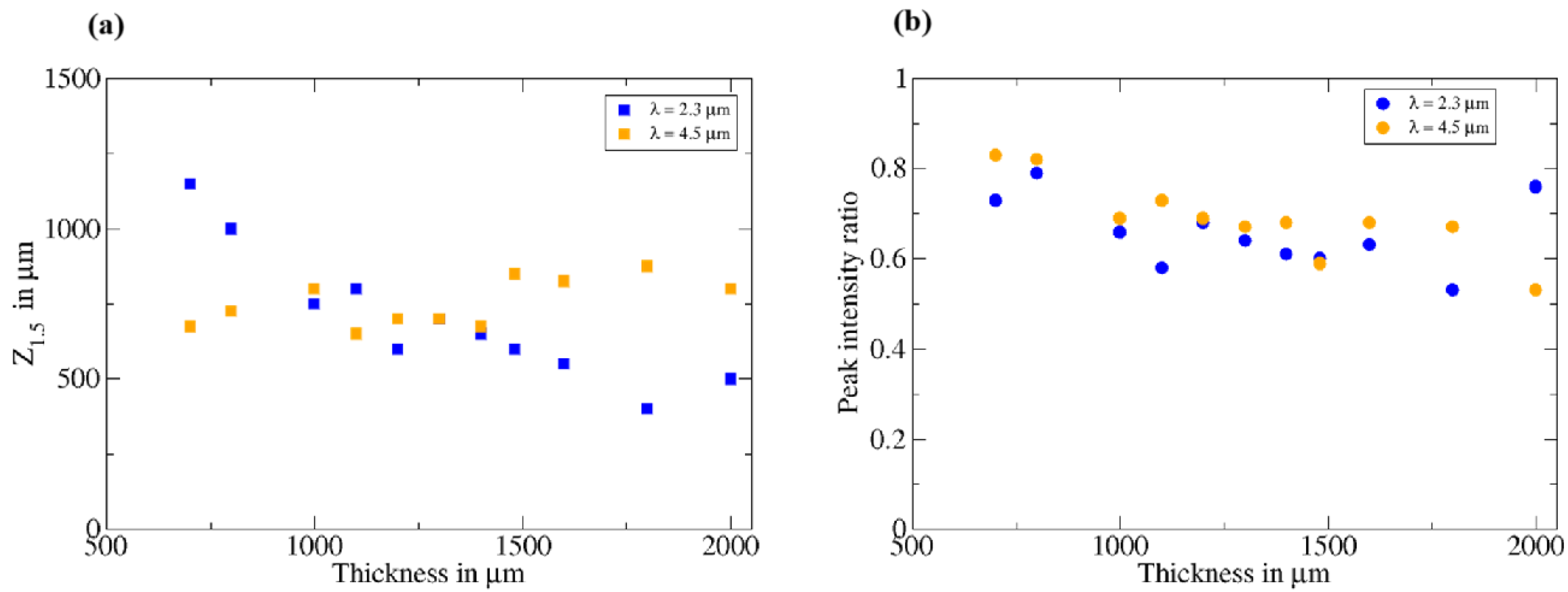
3.2. Micro-Fraxicon
4. Discussion
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Zhang, X.; Hongli, M.A.; Lucas, J. A new class of infrared transmitting glass-ceramics based on controlled nucleation and growth of alkali halide in a sulphide based glass matrix. J. Non Cryst. Solids 2004, 337, 130–135. [Google Scholar] [CrossRef]
- Calvez, L.; Ma, H.L.; Lucas, J.; Zhang, X.H. Glasses and glass-ceramics based on GeSe2–Sb2Se3 and halides for far infrared transmission. J. Non Cryst. Solids 2008, 354, 1123–1127. [Google Scholar] [CrossRef]
- Li, Z.; Olah, A.; Baer, E. Micro-and nano-layered processing of new polymeric systems. Prog. Polym. Sci. 2020, 102, 101210. [Google Scholar] [CrossRef]
- He, C.; Chang, J.; Hu, Q.; Wang, J.; Antonello, J.; He, H.; Liu, S.; Lin, J.; Dai, B.; Elson, D.S.; et al. Complex vectorial optics through gradient index lens cascades. Nat. Commun. 2019, 10, 4264. [Google Scholar] [CrossRef] [PubMed]
- Beadie, G.; Shirk, J.S.; Rosenberg, A.; Lane, P.A.; Fleet, E.; Kamdar, A.R.; Jin, Y.; Ponting, M.; Kazmierczak, T.; Yang, Y.; et al. Optical properties of a bio-inspired gradient refractive index polymer lens. Opt. Express 2008, 16, 11540–11547. [Google Scholar] [CrossRef]
- Gomez-Reino, C.; Perez, M.V.; Bao, C.; Flores-Arias, M.T. Design of GRIN optical components for coupling and interconnects. Laser Photonics Rev. 2008, 2, 203–215. [Google Scholar] [CrossRef]
- Nguyen, V.; Larouche, S.; Landy, N.; Lee, J.S.; Smith, D.R. Quantitative comparison of gradient index and refractive lenses. J. Opt. Soc. Am. A 2012, 29, 2479–2496. [Google Scholar] [CrossRef]
- Michael, A.; Al Hafiz, A.; Puzzer, T.; Kwok, C.Y. Deposition and characterization of thick graded index SixOyFz films with low stress. Sens. Actuator A Phys. 2012, 178, 110–117. [Google Scholar] [CrossRef]
- Fourmentin, C.; Zhang, X.H.; Lavanant, E.; Pain, T.; Rozé, M.; Guimond, Y.; Gouttefangeas, F.; Calvez, L. IR GRIN lenses prepared by ionic exchange in chalcohalide glasses. Sci. Rep. 2021, 11, 11081. [Google Scholar] [CrossRef]
- Lavanant, E.; Calvez, L.; Cheviré, F.; Roze, M.; Hingant, T.; Proux, R.; Guimond, Y.; Zhang, X.H. Radial gradient refractive index (GRIN) infrared lens based on spatially resolved crystallization of chalcogenide glass. Opt. Mater. Express 2020, 10, 860–867. [Google Scholar] [CrossRef]
- Hudelist, F.; Buczynski, R.; Waddie, A.J.; Taghizadeh, M.R. Design and fabrication of nano-structured gradient index microlenses. Opt. Express 2009, 17, 3255–3263. [Google Scholar] [CrossRef] [PubMed]
- Filipkowski, A.; Piechal, B.; Pysz, D.; Stepien, R.; Waddie, A.; Taghizadeh, M.R.; Buczynski, R. Nanostructured gradient index microaxicons made by a modified stack and draw method. Opt. Lett. 2015, 40, 5200–5203. [Google Scholar] [CrossRef] [PubMed]
- Nguyen, H.T.; Kasztelanic, R.; Filipkowski, A.; Pysz, D.; Van Le, H.; Stepien, R.; Omatsu, T.; Krolikowski, W.; Buczynski, R. Broadband optical vortex beam generation using flat-surface nanostructured gradient index vortex phase masks. Sci. Rep. 2023, 13, 20255. [Google Scholar] [CrossRef] [PubMed]
- Nguyen, H.T.; Kasztelanic, R.; Pysz, D.; Van Le, H.; Stepien, R.; Omatsu, T.; Krolikowski, W.; Buczynski, R. Generation of high-order optical vortices with nanostructured phase masks. Opt. Laser Technol. 2024, 172, 110490. [Google Scholar] [CrossRef]
- Le Phu, T.; Le Coq, D.; Masselin, P. Waveguide fabrication with integrated coupling optic. Opt. Laser Technol. 2025, 180, 111522. [Google Scholar] [CrossRef]
- Bhardwaj, V.R.; Simova, E.; Rajeev, P.P.; Hnatovsky, C.; Taylor, R.S.; Rayner, D.M. Corkum, P.B. Optically produced arrays of planar nanostructures inside fused silica. Phys. Rev. Lett. 2006, 96, 057404. [Google Scholar] [CrossRef]
- Gross, S.; Jovanovic, N.; Sharp, A.; Ireland, M.; Lawrence, J.; Withford, M.J. Low loss mid-infrared ZBLAN waveguides for future astronomical applications. Opt. Express 2015, 23, 7946–7956. [Google Scholar] [CrossRef] [PubMed]
- Davis, K.M.; Miura, K.; Sugimoto, N.; Hirao, K. Writing waveguides in glass with a femtosecond laser. Opt. Lett. 1996, 21, 1729–1731. [Google Scholar] [CrossRef]
- Tan, D.; Sharafudeen, K.N.; Yue, Y.; Qiu, J. Femtosecond laser induced phenomena in transparent solid materials: Fundamentals and applications. Prog. Mater. Sci. 2016, 76, 154–228. [Google Scholar] [CrossRef]
- Masselin, P.; Le Coq, D.; Cuisset, A.; Bychkov, E. Spatially resolved Raman analysis of laser induced refractive index variation in chalcogenide glass. Opt. Mater. Express 2012, 2, 1768–1775. [Google Scholar] [CrossRef]
- Minoshima, K.; Kowalevicz, A.M.; Hartl, I.; Ippen, E.P.; Fujimoto, J.G. Photonic device fabrication in glass by use of nonlinear materials processing with a femtosecond laser oscillator. Opt. Lett. 2001, 26, 1516–1518. [Google Scholar] [CrossRef] [PubMed]
- Dias, A.; Muñoz, F.; Alvarez, A.; Moreno-Zárate, P.; Atienzar, J.; Urbieta, A.; Fernandez, P.; Pardo, M.; Serna, R.; Solis, J. Femtosecond laser writing of photonic devices in borate glasses compositionally designed to be laser writable. Opt. Lett. 2018, 43, 2523–2526. [Google Scholar] [CrossRef] [PubMed]
- del Hoyo, J.; Vazquez, R.M.; Sotillo, B.; Fernandez, T.T.; Siegel, J.; Fernández, P.; Osellame, R.; Solis, J. Control of waveguide properties by tuning femtosecond laser induced compositional changes. Appl. Phys. Lett. 2014, 105, 131101. [Google Scholar] [CrossRef]
- Macias-Montero, M.; Dias, A.; Sotillo, B.; Moreno-Zárate, P.; Ariza, R.; Fernandez, P.; Solis, J. Waveguide tapers fabrication by femtosecond laser induced element redistribution in glass. J. Light. Technol. 2020, 38, 6578–6583. [Google Scholar] [CrossRef]
- Lapointe, J.; Bérubé, J.P.; Ledemi, Y.; Dupont, A.; Fortin, V.; Messaddeq, Y.; Vallée, R. Nonlinear increase, invisibility, and sign inversion of a localized fs-laser-induced refractive index change in crystals and glasses. Light Sci. Appl. 2020, 9, 64. [Google Scholar] [CrossRef] [PubMed]
- Masselin, P.; Bychkov, E.; Le Coq, D. Ultrafast laser inscription of high-performance mid-infrared waveguides in chalcogenide glass. IEEE Photon. 2018, 30, 2123–2126. [Google Scholar] [CrossRef]
- Tan, D.; Wang, Z.; Xu, B.; Qiu, J. Photonic circuits written by femtosecond laser in glass: Improved fabrication and recent progress in photonic devices. Adv. Photonics 2021, 3, 024002. [Google Scholar] [CrossRef]
- Tang, H.; Di Franco, C.; Shi, Z.Y.; He, T.S.; Feng, Z.; Gao, J.; Sun, K.; Li, Z.M.; Jiao, Z.Q.; Wang, T.Y.; et al. Experimental quantum fast hitting on hexagonal graphs. Nat. Photonics 2018, 12, 754–758. [Google Scholar] [CrossRef]
- Delullier, P.; Druart, G.; De La Barrière, F.; Calvez, L.; Lancry, M. Femtosecond laser direct writing of gradient index fresnel lens in GeS2-based chalcogenide glass for imaging applications. Appl. Sci. 2022, 12, 4490. [Google Scholar] [CrossRef]
- Stankevič, V.; Karosas, J.; Gečys, P. Fabrication of a multilevel Fresnel axicon deep in fused silica by femtosecond laser machining. Opt. Lett. 2023, 48, 4404–4407. [Google Scholar] [CrossRef]
- Zakery, A.; Elliott, S.R. Optical properties and applications of chalcogenide glasses: A review. J. Non-Cryst. Solids 2003, 330, 1–12. [Google Scholar] [CrossRef]
- DeCorby, R.G.; Ponnampalam, N.; Pai, M.M.; Nguyen, H.T.; Dwivedi, P.K.; Clement, T.J.; Haugen, C.J.; McMullin, J.N.; Kasap, S.O. High index contrast waveguides in chalcogenide glass and polymer. IEEE J. Sel. Top. Quantum Electron. 2005, 11, 539–546. [Google Scholar] [CrossRef]
- D’Amico, C.; Martin, G.; Troles, J.; Cheng, G.; Stoian, R. Multiscale Laser Written Photonic Structures in Bulk Chalcogenide Glasses for Infrared Light Transport and Extraction. Photonics 2021, 8, 211. [Google Scholar] [CrossRef]
- Masselin, P.; Le Coq, D.; Calvez, L.; Petracovschi, E.; Lépine, E.; Bychkov, E.; Zhang, X. CsCl effect on the optical properties of the 80GeS2–20Ga2S3 base glass. Appl. Phys. A 2012, 106, 697–702. [Google Scholar] [CrossRef]
- Roberts, A.; Ampem-Lassen, E.; Barty, A.; Nugent, K.A.; Baxter, G.W.; Dragomir, N.M.; Huntington, S.T. Refractive-index profiling of optical fibers with axial symmetry by use of quantitative phase microscopy. Opt. Lett. 2002, 27, 2061–2063. [Google Scholar] [CrossRef]
- Ampem-Lassen, E.; Huntington, S.T.; Dragomir, N.M.; Nugent, K.A.; Roberts, A. Refractive index profiling of axially symmetric optical fibers: A new technique. Opt. Express 2005, 13, 3277–3282. [Google Scholar] [CrossRef]
- Golub, I. Fresnel axicon. Opt. Lett. 2006, 31, 1890–1892. [Google Scholar] [CrossRef] [PubMed]
- Oskooi, A.F.; Roundy, D.; Ibanescu, M.; Bermel, P.; Joannopoulos, J.D.; Johnson, S.G. MEEP: A flexible free-software package for electromagnetic simulations by the FDTD method. Comput. Phys. Commun. 2010, 181, 687–702. [Google Scholar] [CrossRef]
- Hudelist, F.; Nowosielski, J.M.; Buczynski, R.; Waddie, A.J.; Taghizadeh, M.R. Nanostructured elliptical gradient-index microlenses. Opt. Lett. 2010, 35, 130–132. [Google Scholar] [CrossRef]
- Buczynski, R.; Filipkowski, A.; Piechal, B.; Nguyen, H.T.; Pysz, D.; Stepien, R.; Waddie, A.; Taghizadeh, M.R.; Klimczak, M.; Kasztelanic, R. Achromatic nanostructured gradient index microlenses. Opt. Express 2019, 27, 9588–9600. [Google Scholar] [CrossRef]


Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Le Phu, T.; Ledesma Molinero, M.; Boussard-Plédel, C.; Le Coq, D.; Masselin, P. Femtosecond Laser Fabrication of Gradient Index Micro-Optics in Chalcogenide Glass. Photonics 2024, 11, 1076. https://doi.org/10.3390/photonics11111076
Le Phu T, Ledesma Molinero M, Boussard-Plédel C, Le Coq D, Masselin P. Femtosecond Laser Fabrication of Gradient Index Micro-Optics in Chalcogenide Glass. Photonics. 2024; 11(11):1076. https://doi.org/10.3390/photonics11111076
Chicago/Turabian StyleLe Phu, Thien, Mariel Ledesma Molinero, Catherine Boussard-Plédel, David Le Coq, and Pascal Masselin. 2024. "Femtosecond Laser Fabrication of Gradient Index Micro-Optics in Chalcogenide Glass" Photonics 11, no. 11: 1076. https://doi.org/10.3390/photonics11111076
APA StyleLe Phu, T., Ledesma Molinero, M., Boussard-Plédel, C., Le Coq, D., & Masselin, P. (2024). Femtosecond Laser Fabrication of Gradient Index Micro-Optics in Chalcogenide Glass. Photonics, 11(11), 1076. https://doi.org/10.3390/photonics11111076




