Thermal Analysis of Acousto-Optic Modulators and Its Influence on Ultra-Stable Lasers
Abstract
:1. Introduction
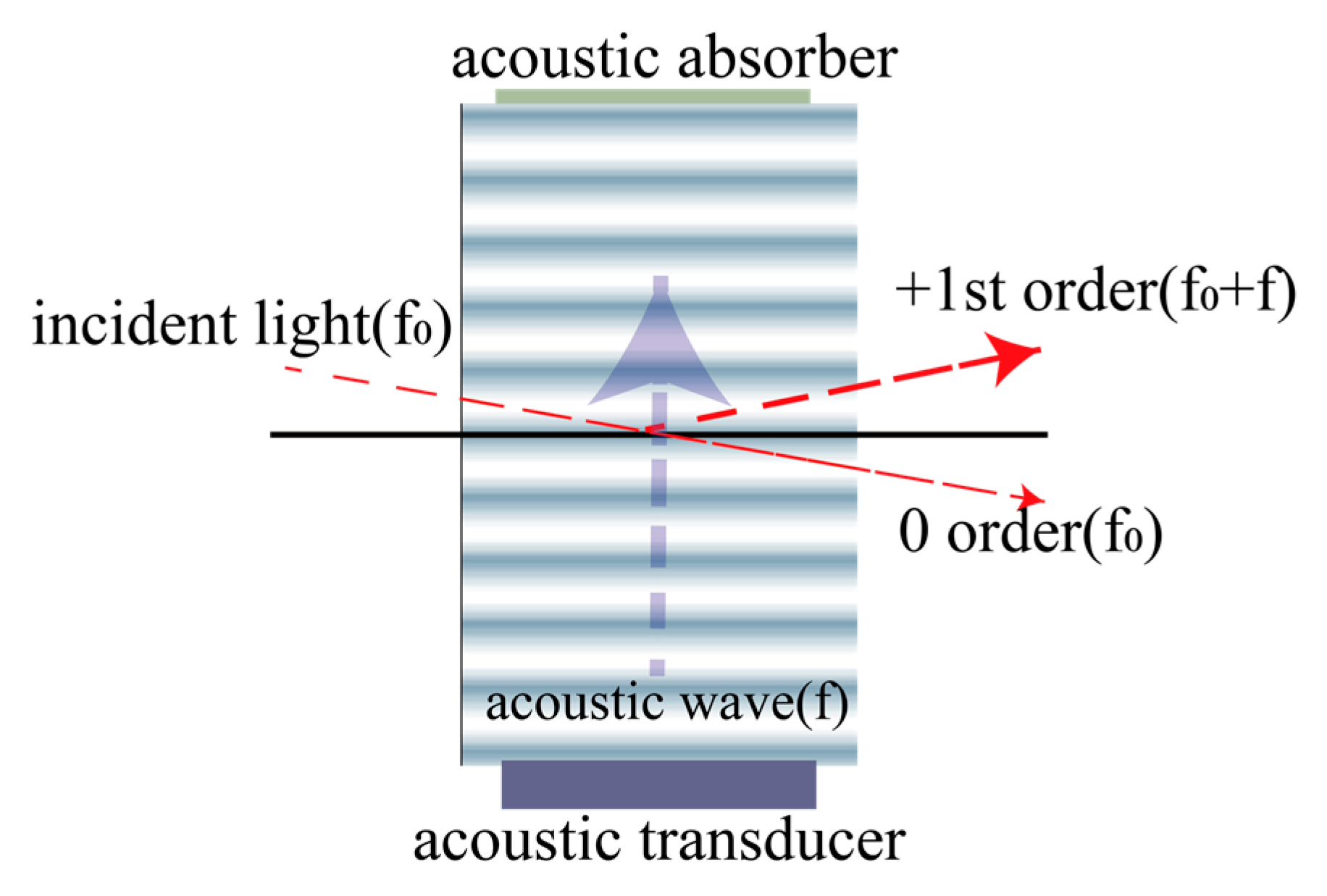
2. Theory and Simulation
3. Temperature Effect Verification Experiment
3.1. Heat Generation and Analysis
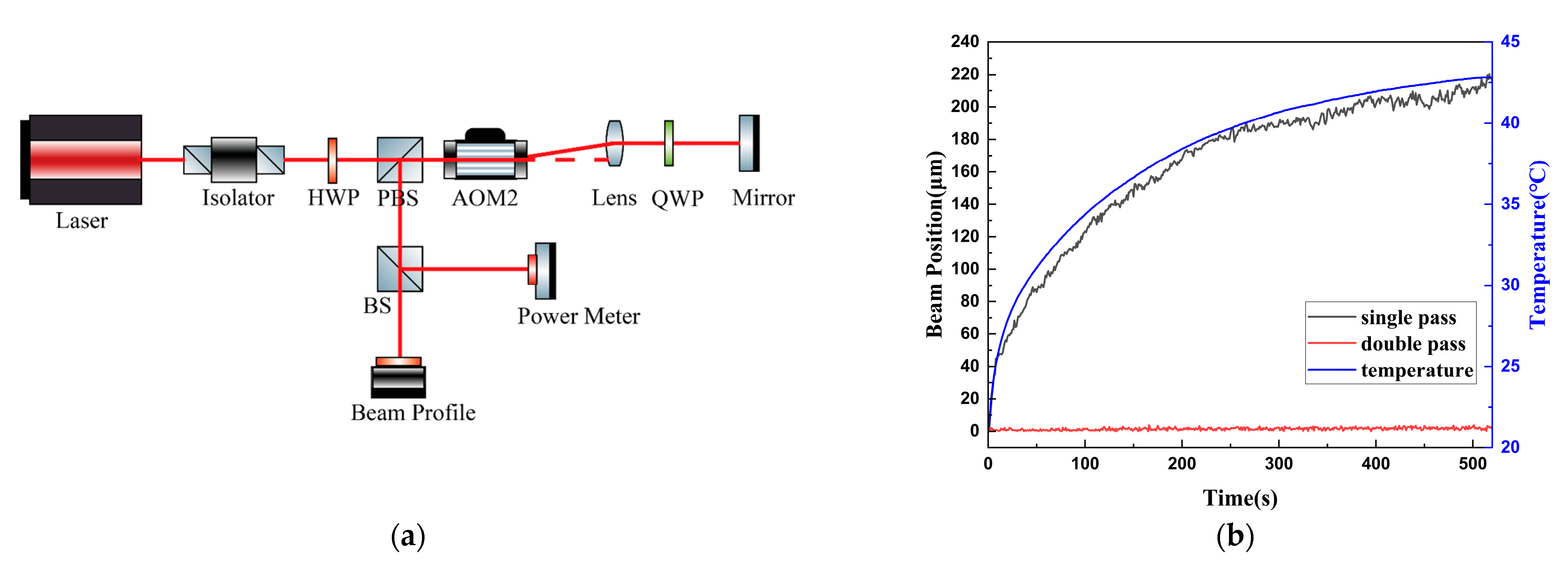
3.2. Diffraction Angle Shift for Single Pass
3.3. Diffraction Angle Shift for Double Pass
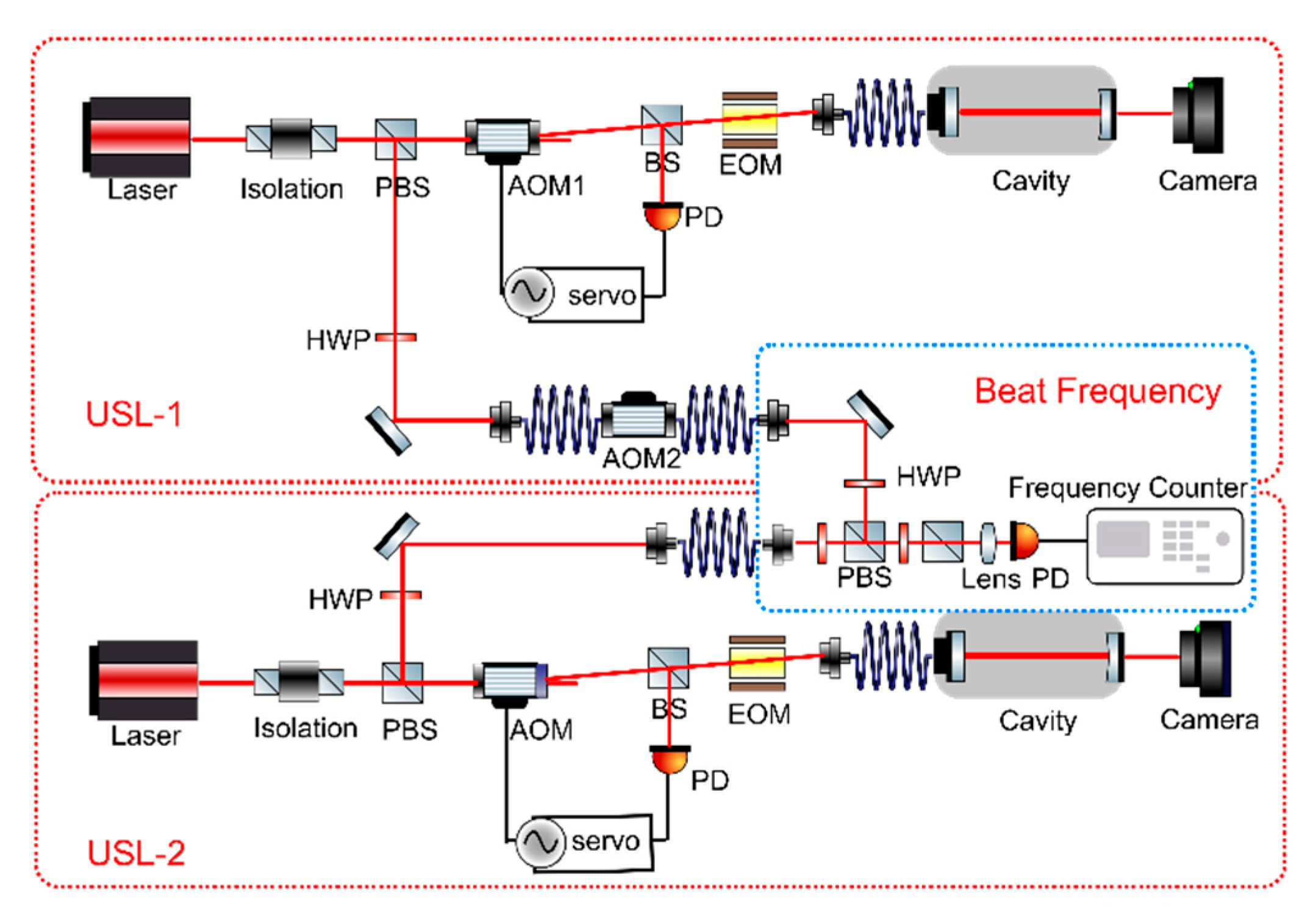
4. Influence and Analysis of AOM on Laser Frequency Stability
5. Discussion
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Zheng, X.; Dolde, J.; Lochab, V.; Merriman, B.N.; Li, H.; Kolkowitz, S. Differential Clock Comparisons with a Multiplexed Optical Lattice Clock. Nature 2022, 602, 425–430. [Google Scholar] [CrossRef]
- Kwee, P.; Bogan, C.; Danzmann, K.; Frede, M.; Kim, H.; King, P.; Pöld, J.; Puncken, O.; Savage, R.L.; Seifert, F.; et al. Stabilized High-Power Laser System for the Gravitational Wave Detector Advanced LIGO. Opt. Express 2012, 20, 10617. [Google Scholar] [CrossRef]
- Oelker, E.; Hutson, R.B.; Kennedy, C.J.; Sonderhouse, L.; Bothwell, T.; Goban, A.; Kedar, D.; Sanner, C.; Robinson, J.M.; Marti, G.E.; et al. Demonstration of 4.8 × 10−17 Stability at 1 s for Two Independent Optical Clocks. Nat. Photonics 2019, 13, 714–719. [Google Scholar] [CrossRef]
- Herbers, S.; Häfner, S.; Dörscher, S.; Lücke, T.; Sterr, U.; Lisdat, C. Transportable Clock Laser System with an Instability of 1.6 × 10−16. Opt. Lett. 2022, 47, 5441. [Google Scholar] [CrossRef] [PubMed]
- Bai, S.; Lu, Y.; Zhang, Z. Mode Field Switching in Narrow Linewidth Mode-Locked Fiber Laser. Chin. Opt. Lett. 2022, 20, 020602. [Google Scholar] [CrossRef]
- He, L.; Zhang, J.; Wang, Z.; Chang, J.; Wu, Q.; Lu, Z.; Zhang, J. Ultra-Stable Cryogenic Sapphire Cavity Laser with an Instability Reaching 2 × 10 −16 Based on a Low Vibration Level Cryostat. Opt. Lett. 2023, 48, 2519–2522. [Google Scholar] [CrossRef]
- Wang, G.; Li, Z.; Huang, J.; Duan, H.; Huang, X.; Liu, H.; Liu, Q.; Yang, S.; Tu, L.; Yeh, H.-C. Analysis and Suppression of Thermal Effect of an Ultra-Stable Laser Interferometer for Space-Based Gravitational Waves Detection. Chin. Opt. Lett. 2022, 20, 011203. [Google Scholar] [CrossRef]
- Chen, X.; Jiang, Y.; Li, B.; Yu, H.; Jiang, H.; Wang, T.; Yao, Y.; Ma, L. Laser Frequency Instability of 6 × 10−16 Using 10-Cm-Long Cavities on a Cubic Spacer. Chin. Opt. Lett. 2020, 18, 030201. [Google Scholar] [CrossRef]
- Yin, Z.; Li, F.; Sun, Y.; Zou, Y.; Wang, Y.; Yang, H.; Hu, P.; Fu, H.; Tan, J. High Synchronization Absolute Distance Measurement Using a Heterodyne and Superheterodyne Combined Interferometer. Chin. Opt. Lett. 2024, 22, 011204. [Google Scholar] [CrossRef]
- Balakshy, V.I.; Kuznetsov, Y.I. Acousto-Optic Stabilization of the Intensity of a Laser Beam. Tech. Phys. 2013, 58, 1812–1816. [Google Scholar] [CrossRef]
- Du, J.-J.; Li, W.-F.; Li, G.; Wang, J.-M.; Zhang, T.-C. Intensity Noise Suppression of Light Field by Optoelectronic Feedback. Opt. Int. J. Light. Electron. Opt. 2013, 124, 3443–3445. [Google Scholar] [CrossRef]
- Balakshy, V.I.; Kuznetsov, Y.I.; Mantsevich, S.N.; Polikarpova, N.V. Dynamic Processes in an Acousto-Optic Laser Beam Intensity Stabilization System. Opt. Laser Technol. 2014, 62, 89–94. [Google Scholar] [CrossRef]
- Liu, C.; Prado, C.A.G.; Tang, C.; Zhong, Z.; Zhao, T.; Zhai, Y. Pulsed Light Power Stabilization of a Semiconductor Laser Using a Mixed Analog-Digital Method with an Acousto-Optic Modulator. Appl. Opt. 2022, 61, 1133. [Google Scholar] [CrossRef] [PubMed]
- Junker, J.; Oppermann, P.; Willke, B. Shot-Noise-Limited Laser Power Stabilization for the AEI 10 m Prototype Interferometer. Opt. Lett. 2017, 42, 755. [Google Scholar] [CrossRef] [PubMed]
- Tricot, F.; Phung, D.H.; Lours, M.; Guérandel, S.; De Clercq, E. Power Stabilization of a Diode Laser with an Acousto-Optic Modulator. Rev. Sci. Instrum. 2018, 89, 113112. [Google Scholar] [CrossRef]
- Ma, L.-S.; Jungner, P.; Ye, J.; Hall, J.L. Delivering the Same Optical Frequency at Two Places: Accurate Cancellation of Phase Noise Introduced by an Optical Fiber or Other Time-Varying Path. Opt. Lett. 1994, 19, 1777. [Google Scholar] [CrossRef]
- Jürss, T.; Grosche, G.; Koke, S. Free-Space Interferometer Design for Optical Frequency Dissemination and out-of-Loop Characterization below the 10−21 -Level. Photonics Res. 2023, 11, 1113. [Google Scholar] [CrossRef]
- Esquivel-Ramírez, E.; Uhthoff-Rodríguez, L.; Alonso-Torres, E.G.; Hernández-López, A.; Gardea-Flores, C.; Paris-Mandoki, A. High-Precision Frequency-Controlled Optical Phase Shifter with Acousto Optic Devices. Opt. Lett. 2024, 49, 2525. [Google Scholar] [CrossRef] [PubMed]
- Zeng, Y.; Fu, Z.; Liu, Y.-Y.; He, X.-D.; Liu, M.; Xu, P.; Sun, X.-H.; Wang, J. Stabilizing a Laser Frequency by the Pound–Drever–Hall Technique with an Acousto-Optic Modulator. Appl. Opt. 2021, 60, 1159. [Google Scholar] [CrossRef]
- Ludlow, A.D.; Boyd, M.M.; Ye, J.; Peik, E.; Schmidt, P.O. Optical Atomic Clocks. Rev. Mod. Phys. 2015, 87, 637–701. [Google Scholar] [CrossRef]
- Lü, T.; Duan, Y.; Xiang, J.; Ren, W.; Lü, D.; Wang, B.; Li, L.; Li, T.; Qu, Q. Temperature Characteristics of 780 nm Acousto-Optic Modulator. Acta Opt. Sin. 2017, 37, 0812001. [Google Scholar] [CrossRef]
- Zhang, X.; Chen, Y.; Fang, J.; Wang, T.; Li, J.; Luo, L. Beam Pointing Stabilization of an Acousto-Optic Modulator with Thermal Control. Opt. Express 2019, 27, 11503. [Google Scholar] [CrossRef] [PubMed]
- Varlamov, A.V.; Agrusov, P.M.; Il’ichev, I.V.; Lebedev, V.V.; Shamrai, A.V.; Stepanov, S.I. Temperature Dependence of Acousto-Optic Polarization Mode Conversion Peak Frequency and Efficiency. In Proceedings of the International Youth Conference on Electronics, Telecommunications and Information Technologies, Petersburg, Russia, 22–23 April 2021; Velichko, E., Vinnichenko, M., Kapralova, V., Koucheryavy, Y., Eds.; Springer International Publishing: Berlin/Heidelberg, Germany, 2021; pp. 299–305. [Google Scholar]
- Nikitin, P.A.; Gerasimov, V.V.; Khasanov, I.S. Temperature Effects in an Acousto-Optic Modulator of Terahertz Radiation Based on Liquefied SF6 Gas. Materials 2021, 14, 5519. [Google Scholar] [CrossRef]
- Dickmann, J.; Neto, L.S.; Gaedtke, M.; Kroker, S. Levitating the Noise Performance of Ultra-Stable Laser Cavities Assisted by a Deep Neural Network: The Non-Intuitive Role of the Mirrors. Opt. Express 2023, 31, 15953–15965. [Google Scholar] [CrossRef]
- Ji, W.-C.; Wang, B.-W.; Hu, Y.; Cui, X.-Y.; Xu, P.; Jiang, X.; Dai, H.-N.; Chen, Y.-A. Characterization of the Pound-Drever-Hall Feedback Loop in an Ultra-Stable Laser System. In Proceedings of the CLEO, Charlotte, NC, USA, 5–10 May 2024; Optica Publishing Group: Washington, DC, USA, 2024; p. JTu2A.21. [Google Scholar]
- Liu, J. Photonic Devices; Cambridge University Press: Cambridge, UK, 2005. [Google Scholar]
- Antonov, S.N. Acousto-Optic Deflector with Heat Removal from the Piezotransducer by Sound Insulation of a Heat Radiator. Acoust. Phys. 2019, 65, 487–494. [Google Scholar] [CrossRef]
- Uchida, N. Optical Properties of Single-Crystal Paratellurite (TeO2). Phys. Rev. B 1971, 4, 3736–3745. [Google Scholar] [CrossRef]
- Thomas, P.A. The Crystal Structure and Absolute Optical Chirality of Paratellurite, α-TeO2. J. Phys. C Solid State Phys. 1988, 21, 4611–4627. [Google Scholar] [CrossRef]
- Li, Y.; Fan, W.; Sun, H.; Cheng, X.; Li, P.; Zhao, X. Structural, Electronic, and Optical Properties of α, β, and γ-TeO2. J. Appl. Phys. 2010, 107, 093506. [Google Scholar] [CrossRef]
- Azrakov, I.V.; Zavarin, S.V.; Nikishin, E.L. The Theoretical and Experimental Research of Diffraction Efficiency Acousto-Optic Bragg Cells Employing Traveling Wave Phase Array Transducers. In Proceedings of the 2014 International Conference on Actual Problems of Electron Devices Engineering (APEDE), Saratov, Russia, 25–26 September 2014; Volume 1, pp. 243–248. [Google Scholar]
- Ahmad, K.A.; Mohammed, F.M. Calculation of Acousto-Optic Figure of Merit for Some of Oxide Crystals. Int. J. Opt. Appl. 2016, 6, 1–6. [Google Scholar]
- Meng, F.; Li, Z.; Li, J.; Meng, L.; Yin, X.; Bian, W.; Jia, J.; Wang, J. An Active Method for Coupling Laser with a High-Finesse Fabry–Pérot Cavity in Ultra-Stable Lasers. Opt. Laser Technol. 2024, 171, 110371. [Google Scholar] [CrossRef]
- Degallaix, J. OSCAR: A MATLAB Based Package to Simulate Realistic Optical Cavities. SoftwareX 2020, 12, 100587. [Google Scholar] [CrossRef]
- Jiang, Y.Y.; Ludlow, A.D.; Lemke, N.D.; Fox, R.W.; Sherman, J.A.; Ma, L.-S.; Oates, C.W. Making Optical Atomic Clocks More Stable with 10−16-Level Laser Stabilization. Nat. Photonics 2011, 5, 158–161. [Google Scholar] [CrossRef]
- Donley, E.A.; Heavner, T.P.; Levi, F.; Tataw, M.O.; Jefferts, S.R. Double-Pass Acousto-Optic Modulator System. Rev. Sci. Instrum. 2005, 76, 063112. [Google Scholar] [CrossRef]








| Parameters | Values |
|---|---|
| Cavity length | 100 mm |
| Mirror 1 radius of curvature | Infinite |
| Mirror 2 radius of curvature | 1000 mm |
| Waist radius | 0.321 mm |
| Free spectral range (FSR) | 1.5 GHz |
| Transmission | 0.01%/0.05% |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhao, P.; Meng, F.; Xiong, J.; Jia, J.; Meng, L.; Qi, H. Thermal Analysis of Acousto-Optic Modulators and Its Influence on Ultra-Stable Lasers. Photonics 2024, 11, 1077. https://doi.org/10.3390/photonics11111077
Zhao P, Meng F, Xiong J, Jia J, Meng L, Qi H. Thermal Analysis of Acousto-Optic Modulators and Its Influence on Ultra-Stable Lasers. Photonics. 2024; 11(11):1077. https://doi.org/10.3390/photonics11111077
Chicago/Turabian StyleZhao, Pengyang, Fanchao Meng, Junyang Xiong, Jianjun Jia, Lingqiang Meng, and Hongxing Qi. 2024. "Thermal Analysis of Acousto-Optic Modulators and Its Influence on Ultra-Stable Lasers" Photonics 11, no. 11: 1077. https://doi.org/10.3390/photonics11111077
APA StyleZhao, P., Meng, F., Xiong, J., Jia, J., Meng, L., & Qi, H. (2024). Thermal Analysis of Acousto-Optic Modulators and Its Influence on Ultra-Stable Lasers. Photonics, 11(11), 1077. https://doi.org/10.3390/photonics11111077





