Influence of Optical Fiber Parameters on the Speckle Pattern and Spectral Observation in Astronomy
Abstract
1. Introduction
2. Mode Noise in the Fiber Spectrum
2.1. Formation of the Modal Noise in FASOT Fiber
2.2. Simulation of the FASOT-Fiber Speckle and Spectrum
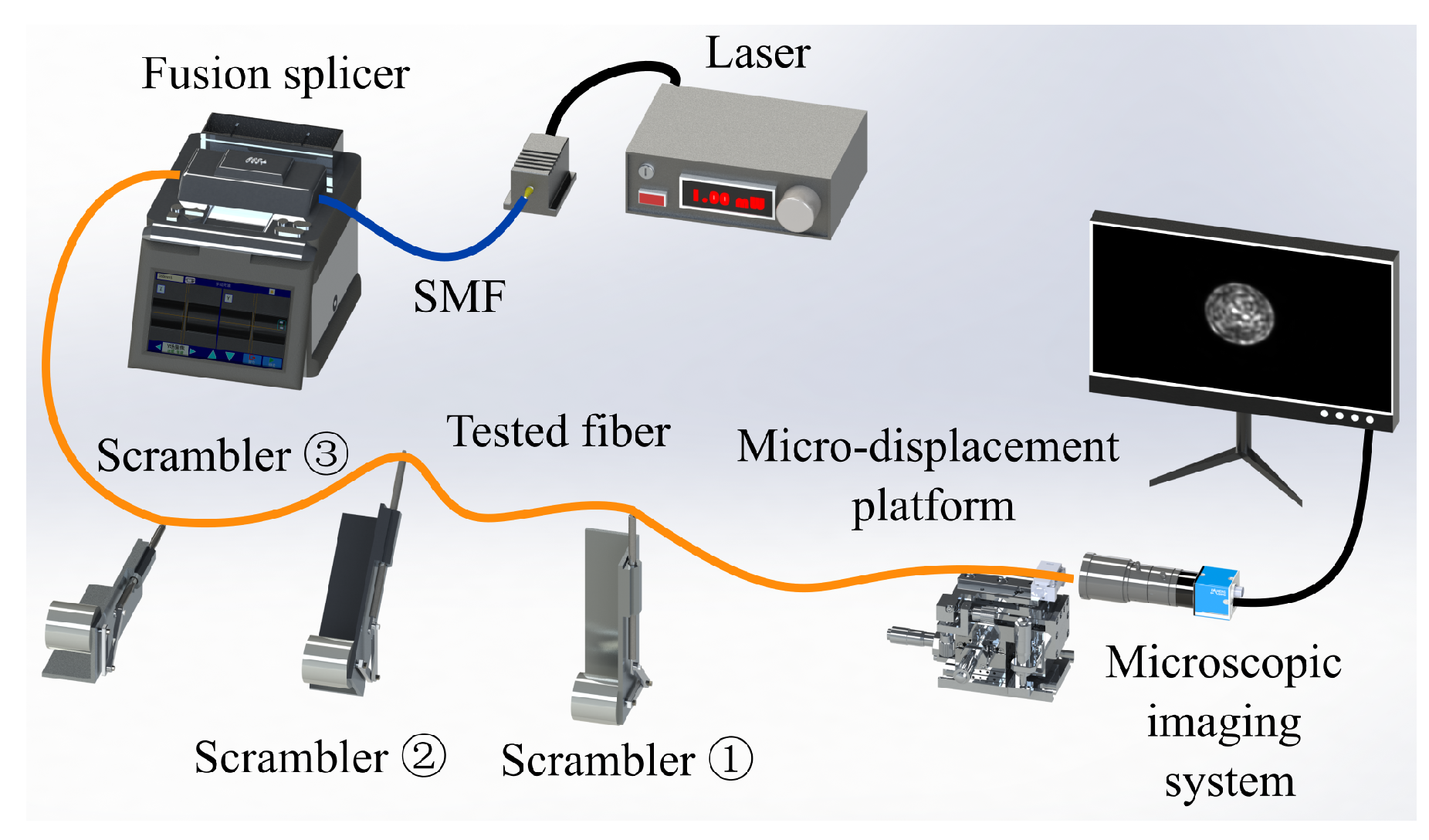
3. Experiments and Results
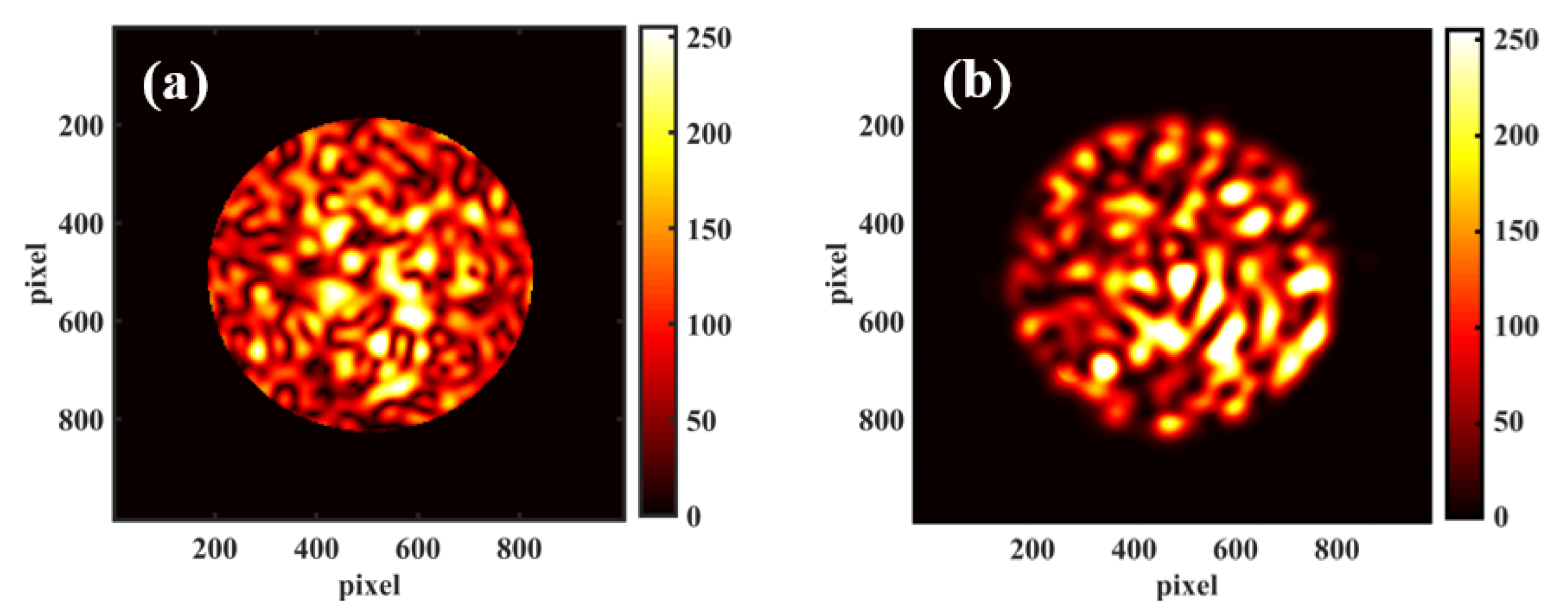
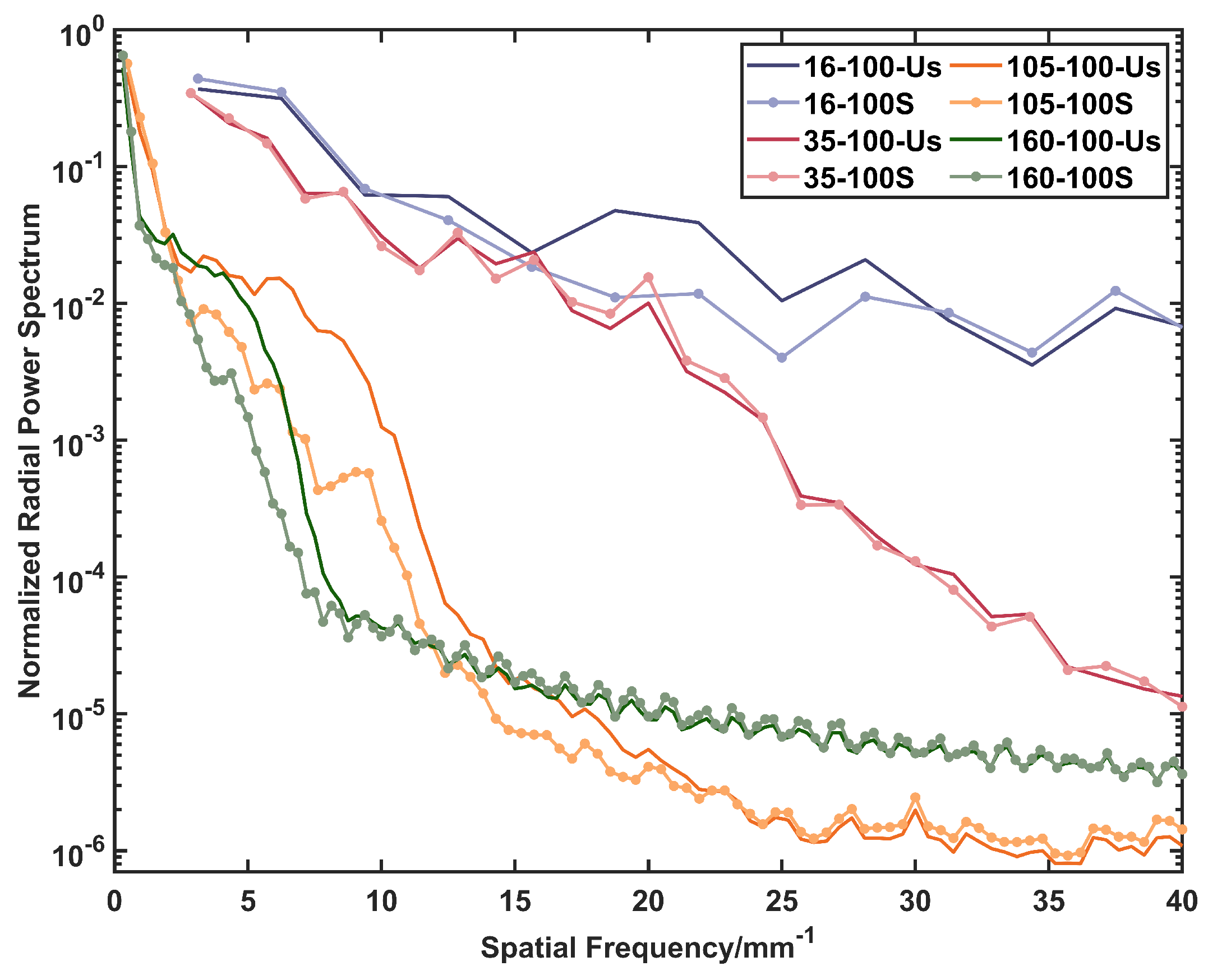
3.1. Fiber Speckle Test
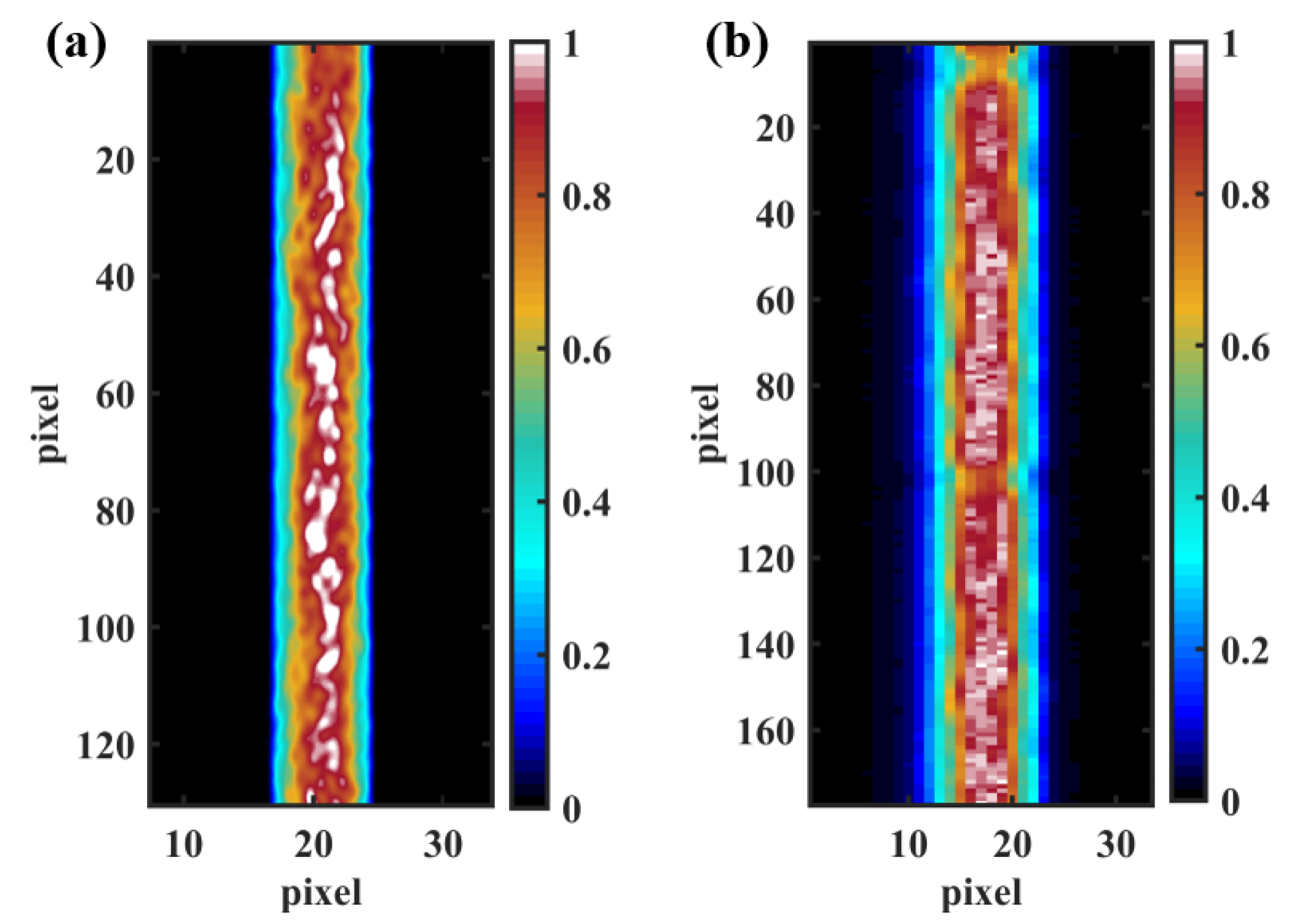
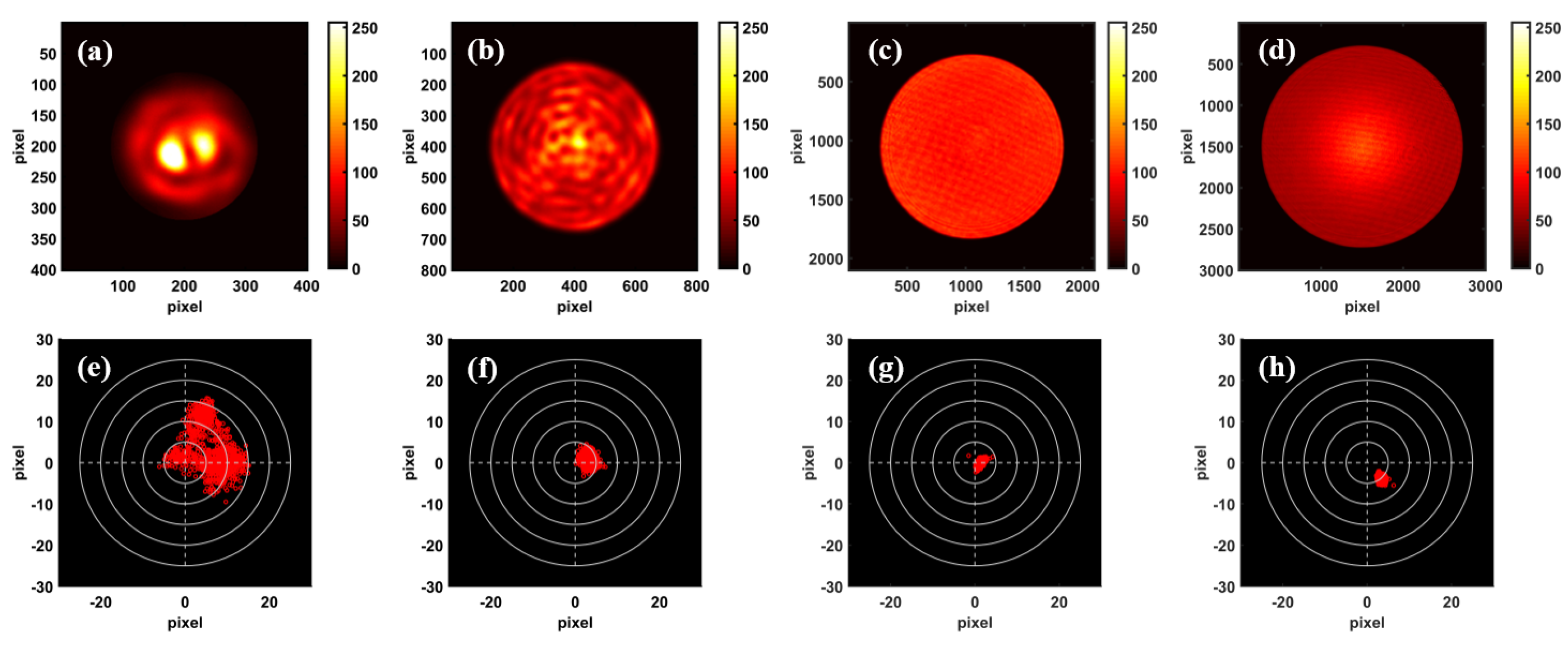
3.2. Fiber Focal Ratio Degradation Test
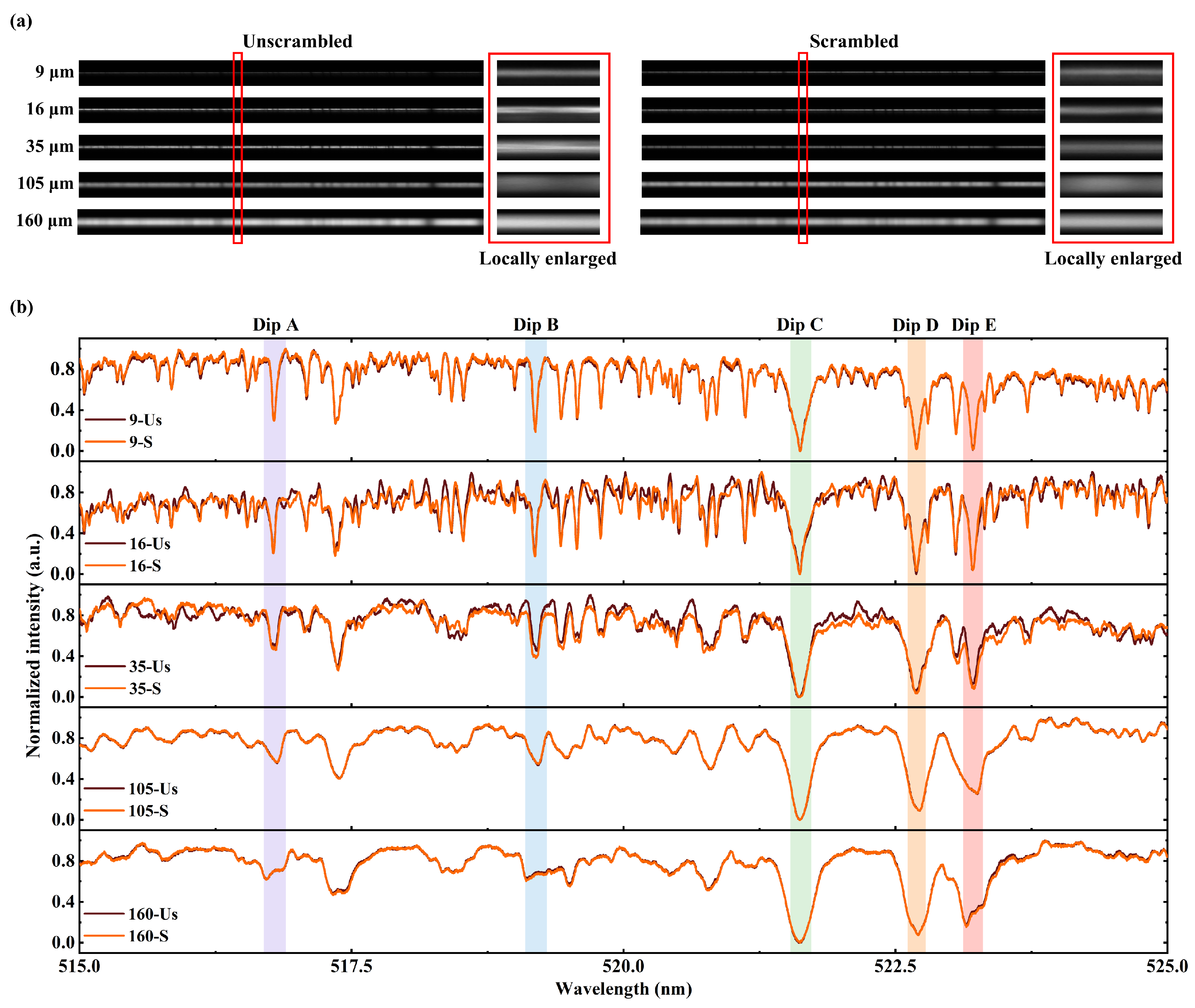
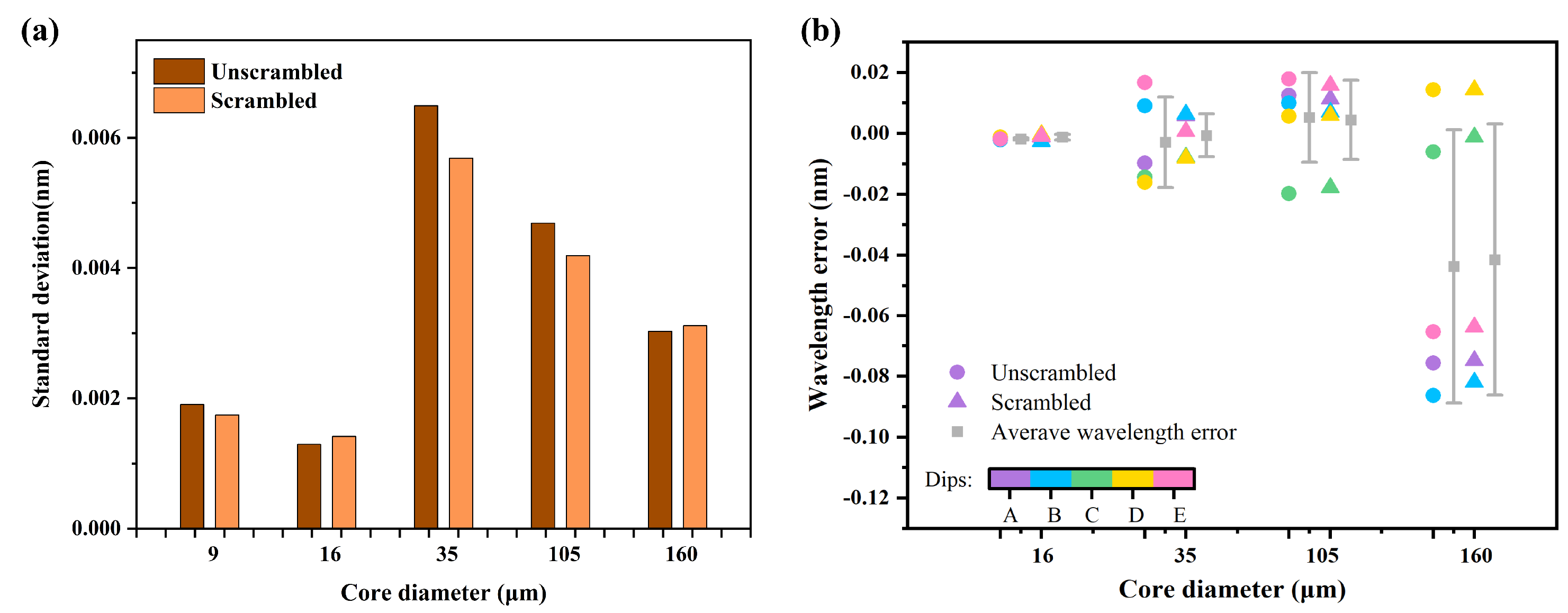
3.3. Solar Spectrum Observation
4. Discussion
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Fang, H.; Xie, Y.; Yuan, Z.; Cai, D.; Zhang, J.; Guo, X.; Tong, L. Parallel fabrication of silica optical microfibers and nanofibers. Light. Adv. Manuf. 2024, 5, 20. [Google Scholar] [CrossRef]
- Kronig, L.; Caseiro, S.; Hug, M.; Charif, M.; Bouri, M.; Kneib, J.P. An easily scalable Theta/Phi fiber positioner to reduce risks, lead times and costs for Multi-Object Spectrographs. Adv. Opt. Mech. Technol. Telesc. Instrum. IV 2020, 11451, 1145125. [Google Scholar] [CrossRef]
- Yan, H.; Li, H.; Wang, S.; Zong, W.; Yuan, H.; Xiang, M.; Huang, Y.; Xie, J.; Dong, S.; Yuan, H.; et al. Overview of the LAMOST survey in the first decade. Innovation 2022, 3, 100224. [Google Scholar] [CrossRef] [PubMed]
- Hahn, C.; Wilson, M.J.; Ruiz-Macias, O.; Cole, S.; Weinberg, D.H.; Moustakas, J.; Kremin, A.; Tinker, J.L.; Smith, A.; Wechsler, R.H.; et al. The DESI Bright Galaxy Survey: Final Target Selection, Design, and Validation. Astron. J. 2023, 165, 253. [Google Scholar] [CrossRef]
- Jaeggli, S.A.; Lin, H.; Onaka, P.; Yamada, H.; Anan, T.; Bonnet, M.; Ching, G.; Huang, X.P.; Kramar, M.; McGregor, H.; et al. The Diffraction-Limited Near-Infrared Spectropolarimeter (DL-NIRSP) of the Daniel K. Inouye Solar Telescope (DKIST). Sol. Phys. 2022, 297, 137. [Google Scholar] [CrossRef]
- Sun, W.; Chen, X.; Yan, Q.; Geng, T.; Yan, Y.; Wang, S.; Wang, A.; Wang, J.; Jin, X.; Jiang, H.; et al. Fiber Integral Field Unit System for Measurement of Solar Spectrum. Spectrosc. Spectr. Anal. 2023, 43, 1168–1174. [Google Scholar] [CrossRef]
- Lee, B.C.; Do, H.; Park, M.; Lim, B.; Choi, Y.; Koo, J.; Bang, T.; Oh, H.; Han, I.; Chang, H. The detection of substellar companions around HD 6860 and HD 112300. Astron. Astrophys. 2023, 678, A106. [Google Scholar] [CrossRef]
- McConnachie, A.W.; Hayes, C.R.; Robertson, J.G.; Pazder, J.; Ireland, M.; Burley, G.; Churilov, V.; Lothrop, J.; Zhelem, R.; Kalari, V.; et al. The Science Performance of the Gemini High Resolution Optical Spectrograph. Publ. Astron. Soc. Pac. 2024, 136, 035001. [Google Scholar] [CrossRef]
- Qu, Z.Q. A Fiber Arrayed Solar Optical Telescope (FASOT). In Proceedings of the 6th Solar Polarization Workshop, Maui, HI, USA, 30 May–4 June 2010; Astronomical Society of the Pacific Conference Series. Astronomical Society of the Pacific: San Francisco, CA, USA, 2011; Volume 437, pp. 423–432. [Google Scholar]
- Bechter, A.; Crass, J.; Ketterer, R.; Crepp, J.R.; Reynolds, R.O.; Bechter, E.; Hinz, P.; Pedichini, F.; Foley, M.; Runburg, E.; et al. On-sky single-mode fiber coupling measurements at the Large Binocular Telescope. In Proceedings of the Adaptive Optics Systems V, Edinburgh, Scotland, 26 June–1 July 2016; Marchetti, E., Close, L.M., Véran, J.P., Eds.; Society of Photo-Optical Instrumentation Engineers (SPIE) Conference Series. SPIE: Bellingham, WA, USA, 2016; Volume 9909, p. 99092X. [Google Scholar] [CrossRef]
- Delorme, J.R.; Jovanovic, N.; Echeverri, D.; Mawet, D.; Wallace, J.K.; Bartos, R.D.; Cetre, S.; Wizinowich, P.; Ragland, S.; Lilley, S.; et al. Keck Planet Imager and Characterizer: A dedicated single-mode fiber injection unit for high-resolution exoplanet spectroscopy. J. Astron. Telesc. Instruments Syst. 2021, 7, 035006. [Google Scholar] [CrossRef]
- Wang, T.; Li, Y.; Xu, B.; Mao, B.; Qiu, Y.; Meng, Y. High-resolution wavemeter based on polarization modulation of fiber speckles. APL Photonics 2020, 5, 126101. [Google Scholar] [CrossRef]
- Takahara, H. Visibility of speckle patterns: Effect of the optical guide length in coherent light. Appl. Opt. 1976, 15, 610. [Google Scholar] [CrossRef] [PubMed]
- Baudrand, J.; Walker, G.A.H. Modal noise in high-resolution, fiber-fed spectra: A study and simple cure. Publ. Astron. Soc. Pac. 2001, 113, 851–858. [Google Scholar] [CrossRef]
- Lemke, U.; Corbett, J.; Allington-Smith, J.; Murray, G. Modal noise prediction in fibre spectroscopy—I. Visibility and the coherent model. Mon. Not. R. Astron. Soc. 2011, 417, 689–697. [Google Scholar] [CrossRef]
- Oliva, E.; Rainer, M.; Tozzi, A.; Sanna, N.; Iuzzolino, M.; Brucalassi, A. Experimental characterization of modal noise in multimode fibers for astronomical spectrometers. Astron. Astrophys. 2019, 632, A21. [Google Scholar] [CrossRef]
- Yan, Y.; Yan, Q.; Wang, G.; Sun, W.; Luo, A.; Ma, Z.; Zhang, Q.; Li, J.; Wang, S. DEEM, a versatile platform of FRD measurement for highly multiplexed fibre systems in astronomy. Mon. Not. R. Astron. Soc. 2018, 476, 4279–4314. [Google Scholar] [CrossRef]
- Kim, J.; Miller, D.T.; Kim, E.; Oh, S.; Oh, J.; Milner, T.E. Optical coherence tomography speckle reduction by a partially spatially coherent source. J. Biomed. Opt. 2005, 10, 064034. [Google Scholar] [CrossRef]
- Redding, B.; Cao, H. Using a multimode fiber as a high-resolution, low-loss spectrometer. Opt. Lett. 2012, 37, 3384–3386. [Google Scholar] [CrossRef]
- Zhou, W.; Liu, Z.; Sun, Y.; Teng, H.; Wang, W.; Bayanheshig; Li, W. Bidirectional Littrow double grating interferometry for quadruple optical interpolation. Opt. Laser Technol. 2024, 175, 110751. [Google Scholar] [CrossRef]
- Zhang, J.; Jirigalantu; Yu, S.; Wang, Y.; Yu, H.; Li, W. Research on manufacturing technology of nanoimprinted grating. J. Manuf. Process. 2024, 131, 891–909. [Google Scholar] [CrossRef]
- Petersburg, R.R.; McCracken, T.M.; Eggerman, D.; Jurgenson, C.A.; Sawyer, D.; Szymkowiak, A.E.; Fischer, D.A. Modal Noise Mitigation through Fiber Agitation for Fiber-fed Radial Velocity Spectrographs. Astrophys. J. 2018, 853, 181. [Google Scholar] [CrossRef]
- Sirk, M.M.; Wishnow, E.H.; Weisfeiler, M.; Jhoti, E.; Curtis, J.; Ishikawa, Y.; Finstad, D.; O’Hanlon, T.; Gibson, S.R.; Edelstein, J.; et al. An Optical Fiber Double Scrambler and Mechanical Agitator System for the Keck Planet Finder Spectrograph. In Proceedings of the Conference on Ground-Based and Airborne Instrumentation for Astronomy VII, Austin, TX, USA, 10–15 June 2018; Proceedings of SPIE. SPIE: Bellingham, WA, USA, 2018; Volume 10702, p. 107026. [Google Scholar] [CrossRef]
- Sablowski, D.P.; Plüschke, D.; Weber, M.; Strassmeier, K.G.; Järvinen, A. Comparing modal noise and FRD of circular and non-circular cross-section fibres. Astron. Nachrichten 2016, 337, 216–225. [Google Scholar] [CrossRef]
- Plavchan, P.P.; Bottom, M.; Gao, P.; Wallace, J.K.; Mennesson, B.; Ciardi, D.; Crawford, S.; Lin, S.; Beichman, C.; Brinkworth, C.; et al. Precision near-infrared radial velocity instrumentation II: Non-Circular Core Fiber Scrambler. Tech. Instrum. Detect. Exopl. VI 2013, 8864, 88640g. [Google Scholar] [CrossRef]
- Wang, Y.; Zhong, L.; Lau, K.Y.; Han, X.; Yang, Y.; Hu, J.; Firstov, S.; Chen, Z.; Ma, Z.; Tong, L.; et al. Precise mode control of laser-written waveguides for broadband, low-dispersion 3D integrated optics. Light. Sci. Appl. 2024, 13, 130. [Google Scholar] [CrossRef]
- Ishizuka, M.; Kotani, T.; Nishikawa, J.; Kurokawa, T.; Mori, T.; Kokubo, T.; Tamura, M. Fiber Mode Scrambler for the Subaru Infrared Doppler Instrument (IRD). Publ. Astron. Soc. Pac. 2018, 130, 065003. [Google Scholar] [CrossRef]
- Raskin, G.; Pember, J.; Rogozin, D.; Schwab, C.; Coutts, D. Fiber modal noise mitigation by a rotating double scrambler. In Proceedings of the Conference on Advances in Optical and Mechanical Technologies for Telescopes and Instrumentation IV, Online, 14–18 December 2020; Society of Photo-Optical Instrumentation Engineers (SPIE) Conference Series. SPIE: Bellingham, WA, USA, 2020; Volume 11451, p. 114516F. [Google Scholar] [CrossRef]
- Norris, B.; Betters, C.; Wei, J.; Yerolatsitis, S.; Amezcua-correa, R.; Leon-saval, S. Optimal broadband starlight injection into a single-mode fibre with integrated photonic wavefront sensing. Opt. Express 2022, 30, 34908–34917. [Google Scholar] [CrossRef] [PubMed]
- Wang, A.; Wang, J.; Yang, X.; Wang, S.; Yan, Y.; Yan, Q.; Lu, C.; Li, S.; Geng, T.; Sun, W.; et al. A Fast and High-precision Alignment Method for IFU Based on Optical Interferometry and Fresnel Diffraction. Publ. Astron. Soc. Pac. 2022, 134, 104503. [Google Scholar] [CrossRef]
- Hernandez, E.; Roth, M.M.; Petermann, K.; Kelz, A.; Moralejo, B.; Madhav, K. Mode expansion theory and application in step-index multimode fibers for astronomical spectroscopy. J. Opt. Soc. Am. B Opt. Phys. 2021, 38, A36–A50. [Google Scholar] [CrossRef]
- Shi, B.; Zhang, C.; Kelly, T.; Wei, X.; Ding, M.; Huang, M.; Fu, S.; Poletti, F.; Radan, S. Splicing Hollow-Core Fiber with Standard Glass-Core Fiber with Ultralow Back-Reflection and Low Coupling Loss. ACS Photonics 2024, 11, 3288–3295. [Google Scholar] [CrossRef]
- Lemke, U.; Corbett, J.; Allington-Smith, J.; Murray, G. Characterising modal noise in fibre-coupled spectrographs for astronomy. In Proceedings of the Modern Technologies in Space- and Ground-Based Telescopes and Instrumentation, Amsterdam, The Netherlands, 1–6 July 2012; Society of Photo-Optical Instrumentation Engineers (SPIE) Conference Series. SPIE: Bellingham, WA, USA, 2010; Volume 7739, p. 773924. [Google Scholar] [CrossRef]






| Astronomical Project | Diameter of Fibers | Numerical Aperture |
|---|---|---|
| MEGERA [2] | 100 µm | 0.2 ± 0.02 |
| LAMOST [3] | 320 µm | 0.22 |
| DESI [4] | 107 µm | 0.22 |
| BiFOIS [5] | 29 × 5 µm (Rectangular core) | 0.25 |
| BOES [7] | 100 µm | 0.2 ± 0.02 |
| GHOST [8] | 53 µm | 0.2 ± 0.02 |
| FASOT [9] | 35 µm | 0.12 |
| LBT [10] | 5.8 µm | 0.14 ± 0.01 |
| KPIC [11] | 6.5 µm | 0.2 ± 0.02 |
| No. | Core Diameter (µm) | Cladding Diameter (µm) | Coating Diameter (µm) | N.A. | Length (m) |
|---|---|---|---|---|---|
| 1 | 16 | 125 | 245 | 0.12 | 5 |
| 2 | 35 | 110 | 125 | 0.12 | 5 |
| 3 | 105 | 125 | 190 | 0.22 | 5 |
| 4 | 160 | 175 | 300 | 0.22 | 5 |
| Core Diameter | 16 µm | 35 µm | 105 µm | 160 µm |
|---|---|---|---|---|
| Unscrambled | 3.34 | 4.76 | 3.65 | 4.27 |
| Scrambled | 3.28 | 4.66 | 3.62 | 4.23 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, A.; Wang, J.; Gan, Z.; Yue, G.; Chen, X.; Yan, Q.; Wang, S.; Yan, Y.; Geng, T.; Chen, S.; et al. Influence of Optical Fiber Parameters on the Speckle Pattern and Spectral Observation in Astronomy. Photonics 2024, 11, 1056. https://doi.org/10.3390/photonics11111056
Wang A, Wang J, Gan Z, Yue G, Chen X, Yan Q, Wang S, Yan Y, Geng T, Chen S, et al. Influence of Optical Fiber Parameters on the Speckle Pattern and Spectral Observation in Astronomy. Photonics. 2024; 11(11):1056. https://doi.org/10.3390/photonics11111056
Chicago/Turabian StyleWang, Anzhi, Jiabin Wang, Zhaoxv Gan, Gang Yue, Xvdong Chen, Qi Yan, Shengjia Wang, Yunxiang Yan, Tao Geng, Shuang Chen, and et al. 2024. "Influence of Optical Fiber Parameters on the Speckle Pattern and Spectral Observation in Astronomy" Photonics 11, no. 11: 1056. https://doi.org/10.3390/photonics11111056
APA StyleWang, A., Wang, J., Gan, Z., Yue, G., Chen, X., Yan, Q., Wang, S., Yan, Y., Geng, T., Chen, S., & Sun, W. (2024). Influence of Optical Fiber Parameters on the Speckle Pattern and Spectral Observation in Astronomy. Photonics, 11(11), 1056. https://doi.org/10.3390/photonics11111056






