High-Extinction Photonic Filters by Cascaded Mach–Zehnder Interferometer-Coupled Resonators
Abstract
1. Introduction
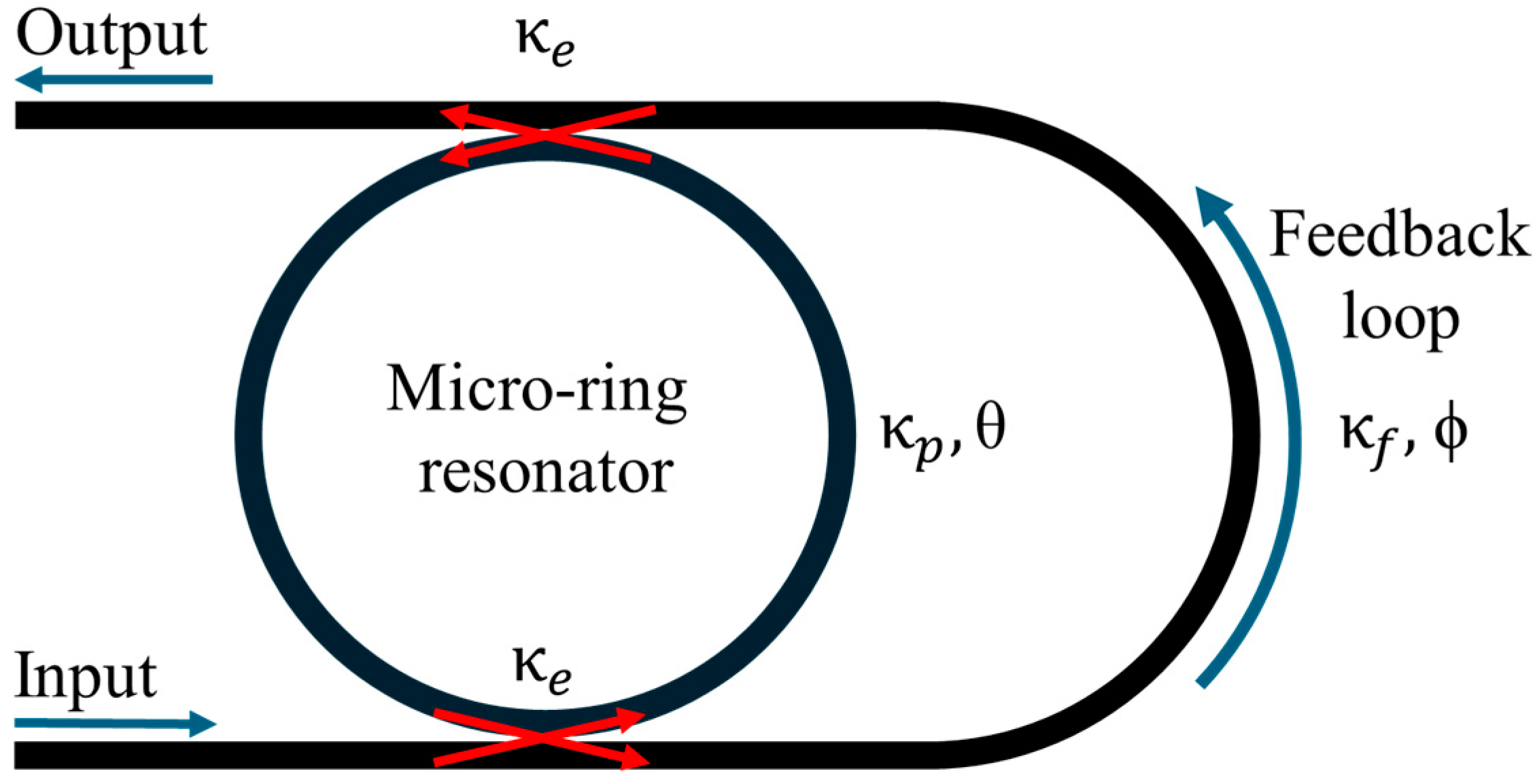
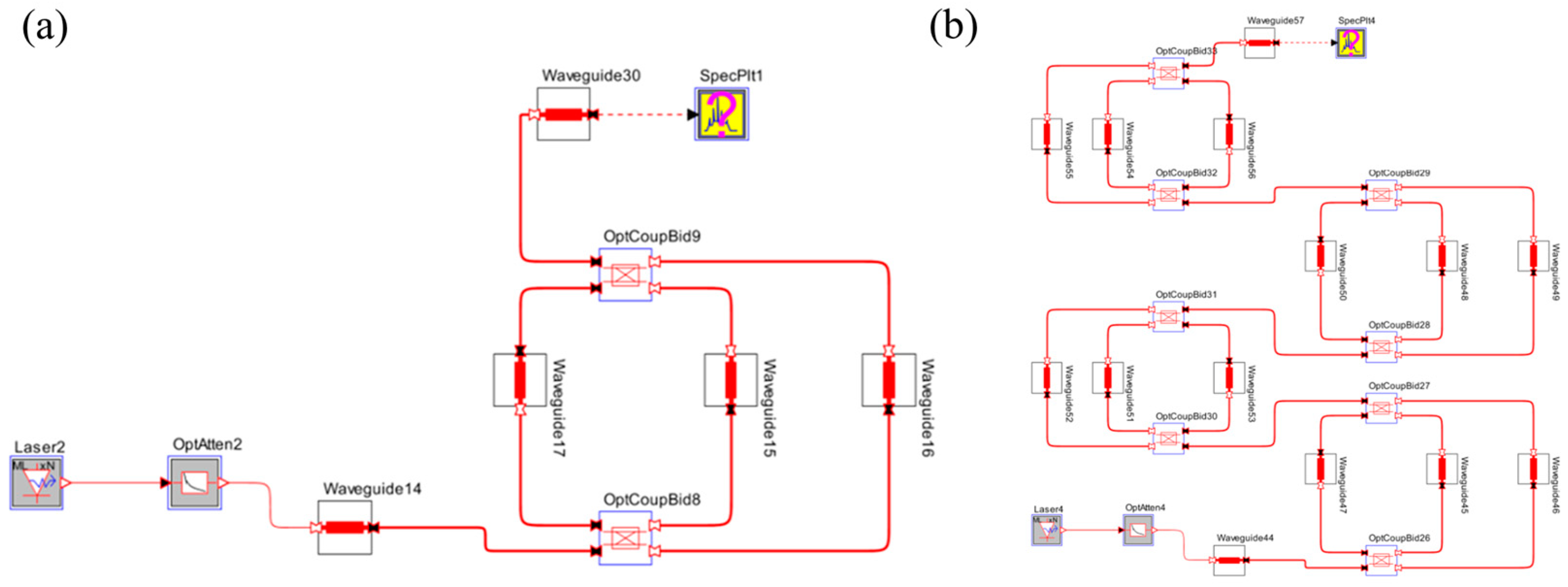
2. Simulation of the Cascaded MZI-Coupled Resonators
3. Fabrication Processes
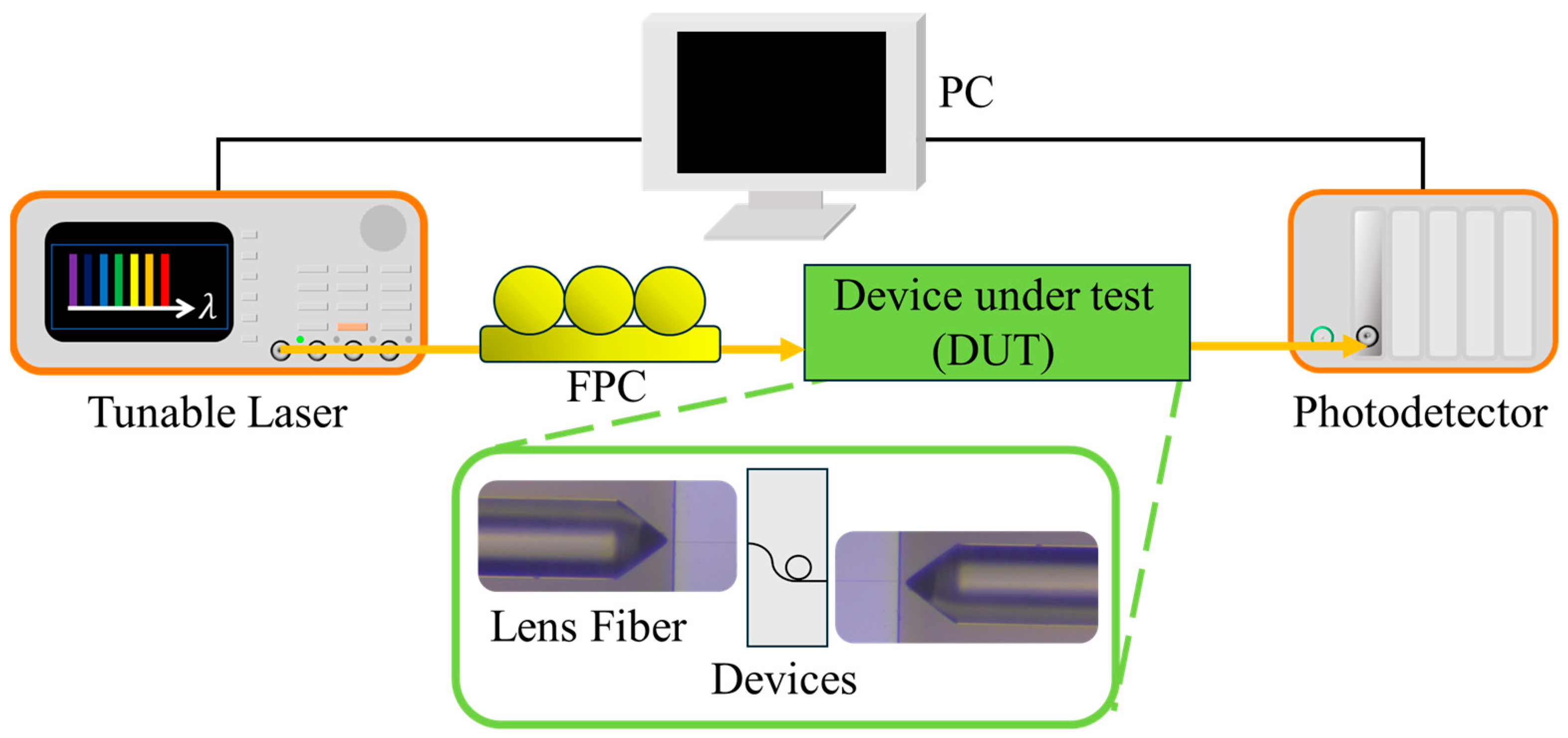
4. Experimental Results
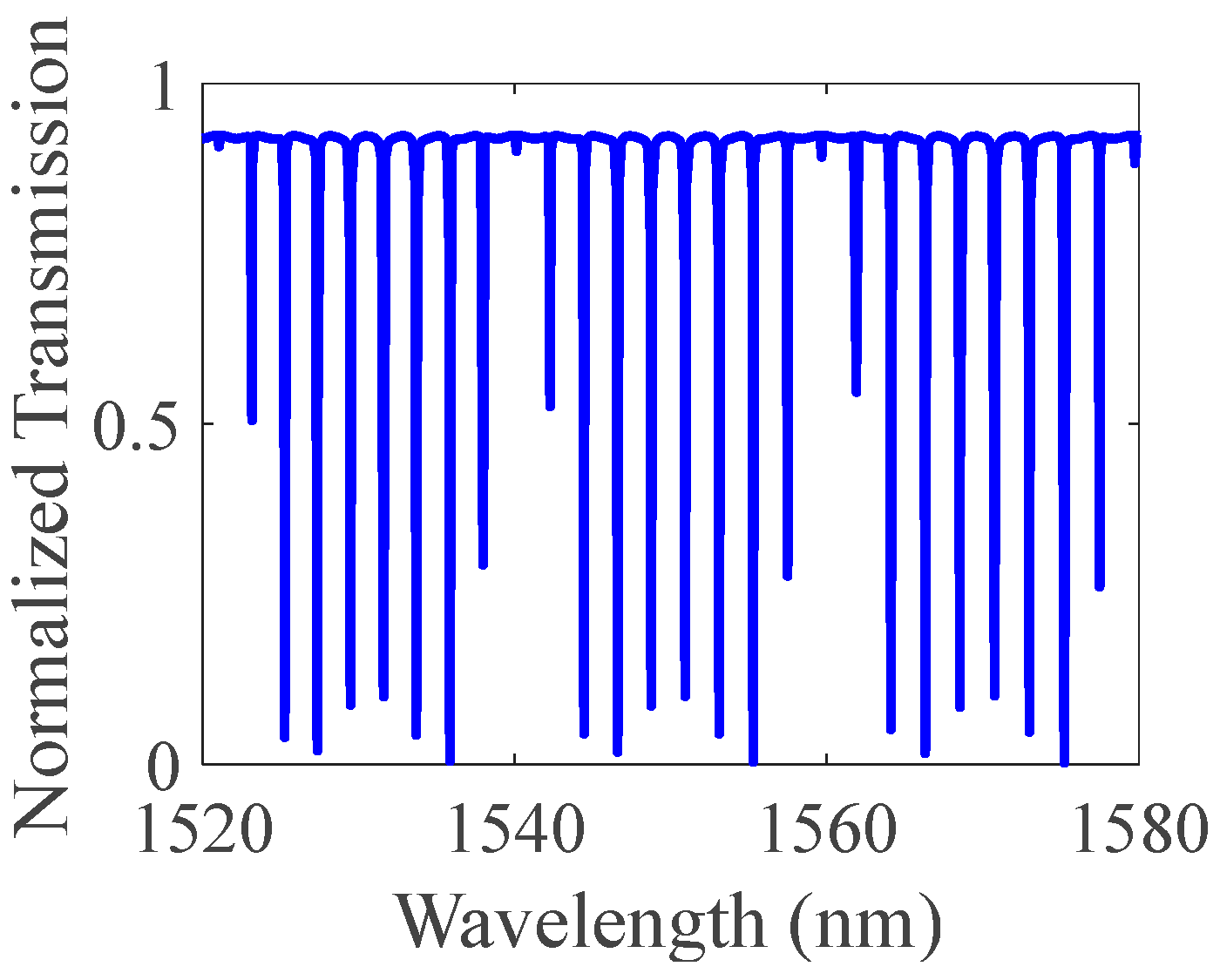
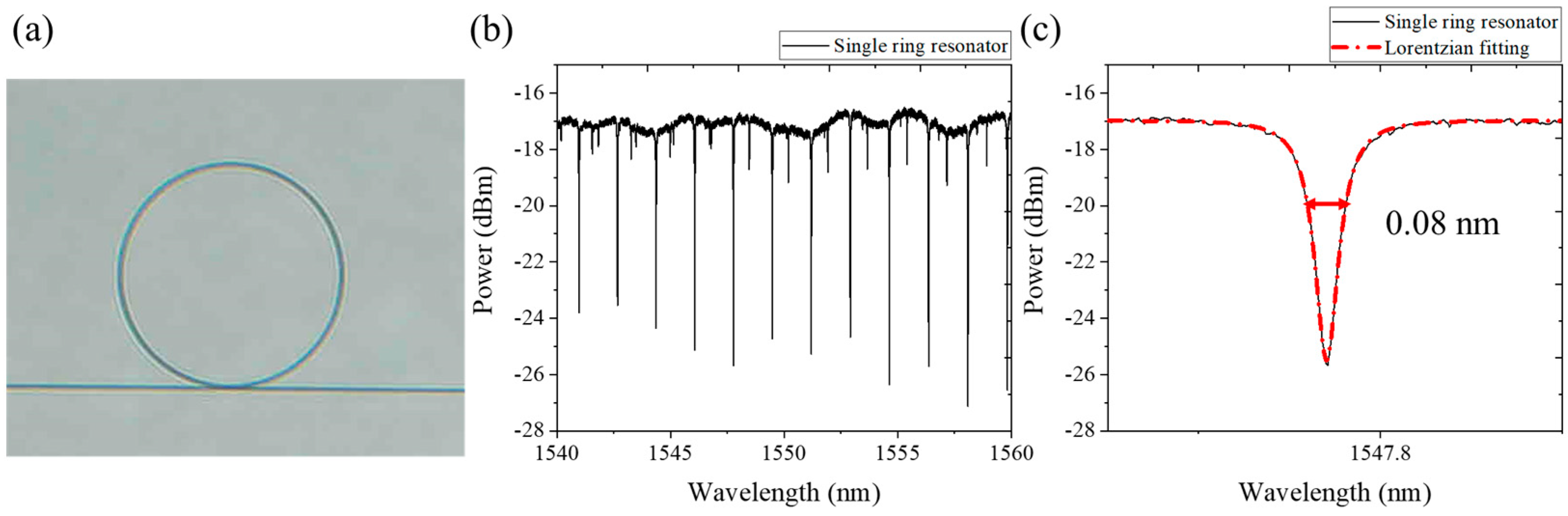
4.1. Insertion Loss and Coupling of a Single-Ring Resonator
4.2. MZI-Coupled Resonator
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Yacobi, B.G. Semiconductor Materials: An Introduction to Basic Principles; Springer Science & Business Media: Berlin/Heidelberg, Germany, 2003. [Google Scholar]
- Grahn, H.T. Introduction to Semiconductor Physics; World Scientific Publishing Company: Singapore, 1999. [Google Scholar]
- Schaller, R.R. Moore’s law: Past, present and future. IEEE Spectr. 1997, 34, 52–59. [Google Scholar] [CrossRef]
- Ghatak, A.; Thyagarajan, K. Introduction to Fiber Optics; Cambridge University Press: Cambridge, CA, USA, 1998. [Google Scholar]
- Jalali, B.; Fathpour, S. Silicon photonics. J. Light. Technol. 2006, 24, 4600–4615. [Google Scholar] [CrossRef]
- Kopp, C.; Bernabé, S.; Bakir, B.B.; Fedeli, J.-M.; Orobtchouk, R.; Schrank, F.; Porte, H.; Zimmermann, L.; Tekin, T. Silicon photonic circuits: On-CMOS integration, fiber optical coupling, and packaging. IEEE J. Sel. Top. Quantum Electron. 2010, 17, 498–509. [Google Scholar] [CrossRef]
- Kazanskiy, N.L.; Khonina, S.N.; Butt, M.A.; Kaźmierczak, A.; Piramidowicz, R. State-of-the-art optical devices for biomedical sensing applications—A review. Electronics 2021, 10, 973. [Google Scholar] [CrossRef]
- Pavesi, L.; Guillot, G. Optical interconnects. In Springer Series in Optical Sciences; Springer: Berlin/Heidelberg, Germany, 2006; Volume 119. [Google Scholar]
- Shi, W.; Tian, Y.; Gervais, A. Scaling capacity of fiber-optic transmission systems via silicon photonics. Nanophotonics 2020, 9, 4629–4663. [Google Scholar] [CrossRef]
- Ohliger, M.A.; Grant, A.K.; Sodickson, D.K. Ultimate intrinsic signal-to-noise ratio for parallel MRI: Electromagnetic field considerations. Magn. Reson. Med. 2003, 50, 1018–1030. [Google Scholar] [CrossRef]
- Dutt, A.; Miller, S.; Luke, K.; Cardenas, J.; Gaeta, A.L.; Nussenzveig, P.; Lipson, M. Tunable squeezing using coupled ring resonators on a silicon nitride chip. Opt. Lett. 2016, 41, 223–226. [Google Scholar] [CrossRef]
- Caspani, L.; Xiong, C.; Eggleton, B.J.; Bajoni, D.; Liscidini, M.; Galli, M.; Morandotti, R.; Moss, D.J. Integrated sources of photon quantum states based on nonlinear optics. Light Sci. Appl. 2017, 6, e17100. [Google Scholar] [CrossRef]
- Harris, N.C.; Grassani, D.; Simbula, A.; Pant, M.; Galli, M.; Baehr-Jones, T.; Hochberg, M.; Englund, D.; Bajoni, D.; Galland, C. Integrated source of spectrally filtered correlated photons for large-scale quantum photonic systems. Phys. Rev. X 2014, 4, 041047. [Google Scholar] [CrossRef]
- Ong, J.R.; Kumar, R.; Mookherjea, S. Ultra-high-contrast and tunable-bandwidth filter using cascaded high-order silicon microring filters. IEEE Photonics Technol. Lett. 2013, 25, 1543–1546. [Google Scholar] [CrossRef]
- Piekarek, M.; Bonneau, D.; Miki, S.; Yamashita, T.; Fujiwara, M.; Sasaki, M.; Terai, H.; Tanner, M.G.; Natarajan, C.M.; Hadfield, R.H.; et al. High-extinction ratio integrated photonic filters for silicon quantum photonics. Opt. Lett. 2017, 42, 815–818. [Google Scholar] [CrossRef] [PubMed]
- Brunetti, G.; Sasanelli, N.; Armenise, M.N.; Ciminelli, C. High performance and tunable optical pump-rejection filter for quantum photonic systems. Opt. Laser Technol. 2021, 139, 106978. [Google Scholar] [CrossRef]
- Kumar, R.R.; Tsang, H.K. High-extinction CROW filters for scalable quantum photonics. Opt. Lett. 2021, 46, 134–137. [Google Scholar] [CrossRef] [PubMed]
- Feng, S.; Lei, T.; Chen, H.; Cai, H.; Luo, X.; Poon, A. Silicon photonics: From a microresonator perspective. Laser Photonics Rev. 2012, 6, 145–177. [Google Scholar] [CrossRef]
- Soltani, M.; Yegnanarayanan, S.; Li, Q.; Adibi, A. Systematic engineering of waveguide-resonator coupling for silicon microring/microdisk/racetrack resonators: Theory and experiment. IEEE J. Quantum Electron. 2010, 46, 1158–1169. [Google Scholar] [CrossRef]
- Hosseini, E.S.; Yegnanarayanan, S.; Atabaki, A.H.; Soltani, M.; Adibi, A. Systematic design and fabrication of high-Q single-mode pulley-coupled planar silicon nitride microdisk resonators at visible wavelengths. Opt. Express 2010, 18, 2127–2136. [Google Scholar] [CrossRef]
- Sethi, P.; Kallega, R.; Haldar, A.; Selvaraja, S.K. Compact broadband low-loss taper for coupling to a silicon nitride photonic wire. Opt. Lett. 2018, 43, 3433–3436. [Google Scholar] [CrossRef]
- Ahmed, A.N.R.; Shi, S.; Zablocki, M.; Yao, P.; Prather, D.W. Tunable hybrid silicon nitride and thin-film lithium niobate electro-optic microresonator. Opt. Lett. 2019, 44, 618–621. [Google Scholar] [CrossRef]
- Zhang, X.-Y.; Zhang, T.; Xue, X.-J.; Zhang, J.-L.; Hong, J.; Wu, P.-Q.; Chen, Q.-Y. Tunable optical ring resonator integrated with asymmetric Mach–Zehnder interferometer. J. Light. Technol. 2010, 28, 2512–2520. [Google Scholar] [CrossRef]
- Boyd, R.W.; Gaeta, A.L.; Giese, E. Nonlinear optics. In Springer Handbook of Atomic, Molecular, and Optical Physics; Springer International Publishing: Cham, Switzerland, 2008; pp. 1097–1110. [Google Scholar]
- Boggio, J.M.C.; Bodenmüller, D.; Ahmed, S.; Wabnitz, S.; Modotto, D.; Hansson, T. Efficient Kerr soliton comb generation in micro-resonator with interferometric back-coupling. Nat. Commun. 2022, 13, 1292. [Google Scholar] [CrossRef]
- Shoman, H.; Jayatilleka, H.; Jaeger, N.A.F.; Shekhar, S.; Chrostowski, L. Measuring on-chip waveguide losses using a single, two-point coupled microring resonator. Opt. Express 2020, 28, 10225–10238. [Google Scholar] [CrossRef] [PubMed]
- Zhao, G.; Zhao, T.; Xiao, H.; Liu, Z.; Liu, G.; Yang, J.; Ren, Z.; Bai, J.; Tian, Y. Tunable Fano resonances based on microring resonator with feedback coupled waveguide. Opt. Express 2016, 24, 20187–20195. [Google Scholar] [CrossRef] [PubMed]
- RSoft FemSIM. RSoft Products.20; Synopsys, Inc.: Sunnyvale, CA, USA, 2024. [Google Scholar]
- OptSIM. RSoft Products.32; Synopsys, Inc.: Sunnyvale, CA, USA, 2024. [Google Scholar]
- Huang, Y.-K.; Wang, P.-H. CMOS-compatible 6-inch wafer integration of photonic waveguides and uniformity analysis. Opt. Express 2024, 32, 7197–7206. [Google Scholar] [CrossRef] [PubMed]
- Cai, L.; Lu, Y.; Zhu, H. Performance enhancement of on-chip optical switch and memory using Ge2Sb2Te5 slot-assisted microring resonator. Opt. Lasers Eng. 2023, 162, 107436. [Google Scholar] [CrossRef]
- Zhou, L.; Poon, A.W. Electrically reconfigurable silicon microring resonator-based filter with waveguide-coupled feedback. Opt. Express 2007, 15, 9194–9204. [Google Scholar] [CrossRef]
- Xiao, S.; Khan, M.H.; Shen, H.; Qi, M. Modeling and measurement of losses in silicon-on-insulator resonators and bends. Opt. Express 2007, 15, 10553–10561. [Google Scholar] [CrossRef]
- Choure, K.K.; Saharia, A.; Mudgal, N.; Pandey, R.; Prajapat, M.; Maddila, R.K.; Tiwari, M.; Singh, G. Implementation of all-optical single qubit gates using Si3N4 based micro ring resonator. Opt. Laser Technol. 2024, 170, 110263. [Google Scholar] [CrossRef]
- Feng, J.; Akimoto, R.; Hao, Q.; Zeng, H. Three-dimensional cross-coupled silicon nitride racetrack resonator-based tunable optical filter. IEEE Photonics Technol. Lett. 2017, 29, 771–774. [Google Scholar] [CrossRef]
- Wang, M.; Chen, X.; Khan, U.; Bogaerts, W. Programmable wavelength filter with double ring loaded MZI. Sci. Rep. 2022, 12, 1482. [Google Scholar] [CrossRef]
- Sun, Q.; Zhou, L.; Lu, L.; Zhou, G.; Chen, J. Reconfigurable high-resolution microwave photonic filter based on dual-ring-assisted MZIs on the Si3N4 platform. IEEE Photonics J. 2018, 10, 1–12. [Google Scholar] [CrossRef]
- Cheng, W.; Lin, D.; Wang, P.; Shi, S.; Lu, M.; Wang, J.; Guo, C.; Chen, Y.; Cang, Z.; Tian, Z.; et al. Tunable bandpass microwave photonic filter with largely reconfigurable bandwidth and steep shape factor based on cascaded silicon nitride micro-ring resonators. Opt. Express 2023, 31, 25648–25661. [Google Scholar] [CrossRef] [PubMed]








| Photonic Filter Structure | Platforms | External Driving | FWHM | Pattern Definition | Max. Extinction Ratio |
|---|---|---|---|---|---|
| Ring resonator [20] | Si3N4 | Without | N.A. | Electron-beam | 10 dB |
| Ring resonator [30] | Si3N4 | Without | N.A. | I-line stepper | 15 dB |
| Ring resonator [34] | Si3N4 | Without | 0.2 nm | Electron-beam | 20 dB |
| Ring resonator [22] | Si3N4+ thin-film lithium niobate | With | 0.013 nm | Electron-beam | 27 dB |
| MZI + Ring resonator [35] | Si3N4 | With | N.A. | Electron-beam | 14 dB |
| MZI + Ring resonator [26] | SOI | With | 0.025 nm | Deep UV | 29 dB |
| MZI + Ring resonator [27] | SOI | With | N.A. | I-line stepper | 31 dB |
| MZI + Double-ring [36] | SOI | Without | N.A. | Deep UV | 30 dB |
| Ring + Multi-stage filter [15] | SOI | Without | N.A. | Deep UV | 86 dB |
| CROW filter [17] | SOI | Without | 0.14 nm | Deep UV | 96 dB |
| Dual-ring-assisted MZIs [37] | Si3N4 | With | 0.06 nm | TriPleX ADS | 18 dB |
| Double-ring [38] | Si3N4 | With | 0.016 nm | TriPleX ADS | 34 dB |
| MZI + Ring resonator (this work) | Si3N4 | Without | 0.04 nm | I-line stepper | 35 dB |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Chen, H.-Z.; Ho, K.-L.; Wang, P.-H. High-Extinction Photonic Filters by Cascaded Mach–Zehnder Interferometer-Coupled Resonators. Photonics 2024, 11, 1055. https://doi.org/10.3390/photonics11111055
Chen H-Z, Ho K-L, Wang P-H. High-Extinction Photonic Filters by Cascaded Mach–Zehnder Interferometer-Coupled Resonators. Photonics. 2024; 11(11):1055. https://doi.org/10.3390/photonics11111055
Chicago/Turabian StyleChen, Hao-Zhong, Kung-Lin Ho, and Pei-Hsun Wang. 2024. "High-Extinction Photonic Filters by Cascaded Mach–Zehnder Interferometer-Coupled Resonators" Photonics 11, no. 11: 1055. https://doi.org/10.3390/photonics11111055
APA StyleChen, H.-Z., Ho, K.-L., & Wang, P.-H. (2024). High-Extinction Photonic Filters by Cascaded Mach–Zehnder Interferometer-Coupled Resonators. Photonics, 11(11), 1055. https://doi.org/10.3390/photonics11111055






