Real-Time Resolution Enhancement of Confocal Laser Scanning Microscopy via Deep Learning
Abstract
1. Introduction
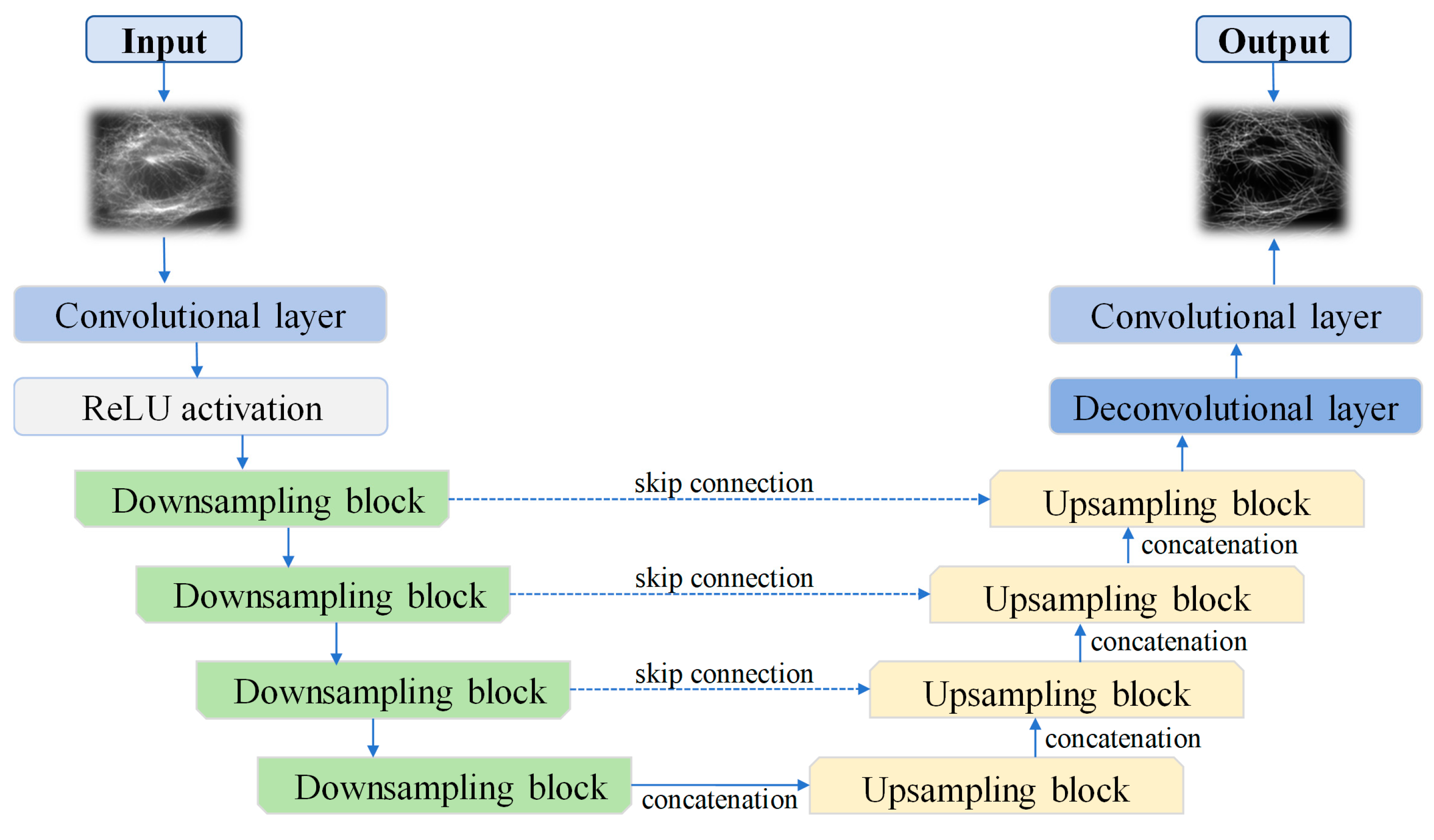
2. Materials and Methods
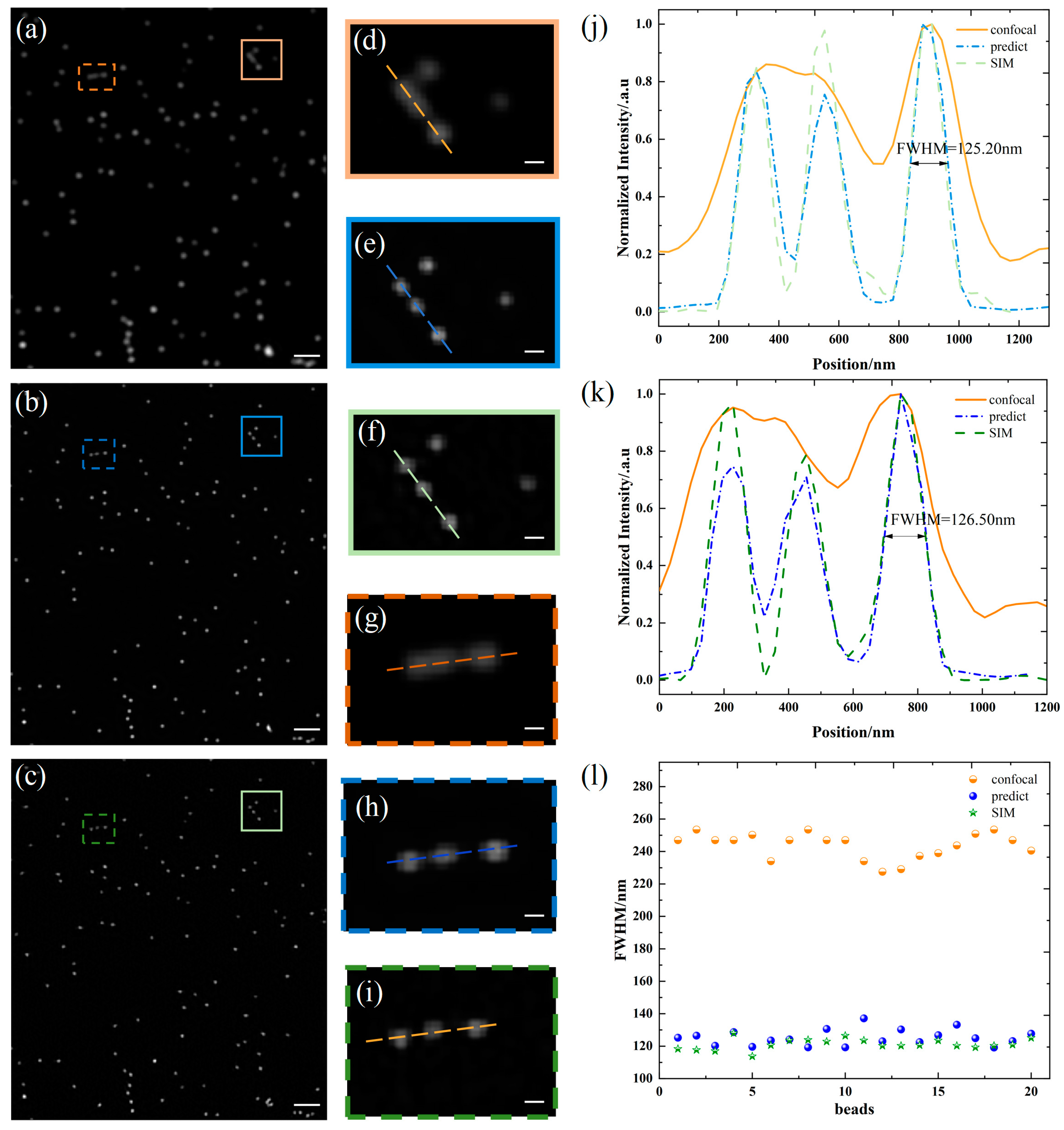
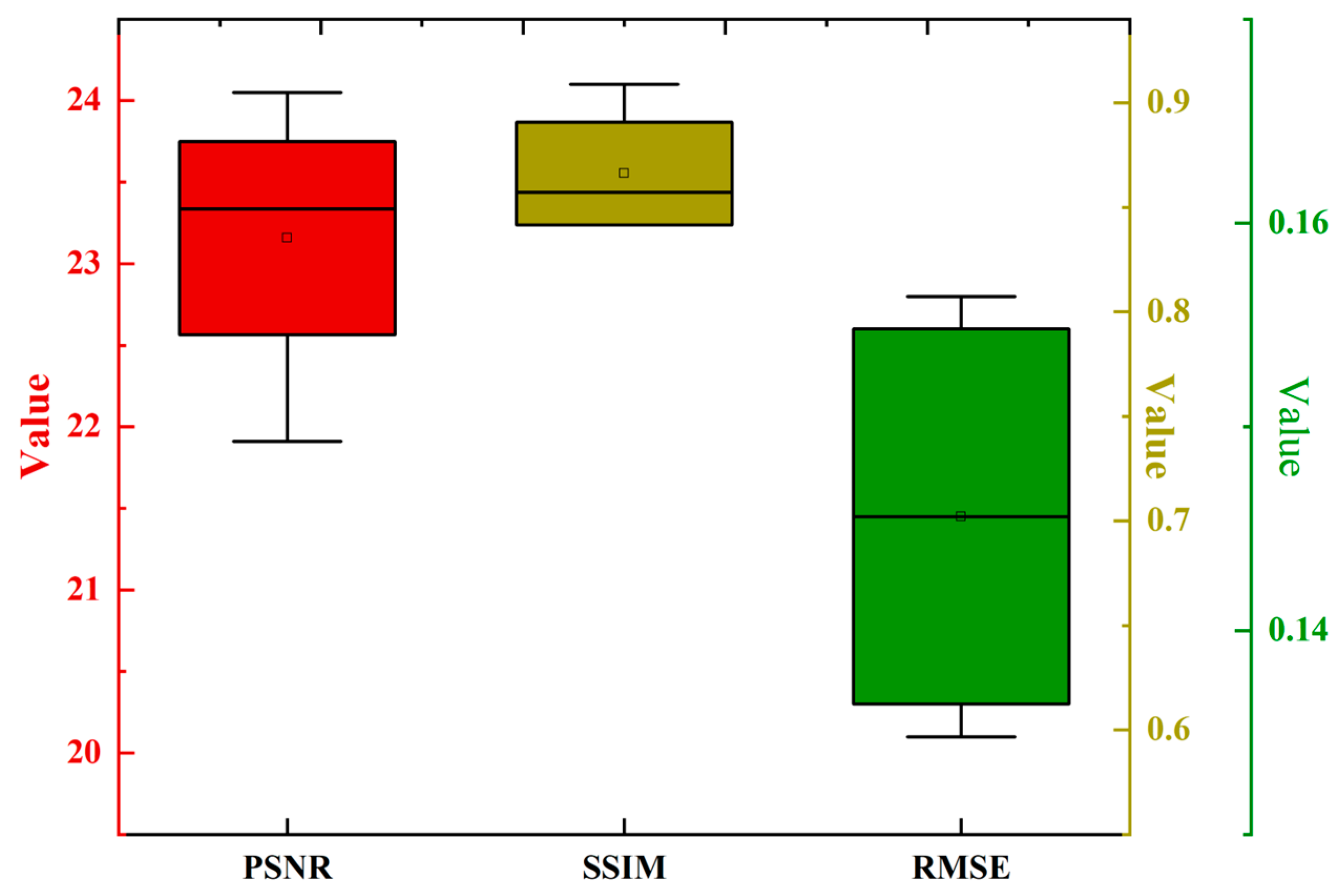
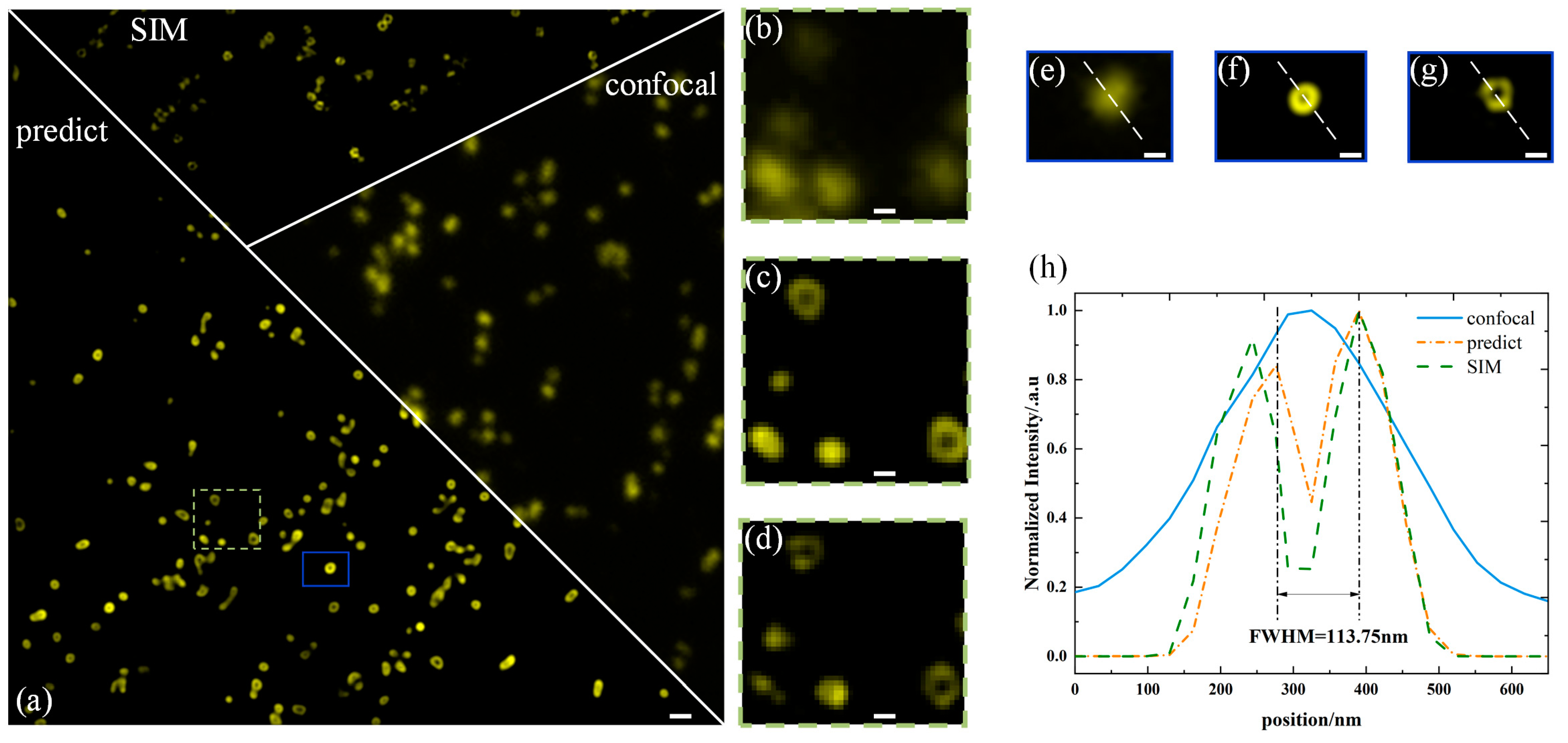
3. Results and Discussion
4. Conclusions
Supplementary Materials
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Heintzmann, R.; Sarafis, V.; Munroe, P.; Nailon, J.; Hanley, Q.S.; Jovin, T.M. Resolution enhancement by subtraction of confocal signals taken at different pinhole sizes. Micron 2003, 34, 293–300. [Google Scholar] [CrossRef] [PubMed]
- Di Franco, E.; Costantino, A.; Cerutti, E.; D’Amico, M.; Privitera, A.P.; Bianchini, P.; Vicidomini, G.; Gulisano, M.; Diaspro, A.; Lanzanò, L. SPLIT-PIN software enabling confocal and super-resolution imaging with a virtually closed pinhole. Sci. Rep. 2023, 13, 2741. [Google Scholar] [CrossRef] [PubMed]
- Kuang, C.; Li, S.; Liu, W.; Hao, X.; Gu, Z.; Wang, Y.; Ge, J.; Li, H.; Liu, X. Breaking the diffraction barrier using fluorescence emission difference microscopy. Sci. Rep. 2013, 3, 1441. [Google Scholar] [CrossRef] [PubMed]
- Dong, W.; Huang, Y.; Zhang, Z.; Xu, L.; Kuang, C.; Hao, X.; Cao, L.; Liu, X. Fluorescence emission difference microscopy based on polarization modulation. J. Innov. Opt. Health Sci. 2022, 15, 2250034. [Google Scholar] [CrossRef]
- Tanaami, T.; Sugiyama, Y.; Kosugi, Y.; Mikuriya, K.; Abe, M. High-speed confocal fluorescence microscopy using a nipkow scanner with microlenses for 3-d imaging of single fluorescent molecule in real time. Bioimages 1996, 4, 57–62. [Google Scholar]
- Hayashi, S.; Okada, Y. Ultrafast superresolution fluorescence imaging with spinning disk confocal microscope optics. Mol. Biol. Cell 2015, 26, 1743–1751. [Google Scholar] [CrossRef]
- Hayashi, S. Resolution doubling using confocal microscopy via analogy with structured illumination microscopy. Jpn. J. Appl. Phys. 2016, 55, 082501. [Google Scholar] [CrossRef]
- Huff, J. The Airyscan detector from ZEISS: Confocal imaging with improved signal-to-noise ratio and super-resolution. Nat. Methods 2015, 12, i–ii. [Google Scholar] [CrossRef]
- Huff, J.; Bergter, A.; Birkenbeil, J.; Kleppe, I.; Engelmann, R.; Krzic, U. The new 2D Superresolution mode for ZEISS Airyscan. Nat. Methods 2017, 14, 1223. [Google Scholar] [CrossRef]
- Dey, N.; Blanc-Feraud, L.; Zimmer, C.; Roux, P.; Kam, Z.; Olivo-Marin, J.-C.; Zerubia, J. Richardson–Lucy algorithm with total variation regularization for 3D confocal microscope deconvolution. Microsc. Res. Tech. 2006, 69, 260–266. [Google Scholar] [CrossRef]
- Dupé, F.X.; Fadili, M.J.; Starck, J.L. Deconvolution of confocal microscopy images using proximal iteration and sparse representations. In Proceedings of the 2008 5th IEEE International Symposium on Biomedical Imaging: From Nano to Macro, Paris, France, 14–17 May 2008; IEEE: Piscataway, NJ, USA, 2008; pp. 736–739. [Google Scholar]
- He, T.; Sun, Y.; Qi, J.; Hu, J.; Huang, H. Image deconvolution for confocal laser scanning microscopy using constrained total variation with a gradient field. Appl. Opt. 2019, 58, 3754–3766. [Google Scholar] [CrossRef] [PubMed]
- Stockbridge, C.; Lu, Y.; Moore, J.; Hoffman, S.; Paxman, R.; Toussaint, K.; Bifano, T. Focusing through dynamic scattering media. Opt. Express 2012, 20, 15086–15092. [Google Scholar] [CrossRef] [PubMed]
- Galaktionov, I.; Nikitin, A.; Sheldakova, J.; Toporovsky, V.; Kudryashov, A. Focusing of a laser beam passed through a moderately scattering medium using phase-only spatial light modulator. Photonics 2022, 9, 296. [Google Scholar] [CrossRef]
- Katz, O.; Small, E.; Guan, Y.; Silberberg, Y. Noninvasive nonlinear focusing and imaging through strongly scattering turbid layers. Optica 2014, 1, 170–174. [Google Scholar] [CrossRef]
- Hillman, T.R.; Yamauchi, T.; Choi, W.; Dasari, R.R.; Feld, M.S.; Park, Y.; Yaqoob, Z. Digital optical phase conjugation for delivering two-dimensional images through turbid media. Sci. Rep. 2013, 3, 1909. [Google Scholar] [CrossRef] [PubMed]
- Tao, X.; Fernandez, B.; Azucena, O.; Fu, M.; Garcia, D.; Zuo, Y.; Chen, D.C.; Kubby, J. Adaptive optics confocal microscopy using direct wavefront sensing. Opt. Lett. 2011, 36, 1062–1064. [Google Scholar] [CrossRef]
- Weigert, M.; Schmidt, U.; Boothe, T.; Müller, A.; Dibrov, A.; Jain, A.; Wilhelm, B.; Schmidt, D.; Broaddus, C.; Culley, S.; et al. Content-aware image restoration: Pushing the limits of fluorescence microscopy. Nat. Methods 2018, 15, 1090–1097. [Google Scholar] [CrossRef]
- Li, X.; Dong, J.; Li, B.; Zhang, Y.; Zhang, Y.; Veeraraghavan, A.; Ji, X. Fast confocal microscopy imaging based on deep learning. In Proceedings of the 2020 IEEE International Conference on Computational Photography (ICCP), St. Louis, MO, USA, 24–26 April 2020; IEEE: Piscataway, NJ, USA, 2020; pp. 1–12. [Google Scholar]
- Wang, W.; Wu, B.; Zhang, B.; Ma, J.; Tan, J. Deep learning enables confocal laser-scanning microscopy with enhanced resolution. Opt. Lett. 2021, 46, 4932–4935. [Google Scholar] [CrossRef]
- Fang, L.; Monroe, F.; Novak, S.W.; Kirk, L.; Schiavon, C.R.; Yu, S.B.; Zhang, T.; Wu, M.; Kastner, K.; Latif, A.A.; et al. Deep learning-based point-scanning super-resolution imaging. Nat. Methods 2021, 18, 406–416. [Google Scholar] [CrossRef]
- Huang, B.; Li, J.; Yao, B.; Yang, Z.; Lam, E.Y.; Zhang, J.; Yan, W.; Qu, J. Enhancing image resolution of confocal fluorescence microscopy with deep learning. PhotoniX 2023, 4, 2. [Google Scholar] [CrossRef]
- Ji, C.; Zhu, Y.; He, E.; Liu, Q.; Zhou, D.; Xie, S.; Wu, H.; Zhang, J.; Du, K.; Chen, Y.; et al. Full field-of-view hexagonal lattice structured illumination microscopy based on the phase shift of electro–optic modulators. Opt. Express 2024, 32, 1635–1649. [Google Scholar] [CrossRef] [PubMed]
- Qiao, C.; Li, D.; Guo, Y.; Liu, C.; Jiang, T.; Dai, Q.; Li, D. Evaluation and development of deep neural networks for image super-resolution in optical microscopy. Nat. Methods 2021, 18, 194–202. [Google Scholar] [CrossRef] [PubMed]
- Xiao, X.; Lian, S.; Luo, Z.; Li, S. Weighted res-unet for high-quality retina vessel segmentation. In Proceedings of the 2018 9th International Conference on Information Technology in Medicine and Education (ITME), Hangzhou, China, 19–21 October 2018; IEEE: Piscataway, NJ, USA, 2018; pp. 327–331. [Google Scholar]
- Qi, J.; Du, J.; Siniscalchi, S.M.; Ma, X.; Lee, C.-H. On mean absolute error for deep neural network based vector-to-vector regression. IEEE Signal Process. Lett. 2020, 27, 1485–1489. [Google Scholar] [CrossRef]
- Zhao, H.; Gallo, O.; Frosio, I.; Kautz, J. Loss functions for image restoration with neural networks. IEEE Trans. Comput. Imaging 2016, 3, 47–57. [Google Scholar] [CrossRef]
- Luebke, D. CUDA: Scalable parallel programming for high-performance scientific computing. In Proceedings of the 2008 5th IEEE International Symposium on Biomedical Imaging: From Nano to Macro, Paris, France, 14–17 May 2008; IEEE: Piscataway, NJ, USA, 2008; pp. 836–838. [Google Scholar]
- Abadi, M.; Agarwal, A.; Barham, P.; Brevdo, E.; Chen, Z.; Citro, C.; Corrado, G.S.; Davis, A.; Dean, J.; Devin, M.; et al. TensorFlow: Large-scale machine learning on heterogeneous systems. arXiv 2015, arXiv:1603.04467. [Google Scholar]
- Ketkar, N. Introduction to keras. In Deep Learning with Python: A Hands-On Introduction; Apress: Berkeley, CA, USA, 2017; pp. 97–111. [Google Scholar]
- Kingma, D.P. Adam: A method for stochastic optimization. arXiv 2014, arXiv:1412.6980. [Google Scholar]
- Qiao, C.; Zeng, Y.; Meng, Q.; Chen, X.; Chen, H.; Jiang, T.; Wei, R.; Guo, J.; Fu, W.; Lu, H.; et al. Zero-shot learning enables instant denoising and super-resolution in optical fluorescence microscopy. Nat. Commun. 2024, 15, 4180. [Google Scholar] [CrossRef]
- Ndajah, P.; Kikuchi, H.; Yukawa, M.; Watanabe, H.; Muramatsu, S. SSIM image quality metric for denoised images. In Proceedings of the 3rd WSEAS Conference International on Visualization, Imaging and Simulation, Faro, Portugal, 3–5 November 2010; pp. 53–58. [Google Scholar]


| Pixels | Ours (frame/s) | Reference [32] (frame/s) |
|---|---|---|
| 512 × 512 | ≈11.11 | ≈2.43 |
| 1024 × 1024 | ≈3.85 | ≈1.45 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Cui, Z.; Xing, Y.; Chen, Y.; Zheng, X.; Liu, W.; Kuang, C.; Chen, Y. Real-Time Resolution Enhancement of Confocal Laser Scanning Microscopy via Deep Learning. Photonics 2024, 11, 983. https://doi.org/10.3390/photonics11100983
Cui Z, Xing Y, Chen Y, Zheng X, Liu W, Kuang C, Chen Y. Real-Time Resolution Enhancement of Confocal Laser Scanning Microscopy via Deep Learning. Photonics. 2024; 11(10):983. https://doi.org/10.3390/photonics11100983
Chicago/Turabian StyleCui, Zhiying, Yi Xing, Yunbo Chen, Xiu Zheng, Wenjie Liu, Cuifang Kuang, and Youhua Chen. 2024. "Real-Time Resolution Enhancement of Confocal Laser Scanning Microscopy via Deep Learning" Photonics 11, no. 10: 983. https://doi.org/10.3390/photonics11100983
APA StyleCui, Z., Xing, Y., Chen, Y., Zheng, X., Liu, W., Kuang, C., & Chen, Y. (2024). Real-Time Resolution Enhancement of Confocal Laser Scanning Microscopy via Deep Learning. Photonics, 11(10), 983. https://doi.org/10.3390/photonics11100983





